W-Ratio Test as an Integer Aperture Estimator: Pull-in Regions and Ambiguity Validation Performance

Abstract

Global Navigation Satellite Systems (GNSS) carrier phase integer ambiguity resolution is an indispensible step in generating highly accurate positioning results. As a quality control step, ambiguity validation, which is an essential procedure in ambiguity resolution, allows the user to make sure the resolved ambiguities are reliable and correct. Many ambiguity validation methods have been proposed in the past decades, such as R-ratio, F-ratio, W-ratio tests, and recently a new theory named integer aperture estimator. This integer aperture estimator provides a framework to compare the other validation methods with the same predefined fail-rate, even though its application in practice can only be based on simulations.

As shown in literature, the pull-in regions of different validation methods may have a variety of shapes which may dictate the closeness of such validation methods to the optimal integer least-squares method. In this contribution, the W-ratio is shown to be connected with the integer aperture theory with an exact formula. The integer least-squares pull-in region for W-ratio is presented and analysed. The results show that the W-ratio’s pull-in region is close to the integer least-squares pull-in region. We have performed numerical experiments which show that the W-ratio is a robust way of validating the resolved ambiguities.

1 Introduction

Nowadays, Global Navigation Satellite Systems (GNSS) are widely used in navigation, surveying, mapping, etc. The demand for high precision GNSS positioning is still increasing. Generally, there are two types of measurements: code and carrier phase. The positioning accuracy based on code measurements and carrier phase measurements are in meter level and centimeter to millimeter level, respectively. Hence, carrier phase measurements are essential for precise positioning.

As a drawback, each carrier phase contains an integer ambiguity in the number of wavelengths that needs to be resolved. Traditionally used estimation methods, e.g. Least-squares, or Kalman filtering, can only provide us with float (or the real-valued) solutions and fixing the float ambiguities (ambiguity resolution) to integers is not an easy task. An amount of literature (e.g. Teunissen 1995; Han 1997; Wang et al. 1998) can be found to study the integer ambiguity resolution problem, and one of the most popular approaches is the so-called LAMBDA (Least-squares AMBiguity Decorrelation Adjustment) proposed by Teunissen (1995). With the float solution and variance–covariance matrix of the ambiguities from Least-squares, a search is carried out to find out integer ambiguity candidates inside the hyper-ellipsoid which is defined based on the float solution and the variance–covariance matrix. Instead of one integer candidate, usually the first best and the second best ambiguity combinations are compared to make sure there is strong confidence in using the best combination in positioning. Consequently another problem called integer ambiguity validation emerged.

Various ambiguity validation methods have been proposed, such as F-ratio test, R-ratio, difference test, project test (Verhagen 2005), and W-ratio (Wang et~al. 1998, 2000). From a statistical point of view, the critical values to validate the resolved ambiguity of these methods can be generated according to their distributions or empirical values. In another approach to ambiguity validation, Integer Aperture (IA) estimator (Teunissen 2003a, 2003b) has been developed. In Verhagen (2005), the IA estimator was considered as a framework for all the other classical validation methods, and the geometries of different validation methods are then reflected through various aperture pull-in regions.

In this contribution, the W-ratio test is first presented, and then the deduction of the W-ratio test as an integer aperture estimator is given, as well as its aperture pull-in region, finally the performance of the W-ratio is analysed with real data.

2 Parameter Estimation

The raw GNSS measurements are affected by many error sources, such as troposphere delay, ionosphere delay, clock error, etc. Through a double-differencing procedure, such systematic errors can be reduced over a short baseline, and the baseline components and integer ambiguities are the remaining parameters to be estimated. Without loss of generality, the double differenced functional models are given as follows:

$$ \Delta \nabla \varnothing =\frac{1}{\uplambda}\Delta \nabla \uprho +\Delta \nabla \mathrm{N}+{\upvarepsilon}_{\varnothing} $$

(1)

$$ \Delta \nabla \mathrm{P}=\Delta \nabla \uprho +{\upvarepsilon}_{\mathrm{P}} $$

(2)

where Δ∇ is the double differencing operator between satellites and receivers, ∅ and P are carrier phase measurements and code measurements respectively, λ is the carrier phase wavelength, ρ is the geometric distance between satellites and receivers, N are the integer ambiguities in cycles, and $\upvarepsilon$ represents the noise of the two types of measurements.

With an approximate rover position given, the above models can be linearized as

$$ \mathrm{l}=\mathrm{Ax}+\mathrm{v} $$

(3)

where l is the vector of the observations, v is the vector of observation errors, x is the vector of unknowns x = (x_r, Δ∇N)^T, A is the design matrix of both coordinates ${\mathrm{A}}_{{\mathrm{x}}_{\mathrm{r}}}$ and ambiguities A_a, and x_r are the coordinates.

It is interesting to note that Eq. (3) and the double differenced stochastic model in the following are the so-called Gauss–Markov model:

$$ \mathrm{D}\left(\mathrm{l}\right)={\upsigma}_0^2\mathrm{Q}={\upsigma}_0^2{\mathrm{P}}^{-1} $$

(4)

where D is the covariance matrix, σ ²₀ is an a priori variance factor, Q and P are the cofactor matrix and weight matrix of the measurements.

By applying the classical least-squares approach, which minimizes v^TPv, the unknown parameters and their covariance are uniquely estimated as:

$$ \widehat{\mathrm{x}}={\left({\widehat{\mathrm{x}}}_{\mathrm{r}},\ \widehat{\mathrm{a}}\right)}^{\mathrm{T}}={\left({\mathrm{A}}^{\mathrm{T}}\mathrm{PA}\right)}^{-1}{\mathrm{A}}^{\mathrm{T}}\mathrm{Pl}, $$

$$ {\widehat{\mathrm{Q}}}_{\hat{\mathrm{x}}}={\left({\mathrm{A}}^{\mathrm{T}}\mathrm{PA}\right)}^{-1}=\left[\begin{array}{cc}\hfill {\mathrm{Q}}_{{\hat{\mathrm{x}}}_{\mathrm{r}}}\hfill & \hfill {\mathrm{Q}}_{{\hat{\mathrm{x}}}_{\mathrm{r}}\hat{\mathrm{a}}}\hfill \\ {}\hfill {\mathrm{Q}}_{{\hat{\mathrm{a}}\hat{\mathrm{x}}}_{\mathrm{r}}}\hfill & \hfill {\mathrm{Q}}_{\hat{\mathrm{a}}}\hfill \end{array}\right] $$

(5)

where $\widehat{\mathrm{a}}$ represents the float solution of the integer ambiguities. Then the posteriori variance is

$$ {\widehat{\mathrm{s}}}_0^2=\frac{{\widehat{\mathrm{v}}}^{\mathrm{T}}\mathrm{P}\widehat{\mathrm{v}}}{\mathrm{f}}=\frac{\Omega_0}{\mathrm{f}} $$

(6)

with f is the degree of freedom.

3 W-Ratio Statistical Test

The W-ratio has been proposed by Wang et~al. (1998), with the purpose of discriminating two sets of best integer candidates—the most likely candidate and the second most likely candidate. The likelihood ratio method (Koch 1988) and the artificial nesting method (Hoel 1947) may be applied to construct the discrimination tests, which both yield the following test statistic:

$$ \mathrm{W}=\frac{\mathrm{d}}{\sqrt{\mathrm{Var}\left(\mathrm{d}\right)}}\ge \mathrm{c} $$

(7)

where

$$ \mathrm{d}={\Omega}_2-{\Omega}_1,\ \mathrm{Var}\left(\mathrm{d}\right)={\uprho}^2{\mathrm{Q}}_{\mathrm{d}} $$

(8)

$$ {\Omega}_{\mathrm{i}}={\Omega}_0+{\left({\check{\mathrm{a}}}_{\mathrm{i}}-\widehat{\mathrm{a}}\right)}^{\mathrm{T}}{{\mathrm{Q}}_{\hat{\mathrm{a}}}}^{-1}\left({\check{\mathrm{a}}}_{\mathrm{i}}-\widehat{\mathrm{a}}\right) $$

(9)

c is the critical value, and ρ² could be decided by users either from an a priori variance σ ²₀ or from an a posteriori variance ${\widehat{\mathrm{s}}}_0^2$; ${\check{\mathrm{a}}}_{\mathrm{i}}$ represents the integer ambiguities. By applying the variance–covariance propagation law, the variance for d can be derived as ${\mathrm{Q}}_{\mathrm{d}}=4\times {\left({\check{\mathrm{a}}}_2-{\check{\mathrm{a}}}_1\right)}^{\mathrm{T}}{\mathrm{Q}}_{\hat{\mathrm{a}}}^{-1}\left({\check{\mathrm{a}}}_2-{\check{\mathrm{a}}}_1\right).$ Assuming that W_a and W_s are the two ratios corresponding to a priori variance σ ²₀ and a posteriori variance ${\widehat{\mathrm{s}}}_0^2$, and under the assumption that the fixed ambiguities are deterministic quantities, they are supposed to have a truncated standard normal distribution (TSND) and a truncated student t distribution (TSD) respectively, from which the critical values can be easily obtained (Wang et~al. 1998).

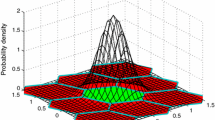
From the definition of the TSND, TSD and one constraint of the W-ratio (d ≥ 0), we can obtain the probability density function (PDF) and cumulative distribution function (CDF) for the W-ratio. Figure 1 shows the PDF of both Wa-ratio and Ws-ratio.

Fig. 1

Probability density function of SND, TSND, SD, TSD (degree of freedom 4)

Apparent from Fig. 1, due to the constraint of d ≥ 0, the PDF of TSND and standard normal distribution (SND) are different, as well as the TSD and student t distribution (SD). The critical value for TSND is in fact a special case of SND, and it is slightly larger than the SND critical value, which implies that the accepted number of epochs for TSND will be less than SND, however, more reliable.

4 W-Ratio as an Integer Aperture Estimator

On the basis of the integer estimator, the IA theory was first introduced by Teunissen (2003a), and the IA estimator $\overline{\mathrm{a}}$ is developed as:

$$ \overline{{a}}={\displaystyle \sum_{z\in {Z}^n}}z{\omega}_z\left(\widehat{a}\right)+\widehat{a}\left(1-{\displaystyle \sum_{z\in {Z}^n}}{\omega}_z\left(\widehat{a}\right)\right) $$

(10)

with the indicator function ω _z (x) defined as:

$$ {\omega}_z(x)=\left\{\begin{array}{c}\hfill 1\kern1.25em {\it if}\ x\in {\Omega}_z\hfill \\ {}\hfill 0\kern1.25em {\it otherwise}\hfill \end{array}\right. $$

(11)

where z is an integer vector and the centre of Ω _z . x represents the float ambiguity vector. The Ω _z are the aperture pull-in regions, and their union Ω ⊂ R ⁿ is the aperture space, which is also translational invariant.

With the above definition, three outcomes can be distinguished as: (1) $\widehat{a}\in$ Ω _a Success: correct integer estimation; (2) $\widehat{a}\in$ Ω\Ω _a Failure: incorrect integer estimation; (3) $\widehat{a}\notin$ Ω Undecided: ambiguity not fixed to an integer. Then the probabilities of success (P _s ), failure (P _f ) and undecided (P _u ) can be derived accordingly.

In the case of a GNSS model, ${f}_{\widehat{a}}(x)$ represents the probability density function of the float ambiguities, and is usually assumed to be normally distributed. The IA estimator allows the user to choose a pre-defined fail-rate, and then determine the critical value accordingly.

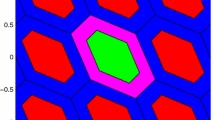
In Verhagen (2005), the pull-in regions of integer aperture bootstrapping, integer aperture least-squares have been explored, as well as other IA estimators. Since integer least-squares is optimal, the IA least-squares estimator can be considered to be a better solution than the others, and the pull-in region has been shown to be a hexagon. According to simulations, the success-rate, fail-rate and undecided-rate can be obtained respectively.

In a similar way, assume σ ²₀  = 1, the W-ratio can be considered as one of the integer aperture estimators and its pull-in region is derived as follows:

$$ \frac{\Omega_2-{\Omega}_1}{2\sqrt{{\left({\check{\mathrm{a}}}_2-{\check{\mathrm{a}}}_1\right)}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\left({\check{\mathrm{a}}}_2-{\check{\mathrm{a}}}_1\right)}}\ge \mathrm{c} $$

$$ \Leftrightarrow \frac{{\left({\check{\mathrm{a}}}_2-\widehat{\mathrm{a}}\right)}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\left({\check{\mathrm{a}}}_2-\widehat{\mathrm{a}}\right)-{\left({\check{\mathrm{a}}}_1-\widehat{\mathrm{a}}\right)}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\left({\check{\mathrm{a}}}_1-\widehat{\mathrm{a}}\right)}{2\sqrt{{\left({\check{\mathrm{a}}}_2-{\check{\mathrm{a}}}_1\right)}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\left({\check{\mathrm{a}}}_2-{\check{\mathrm{a}}}_1\right)}}\ge \mathrm{c} $$

replace a with a generic form of x, we have:

$$ \Leftrightarrow\frac{{\left({\check{\mathrm{x}}}_2-\widehat{\mathrm{x}}\right)}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\left({\check{\mathrm{x}}}_2-\widehat{\mathrm{x}}\right)-{\left({\check{\mathrm{x}}}_1-\widehat{\mathrm{x}}\right)}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\left({\check{\mathrm{x}}}_1-\widehat{\mathrm{x}}\right)}{2\sqrt{{\left({\check{\mathrm{x}}}_2-{\check{\mathrm{x}}}_1\right)}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\left({\check{\mathrm{x}}}_2-{\check{\mathrm{x}}}_1\right)}}\ge \mathrm{c} $$

with the property of integer translation, ${\check{\mathrm{x}}}_1$ has been moved to the zero vector. By defining $\mathrm{z}={\check{\mathrm{x}}}_2-{\check{\mathrm{x}}}_1={\check{\mathrm{x}}}_2$, the deduction goes as follows:

$$ \Leftrightarrow \frac{{\left(\mathrm{z}-\widehat{\mathrm{x}}\right)}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\left(\mathrm{z}-\widehat{\mathrm{x}}\right)-{\widehat{\mathrm{x}}}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\widehat{\mathrm{x}}}{2\sqrt{{\mathrm{z}}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\mathrm{z}}}\ge \mathrm{c} $$

$$ \Leftrightarrow{\mathrm{z}}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\mathrm{z}-2{\mathrm{z}}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\widehat{\mathrm{x}}\ge 2\mathrm{c}\sqrt{{\mathrm{z}}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\mathrm{z}} $$

$$ \Leftrightarrow\frac{{\mathrm{z}}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\widehat{\mathrm{x}}}{\sqrt{{\mathrm{z}}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\mathrm{z}}}\le \frac{1}{2}\sqrt{{\mathrm{z}}^{\mathrm{T}}{\mathrm{Q}}_{\widehat{\mathrm{a}}}^{-1}\mathrm{z}}-\mathrm{c} $$

where z is the closest integer other than zero vector. Note that the final formula for the pull-in region of W-ratio is different from the difference test and the projector test, whose pull-in regions as an integer aperture estimator are provided in Verhagen (2005). By comparing these three ambiguity validation methods, a noticeable difference is that the determination of critical values for the difference test and the projector test are either empirical or based on non-strict distribution, whereas W-ratio is based on the truncated normal distribution or truncated student t distribution. Consequently, the size of their pull-in regions varies with the critical values.

Fig. 2

W-ratio aperture pull-in region (black dash for critical value of 0.5, blue dash dot for critical value of 1) and integer least-squares pull-in region (red, solid line)

The shape of the W-ratio’s pull-in region, however, is similar to those of the integer aperture least-squares, the integer aperture difference test and the projector’s pull-in region; see Figures 5 and 10 in Verhagen (2005). For a two dimensional case, the W-ratio’s pull-in region can be constructed with six intersecting half-spaces which are bounded by the planes orthogonal to z with the condition above. Figure 2 shows the pull-in region of the W-ratio test, with

$$ \mathrm{Q} = \left[0.1392 - 0.0486; - 0.0486\ 0.1583\right]; $$

In this case, the a priori variance for the W-ratio test is considered as 1.0. The pull-in region of the integer least-squares is shown as red solid line, with the other twopull-in regions of the W-ratio tests shown in black and blue. Obviously the W-ratio pull-in region is also close to the integer least-squares pull-in region.

5 Numerical Analysis

Under the framework of the integer aperture estimator, the W-ratio could be applied in another way instead of depending on its truncated distribution. As suggested in Teunissen (2003a), Verhagen (2005), the critical value should be determined from a given fail-rate. Based on the fail-rate, simulations are carried out to find the corresponding critical value. The exact procedures are: (1) given variance–covariance matrix of the ambiguities and the fail-rate; (2) determine the critical value according to the given fail-rate and then use the critical value to perform the ambiguity validation test. For the purpose of reliable results, the sample size should be as large as possible. A discussion about the influence of the sample size on the ambiguity validation results can be found in Li and Wang (2012).

With the purpose of analysing the W-ratio’s performance in real applications, a 30 min static data set with six satellites was utilized, and the data was gathered on 6th, June, 2010, Sydney, Australia, with a sampling rate and an elevation angle as 1 s and 15 degrees, respectively. After least-squares estimation, we can obtain the float solution together with their variance–covariance matrix, and using the exact procedures above and a pre-defined fail-rate, simulations can be applied to determine the critical values.

Due to the heavy computational burden of simulation for each epoch, a certain epoch was selected to illustrate the application of the W-ratio instead. In Figs. 3 and 4, both the ADOP (ambiguity dilution of precision) values and Wa-ratio values are plotted. It is shown that there is just a minor change in the ADOP values, so the variance–covariance matrix of the nine hundredth epoch was chosen to simulate the critical value with a pre-defined fail rate as 0.001.

The results are listed in Table 1, with a critical value of 2.81 for TSND and 2.85 for WIA (W-ratio IA estimator). For both approaches, the correct acceptances are quite similar (1794, 1792), as well as the wrongly rejected ones (6, 8). These results are extremely close to the truth so that for all the resolved ambiguities it can be assumed to be correct.

Another 20 min kinematic data set, which was collected on 9th, June, 2010, Sydney, Australia, has been used to describe the W-ratio’s performance. There were six GPS satellites tracked with dual-frequency observations available, and the sampling rate and the elevation angle are the same as in the previous data set.

Fig. 3

ADOP values changing with epoch number in static case

Fig. 4

Wa-ratio statistical values in static case

Table 1 Wa-ratio performance in static case, CA = correct acceptance; WA = wrong acceptance; CR = correct rejection; WR = wrong rejection

Fig. 5

ADOP values changing with epoch number in kinematic case

Fig. 6

Wa-ratio statistical values in kinematic case

After estimation on an epoch by epoch basis, the float solution and its variance and covariance were obtained. The ADOP values plotted in Fig. 5 are roughly ranging from 0.176 to 0.183 cycles, and in order to effectively apply the IA for the W-ratio test, the geometry of the six hundredth epoch was chosen to determine the critical value. In Fig. 6, the statistical values of the Wa-ratio were plotted. Table 2 shows the validation results with respect to different way of determining the critical values. A 95 % confidence level yields a significance level of 1.96 for TSND, and theW-ratio as an integer aperture estimator (WIA), with a pre-defined fail-rate of 0.015 generates a critical value of 1.81. Comparing with the WIA, the number of correctly accepted (CA) epochs for the W-Ratio with TSND is smaller, which means that the critical value for TSND is conservative. However, the wrongly accepted (WA) number, correctly rejected (CR) number and the wrongly rejected number (WR) change significantly.

Table 2 Wa-ratio performance in the kinematic case, CA = correct acceptance; WA = wrong acceptance; CR = correct rejection; WR = wrong rejection

Concluding Remarks

In this contribution, various ways of utilizing the W-ratio test have been discussed. Instead of determining the critical value from the standard normal distribution, a preferable way is to consider the constraint and thus, to apply the truncated normal distribution, with a creation of the look-up table to specify the critical values. Besides, under the framework of the integer aperture estimator, the pull-in region of W-ratio is presented, and the critical value could be generated with a given fail-rate according to simulations, which is also another way to apply the W-ratio. In case of a short observation period, as the satellite geometry doesn’t change too much, the user is capable of obtaining the critical values by simulating the critical values with one epoch data. However, more investigations should be carried out in the future to study the performance of the W-ratio test as an integer aperture estimator. The application of integer aperture theory mainly depends on simulation, which only requires geometry information regardless of the float solution (or the quality of the observations). This issue needs further analysis.