Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Reliability theory has become a great anxiety in recent years, because high-tech industry processes, computer networking with increasing levels of sophistication comprise most engineering systems today (Verma et al. 2010; Ram 2013). Reliability can be defined as the probability that it will produce correct outputs up to given time period, according to McClusky and Mitra (2004). Reliability is enhanced by features that help to avoid, detect, and repair hardware faults. A reliable system does not mutely continue and deliver results that include corrupted data.

In the field of reliability theory, the remarkable work has been done by many researchers. Soi and Aggarwal (1980) discussed the future trends in the digital communication system and presented a system analysis model in the form of a state diagram to study the overall availability behavior of next generation digital communication system. Goel et al. (1993) investigated a model for satellite based computer communication network system. In that work, a master station is connected to the remote micro earth stations in the country. A micro earth station fails due to a transient fault. Azaron et al. (2005) discussed reliability evaluation and optimization of dissimilar component cold standby redundant system which was the combination of series–parallel subsystems combination. They applied the shortest path technique for reliability evaluation. Elyasi-Komari et al. (2011) described the techniques and basic principles of dependable development and deployment of computer networks that are based on the results of FME(C)A (Failure Modes and Effects (Criticality) Analysis) analysis. Further, Nagiya and Ram (2013) investigated the various reliability characteristics of a satellite communication system which includes the earth station and terrestrial system and found the important reliability analysis.

In the context of computer systems, it is a universal purpose of device that can be planned to carry out every work in daily life. In today’s fast life, everything depends on computer based systems. Now-a-days, it is quite impossible to overestimate the importance of computer systems in the environment around us. Embedded computer systems can be found in many devices around the home. Televisions, refrigerators, washing machines, telephones, just the few names. As a source of communication, computer plays a very crucial role. Information can be shared by anyone in the rest of the world and email has made written communication with anyone in the world potentially instantaneous. Usually, a computer system consists of at least one processing element, a central processing unit (CPU), and some form of memory. The processing element carries out arithmetic and logic operations, and a sequencing and control unit that can change the order of operations based on stored information. Peripheral devices allow information to be retrieved from an external source, and the result of operations saved and retrieved (Rajaraman 2010).

In computer hardware, availability refers to the overall uptime of the system. Reliability in general is likelihood of a failure occurring in a running system. A perfectly reliable system will also enjoy perfect availability within an intended period of time. The industry uses the concept of “high availability” to refer the systems and technologies specially engineered for reliability, availability, and sensitivity such systems include redundant hardware. By Lyu (1996), the demand for complex hardware systems has increased for more speedily than the ability to design implement, test, and maintain them. When the requirements for and dependencies on computer increases, the possibilities of calamities from computer failure also increase. The impact of these failures ranges from inconvenience, economic, damages, to loss of life. Hence the reliable performance of the computer systems has become a major concern. Hardware reliability can be described by exponential distribution. Also, hardware reliability decreases with time. The hardware reliability theory relies on the analysis of stationary processes because only physical faults are considered.

In the field of reliability-copula concept, Ram and Singh (2008, 2010a, b) studied the reliability indices of complex systems under two types of failure and repair using Gumbel–Hougaard family copula. Recently, the authors (Singh et al. 2013a, b) studied the complex systems under k-out-of-n types, which consist of two subsystems in series configuration using Gumbel–Hougaard family copula distribution in repair. Although they have done a good work by applying the copula approach, they did not think about the home or office based computer system performance under copula approach, which is a very important issue in today’s work culture.

The present chapter reflects the performance of a home or office based computer system constructed with hardware connectivity under the concept of Gumbel–Hougaard family copula. The designed system is studied by using the Markov process, supplementary variable technique, and the Laplace transformation to obtain the various reliability measures.

2 Brief Introduction of Gumbel–Hougaard Family Copula

Several authors, including Nelsen (2006), have studied the family of copulas extensively. The Gumbel–Hougaard family copula is defined as:

$$ {C}_{\theta}\left({u}_1,{u}_2\right)= \exp \left(-{\left({\left(- \log {u}_1\right)}^{\theta}+{\left(- \log {u}_2\right)}^{\theta}\right)}^{1/\theta}\right),\kern0.6em 1\le \theta \le \infty $$

For θ = 1 the Gumbel–Hougaard copula models independence, for θ → ∞ it converges to comonotonicity.

Gumbel–Hougaard family copula gives the good results, when the system is in the complete failure mode. The best policy is to repair the failed system as soon as it is possible by Gumbel–Hougaard family copula when two distributions are coupled.

3 Mathematical Model Details

3.1 Nomenclature

Notations associated with work are shown in Table 1.

3.2 System Description

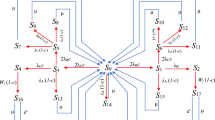
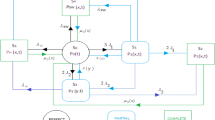
This chapter represents the reliability based mathematical modeling of a home or office based computer system under copula technique. Although the problem looks like general in daily routine, but here authors applied Gumbel–Hougaard family copula, makes the problem interesting. A general computer system has been converted into multi-states, which are good, degraded, and failed. The system has two types of failure, namely minor and major. From the good state after minor failure, the system goes to degraded state and after major failure, the system goes into a complete failure mode. Minor failure means any component of the system failed partially and the system could be worked with less efficiency while the major failure means the failure of any important component of the system, without which system could not be workable. After repairing, the system comes back in good state. A failed state could be repaired with the help of Gumbel–Hougaard family copula (Ram and Singh 2008, 2010; Ram 2010; Ram et al. 2013). The configuration and state transition diagram of the designed system have been shown in Fig. 1a, b.

Fig. 1
figure 1figure 1

(a) System configuration. (b) Transition state diagram

Full size image
Table 1 Notations
Full size table
Table 2 State description of the system
Full size table

3.3 State Description

All the states of the state transition diagram are described in Table 2.

3.4 Assumptions

The following assumptions are associated with the model

  1. 1.

    Initially, all the components are working that means system is in good state.

  2. 2.

    At any time, the system can cover from degraded or failed states.

  3. 3.

    All the components can be repaired.

  4. 4.

    Sufficient repair facilities are available.

  5. 5.

    After repair, the system works like a new one.

  6. 6.

    The failure and repair rate are constant. The value of different failure and repair rates are based on previous literature and work experience.

  7. 7.

    The expression for the joint probability distribution of repair of the complete failed states S P, S ST and degraded state S KMS are computed with the help of Gumbel–Hougaard family copula.

3.5 Formulation and Solution of Model

On the basis of the transition state diagram by the consideration of possible transition state, we can obtain the following set of differential equations for the present model after applying Markov process:

$$ \begin{aligned}[b]&\left[\frac{\partial }{\partial t}+{\lambda}_{\mathrm{C}}+{\lambda}_{\mathrm{S}\mathrm{T}}+{\lambda}_{\mathrm{U}}+{\lambda}_{\mathrm{MN}}+{\lambda}_{\mathrm{MS}}+{\lambda}_{\mathrm{K}}\right]{P}_{\mathrm{S}}(t)=\mu (y)\big[{P}_{\mathrm{C}\mathrm{U}}\big( t\big)+{P}_{\mathrm{U}}(t)\nonumber\\ &\quad+\,{P}_{\mathrm{MS}}(t)+{P}_{\mathrm{K}}(t)\big]+ \exp \big[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\big]{}^{\frac{1}{\theta}}{P}_{\mathrm{K}\mathrm{MS}}\big( t\big)\nonumber\\ &\quad+\,{\displaystyle \underset{0}{\overset{\infty }{\int }}{P}_{\mathrm{MN}}}\left( y, t\right)\mu (y) dy+{\displaystyle \underset{0}{\overset{\infty }{\int }}{P}_{\mathrm{S}\mathrm{T}}}\left( x, t\right) \exp \left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]{}^{\frac{1}{\theta}} dx \nonumber\\ &\quad+\,{\displaystyle \underset{0}{\overset{\infty }{\int }}{P}_{\mathrm{P}}}\left( x, t\right) \exp \left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]{}^{\frac{1}{\theta}} dx\end{aligned} $$
(1)
$$ \left[\frac{\partial }{\partial t}+{\lambda}_{\mathrm{S}\mathrm{T}}+\mu (y)\right]{P}_{\mathrm{C}\mathrm{U}}(t)={\lambda}_{\mathrm{C}}{P}_{\mathrm{S}}(t) $$
(2)
$$ \left[\frac{\partial }{\partial t}+{\lambda}_{\mathrm{P}}+\mu (y)\right]{P}_{\mathrm{U}}(t)={\lambda}_{\mathrm{U}}{P}_{\mathrm{S}}(t) $$
(3)
$$ \left[\frac{\partial }{\partial t}+{\lambda}_{\mathrm{K}}+\mu (y)\right]{P}_{\mathrm{MS}}(t)={\lambda}_{\mathrm{MS}}{P}_{\mathrm{S}}(t) $$
(4)
$$ \left[\frac{\partial }{\partial t}+{\lambda}_{\mathrm{MS}}+\mu (y)\right]{P}_{\mathrm{K}}(t)={\lambda}_{\mathrm{K}}{P}_{\mathrm{S}}(t) $$
(5)
$$ \left[\frac{\partial }{\partial t}+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right]{P}_{\mathrm{K}\mathrm{MS}}(t)={\lambda}_{\mathrm{K}}{P}_{\mathrm{MS}}(t)+{\lambda}_{\mathrm{MS}}{P}_{\mathrm{K}}(t) $$
(6)
$$ \left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right]{P}_{\mathrm{ST}}\left( x, t\right)=0 $$
(7)
$$ \left[\frac{\partial }{\partial t}+\frac{\partial }{\partial x}+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right]{P}_{\mathrm{P}}\left( x, t\right)=0 $$
(8)
$$ \left[\frac{\partial }{\partial t}+\frac{\partial }{\partial y}+\mu (y)\right]{P}_{\mathrm{MN}}\left( y, t\right)=0 $$
(9)

Boundary conditions

$$ {P}_{\mathrm{S}\mathrm{T}}\left(0, t\right)={\lambda}_{\mathrm{S}\mathrm{T}}\left[{P}_{\mathrm{S}}(t)+{P}_{\mathrm{CU}}(t)\right] $$
(10)
$$ {P}_{\mathrm{P}}\left(0, t\right)={\lambda}_{\mathrm{P}}{P}_{\mathrm{U}}(t) $$
(11)
$$ {P}_{\mathrm{MN}}\left(0, t\right)={\lambda}_{\mathrm{MN}}{P}_{\mathrm{S}}(t) $$
(12)

Initial condition

$$ {P}_{\mathrm{S}}(0)\kern0.75em \mathrm{and}\ \mathrm{other}\ \mathrm{state}\ \mathrm{probabilities}\ \mathrm{are}\ \mathrm{zero}\ \mathrm{at}\kern0.5em t=0 $$
(13)

Solving Eqs. (1–12) with the help of Laplace transformation, and using Eq. (13), we obtain

$$ \begin{aligned}[b]&\left[ s+{\lambda}_{\mathrm{C}}+{\lambda}_{\mathrm{S}\mathrm{T}}+{\lambda}_{\mathrm{U}}+{\lambda}_{\mathrm{MN}}+{\lambda}_{\mathrm{MS}}+{\lambda}_{\mathrm{K}}\right]{\overline{P}}_{\mathrm{S}}(s)=1+\mu (y)\left[{\overline{P}}_{\mathrm{C}\mathrm{U}}\right( s\Big)\nonumber\\ &\quad+\,{\overline{P}}_{\mathrm{U}}(s)+{\overline{P}}_{\mathrm{MS}}(s)+{\overline{P}}_{\mathrm{K}}(s)\left]+ \exp \right[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\left]{}^{\frac{1}{\theta}}{\overline{P}}_{\mathrm{K}\mathrm{MS}}\right( s\Big)\nonumber\\ &\quad+\,{\displaystyle \underset{0}{\overset{\infty }{\int }}{\overline{P}}_{\mathrm{MN}}}\left( y, s\right)\mu (y) dy+{\displaystyle \underset{0}{\overset{\infty }{\int }}{\overline{P}}_{\mathrm{S}\mathrm{T}}}\left( x, s\right) \exp \left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]{}^{\frac{1}{\theta}} dx\nonumber\\ &\quad+\,{\displaystyle \underset{0}{\overset{\infty }{\int }}{\overline{P}}_{\mathrm{P}}}\left( x, s\right) \exp \left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]{}^{\frac{1}{\theta}} dx\end{aligned} $$
(14)
$$ \left[ s+{\lambda}_{\mathrm{S}\mathrm{T}}+\mu (y)\right]{\overline{P}}_{\mathrm{C}\mathrm{U}}(s)={\lambda}_{\mathrm{C}}{\overline{P}}_{\mathrm{S}}(s) $$
(15)
$$ \left[ s+{\lambda}_{\mathrm{P}}+\mu (y)\right]{\overline{P}}_{\mathrm{U}}(s)={\lambda}_{\mathrm{U}}{\overline{P}}_{\mathrm{S}}(s)$$
(16)
$$ \left[ s+{\lambda}_{\mathrm{K}}+\mu (y)\right]{\overline{P}}_{\mathrm{MS}}(s)={\lambda}_{\mathrm{MS}}{\overline{P}}_{\mathrm{S}}(s) $$
(17)
$$ \left[ s+{\lambda}_{\mathrm{MS}}+\mu (y)\right]{\overline{P}}_{\mathrm{K}}(s)={\lambda}_{\mathrm{K}}{\overline{P}}_{\mathrm{S}}(s)$$
(18)
$$ \left[ s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right]{\overline{P}}_{\mathrm{K}\mathrm{MS}}(s)={\lambda}_{\mathrm{K}}{\overline{P}}_{\mathrm{MS}}(s)+{\lambda}_{\mathrm{MS}}{\overline{P}}_{\mathrm{K}}(s) $$
(19)
$$ \left[ s+\frac{\partial }{\partial x}+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right]{\overline{P}}_{\mathrm{ST}}\left( x, s\right)=0 $$
(20)
$$ \left[ s+\frac{\partial }{\partial x}+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right]{\overline{P}}_{\mathrm{P}}\left( x, s\right)=0 $$
(21)
$$ \left[ s+\frac{\partial }{\partial y}+\mu (y)\right]{\overline{P}}_{\mathrm{MN}}\left( y, s\right)=0 $$
(22)
$$ {\overline{P}}_{\mathrm{S}\mathrm{T}}\left(0, s\right)={\lambda}_{\mathrm{S}\mathrm{T}}\left[{\overline{P}}_{\mathrm{S}}(s)+{\overline{P}}_{\mathrm{CU}}(s)\right] $$
(23)
$$ {\overline{P}}_{\mathrm{P}}\left(0, s\right)={\lambda}_{\mathrm{P}}{\overline{P}}_{\mathrm{U}}(s) $$
(24)
$$ {\overline{P}}_{\mathrm{MN}}\left(0, s\right)={\lambda}_{\mathrm{MN}}{\overline{P}}_{\mathrm{S}}(s) $$
(25)

Solving Eqs. (14–22) with the help of Eqs. (23–25), we get

$$ {\overline{P}}_{\mathrm{S}}(s)=\frac{1}{D(s)} $$
(26)
$$ {\overline{P}}_{\mathrm{C}\mathrm{U}}(s)=\frac{\lambda_{\mathrm{C}}}{s+{\lambda}_{\mathrm{S}\mathrm{T}}+\mu (y)}{\overline{P}}_{\mathrm{S}}(s) $$
(27)
$$ {\overline{P}}_{\mathrm{U}}(s)=\frac{\lambda_{\mathrm{U}}}{s+{\lambda}_{\mathrm{P}}+\mu (y)}{\overline{P}}_{\mathrm{S}}(s)$$
(28)
$$ {\overline{P}}_{\mathrm{MS}}(s)=\frac{\lambda_{\mathrm{MS}}}{s+{\lambda}_{\mathrm{K}}+\mu (y)}{\overline{P}}_{\mathrm{S}}(s)$$
(29)
$$ {\overline{P}}_{\mathrm{K}}(s)=\frac{\lambda_{\mathrm{K}}}{s+{\lambda}_{\mathrm{MS}}+\mu (y)}{\overline{P}}_{\mathrm{S}}(s)$$
(30)
$$\setcounter{equation}{30}\begin{array}{lll} {\overline{P}}_{\mathrm{K}\mathrm{MS}}(s)& = & \frac{\lambda_{\mathrm{K}}{\lambda}_{\mathrm{MS}}}{\left( s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right)}\nonumber\\ & & \times \left(\frac{1}{s+{\lambda}_{\mathrm{K}}+\mu (y)}+\frac{1}{s+{\lambda}_{\mathrm{MS}}+\mu (y)}\right)\;{\overline{P}}_{\mathrm{S}}(s)\end{array}$$
(31)
$$\begin{array}{lll} {\overline{P}}_{S T}(s) & = & \frac{1}{s}\left({\lambda}_{S T}+\frac{\lambda_{S T}}{s+{\lambda}_{S T}+\mu (y)}\right)\nonumber \\&& \times \left(1-\frac{ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}}{\left( s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right)}\right)\;{\overline{P}}_S(s) \end{array}$$
(32)
$$ {\overline{P}}_{\mathrm{MN}}(s)=\frac{1}{s}{\lambda}_{\mathrm{MN}}\left(1-\frac{\mu (y)}{\left( s+\mu (y)\right)}\right){\overline{P}}_{\mathrm{S}}(s) $$
(33)
$$ {\overline{P}}_{\mathrm{P}}(s)=\frac{\lambda_{\mathrm{P}}{\lambda}_{\mathrm{U}}}{s\left\{ s+{\lambda}_{\mathrm{P}}+\mu (y)\right\}}\left(1-\frac{ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}}{\left( s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right)}\right){\overline{P}}_{\mathrm{S}}(s) $$
(34)

where

$$ \begin{aligned}[b] D(s)&=\left[\left( s+{C}_1\right)-\mu (y)\left[\frac{\lambda_{\mathrm{C}}}{\left( s+{C}_2\right)}+\frac{\lambda_{\mathrm{U}}}{\left( s+{C}_3\right)}+\frac{\lambda_{\mathrm{MS}}}{\left( s+{C}_4\right)}+\frac{\lambda_{\mathrm{K}}}{\left( s+{C}_5\right)}\right]\right]\nonumber\\ &\quad-\,\frac{ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}}{\left( s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right)}{\lambda}_{\mathrm{K}}{\lambda}_{\mathrm{MS}}\left[\frac{1}{\left( s+{C}_4\right)}+\frac{1}{\left( s+{C}_5\right)}\right]\nonumber\\ &\quad-\,\frac{ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}}{\left( s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right)}\left[{\lambda}_{\mathrm{ST}}+\frac{\lambda_{\mathrm{ST}}{\lambda}_{\mathrm{C}}}{\left( s+{C}_2\right)}+\frac{\lambda_{\mathrm{P}}{\lambda}_{\mathrm{U}}}{\left( s+{C}_3\right)}\right]\nonumber\\ &\quad-\,\frac{\mu (y)}{\left\{ s+\mu (y)\right\}}{\lambda}_{\mathrm{MN}}\end{aligned} $$
$$ {C}_1={\lambda}_{\mathrm{C}}+{\lambda}_{\mathrm{ST}}+{\lambda}_{\mathrm{U}}+{\lambda}_{\mathrm{MN}}+{\lambda}_{\mathrm{MS}}+{\lambda}_{\mathrm{K}},\kern0.5em {C}_2={\lambda}_{\mathrm{ST}}+\mu (y),$$
$$ {C}_3={\lambda}_{\mathrm{P}}+\mu (y),\kern0.5em {C}_4={\lambda}_{\mathrm{K}}+\mu (y),\kern0.5em {C}_5={\lambda}_{\mathrm{MS}}+\mu (y) $$

The Laplace transformation of the probabilities that the system is in upstate (i.e., either good or degraded):

$$ \begin{aligned}[b]{\overline{P}}_{\mathrm{up}}(s)&={\overline{P}}_{\mathrm{S}}(s)+{\overline{P}}_{\mathrm{C}\mathrm{U}}(s)+{\overline{P}}_{\mathrm{U}}(s)+{\overline{P}}_{\mathrm{MS}}(s)+{\overline{P}}_{\mathrm{K}}(s)+{\overline{P}}_{\mathrm{K}\mathrm{MS}}(s)\nonumber\\ {}&=\left\{\vphantom{\left.\kern1.24em +\frac{\lambda_{\mathrm{K}}{\lambda}_{\mathrm{MS}}}{s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}}\left(\frac{1}{\left( s+{C}_4\right)}+\frac{1}{\left( s+{C}_5\right)}\right)\right\}}1+\frac{\lambda_{\mathrm{C}}}{\left( s+{C}_2\right)}+\frac{\lambda_{\mathrm{U}}}{\left( s+{C}_3\right)}+\frac{\lambda_{\mathrm{MS}}}{\left( s+{C}_4\right)}+\frac{\lambda_{\mathrm{K}}}{\left( s+{C}_5\right)}\right.\nonumber\\ &\quad+\,\left.\frac{\lambda_{\mathrm{K}}{\lambda}_{\mathrm{MS}}}{s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}}\left(\frac{1}{\left( s+{C}_4\right)}+\frac{1}{\left( s+{C}_5\right)}\right)\right\}{\overline{P}}_{\mathrm{S}}(s)\end{aligned} $$
(35)

The Laplace transformation of the probabilities that the system is in downstate (i.e., failed):

$$ \begin{aligned}[b] {\overline{P}}_{\mathrm{down}}(s)&={\overline{P}}_{\mathrm{P}}(s)+{\overline{P}}_{\mathrm{S}\mathrm{T}}(s)+{\overline{P}}_{\mathrm{MN}}(s)\nonumber\\ &=\left\{\frac{1}{s}\left(1-\frac{ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}}{\left( s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right)}\right)\right.\nonumber\\ &\quad\times \left.\left({\lambda}_{\mathrm{S}\mathrm{T}}+\frac{\lambda_{\mathrm{S}\mathrm{T}}{\lambda}_{\mathrm{C}}}{\left( s+{C}_2\right)}+\frac{\lambda_{\mathrm{P}}{\lambda}_{\mathrm{U}}}{\left( s+{C}_3\right)}\right)+{\lambda}_{\mathrm{MN}}\frac{1}{s}\left[1-\frac{\mu (y)}{s+\mu (y)}\right]\vphantom{\left\{\frac{1}{s}\left(1-\frac{ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}}{\left( s+ \exp {\left[{x}^{\theta}+{\left\{ \log \varphi (x)\right\}}^{\theta}\right]}^{\frac{1}{\theta}}\right)}\right)\times \left({\lambda}_{\mathrm{S}\mathrm{T}}+\frac{\lambda_{\mathrm{S}\mathrm{T}}{\lambda}_{\mathrm{C}}}{\left( s+{C}_2\right)}+\frac{\lambda_{\mathrm{P}}{\lambda}_{\mathrm{U}}}{\left( s+{C}_3\right)}\right)\right.}\right\}{\overline{P}}_{\mathrm{S}}(s)\end{aligned}$$
(36)

4 Particular Cases and Numerical Computations

4.1 Availability Analysis

4.1.1 When the System in Comprehensive State

Initially, the system works properly, for this, setting the value of different failure and repair rates as λ C = 0.2, λ ST = 0.3, λ U = 0.2, λ MN = 0.1, λ MS = 0.5, λ K = 0.4, λ P = 0.3, φ(x) = 1, μ(y) = 1 in Eq. (35), one can obtain the availability of the system

$$ \begin{aligned}[b]{P}_{\mathrm{up}}(t)&=\left\{ \vphantom{+0.003352035390\kern0.5em {\mathrm{e}}^{\left(-1.334602761 t\right)}+0.8927202294\Big\} }0.08747435461\kern0.5em {\mathrm{e}}^{\left(-2.903649803 t\right)} \cos \kern0.5em \right(0.3135682026 t\Big)\\ &\quad-0.3968940408\kern0.5em {\mathrm{e}}^{\left(-2.903649803 t\right)} \sin \kern0.5em \left(0.3135682026 t\right)\\ &\quad+0.0007440467225\kern0.5em {\mathrm{e}}^{\left(-1.458316302 t\right)}+0.01570933388\kern0.5em {\mathrm{e}}^{\left(-1.018061332 t\right)}\\ &\quad+0.003352035390\kern0.5em {\mathrm{e}}^{\left(-1.334602761 t\right)}+0.8927202294\Big\}\end{aligned} $$
(37a)

4.1.2 When No Failure in Control and Storage Unit

The control and storage units are perfect, i.e., no failure occurrence in both the units, putting other failure and repair rates as λ U = 0.2, λ MN = 0.1, λ MS = 0.5, λ K = 0.4, λ P = 0.3, φ(x) = 1, μ(y) = 1 in Eq. (35), we have,

$$\renewcommand\theequation{\arabic{equation}b}\setcounter{equation}{36}\begin{array}{lll}{P}_{\mathrm{up}}(t) & = & \left\{0.03538863784\kern0.5em {\mathrm{e}}^{(-2.660026210 t} \cos \kern0.5em (0.6818499005 t)\right.\nonumber\\ &&\left. +0.2778239624\kern0.5em {\mathrm{e}}^{\left(-2.660026210 t\right)} \sin \kern0.5em (0.6818499005 t)\right.\nonumber\\ && \left.+0.0007092452156\kern0.5em {\mathrm{e}}^{(-1.455748534 t)}+0.01988553985\kern0.5em {\mathrm{e}}^{(-1.021910991 t)}\right.\nonumber\\ &&\left.+0.002616287337\kern0.5em {\mathrm{e}}^{(-1.320568054 t)}+0.9414002897\right\}\end{array} $$
(37b)

4.1.3 When No Failure in Power and Monitor

The power and monitor of the system are in perfect working condition, then setting different failure and repair rates as: λ C = 0.2, λ ST = 0.3, λ U = 0.2, λ MN = 0, λ MS = 0.5, λ K = 0.4, λ P = 0, φ(x) = 1, μ(y) = 1. Substituting all these values in Eq. (35), one can obtain

$$ \begin{aligned}[b]{P}_{\mathrm{up}}(t)&=\left\{\vphantom{\quad+0.00009129208258\;{\mathrm{e}}^{\left(-1.455712754 t\right)}+0.9422900542\Big\}}0.5785670001\kern0.5em {\mathrm{e}}^{\left(-2.850684518 t\right)} \cos \kern0.5em \right(0.2437004362 t\Big)\\ &\quad -0.5523608006\kern0.5em {\mathrm{e}}^{\left(-2.850684518 t\right)} \sin \kern0.5em \left(\mathrm{0.0.2437004362} t\right)\\ &\quad -0.002282954416\kern0.5em {\mathrm{e}}^{\left(-1.040489494 t\right)}+0.002044908119\kern0.5em {\mathrm{e}}^{\left(-1.320708716 t\right)}\\ & \quad+0.00009129208258\;{\mathrm{e}}^{\left(-1.455712754 t\right)}+0.9422900542\Big\}\end{aligned}\qquad\qquad\quad$$
(37c)

4.1.4 When No Failure in Keyboard and Mouse

When keyboard and mouse have no failure, putting the value of different failure and repair rates as λ C = 0.2, λ ST = 0.3, λ U = 0.2, λ MN = 0.1, λ MS = 0, λ K = 0, λ P = 0.3, φ(x) = 1, in Eq. (35), one can obtain

$$ \begin{aligned}[b]{P}_{\mathrm{up}}(t)&=\Big\{0.1110157824\kern0.5em {\mathrm{e}}^{\left(-3.038692672 t\right)}+0.0206201604\kern0.5em {\mathrm{e}}^{\left(-1.745678579 t\right)}\nonumber\\ &\quad+0.02578659225\kern0.5em {\mathrm{e}}^{\left(-1.033908748 t\right)}+0.8425774650\Big\}\end{aligned} $$
(37d)

Varying the time unit t from 0 to 20 in each case of availability, the computed value in all four cases of availability is shown in Table 3 and demonstrated by the graphs in Fig. 2, respectively.

Table 3 Availability as function of time
Full size table
Fig. 2
figure 2

Availability as function of time

Full size image

4.2 Reliability Analysis

The reliability of the design system can be found by fixing the repair rates equal to zero.

4.2.1 When the System in Comprehensive State

When the system is fully functioning, taking the value of different failure rates as λ C = 0.2, λ ST = 0.3, λ U = 0.2, λ MN = 0.1, λ MS = 0.5, λ K = 0.4, λ P = 0.3. Substituting all these values in Eq. (35), one can obtain the reliability of the system

$$ R(t)=0.1848739496\kern0.5em {\mathrm{e}}^{\left(-1.7 t\right)}+0.5294117647+0.2857142857\kern0.5em {\mathrm{e}}^{\left(-0.3 t\right)} $$
(38a)

4.2.2 When No Control Unit and Storage Unit Are failed

The control unit and storage unit are not failed, then their corresponding failure rates are zero, and other rates as λ C = 0, λ ST = 0, λ U = 0.2, λ MN = 0.1, λ MS = 0.5, λ K = 0.4, λ P = 0.3. Putting all values in Eq. (35), we have

$$ R(t)=0.02777777778\kern0.5em {\mathrm{e}}^{\left(-1.2 t\right)}+0.75+0.2222222222\kern0.5em {\mathrm{e}}^{\left(-0.3 t\right)} $$
(38b)

4.2.3 When No Power and Monitor Are failed

Taking the value of different failure rates as λ C = 0.2, λ ST = 0.3, λ U = 0.2, λ MN = 0, λ MS = 0.5, λ K = 0.4, λ P = 0. Substituting all values in Eq. (35), we can obtain the reliability of the system as

$$ R(t)=0.1586538462\kern0.5em {\mathrm{e}}^{\left(-1.6 t\right)}+0.6875+0.1538461538\kern0.5em {\mathrm{e}}^{\left(-0.3 t\right)} $$
(38c)

4.2.4 When No Keyboard and Mouse Are failed

The keyboard and mouse are not failed, setting the value of different failure rates as λ C = 0.2, λ ST = 0.3, λ U = 0.2, λ MN = 0.1, λ MS = 0, λ K = 0, λ P = 0.3,. Putting all the values in Eq. (35), we can obtain the reliability of the system as:

$$ R(t)=0.2\kern0.5em {\mathrm{e}}^{\left(-0.55 t\right)}\left(5. \cosh (0.25)+3. \sinh \left(0.25 t\right)\right) $$
(38d)

Varying the time unit t from 0 to 20 in each case of reliability, the computed numeric values are given in Table 4 and correspondingly shown the graph of reliability with respect to time in Fig. 3.

Table 4 Reliability as function of time
Full size table
Fig. 3
figure 3

Reliability as function of time

Full size image

4.3 Expected Profit

For an organization and an official point of view, the expected profit during the interval [0, t) is given as

$$ {E}_{\mathrm{P}}(t)={C}_1{\displaystyle \underset{0}{\overset{t}{\int }}{P}_{\mathrm{up}}(t) dt}- t{C}_2 $$
(39)

Using Eq. (37a) for a the comprehensive state only in Eq. (39), the cost for the same set of parameters is obtained as

$$ \begin{aligned}[b]{E}_{\mathrm{P}}(t)&={C}_1\left\{-0.01518745908\;{\mathrm{e}}^{\left(-2.903649803 t\right)}\vphantom{\quad +0.8927202294 t-0.01543063604\;{\mathrm{e}}^{\left(-1.018061332 t\right)}\Big\}} \cos \right(0.3135682026 t\Big)\nonumber\\ &\quad +0.1383280947\;{\mathrm{e}}^{\left(-2.903649803 t\right)} \sin \left(0.3135682026 t\right)+0.3363993984\nonumber\\ &\quad -0.0005102094254\;{\mathrm{e}}^{\left(-1.458316302 t\right)}-0.002511635288\;{\mathrm{e}}^{\left(-1.334602761 t\right)}\nonumber\\ &\quad +0.8927202294 t-0.01543063604\;{\mathrm{e}}^{\left(-1.018061332 t\right)}\Big\}- t{C}_2\end{aligned} $$
(40)

Setting C 1 = 1 and C 2 = 0.1, 0.2, 0.3, 0.4, 0.5, respectively, in Eq. (40), we get the Table 5 and obtained results are demonstrated by Fig. 4.

Table 5 Expected profit as function of time
Full size table
Fig. 4
figure 4

Expected profit as function of time

Full size image

4.4 Sensitivities

Sensitivity of a function is explained as the partial derivative of the function with respect to their input factors. Sensitivity analysis, also called importance analysis (Henley and Kumamoto 1992; Andrews and Moss 1993), help detect which parameter contribute most to system performance and thus would be good ones for elevate. Sensitivity to a factor is defined as the partial derivative of the function with respect to input parameters. Here, these input parameters are the failure rates of the system.

4.4.1 Availability Sensitivity

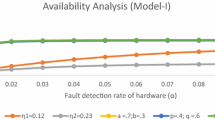
Availability sensitivity can be obtained by partial differentiation of Eq. (35) with respect to the failure rates of control unit, storage unit, UPS, monitor, mouse, keyboard, power supply, respectively after taking unity as the repair rates. Using the values of the failure rates as λ C = 0.2, λ ST = 0.3, λ U = 0.2, λ MN = 0.1, λ MS = 0.5, λ K = 0.4, λ P = 0.3, we have obtained the values of partial derivatives \( \frac{\partial {P}_{\mathrm{up}}(t)}{\partial {\lambda}_{\mathrm{C}}} \), \( \frac{\partial {P}_{\mathrm{up}}(t)}{\partial {\lambda}_{\mathrm{ST}}} \), \( \frac{\partial {P}_{\mathrm{up}}(t)}{\partial {\lambda}_{\mathrm{U}}} \), \( \frac{\partial {P}_{\mathrm{up}}(t)}{\partial {\lambda}_{\mathrm{MN}}} \), \( \frac{\partial {P}_{\mathrm{up}}(t)}{\partial {\lambda}_{\mathrm{MS}}} \), \( \frac{\partial {P}_{\mathrm{up}}(t)}{\partial {\lambda}_{\mathrm{K}}} \), \( \frac{\partial {P}_{\mathrm{up}}(t)}{\partial {\lambda}_{\mathrm{P}}} \). Taking the time unit from 0 to 20, we obtain the Table 6 and correspondingly Fig. 5.

Table 6 Availability sensitivity as function of time
Full size table
Fig. 5
figure 5

Availability sensitivity as function of time

Full size image

4.4.2 Reliability Sensitivity

Sensitivity of reliability can be analyzed by partial differentiation of Eq. (38a) with respect to the failure rates of control unit, storage unit, UPS, monitor, mouse, keyboard, power supply, respectively. Using the values of the failure rates λ C = 0.2, λ ST = 0.3, λ U = 0.2, λ MN = 0.1, λ MS = 0.5, λ K = 0.4, λ P = 0.3, we have obtained the values of \( \frac{\partial R(t)}{\partial {\lambda}_{\mathrm{C}}} \), \( \frac{\partial R(t)}{\partial {\lambda}_{\mathrm{ST}}} \), \( \frac{\partial R(t)}{\partial {\lambda}_{\mathrm{U}}} \), \( \frac{\partial R(t)}{\partial {\lambda}_{\mathrm{MN}}} \), \( \frac{\partial R(t)}{\partial {\lambda}_{\mathrm{MS}}} \), \( \frac{\partial R(t)}{\partial {\lambda}_{\mathrm{K}}} \), \( \frac{\partial R(t)}{\partial {\lambda}_{\mathrm{P}}} \). Taking the time unit from 0 to 20 units, one can obtain the Table 7 and corresponding Fig. 6.

Table 7 Reliability sensitivity as function of time
Full size table
Fig. 6
figure 6

Reliability sensitivity as function of time

Full size image

5 Result Discussion

From Fig. 2, we have analyzed that when the system is in the comprehensive state, the availability of the system first decreases quickly and then becomes constant. When control and storage unit are not failed, then availability of the system decreases quickly and then becomes constant. But in this case, availability is high as compare to comprehensive state. In the same manner, when power supply and monitor are not failed, availability first decreases sharply and coincide with the availability of the system when control and storage unit are not failed. Further, when the keyboard and mouse are not failed, availability of the system is lowest. Firstly, it decreases quickly and then becomes constant.

Figure 3 shows the reliability of the system. When the system is in a comprehensive state, the reliability of the system first decreases smoothly and then becomes constant. Similarly, when storage and control unit are not failed, and power supply with the monitor are not failed, reliability of the system first decreases smoothly and then becomes constant, but the reliability of the system in case when storage and control unit are not failed, is highest. When keyboard and mouse are not failed reliability of the system is lowest. In this case also, reliability first decreases, quickly in the shape of a curve and then becomes constant.

Figure 4 shows the expected profit, when the revenue per unit time fixed at one and varying service cost from 0.1 to 0.5. It is clear from the graph that the profit decrease as the service cost increase.

From Fig. 5, availability sensitivity of the system decreases swiftly (as a straight line) and then becomes constant as time increases with respect to the failure rates of storage unit and monitor. Availability sensitivity with respect to the failure rate of keyboard and mouse increase, but after a short curve, it becomes constant as time increase. With respect to the failure rate of power supply, UPS and control unit, it decreases shortly and then becomes constant. From Fig. 6, reliability sensitivity of the system with respect to the failure rate of the monitor and storage unit, are first to decrease as a straight line but again after some increment, it becomes constant. With respect to the failure rate of power supply, reliability sensitivity decreases in the form of a smooth curve and then it comes back to near zero and then becomes constant as time increases. Reliability sensitivity with respect to the failure rate of keyboard and mouse increases and after some times, it also becomes constant. Reliability sensitivity with respect to the failure rate of UPS firstly becomes constant for a very short time after that, this decrease as time unit increases in the form of the hyperbola and becomes constant.

6 Conclusion

In this chapter, we have analyzed the availability, reliability, cost, and sensitivity of the home or office based computer system by introducing a mathematical model. The availability, reliability, and sensitivity become constant over a certain period of time. The system based profit decreases as service cost increases. It is also noticeable, the system could make less sensitive by controlling its failure rates. With the help of this developed model, one can conclude that the results achieved in this work are valuable in the study of improving the performance of the computer systems that contain multi-stages. Hence the present work evidently shows the importance of copula repair modeling, which seems very much to be possible at home or office based computer systems. The future work in this area can be keen to the elaboration of more complexities for specific computer networks.