Stochastic modeling and cost-benefit analysis of computing device with fault detection subject to expert repair facility

Abstract

In the present study, two stochastic models of a computing device are studied using the concept of imperfect fault detection in the presence of regular and expert repairman. The computing device is a combination of hardware and software components which works together but fails independently. In both models, the unit is under observation for fault detection by the regular repairman. In first model, if the unit is seriously damaged then it undergoes for replacement by regular repairman otherwise it is sent back to operation after maintenance. In second model, if the unit is seriously damaged then it undergoes for repair by expert repairman otherwise it is sent back to operation after maintenance. Various reliability measures for both the system models are obtained using semi-Markov process and regenerative point technique. Finally to highlight the importance of the study empirical results have been obtained with respect to fault detection rate.

1 Introduction

In today’s scientific environment virtually everyone be contingent on the persistent functioning of computing machinery and systems for our security, safety and economic prosperity. Most of automated machines, advanced airliners, hospital observing appliances, information exchange systems, computer networks in industries and academic institutions and mobile networks have been heavily depends on computing devices and customers anticipate that these systems works properly as and when required because if they fail results can be very calamitous. With the passes of time, society propagates in complication and new dire challenges arises in the arena of computing machines due to hardware and software component failures which plays key role in the manufacturing of these systems. The failure of these components directly disturb the reliability of the whole system. A lot of research work has been carried out by reliability engineers and academicians to make improvement in systems reliability and many techniques have been developed for reliability improvement like, redundancy, priority in repair disciplines, inspection etc. In most of the studies either hardware components or software components has been analyzed only. First of all, Friedman and Tran [1] and Welke et al. [2] annoyed to improve a joint reliability model for the whole computer system including both hardware and software together. The software growth model under operational and testing has been studied by Yang and Xie [3]. Biswas et al. [4] obtained the availability of a system under the concept of imperfect repairs before the replacement. Teng and Pham [5] studied the concept of imperfect debugging and derived the transient solution of software model. Levitin [6] provided a procedure for assessing reliability of systems involving fault-tolerant software components. Kharoufeh et al. [7] obtained availability using Markovian approach under the effect of shocks of a occasionally inspected systems. Wang and Chen [8] and Hsu et al. [9] studied the availability under concepts of general repair times, reboot delay, standby switching failure, unreliable repair facility and switching failures. Smidt-Destombes et al. [10] developed a spare part model on system level using cold standby redundancy technique. Hajeeh [11] derived the availability for a series alignment with two types of redundancy and common cause failure. Anand and Malik [12] analyzed a computer system with arbitrary distributions for h/w and s/w replacement and priority to repair activities of h/w over replacement of the s/w components. Malik and Barak [13] obtained various reliability measures of a cold standby redundant system with preventive maintenance and repair. Malik [14] performed the reliability modeling of a computer system with preventive maintenance and priority subject to maximum operation and repair times. Kumar and Malik [15] carried out the cost-benefit analysis of a computer system with priority to S/W replacement over H/W repair activities subject to maximum operation and repair times. A stochastic model has been developed for a redundant computer system using the concepts of cold stand by redundancy and independent hardware and software failure. Kumar et al. [16] carried out a performance analysis of computer systems with imperfect fault detection. Malik [17] analyzed a 2-out-of-2: G system with single cold standby unit with priority to repair and arrival time of the server. A comparative analysis of various reliability measures of a computer system has been done by Kumar and Saini [18]. Mishra et al. [19] assessed the reliability of a mobile agent based system in suspicious MANET. Kumar et al. [20] carried out the profit analysis of a computing machine with priority and s/w rejuvenation. The above highlighted literature demonstrated that not much work in the field of computing machines has been carried out. The concept of expert repairman has not been studied so far.

By keeping it in mind, two stochastic models of a computing device are studied using the concept of imperfect fault detection in the presence of regular and expert repairman. The computing device is a combination of hardware and software components which works together but fails independently. In both models, the unit is under observation for fault detection by the regular repairman. In first model, if the unit is seriously damaged then it undergoes for replacement by regular repairman otherwise it is sent back to operation after maintenance. In second model, if the unit is seriously damaged then it undergoes for repair by expert repairman otherwise it is sent back to operation after maintenance. Various reliability measures for both the system models are obtained using semi-Markov process and regenerative point technique. Finally to highlight the importance of the study empirical results have been obtained with respect to fault detection rate.

2 Assumptions

• a) Two unit cold standby system with one operative and other standby.

• b) Replacement of components after fault detection in hardware and software.

• c) Replacement takes time.

• d) Repairs are perfect.

• e) Regular repairman available in Model-I.

• f) Expert repairman available immediately in Model-II.

• g) All time dependent random variables are independent.

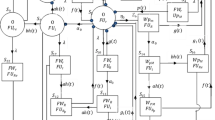
3 System model description

Two stochastic models have been formulated under the above stated assumptions. The state description of the models is as follows:

4 Transition probabilities

By probabilistic considerations, the expression of transition probabilities have been derived as follows:

For both models

$$\varepsilon_{01} = \int\limits_{0}^{\infty } {p\eta_{1} e^{{ - p\eta_{1} t}} e^{{ - q\eta_{2} t}} e^{ - st} dt} = p\eta_{1} \int\limits_{0}^{\infty } {e^{{ - (p\eta_{1} + q\eta_{2} + s)t}} dt = \frac{p\eta_{1} }{p\eta_{1} + q\eta_{2} + s}}.$$

(1)

Taking limit $s \to 0$ in Eq. (1), we get

$$\varepsilon_{01} = \lim \frac{{p\eta_{1} }}{{p\eta_{1} + q\eta_{2} + s}} = \frac{{p\eta_{1} }}{{p\eta_{1} + q\eta_{2} }}.$$

(2)

$$\begin{aligned} \varepsilon_{02} &= \frac{{q\eta_{2} }}{{p\eta_{1} + q\eta_{2} }},\;\varepsilon_{10} = ag^{*} (p\eta_{1} + q\eta_{2} ),\;\varepsilon_{13} = bg^{*} (p\eta_{1} + q\eta_{2} ),\;\varepsilon_{17} = \frac{{p\eta_{1} }}{{p\eta_{1} + q\eta_{2} }}\left[ {1 - g^{*} (p\eta_{1} + q\eta_{2} )} \right], \hfill \\ \varepsilon_{18} &= \frac{{q\eta_{2} }}{{p\eta_{1} + q\eta_{2} }}\left[ {1 - g^{*} (p\eta_{1} + q\eta_{2} )} \right],\;\varepsilon_{20} = ch^{*} (p\eta_{1} + q\eta_{2} ),\;\varepsilon_{24} = dh^{*} (p\eta_{1} + q\eta_{2} ),\;\varepsilon_{8.15} = bg^{*} (0), \hfill \\ \varepsilon_{25} &= \frac{{p\eta_{1} }}{{p\eta_{1} + q\eta_{2} }}[1 - h^{*} (p\eta_{1} + q\eta_{2} )],\;\varepsilon_{26} = \frac{{q\eta_{2} }}{{p\eta_{1} + q\eta_{2} }}[1 - h^{*} (p\eta_{1} + q\eta_{2} )],\;\varepsilon_{01} = \frac{{p\eta_{1} }}{{p\eta_{1} + q\eta_{2} }}, \hfill \\ \varepsilon_{52} &= ch^{*} (0),\;\varepsilon_{5.14} = dh^{*} (0),\;\varepsilon_{6.13} = dh^{*} (0),\;\varepsilon_{62} = \,ch^{*} (0),\;\varepsilon_{71} = ag^{*} (0),\;\varepsilon_{7.16} = bg^{*} (0), \hfill \\ \varepsilon_{81} &= ag^{*} (0) \hfill \\ \end{aligned}$$

For Model-I

$$\begin{aligned} \varepsilon_{30} &= f^{*} (p\eta_{1} + q\eta_{2} ),\;\varepsilon_{39} = \frac{{p\eta_{1} }}{{p\eta_{1} + q\eta_{2} }}[1 - f^{*} (p\eta_{1} + q\eta_{2} )],\;\varepsilon_{3.10} = \frac{{q\eta_{2} }}{{p\eta_{1} + q\eta_{2} }}[1 - f^{*} (p\eta_{1} + q\eta_{2} )], \hfill \\ \varepsilon_{40} &= f_{1}^{*} (p\eta_{1} + q\eta_{2} ),\;\varepsilon_{4.11} = \frac{{p\eta_{1} }}{{p\eta_{1} + q\eta_{2} }}[1 - f_{1}^{*} (p\eta_{1} + q\eta_{2} )],\;\varepsilon_{4.12} = \frac{{q\eta_{2} }}{{p\eta_{1} + q\eta_{2} }}[1 - f_{1}^{*} (p\eta_{1} + q\eta_{2} )], \hfill \\ \varepsilon_{91} &= f^{*} (0),\;\varepsilon_{10.2} = f^{*} (0),\;\varepsilon_{11.1} = f_{1}^{*} (0),\;\varepsilon_{12.2} = f_{1}^{*} (0),\;\varepsilon_{13.2} = f_{1}^{*} (0),\;\varepsilon_{14.1} = f_{1}^{*} (0),\;\varepsilon_{15.2} = f^{*} (0), \hfill \\ \varepsilon_{16.1} &= f^{*} (0) \hfill \\ \end{aligned}$$

For Model-II

$$\begin{aligned} \varepsilon_{30} &= X^{*} (p\eta_{1} + q\eta_{2} ),\;\varepsilon_{39} = \frac{{p\eta_{1} }}{{p\eta_{1} + q\eta_{2} }}[1 - X^{*} (p\eta_{1} + q\eta_{2} )],\;\varepsilon_{3.10} = \frac{{q\eta_{2} }}{{p\eta_{1} + q\eta_{2} }}[1 - X^{*} (p\eta_{1} + q\eta_{2} )], \hfill \\ \varepsilon_{40} &= Y^{*} (p\eta_{1} + q\eta_{2} ),\;\varepsilon_{4.11} = \frac{{p\eta_{1} }}{{p\eta_{1} + q\eta_{2} }}[1 - Y^{*} (p\eta_{1} + q\eta_{2} )],\;\varepsilon_{4.12} = \frac{{q\eta_{2} }}{{p\eta_{1} + q\eta_{2} }}[1 - Y^{*} (p\eta_{1} + q\eta_{2} )], \hfill \\ \varepsilon_{91} &= X^{*} (0),\;\varepsilon_{10.2} = X^{*} (0),\;\varepsilon_{11.1} = Y^{*} (0),\;\varepsilon_{12.2} = Y^{*} (0),\;\varepsilon_{13.2} = Y^{*} (0),\;\varepsilon_{14.1} = Y^{*} (0),\;\varepsilon_{15.2} = X^{*} (0), \hfill \\ \varepsilon_{16.1} &= X^{*} (0). \hfill \\ \end{aligned}$$

Via state probabilities for both models:

$$\begin{aligned} & \varepsilon_{11.8} = \varepsilon_{18} \times \varepsilon_{81},\;\varepsilon_{12.8,15} = \varepsilon_{18} \times \varepsilon_{8.15} \times \varepsilon_{15.2},\;\varepsilon_{11.7} = \varepsilon_{17} \times \varepsilon_{71},\;\varepsilon_{11.7,16} = \varepsilon_{17} \times \varepsilon_{7.16} \times \varepsilon_{16.1},\;\varepsilon_{31.9} = \varepsilon_{39} \times \varepsilon_{91}, \hfill \\ & \varepsilon_{32.10} = \varepsilon_{3.10} \times \varepsilon_{10.2},\;\varepsilon_{4.1,11} = \varepsilon_{4.11} \times \varepsilon_{11.1},\;\varepsilon_{4.2,12} = \varepsilon_{4.12} \times \varepsilon_{12.2},\;\varepsilon_{22.5} = \varepsilon_{25} \times \varepsilon_{52},\;\varepsilon_{22.6} = \varepsilon_{26} \times \varepsilon_{62}, \hfill \\ & \varepsilon_{21.5,14} = \varepsilon_{25} \times \varepsilon_{5.14} \times \varepsilon_{14.1},\;\varepsilon_{22.6,13} = \,\varepsilon_{26} \times \varepsilon_{6.13} \times \varepsilon_{13.2}. \hfill \\ \end{aligned}$$

5 Mean sojourn times

The mean sojourn time for regenerative states in both models by using probabilistic arguments is as follows:

$$\mu_{0} = m_{01} + m_{02} = - \frac{d}{ds}\left\{ {\frac{{p\eta_{1} }}{{s + p\eta_{1} + q\eta_{2} }} + \frac{{q\eta_{2} }}{{s + p\eta_{1} + q\eta_{2} }}} \right\} = - \left\{ {\frac{{p\eta_{1} }}{{(s + p\eta_{1} + q\eta_{2} )^{2} }} + \frac{{q\eta_{2} }}{{(s + p\eta_{1} + q\eta_{2} )^{2} }}} \right\}.$$

(3)

Taking limit $s \to 0$ in Eq. (1), we get

$$\begin{aligned} \mu_{0} &= \frac{1}{{(p\eta_{1} + q\eta_{2} )}},\;\mu_{1} = \frac{1}{{(\alpha + p\eta_{1} + q\eta_{2} )}},\;\mu_{2} = \frac{1}{{(\beta + p\eta_{1} + q\eta_{2} )}},\;\mu_{1} = \frac{1}{{(\gamma + p\eta_{1} + q\eta_{2} )}}, \hfill \\ \mu_{4} &= \frac{1}{{(\lambda + p\eta_{1} + q\eta_{2} )}},\;\mu_{1}^{\prime } = \frac{1}{\alpha },\;\mu_{2}^{\prime } = \frac{1}{\beta },\;\mu_{3}^{\prime } = \frac{1}{\gamma },\;\mu_{4}^{\prime } = \frac{1}{\lambda }. \hfill \\ \end{aligned}$$

6 Mean time to system failure

Let $R_{i} \left( t \right)$ be the cumulative density function of first transition time of the system from regenerative states. By probabilistic arguments, the recurrence equations for $R_{i} \left( t \right)$ are as follows:

$$\begin{aligned} R_{0} \left( t \right) &= Q_{01} (t)\varTheta R_{1} \left( t \right) + Q_{02} (t)\varTheta R_{2} \left( t \right) \hfill \\ R_{1} \left( t \right) &= Q_{10} (t)\varTheta R_{0} \left( t \right) + Q_{13} (t)\varTheta R_{3} \left( t \right) + \sum\limits_{j = 7,8} {Q_{1j} (t)} ; {R_{3} \left( t \right) = Q_{30} (t)\varTheta R_{0} \left( t \right) + }\sum\limits_{j = 9,10} {Q_{3j} (t)} \hfill \\ R_{2} \left( t \right) &= Q_{20} (t)\varTheta R_{0} \left( t \right) + Q_{24} (t)\varTheta R_{4} \left( t \right) + \sum\limits_{j = 5,6} {Q_{2j} (t); {R_{4} \left( t \right) = Q_{40} (t)\varTheta R_{0} \left( t \right) + }\sum\limits_{j = 11,12} {Q_{4j} (t)} } . \hfill \\ \end{aligned}$$

(4)

By using Laplace Stieltjes transformation and Cramer rule on the above system of recurrence relations (4) the value of $R_{0}^{**} (s)$ has been derived. Mean time to system failure has been derived by the expression given below: ${\text{MTSF}} = \mathop {\lim }\limits_{s \to 0} {\frac{{1 - R_{0}^{**} (s)}}{s}} = \frac{N}{D}$. Where

$$N = {\mu_{0} + p_{01} \mu_{1} + p_{02} \mu_{2} } + p_{13} p_{01} \mu_{3} + p_{02} p_{24} \mu_{4} \quad \& \quad D = 1 - p_{01} p_{10} - p_{02} p_{20} - p_{01} p_{13} p_{30} - p_{24} p_{02} p_{40} .$$

(5)

7 Steady state availability analysis

By probabilistic arguments, semi-Markovian approach and regenerative point technique the recurrence relation for the SA have been derived. The probability of the system in operating state at any point of time ‘t’ has been denoted by $\tau_{i} (t)$. The recurrence relation of transition from one regenerative state to another regenerative state through via states for SA are as follows:

$$\begin{aligned} \tau_{0} (t) &= Z_{0} (t) + q_{01} (t)\copyright\tau_{1} (t) + q_{02} (t)\copyright\tau_{2} (t) \hfill \\ \tau_{1} (t) &= Z_{1} (t) + q_{10} (t)\copyright\tau_{0} (t) + \left[ {q_{11.7} (t) + q_{11.7,16} (t)} \right]\copyright\tau_{1} (t) + \left[ {q_{12.8} (t) + q_{12.8,15} (t)} \right]\copyright\tau_{2} (t) + q_{13} (t)\copyright\tau_{3} (t) \hfill \\ \tau_{2} (t) &= Z_{2} (t) + q_{20} (t)\copyright\tau_{0} (t) + \left[ {q_{21.5} (t) + q_{21.5,14} (t)} \right]\copyright\tau_{1} (t) + \left[ {q_{22.6} (t) + q_{22.6,13} (t)} \right]\copyright\tau_{2} (t) + q_{24} (t)\copyright\tau_{4} (t) \hfill \\ \tau_{3} (t) &= Z_{3} (t) + q_{30} (t)\copyright\tau_{0} (t) + q_{31.9} (t)\copyright\tau_{1} (t) + q_{32.10} (t)\copyright\tau_{2} (t) \hfill \\ \tau_{4} (t) &= Z_{4} (t) + q_{40} (t)\copyright\tau_{0} (t) + q_{41.11} (t)\copyright\tau_{1} (t) + q_{42.12} (t)]\copyright\tau_{2} (t), \hfill \\ \end{aligned}$$

(6)

where $Z_{i} (t);i = 0,1,2,3,4$ is the probability of to remain in the upstate without transiting to any other state.

For Model-I

$$\begin{aligned} Z_{0} (t) &= e^{ - (p\eta_{1} + q\eta_{2} )t}, Z_{1} (t) = e^{ - (p\eta_{1} + q\eta_{2})t} \overline{G(t)}, Z_{2} (t) = e^{ - (p\eta_{1} + q\eta_{2})t} \overline{H(t)}, Z_{3} (t) = e^{ - (p\eta_{1} + q\eta_{2})t} \overline{F(t)}, \hfill \\ Z_{4} (t) &= e^{ - (p\eta_{1} + q\eta_{2})t} \overline{F_{1}} (t). \hfill \\ \end{aligned}$$

(7)

For Model-II

$$\begin{aligned} & Z_{0} (t) = e^{{- (p\eta_{1} + q\eta_{2} )t }} , {Z_{1} (t) = e^{{ - (p\eta_{1} + q\eta_{2} )t}} \overline{G(t)} }, {Z_{2} (t) = e^{{ - (p\eta_{1} + q\eta_{2} )t}} \overline{H(t)} },\\&{Z_{3} (t) = e^{{ - (p\eta_{1} + q\eta_{2} )t}} \overline{X(t)}}, Z_{4} (t) = e^{{ - (p\eta_{1} + q\eta_{2} )t}} \overline{Y(t)}.\end{aligned}$$

(8)

Taking Laplace transform on above system of Eqs. (6), (7) and (8) the expression for $\tau_{0}^{*} (s)$ has been derived using Cramer’s rule. The SSA has been given by

$$\begin{aligned} A_{0} (\infty ) & = \mathop {\lim }\limits_{s \to 0} s\tau_{0}^{*} (s) = \frac{{N_{1} }}{{D_{1} }},\quad {\text{where}} \\ N_{1} & = (Z_{0} (t)[(1 - \varepsilon_{11.7} - \varepsilon_{11.7,16} - \varepsilon_{31.9} \varepsilon_{13} )(1 - \varepsilon_{22.6} - \varepsilon_{22.6,13} - \varepsilon_{42.12} \varepsilon_{24} ) - (\varepsilon_{12.8} + \varepsilon_{12.8,15} + \varepsilon_{32.10} \varepsilon_{13} ) \\ & \quad \times (\varepsilon_{21.5} + \varepsilon_{21.5,14} + \varepsilon_{41.11} \varepsilon_{24} )] + (Z_{1} (t) + \varepsilon_{13} Z_{3} (t))[\varepsilon_{01} (1 - \varepsilon_{22.6} - \varepsilon_{22.6,13} - \varepsilon_{42.12} \varepsilon_{24} ) + \varepsilon_{02} (\varepsilon_{21.5} + \\ & \quad \times \varepsilon_{21.5,14} + \varepsilon_{41.11} \varepsilon_{24} )] + (Z_{2} (t) + \varepsilon_{24} Z_{4} (t))[\varepsilon_{01} (\varepsilon_{12.8} + \varepsilon_{12.8,15} + \varepsilon_{32.10} \varepsilon_{13} ) + \varepsilon_{02} (1 - \varepsilon_{11.7} - \varepsilon_{11.7,16} \\ & \quad - \varepsilon_{31.9} \varepsilon_{13} )] \\ D_{1} & = (\mu_{0} (t)[(1 - \varepsilon_{11.7} - \varepsilon_{11.7,16} - \varepsilon_{31.9} \varepsilon_{13} )(1 - \varepsilon_{22.6} - \varepsilon_{22.6,13} - \varepsilon_{42.12} \varepsilon_{24} ) - (\varepsilon_{12.8} + \varepsilon_{12.8,15} + \varepsilon_{32.10} \varepsilon_{13} ) \\ & \quad \times (\varepsilon_{21.5} + \varepsilon_{21.5,14} + \varepsilon_{41.11} \varepsilon_{24} )] + (\mu_{1}^{\prime } (t) + \varepsilon_{13} \mu_{3}^{\prime } (t))[\varepsilon_{01} (1 - \varepsilon_{22.6} - \varepsilon_{22.6,13} - \varepsilon_{42.12} \varepsilon_{24} ) + \varepsilon_{02} (\varepsilon_{21.5} \\ & \quad + \varepsilon_{21.5,14} + \varepsilon_{41.11} \varepsilon_{24} )] + (\mu_{2}^{\prime } (t) + \varepsilon_{24} \mu_{4}^{\prime } (t))[\varepsilon_{01} (\varepsilon_{12.8} + \varepsilon_{12.8,15} + \varepsilon_{32.10} \varepsilon_{13} ) + \varepsilon_{02} (1 - \varepsilon_{11.7} - \varepsilon_{11.7,16} \\ & \quad - \varepsilon_{31.9} \varepsilon_{13} )]. \\ \end{aligned}$$

(9)

8 The busy period analysis of repairman

By probabilistic arguments, semi-Markovian approach and regenerative point technique the recurrence relation for the BPR have been derived. The probability that the server is busy in repairing hardware, software, fault detection of hardware and software, replacement, software up-gradation and hardware repair at any point of time ‘t’ has been denoted by $\prod_{i} (t)$. The recurrence relation of transition from one regenerative state to another regenerative state through via states for BPR are as follows:

$$\begin{aligned} \prod_{0} (t) &= \aleph_{0} (t) + q_{01} (t)\copyright\prod_{1} (t) + q_{02} (t)\copyright\prod_{2} (t) \hfill \\ \prod_{1} (t) &= \aleph_{1} (t) + \prod_{10} (t)\copyright\tau_{0} (t) + \left[ {q_{11.7} (t) + q_{11.7,16} (t)} \right]\copyright\prod_{1} (t) + \left[ {q_{12.8} (t) + q_{12.8,15} (t)} \right]\copyright\prod_{2} (t) + q_{13} (t)\copyright\prod_{3} (t) \hfill \\ \prod_{2} (t) &= \aleph_{2} (t) + q_{20} (t)\copyright\prod_{0} (t) + \left[ {q_{21.5} (t) + q_{21.5,14} (t)} \right]\copyright\prod_{1} (t) + \left[ {q_{22.6} (t) + q_{22.6,13} (t)} \right]\copyright\prod_{2} (t) + q_{24} (t)\copyright\prod_{4} (t) \hfill \\ \prod_{3} (t) &= \aleph_{3} (t) + q_{30} (t)\copyright\prod_{0} (t) + q_{31.9} (t)\copyright\prod_{1} (t) + q_{32.10} (t)\copyright\prod_{2} (t) \hfill \\ \prod_{4} (t) &= \aleph_{4} (t) + q_{40} (t)\copyright\prod_{0} (t) + q_{41.11} (t)\copyright\prod_{1} (t) + q_{42.12} (t)]\copyright\prod_{2} (t). \hfill \\ \end{aligned}$$

(10)

where $\aleph_{i} (t);i = 0,1,2,3,4$ is the probability of to remain busy in any repair activity at any regenerative state without transiting to any other states.

For Model-I

$$\begin{aligned} \aleph_{1} (t) &= e^{{ - (p\eta_{1} + q\eta_{2})t}} \overline{G(t)},{\aleph_{2} (t)} = e^{{ - (p\eta_{1} + q\eta_{2})t}} \overline{H(t)},{\aleph_{3} (t)} = e^{{ - (p\eta_{1} + q\eta_{2} )t}} \overline{F(t)}, \hfill \\ \aleph_{4} (t) &= e^{{ - (p\eta_{1} + q\eta_{2} )t}} \overline{{F_{1} (t)}}. \hfill \\ \end{aligned}$$

(11)

For Model-II

$$\begin{aligned} \aleph_{1} (t) &= e^{ - (p\eta_{1} + q\eta_{2} )t} \overline{G(t)},{\aleph_{2} (t)} = e^{ - (p\eta_{1} + q\eta_{2} )t} \overline{H(t)},{\aleph_{3} (t)} = e^{ - (p\eta_{1} + q\eta_{2} )t} \overline{X(t)}, \hfill \\ \aleph_{4} (t) &= e^{ - (p\eta_{1} + q\eta_{2} )t} \overline{Y(t)}. \hfill \\ \end{aligned}$$

(12)

Taking Laplace transform on above system of Eqs. (10), (11) and (12) the expression for $\prod_{0}^{*} (s)$ has been derived using Cramer’s rule. The SBPR has been given by

$$\begin{aligned} \prod_{0} (\infty ) & = \mathop {\lim }\limits_{s \to 0} s\prod_{0}^{*} (s) = \frac{{N_{2} }}{{D_{1} }}\quad {\text{where}} \\ N_{2} & = \left( {\aleph_{1} (t) + \varepsilon_{13} \aleph_{3} (t)} \right)\left[ {\varepsilon_{01} (1 - \varepsilon_{22.6} - \varepsilon_{22.6,13} - \varepsilon_{42.12} \varepsilon_{24} ) + \varepsilon_{02} (\varepsilon_{21.5} + \varepsilon_{21.5,14} + \varepsilon_{41.11} \varepsilon_{24} )} \right] \\ & \quad + \left( {\aleph_{2} (t) + \varepsilon_{24} \aleph_{4} (t)} \right)\left[ {\varepsilon_{01} (\varepsilon_{12.8} + \varepsilon_{12.8,15} + \varepsilon_{32.10} \varepsilon_{13} ) + \varepsilon_{02} (1 - \varepsilon_{11.7} - \varepsilon_{11.7,16} - \varepsilon_{31.9} \varepsilon_{13} )} \right]. \\ \end{aligned}$$

(13)

9 Expected number of visits by repairman (ENVR)

By probabilistic arguments, semi-Markovian approach and regenerative point technique the recurrence relation for the ENVR have been derived. The ENV by repairman during time interval (0, t] has been denoted by $\Im_{i} (t)$. The recurrence relation of transition from one regenerative state to another regenerative state through via states for ENVR are as follows:

$$\begin{aligned} \Im_{0} (t) = Q_{01} (t)\copyright[1 + \Im_{1} (t)] + Q_{02} (t)\copyright[1 + \Im_{2} (t)] \hfill \\ \Im_{1} (t) = Q_{10} (t)\copyright\Im_{0} (t) + [Q_{11.7} (t) + Q_{11.7,16} (t)]\copyright\Im_{1} (t) + [Q_{12.8} (t) + Q_{12.8,15} (t)]\copyright\Im_{2} (t) + Q_{13} (t)\copyright\Im_{3} (t) \hfill \\ \Im_{2} (t) = Q_{20} (t)\copyright\Im_{0} (t) + [Q_{21.5} (t) + Q_{21.5,14} (t)]\copyright\Im_{1} (t) + [Q_{22.6} (t) + Q_{22.6,13} (t)]\copyright\Im_{2} (t) + Q_{24} (t)\copyright\Im_{4} (t) \hfill \\ \Im_{3} (t) = Q_{30} (t)\copyright\Im_{0} (t) + Q_{31.9} (t)\copyright\Im_{1} (t) + Q_{32.10} (t)\copyright\Im_{2} (t) \hfill \\ \Im_{4} (t) = Q_{40} (t)\copyright\Im_{0} (t) + Q_{41.11} (t)\copyright\Im_{1} (t) + Q_{42.12} (t)]\copyright\Im_{2} (t). \hfill \\ \end{aligned}$$

(14)

Taking Laplace transform on above system of Eq. (14), the expression for $\prod_{0}^{*} (s)$ has been derived using Cramer’s rule. The SBPR has been given by

$$\begin{aligned} \Im_{0} (\infty ) & = \mathop {\lim }\limits_{s \to 0} s\Im_{0}^{*} (s) = \frac{{N_{3} }}{{D_{1} }}\quad {\text{where}} \\ N_{3} & = (\varepsilon_{01} + \varepsilon_{02} )[(1 - \varepsilon_{11.7} - \varepsilon_{11.7,16} - \varepsilon_{31.9} \varepsilon_{13} )(1 - \varepsilon_{22.6} - \varepsilon_{22.6,13} - \varepsilon_{42.12} \varepsilon_{24} ) - (\varepsilon_{12.8} + \varepsilon_{12.8,15} + \varepsilon_{32.10} \varepsilon_{13} ) \\ & \quad \times (\varepsilon_{21.5} + \,\varepsilon_{21.5,14} + \varepsilon_{41.11} \varepsilon_{24} )] \\ \end{aligned}$$

(15)

10 The cost-benefit analysis

The expected steady state profit incurred to the computing system per unit time for both models is given by the following functions: For Models-I and II $CBA = (\psi_{0} )SSA - (\psi_{1} )BPR - (\psi_{2} )ENVR\quad \& \quad CBA = (\psi_{0} )SSA - (\psi_{1} )BPR - (\psi_{2} )ENVR - \psi_{3} ,$where $\psi_{0}$ the revenue generated by computing system per unit up-time, $\psi_{1}$ the outlay on repairman for performing repair activities on per failure of unit, $\psi_{2}$ the outlay on per visit of regular server; $\psi_{3}$ The fixed outlay on expert server.

11 Empirical study

The empirical study of both stochastic models have been carried out by considering all the time dependent random variables as exponential distributed (Table 1). For a particular set of values of the parameters, the numerical and graphical results have been depicted with respect to fault detection rate of hardware. The initial values has been taken as follows:

Table 1 Models state description

Table 2 Mean time to system failure (in time units) vs. fault detection rate

For Model-I: denoted by $\varOmega$$\varOmega :a = 0.3;\;b = 0.7;\;p = 0.6;\;q = 0.4;\;c = 0.25;\;d = 0.75;\;\beta = 0.04;\;\lambda = 0.9;\;\gamma = 0.8;\;\eta_{1} = 0.005;\;\eta_{2} = 0.008.$For Model-II: denoted by $\varSigma$

$$\varSigma :a = 0.3;\;b = 0.7;\;p = 0.6;\;q = 0.4;\;c = 0.25;\;d = 0.75;\;\beta = 0.04;\;\lambda_{1} = 1.9;\;\gamma_{1} = 2.1;\;\eta_{1} = 0.005;\;\eta_{2} = 0.008.$$

From Table 2, we analyze that mean time to system failure increases with respect to fault detection rate. By making a variation in software failure rate and hardware failure rate, i.e., $\eta_{2} = 0.008\quad {\text{to}}\quad \eta_{2} = 0.23$; $\eta_{1} = 0.005\quad {\text{to}}\quad \eta_{1} = 0.12$, respectively the mean time to system failure sharply declined. If the chances of fault detection by regular repairman is more than the mean time to system increased. If $\alpha > 0.01$ and chances of software failure is more than mean time to system failure decreased. The mean time to system failure rapidly increased by increasing the software fault detection rate, i.e., $\beta = 0.04\quad {\text{to}}\quad \beta = 0.5$.

From Table 3, we analyze that steady state availability of the system increases with respect to fault detection rates of hardware as well as software. But any variation in software failure rate and hardware failure rate, i.e., $\eta_{2} = 0.008\quad {\text{to}}\quad \eta_{2} = 0.23$; $\eta_{1} = 0.005\quad {\text{to}}\quad \eta_{1} = 0.12$, respectively resulted in the sharp decline in the availability of the system. If the chances of fault detection of hardware by regular repairman is more than the system availability increased. As soon as the chances of software failure increased the availability decreased.

Table 3 Steady state availability vs. fault detection rate of hardware

From Table 4, we analyze that expected profit generated by the system increases with respect to fault detection rates of hardware as well as software. But any variation in software failure rate and hardware failure rate, i.e., $\eta_{2} = 0.008\quad {\text{to}}\quad \eta_{2} = 0.23$; $\eta_{1} = 0.005\quad {\text{to}}\quad \eta_{1} = 0.12$, respectively resulted in the sharp decline in the availability of the system. For $\alpha \, < \, 0.02$ and $\eta_{2} = 0.23$ system operates in loss. If the chances of fault detection of hardware by regular repairman is more than the system profit increased. As soon as the chances of software failure increased the expected profit generated by system decreased.

Table 4 Expected profit (in rupees) vs. fault detection rate of hardware

From Table 5, we analyze that mean time to system failure increases with respect to fault detection rate. By making a variation in software failure rate and hardware failure rate, i.e., $\eta_{2} = 0.008\quad {\text{to}}\quad \eta_{2} = 0.23$; $\eta_{1} = 0.005\quad {\text{to}}\quad \eta_{1} = 0.12$, respectively the mean time to system failure sharply declined. If the chances of fault detection by regular repairman is more than the mean time to system increased. If $\alpha > 0.01$ and chances of software failure is more than mean time to system failure decreased. The mean time to system failure rapidly increased by increasing the software fault detection rate, i.e., $\beta = 0.04\quad {\text{to}}\quad \beta = 0.5$.

Table 5 Mean time to system failure (in time units) vs. fault detection rate

From Table 6, we analyze that steady state availability of the system increases with respect to fault detection rates of hardware as well as software. But any variation in software failure rate and hardware failure rate, i.e.,$\eta_{2} = 0.008\quad {\text{to}}\quad \eta_{2} = 0.23$; $\eta_{1} = 0.005\quad {\text{to}}\quad \eta_{1} = 0.12$, respectively resulted in the sharp decline in the availability of the system. If the chances of fault detection of hardware by regular repairman is more than the system availability increased. As soon as the chances of software failure increased the availability decreased.

Table 6 Steady state availability vs. fault detection rate of hardware

From Table 7, we analyze that expected profit generated by the system increases with respect to fault detection rates of hardware as well as software. But any variation in software failure rate and hardware failure rate, i.e., $\eta_{2} = 0.008\quad {\text{to}}\quad \eta_{2} = 0.23$; $\eta_{1} = 0.005\quad {\text{to}}\quad \eta_{1} = 0.12$, respectively resulted in the sharp decline in the availability of the system. For $\alpha \, < \, 0.03,\quad \eta_{2} = 0.23$ and $\alpha \, < \, 0.02,\quad \eta_{1} = 0.12$ system operates in loss. If the chances of fault detection of hardware by regular repairman is more than the system profit increased. As soon as the chances of software failure increased the expected profit generated by system decreased.

Table 7 Expected profit (in rupees) vs. fault detection rate of hardware

12 Conclusion

In the above section, empirical study for two stochastic models of a computing machine has been carried out using the concept of fault detection and expert server. The following results have been depicted:

• By increasing fault detection rate of hardware and software components, the system can be made more available and profitable.

• Systems should be operated under such conditions that chances of hardware and software failures can be decreased.

• From Tables 2 and 5, we find that in the presence of expert server the mean time to system failure increased.

• From Tables 3 and 6 and Figs. 1 and 2, we find that if the rate of hardware and software failure increase then the system availability slightly decreased because it takes the unit under repair until the unit repaired while the regular server replace the unit immediately.

  Fig. 1

  

  Availability analysis vs. fault detection rate (Model-I)

  Fig. 2

  

  Availability analysis vs. fault detection rate (Model-II)

• From Tables 4 and 7 and Figs. 3 and 4, we find that the profit of Model-I is more in comparison to model-II in which expert repairman is called of hardware and software repairs. So, visits of expert server creates extra financial burden.

  Fig. 3

  

  Profit analysis vs. fault detection rate (Model-I)

  Fig. 4

  

  Profit analysis vs. fault detection rate (Model-II)

Finally, we conclude that a computing machine can be made more available and profit by apply proper fault detection policies, controlling hardware and software failures and giving the preference to replacement of hardware and software components by regular repairman in place of repair by expert repairman when fault is not properly detected and its repair is not feasible by regular repairman.