Availability, MTTF and cost analysis of a system having two units in series configuration with controller

Abstract

The paper deals with the availability analysis of a system, which consists of two subsystems namely subsystem-1 and subsystem-2. Subsystem-1 is working under k-out of n: good configuration while subsystem-2 has two identical units connected in parallel configuration. A controller is attached with each subsystem for proper functioning of the system. All failure rates are constant but repairs follow general and exponential distributions. The transitional state probabilities, asymptotic behavior and some characteristics such as reliability, availability, MTTF and the cost effectiveness of the system have been evaluated with the help of supplementary variable technique, Laplace transformations and copula methodology. At last, some particular cases and numerical examples have been taken to describe the model.

1 Introduction

The reliability of a system and its maintenance employs an increasing important issue in modern day electronic, manufacturing and industrial systems. In real life, one comes across many complexities of modern day engineering systems. Earlier different researchers have discussed the reliability characteristics of systems assuming different types of failures and one way of repair between successive transitional states. To cite a few, (Govil 1974) studied operational behaviour of a complex system. Ref. (Gupta and Sharma 1993) discussed reliability measures of two duplex-unit standby system. Ref. (Singh et al. 1992, 2001) worked on reliability measures with head-of-line repair policy and analyzed two units cold standby system assuming various parameters. Zhang et al. (2010) and Verma et al. (2010) have studied reliability models for systems with internal and external redundancy.

Keeping facts like complexity of advanced technology and modern demand of electronic equipments, one needs to incorporate the study of controller as discussed by Ogata (2009), which is used in various electronic devices and systems to improve productivity as well as performance that relieves the drudgery of many routine repetitive manual operations. Nonetheless, engineers and scientists must now have a good understanding of this field. Controller is a device that monitors the operational conditions of given dynamical systems. The operational conditions are typically revered to as output variables of the system, which function by adjusting the certain input variables. The concept of using controller is new for scientists and engineers. Since 1980 to the present, developments in the modern control theory centered around robust control and associated topics. At present, the digital computers are used as integral part of control systems. The controllers are not only used in engineering systems (in industry, they are used for electricity or pressurize fluid such as oil or air as power sources etc.) but also for non-engineering systems like biological, biomedical, economic and socioeconomic systems. They are used in various complex systems to control output variables such as speed controller (controlling centrifugal force), temperature (control temperature of furnace), thermostat controller (controlling room temperature) and many other tasks. Since they are widely used in industry now a days and hence classified according to their control actions as : (i) to position or on–off controllers (ii) proportional controllers (iii) integral controllers (iv) proportional-plus integral controllers (v) proportional-plus-derivative controllers (vi) proportional-plus-integral-plus-derivative controllers. Controllers may also be classified according to the kind of power employed in operations such as pneumatics controller, hydraulic controllers, or electronic controllers. The use of controller in plant is based on the nature of plant and operational conditions, including such considerations as safety, cost, availability, reliability, accuracy, weight and size.

Apart from the importance of incorporation of controller, human factors play a very important role during the design, production and maintenance phases of a system. Human error or failure may be defined as the failure to perform a specific task that could lead to disruption of scheduled operations or result in damage to property and equipment. There are various reasons for the occurrence of human errors such as inadequate work area, inadequate training, poor equipment design, high noise level, improper tools and poorly written equipment maintenance and operating procedures (Dhillon and Yang 1992, 1993; Dhillon and Liu 2006; Giuntini 2000).

Keeping the above facts in view, authors have considered a system, which consists of two subsystems viz. subsystem-1 and subsystem-2. The subsystem-1 follows k-out of-n: good configuration and subsystem-2 has two independent identical units in parallel configuration. Both subsystems are connected in series and each linked with a controller for the proper functioning of the system. The considered system can fail in following ways:

• (i) More than k units of subsystem-1 fail but both units of subsystem-2 are in good working condition.

• (ii) Human error occurs in the system.

• (iii) Controller of the subsystem-1 fails.

• (iv) Controller of the subsystem-2 fails.

• (v) Both units of the subsystem-2 fail.

The system will be in degraded state due to partial failure that can occur in following situations:

• (i) All units of subsystem-1 are good and one unit of subsystem-2 fails.

• (ii) At least k units of subsystem-1 are good and one unit of subsystem-2 fails.

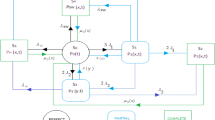
In the past, researchers (Ram and Singh 2008, 2009, 2010) have considered reliability and MTTF of complex systems, with different types of failures and one type of repair. However, in their study one of the important aspects of modern engineered system, i.e., controller is not included. When this possibility exists, reliability of the system can be analysed with the help of copula (Melchiori 2003; Nelsen 2006). Therefore, in contrast to the earlier models, here authors have considered a model in which they tried to address a problem where two different repair facilities are available between adjacent states i.e., the initial state and complete failed state incorporating copula. All failure rates are constant but repairs follow general and exponential distributions. In the present paper, S₀ is a state where the system is in good working condition. S₁, S₃ and S₄ are the states where the system is in partially failed or degraded state and S₂, S₅, S₆, S₇, S₈ and S₉ are the states where the system is in completely failure mode. When the system is in degraded mode, the general repair is employed, but whenever the system is in complete failure mode, it is repaired by using joint distribution with the help of Gumbel-Hougaard family copula.

The system is studied by using the supplementary variable technique Cox (1955) and Oliveira et al. (2005), Laplace transformation and Gumbel-Hougaard family of copula to obtain various reliability measures such as, transitional state probabilities, steady state probabilities, i.e., asymptotic behaviour, availability, mean time to failure and cost analysis. At last, some particular cases of the system have been analysed to highlight the different possibilities of the system.

2 Brief introduction of Gumbel-Hougaard family copula

A number of authors including Nelsen (2006) have studied the family of copulas extensively. The Gumbel-Hougaard family copula is defined as:

$$ C_{\theta } (u_{1} ,u_{2} ) = \exp ( - (( - \log u_{1} )^{\theta } + ( - \log u_{2} )^{\theta } )^{{{1 \mathord{\left/ {\vphantom {1 \theta }} \right. \kern-\nulldelimiterspace} \theta }}} ),\quad 1 \le \theta \le \infty $$

For θ = 1 the Gumbel-Hougaard copula models independence, for θ → ∞ it converges to comonotonicity.

3 State description

State	State description
S0	All units of subsystem-1 and 2 are in good working condition.
S1	k units of subsystem-1 are in good working condition.
S2	System has completely failed due to failure of (k + i) units of subsystem-1.
S3	One unit of subsystem-2 has failed and the system is in degraded state.
S4	All units of subsystem-1 are in good state and one unit of subsystem-2 has failed.
S5	k units of subsystem-1 are good but both units of subsystem-2 have failed. The system is in completely failed state.
S6	All unit of subsystem-1 are good but both units of subsystem-2 have failed. The system is in completely failed state.
S7	System has failed due to the failure of controller in subsystem-1.
S8	System has failed due to the failure of controller in subsystem-2.
S9	System has completely failed due to human error.

4 Assumptions

The following assumptions are taken throughout the discussion of the model:

• (i) Initially the system is in good state and all the units of subsystems-1 and 2 are in good working condition.

• (ii) The subsystem-1 works successfully until at least k units of it are in good working condition.

• (iii) Subsystem-1 fails if more than k units fail.

• (iv) Subsystem-2 works successfully if at least one unit is in good state.

• (v) Subsystem-2 can be repaired when one unit fails or both units fail and controller fails.

• (vi) All failure rates are constant and follow negative exponential distribution.

• (vii) Degraded system is repaired by a general time distribution.

• (viii) In the repairing of complete failed state Gumbel-Hougaard family copula is applied.

• (ix) Repaired system works like a new system and repair did not damage anything.

• (x) Only one change is allowed at a time in the transitions.

The state transition diagram of model is shown in Fig. 1, and the notations pertaining to the model is shown in Table 1.

Fig. 1

State transition diagram of model

Table 1 Notations

5 Formulation of mathematical model

By probability of considerations and continuity arguments, we can obtain the following set of difference differential equations governing the present mathematical model

$$ \begin{aligned} \left[ {\frac{\partial }{\partial t} + \lambda_{1} + \lambda_{C} + \lambda_{CB} + \lambda_{h} + 2\lambda } \right]P_{0} (t) & = \int\limits_{0}^{\infty } {\phi (x)P_{1} (x,t)} {{dx}} \\ + & \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{2} } (x,t){{dx}} + \int\limits_{0}^{\infty } {\phi (x)P_{4} } (x,t){{dx}} \\ + & \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{5} } (x,t){{dx}} \\ + & \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{6} } (x,t){{dx}} \\ + & \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{7} } (x,t){{dx}} \\ + & \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{8} } (x,t){{dx}} \\ + & \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{9} } (x,t){{dx}} \\ \end{aligned} $$

(1)

$$ \left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \lambda_{2} + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} + 2\lambda + \phi (x)} \right]P_{1} (x,t) = 0 $$

(2)

$$ \left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]P_{2} (x,t) = 0 $$

(3)

$$ \left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} + \lambda + \phi (x)} \right]P_{3} (x,t) = 0 $$

(4)

$$ \left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} + \lambda + \phi (x)} \right]P_{4} (x,t) = 0 $$

(5)

$$ \left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]P_{5} (x,t) = 0 $$

(6)

$$ \left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]P_{6} (x,t) = 0 $$

(7)

$$ \left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]P_{7} (x,t) = 0 $$

(8)

$$ \left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]P_{8} (x,t) = 0 $$

(9)

$$ \left[ {\frac{\partial }{\partial t} + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]P_{9} (x,t) = 0 $$

(10)

The method of formation of Eqs. 1–10 has been given in Appendix 1.

The boundary conditions of designed system are defined as:

The state transition probability of the system in a state = failure rate × probability of the previous state. Therefore

$$ P_{1} (0,t) = \lambda_{1} P_{0} (t) + \int\limits_{0}^{\infty } {\phi (x)} P_{3} (x,t){{dx}} $$

(11)

$$ P_{2} (0,t) = \lambda_{2} P_{1} (t) $$

(12)

$$ P_{3} (0,t) = 2\lambda_{1} P_{0} (t) $$

(13)

$$ P_{4} (0,t) = 2\lambda P_{0} (t) $$

(14)

$$ P_{5} (0,t) = 2\lambda^{2} P_{1} (0,t) $$

(15)

$$ P_{6} (0,t) = 2\lambda^{2} P_{0} (t) $$

(16)

$$ P_{7} (0,t) = \lambda_{{C}} [P_{0} (t) + P_{1} (0,t) + P_{3} (0,t) + P_{4} (0,t)] $$

(17)

$$ P_{8} (0,t) = \lambda_{{CB}} [P_{0} (t) + P_{1} (0,t) + P_{3} (0,t) + P_{4} (0,t)] $$

(18)

$$ P_{9} (0,t) = \lambda_{{h}} [P_{0} (t) + P_{1} (0,t) + P_{3} (0,t) + P_{4} (0,t)] $$

(19)

Initials condition:

$$ P_{0} (0) = 1\;{\text{and other state probabilities are zero at }}t \, = \, 0 $$

(20)

In the above equations, t and x both represent times. The supplementary variable x, which represents the elapsed repair time of the system, varies only when the system is in degraded or failed state, and its rate of variation is exactly equal to that of the schedule time, represented by t.

6 Solution of the model

Taking Laplace transformation of Eqs. 1–19 and using Eq. 20, we obtain

$$ \begin{aligned} \left[ {s + \lambda_{1} + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} + 2\lambda } \right]\bar{P}_{0} (s) & = \left[ {1 + \int\limits_{0}^{\infty } {\bar{P}_{1} (x,s)\phi } (x){{dx}} + \int\limits_{0}^{\infty } {\bar{P}_{2} } (x,s)\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } {{dx}}} \right. \\ + & \int\limits_{0}^{\infty } {\bar{P}_{4} (x,s)\phi } (x){{dx}} + \int\limits_{0}^{\infty } {\bar{P}_{5} } (x,s)\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } {{dx}} \\ + & \int\limits_{0}^{\infty } {\bar{P}_{6} } (x,s)\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } {{dx}} + \int\limits_{0}^{\infty } {\bar{P}_{7} } (x,s)\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } {{dx}} \\ + & \left.\int\limits_{0}^{\infty } {\bar{P}_{8} } (x,s)\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } {{dx}} + \int\limits_{0}^{\infty } {\bar{P}_{9} } (x,s)\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } {{dx}}\right] \\ \end{aligned} $$

(21)

$$ \left[ {s + \frac{\partial }{\partial x} + \lambda_{2} + 2\lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} + \phi (x)} \right]\bar{P}_{1} (x,s) = 0 $$

(22)

$$ \left[ {s + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]\bar{P}_{2} (x,s) = 0 $$

(23)

$$ \left[ {s + \frac{\partial }{\partial x} + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} + \phi (x)} \right]\bar{P}_{3} (x,s) = 0 $$

(24)

$$ \left[ {s + \frac{\partial }{\partial x} + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} + \phi (x)} \right]\bar{P}_{4} (x,s) = 0 $$

(25)

$$ \left[ {s + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]\bar{P}_{5} (x,s) = 0 $$

(26)

$$ \left[ {s + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]\bar{P}_{6} (x,s) = 0 $$

(27)

$$ \left[ {s + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]\bar{P}_{7} (x,s) = 0 $$

(28)

$$ \left[ {s + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]\bar{P}_{8} (x,s) = 0 $$

(29)

$$ \left[ {s + \frac{\partial }{\partial x} + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } } \right]\bar{P}_{9} (x,s) = 0 $$

(30)

$$ \bar{P}_{1} (0,s) = \lambda_{1} \bar{P}_{0} (s) + \int\limits_{0}^{\infty } {\phi (x)} \bar{P}_{3} (x,s){{dx}} $$

(31)

$$ \bar{P}_{2} (0,s) = \lambda_{2} \bar{P}_{1} (0,s) $$

(32)

$$ \bar{P}_{3} (0,s) = 2\lambda \bar{P}_{0} (0,s) $$

(33)

$$ \bar{P}_{4} (0,s) = 2\lambda \bar{P}_{0} (s) $$

(34)

$$ \bar{P}_{5} (0,s) = 2\lambda^{2} \bar{P}_{0} (s) $$

(35)

$$ \bar{P}_{6} (0,s) = 2\lambda^{2} \bar{P}_{0} (s) $$

(36)

$$ \bar{P}_{7} (0,s) = \lambda_{{C}} [\bar{P}_{0} (s) + \bar{P}_{1} (0,s) + \bar{P}_{3} (0,s) + \bar{P}_{4} (0,s)] $$

(37)

$$ \bar{P}_{8} (0,s) = \lambda_{{CB}} [\bar{P}_{0} (s) + \bar{P}_{1} (0,s) + \bar{P}_{3} (0,s) + \bar{P}_{4} (0,s)] $$

(38)

$$ \bar{P}_{9} (0,s) = \lambda_{{h}} [\bar{P}_{0} (s) + \bar{P}_{1} (0,s) + \bar{P}_{3} (0,s) + \bar{P}_{4} (0,s)] $$

(39)

Solving (21–30) with the help of (31–39), one can get the transition state probabilities of the system as:

$$ \, \bar{P}_{0} (s) = \frac{1}{{{{D}}(s)}} $$

(40)

$$ \, \bar{P}_{1} (s) = \frac{1}{{{{D}}(s)}}\left( {\lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )}}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}}} \right)\left( {\frac{{(1 - S_{\phi } (s + \lambda_{2} + 2\lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} ))}}{{(s + \lambda_{2} + 2\lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )}}} \right) $$

(41)

$$ \, \bar{P}_{2} (s) = \frac{{\lambda_{2} }}{{{{D}}(s)}}\left( {\lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )}}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}}} \right)\left( {\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s}} \right) $$

(42)

$$ \, \bar{P}_{3} (s) = \frac{1}{{{{D}}(s)}}\left( {\frac{{2\lambda \lambda_{1} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )} \right)}}} \right)\left( {\frac{{(1 - S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} ))}}{{(s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )}}} \right) $$

(43)

$$ \, \bar{P}_{4} (s) = \frac{2\lambda }{D(s)}\left\{ {\frac{{(1 - S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{{h}} )}}{{(s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{{h}} )}}} \right\} $$

(44)

$$ \, \bar{P}_{5} (s) = \frac{{2\lambda^{2} }}{{{{D}}(s)}}\left( {\lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )}}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}}} \right)\left( {\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s}} \right) $$

(45)

$$ \, \bar{P}_{6} (s) = \frac{{2\lambda^{2} }}{{{{D}}(s)}}\left( {\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s}} \right) $$

(46)

$$ \, \bar{P}_{7} (s) = \left( {\frac{{\lambda_{C} }}{D(s)}\left( {1 + \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} ) + 2\lambda \lambda_{1} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{CB} + \lambda_{{h}} )} \right)}} + 2\lambda } \right)} \right)\left( {\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s}} \right) $$

(47)

$$ \, \bar{P}_{8} (s) = \left( {\frac{{\lambda_{CB} }}{{{{D}}(s)}}\left( {1 + \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} ) + 2\lambda \lambda_{1} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}} + 2\lambda } \right)} \right)\left( {\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s}} \right) $$

(48)

$$ \, \bar{P}_{9} (s) = \left( {\frac{{\lambda_{h} }}{D(s)}\left( {1 + \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda_{2} + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} ) + 2\lambda \lambda_{1} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda_{2} + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}} + 2\lambda } \right)} \right)\left( {\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s}} \right) $$

(49)

where

$$ \begin{aligned} {{D}}(s) & = s + \lambda_{1} + \lambda_{{C}} + \lambda_{{h}} + \lambda_{{CB}} + 2\lambda \\ - & \left( {\lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + {{\uplambda}}_{{h}} )}}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}}} \right)\bar{S}_{\phi } (s + \lambda_{1} + \lambda_{{C}} + \lambda_{{h}} + \lambda_{{CB}} + 2\lambda ) \\ - & \left( {\lambda_{2} \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )}}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}}} \right)S_{{\mu_{0} }} (x) + 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{CB} + \lambda_{h} ) \\ - & 2\lambda^{2} \left( {\lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )}}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}}} \right)S_{{\mu_{0} }} (x) \\ - & \lambda_{h} \left( {1 + \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} ) + 2\lambda \lambda_{{}} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}} + 2\lambda } \right)S_{{\mu_{0} }} (x) \\ - & \lambda_{C} \left( {1 + \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} ) + 2\lambda \lambda_{{}} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}} + 2\lambda } \right)S_{{\mu_{0} }} (x) \\ - & \lambda_{CB} \left( {1 + \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} ) + 2\lambda \lambda_{{}} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )} \right)}} + 2\lambda } \right)S_{{\mu_{0} }} (x) \\ \end{aligned} $$

The information related to solution of Eqs. 21–30 is given in Appendix 2.

The Laplace transformations of the probabilities that the system is in up (i.e., either good or degraded state) and failed state at any time are as follows:

$$ \begin{aligned} \bar{P}_{up} (s) & = \bar{P}_{0} (s) + \bar{P}_{1} (s) + \bar{P}_{3} (s) + \bar{P}_{4} (s) \\ \, & = \frac{1}{{{{D}}(s)}}\left[ {1 + \frac{{\lambda_{1} (1 - S_{\phi } (s + \lambda_{2} + 2\lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} ))}}{{(s + \lambda_{2} + 2\lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )}} + \left\{ {\frac{{(1 - S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}})}}{{(s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )}}} \right\}} \right. \\ + & \, \left. {\left\{ {\frac{{(1 - S_{\phi } (s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} ))}}{{(s + \lambda + \lambda_{{C}} + \lambda_{{CB}} + \lambda_{{h}} )}}} \right\}} \right] \\ \end{aligned} $$

(50)

$$ \begin{aligned} \, \bar{P}_{failed} (s) & = \bar{P}_{2} (s) + \bar{P}_{5} (s) + \bar{P}_{6} (s) + \bar{P}_{7} (s) + \bar{P}_{8} (s) + \bar{P}_{9} (s) \\ & = \, \frac{{\lambda_{1} \lambda_{2} }}{{{{D}}(s)}}\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s} + \frac{{2\lambda_{1} \lambda^{2} }}{{{{D}}(s)}}\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s} \\ + & \frac{{\lambda^{2} }}{{{{D}}(s)}}\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s} \\ + & \frac{{\lambda_{C} (1 + \lambda_{1} )(1 + 2\lambda )}}{{{{D}}(s)}}\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s} + \frac{{\lambda_{CB} (1 + \lambda_{1} )(1 + 2\lambda )}}{{{{D}}(s)}}\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s} \\ + & \frac{{\lambda_{h} (1 + \lambda_{1} )(1 + 2\lambda )}}{{{{D}}(s)}}\frac{{(1 - S_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s))}}{s} \\ \end{aligned} $$

(51)

7 Asymptotic behaviour of the system

In long run as t tends to infinity, the state transition probability of system can be obtained using Abel’s lemma in Laplace transformation i.e. $\mathop {\lim }\limits_{t \to \infty } F(t) = \mathop {\lim }\limits_{s \to 0} sF(s) = F(say)$, provided that the limit of the right hand side exists. Time independent i.e. steady state probabilities of the system in different states are given by

$$ P_{0} = \frac{1}{{{{D}}^{ '} (0)}} $$

(52)

$$ P_{1} = \frac{{\lambda_{1} }}{{{{D}}^{ '} (0)(\lambda_{2} + 2\lambda + \lambda_{{c}} + \lambda_{{CB}} + \lambda_{{h}} + \phi )}} $$

(53)

$$ P_{2} = \frac{{\lambda_{1} \lambda_{2} }}{{{{D}}^{ '} (0)(\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } )}} $$

(54)

$$ P_{3} = \frac{{2\lambda \lambda_{1} }}{{{{D}}^{ '} (0)(\lambda + \lambda_{{c}} + \lambda_{{CB}} + \lambda_{{h}} + \phi )}} $$

(55)

$$ P_{4} = \frac{2\lambda }{{(\lambda + \lambda_{{c}} + \lambda_{{CB}} + \lambda_{{h}} + \phi )}}\frac{1}{{{\text D}}^{ '} (0)} $$

(56)

$$ P_{5} = \frac{{2\lambda_{1} \lambda^{2} }}{{{{D}}^{ '} (0)(\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } )}} $$

(57)

$$ P_{6} = \frac{{2\lambda^{2} }}{{{{D}}^{ '} (0)(\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } )}} $$

(58)

$$ P_{7} = \frac{{\lambda_{C} (1 + \lambda_{1} )(1 + 2\lambda )}}{{{{D}}^{ '} (0)(\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } )}} $$

(59)

$$ P_{8} = \frac{{\lambda_{CB} (1 + \lambda_{1} )(1 + 2\lambda )}}{{{{D}}^{ '} (0)(\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } )}} $$

(60)

$$ P_{9} = \frac{{\lambda_{h} (1 + \lambda_{1} )(1 + 2\lambda )}}{{{{D}}^{ '} (0)(\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } )}} $$

(61)

where

$$ {{D}}^{ '} (0) = \frac{{d}}{{ds}}{{D}}(s),\quad as\;s \to 0 $$

.

The more information related to asymptotic behaviour of the system is given in Appendix 3.

8 Particular cases

8.1 Availability

When repair follows exponential distribution. Setting

$\bar{S}_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s) = \frac{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }{s + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } },\,\bar{S}_{\phi } (s) = \frac{\phi }{s + \phi }$ in Eq. 50, fixing the values of different parameters as λ_C = 0.01, λ_CB = 0.02, λ_h = 0.001, λ = 0.05, λ₁ = 0.05, λ₂ = 0.06, $\phi = { 1}, \, \theta \, = { 1},x = { 1}$ and then taking inverse Laplace transform, one get P _up (t) as

$$ P_{up} (t) = - 0.0001485702 e^{( - 1.071000t)} - 0.03408091688 e^{( - 1.21100t)} - 0.003516569 e^{( - 2.70956548t)} \\ + 0.1235797 e^{( - 1.2230648t)} + 0.00625443789 e^{( - 1.089127739t)} - 0.005839177 e^{( - 1.08599944t)} \\ + 0.0002895 e^{( - 1.06672t)} + 0.9134666 e^{( - 0.04381t)} \\ $$

(62)

To observe the variation pattern of P _up (t) with respect to change in λ₁ and λ₂ substitute λ₁ = 0.06, 0.07, 0.08, 0.09 corresponding to λ₂ = 0.07, 0.08, 0.09, 0.10 respectively in (50) and take inverse Laplace transform provided other parameters remain same. For, t = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 units of time, one may obtain the different values of P _up (t) as shown in Table 2 and the corresponding graph is shown in Fig. 2.

Table 2 Time versus availability

Fig. 2

Time versus availability

8.2 Mean time to failure (MTTF)

Setting $\bar{S}_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} (s) = \frac{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }}{{s + \exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }},\,\,\bar{S}_{\phi } (s) = \frac{\phi }{s + \phi }$ and taking all repairs to zero in Eq. 50, one can obtain the MTTF as given below:

$$ {\text{MTTF}} = \mathop {\lim }\limits_{s \to 0} \bar{P}_{up} (s) = \frac{1}{{(\lambda_{1} + \lambda_{C} + \lambda_{CB} + \lambda_{h} + 2\lambda )}} $$

(63)

Setting λ_C = 0.01, λ_CB = 0.02, λ_h = 0.001, λ = 0.05 and varying λ₁ as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09 in (63) one may obtain the variations of MTTF with respect to λ₁.

Setting λ₁ = 0.05, λ_CB = 0.02, λ_h = 0.001, λ = 0.05 and varying λ_c as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09 in (63) one may obtain the changes of MTTF with respect to λ_c.

Setting λ₁ = 0.05, λ_C = 0.01, λ_h = 0.001, λ = 0.05 and varying λ_CB as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09 in 63 one can get the variations of MTTF with respect to λ_CB.

Setting λ₁ = 0.05, λ_C = 0.01, λ_CB = 0.02, λ = 0.05 and varying λ_h as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09 in (63) one may obtain the changes of MTTF with respect to λ_h.

Setting λ₁ = 0.05, λ_C = 0.01, λ_CB = 0.02, λ_h = 0.001 and varying λ as 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09 in (63) one may obtain the variation of MTTF with respect to λ.

The combined numerical values of MTTF with respect to λ₁, λ_C, λ_CB, λ_h and λ have been shown in Table 3 and corresponding graphs are displayed in Fig. 3.

Table 3 MTTF versus failure rates

Fig. 3

MTTF versus failure rates

8.3 Cost analysis

Let the service facility be always available, then expected profit during the interval [0, t] is given by

$$ E_{p} (t) = K_{1} \int\limits_{0}^{t} {P_{up} (t)} dt - K_{2} t $$

(64)

Assuming the values of various parameters as λ₁ = 0.05, λ_h = 0.001, λ₂ = 0.06, λ_C = 0.01, λ_CB = 0.02, λ = 0.05, mean time to repair $\phi (x) = 1,\,x = 1,\theta = 1,\phi (x) = 1$ and setting $\bar{S}_{{_{{\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } }} }} (s) = \frac{{\exp [x^{\theta } + \{ \log \phi_{A} (x)\}^{\theta } ]^{1/\theta } }}{{s + \exp [x^{\theta } + \{ \log \phi_{A} (x)\}^{\theta } ]^{1/\theta } }},\,\bar{S}_{\phi } (s) = \frac{\phi }{s + \phi },$ in Eq. 50, then taking inverse Laplace transform, one can obtain

$$ \begin{aligned} E_{p} (t) & = K_{1} (0.02814278751 e^{( - 1.21100\;t)} + 0.0001387211 e^{( - 1.071000\;t)} + 0.001295651 e^{( - 2.7095548\;t)} \\ - & 0.1010410148 e^{( - 1.2230648\;t)} - 0.005742612 e^{( - 1.0891277 t)} + 0.0053767760 e^{( - 1.08599984\;t)} \\ - & 0.0002714152 e^{( - 1.066732535\;t)} + 20.850608 e^{( - 0.043809544\;t)} + 20.92270) - K_{2} t \\ \end{aligned} $$

(65)

Let K ₁ = 1 and K ₂ = 0.5, 0.4, 0.3, 0.2, 0.1, 0.05, 0.01 and varying t = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 one can get Table 4, and the corresponding graph is shown in Fig. 4.

Table 4 Time versus expected profit

Fig. 4

Time versus expected profit

9 Conclusion

Table 2 and corresponding Fig. 2 provide information about the changes of availability of the repairable system with respect to time when failure rates are fixed at different values. When failure rates are fixed at lower values λ₁ = 0.05, λ₂ = 0.06, λ_C = 0.01, λ_CB = 0.02, λ = 0.05, λ_h = 0.001, availability of the system decreases and probability of failure increases, with passage of time and ultimately becomes steady to the value zero after a sufficient long interval of time. From this, one can safely predict the future behavior of the system at any time for any given set of parametric values, as is evident by the graphical consideration of the model.

Table 3 and Fig. 3 yield the MTTF of the system with respect to variation in λ₁, λ_C, λ_CB, λ_h and λ respectively when other parameters have been kept constant. By critical observation of this figure, we can say that MTTF of the system is decreasing with respect to different failure rates. MTTF of the system is highest with respect to failure rate of subsystem-2 and is lowest with respect to any human failure. The MTTF of subsystem-2 is precisely same on failure rate variation value at 0.5 with subsystem-1 when most of the k units have failed during operational mode, at 0.8 with its controller failure and at 0.9 with controller failure of subsystem-1.

When revenue cost per unit time K ₁ fixed at one, service cost K ₂ = 0.5, 0.4, 0.3, 0.2, 0.1, 0.05, 0.01, profit has been calculated (Table 4) and results are demonstrated by graphs (Fig. 4). The observation outlines that as the service cost decreases profit increases.

Thus, in general with this study, behaviour of such systems can be analyzed and prognosticate in advance.

Appendices

Appendix 1

Equation 1 has been obtained by limiting case of following probabilistic difference equation:

$$ \begin{aligned} P_{0} (t + \Updelta ) & = (1 - \lambda_{1} \Updelta t)(1 - \lambda_{C} \Updelta t)(1 - \lambda_{CB} \Updelta t)(1 - \lambda_{h} \Updelta t)(1 - 2\lambda \Updelta t)P_{0} (t) + \int\limits_{0}^{\infty } {\phi (x)P_{1} (x,t)} {{dx}}\Updelta t \\ + & \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{2} } (x,t){{dx}}\Updelta t + \int\limits_{0}^{\infty } {\phi (x)P_{3} (x,t)} {{dx}}\Updelta t + \int\limits_{0}^{\infty } {\phi (x)P_{4} } (x,t){{dx}}\Updelta t \\ + & \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{5} } (x,t){{dx}}\Updelta t + \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{6} } (x,t){{dx}}\Updelta t \\ + & \int\limits_{0}^{\infty } {\exp [x^{\theta } + \{ \log \phi (x)\}^{\theta } ]^{1/\theta } P_{9} } (x,t){{dx}}\Updelta t \\ \end{aligned} $$

Now $\mathop {\lim }\limits_{\Updelta t \to 0\;} \;\frac{{P_{0} (t + \Updelta ) - P_{0} (t)}}{\Updelta t} + (\lambda_{1} + \lambda_{C} + \lambda_{CB} + \lambda_{h} + 2\lambda ) \cdots = \int\limits_{0}^{\infty } {\phi (x)P_{1} (x,t)} {{dx}} + \cdots P_{0} (t)$ yield Eq. 1 and similarly Eqs. 2–10 have been obtained.

Appendix 2

Solving 22–30, one can have

$$ \bar{P}_{1} (x,s) = \bar{P}_{1} (0,s)\exp \left( {( - (s + \lambda_{2} + 2\lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} } \right)e^{{ - \int\limits_{0}^{x} {\phi (x){{dx}}} }} $$

where

$$\bar{P}_{1} (0,s) = \lambda_{1} \bar{P}_{0} (s),\quad S_{\phi } (x) = \phi (x)e^{{\int\limits_{0}^{x} {\phi (x){{dx}}} }} ,\quad S_{\phi } (s) = \int\limits_{0}^{\infty } {e^{ - sx} } \phi (x)e^{{\int\limits_{0}^{x} {\phi (x){{dx}}} }} {{dx}}. $$

This implies that

$$\bar{P}_{1} (s) = \int\limits_{0}^{\infty } {\bar{P}_{1} (x,s){{dx}}} $$

. So on. Using values obtained by solving 22–30, one can get the transition state probabilities of the system.

Appendix 3

We have

$$ \begin{aligned} {{D}}(s) = s + \lambda_{1} + \lambda_{C} + \lambda_{h} + \lambda_{CB} + 2\lambda \\ - \left( {\lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )}}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )} \right)}}} \right)\bar{S}_{\phi } (s + \lambda_{1} + \lambda_{C} + \lambda_{h} + \lambda_{CB} + 2\lambda ) \\ - \left( {\lambda_{2} \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )}}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )} \right)}}} \right)S_{{\mu_{0} }} (x) + 2\lambda S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} ) \\ - 2\lambda^{2} \left( {\lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )}}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )} \right)}}} \right)S_{{\mu_{0} }} (x) \\ - \lambda_{h} \left( {1 + \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} ) + 2\lambda \lambda_{{}} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )} \right)}} + 2\lambda } \right)S_{{\mu_{0} }} (x) \\ - \lambda_{C} \left( {1 + \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} ) + 2\lambda \lambda_{{}} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )} \right)}} + 2\lambda } \right)S_{{\mu_{0} }} (x) \\ - \lambda_{CB} \left( {1 + \lambda_{1} + \frac{{2\lambda \lambda_{1} S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} ) + 2\lambda \lambda_{{}} }}{{\left( {1 - 2\lambda S_{\phi } (s + \lambda + \lambda_{C} + \lambda_{CB} + \lambda_{h} )} \right)}} + 2\lambda } \right)S_{{\mu_{0} }} (x) \\ \end{aligned} $$

when s = 0, D(s) becomes zero and $P_{0} (0) = \mathop {\lim }\nolimits_{s \to 0} sP_{0} (s) = \mathop {\lim }\nolimits_{s \to 0} \frac{s}{{{{D}}(s)}} = \frac{1}{{{{D}}^{ '} (0)}}$ by D’L Hospital rule $S_{\phi } (s) = \int\nolimits_{0}^{\infty } {e^{ - sx} } \phi (x)e^{{\int\nolimits_{0}^{x} {\phi (x){{dx}}} }} {{dx}} = \frac{\phi }{s + \phi }$ implies that $S_{\phi } (0)\; = \frac{\phi }{0 + \phi } = 1$and so on.