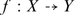Lagrangian Fibrations of Holomorphic-Symplectic Varieties of K3^[n]-Type

Abstract

Let X be a compact Kähler holomorphic-symplectic manifold, which is deformation equivalent to the Hilbert scheme of length n subschemes of a K3 surface. Let $\mathcal{L}$ be a nef line-bundle on X, such that the top power $c_{1}(\mathcal{L})^{2n}$ vanishes and $c_{1}(\mathcal{L})$ is primitive. Assume that the two dimensional subspace H ^2, 0(X) ⊕ H ^0, 2(X) of $H^{2}(X, \mathbb{C})$ intersects $H^{2}(X, \mathbb{Z})$ trivially. We prove that the linear system of $\mathcal{L}$ is base point free and it induces a Lagrangian fibration on X. In particular, the line-bundle $\mathcal{L}$ is effective. A determination of the semi-group of effective divisor classes on X follows, when X is projective. For a generic such pair $(X,\mathcal{L})$, not necessarily projective, we show that X is bimeromorphic to a Tate-Shafarevich twist of a moduli space of stable torsion sheaves, each with pure one dimensional support, on a projective K3 surface.

Partially supported by Simons Foundation Collaboration Grant 245840 and by NSA grant H98230-13-1-0239.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

An irreducible holomorphic symplectic manifold is a simply connected compact Kähler manifold such that $H^{0}(X,\wedge ^{2}T^{{\ast}}X)$ is generated by an everywhere non-degenerate holomorphic 2-form [4]. A compact Kähler manifold X is said to be of K3 ^[n] -type, if it is deformation equivalent to the Hilbert scheme S ^[n] of length n subschemes of a K3 surface S. Any manifold of K3^[n]-type is irreducible holomorphic symplectic [4]. The second integral cohomology of an irreducible holomorphic symplectic manifold X admits a natural symmetric non-degenerate integral bilinear pairing (•, •) of signature (3, b ₂(X) − 3), called the Beauville-Bogomolov-Fujiki pairing. The Beauville-Bogomolov-Fujiki pairing is monodromy invariant, and is thus an invariant of the deformation class of X.

Definition 1.1.

An irreducible holomorphic symplectic manifold X is said to be special, if the intersection in $H^{2}(X, \mathbb{C})$ of $H^{2}(X, \mathbb{Z})$ and H ^2, 0(X) ⊕ H ^0, 2(X) is a non-zero subgroup.

The locus of special periods forms a countable union of real analytic subvarieties of half the dimension in the corresponding moduli space.

Definition 1.2.

Let X be a 2n-dimensional irreducible holomorphic symplectic manifold and $\mathcal{L}$ a line bundle on X. We say that $\mathcal{L}$ induces a Lagrangian fibration, if it satisfies the following two conditions.

• 1. $h^{0}\left (X,\mathcal{L}\right ) = n + 1$.

• 2. The linear system $\mid \mathcal{L}\mid$ is base point free, and the generic fiber of the morphism $\pi: X \rightarrow \mid \mathcal{L}\mid ^{{\ast}}$ is a connected Lagrangian subvariety.

A line bundle $\mathcal{L}$ on a holomorphic symplectic manifold X is said to be nef, if $c_{1}(\mathcal{L})$ belongs to the closure in $H^{1,1}(X, \mathbb{R})$ of the Kähler cone of X.

Theorem 1.3.

Let X be an irreducible holomorphic symplectic manifold of K3 ^[n] -type and $\mathcal{L}$ a nef line-bundle, such that $c_{1}(\mathcal{L})$ is primitive and isotropic with respect to the Beauville-Bogomolov-Fujiki pairing. Assume that X is non-special. Then the line bundle $\mathcal{L}$ induces a Lagrangian fibration $\pi: X \rightarrow \mid \mathcal{L}\mid ^{{\ast}}$ .

See Theorem 6.3 for a variant of Theorem 1.3 dropping the assumption that $\mathcal{L}$ is nef. Theorem 1.3 is proven in Sect. 6. The proof relies on Verbitsky’s Global Torelli Theorem [14, 40], on the determination of the monodromy group of X [21, 22], and on a result of Matsushita that Lagrangian fibrations form an open subset in the moduli space of pairs $(X,\mathcal{L})$ [27]. Let us sketch the three main new ingredients in the proof of Theorem 1.3.

• (1) We associate to the pair $(X,\mathcal{L})$ in Theorem 1.3 a projective K3 surface S with a nef line bundle $\mathcal{B}$ of degree $\frac{2n-2} {d^{2}}$, where $d:=\gcd \{ (c_{1}(\mathcal{L}),\lambda )\:\ \lambda \in H^{2}(X, \mathbb{Z})\}$. The sub-lattice $c_{1}(\mathcal{B})^{\perp }$ orthogonal to $c_{1}(\mathcal{B})$ in $H^{2}(S, \mathbb{Z})$ is Hodge-isometric to $c_{1}(\mathcal{L})^{\perp }/\mathbb{Z}c_{1}(\mathcal{L})$. The construction realizes the period domain Ω ₂₀ of the pairs $(X,\mathcal{L})$ as an affine line bundle over a period domain Ω ₁₉ of semi-polarized K3 surfaces (Sect. 4).

• (2) The bundle map q: Ω ₂₀ → Ω ₁₉ is invariant with respect to a subgroup Q of the monodromy group (Lemma 5.3). The group Q is isomorphic to $c_{1}(\mathcal{B})^{\perp }$. Q acts on the fiber of q over the period of a semi-polarized K3 surface $(S,\mathcal{B})$. Similarly, the lattice $c_{1}(\mathcal{B})^{\perp }$ projects to a subgroup of H ^0, 2(S), which acts on H ^0, 2(S) by translations. There exists an isomorphism, of the fiber of q with H ^0, 2(S), which is equivariant with respect to the two actions (Lemma 5.4).

• (3) The fiber of q over the period of a semi-polarized K3 surface $(S,\mathcal{B})$ contains the period of a moduli space of sheaves on S with pure one-dimensional support in the linear system $\mid \mathcal{B}^{d}\mid$ (Sect. 5.1). Each such moduli space of sheaves is known to be a Lagrangian fibration [34].

The assumption that X is non-special in Theorem 1.3 is probably not necessary. Unfortunately, our proof will rely on it. When X is non-special the Q-orbit, of every point in the fiber of q through the period of X, is a dense subset of the fiber (Lemma 5.4). This density will have a central role in this paper due to the following elementary observation.

Observation 1.4.

Let T be a topological space and Q a group acting on T. Assume that the Q-orbit of every point of T is dense in T. Then any nonempty Q-invariant open subset of T must be the whole of T.

The above observation will be used in an essential way in three different proofs (Theorem 6.1, Proposition 7.7, and Theorem 7.11).

The statement of the next result requires the notion of a Tate-Shafarevich twist, which we now recall. Let M be a complex manifold and π: M → B a proper map with connected fibers of pure dimension n. Assume that the generic fiber of π is a smooth abelian variety. Let {U _i } be an open covering of B in the analytic topology. Set $U_{\mathit{ij}}:= U_{i} \cap U_{j}$ and $M_{\mathit{ij}}:=\pi ^{-1}(U_{\mathit{ij}})$. Assume given a 1-co-cycle g _ij of automorphisms of M _ij , satisfying $\pi \circ g_{\mathit{ij}} =\pi$, and acting by translations on the smooth fibers of π. We can re-glue the open covering {M _i } of M using the co-cycle $\{g_{\mathit{ij}}\}$ to get a complex manifold M ^′ and a proper map π ^′: M ^′ → B, whose fibers are isomorphic to those of π. We refer to (M ^′, π ^′) as the Tate-Shafarevich twist of (M, π) associated to the co-cycle {g _ij }. Tate-Shafarevich twists are standard in the study of elliptic fibrations [10, 17].

Let $\mathcal{L}$ be a semi-ample line bundle on a K3 surface S with an indivisible class $c_{1}(\mathcal{L})$. Given an ample line bundle H on S and an integer χ, denote by $M_{H}(0,\mathcal{L}^{d},\chi )$ the moduli space of H-stable coherent sheaves on S of rank zero, determinant $\mathcal{L}^{d}$, and Euler characteristic χ. Assume that d and χ are relatively prime. For a generic polarization H, the moduli space $M_{H}(0,\mathcal{L}^{d},\chi )$ is smooth and projective and it admits a Lagrangian fibration over the linear system $\mid \mathcal{L}^{d}\mid$ [34].

Let X be an irreducible holomorphic symplectic manifold of K3^[n]-type and $\pi: X \rightarrow \mathbb{P}^{n}$ a Lagrangian fibration. Set $\alpha:=\pi ^{{\ast}}c_{1}(\mathcal{O}_{\mathbb{P}^{n}}(1))$. The divisibility of (α, •) is the positive integer $d:=\gcd \{ (\alpha,\lambda )\:\ \lambda \in H^{2}(X, \mathbb{Z})\}$. The integer d ² divides n − 1 (Lemma 2.5).

Theorem 1.5.

Assume that X is non-special and the intersection $H^{1,1}(X, \mathbb{Z}) \cap \alpha ^{\perp }$ is $\mathbb{Z}\alpha$ . There exists a K3 surface S, a semi-ample line bundle $\mathcal{L}$ on S of degree $\frac{2n-2} {d^{2}}$ with an indivisible class $c_{1}(\mathcal{L})$ , an integer χ relatively prime to d, and a polarization H on S, such that X is bimeromorphic to a Tate-Shafarevich twist of the Lagrangian fibration $M_{H}(0,\mathcal{L}^{d},\chi ) \rightarrow \mid \mathcal{L}^{d}\mid$ .

Theorem 1.5 is proven in Sect. 7. The semi-polarized K3 surface $(S,\mathcal{L})$ in Theorem 1.5 is the one mentioned already above, which is associated to (X, α) in Sect. 4.1. The equality $H^{1,1}(X, \mathbb{Z}) \cap \alpha ^{\perp } = \mathbb{Z}\alpha$ is equivalent to the statement that $\mathrm{Pic}(S)$ is cyclic generated by $\mathcal{L}$. This condition is relaxed in Theorem 7.13, which strengthens Theorem 1.5.

A reduced and irreducible divisor on X is called prime exceptional, if it has negative Beauville-Bogomolov-Fujiki degree. A divisor D on X is called movable, if the base locus of the linear system ∣D∣ has co-dimension ≥ 2 in X. The movable cone $\mathcal{M}\mathcal{V}_{X}$ of X is the cone in $N^{1}(X):= H^{1,1}(X, \mathbb{Z}) \otimes _{\mathbb{Z}}\mathbb{R}$ generated by classes of movable divisors. Assume that X is a projective irreducible holomorphic symplectic manifold of K3^[n]-type and let h ∈ N ¹(X) be an ample class. Denote by $\mathcal{P}\mathit{ex}_{X} \subset H^{1,1}(X, \mathbb{Z})$ the set of classes of prime exceptional divisors. The set $\mathcal{P}\mathit{ex}_{X}$ is determined in [24, Theorem 1.11 and Sec. 1.5]. The closure of the movable cone in N ¹(X) is determined as follows:

$$\displaystyle{\overline{\mathcal{M}\mathcal{V}}_{X}\,=\,\{c \in N^{1}(X)\:\ (c,c)\,\geq \,0,\ (c,h)\,\geq \,0,\ \mbox{ and}\ (c,e)\,\geq \,0,\ \mbox{ for all}\ e \in \mathcal{P}\mathit{ex}_{ X}\},}$$

by a result of Boucksom [6, 23, Prop. 5.6 and Lemma 6.22].¹

Corollary 1.6.

Let X be a projective irreducible holomorphic symplectic manifold of K3 ^[n] -type. The semi-group of effective divisor classes on X is generated by the classes of prime exceptional divisors and integral points in the closure of the movable cone in N ¹ (X).

Corollary 1.6 was shown to follow from Theorem 1.3 in [23, Paragraph following Question 10.11].

We classify the deformation types of pairs $(X,\mathcal{L})$, consisting of an irreducible holomorphic symplectic manifold X of K3^[n]-type, n ≥ 2, and a line bundle $\mathcal{L}$ on X with a primitive and isotropic first Chern class, such that $(c_{1}(\mathcal{L}),\kappa ) > 0$, for some Kähler class κ. The following proposition is proven in Sect. 4.3, using monodromy invariants introduced in Lemma 2.5.

Proposition 1.7.

Let d be a positive integer, such that d ² divides n − 1. If 1 ≤ d ≤ 4, then there exists a unique deformation type of pairs $(X,\mathcal{L})$ , with $c_{1}(\mathcal{L})$ primitive and isotropic, such that $(c_{1}(\mathcal{L}),\bullet )$ has divisibility d. For d ≥ 5, let ν(d) be half the number of multiplicative units in the ring $\mathbb{Z}/d\mathbb{Z}$ . Then there are ν(d) deformation types of pairs $(X,\mathcal{L})$ as above, with $(c_{1}(\mathcal{L}),\bullet )$ of divisibility d.

A generalized Kummer variety of dimension 2n is the fiber of the Albanese map S ^[n+1] → S from the Hilbert scheme of length n subschemes of an abelian surface S to S itself [4]. We expect all of the above results to have analogues for X an irreducible holomorphic-symplectic manifold deformation equivalent to a generalized Kummer variety. Yoshioka proved Theorem 1.3 for those X associated to a moduli space of sheaves on an abelian surface [43]. Let the pair $(X,\mathcal{L})$ consist of X, deformation equivalent to a generalized Kummer, and a line bundle $\mathcal{L}$ with a primitive and isotropic first Chern class. The basic construction of Sect. 4.1 associates to the pair $(X,\mathcal{L})$, with $\dim (X) = 2n$, n ≥ 2, and with $(c_{1}(\mathcal{L}),\bullet )$ of divisibility d, two dual pairs (S ₁, α ₁) and (S ₂, α ₂), each consisting of an abelian surface S _i and a class α _i in the Neron-Severi group of S _i of self intersection $\frac{2n+2} {d^{2}}$, such that $S_{2}\mathop{\cong}S_{1}^{{\ast}}$ and the natural isometry $H^{2}(S_{1}, \mathbb{Z})\mathop{\cong}H^{2}(S_{2}, \mathbb{Z})$ maps α ₁ to α ₂. A conjectural determination of the monodromy group of generalized Kummer varieties was suggested in the comment after [25, Prop. 4.8]. Assuming that the monodromy group is as conjectured, we expect that the proofs of all the results above can be adapted to this deformation type.

A version of Theorem 1.3 has been conjectured for irreducible holomorphic symplectic manifolds of all deformation types [5, 26, 39, Conjecture 2]. Markushevich, Sawon, and Yoshioka proved a version of Theorem 1.3, when X is the Hilbert scheme of n points on a K3 surface and $(c_{1}(\mathcal{L}),\bullet )$ has divisibility 1 [26, Cor. 4.4] and [39] (the regularity of the fibration, in Sect. 5 of [39], is due to Yoshioka). Bayer and Macri recently proved a strong version of Theorem 1.3 for moduli spaces of sheaves on a projective K3 surface [3].

Remark 1.8 (Added in the final revision).

Let X ₀ be an irreducible holomorphic symplectic manifold and $\mathcal{L}_{0}$ a nef line bundle on X ₀, such that $c_{1}(\mathcal{L}_{0})$ is primitive and isotropic with respect to the Beauville-Bogomolov-Fujiki pairing. Matsushita proved that if $\mathcal{L}_{0}$ induces a Lagrangian fibration, then so does $\mathcal{L}$ for every pair $(X,\mathcal{L})$ deformation equivalent to $(X_{0},\mathcal{L}_{0})$, with X irreducible holomorpic symplectic and $\mathcal{L}$ nef (preprint posted very recently [28], announced earlier in his talk [31]). It follows that Theorem 1.3 above holds also without the assumption that X is non-special, since a pair $(X,\mathcal{L})$ with X special is a deformation of a pair $(X_{0},\mathcal{L}_{0})$ with X ₀ non-special. In fact, this stronger version of Theorem 1.3, dropping the non-speciality, follows already from the combination of Matsushita’s result and Example 3.1 below, since Example 3.1 exhibits a pair $(X_{0},\mathcal{L}_{0})$, with a line bundle $\mathcal{L}_{0}$ inducing a Lagrangian fibration, in each deformation class of pairs $(X,\mathcal{L})$ with X of K3^[n]-type and $c_{1}(\mathcal{L})$ primitive, isotropic, and on the boundary of the positive cone. Matsushita’s result does not seem to provide an alternative proof of Theorem 1.5 and the only proof we know is presented in Sect. 7 and relies on the preceding sections.

2 Classification of Primitive-Isotropic Classes

A lattice, in this note, is a finitely generated free abelian group with a symmetric bilinear pairing $(\bullet,\bullet ): L \otimes _{\mathbb{Z}}L \rightarrow \mathbb{Z}$. The pairing may be degenerate. The isometry group O(L) is the group of automorphisms of L preserving the bilinear pairing.

Definition 2.1.

Two pairs (L _i , v _i ), i = 1, 2, each consisting of a lattice L _i and an element v _i  ∈ L _i , are said to be isometric, if there exists an isometry g: L ₁ → L ₂, such that g(v ₁) = v ₂.

Let X be an irreducible holomorphic symplectic manifold of K3^[n]-type, n ≥ 2. Set $\varLambda:= H^{2}(X, \mathbb{Z})$. We will refer to Λ as the K3 ^[n] -lattice. Let $\tilde{\varLambda }$ be the Mukai lattice, i.e., the orthogonal direct sum of two copies of the negative definite E ₈(−1) lattice and four copies of the even unimodular rank two lattice with signature (1, −1).

Theorem 2.2 ([22], Theorem 1.10).

X comes with a natural $O(\tilde{\varLambda })$ -orbit $\iota _{X}$ of primitive isometric embeddings $\iota: H^{2}(X, \mathbb{Z})\hookrightarrow \tilde{\varLambda }$ .

Choose a primitive isometric embedding $\iota:\varLambda \hookrightarrow \tilde{\varLambda }$ in the canonical $O(\tilde{\varLambda })$-orbit ι _X provided by Theorem 2.2. Choose a generator $v \in \tilde{\varLambda }$ of the rank 1 sub-lattice orthogonal to $\iota (\varLambda )$. We say that an isometry g ∈ O(Λ) stabilizes the $O(\tilde{\varLambda })$-orbit ι _X , if given a representative isometric embedding ι in the orbit ι _X , there exists an isometry $\tilde{g} \in O(\tilde{\varLambda })$ satisfying $\iota \circ g =\tilde{ g}\circ \iota$. Note that $\tilde{g}$ necessarily maps v to ± v.

Set $\varLambda _{\mathbb{R}}:=\varLambda \otimes _{\mathbb{Z}}\mathbb{R}$. Let $\tilde{\mathcal{C}}\subset \varLambda _{\mathbb{R}}$ be the positive cone $\{x \in \varLambda _{\mathbb{R}}\:\ (x,x) > 0\}$. Then $H^{2}(\tilde{\mathcal{C}}, \mathbb{Z})$ is isomorphic to $\mathbb{Z}$ and is a natural character of the isometry group O(Λ) [23, Lemma 4.1]. Denote by O ⁺(Λ) the kernel of this orientation character. Isometries in O ⁺(Λ) are said to be orientation preserving.

Definition 2.3.

Let X, X ₁, and X ₂ be irreducible holomorphic symplectic manifolds. An isometry $g: H^{2}(X_{1}, \mathbb{Z}) \rightarrow H^{2}(X_{2}, \mathbb{Z})$ is a parallel transport operator, if there exists a family $\pi: \mathcal{X} \rightarrow B$ (which may depend on g) of irreducible holomorphic symplectic manifolds, points b ₁ and b ₂ in B, isomorphisms $X_{i}\mathop{\cong}\mathcal{X}_{b_{i}}$, where $\mathcal{X}_{b_{i}}$ is the fiber over b _i , i = 1, 2, and a continuous path γ from b ₁ to b ₂, such that parallel transport along γ in the local system $R^{2}\pi _{{\ast}}\mathbb{Z}$ induces the isometry g. When $X = X_{1} = X_{2}$, we call g a monodromy operator. The monodromy group Mon ²(X) of X is the subgroup, of the isometry group of $H^{2}(X, \mathbb{Z})$, generated by monodromy operators.

Theorem 2.4 ([22], Theorem 1.2 and Lemma 4.2).

The subgroup Mon ² (X) of O(Λ) consists of orientation preserving isometries stabilizing the orbit ι _X .

Given a lattice L, let I _n (L) ⊂ L be the subset of primitive classes v with $(v,v) = 2n - 2$. Notice that the orbit set I _n (L)∕O(L) parametrizes the set of isometry classes of pairs (L ^′, v ^′), such that L ^′ is isometric to L and v ^′ is a primitive class in L ^′ with $(v^{{\prime}},v^{{\prime}}) = 2n - 2$ [23, Lemma 9.14].

Let n be an integer ≥ 2, let Λ be the K3^[n]-lattice, and let α ∈ Λ be a primitive isotropic class. Let div(α, •) be the largest positive integer, such that (α, •)∕div(α, •) is an integral class of Λ ^∗. Set d: = div(α, •) and

$$\displaystyle{\beta:=\iota (\alpha ).}$$

Let $L \subset \tilde{\varLambda }$ be the saturation² of $\mathrm{span}_{\mathbb{Z}}\{\beta,v\}$. Clearly, the isometry class of (L, v) depends only on α and the $O(\tilde{\varLambda })$-orbit of ι. Consequently, the isometry class of (L, v) depends only on α, as the $O(\tilde{\varLambda })$-orbit ι _X of ι is natural, by Theorem 2.2. We denote by [L, v](α) the isometry class of the pair (L, v) associated to α.

Lemma 2.5.

• (1) d ² divides n − 1.

• (2) L is isometric to the lattice L _n,d with Gram matrix $\frac{2n-2} {d^{2}} \left (\begin{array}{cc} 1&0\\ 0 &0\end{array} \right ).$

• (3) Let d ≥ 1 be an integer, such that d ² divides n − 1. The map α↦[L,v](α) induces a one-to-one correspondence between the set of Mon ² (X)-orbits, of primitive isotropic classes α with div (α,• ) = d, and the set of isometry classes I _n (L _n,d )∕O(L _n,d ).

• (4) There exists an integer b, such that $(\beta -bv)/d$ is an integral class of L. The isometry class [L,v](α) is represented by (L _n,d ,(d,b)), for any such integer b.

Proof.

Part (1): There exists a class δ ∈ Λ, such that $(\delta,\delta ) = 2 - 2n$ and the sub-lattice $\delta _{\varLambda }^{\perp }$ of Λ, orthogonal to δ, is a unimodular lattice isometric to the K3-lattice. The sub-lattice $[\iota (\delta _{\varLambda }^{\perp })]_{\tilde{\varLambda }}^{\perp }$ of $\tilde{\varLambda }$, which is the saturation of span{ι(δ), v}, is unimodular, hence isometric to the unimodular hyperbolic plane U with Gram matrix $\left (\begin{array}{cc} 0 & - 1\\ - 1 & 0 \end{array} \right ).$ We may further assume that $v = (1,1 - n)$ and $\iota (\delta ) = (1,n - 1)$, under this isomorphism. If X is the Hilbert scheme S ^[n] of a K3-surface and δ is half the class of the big diagonal, then δ satisfies the above properties. Write $\alpha = a\xi + b\delta$, where ξ is a primitive class of the K3-lattice $\delta _{\varLambda }^{\perp }$, a > 0, and $\gcd (a,b) = 1$. We get

$$\displaystyle{0 = (\alpha,\alpha ) = a^{2}(\xi,\xi ) - (2n - 2)b^{2},}$$

and (ξ, ξ) is even. Hence, a ² divides n − 1. Furthermore, $\mathrm{div}(\delta,\bullet ) = 2n - 2$, div(ξ, •) = 1, since $\delta _{\varLambda }^{\perp }$ is unimodular, and $\mathrm{div}(\alpha,\bullet ) =\gcd (\mathrm{div}(a\xi,\bullet ),\mathrm{div}(b\delta,\bullet )) =\gcd (a,(2n - 2)b) = a$. Thus, $a = d:= \mathrm{div}(\alpha,\bullet )$.

Part (2): Note that $\iota (\delta ) - v = (2n - 2)e$, where e is a primitive isotropic class of $\tilde{\varLambda }$. Set $\gamma:= \frac{1} {d}(\beta -bv) =\iota (\xi ) + \frac{b(2n-2)} {d} e$. We claim that the lattice $L:= \mathrm{span}_{\mathbb{Z}}\{v,\gamma \}$ is saturated in $\tilde{\varLambda }$. Indeed, choose $\eta \in \delta _{\varLambda }^{\perp }$, such that (ξ, η) = 1. Then $\left (\begin{array}{cc} (v,e)&(v,\eta )\\ (\gamma, e) & (\gamma,\eta ) \end{array} \right ) = \left (\begin{array}{cc} - 1&0\\ 0 &1 \end{array} \right )$.

Let G be the Gram matrix of L in the basis {v, γ}. Then

$$\displaystyle{G = \frac{2n - 2} {d^{2}} \left (\begin{array}{cc} d^{2} & -\mathit{bd} \\ -\mathit{bd}& b^{2} \end{array} \right ) = \frac{2n - 2} {d^{2}} \left (\begin{array}{c} d\\ -b \end{array} \right )\left (\begin{array}{cc} d& - b \end{array} \right ).}$$

Choose a 2 × 2 invertible matrix A, with integer coefficients, such that $A\left (\begin{array}{c} d\\ -b \end{array} \right ) = \left (\begin{array}{c} 1\\ 0 \end{array} \right )$. Then AGA ^t is the Gram matrix of L _n, d .

Part (3): Assume given two primitive isotropic classes α ₁ and α ₂ in $\varLambda:= H^{2}(X, \mathbb{Z})$ and let (L _i , v _i ) be the pair associated to α _i as above, for i = 1, 2. In other words, $\iota _{i}:\varLambda \hookrightarrow \tilde{\varLambda }$ is a primitive embedding in the orbit ι _X , v _i generates the sub-lattice of $\tilde{\varLambda }$ orthogonal to the image of ι _i , and L _i is the saturation of $\mathrm{span}_{\mathbb{Z}}\{\iota (\alpha _{i}),v_{i}\}$.

Let us check that the map α↦[L, v](α) is constant on Mon ²(X)-orbits. Assume that there exists an element μ ∈ Mon ²(X), such that μ(α ₁) = α ₂. Then there exists an isometry $\tilde{\mu }\in O(\tilde{\varLambda })$, satisfying $\tilde{\mu }\circ \iota _{1} =\iota _{2}\circ \mu$, by Theorem 2.4. We get that $\tilde{\mu }(L_{1}) = L_{2}$ and $\tilde{\mu }(v_{1}) = v_{2}$, or $\tilde{\mu }(v_{1}) = -v_{2}$. So, the isometry $\tilde{\mu }$ or $-\tilde{\mu }$ from L ₁ onto L ₂ provides an isometry of the pairs (L _i , v _i ), i = 1, 2.

We show next that the map α↦[L, v](α) is injective, i.e., that the isometry class of the pair (L, v) determines the Mon ²(X)-orbit of α. Assume that there exists as isometry f: L ₁ → L ₂, such that f(v ₁) = v ₂. Then there exists an isometry $\tilde{f} \in O(\tilde{\varLambda })$, such that $\tilde{f}(L_{1}) = L_{2}$ and the restriction of $\tilde{f}$ to L ₁ is f, by ([36], Proposition 1.17.1 and Theorem 1.14.4, see also [21], Lemma 8.1 for more details). In particular, $\tilde{f}(v_{1}) = v_{2}$. There exists a unique isometry h ∈ O(Λ) satisfying $\iota _{2} \circ h =\tilde{ f} \circ \iota _{1}$. There exists an isometry $\phi \in O(\tilde{\varLambda })$, such that $\phi \circ \iota _{2} =\iota _{1}$, since both ι _i belong to the same $O(\tilde{\varLambda })$-orbit ι _X . We get the equality $\iota _{1} \circ h =\phi \circ \iota _{2} \circ h = (\phi \circ \tilde{f}) \circ \iota _{1}$. If h is orientation preserving, then h belongs to Mon ²(X), otherwise, − h does, by Theorem 2.4. Let μ = h, if it is orientation preserving. Otherwise, set $\mu:= -h$. Then μ is a monodromy operator and $\iota _{2}(\mu (\alpha _{1})) = \pm \iota _{2}(h(\alpha _{1})) = \pm \tilde{f}(\iota _{1}(\alpha _{1}))$. The class ι ₁(α ₁) spans the null space of L ₁, and $\tilde{f}$ restricts to an isometry from L ₁ to L ₂. Hence, ι ₂(μ(α ₁)) spans the null space of L ₂. Hence, μ(α ₁) = ±α ₂.

Finally we show that α ₂ and −α ₂ belong to the same Mon ²(X)-orbit. There exists an element τ ∈ Λ satisfying (τ, τ) = 2, and (τ, α ₂) = 0. The isometry ρ _τ  ∈ O(Λ), given by $\rho _{\tau }(\lambda ) = -\lambda + (\lambda,\tau )\tau$, belongs to Mon ²(X), by ([21], Corollary 1.8), and it sends α ₂ to −α ₂.

It remains to prove that the map α↦[L, v](α) is surjective. Assume given a primitive class v ∈ L _n, d with $(v,v) = 2n - 2$. There exists a primitive isometric embedding $f: L_{n,d}\hookrightarrow \tilde{\varLambda }$, by ([36], Proposition 1.17.1). The lattice $f(v)_{\tilde{\varLambda }}^{\perp }$, orthogonal to f(v) in $\tilde{\varLambda }$, is isometric to the K3^[n]-lattice Λ. Choose such an isometry $h: f(v)_{\tilde{\varLambda }}^{\perp }\rightarrow \varLambda$, with the property that $h^{-1}:\varLambda \hookrightarrow \tilde{\varLambda }$ belongs to the $O(\tilde{\varLambda })$-orbit ι _X . Such a choice exists, since O(Λ) acts transitively on the orbit space $O(\varLambda,\tilde{\varLambda })/O(\tilde{\varLambda })$, by ([22], Lemma 4.3). Above, $O(\varLambda,\tilde{\varLambda })$ denotes the set of primitive isometric embeddings of Λ in $\tilde{\varLambda }$. Denote by β ∈ L _n, d a generator of the null space of L _n, d . Set α: = h(f(β)). Then α is a class in Λ, such that [L, v](α) is represented by (L _n, d , v).

Part (4): The existence of such an integer b was established in the course of proving part (1). The rest of the statement follows from Lemma 2.6. □ 

If d = 2, set ν(d): = 1. If d > 2, let ν(d) be half the number of multiplicative units in the ring $\mathbb{Z}/d\mathbb{Z}$.

Lemma 2.6.

A vector (x,y) ∈ L _n,d is primitive of degree 2n − 2, if and only if  $\left \vert \!x\!\right \vert = d$ and gcd (d,y) = 1. Two primitive vectors (d,y), (d,z) belong to the same O(L _n,d )-orbit, if and only if y ≡ z modulo d, or y ≡−z modulo d. Consequently, ν(d) is equal to the number of O(L _n,d )-orbits of primitive vectors in L _n,d of degree 2n − 2.

Proof.

The isometry group of L _n, d consists of matrices of the form $\left (\begin{array}{cc} \pm 1& 0\\ c & \pm 1 \end{array} \right )$. The orbit O(L _n, d )(d, y) consists of vectors of the form (±d, cd ± y). Consequently, the number of O(L _n, d )-orbits of primitive vectors in L _n, d of degree 2n − 2 is equal to the number of orbits in $\{y:\ 0 < y < d\ \mbox{ and}\ \gcd (y,d) = 1\}$ under the action y↦d − y. The latter number is ν(d). □ 

3 An Example of a Lagrangian Fibration for Each Value of the Monodromy Invariants

Let S be a projective K3 surface, K(S) its topological K-group, generated by classes of complex vector bundles, and $H^{{\ast}}(S, \mathbb{Z})$ its integral cohomology ring. Let $\mathit{td}_{S}:= 1 + \frac{c_{2}(S)} {12}$ be the Todd class of S and $\sqrt{ \mathit{td}_{S}}:= 1 + \frac{c_{2}(S)} {24}$ its square root. The homomorphism $v: K(S) \rightarrow H^{{\ast}}(S, \mathbb{Z})$, given by $v(x) = \mathit{ch}(x)\sqrt{\mathit{td } _{S}}$ is an isomorphism of free abelian groups. Given a coherent sheaf E on S, the class v(E) is called the Mukai vector of E. Given integers r and s and a class $c \in H^{2}(S, \mathbb{Z})$, we will denote by (r, c, s) the class of $H^{{\ast}}(S, \mathbb{Z})$, whose graded summand in $H^{0}(S, \mathbb{Z})$ is r times the class Poincare dual to S, its graded summand in $H^{2}(S, \mathbb{Z})$ is c, and its graded summand in $H^{4}(S, \mathbb{Z})$ is s times the class Poincare dual to a point. We endow $H^{{\ast}}(S, \mathbb{Z})$ with the Mukai pairing

$$\displaystyle{((r,c,s),(r^{{\prime}},c^{{\prime}},s^{{\prime}}))\ \:=\ \ (c,c^{{\prime}}) -\mathit{rs}^{{\prime}}- r^{{\prime}}s,}$$

where $(c,c^{{\prime}}):=\int _{S}c \cup c^{{\prime}}.$ Then $(v(x),v(y)) = -\chi (x \otimes y)$, where $\chi: K(S) \rightarrow \mathbb{Z}$ is the Euler characteristic [35]. $H^{{\ast}}(S, \mathbb{Z})$, endowed with the Mukai pairing, is called the Mukai lattice. The Mukai lattice is an even unimodular lattice of rank 24, which is isometric to the orthogonal direct sum of two copies of the negative definite E ₈(−1) lattice and four copies of the even unimodular rank 2 hyperbolic lattice U.

Let v ∈ K(S) be the class with Mukai vector (0, d ξ, s) in $H^{{\ast}}(S, \mathbb{Z})$, such that ξ a primitive effective class in $H^{1,1}(S, \mathbb{Z})$, (ξ, ξ) > 0, d is a positive integer, and $\gcd (d,s) = 1$. There is a system of hyperplanes in the ample cone of S, called v-walls, that is countable but locally finite [15, Ch. 4C]. An ample class is called v-generic, if it does not belong to any v-wall. Choose a v-generic ample class H. Let M _H (v) be the moduli space of H-stable sheaves on the K3 surface S with class v. M _H (v) is a smooth projective irreducible holomorphic symplectic variety of K3^[n]-type, with $n = \frac{(v,v)+2} {2} = \frac{d^{2}(\xi,\xi )+2} {2}$. This is a special case of a result, which is due to several people, including Huybrechts, Mukai, O’Grady [38], and Yoshioka [44]. It can be found in its final form in [44].

Over S × M _H (v) there exists a universal sheaf $\mathcal{F}$, possibly twisted with respect to a non-trivial Brauer class pulled-back from M _H (v). Associated to $\mathcal{F}$ is a class $[\mathcal{F}]$ in $K(S \times M_{H}(v))$ ([20], Definition 26). Let π _i be the projection from S × M _H (v) onto the i-th factor. Denote by v ^⊥ the sub-lattice in $H^{{\ast}}(S, \mathbb{Z})$ orthogonal to v. The second integral cohomology $H^{2}(M_{H}(v), \mathbb{Z})$, its Hodge structure, and its Beauville-Bogomolov-Fujiki pairing, are all described by Mukai’s Hodge-isometry

$$\displaystyle{ \theta \:\ v^{\perp }\ \ \ \longrightarrow \ \ \ H^{2}(M_{ H}(v), \mathbb{Z}), }$$

(3.1)

given by $\theta (x):= c_{1}\left (\pi _{2_{!}}\{\pi _{1}^{!}(x^{\vee }) \otimes [\mathcal{F}]\}\right )$ (see [44]).

We provide next an example of a moduli space M _H (v) and a primitive isotropic class $\alpha \in H^{1,1}(M_{H}(v), \mathbb{Z})$, such that [L, v](α) is represented by (L _n, d , (d, b)), for every integer n ≥ 2, for every positive integer d, such that d ² divides n − 1, and for every integer b satisfying gcd(b, d) = 1.

Example 3.1.

Let d be a positive integer, such that d ² divides n − 1. Let S be a K3 surface with a nef line bundle $\mathcal{L}$ of degree $\frac{2n-2} {d^{2}}$. Let λ be the class $c_{1}(\mathcal{L})$ in $H^{2}(S, \mathbb{Z})$. Fix an integer b satisfying gcd(b, d) = 1. Set v: = (0, d λ, s), where s is an integer satisfying sb = 1 (modulo d). Then v is a primitive Mukai vector and $(v,v) = 2n - 2$. Choose a v-generic ample line bundle H. A sheaf F of class v is H-stable, if and only if it is H-semi-stable. The moduli space M _H (v), of H-stable sheaves of class v, is smooth, projective, holomorphic symplectic, and of K3^[n]-type. Set α: = θ((0, 0, 1)). Let $\iota: H^{2}(M_{H}(v), \mathbb{Z}) \rightarrow H^{{\ast}}(S, \mathbb{Z})$ be the composition of θ ⁻¹ with the inclusion of v ^⊥ into $H^{{\ast}}(S, \mathbb{Z})$. A Mukai vector (r, c, t) belongs to v ^⊥, if and only if rs = d(c, λ). It follows that d divides r, since gcd(d, s) = 1. Thus, div(α, •) = d. Now

$$\displaystyle{\iota (\alpha ) -\mathit{bv} = (0,-\mathit{bd}\lambda,1 -\mathit{bs})}$$

is divisible by d, by our assumption on s. Hence, the monodromy invariant [L, v](α) is equal to the isometry class of (L _n, d , (d, b)), by Lemma 2.5. The cohomology $H^{1}(S,\mathcal{L}^{d})$ vanishes, since $\mathcal{L}$ is a nef divisor of positive degree [32, Prop. 1]. Thus, the vector space $H^{0}(S,\mathcal{L}^{d})$ has dimension $\chi (\mathcal{L}^{d}) = n + 1$. The support morphism $\pi: M_{H}(v) \rightarrow \mid \mathcal{L}^{d}\mid$ realizes M _H (v) as a completely integrable system. The equality $\pi ^{{\ast}}c_{1}(\mathcal{O}_{\mid \mathcal{L}^{d}\mid }(1)) =\alpha$ is easily verified.

4 Period Domains and Period Maps

4.1 A Projective K3 Surface Associated to an Isotropic Class

Let X be an irreducible holomorphic symplectic manifold of K3^[n]-type, n ≥ 2. Assume that there exists a non-zero primitive isotropic class $\alpha \in H^{1,1}(X, \mathbb{Z})$. Let $\tilde{\varLambda }$ be the Mukai lattice. Choose a primitive isometric embedding $\iota: H^{2}(X, \mathbb{Z}) \rightarrow \tilde{\varLambda }$ in the canonical $O(\tilde{\varLambda })$-orbit ι _X of Theorem 2.2. Set $\tilde{\varLambda }_{\mathbb{C}}:=\tilde{\varLambda } \otimes _{\mathbb{Z}}\mathbb{C}$. Endow $\tilde{\varLambda }_{\mathbb{C}}$ with the weight 2 Hodge structure, so that $\tilde{\varLambda }_{\mathbb{C}}^{2,0} =\iota (H^{2,0}(X))$. Set β: = ι(α). Then β belongs to $\tilde{\varLambda }_{\mathbb{C}}^{1,1}$. Set

$$\displaystyle{\varLambda _{k3}\ \:=\ \ \beta _{ \tilde{\varLambda }}^{\perp }/\mathbb{Z}\beta }$$

and endow Λ _k3 with the induced Hodge structure. Let U be the even unimodular rank 2 lattice of signature (1, 1), and E ₈(−1) the negative definite E ₈ lattice. Then Λ _k3 is isometric to the K3 lattice, which is the orthogonal direct sum of two copies of E ₈(−1) and three copies of U. Indeed, this is clear if β is a class in a direct summand of $\tilde{\varLambda }$ isometric to U. It follows in general, since the isometry group of $\tilde{\varLambda }$ acts transitively on the set of primitive isotropic classes in $\tilde{\varLambda }$. The induced Hodge structure on Λ _k3 is the weight 2 Hodge structure of some K3 surface S(α), by the surjectivity of the period map.

Let v be a generator of the rank 1 sub-lattice of $\tilde{\varLambda }$ orthogonal to the image of ι. Then v is of Hodge-type (1, 1). Set $\varLambda:= H^{2}(X, \mathbb{Z})$. Then v ^⊥ is isometric to Λ. We claim that $(v,v) = 2n - 2$. Indeed, the pairing induces an isomorphism of the two discriminant groups $(\mathbb{Z}v)^{{\ast}}/\mathbb{Z}v$ and Λ ^∗∕Λ, since $\mathbb{Z}v$ and Λ are a pair of primitive sublattices, which are orthogonal complements in the unimodular lattice $\tilde{\varLambda }$. We conclude that the order | (v, v) | of $(\mathbb{Z}v)^{{\ast}}/\mathbb{Z}v$ is equal to the order 2n − 2 of Λ ^∗∕Λ. Finally, (v, v) > 0, by comparing the signatures of Λ and $\tilde{\varLambda }$.

Let $\bar{v}$ be the coset $v + \mathbb{Z}\beta$ in Λ _k3. Then $\bar{v}$ is of Hodge-type (1, 1) and $(\bar{v},\bar{v}) = 2n - 2$. Hence S(α) is a projective K3 surface (even if X is not projective). We may further choose the Hodge isometry $\eta: H^{2}(S(\alpha ), \mathbb{Z}) \rightarrow \varLambda _{k3}$, so that that $\bar{v}$ corresponds to a class in the positive cone of S(α), possibly after replacing v by − v. We may further assume that $\bar{v}$ corresponds to a nef class of S(α), possibly after replacing η with η ∘ w, where w is an element of the subgroup $W \subset O^{+}(H^{2}(S(\alpha ), \mathbb{Z}))$, generated by reflections by classes of smooth rational curves on S(α) [19, Prop. 1.9].

4.2 A Period Domain as an Affine Line Bundle Over Another

Keep the notation of Sect. 4.1. Set $\varLambda:= H^{2}(X, \mathbb{Z})$. Set d: = div(α, •). Let $\alpha _{\varLambda }^{\perp }$ be the (degenerate) lattice orthogonal to α in Λ. Set $Q_{\alpha }:=\alpha _{ \varLambda }^{\perp }/\mathbb{Z}\alpha.$

Lemma 4.1.

Q _α is isometric to the sub-lattice $\bar{v}^{\perp }$ of Λ _k3 and both are isometric to the orthogonal direct sum

$$\displaystyle{E_{8}(-1) \oplus E_{8}(-1) \oplus U \oplus U \oplus \mathbb{Z}\lambda,}$$

where $(\lambda,\lambda ) = \frac{2-2n} {d^{2}}$ .

Proof.

The K3 lattice $\varLambda _{k3}:= [\beta _{\tilde{\varLambda }}^{\perp }]/\mathbb{Z}\beta$ is isometric to $E_{8}(-1) \oplus E_{8}(-1) \oplus U \oplus U \oplus U$. Let L be the saturation of $\mathrm{span}_{\mathbb{Z}}\{v,\beta \}$ in $\tilde{\varLambda }$. Then L is contained in $\beta _{\tilde{\varLambda }}^{\perp }$ and the image of L in Λ _k3 is spanned by a class ξ of self-intersection $\frac{2n-2} {d^{2}}$, such that $\bar{v} = d\xi$, by Lemma 2.5.

It remains to prove that Q _α is isometric to $\xi _{\varLambda _{k3}}^{\perp }$. Consider the following commutative diagram.

$$\displaystyle{\begin{array}{ccccccc} 0 \rightarrow & \mathbb{Z}\beta & \rightarrow & \beta _{\tilde{\varLambda }}^{\perp } &\rightarrow & \varLambda _{k3} & \rightarrow 0 \\ & =\ \uparrow \ & & \uparrow & & \ \uparrow \ j \\ 0 \rightarrow & \mathbb{Z}\beta & \rightarrow &L_{\tilde{\varLambda }}^{\perp }&\rightarrow &L_{\tilde{\varLambda }}^{\perp }/\mathbb{Z}\beta & \rightarrow 0 \\ & \mathop{\cong}\ \uparrow \ & & \mathop{\cong}\ \uparrow \ \iota & & \ \uparrow \ \bar{\iota } \\ 0 \rightarrow & \mathbb{Z}\alpha & \rightarrow & \alpha _{\varLambda }^{\perp } &\rightarrow & Q_{\alpha } & \rightarrow 0. \end{array} }$$

The lower vertical arrow $\bar{\iota }$ in the rightmost column is evidently an isomorphism. The image of the upper one j is precisely $\xi _{\varLambda _{k3}}^{\perp }$. □ 

Let Ω _Λ be the period domain

$$\displaystyle{ \varOmega _{\varLambda }:=\{\ell\in \mathbb{P}[H^{2}(X, \mathbb{C})]\:\ (\ell,\ell) = 0\ \mbox{ and}\ (\ell,\bar{\ell}) > 0\}. }$$

(4.1)

Set

$$\displaystyle{ \varOmega _{\alpha ^{\perp }}:=\{\ell\in \varOmega _{\varLambda }\:\ (\ell,\alpha ) = 0\}. }$$

(4.2)

Then $\varOmega _{\alpha ^{\perp }}$ is an affine line-bundle over the period domain

$$\displaystyle{\varOmega _{Q_{\alpha }}\ \:=\ \ \{\ell\in \mathbb{P}[Q_{\alpha } \otimes _{\mathbb{Z}}\mathbb{C}]\:\ (\ell,\ell) = 0\ \mbox{ and}\ (\ell,\bar{\ell}) > 0\}.}$$

Given a point of $\varOmega _{Q_{\alpha }}$, corresponding to a one-dimensional subspace ℓ of $Q_{\alpha } \otimes _{\mathbb{Z}}\mathbb{C}$, we get a two dimensional subspace V _ℓ of $H^{2}(X, \mathbb{C})$ orthogonal to α and containing α. The line in $\varOmega _{\alpha ^{\perp }}$, over the point ℓ of $\varOmega _{Q_{\alpha }}$, is $\mathbb{P}[V _{\ell}]\setminus \{\mathbb{P}[\mathbb{C}\alpha ]\}$. Denote by

$$\displaystyle{ q\:\ \varOmega _{\alpha ^{\perp }}\ \ \rightarrow \ \ \varOmega _{Q_{\alpha }} }$$

(4.3)

the bundle map. A semi-polarized K3 surface of degree k is a pair consisting of a K3 surface together with a nef line bundle of degree k (also known as weak algebraic polarization of degree k in [33, Section 5]). Note that each component of $\varOmega _{Q_{\alpha }}$ is isomorphic to the period domain of the moduli space of semi-polarized K3 surfaces of degree $\frac{2n-2} {d^{2}}$.

Definition 4.2.

Fibers of q will be called Tate-Shafarevich lines for reasons that will become apparent in Sect. 7.

Tate-Shafarevich lines are limits of twistor lines, as will be explained in Remark 4.6.

4.3 The Period Map

Given a period ℓ ∈ Ω _Λ , set $\varLambda ^{1,1}(\ell, \mathbb{Z}):=\{\lambda \in \varLambda \:\ (\lambda,\ell) = 0\}$. Define $Q_{\alpha }^{1,1}(q(\ell), \mathbb{Z})$ similarly. We get the short exact sequence

$$\displaystyle{0 \rightarrow \mathbb{Z}\alpha \rightarrow \left [\alpha ^{\perp }\cap \varLambda ^{1,1}(\ell, \mathbb{Z})\right ] \rightarrow Q_{\alpha }^{1,1}(q(\ell), \mathbb{Z}) \rightarrow 0.}$$

$\varOmega _{\alpha ^{\perp }}$ has two connected components, since $\varOmega _{Q_{\alpha }}$ has two connected components. Indeed, Q _α has signature (2, b ₂(X) − 4), and a period ℓ comes with an oriented positive definite plane $[\ell\oplus \bar{\ell}] \cap [\varLambda _{\mathbb{R}}]$, which, in turn, determines the orientation of the positive cone in $Q_{\alpha } \otimes _{\mathbb{Z}}\mathbb{R}$.

The positive cone $\tilde{\mathcal{C}}_{\varLambda }$ in $\varLambda _{\mathbb{R}}$ is the cone

$$\displaystyle{ \tilde{\mathcal{C}}_{\varLambda }:=\{ x \in \varLambda _{\mathbb{R}}\:\ (x,x) > 0\}. }$$

(4.4)

The cohomology group $H^{2}(\tilde{\mathcal{C}}_{\varLambda }, \mathbb{Z})$ is isomorphic to $\mathbb{Z}$ and an orientation of $\tilde{\mathcal{C}}_{\varLambda }$ is the choice of one of the two generator of $H^{2}(\tilde{\mathcal{C}}_{\varLambda }, \mathbb{Z})$. An orientation of $\tilde{\mathcal{C}}_{\varLambda }$ determines an orientation of every positive definite three dimensional subspace of $\varLambda _{\mathbb{R}}$ [23, Lemma 4.1]. A choice of an orientation of $\tilde{\mathcal{C}}_{\varLambda }$ determines a choice of a component of $\varOmega _{\alpha ^{\perp }}$ as follows. A period ℓ ∈ Ω _Λ determines the subspace $\varLambda ^{1,1}(\ell, \mathbb{R})$ and the cone $\mathcal{C}_{\ell}^{{\prime}}:=\{ x \in \varLambda ^{1,1}(\ell, \mathbb{R})\:\ (x,x) > 0\}$ in $\varLambda ^{1,1}(\ell, \mathbb{R})$ has two connected components. A choice of a connected component of $\mathcal{C}_{\ell}^{{\prime}}$ is equivalent to a choice of an orientation of the positive cone of $\tilde{\mathcal{C}}_{\varLambda }$. Indeed, a non-zero element σ ∈ ℓ and an element $\omega \in \mathcal{C}_{\ell}^{{\prime}}$ determine a basis $\{\mbox{ R}e(\sigma ),\mbox{ I}m(\sigma ),\omega \}$, hence an orientation, of a positive definite three dimensional subspace of $\varLambda _{\mathbb{R}}$, and the corresponding orientation of $\tilde{\mathcal{C}}_{\varLambda }$ is independent of the choice of σ and ω. Thus, the choice of the orientation of the positive cone $\tilde{\mathcal{C}}_{\varLambda }$ determines a connected component $\mathcal{C}_{\ell}$ of $\mathcal{C}_{\ell}^{{\prime}}$, called the positive cone (for the orientation). If ℓ belongs to $\varOmega _{\alpha ^{\perp }}$, then the class α belongs to $\varLambda ^{1,1}(\ell, \mathbb{R})$ and α is in the closure of precisely one of the two connected components of $\mathcal{C}_{\ell}^{{\prime}}$. The connected component of $\varOmega _{\alpha ^{\perp }}$, compatible with the chosen orientation of $\tilde{\mathcal{C}}_{\varLambda }$, is the one for which α belongs to the boundary of the positive cone $\mathcal{C}_{\ell}$ for the chosen orientation.

A marked pair (Y, ψ) consists of an irreducible holomorphic symplectic manifold Y and an isometry ψ from $H^{2}(Y, \mathbb{Z})$ onto a fixed lattice. The moduli space of isomorphism classes of marked pairs is a non-Hausdorff complex manifold [13]. Let $\mathfrak{M}_{\varLambda }^{0}$ be a connected component of the moduli space of marked pairs of K3^[n]-type, where the fixed lattice is Λ. The period map

$$\displaystyle{P_{0}: \mathfrak{M}_{\varLambda }^{0} \rightarrow \varOmega _{\varLambda }}$$

sends a marked pair (Y, ψ) to the point ψ(H ^2, 0(Y )) of Ω _Λ . P ₀ is a holomorphic map and a local homeomorphism [4]. The positive cone $\mathcal{C}_{Y }$ is the connected component of the cone $\{x \in H^{1,1}(Y, \mathbb{R})\:\ (x,x) > 0\}$ containing the Kähler cone. Hence, the positive cone in $H^{2}(Y, \mathbb{R})$ comes with a canonical orientation and the marking ψ determines an orientation of the positive cone in $\tilde{\mathcal{C}}_{\varLambda }$. We conclude that $\mathfrak{M}_{\varLambda }^{0}$ determines an orientation of the positive cone $\tilde{\mathcal{C}}_{\varLambda }$ [23, Sec. 4]. Let

$$\displaystyle{ \varOmega _{\alpha ^{\perp }}^{+} }$$

(4.5)

be the connected component of $\varOmega _{\alpha ^{\perp }}$, inducing the same orientation of $\tilde{\mathcal{C}}_{\varLambda }$ as $\mathfrak{M}_{\varLambda }^{0}$. Let

$$\displaystyle{ \mathfrak{M}_{\alpha ^{\perp }}^{0} }$$

(4.6)

be the inverse image $P_{0}^{-1}(\varOmega _{\alpha ^{\perp }}^{+})$.

Theorem 4.3 (The Global Torelli Theorem [14, 40]).

The period map $P_{0}: \mathfrak{M}_{\varLambda }^{0} \rightarrow \varOmega _{\varLambda }$ is surjective. Any two points in the same fiber of P ₀ are inseparable. If (X ₁ ,η ₁ ) and (X ₂ ,η ₂ ) correspond to two inseparable points in $\mathfrak{M}_{\varLambda }^{0}$ , then X ₁ and X ₂ are bimeromorphic. If the Kähler cone of X is equal to its positive cone and (X,η) corresponds to a point of $\mathfrak{M}_{\varLambda }^{0}$ , then this point is separated.

Lemma 4.4.

$\mathfrak{M}_{\alpha ^{\perp }}^{0}$ is path-connected.

Proof.

The statement follows from the Global Torelli Theorem 4.3 and the fact that $\varOmega _{\alpha ^{\perp }}^{+}$ is connected. The proof is similar to that of [24, Proposition 5.11]. □ 

Proposition 4.5.

Let X ₁ and X ₂ be two irreducible holomorphic symplectic manifolds of K3 ^[n] -type and $\eta _{j}: H^{2}(X_{j}, \mathbb{Z}) \rightarrow \varLambda$ , j = 1,2, isometries. The marked pairs (X ₁ ,η ₁ ) and (X ₂ ,η ₂ ) belong to the same connected moduli space $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ , provided the following conditions hold.

• (1) The $O(\tilde{\varLambda })$ orbits $\iota _{X_{j}} \circ \eta _{j}^{-1}$ , j = 1,2, are equal. Above $\iota _{X_{j}}$ is the canonical $O(\tilde{\varLambda })$ -orbit of primitive isometric embeddings of $H^{2}(X_{j}, \mathbb{Z})$ into $\tilde{\varLambda }$ mentioned in Theorem  2.2.

• (2) $\eta _{2}^{-1} \circ \eta _{1}: H^{2}(X_{1}, \mathbb{Z}) \rightarrow H^{2}(X_{2}, \mathbb{Z})$ is orientation preserving.

• (3) $\eta _{j}^{-1}(\alpha )$ is of Hodge type (1,1) and it belongs to the boundary of the positive cone $\mathcal{C}_{X_{j}}$ in $H^{1,1}(X_{j}, \mathbb{R})$ , for j = 1,2.

Proof.

Conditions 1 and 2 imply that $\eta _{2}^{-1} \circ \eta _{1}$ is a parallel-transport operator, by Theorem 2.4. Hence, the two marked pairs belong to the same connected component $\mathfrak{M}_{\varLambda }^{0}$ of $\mathfrak{M}_{\varLambda }$. Condition 3 implies that both belong to $\mathfrak{M}_{\alpha ^{\perp }}^{0}$, and the latter is connected, by Lemma 4.4. □ 

Proof (of Proposition 1.7).

Lemma 2.5 introduced the monodromy invariant $[L,v](c_{1}(\mathcal{L}))$ of the pair $(X,\mathcal{L})$. The claimed number of deformation types in the statement of the proposition is equal to the number of values of the monodromy invariant [L, v](•) for fixed n and d, by Lemma 2.6. Assume given another pair $(X^{{\prime}},\mathcal{L}^{{\prime}})$ as above, such that the monodromy invariants $[L,v](c_{1}(\mathcal{L}^{{\prime}}))$ and $[L,v](c_{1}(\mathcal{L}))$ are equal. Choose a parallel transport operator $g: H^{2}(X^{{\prime}}, \mathbb{Z}) \rightarrow H^{2}(X, \mathbb{Z})$. We do not assume that $g(c_{1}(\mathcal{L}^{{\prime}}))$ is of Hodge type (1, 1). Set $\alpha:= c_{1}(\mathcal{L})$ and $\alpha ^{{\prime}}:= c_{1}(\mathcal{L}^{{\prime}})$. The monodromy invariant $[L,v](g(\alpha ^{{\prime}}))$ is equal to [L, v](α ^′) and hence also to [L, v](α). Hence, there exists a monodromy operator f ∈ Mon ²(X), such that fg(α ^′) = α, by Lemma 2.5. Choose a marking $\eta: H^{2}(X, \mathbb{Z}) \rightarrow \varLambda$. Then η ^′: = η ∘ f ∘ g is a marking of X ^′ satisfying η(α) = η ^′(α ^′). Hence, the triples (X, α, η) and (X ^′, α ^′, η ^′) both belong to the moduli space $\mathfrak{M}_{\eta (\alpha )^{\perp }}^{0}$, by Proposition 4.5. $\mathfrak{M}_{\eta (\alpha )^{\perp }}^{0}$ is connected, by Lemma 4.4. Hence, $(X,\mathcal{L})$ and $(X^{{\prime}},\mathcal{L}^{{\prime}})$ are deformation equivalent. □ 

Remark 4.6.

Tate-Shafarevich lines (Definition 4.2) are limits of twistor lines in the following sense. Let ℓ be a point of Ω _Λ and ω a class in the positive cone $\mathcal{C}_{\ell}$ in $\varLambda ^{1,1}(\ell, \mathbb{R})$. Assume that ω is not orthogonal to any class in $\varLambda ^{1,1}(\ell, \mathbb{Z})$. Then there exists a marked pair (X, η) in each connected component $\mathfrak{M}_{\varLambda }^{0}$ of the moduli space of marked pairs, such that P(X, η) = ℓ and η ⁻¹(ω) is a Kähler class of X [13, Cor. 5.7]. Set $W^{{\prime}}:=\ell \oplus \bar{\ell}\oplus \mathbb{C}\omega$. $\mathbb{P}(W^{{\prime}}) \cap \varOmega _{\varLambda }$ is a twistor line for (X, η); it admits a canonical lift to a smooth rational curve in $\mathfrak{M}_{\varLambda }^{0}$ containing the point (X, η) [13, Cor. 5.8]. This lift corresponds to an action of the quaternions $\mathbb{H}$ on the real tangent bundle of the differentiable manifold X, such that the unit quaternions act as integrable complex structures, one of which is the complex structure of X. Let α ∈ Λ be the primitive isotropic class as above. Assume that ℓ belongs to $\varOmega _{\alpha ^{\perp }}^{+}$. Consider the three dimensional subspace $W:=\ell \oplus \bar{\ell}\oplus \mathbb{C}\alpha$ of $H^{2}(X, \mathbb{C})$. Then W is a limit of a sequence of three dimensional subspaces $W_{i}^{{\prime}}$, associated to some sequence of classes ω _i as above, since α belongs to the boundary of the positive cone $\mathcal{C}_{\ell}$. Now W is contained in $\alpha ^{\perp }$, and so $\mathbb{P}(W) \cap \varOmega _{\alpha ^{\perp }} = \mathbb{P}(W) \cap \varOmega _{\varLambda }.$ In this degenerate case, the conic $\mathbb{P}(W) \cap \varOmega _{\varLambda }$ consists of two irreducible components, the Tate-Shafarevich line $\mathbb{P}[\ell\oplus \mathbb{C}\alpha ]\setminus \{\mathbb{P}[\mathbb{C}\alpha ]\}$ in $\varOmega _{\alpha ^{\perp }}^{+}$ and the line $\mathbb{P}[\bar{\ell}\oplus \mathbb{C}\alpha ]\setminus \{\mathbb{P}[\mathbb{C}\alpha ]\}$ in the other connected component $\varOmega _{\alpha ^{\perp }}^{-}$ of $\varOmega _{\alpha ^{\perp }}$. Theorem 7.11 will provide a lift of a generic Tate-Shafarevich line in the period domain to a line in the moduli space of marked pairs.

A summary of notation related to lattices and period domains
U	The rank 2 even unimodular lattice of signature (1, 1)
E 8(−1)	The root lattice of type E 8 with a negative definite pairing
$\tilde{\varLambda }$	The Mukai lattice; the orthogonal direct sum $U^{\oplus 4} \oplus E_{8}(-1)^{\oplus 2}$
Λ	The K3[n]-lattice; the orthogonal direct sum $U^{\oplus 3} \oplus E_{8}(-1)^{\oplus 2} \oplus \langle 2 - 2n\rangle$,
	where $\langle 2 - 2n\rangle$ is the rank 1 lattice generated by a class of self-intersection 2 − 2n
α	A primitive isotropic class in Λ
Q α	The subquotient $\alpha ^{\perp }/\mathbb{Z}\alpha$
ι	A primitive embedding of Λ in $\tilde{\varLambda }$
β	The primitive isotropic class ι(α) in $\tilde{\varLambda }$
Λ k3	The subquotient $\beta ^{\perp }/\mathbb{Z}\beta$, which is isomorphic to the K3 lattice $U^{\oplus 3} \oplus E_{8}(-1)^{\oplus 2}$
v	A generator of the rank 1 sublattice of $\tilde{\varLambda }$ orthogonal to $\iota (\varLambda )$
$\bar{v}$	The coset $v + \mathbb{Z}\beta$ in Λ k3
d	The divisibility of (α, •) in Λ ∗; d: = gcd{(α, λ) :  λ ∈ Λ}
ξ	The integral element $(1/d)\bar{v}$ of Λ k3. We have $(\xi,\xi ) = \frac{2n-2} {d^{2}}$
Ω Λ	The period domain given in (4.1)
$\tilde{\mathcal{C}}_{\varLambda }$	The positive cone given in (4.4)
Ω Λ +	The connected component of Ω Λ determined by the orientation of $\tilde{\mathcal{C}}_{\varLambda }$
$\varOmega _{\alpha ^{\perp }}$	The hyperplane section of Ω Λ given in (4.2)
$\varOmega _{\alpha ^{\perp }}^{+}$	The connected component of $\varOmega _{\alpha ^{\perp }}$ given in (4.5)
$\varOmega _{Q_{\alpha }}$	The period domain of the lattice $Q_{\alpha }$
q	The fibration $q:\varOmega _{\alpha ^{\perp }} \rightarrow \varOmega _{Q_{\alpha }}$ by Tate-Shafarevich lines given in (4.3)
$\mathfrak{M}_{\varLambda }^{0}$	A connected component of the moduli space of marked pairs
P 0	The period map $P_{0}: \mathfrak{M}_{\varLambda }^{0} \rightarrow \varOmega _{\varLambda }^{+}$
$\mathfrak{M}_{\alpha ^{\perp }}^{0}$	The inverse image of $\varOmega _{\alpha ^{\perp }}^{+}$ in $\mathfrak{M}_{\varLambda }^{0}$ via P 0
[L, v](α)	The monodromy invariant associated to the class α in Lemma 2.5 (4)

5 Density of Periods of Relative Compactified Jacobians

We keep the notation of Sect. 4. In Sect. 5.1 we construct a section $\tau:\varOmega _{ Q_{\alpha }}^{+} \rightarrow \varOmega _{\alpha ^{\perp }}^{+}$, given in (5.2), of the fibration $q:\varOmega _{ \alpha ^{\perp }}^{+} \rightarrow \varOmega _{Q_{\alpha }}^{+}$ by Tate-Shafarevich lines. We then show that τ maps a period $\underline{\ell}$, of a semi-polarized K3 surface $(S,\mathcal{B})$ in the period domain $\varOmega _{Q_{\alpha }}^{+}$, to the period $\tau (\underline{\ell})$ of a moduli space M of sheaves on S with pure one-dimensional support in the linear system $\mid \mathcal{B}^{d}\mid$. The moduli space M admits a Lagrangian fibration over $\mid \mathcal{B}^{d}\mid$. In Sect. 5.2 we construct an injective homomorphism $g: Q_{\alpha } \rightarrow O(\varLambda )$, whose image is contained in the subgroup of the monodromy group which stabilizes α. We get an action of Q _α on the period domain $\varOmega _{\alpha ^{\perp }}^{+}$, which lifts to an action on connected components $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ of the moduli space of marked pairs given in Eq. (4.6). We then show that the fibration q by Tate-Shafarevich lines is g(Q _α )-invariant. In Sect. 5.3 we prove that the g(Q _α )-orbit of every point in a non-special Tate-Shafarevich line is dense in that line. Consequently, the non-special Tate-Shafarevich line $q^{-1}(\underline{\ell})$ contains the dense orbit $g(Q_{\alpha })\tau (\underline{\ell})$ of periods of marked pairs in $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ admitting a Lagrangian fibration.

Conventions: The discussion in the current Sect. 5 concerns only period domains, so we are free to choose the embedding ι. When we consider in subsequent sections a component $\mathfrak{M}_{\varLambda }^{0}$ of the moduli space of marked pairs (X, η) of K3^[n]-type, together with such an embedding $\iota:\varLambda \rightarrow \tilde{\varLambda }$, we will always assume that ι is chosen so that ι ∘η belongs to the canonical $O(\tilde{\varLambda })$-orbit ι _X of Theorem 2.2, for all (X, η) in $\mathfrak{M}_{\varLambda }^{0}$. We choose the orientation of the positive cone $\tilde{\mathcal{C}}_{\varLambda }$ of Λ, so that α belongs to the boundary of the positive cone in $\varLambda ^{1,1}(\ell, \mathbb{R})$, for every $\ell\in \varOmega _{\alpha ^{\perp }}^{+}$. We choose the orientation of the positive cone $\tilde{\mathcal{C}}_{\varLambda _{k3}}$, so that $\bar{v}$ belongs to the positive cone in $\varLambda _{k3}^{1,1}(\underline{\ell}, \mathbb{R})$, for every $\underline{\ell}\in \varOmega _{\bar{v}^{\perp }}^{+}$. Note that the composition $\alpha _{\varLambda }^{\perp }\stackrel{\iota }{\rightarrow }\beta _{\tilde{\varLambda }}^{\perp }\rightarrow \varLambda _{k3}$ induces an isometry from $Q_{\alpha }:=\alpha _{ \varLambda }^{\perp }/\mathbb{Z}\alpha$ onto $\bar{v}_{\varLambda _{k3}}^{\perp }$, by Lemma 4.1. The choice of orientation of the positive cone of Λ _k3 determines an orientation of the positive cone of Q _α .

5.1 A Period of a Lagrangian Fibration in Each Tate-Shafarevich Line

Choose a class γ in $\tilde{\varLambda }$ satisfying $(\gamma,\beta ) = -1$ and (γ, γ) = 0. Note that β and γ span a unimodular sub-lattice of $\tilde{\varLambda }$ of signature (1, 1). We construct next a section of the affine bundle $q:\varOmega _{\alpha ^{\perp }} \rightarrow \varOmega _{Q_{\alpha }}$, given in Eq. (4.3), in terms of γ. We have the following split short exact sequence.

(5.1)

Above, $\sigma _{\gamma }(x) = -(x,\gamma )\beta$, and $\tilde{\tau }_{\gamma }(y) =\tilde{ y} + (\tilde{y},\gamma )\beta$, where $\tilde{y}$ is any element of $\beta _{\tilde{\varLambda }}^{\perp }$ satisfying $j(\tilde{y}) = y$. One sees that $\tilde{\tau }_{\gamma }$ is well defined as follows. If $\tilde{y}_{1}$ and $\tilde{y}_{2}$ satisfy $j(\tilde{y}_{k}) = y$, then the difference $[\tilde{y}_{1} + (\tilde{y_{1}},\gamma )\beta ] - [\tilde{y}_{2} + (\tilde{y_{2}},\gamma )\beta ]$ belongs to the kernel of j and is sent to 0 via σ _γ , so the difference is equal to 0. Note that $\tilde{\tau }_{\gamma }$ is an isometric embedding and its image is precisely $\{\beta,\gamma \}_{\tilde{\varLambda }}^{\perp }$.

We regard $\varOmega _{Q_{\alpha }}^{+}$ as the period domain for semi-polarized K3 surfaces, with a nef line bundle of degree $\frac{2n-2} {d^{2}}$, via the isomorphism $\bar{v}_{\varLambda _{k3}}^{\perp }\mathop{\cong}Q_{\alpha }$ of Lemma 4.1. The homomorphism $\iota ^{-1} \circ \tilde{\tau }_{\gamma }$ induces an isometric embedding of Q _α in $\alpha _{\varLambda }^{\perp }$. We get a section

$$\displaystyle{ \tau _{\gamma }\:\ \varOmega _{ Q_{\alpha }}^{+} \rightarrow \varOmega _{\alpha ^{ \perp }}^{+} }$$

(5.2)

of $q:\varOmega _{ \alpha ^{\perp }}^{+} \rightarrow \varOmega _{Q_{\alpha }}^{+}.$ Following is an explicit description of τ _γ . Let $\underline{\ell}$ be a period in $\varOmega _{Q_{\alpha }}^{+}$. Choose a period ℓ in $\varOmega _{\alpha ^{\perp }}^{+}$ satisfying $q(\ell) =\underline{\ell}$. Let x be a non-zero element of the line ℓ in $\alpha _{\varLambda }^{\perp }\otimes _{\mathbb{Z}}\mathbb{C}$. Then

$$\displaystyle{ \tau _{\gamma }(\underline{\ell}) = \mathrm{span}_{\mathbb{C}}\{x + (\iota (x),\gamma )\alpha \}. }$$

(5.3)

We see that γ belongs to $\tilde{\varLambda }^{1,1}(\tau _{\gamma }(\underline{\ell}))$, for every $\underline{\ell}$ in $\varOmega _{Q_{\alpha }}^{+}$.

Fix a period $\underline{\ell}$ in $\varOmega _{Q_{\alpha }}^{+}$. We construct next a marked pair (M _H (u), η ₁) with period $\tau _{\gamma }(\underline{\ell})$, such that $\eta _{1}^{-1}(\alpha )$ induces a Lagrangian fibration. Let S be a K3 surface and $\eta: H^{2}(S, \mathbb{Z}) \rightarrow \varLambda _{k3}$ a marking, such that the period η(H ^2, 0(S)) is $\underline{\ell}$. Such a marked pair (S, η) exists, by the surjectivity of the period map. Extend η to the Hodge isometry

$$\displaystyle{\tilde{\eta }\:\ H^{{\ast}}(S, \mathbb{Z}) \rightarrow \tilde{\varLambda },}$$

given by $\tilde{\eta }((0,0,1)) =\beta$, $\tilde{\eta }((1,0,0)) =\gamma$, and $\tilde{\eta }$ restricts to $H^{2}(S, \mathbb{Z})$ as $\tilde{\tau }_{\gamma }\circ \eta$. We have the equality $v =\sigma _{\gamma }(v) +\tilde{\tau } _{\gamma }(\bar{v}) = -(\gamma,v)\beta +\tilde{\tau } _{\gamma }(\bar{v})$. Set $a:= -(\gamma,v)$ and $u:= (0,\eta ^{-1}(\bar{v}),a)$. Then $\tilde{\eta }(u) = v$. We may choose the marking η so that the class $\eta ^{-1}(\bar{v})$ is nef, possibly after replacing η by $\pm \eta \circ w$, where w is an element of the group of isometries of $H^{2}(S, \mathbb{Z})$, generated by reflections by − 2 curves [2, Ch. VIII Prop. 3.9]. Choose a u-generic polarization H of S. Then M _H (u) is a projective irreducible holomorphic symplectic manifold. Let

$$\displaystyle{\theta: u^{\perp }\rightarrow H^{2}(M_{ H}(u), \mathbb{Z})}$$

be Mukai’s isometry, given in Eq. (3.1). We get the commutative diagram:

(5.4)

where η ₂ is the restriction of $\tilde{\eta }$ and $\eta _{1} =\iota ^{-1} \circ \eta _{2} \circ \theta ^{-1}$. Note that $\eta _{1}(\theta (0,0,1)) =\alpha$. Let L be the saturation in $H^{{\ast}}(S, \mathbb{Z})$ of the sub-lattice spanned by (0, 0, 1) and u. Let b be an integer satisfying ab ≡ 1 (modulo d). The monodromy invariant [L, u](θ(0, 0, 1)) of Lemma 2.5 is the isometry class of the pair (L _n, d , (d, b)), by the commutativity of the above diagram. Furthermore, η ₁ is a Hodge isometry with respect to the Hodge structure on Λ induced by $\tau _{\gamma }(\underline{\ell})$. In particular, (M _H (u), η ₁) is a marked pair with period $\tau _{\gamma }(\underline{\ell})$. Example 3.1 exhibits θ(0, 0, 1) as the class $\pi ^{{\ast}}c_{1}(\mathcal{O}_{\mid \mathcal{L}^{d}\mid }(1))$, for a Lagrangian fibration $\pi: M_{H}(u) \rightarrow \mid \mathcal{L}^{d}\mid$, where $\mathcal{L}$ is the line bundle over S with class η ⁻¹(ξ).

Remark 5.1.

The isometry η ₁ is compatible with the orientations of the positive cones, the canonical one of $H^{2}(M_{H}(u), \mathbb{Z})$ and the chosen one of Λ. Indeed, it maps the class θ(0, 0, 1), on the boundary of the positive cone of $H^{1,1}(M_{H}(u), \mathbb{R})$, to the class α on the boundary of the positive cone of $\varLambda ^{1,1}(\tau _{\gamma }(\underline{\ell}), \mathbb{R})$. The composition $\tilde{\eta }\circ \theta ^{-1}$ in Diagram (5.4) belongs to the canonical orbit $\iota _{M_{H}(u)}$ of Theorem 2.2, by [22, Theorem 1.14]. The commutativity of the Diagram implies that the isometric embedding ι ∘η ₁ also belongs to the orbit $\iota _{M_{H}(u)}$.

5.2 Monodromy Equivariance of the Fibration by Tate-Shafarevich Lines

Denote by $O(\tilde{\varLambda })_{\beta,v}^{+}$ the subgroup of $O(\tilde{\varLambda })^{+}$ stabilizing both β and v. Following is a natural homomorphism

$$\displaystyle{ h: O(\tilde{\varLambda })_{\beta,v}^{+} \rightarrow O(\varLambda _{ k3})_{\bar{v}}. }$$

(5.5)

If ψ belongs to $O(\tilde{\varLambda })_{\beta,v}^{+}$, then ψ(β) = β and $\beta _{\tilde{\varLambda }}^{\perp }$ is ψ-invariant. Thus ψ induces an isometry h(ψ) of $\varLambda _{k3}:=\beta _{ \tilde{\varLambda }}^{\perp }/\mathbb{Z}\beta$. We construct next a large subgroup in the kernel of h.

Given an element z of $\tilde{\varLambda }$, orthogonal to β and v, define the map $\tilde{g}_{z}:\tilde{\varLambda }\rightarrow \tilde{\varLambda }$ by

$$\displaystyle{\tilde{g}_{z}(x)\ \:=\ \ x - (x,\beta )z + \left [(x,z) -\frac{1} {2}(x,\beta )(z,z)\right ]\beta.}$$

Lemma 5.2.

The map $\tilde{g}_{z}$ is the unique isometry in $O(\tilde{\varLambda })_{\beta,v}$ , which sends γ to an element of $\tilde{\varLambda }$ congruent to γ + z modulo $\mathbb{Z}\beta$ and belongs to the kernel of h. The isometry $\tilde{g}_{z}$ is orientation preserving.

Proof.

We first define an isometry f with the above property, then prove its uniqueness, and finally prove that it is equal to $\tilde{g}_{z}$. Set $\gamma _{1}:=\gamma +z + \left [(\gamma,z) + \frac{1} {2}(z,z)\right ]\beta$. Then (γ ₁, γ ₁) = 0, $(\gamma _{1},\beta ) = -1$, and γ ₁ is the unique element of $\tilde{\varLambda }$ satisfying the above equalities and congruent to $\gamma +z$ modulo $\mathbb{Z}\beta$. Define $\tilde{\sigma }_{\gamma }:\tilde{\varLambda }\rightarrow \mathbb{Z}\beta + \mathbb{Z}\gamma$ by $\tilde{\sigma }_{\gamma }(x):= -(x,\beta )\gamma - (x,\gamma )\beta$. We get the commutative diagram with split short exact rows:

Above $\tilde{\tau }_{\gamma }$ and j are the homomorphisms given in Eq. (5.1), $\tilde{j}(x) = j(x + (x,\beta )\gamma )$, and $\tilde{\sigma }_{\gamma _{1}}$, $\tilde{\tau }_{\gamma _{ 1}}$, and $\tilde{j}_{1}$ are defined similarly, replacing γ by γ ₁. The map f is defined by f(β) = β, f(γ) = γ ₁, and $f(\tilde{\tau }_{\gamma }(y)) =\tilde{\tau } _{\gamma _{1}}(y)$. Then f is clearly an isometry.

The isometry f can be extended to an isometry of $\tilde{\varLambda }_{\mathbb{R}}$ and we can continuously deform z to 0 in $\{\beta,v\}^{\perp }\otimes _{\mathbb{Z}}\mathbb{R}$, resulting in a continuous deformation of f to the identity. Hence, f is orientation preserving.

Note the equalities $\tilde{\sigma }_{\gamma }(v) = -(v,\gamma )\beta = -(v,\gamma _{1})\beta =\tilde{\sigma } _{\gamma _{1}}(v)$, where the middle one follows from that fact that both z and β are orthogonal to v. We get the equality

$$\displaystyle{\tilde{\tau }_{\gamma }(\bar{v}) = v -\tilde{\sigma }_{\gamma }(v) = v -\tilde{\sigma }_{\gamma _{1}}(v) =\tilde{\tau } _{\gamma _{1}}(\bar{v}).}$$

Thus f(v) = v and f belongs to $O(\tilde{\varLambda })_{\beta,v}^{+}$. Let x be an element of β ^⊥. Then $\tilde{j}(x) = j(x) =\tilde{ j}_{1}(x)$. Set y: = j(x). Now $\tilde{\tau }_{\gamma }(y) \equiv \tilde{\tau }_{\gamma _{1}}(y)$ modulo $\mathbb{Z}\beta$, by definition of both. Hence, h(f) is the identity isometry of Λ _k3.

Let f ^′ be another isometry of $\tilde{\varLambda }$ satisfying the assumptions of the Lemma. Then f ^′(γ) = γ ₁, by the characterization of γ ₁ mentioned above. Set $e:= f^{-1} \circ f^{{\prime}}$. Then e(β) = β, e(γ) = γ, e(v) = v, and h(e) = id. Given x ∈ β ^⊥, we get that e(x) ≡ x modulo $\mathbb{Z}\beta$. Now $(e(x),\gamma ) = (e(x),e(\gamma )) = (x,\gamma )$. Thus, e restricts to the identity on β ^⊥. We conclude that e is the identity of $\tilde{\varLambda }$, as the latter is spanned by γ and β ^⊥. Thus f ^′ = f.

It remains to prove the equality $f =\tilde{ g}_{z}$. We already know that $f(\gamma ) =\gamma _{1} =\tilde{ g}_{z}(\gamma )$ and $f(\beta ) =\beta =\tilde{ g}_{z}(\beta )$. Given y ∈ Λ _k3, we have

$$\displaystyle{\tilde{g}_{z}(\tilde{\tau }_{\gamma }(y)) =\tilde{\tau } _{\gamma }(y) + (\tilde{\tau }_{\gamma }(y),z)\beta =\tilde{\tau } _{\gamma _{1}}(y) = f(\tilde{\tau }_{\gamma }(y)).}$$

Hence, $\tilde{g}_{z} = f$. □ 

Let

$$\displaystyle{\tilde{g}:\alpha _{ \varLambda }^{\perp }\rightarrow O(\tilde{\varLambda })_{\beta,v}^{+}}$$

be the map sending z to $\tilde{g}_{\iota (z)}$. Denote by $\mathit{Mon}^{2}(\varLambda,\iota )$ the subgroup of O ⁺(Λ) of isometries stabilizing the orbit $O(\tilde{\varLambda })\iota$. Note that $O(\tilde{\varLambda })_{v}^{+}$ is conjugated via ι onto $\mathit{Mon}^{2}(\varLambda,\iota )$, if n = 2, and to an index 2 subgroup of Mon ²(Λ, ι), if n ≥ 2 [21, Lemma 4.10]. Let $\mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$ be the subgroup of Mon ²(Λ, ι) stabilizing α.

Lemma 5.3.

• (1) The map $\tilde{g}$ is a group homomorphism with kernel $\mathbb{Z}\alpha$ . It thus factors through an injective homomorphism

  $$\displaystyle{g: Q_{\alpha } \rightarrow \mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }.}$$

• (2) Let z be an element of $\alpha _{\varLambda }^{\perp }$ and [z] its coset in Q _α . Then $g_{[z]}:\alpha ^{\perp }\rightarrow \alpha ^{\perp }$ sends x ∈α ^⊥ to x + (x,z)α.

• (3) The map $q:\varOmega _{ \alpha ^{\perp }}^{+} \rightarrow \varOmega _{Q_{\alpha }}^{+}$ is $\mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$ -equivariant and it is invariant with respect to the image $g(Q_{\alpha }) \subset \mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$ of g.

• (4) The image of $\tilde{g}$ is equal to the kernel of the homomorphism h, given in Eq. (5.5).

Proof.

Part (1) follows from the characterization of $\tilde{g}_{z}$ in Lemma 5.2. Part (2) is straightforward as is the $\mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$-equivariance of q. The g(Q _α )-invariance of q follows from part (2). Part (3) is thus proven.

Part (4): The image of $\tilde{g}$ is contained in the kernel of h, by Lemma 5.2. Let $f \in O(\tilde{\varLambda })_{\beta,v}$ belong to the kernel of h. Set γ ₁: = f(γ) and $z:=\gamma _{1}-\gamma$. Then $(\gamma _{1},\beta ) = (f(\gamma ),\beta ) = (f(\gamma ),f(\beta )) = (\gamma,\beta )$ and similarly (γ ₁, v) = (γ, v). Hence, (z, β) = 0 and (z, v) = 0. The isometry $\tilde{g}_{z}$ is thus well defined and it is equal to f, by Lemma 5.2. □ 

5.3 Density

A period $\underline{\ell}$ in $\varOmega _{\varLambda _{k3}}$ is said to be special, if it satisfies the condition analogous to the one in Definition 1.1. We identify $\varOmega _{Q_{\alpha }}$ as a submanifold of $\varOmega _{\varLambda _{ k3}}$, via Lemma 4.1. Note that a period $\ell\in \varOmega _{\alpha ^{\perp }}$ is special, if and only if the period q(ℓ) is.

Lemma 5.4.

• 1. g(Q _α ) has a dense orbit in $q^{-1}(\underline{\ell})$ , if and only if $\underline{\ell}$ is non-special.

• 2. If g(Q _α ) has a dense orbit in $q^{-1}(\underline{\ell})$ , then every g(Q _α )-orbit in $q^{-1}(\underline{\ell})$ is dense.

Proof.

Part 2 follows from the description of the action in Lemma 5.3 part 2. We prove part 1. Fix a period ℓ such that $q(\ell) =\underline{\ell}$ and choose a non-zero element t of the line ℓ in $\alpha _{\varLambda }^{\perp }\otimes _{\mathbb{Z}}\mathbb{C}$. Then $q^{-1}(\underline{\ell}) = \mathbb{P}[\mathbb{C}\alpha + \mathbb{C}t]\setminus \{\mathbb{P}[\mathbb{C}\alpha ]\}$ and $g_{[z]}(a\alpha + t) = (a + (t,z))\alpha + t$, by Lemma 5.3 part 2. The fiber $q^{-1}(\underline{\ell})$ has a dense g(Q _α )-orbit, if and only if the image of

$$\displaystyle{ (t,\bullet ): Q_{\alpha } \rightarrow \mathbb{C} }$$

(5.6)

is dense in $\mathbb{C}$.

Suppose first that $\underline{\ell}$ is special. Set $V:= [\underline{\ell}\oplus \bar{\underline{\ell}}] \cap [Q_{\alpha } \otimes _{\mathbb{Z}}\mathbb{R}]$. Let λ be a non-zero element in $V \cap Q_{\alpha }$. There exists an element $t \in \underline{\ell}$, such that $\lambda = t +\bar{ t}$. Given an element z ∈ Q _α , then $2Re(z,t) = (z,t) + (z,\bar{t}) = (z,\lambda )$ is an integer. Thus, Re(z, t) belongs to the discrete subgroup $\frac{1} {2}\mathbb{Z}$ of $\mathbb{R}$. Hence, the image of the homomorphism (5.6) is not dense in $\mathbb{C}$.

Assume next that $\underline{\ell}$ is non-special. Denote by $\varTheta (\underline{\ell}) \subset Q_{\alpha }$ the lattice orthogonal to the kernel of the homomorphism (5.6). $\varTheta (\underline{\ell})$ is the transcendental lattice of the K3-surface with period $\underline{\ell}$. We know that $\varTheta (\underline{\ell})$ has rank at least two, and if the rank of $\varTheta (\underline{\ell})$ is 2, then the Hodge decomposition is defined over $\mathbb{Q}$ and so $\underline{\ell}$ is special. Thus, the rank of $\varTheta (\underline{\ell})$ is at least three. Let $G \subset \varTheta (\underline{\ell})$ be a co-rank 1 subgroup. We claim that the image (t, G), of G via the homomorphism (5.6), spans $\mathbb{C}$ as a 2-dimensional real vector space. The latter statement is equivalent to the statement that the image of G in V ^∗, under the map z↦(z, •) which has real values on V, spans V ^∗. The equivalence is clear considering the following isomorphisms of two dimensional real vector spaces:

where ev _t is evaluation at t, Re takes (z, •) to its real part Re(z, •), and p ^∗ is pullback via the projection p: V → ℓ on the (2, 0) part. Assume that the image of G in V ^∗ spans a one-dimensional subspace W. Let U be the subspace of V annihilated by W, and hence also by (z, •), z ∈ G. Then the kernel of the homomorphism $\varLambda _{k3} \rightarrow U^{{\ast}}$, given by z↦(z, •), has co-rank 1 in Λ _k3. It follows that the decomposition $\varLambda _{k3} \otimes _{\mathbb{Z}}\mathbb{R} = U \oplus U^{\perp }$ is defined over $\mathbb{Q}$. Thus, U ∩Λ _k3 is non-trivial and $\underline{\ell}$ is special. A contradiction. Thus, indeed, the image (t, G) of G spans $\mathbb{C}$. Let $Z \subset \mathbb{C}$ be the image $(t,\varTheta (\underline{\ell}))$ of $\varTheta (\underline{\ell})$ via the homomorphism (5.6). We have established that Z satisfies the hypothesis of Lemma 5.5 below, which implies that the image of the homomorphism (5.6) is dense in $\mathbb{C}$. □ 

Lemma 5.5.

Let $Z \subset \mathbb{R}^{2}$ be a free additive subgroup of rank ≥ 3. Assume that any co-rank 1 subgroup of Z spans $\mathbb{R}^{2}$ as a real vector space. Then Z is dense in $\mathbb{R}^{2}$ .

Proof.

Let Σ be the set of all bases of $\mathbb{R}^{2}$, consisting of elements of Z. Given a basis β ∈ Σ, $\beta =\{ z_{1},z_{2}\}$, set $\left \vert \!\beta \!\right \vert = \left \vert \!z_{1}\!\right \vert + \left \vert \!z_{2}\!\right \vert$. Set $I:=\inf \{ \left \vert \!\beta \!\right \vert \:\ \beta \in \varSigma \}.$ Note that the closed parallelogram P _β with vertices {0, z ₁, z ₂, z ₁ + z ₂} has diameter $< \left \vert \!\beta \!\right \vert$. Furthermore, every point of the plane belongs to a translate of P _β by an element of the subset $\mathrm{span}_{\mathbb{Z}}\{z_{1},z_{2}\}$ of Z. Hence, it suffices to prove that I = 0.

The proof is by contradiction. Assume that I > 0. Let β = { z ₁, z ₂} be a basis satisfying $I \leq \left \vert \!\beta \!\right \vert < \frac{12} {11}I$. We may assume, without loss of generality, that $\left \vert \!z_{1}\!\right \vert \geq \left \vert \!z_{2}\!\right \vert$.

We prove next that there exists an element w ∈ Z, such that $w = c_{1}z_{1} + c_{2}z_{2}$, where the coefficients c _i are irrational. Set r: = rank(Z). Let $z_{3},\ldots,z_{r}$ be elements of Z completing {z ₁, z ₂} to a subset, which is linearly independent over $\mathbb{Q}$. Write $z_{j} = c_{j,1}z_{1} + c_{j,2}z_{2}$, for 3 ≤ j ≤ r. Assume that c _j, 1 are rational, for 3 ≤ j ≤ r. Then there exists a positive integer N, such that Nc _j, 1 are integers, for all 3 ≤ j ≤ r. Then

$$\displaystyle{\{z_{2},\mathit{Nz}_{3} -\mathit{Nc}_{3,1}z_{1},\ldots,\mathit{Nz}_{r} -\mathit{Nc}_{r,1}z_{1}\}}$$

spans a co-rank 1 subgroup of Z, which lies on $\mathbb{R}z_{2}$. This contradicts the assumption on Z. Hence, there exists an element w ∈ Z, such that $w = c_{1}z_{1} + c_{2}z_{2}$, where the coefficient c ₁ is irrational. Repeating the above argument for c ₂, we get the desired conclusion.

Choose an element w as above. By adding vectors in $\mathrm{span}_{\mathbb{Z}}\{z_{1},z_{2}\}$, and possibly after changing the signs of z ₁ or z ₂, we may assume that $w = c_{1}z_{1} + c_{2}z_{2}$, with $0 < c_{1} < \frac{1} {2}$ and $0 < c_{2} < \frac{1} {2}$. Then w belongs to the parallelogram $\frac{1} {2}P_{\beta }$ with vertices $\{0, \frac{z_{1}} {2}, \frac{z_{2}} {2}, \frac{z_{1}+z_{2}} {2} \}$. If c ₁ and c ₂ are both larger than $\frac{1} {3}$ replace w by $z_{1} + z_{2} - 2w$. We may thus assume further, that at least one c _i is $\leq \frac{1} {3}$. In particular, $\left \vert \!w\!\right \vert \leq c_{1}\left \vert \!z_{1}\!\right \vert + c_{2}\left \vert \!z_{2}\!\right \vert < \frac{5} {6}\left \vert \!z_{1}\!\right \vert.$ Consider the new basis $\tilde{\beta }:=\{ w,z_{2}\}$ of $\mathbb{R}^{2}$. Then $\left \vert \!\tilde{\beta }\!\right \vert = \left \vert \!w\!\right \vert + \left \vert \!z_{2}\!\right \vert < \frac{5} {6}\left \vert \!z_{1}\!\right \vert + \left \vert \!z_{2}\!\right \vert = \left \vert \!\beta \!\right \vert -\frac{1} {6}\left \vert \!z_{1}\!\right \vert \leq \frac{11} {12}\left \vert \!\beta \!\right \vert < I.$ We obtain the desired contradiction. □ 

Denote by $J_{\alpha } \subset \varOmega _{\alpha ^{\perp }}$ the union of all the g(Q _α ) translates of the section τ _γ constructed in Eq. (5.2) above.

$$\displaystyle{J_{\alpha }:=\bigcup _{y\in Q_{\alpha }}g_{y}\left [\tau _{\gamma }\left (\varOmega _{Q_{\alpha }}^{+}\right )\right ].}$$

One easily checks that $g_{[z]} \circ \tau _{\gamma } =\tau _{\delta }$, where $\delta:=\gamma +\iota (z) + (\gamma,\iota (z))\beta + \frac{(z,z)} {2} \beta$, for all $z \in \alpha _{\varLambda }^{\perp }$, and so J _α is independent of the choice of γ.

Proposition 5.6.

• (1) J _α is a dense subset of $\varOmega _{\alpha ^{\perp }}^{+}$ .

• (2) If V is a g(Q _α )-invariant open subset of $\varOmega _{\alpha ^{\perp }}^{+}$ , which contains J _α , then V contains every non-special period in $\varOmega _{\alpha ^{\perp }}^{+}$ .

• (3) For every ℓ ∈ J _α , there exists a marked pair (M,η), consisting of a smooth projective irreducible holomorphic symplectic manifold M of K3 ^[n] -type and a marking $\eta: H^{2}(M, \mathbb{Z}) \rightarrow \varLambda$ with period ℓ satisfying the following properties.

  • (a) The composition $\iota \circ \eta: H^{2}(M, \mathbb{Z}) \rightarrow \tilde{\varLambda }$ belongs to the canonical $O(\tilde{\varLambda })$ -orbit ι _M of Theorem  2.2.

  • (b) There exists a Lagrangian fibration $\pi: M \rightarrow \mathbb{P}^{n}$ , such that the class η ⁻¹ (α) is equal to $\pi ^{{\ast}}c_{1}(\mathcal{O}_{\mathbb{P}^{n}}(1))$ .

Proof.

• (1) The density of J _α follows from Lemma 5.4.

• (2) V intersects every non-special fiber $q^{-1}(\underline{\ell})$ in a non-empty open g(Q _α )-equivariant subset of the latter. The complement $q^{-1}(\underline{\ell})\setminus V$ is thus a closed g(Q _α )-equivariant proper subset of the fiber. But any g(Q _α )-orbit in the non-special fiber $q^{-1}(\underline{\ell})$ is dense in $q^{-1}(\underline{\ell})$, by Lemma 5.4. Hence, the complement $q^{-1}(\underline{\ell})\setminus V$ must be empty.

• (3) If ℓ ₀ belongs to the section $\tau _{\gamma }\left (\varOmega _{Q_{\alpha }}^{+}\right )$, then such a pair (M, η): = (M _H (u), η ₁) was constructed in Diagram (5.4) as mentioned in Remark 5.1. If ℓ = g _z (ℓ ₀), $z \in \alpha _{\varLambda }^{\perp }$, set $(M,\eta ) = (M_{H}(u),g_{z} \circ \eta _{1})$. □ 

6 Primitive Isotropic Classes and Lagrangian Fibrations

We prove Theorem 1.3 in this section using the geometry of the moduli space $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ given in Eq. (4.6). Recall that $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ is a connected component of the moduli space of marked pairs (X, η) with X of K3^[n]-type and such that η ⁻¹(α) is a primitive isotropic class of Hodge type (1, 1) in the boundary of the positive cone in $H^{1,1}(X, \mathbb{R})$.

Fix a connected moduli space $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ as in Eq. (4.6). Denote by $\mathcal{L}_{\eta ^{-1}(\alpha )}$ the line bundle on X with $c_{1}(\mathcal{L}) =\eta ^{-1}(\alpha )$. Let V be the subset of $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ consisting of all pairs (X, η), such that $\mathcal{L}_{\eta ^{-1}(\alpha )}$ induces a Lagrangian fibration.

Theorem 6.1.

The image of V via the period map contains every non-special period in $\varOmega _{\alpha ^{\perp }}^{+}$ .

Proof.

Let (X, η) be a marked pair in $\mathfrak{M}_{\alpha ^{\perp }}^{0}$. The property that η ⁻¹(α) is the first Chern class of a line-bundle $\mathcal{L}$ on X, which induces a Lagrangian fibration $X \rightarrow \mid \mathcal{L}\mid ^{{\ast}}$, is an open property in the moduli space of marked pairs, by a result of Matsushita [27]. V is thus an open subset.

Choose a primitive embedding $\iota:\varLambda \rightarrow \tilde{\varLambda }$ with the property that ι ∘η belongs to the canonical $O(\tilde{\varLambda })$-orbit ι _X of Theorem 2.2, for all $(X,\eta )$ in $\mathfrak{M}_{\varLambda }^{0}$. Let Mon ²(Λ, ι) and its subgroup $\mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$ be the subgroups of O ⁺(Λ) introduced in Lemma 5.3. The component $\mathfrak{M}_{\varLambda }^{0}$ of the moduli space of marked pairs is invariant under $\mathit{Mon}^{2}(\varLambda,\iota )$, by Theorem 2.4. The subset $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ of $\mathfrak{M}_{\varLambda }^{0}$ is invariant under the subgroup $\mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$. Hence, the subset V is $\mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$ invariant. The construction in Sect. 5.1 yields a marked pair (M _H (u), η ₁) with period in the image of the section $\tau _{\gamma }:\varOmega _{ Q_{\alpha }}^{+} \rightarrow \varOmega _{\alpha ^{\perp }}^{+}$, given in Eq. (5.2). Furthermore, the class $\eta _{1}^{-1}(\alpha )$ induces a Lagrangian fibration of M _H (u). The marked pair $(M_{H}(u),\eta _{1})$ belongs to $\mathfrak{M}_{\alpha ^{\perp }}^{0}$, by Proposition 4.5 (Remark 5.1 verifies the conditions of Proposition 4.5). Hence, (M _H (u), η ₁) belongs to V and the image of the section $\tau _{\gamma }:\varOmega _{ Q_{\alpha }}^{+} \rightarrow \varOmega _{\alpha ^{\perp }}^{+}$ is thus contained in the image of V via the period map. The period map P ₀ is $\mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$ equivariant and a local homeomorphism, by the Local Torelli Theorem [4]. Hence, the image P ₀(V ) is an open and $\mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$ invariant subset of $\varOmega _{\alpha ^{\perp }}^{+}$. Any $\mathit{Mon}^{2}(\varLambda,\iota )_{\alpha }$ invariant subset, which contains the section $\tau _{\gamma }(\varOmega _{Q_{\alpha }}^{+})$, contains also the dense subset J _α of Proposition 5.6. P ₀(V ) thus contains every non-special period in $\varOmega _{\alpha ^{\perp }}^{+}$, by Proposition 5.6 (2). □ 

We will need the following criterion of Kawamata for a line bundle to be semi-ample. Let X be a smooth projective variety and D a divisor class on X. Set $\nu (X,D):=\max \{ e\:\ D^{e}\not\equiv 0\}$, where $\equiv$ denotes numerical equivalence. If D ≡ 0, we set ν(X, D) = 0. Denote by

the rational map, defined whenever the linear system is non-empty. Set $\kappa (X,D):=\max \{\dim \varPhi _{kD}(X)\:\ k > 0\}$, if ∣kD∣ is non-empty for some positive integer k, and $\kappa (X,D):= -\infty$, otherwise.

Theorem 6.2 (A special case of [16, Theorem 6.1]).

Let X be a smooth projective variety with a trivial canonical bundle and D a nef divisor. Assume that ν(X,D) = κ(X,D) and κ(X,D) ≥ 0. Then D is semi-ample, i.e., there exists a positive integer k such that the linear system ∣kD∣ is base point free.

An alternate proof of Kawamata’s Theorem is provided in [11]. A reduced and irreducible divisor E on X is called prime-exceptional, if the class $e \in H^{2}(X, \mathbb{Z})$ of E satisfies (e, e) < 0. Consider the reflection $R_{E}: H^{2}(X, \mathbb{Z}) \rightarrow H^{2}(X, \mathbb{Z})$, given by

$$\displaystyle{R_{E}(x) = x -\frac{2(x,e)} {(e,e)} e.}$$

It is known that the reflection R _E by the class of a prime exceptional divisor E is a monodromy operator, and in particular an integral isometry [24, Cor. 3.6]. Let $W(X) \subset O(H^{2}(X, \mathbb{Z}))$ be the subgroup generated by reflections R _E by classes of prime exceptional divisors E ⊂ X. Elements of W(X) preserve the Hodge structure, hence W(X) acts on $H^{1,1}(X, \mathbb{Z})$.

Let $\mathcal{P}\mathit{ex}_{X} \subset H^{1,1}(X, \mathbb{Z})$ be the set of classes of prime exceptional divisors. The fundamental exceptional chamber of the positive cone $\mathcal{C}_{X}$ is the set

$$\displaystyle{\mathcal{F}\mathcal{E}_{X}\ \:=\ \ \{ a \in \mathcal{C}_{X}\:\ (a,e) > 0,\ \mbox{ for all}\ e \in \mathcal{P}\mathit{ex}_{X}\}.}$$

The closure of $\mathcal{F}\mathcal{E}_{X}$ in $\mathcal{C}_{X}$ is a fundamental domain for the action of W(X) [23, Theorem 6.18]. Let

be a bimeromorphic map to an irreducible holomorphic symplectic manifold Y and $\mathcal{K}_{Y }$ the Kähler cone of Y. Then $f^{{\ast}}\mathcal{K}_{Y }$ is an open subset of $\mathcal{F}\mathcal{E}_{X}$. Furthermore, the union of $f^{{\ast}}\mathcal{K}_{Y }$, as f and Y vary over all such pairs, is a dense open subset of $\mathcal{F}\mathcal{E}_{X}$, by a result of Boucksom [6] (see also [23, Theorem 1.5]).

Proof (of Theorem 1.3).

Step 1: Keep the notation in the opening paragraph of Sect. 5. Choose a marking $\eta: H^{2}(X, \mathbb{Z}) \rightarrow \varLambda$, such that ι ∘η belongs to the canonical $O(\tilde{\varLambda })$-orbit ι _X . Set $\alpha:=\eta (c_{1}(\mathcal{L}))$. Then (X, η) belongs to a component $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ of the moduli space of marked pairs of K3^[n]-type considered in Theorem 6.1. We use here the assumption that $\mathcal{L}$ is nef in order to deduce that η ⁻¹(α) belongs to the boundary of the positive cone of X, used in Theorem 6.1.

The period P ₀(X, η) is non-special, by assumption. There exists a marked pair (Y, ψ) in $\mathfrak{M}_{\alpha ^{\perp }}^{0}$ satisfying P ₀(Y, ψ) = P ₀(X, η), such that the class ψ ⁻¹(α) induces a Lagrangian fibration, by Theorem 6.1. The marked pairs (X, η) and (Y, ψ) correspond to inseparable points in the moduli space $\mathfrak{M}_{\alpha ^{\perp }}^{0}$, by the Global Torelli Theorem 4.3. Hence, there exists an analytic correspondence Z ⊂ X × Y, $Z =\sum _{ i=0}^{k}Z_{i}$ in X × Y, of pure dimension 2n, with the following properties, by results of Huybrechts [13, Theorem 4.3] (see also [23, Sec. 3.2]).

• (1) The homomorphism $Z_{{\ast}}: H^{{\ast}}(X, \mathbb{Z}) \rightarrow H^{{\ast}}(Y, \mathbb{Z})$ is a Hodge isometry, which is equal to ψ ⁻¹ ∘η. The irreducible component Z ₀ of the correspondence is the graph of a bimeromorphic map

  

  .

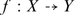
• (2) The images in X and Y of all other components Z _i , i > 0, are of positive co-dimension.

Step 2: We prove next that the line bundle $\mathcal{L}$ over X is semi-ample. We consider separately the projective and non-algebraic cases.

Step 2.1: Assume that X is not projective.³ We claim that $f_{{\ast}}(c_{1}(\mathcal{L})) =\psi ^{-1}(\alpha )$. The Neron-Severi group NS(X) does not contain any positive class, by Huybrechts projectivity criterion [13]. Hence, the Beauville-Bogomolov-Fujiki pairing restricts to NS(X) as a non-positive pairing with a rank one null sub-lattice spanned by the class $c_{1}(\mathcal{L})$. Similarly, the Beauville-Bogomolov-Fujiki pairing restricts to NS(Y ) with a rank one null space spanned by ψ ⁻¹(α). Hence, $f_{{\ast}}(c_{1}(\mathcal{L})) = \pm \psi ^{-1}(\alpha )$. Now ψ ⁻¹(α) is semi-ample and hence belongs to the closure of $\mathcal{F}\mathcal{E}_{Y }$. The class $c_{1}(\mathcal{L})$ is assumed nef, and hence belongs to the closure of $\mathcal{F}\mathcal{E}_{X}$. The bimeromorphic map f induces a Hodge-isometry $f_{{\ast}}: H^{2}(X, \mathbb{Z}) \rightarrow H^{2}(Y, \mathbb{Z})$, which maps $\mathcal{F}\mathcal{E}_{X}$ onto $\mathcal{F}\mathcal{E}_{Y }$ [6]. Hence, $f_{{\ast}}(c_{1}(\mathcal{L}))$ belongs to $\overline{\mathcal{F}\mathcal{E}}_{Y }$ as well. We conclude the equality $f_{{\ast}}(c_{1}(\mathcal{L})) =\psi ^{-1}(\alpha )$.

Let $\mathcal{L}_{2}$ be the line bundle with $c_{1}(\mathcal{L}_{2}) =\psi ^{-1}(\alpha )$. The bimeromorphic map

is holomorphic in co-dimension one, and so induces an isomorphism $f_{1}: \mid \mathcal{L}\mid \rightarrow \mid \mathcal{L}_{2}\mid$ of the two linear systems. Denote by $\varPhi _{\mathcal{L}_{2}}: Y \rightarrow \mid \mathcal{L}_{2}\mid ^{{\ast}}$ the Lagrangian fibration induced by $\mathcal{L}_{2}$. We conclude that $\mid \mathcal{L}\mid$ is n dimensional and the meromorphic map

is an algebraic reduction of X (see [8]). By definition, an algebraic reduction of X is a dominant meromorphic map

to a normal projective variety B, such that π ^∗ induces an isomorphism of the function fields of meromorphic functions [8]. Only the birational class of B is determined by X. Fibers of the algebraic reduction π are defined via a resolution of indeterminacy, and are closed connected analytic subsets of X. In our case, the generic fiber of $\varPhi _{\mathcal{L}}$ is bimeromorphic to the generic fiber of $\varPhi _{\mathcal{L}_{2}}$. The generic fiber of $\varPhi _{\mathcal{L}_{2}}$ is a complex torus, and hence algebraic, by [7, Prop. 2.1]. Hence, the generic fiber of $\varPhi _{\mathcal{L}}$ has algebraic dimension n. It follows that the line bundle $\mathcal{L}$ is semi-ample, it is the pullback of an ample line-bundle over B, via a holomorphic reduction map π: X → B which is a regular morphism, by [8, Theorems 1.5 and 3.1].

Step 2.2: When X is projective there exists an element w ∈ W(X), such that Huybrecht’s birational map

satisfies $f^{{\ast}}\circ \psi ^{-1}\circ \eta = w$, by [23, Theorem 1.6]. Set $\alpha _{X}:=\eta ^{-1}(\alpha )$ and $\alpha _{Y }:=\psi ^{-1}(\alpha )$. We get the equality w(α _X ) = f ^∗(α _Y ).

Let $\overline{\mathcal{F}\mathcal{E}}_{X}$ be the closure of the fundamental exceptional chamber $\mathcal{F}\mathcal{E}_{X}$ in $H^{1,1}(X, \mathbb{R})$. The class α _X is nef, by assumption, and it thus belongs to $\overline{\mathcal{F}\mathcal{E}}_{X}$. We already know that α _Y is the class of a line bundle, which induces a Lagrangian fibration. Hence, $f^{{\ast}}(\alpha _{Y })$ belongs to $\overline{\mathcal{F}\mathcal{E}}_{X}$. The class w(α _X ) thus belongs to the intersection $w\left (\overline{\mathcal{F}\mathcal{E}}_{X}\right ) \cap \overline{\mathcal{F}\mathcal{E}}_{X}$.

Let J be the subset of $\mathcal{P}\mathit{ex}_{X}$ given by $J =\{ e \in \mathcal{P}\mathit{ex}_{X}\:\ (e,\alpha _{X}) = 0\}$. Denote by W _J the subgroup of W(X) generated by reflections R _e , for all e ∈ J. Then W _J is equal to

$$\displaystyle{\{w \in W(X)\:\ w(\alpha _{X}) \in \overline{\mathcal{F}\mathcal{E}}_{X}\},}$$

by a general property of crystalographic hyperbolic reflection groups [12, Lecture 3, Proposition on page 15]. We conclude that w(α _X ) = α _X and

$$\displaystyle{ \alpha _{X} = f^{{\ast}}(\alpha _{ Y }). }$$

(6.1)

We are ready to prove⁴ that $\mathcal{L}$ is semi-ample. The rational map f is regular in co-dimension one. The map f thus induces an isomorphism $f_{m}: \mid \mathcal{L}^{m}\mid \rightarrow \mid \mathcal{L}_{2}^{m}\mid$, for every integer m. Hence, $\kappa (X,\mathcal{L}) =\kappa (Y,\mathcal{L}_{2}) = n$. Any non-zero isotropic divisor class D on a 2n dimensional irreducible holomorphic symplectic manifold satisfies ν(X, D) = n, by a result of Verbitsky [41]. Hence, $\nu (X,\mathcal{L}) = n$. The line bundle $\mathcal{L}$ is assumed to be nef. Hence, $\mathcal{L}$ is semi-ample, by Theorem 6.2.

Step 3: We return to the general case, where X may or may not be projective. In both cases we have seen that there exists a positive integer m, such that the linear system $\mid \mathcal{L}^{m}\mid$ is base point free and $\varPhi _{\mathcal{L}^{m}}$ is a regular morphism. Furthermore, the bimeromorphic map

is regular in co-dimension one and thus induces an isomorphism $f_{k}: \mid \mathcal{L}^{k}\mid \rightarrow \mid \mathcal{L}_{2}^{k}\mid$, for every positive integer k. Denote by $f_{k}^{{\ast}}: \mid \mathcal{L}_{2}^{k}\mid ^{{\ast}}\rightarrow \mid \mathcal{L}^{k}\mid ^{{\ast}}$ the transpose of f _k . We get the equality $\varPhi _{\mathcal{L}^{k}} = f_{k}^{{\ast}}\circ \varPhi _{\mathcal{L}_{2}^{k}} \circ f,$ for all k. Let $V _{m}: \mid \mathcal{L}_{2}\mid ^{{\ast}}\rightarrow \mid \mathcal{L}_{2}^{m}\mid ^{{\ast}}$ be the Veronese embedding. We get the equalities

$$\displaystyle{ V _{m} \circ (f_{1}^{{\ast}})^{-1} \circ \varPhi _{ \mathcal{L}} = V _{m} \circ \varPhi _{\mathcal{L}_{2}} \circ f =\varPhi _{\mathcal{L}_{2}^{m}} \circ f = (f_{m}^{{\ast}})^{-1} \circ \varPhi _{ \mathcal{L}^{m}}. }$$

(6.2)

Now, $V _{m} \circ (f_{1}^{{\ast}})^{-1}: \mid \mathcal{L}\mid ^{{\ast}}\rightarrow \mid \mathcal{L}_{2}^{m}\mid ^{{\ast}}$ is a closed immersion and the morphism on the right hand side of (6.2) is regular. Hence, the rational map $\varPhi _{\mathcal{L}}$ is a regular morphism. The base locus of the linear system $\mid \mathcal{L}\mid$ is thus either empty, or a divisor. The latter is impossible, since f is regular in co-dimension one and $\mid \mathcal{L}_{2}\mid$ is base point free. Hence, $\mid \mathcal{L}\mid$ is base point free. □ 

Let X and $\mathcal{L}$ be as in Theorem 1.3, except that we drop the assumption that $\mathcal{L}$ is nef and assume only that $c_{1}(\mathcal{L})$ belongs to the boundary of the positive cone. Assume that X is projective.

Theorem 6.3.

There exists an element w ∈ W(X), a projective irreducible holomorphic symplectic manifold Y, a birational map

, and a Lagrangian fibration $\pi: Y \rightarrow \mathbb{P}^{n}$ , such that $w(\mathcal{L}) = f^{{\ast}}\pi ^{{\ast}}\mathcal{O}_{\mathbb{P}^{n}}(1)$ .

Proof.

Let (Y, ψ) be the marked pair constructed in Step 1 of the proof of Theorem 1.3. Then Y admits a Lagrangian fibration $\pi: Y \rightarrow \mathbb{P}^{n}$ and the class $\pi ^{{\ast}}c_{1}(\mathcal{O}_{\mathbb{P}^{n}}(1))$ was denoted α _Y in that proof. In step 2.2 of that proof we showed the existence of a birational map

and an element w ∈ W(X), such that $w(c_{1}(\mathcal{L})) = f^{{\ast}}(\alpha _{Y })$ (see Equality (6.1)). □ 

7 Tate-Shafarevich Lines and Twists

7.1 The Geometry of the Universal Curve

Let S be a projective K3 surface, d a positive integer, and $\mathcal{L}$ a nef line bundle on S of positive degree, such that the class $c_{1}(\mathcal{L})$ is indivisible. Set $n:= 1 + \frac{d^{2}\deg (\mathcal{L})} {2}$. Let $\mathcal{C}\subset S \times \mid \mathcal{L}^{d}\mid$ be the universal curve, $\pi _{i}$ the projection from $S \times \mid \mathcal{L}^{d}\mid$ to the i-th factor, i = 1, 2, and p _i the restriction of π _i to $\mathcal{C}$. We assume in this section the following assumptions about the line bundle $\mathcal{L}$.

Assumption 7.1.

• (1) The linear system $\mid \mathcal{L}^{d}\mid$ is base point free.

• (2) The locus in $\mid \mathcal{L}^{d}\mid$ , consisting of divisors which are non-reduced, or reducible having a singularity which is not an ordinary double point, has co-dimension at least 2.

Remark 7.2.

Assumption 7.1 holds whenever $\mathrm{Pic}(S)$ is cyclic generated by $\mathcal{L}$. The base point freeness Assumption 7.1 (1) follows from [32, Prop. 1]. Assumption 7.1 (2) is verified as follows. If $a + b = d$, a ≥ 1, b ≥ 1, then the image of $\mid \mathcal{L}^{a}\mid \times \mid \mathcal{L}^{b}\mid$ in $\mid \mathcal{L}^{d}\mid$ has co-dimension $2ab\left (\frac{n-1} {d^{2}} \right ) - 1$. The co-dimension is at least two, except in the case (n, d) = (5, 2). In the latter case $\mid \mathcal{L}\mid \mathop{\cong}\mathbb{P}^{2}$, $\mid \mathcal{L}^{2}\mid \mathop{\cong}\mathbb{P}^{5}$ and the generic curve in the image of $\mid \mathcal{L}\mid \times \mid \mathcal{L}\mid$ in $\mid \mathcal{L}^{2}\mid$ is the union of two smooth curves of genus 2 meeting transversely at two points. Hence, Assumption 7.1 (2) holds in this case as well.

The morphism $p_{1}: \mathcal{C}\rightarrow S$ is a projective hyperplane sub-bundle of the trivial bundle over S with fiber $\mid \mathcal{L}^{d}\mid$, by the base point freeness Assumption 7.1 (1). Assumption 7.1 (2) will be used in the proof of Lemma 7.9. Consider the exponential short exact sequence over $\mathcal{C}$

$$\displaystyle{0 \rightarrow \mathbb{Z} \rightarrow \mathcal{O}_{\mathcal{C}}\rightarrow \mathcal{O}_{\mathcal{C}}^{{\ast}}\rightarrow 0.}$$

We get the exact sequence of sheaves of abelian groups over $\mid \mathcal{L}^{d}\mid$

$$\displaystyle{ 0\longrightarrow R^{1}p_{ 2_{{\ast}}}\mathbb{Z}\longrightarrow R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}\longrightarrow R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}\stackrel{\deg }{\longrightarrow }R^{2}p_{ 2_{{\ast}}}\mathbb{Z}\longrightarrow 0, }$$

(7.1)

where we work in the complex analytic category. Note that deg above is surjective, since $R^{2}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}$ vanishes. Set

and

. Set $Br^{{\prime}}(S):= H_{}^{2}(S,\mathcal{O}_{S}^{{\ast}})$ and $Br^{{\prime}}(\mathcal{C}):= H_{}^{2}(\mathcal{C},\mathcal{O}_{\mathcal{C}}^{{\ast}})$.

Lemma 7.3.

• (1) There is a natural isomorphism

  $$\displaystyle{R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}\mathop{\cong}T^{{\ast}}\mid \mathcal{L}^{d}\mid \otimes _{ \mathbb{C}}H^{2,0}(S)^{{\ast}}.}$$
• (2)

  is naturally isomorphic to $H^{0,2}(\mathcal{C})$ . Consequently,

  

  is one dimensional.

• (3) $H^{2}(\mathcal{C}, \mathbb{Z})$ decomposes as a direct sum

  $$\displaystyle{H^{2}(\mathcal{C}, \mathbb{Z}) = p_{ 1}^{{\ast}}H^{2}(S, \mathbb{Z}) \oplus p_{ 2}^{{\ast}}H^{2}(\mid \mathcal{L}^{d}\mid, \mathbb{Z}).}$$

  The groups $H^{i}(\mathcal{C}, \mathbb{Z})$ vanish for odd i. The Dolbeault cohomologies $H^{p,q}(\mathcal{C})$ vanish, if $\left \vert \!p - q\!\right \vert > 2$ .

• (4) The pullback homomorphism $p_{1}^{{\ast}}: H_{}^{2}(S,\mathcal{O}_{S}^{{\ast}}) \rightarrow H_{}^{2}(\mathcal{C},\mathcal{O}_{\mathcal{C}}^{{\ast}})$ is an isomorphism. The Leray spectral sequence yields an isomorphism

  $$\displaystyle{b: H_{}^{2}(\mathcal{C},\mathcal{O}_{ \mathcal{C}}^{{\ast}}) \rightarrow H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}).}$$

  Consequently, we have the isomorphisms

  

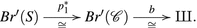
Let $\mathcal{F}$ be a sheaf of abelian groups over $\mathcal{C}$. Let $F^{p}H^{k}(\mathcal{C},\mathcal{F})$ be the Leray filtration associated to the morphism $p_{2}: \mathcal{C}\rightarrow \mid \mathcal{L}^{d}\mid$ and $E_{\infty }^{p,q}:= F^{p}H^{p+q}(\mathcal{C},\mathcal{F})/F^{p+1}H^{p+q}(\mathcal{C},\mathcal{F})$ its graded pieces. Recall that the $E_{2}^{p,q}$ terms are $E_{2}^{p.q}:= H^{p}(\mid \mathcal{L}^{d}\mid,R^{q}p_{2_{{\ast}}}\mathcal{F})$ and the differential at this step is $d_{2}: E_{2}^{p,q} \rightarrow E_{2}^{p+2,q-1}$.

Proof.

• (1) We have the isomorphism $\mathcal{O}_{S\times \mid \mathcal{L}^{d}\mid }(\mathcal{C})\mathop{\cong}\pi _{1}^{{\ast}}\mathcal{L}^{d} \otimes \pi _{2}^{{\ast}}\mathcal{O}_{\mid \mathcal{L}^{d}\mid }(1)$. Apply the functor $R\pi _{2_{{\ast}}}$ to the short exact sequence $0 \rightarrow \mathcal{O}_{S\times \mid \mathcal{L}^{d}\mid } \rightarrow \mathcal{O}_{S\times \mid \mathcal{L}^{d}\mid }(\mathcal{C}) \rightarrow \mathcal{O}_{\mathcal{C}}(\mathcal{C}) \rightarrow 0$ to obtain the Euler sequence of the tangent bundle.

  $$\displaystyle{0 \rightarrow \mathcal{O}_{\mid \mathcal{L}^{d}\mid } \rightarrow H^{0}(S,\mathcal{L}^{d}) \otimes _{ \mathbb{C}}\mathcal{O}_{\mid \mathcal{L}^{d}\mid }(1) \rightarrow T\mid \mathcal{L}^{d}\mid \rightarrow 0.}$$

  Now $\mathcal{O}_{\mathcal{C}}(\mathcal{C}) \otimes _{\mathbb{C}}H^{2,0}(S)$ is isomorphic to the relative dualizing sheaf $\omega _{p_{2}}$. We get the isomorphisms

  $$\displaystyle\begin{array}{rcl} R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}&\mathop{\cong}& [R^{0}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}(\mathcal{C}) \otimes _{\mathbb{C}}H^{2,0}(S)]^{{\ast}}\mathop{\cong}[R^{0}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}(\mathcal{C})]^{{\ast}}\otimes _{ \mathbb{C}}H^{2,0}(S)^{{\ast}} {}\\ &\mathop{\cong}& T^{{\ast}}\mid \mathcal{L}^{d}\mid \otimes _{ \mathbb{C}}H^{2,0}(S)^{{\ast}}. {}\\ \end{array}$$

• (2) $R^{2}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}$ vanishes, since p ₂ has one-dimensional fibers. $H^{2}(\mid \mathcal{L}^{d}\mid,p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}})$ vanishes, since $p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}\mathop{\cong}\mathcal{O}_{\mid \mathcal{L}^{d}\mid }$. The latter isomorphism follow from the fact that p ₂ has connected fibers. We conclude that $H^{2}(\mathcal{C},\mathcal{O}_{\mathcal{C}})$ is isomorphic to the $E_{\infty }^{1,1}$ graded summand of its Leray filtration. The differential $d_{2}: H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}) \rightarrow H^{3}(\mid \mathcal{L}^{d}\mid,p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}})$ vanishes, since $H^{0,3}(\mid \mathcal{L}^{d}\mid )$ vanishes. Hence, the $E_{2}^{1,1}$ term

  

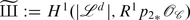
  is isomorphic to $H^{2}(\mathcal{C},\mathcal{O}_{\mathcal{C}})$.

• (3) The statement is topological and so it suffices to prove it in the case where Pic(S) is cyclic generated by $\mathcal{L}$. In this case $\mathcal{L}$ is ample, and so the line bundle $\pi _{1}^{{\ast}}\mathcal{L}^{d} \otimes \pi _{2}^{{\ast}}\mathcal{O}_{\mid \mathcal{L}^{d}\mid }(1)$ is ample. The Lefschetz Theorem on Hyperplane sections implies that the restriction homomorphism $H^{2}(S \times \mid \mathcal{L}^{d}\mid, \mathbb{Z}) \rightarrow H^{2}(\mathcal{C}, \mathbb{Z})$ is an isomorphism.

  $\mathcal{C}$ is the projectivization of a rank n vector bundle F over S. Hence, $H^{{\ast}}(\mathcal{C}, \mathbb{Z})$ is the quotient of $H^{{\ast}}(S, \mathbb{Z})[x]$, with x of degree 2, by the ideal generated by $\sum _{i=0}^{n+1}c_{i}(F)x^{i}$. The image of x in $H^{{\ast}}(\mathcal{C}, \mathbb{Z})$ corresponds to the class $\bar{x}:= c_{1}(\mathcal{O}_{\mathcal{C}}(1))$ of Hodge type (1, 1). In particular, $H^{{\ast}}(\mathcal{C}, \mathbb{Z})$ is a free $H^{{\ast}}(S, \mathbb{Z})$-module of rank n generated by 1, $\bar{x}$, …, $\bar{x}^{n-1}$.

• (4) The vanishing of $H^{3}(S, \mathbb{Z})$ and $H^{3}(\mathcal{C}, \mathbb{Z})$ yields the commutative diagram with exact rows:

  

  Part (3) of the Lemma implies that the left and middle vertical homomorphism are isomorphisms. It follows that the right vertical homomorphism is an isomorphism as well.

The sheaf $R^{2}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}$ vanishes, by the exactness of $R^{2}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}\rightarrow R^{2}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}\rightarrow R^{3}p_{2_{{\ast}}}\mathbb{Z}$ and the vanishing of the left and right sheaves due to the fact that p ₂ has one-dimensional fibers. The sheaf $p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}$ is isomorphic to $\mathcal{O}_{\mid \mathcal{L}^{d}\mid }^{{\ast}}$, since p ₂ has connected complete fibers. Thus, $H^{2}(\mathcal{C},\mathcal{O}_{\mathcal{C}}^{{\ast}})$ is isomorphic to the kernel of the differential

$$\displaystyle{ d_{2}: E_{2}^{1,1}:= H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}) \rightarrow E_{ 2}^{3,0}:= H^{3}(\mid \mathcal{L}^{d}\mid,\mathcal{O}_{\mid \mathcal{L}^{d}\mid }^{{\ast}}). }$$

(7.2)

We prove next that d ₂ vanishes. The co-kernel of d ₂ is equal to $F^{3}H^{3}(\mathcal{C},\mathcal{O}_{\mathcal{C}}^{{\ast}})$. Now $F^{3}H^{3}(\mathcal{C},\mathcal{O}_{\mathcal{C}}^{{\ast}})$ is equal to the image of $p_{2}^{{\ast}}: H^{3}(\mid \mathcal{L}^{d}\mid,\mathcal{O}_{\mid \mathcal{L}^{d}\mid }^{{\ast}}) \rightarrow H^{3}(\mathcal{C},\mathcal{O}_{\mathcal{C}}^{{\ast}})$. We have a commutative diagram

The horizontal homomorphisms, induced by the connecting homomorphism of the exponential sequence, are isomorphisms, since $h^{0,3}(\mathcal{C}) = h^{0,3}(\mid \mathcal{L}^{d}\mid ) = 0$ and $h^{0,4}(\mathcal{C}) = h^{0,4}(\mid \mathcal{L}^{d}\mid ) = 0$. The right vertical homomorphism is injective. We conclude that the left vertical homomorphism is injective. Hence the differential d ₂ in (7.2) vanishes and $H^{2}(\mathcal{C},\mathcal{O}_{\mathcal{C}}^{{\ast}})$ is isomorphism to $H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}})$, yielding the isomorphism b. □ 

Let $\varSigma \subset H^{2}(S, \mathbb{Z})$ be the sub-lattice generated by classes of irreducible components of divisors in the linear system $\mid \mathcal{L}^{d}\mid$. Denote by Σ ^⊥ the sub-lattice of $H^{2}(S, \mathbb{Z})$ orthogonal to Σ.

Lemma 7.4.

• (1) The Leray filtration of $H^{2}(\mathcal{C}, \mathbb{Z})$ associated to p ₂ is identified as follows:

  $$\displaystyle\begin{array}{rcl} F^{2}H^{2}(\mathcal{C}, \mathbb{Z})& =& p_{ 2}^{{\ast}}H^{2}(\mid \mathcal{L}^{d}\mid, \mathbb{Z}), {}\\ F^{1}H^{2}(\mathcal{C}, \mathbb{Z})& =& p_{ 2}^{{\ast}}H^{2}(\mid \mathcal{L}^{d}\mid, \mathbb{Z})\ \oplus \ p_{ 1}^{{\ast}}\varSigma ^{\perp }. {}\\ \end{array}$$

• (2) $E_{2}^{p,q} = E_{\infty }^{p,q}$ , if (p,q) = (2,0), or (1,1). Consequently, we get the following isomorphisms.

  $$\displaystyle\begin{array}{rcl} E_{2}^{2,0}:= H^{2}(\mid \mathcal{L}^{d}\mid,p_{ 2_{{\ast}}}\mathbb{Z})& \mathop{\cong}& p_{2}^{{\ast}}H^{2}(\mid \mathcal{L}^{d}\mid, \mathbb{Z}), {}\\ E_{2}^{1,1}:= H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{ 2_{{\ast}}}\mathbb{Z})& \mathop{\cong}& p_{1}^{{\ast}}\varSigma ^{\perp }, {}\\ \end{array}$$

• (3) If the sub-lattice Σ is saturated in $H^{2}(S, \mathbb{Z})$ , then $H^{2}(\mid \mathcal{L}^{d}\mid,R^{1}p_{2_{{\ast}}}\mathbb{Z})$ vanishes.

Proof.

(1), (2) The sheaf $p_{2_{{\ast}}}\mathbb{Z}$ is the constant sheaf $\mathbb{Z}$, since p ₂ has connected fibers. Then $E_{2}^{3,0} = H^{3}(\mid \mathcal{L}^{d}\mid, \mathbb{Z}) = 0$, and so $E_{\infty }^{1,1} = E_{2}^{1,1} = H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{2_{{\ast}}}\mathbb{Z})$. $E_{2}^{2,0}:= H^{2}(\mid \mathcal{L}^{d}\mid,p_{2_{{\ast}}}\mathbb{Z})$ has rank 1 and it maps injectively into $H^{2}(\mathcal{C}, \mathbb{Z})$, with image equal to $p_{2}^{{\ast}}H^{2}(\mid \mathcal{L}^{d}\mid, \mathbb{Z})$. Thus, $E_{2}^{2,0} = E_{\infty }^{2,0}$ and $E_{\infty }^{1,1}:= F^{1}H^{2}(\mathcal{C}, \mathbb{Z})/E_{\infty }^{2,0}$ is isomorphic to $F^{1}H^{2}(\mathcal{C}, \mathbb{Z})/p_{2}^{{\ast}}H^{2}(\mid \mathcal{L}^{d}\mid, \mathbb{Z})$. Finally, $E_{2}^{0,2}$ is the kernel of

$$\displaystyle{d_{2}: H^{0}(\mid \mathcal{L}^{d}\mid,R^{2}p_{ 2_{{\ast}}}\mathbb{Z}) \rightarrow H^{2}(\mid \mathcal{L}^{d}\mid,R^{1}p_{ 2_{{\ast}}}\mathbb{Z}).}$$

Thus, $F^{1}H^{2}(\mathcal{C}, \mathbb{Z})$ is the kernel of the homomorphism $H^{2}(\mathcal{C}, \mathbb{Z}) \rightarrow H^{0}(\mid \mathcal{L}^{d}\mid,R^{2}p_{2_{{\ast}}}\mathbb{Z})$. The latter kernel is equal to $p_{1}^{{\ast}}\varSigma ^{\perp }\oplus p_{2}^{{\ast}}H^{2}(\mid \mathcal{L}^{d}\mid, \mathbb{Z})$, by Lemma 7.3 (3). We conclude that $F^{1}H^{2}(\mathcal{C}, \mathbb{Z})/p_{2}^{{\ast}}H^{2}(\mid \mathcal{L}^{d}\mid, \mathbb{Z})$ is isomorphic to both $H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{2_{{\ast}}}\mathbb{Z})$ and $p_{1}^{{\ast}}\varSigma ^{\perp }$.

(3) The composition $H^{2}(\mathcal{C}, \mathbb{Z}) \rightarrow H^{0}(R^{2}p_{2_{{\ast}}}\mathbb{Z})\hookrightarrow \varSigma ^{{\ast}}$ factors through $H^{2}(S, \mathbb{Z})$. If Σ is saturated, then the composition is surjective, since $H^{2}(S, \mathbb{Z})$ is unimodular. Thus, $d_{2}^{0,2}: H^{0}(R^{2}p_{2_{{\ast}}}\mathbb{Z}) \rightarrow H^{2}(R^{1}p_{2_{{\ast}}}\mathbb{Z})$ vanishes. The sheaf $p_{2_{{\ast}}}\mathbb{Z}$ is the trivial local system and the homomorphism $H^{4}(\mid \mathcal{L}^{d}\mid,p_{2_{{\ast}}}\mathbb{Z})\mathop{\cong}H^{4}(\mid \mathcal{L}^{d}\mid, \mathbb{Z}) \rightarrow H^{4}(\mathcal{C}, \mathbb{Z})$ is the injective pull-back homomorphism p ₂ ^∗. Thus the differential $d_{2}^{2,1}: H^{2}(R^{1}p_{2_{{\ast}}}\mathbb{Z}) \rightarrow H^{4}(p_{2_{{\ast}}}\mathbb{Z})$ vanishes. We conclude that $E_{2}^{2,1}:= H^{2}(R^{1}p_{2_{{\ast}}}\mathbb{Z})$ is isomorphic to $E_{\infty }^{2,1}$. Now $E_{\infty }^{2,1}$ vanishes, since $H^{3}(\mathcal{C}, \mathbb{Z})$ vanishes. □ 

Let $\mathcal{A}^{0}$ be the kernel of the homomorphism deg, given in (7.1). Then $\mathcal{A}^{0}$ is a subsheaf of $R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}$ and we get the short exact sequences

$$\displaystyle\begin{array}{rcl} 0\longrightarrow \mathcal{A}^{0}\longrightarrow R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}\stackrel{\deg }{\longrightarrow }R^{2}p_{ 2_{{\ast}}}\mathbb{Z}\longrightarrow 0,& &{}\end{array}$$

(7.3)

$$\displaystyle\begin{array}{rcl} 0\longrightarrow R^{1}p_{ 2_{{\ast}}}\mathbb{Z}\longrightarrow R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}\longrightarrow \mathcal{A}^{0}\longrightarrow 0,& &{}\end{array}$$

(7.4)

and the long exact

$$\displaystyle{\cdots \rightarrow H_{}^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{ 2_{{\ast}}}\mathbb{Z}) \rightarrow H_{}^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}})\stackrel{}{\rightarrow }H_{}^{1}(\mid \mathcal{L}^{d}\mid,\mathcal{A}^{0}) \rightarrow \cdots }$$

Lemma 7.5.

The group $H^{0}(\mid \mathcal{L}^{d}\mid,\mathcal{A}^{0})$ is isomorphic to NS(S) ∩Σ ^⊥ . The composite homomorphism

factors through an injective homomorphism from $H^{2}(S, \mathbb{Z})/[\varSigma ^{\perp } + \mathit{NS}(S)]$ into the kernel of the homomorphism

.

Proof.

The space $H^{0}(\mid \mathcal{L}^{d}\mid,R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}})$ vanishes, by Lemma 7.3 (1). Hence, $H^{0}(\mid \mathcal{L}^{d}\mid,\mathcal{A}^{0})$ is the kernel of the homomorphism

. Compose the above homomorphism with the isomorphism $\varSigma ^{\perp }\mathop{\cong}H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{2_{{\ast}}}\mathbb{Z})$ of Lemma 7.4 in order to get the isomorphism $H^{0}(\mid \mathcal{L}^{d}\mid,\mathcal{A}^{0})\mathop{\cong}\mathit{NS}(S) \cap \varSigma ^{\perp }$.

We have a commutative diagram with short exact rows

(7.5)

The top row is obtained from the long exact sequence of sheaf cohomologies associated to the short exact sequence (7.4). The left vertical homomorphism is injective and the right vertical homomorphism is surjective. The co-kernel of the former is isomorphic to the kernel of the latter and both are isomorphic to $H^{2}(S, \mathbb{Z})/[\varSigma ^{\perp } + \mathit{NS}(S)]$. Setting

(7.6)

we see that the right vertical homomorphism fits in the short exact sequence

(7.7)

The statement of the Lemma follows. □ 

Let

be the group given in Eq. (7.6). Classes of

represent torsors for the relative Picard group scheme, while classes of

represent torsors for the relative Pic⁰ group scheme. This comment will be illustrated in Example 7.8 below.

7.2 A Universal Family of Tate-Shafarevich Twists

Let S be the marked K3 surface in Diagram (5.4) and M _H (u) the moduli space of H-stable sheaves of pure one-dimensional support on S in that Diagram. Recall that c ₁(u) is the first Chern class of $\mathcal{L}^{d}$, for a nef line-bundle $\mathcal{L}$ on S, and the support map $\pi: M_{H}(u) \rightarrow \mid \mathcal{L}^{d}\mid$ is a Lagrangian fibration.

Let σ be a section of $R^{1}p_{2_{{\ast}}}(\mathcal{O}_{\mathcal{C}}^{{\ast}})$ over an open subset U of $\mid \mathcal{L}^{d}\mid$. Assume that σ is the image of a section $\tilde{\sigma }$ of $R^{1}p_{2_{{\ast}}}(\mathcal{O}_{\mathcal{C}})$ over U. Then σ lifts to an automorphism of the open subset π ⁻¹(U) of M _H (u). This is seen as follows. Fix a point $t \in \mid \mathcal{L}^{d}\mid$ and denote by C _t the corresponding divisor in S. Denote by σ(t) the image of σ in $H^{1}(C_{t},\mathcal{O}_{C_{t}}^{{\ast}})$ and by L _σ(t) the line-bundle over C _t with class σ(t). A sheaf F over C _t is H-stable, if and only if $F \otimes L_{\sigma (t)}$ is H-stable, since tensorization by L _σ(t) induces a one-to-one correspondence between the set of subsheaves, which is slope-preserving, since L _σ(t) belongs to the identity component of the Picard group of C _t .

Let s be an element of

. We can choose a Čech 1-co-cycle $\sigma:=\{\sigma _{\mathit{ij}}\}$ for the sheaf $\mathcal{A}^{0}$ representing s in

, with respect to an open covering {U _i } of $\mid \mathcal{L}^{d}\mid$, such that each σ _ij is the image of a section $\tilde{\sigma }_{\mathit{ij}}$ of $R^{1}p_{2_{{\ast}}}(\mathcal{O}_{\mathcal{C}})$, since the homomorphism $R^{1}p_{2_{{\ast}}}(\mathcal{O}_{\mathcal{C}}) \rightarrow \mathcal{A}^{0}$ is surjective. The co-cycle {σ _ij } may be used to re-glue the open covering $\pi ^{-1}(U_{i})$ of M _H (u) to obtain a separated complex manifold M _σ together with a proper map $\pi _{\sigma }: M_{\sigma } \rightarrow \mid \mathcal{L}^{d}\mid.$ The latter is independent of the choice of the co-cycle, by the following Lemma, so we denote it by

$$\displaystyle{ \pi _{s}: M_{s} \rightarrow \mid \mathcal{L}^{d}\mid. }$$

(7.8)

Lemma 7.6.

Let $\sigma:=\{\sigma _{\mathit{ij}}\}$ and $\sigma ^{{\prime}}:=\{\sigma _{ \mathit{ij}}^{{\prime}}\}$ be two co-cycles representing the same class in

. Then there exists an isomorphism $h: M_{\sigma } \rightarrow M_{\sigma ^{{\prime}}}$ satisfying the equation $\pi _{\sigma ^{{\prime}}}\circ h =\pi _{\sigma }$ . If the lattice Σ of Lemma  7.4 has finite index in NS(S), then h depends canonically on σ and σ ^′ .

Proof.

There exists a co-chain $h:=\{ h_{i}\}$ in $C^{0}(\{U_{i}\},\mathcal{A}^{0})$, such that $h_{i}\sigma _{\mathit{ij}} =\sigma _{ \mathit{ij}}^{{\prime}}h_{j}$, possibly after refining the covering and restricting the co-cycles σ and σ ^′ to the refinement. Each h _i is the image of a section $\tilde{h}_{i}$ of $R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}$, possibly after further refinement of the covering, since the sheaf homomorphism $R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}\rightarrow \mathcal{A}^{0}$ is surjective. Hence, h _i lifts canonically to an automorphism of $\pi ^{-1}(U_{i})$. The co-chain $\{h_{i}\}$ of automorphisms glues to a global isomorphism from $M_{\sigma ^{{\prime}}}$ to M _σ , by the equality $h_{i}\sigma _{\mathit{ij}} =\sigma _{ \mathit{ij}}^{{\prime}}h_{j}$.

If $h^{{\prime}}:=\{ h_{i}^{{\prime}}\}$ is another co-chain satisfying the equality $\delta (h) =\sigma (\sigma ^{{\prime}})^{-1}$, then h ⁻¹ h ^′ is a global section of $\mathcal{A}^{0}$. The assumption that Σ has finite index in NS(S) implies that $H^{0}(\mathcal{A}^{0})$ vanishes, by Lemma 7.5. Hence h = h ^′ and the above refinements are not needed. □ 

In the relative setting the above construction gives rise to a natural proper family

which restricts over $\{0\} \times \mid \mathcal{L}^{d}\mid$ to $\pi: M_{H}(u) \rightarrow \mid \mathcal{L}^{d}\mid$, and over

to $\pi _{j(\tilde{s})}: M_{j(\tilde{s})} \rightarrow \mid \mathcal{L}^{d}\mid.$ Indeed, let $(\{U_{i}\},\tilde{\sigma }_{\mathit{ij}})$ be a Čech co-cycle representing a non-zero class $\tilde{\sigma }$ in $H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{{\ast}}\mathcal{O}_{\mathcal{C}})$. Let

(7.9)

be the function satisfying $\tau (x)\tilde{\sigma } = x$. Then

is a global co-cycle representing the desired family. Let

be the composition of $\tilde{\pi }$ with the projection to

.

Proposition 7.7.

If the weight 2 Hodge structure of S is non-special, then M _s is Kähler, for all

.

Proof.

There is an open neighborhood of the origin in

, over which the fibers of f are Kähler, by the stability of Kähler manifolds [42, Theorem 9.3.3]. Let

be the homomorphism given in Eq. (7.5) The kernel $\ker (j)$ is isomorphic to the group $[\varSigma ^{\perp } + \mathit{NS}(S)]/\mathit{NS}(S)$, by Lemma 7.5. As a subgroup of the base

of the family f, the kernel $\ker (j)$ acts on the base. Let z be an element of $\ker (j)$ and $\tilde{s}$ an element of

. The fibers $M_{\tilde{s}}$ and $M_{\tilde{s}+z}$ of f are both isomorphic to $M_{j(\tilde{s})}$ by Lemma 7.6. Let

be the subset consisting of points over which the fiber of f is Kähler. Then V is an open and ker(j)-invariant subset of

. Note that ker(j) is a finite index subgroup of $H^{2}(S, \mathbb{Z})/\mathit{NS}(S)$. The kernel ker(j) is a dense subgroup of

, if and only if the image of $H^{2}(S, \mathbb{Z})/\mathit{NS}(S)$ is dense in H ^0, 2(S), by Lemma 7.3 (4). This is indeed the case, by the assumption that the weight 2 Hodge structure of S is non-special, and Lemmas 5.4 and 5.5. The complement V ^c of V in

is ker(j) invariant. If non-empty, then V ^c is dense and closed and so equal to

. But we know that V is non-empty. Hence,

. □ 

Example 7.8.

Consider the case where d = 1 and $\mathrm{Pic}(S)$ is cyclic generated by the line bundle $\mathcal{L}$ of degree 2n − 2, n ≥ 2. Then $H^{2}(\mid \mathcal{L}^{d}\mid,R^{1}p_{2_{{\ast}}}\mathbb{Z})$ vanishes, by Lemma 7.4 (3), and

. The linear system $\mid \mathcal{L}\mid$ consists of integral curves, and so we can find an open covering {U _i } of $\mid \mathcal{L}\mid$, and sections $\zeta _{i}: U_{i} \rightarrow \mathcal{C}$, such that p ₂ ∘ζ _i is the identity. Set $D_{i}:=\zeta _{i}(U_{i})$. We get the line bundle $\mathcal{O}_{p_{2}^{-1}(U_{i})}(D_{i})$, which restricts to a line bundle of degree 1 on fibers of p ₂ over points of U _i . Let h _i be the section of $R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}$ over U _i corresponding to $\mathcal{O}_{p_{2}^{-1}(U_{i})}(D_{i})$ and denote by h: = { h _i } the corresponding co-chain in $C^{0}(\{U_{i}\},R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}})$.

Consider the Lagrangian fibrations $\pi _{0}: M_{\mathcal{L}}(0,\mathcal{L},\chi ) \rightarrow \mid \mathcal{L}\mid$ and $\pi _{1}: M_{\mathcal{L}}(0,\mathcal{L},\chi +1) \rightarrow \mid \mathcal{L}\mid$, for some integer χ. The push-forward of every rank 1 torsion free sheaf on a curve in the linear system $\mid \mathcal{L}\mid$ is an $\mathcal{L}$-stable sheaf on S, since the curve is integral. Hence, the section h _i induces an isomorphism $h_{i}:\pi _{ 0}^{-1}(U_{i}) \rightarrow \pi _{1}^{-1}(U_{i})$. The co-boundary $(\delta h)_{\mathit{ij}}:= h_{j}h_{i}^{-1}$ is a co-cycle in $Z^{1}(\{U_{i}\},\mathcal{A}^{0})$ representing a class

mapping to the identity in

. The Lagrangian fibration $\pi _{s}: M_{s} \rightarrow \mid \mathcal{L}\mid$, associated to the class s in Eq. (7.8) with $u = (0,\mathcal{L},\chi )$, coincides with $\pi _{1}: M_{\mathcal{L}}(0,\mathcal{L},\chi +1) \rightarrow \mid \mathcal{L}\mid,$ by the commutativity of the following diagram.

The moduli spaces $M_{\mathcal{L}}(0,\mathcal{L},\chi )$ and $M_{\mathcal{L}}(0,\mathcal{L},\chi +1)$ are not isomorphic for generic $(S,\mathcal{L})$, since their weight 2 Hodge structures are not Hodge isometric.

The kernel of

is cyclic of order 2n − 2, by the exactness of the sequence (7.7). The class s constructed above generates the kernel. This is seen as follows. The sheaf $R^{2}p_{2_{{\ast}}}\mathbb{Z}$ is trivial, in our case, and the homomorphism deg, given in (7.3), maps the 0-co-chain h to a global section of $R^{2}p_{2_{{\ast}}}\mathbb{Z}$, which generates $H^{0}(R^{2}p_{2_{{\ast}}}\mathbb{Z}).$ Hence, δ h generates the image of the connecting homomorphism $H^{0}(R^{2}p_{2_{{\ast}}}\mathbb{Z}) \rightarrow H^{1}(\mathcal{A}^{0})$ associated to the short exact sequence (7.3). The latter image is precisely the kernel of

.

7.3 The Period Map of the Universal Family is Étale

Denote by $T_{\pi _{s}}:=\ker \left [d\pi _{s}: \mathit{TM}_{s} \rightarrow \pi _{s}^{{\ast}}T\mid \mathcal{L}^{d}\mid \right ]$ the relative tangent sheaf of $\pi _{s}: M_{s} \rightarrow \mid \mathcal{L}^{d}\mid$.

Lemma 7.9.

The vertical tangent sheaf $T_{\pi _{s}}$ is isomorphic to $\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid$ .

Proof.

Let sing(π _s ) be the support of the co-kernel of the differential $d\pi _{s}: \mathit{TM}_{s} \rightarrow \pi _{s}^{{\ast}}T\mid \mathcal{L}^{d}\mid$. We use Assumption 7.1 to prove that the co-dimension of sing(π _s ) in M _s is ≥ 2. The generic fiber of π _s is smooth, since M _s is smooth. All fibers of π _s have pure dimension n [29]. Hence, the only way sing(π _s ) could contain a divisor is if π _s has fibers with a non-reduced irreducible component over some divisor in $\mid \mathcal{L}^{d}\mid$. The generic divisor in the linear system $\mid \mathcal{L}^{d}\mid$ is a smooth curve, by Assumption 7.1 (1) and [32, Prop. 1]. The fiber of π _s , over a reduced divisor $C \in \mid \mathcal{L}^{d}\mid$, is isomorphic to the compactified Picard of C, consisting of $\mathcal{L}$-stable sheaves of Euler characteristic χ with pure one-dimensional support C, which are the push forward of rank 1 torsion free sheaves over C. If C is an integral curve, then the moduli space of rank 1 torsion free sheaves over C with a fixed Euler characteristic is irreducible and reduced [1]. If C is reduced (possibly reducible) with at worst ordinary double point singularities, then the compactified Picard is reduced, by a result of Oda and Seshadri [37]. Assumption 7.1 (2) thus implies that sing(π _s ) has co-dimension ≥ 2 in M _s .

Let U be the complement of $\mbox{ sing}(\pi _{s})$ in M _s . The isomorphism $\mathit{TM}_{s} \rightarrow T^{{\ast}}M_{s}$, induced by a non-degenerate global holomorphic 2-form, maps the restriction of $T_{\pi _{s}}$ to U isomorphically onto the restriction of $\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid$. The isomorphism $\mathit{TM}_{s} \rightarrow T^{{\ast}}M_{s}$ must map $T_{\pi _{s}}$ as a subsheaf of the locally free $\pi _{s}^{{\ast}}T\mid \mathcal{L}^{d}\mid$, by the fact that sing(π _s ) has codimension ≥ 2. But $T_{\pi _{s}}$ is a saturated subsheaf of TM _s . Hence, the image of $T_{\pi _{s}}$ is also saturated in $T^{{\ast}}M_{s}$, and is thus equal to $\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid$. □ 

When the K3 surface S is non-special, the fibers of the family f are irreducible holomorphic symplectic manifolds, by Proposition 7.7 and the fact that Kähler deformations of an irreducible holomorphic symplectic manifold remain such [4]. Denote by

(7.10)

the trivialization, which restricts to the marking η ₁ in Diagram (5.4) over the point

. Let

be the period map of the family f and the marking η. Let

be the differential at $\tilde{s}$ of the period map.

Lemma 7.10.

The differential dP _f is injective, for all $\tilde{s}$ in

, and its image is equal to $H^{2,0}(M_{s})^{{\ast}}\otimes \pi _{s}^{{\ast}}H^{1,1}(\mid \mathcal{L}^{d}\mid )$ .

Proof.

Let $\psi: H^{2,0}(M_{s})^{{\ast}}\otimes H^{1}(\mid \mathcal{L}^{d}\mid,T^{{\ast}}\mid \mathcal{L}^{d}\mid ) \rightarrow H^{1}(M_{s},T_{\pi _{s}})$ be the composition of

$$\displaystyle{1 \otimes \pi _{s}^{{\ast}}:H^{2,0}(M_{ s})^{{\ast}}\!\otimes \!H^{1}(\mid \mathcal{L}^{d}\mid,T^{{\ast}}\mid \mathcal{L}^{d}\mid )\rightarrow H^{0}(M_{ s},\wedge ^{2}\mathit{TM}_{ s}) \otimes H^{1}(M_{ s},\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid )}$$

with the contraction homomorphism $H^{0}(M_{s},\wedge ^{2}\mathit{TM}_{s}) \otimes H^{1}(M_{s},\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid ) \rightarrow H^{1}(M_{s},T_{\pi _{s}})$. Let

be the Kodaira-Spencer map. We have the commutative diagram.

Above, the right vertical homomorphism is induced by the sheaf homomorphism $\mathit{TM}_{s} \rightarrow T^{{\ast}}M_{s}$, associated to a holomorphic 2-form, and γ is induced by the inclusion of the relative tangent sheaf $T_{\pi _{s}}$ as a subsheaf of TM _s . The homomorphism ν is defined as follows. A tangent vector ξ at a class $\tilde{s}$ of

is represented by a co-cycle of infinitesimal automorphisms – tangent vector fields – which are vertical, being a limit of translations by local sections of the image of $R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}$ in $R^{1}p_{2_{{\ast}}}\mathcal{O}_{\mathcal{C}}^{{\ast}}$. So ξ corresponds to an element ν(ξ) in $H^{1}(M_{s},T_{\pi _{s}})$.

The top right triangle commutes, by Griffiths’ identification of the differential of the period map [9]. The middle triangle commutes, by definition of the family f. The commutativity of the outer polygon is easily verified. The top horizontal homomorphism 1 ⊗ π _s ^∗ is injective, with image equal to the tangent line to the fiber of q. Hence, it suffices to prove that ψ and ν have the same image in $H^{1}(M_{s},T_{\pi _{s}})$. The latter statement would follow once we prove that ν is an isomorphism.

The homomorphism ν is induced by the pullback

$$\displaystyle{\pi _{s}^{{\ast}}H^{1}(\mid \mathcal{L}^{d}\mid,R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}) \rightarrow H^{1}(M_{ s},\pi _{s}^{{\ast}}R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}),}$$

followed by the homomorphism of sheaf cohomologies induced by an injective sheaf homomorphism

$$\displaystyle{\tilde{\nu }\:\ \pi _{ s}^{{\ast}}R^{1}p_{ 2_{{\ast}}}\mathcal{O}_{\mathcal{C}}\rightarrow T_{\pi _{s}}.}$$

The domain of $\tilde{\nu }$ is isomorphic to $\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid$, by Lemma 7.3, and its target is isomorphic to $\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid$, by Lemma 7.9. Hence, $\tilde{\nu }$ is an isomorphism. It remains to prove that $H^{1}(M_{s},\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid )$ is one dimensional. We have the exact sequence

$$\displaystyle\begin{array}{rcl} 0& \rightarrow & H^{1}(\mid \mathcal{L}^{d}\mid,\pi _{ s_{{\ast}}}\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid ) \rightarrow H^{1}(M_{ s},\pi _{s}^{{\ast}}T^{{\ast}}\mid \mathcal{L}^{d}\mid ) {}\\ & \rightarrow & H^{0}(\mid \mathcal{L}^{d}\mid,T^{{\ast}}\mid \mathcal{L}^{d}\mid \otimes R^{1}\pi _{ s_{{\ast}}}\mathcal{O}_{M_{s}}). {}\\ \end{array}$$

The left hand space is one-dimensional. It remains to prove that the right hand one vanishes. It suffices to prove that $R^{1}\pi _{s_{{\ast}}}\mathcal{O}_{M_{s}}$ is isomorphic to $T^{{\ast}}\mid \mathcal{L}^{d}\mid$, since $T^{{\ast}}\mid \mathcal{L}^{d}\mid \otimes T^{{\ast}}\mid \mathcal{L}^{d}\mid$ does not have any non-zero global sections.

When s = 0 and M ₀ = M _H (u), then M ₀ is projective and $R^{1}\pi _{0_{{\ast}}}\mathcal{O}_{M_{0}}$ is isomorphic to $T^{{\ast}}\mid \mathcal{L}^{d}\mid$, by [30, Theorem 1.3]. Let us show that the sheaves $R^{1}\pi _{s_{{\ast}}}\mathcal{O}_{M_{s}}$ are naturally isomorphic to $R^{1}\pi _{0_{{\ast}}}\mathcal{O}_{M_{0}}$, for all s in

. The fibrations π _s agree, by definition, over the open sets in a Čech covering of $\mid \mathcal{L}^{d}\mid$, and the gluing transformations for the co-cycle representing the class s do not change the induced sheaf transition functions for the sheaves $R^{1}\pi _{s_{{\ast}}}\mathcal{O}_{M_{s}}$, as we show next. The gluing transformations glue locally free sheaves, so it suffices to prove that they agree with those of π ₀ over a dense open subset of $\mid \mathcal{L}^{d}\mid$. Indeed, if the fiber of M _H (u) over $t \in \mid \mathcal{L}^{d}\mid$ is a smooth and projective $\mathrm{Pic}^{d}(C_{t})$, then an automorphism of an abelian variety $\mathrm{Pic}^{d}(C_{t})$, acting by translation, acts trivially on the fiber $H^{1}(\mathrm{Pic}^{d}(C_{t}),\mathcal{O}_{\mathrm{Pic}^{d}(C_{t})})$ of $R^{1}\pi _{{\ast}}\mathcal{O}_{M_{H}(u)}$. □ 

7.4 The Tate-Shafarevich Line as the Base of the Universal Family

Let $q:\varOmega _{ \alpha ^{\perp }}^{+} \rightarrow \varOmega _{Q_{\alpha }}^{+}$ be the morphism given in Eq. (4.3).

Theorem 7.11.

Assume that the weight 2 Hodge structure of S is non-special and Assumption  7.1 holds. Then the period map P _f of the family f maps

isomorphically onto the fiber of the morphism q through the period of M _H (u).

Proof.

We already know that P _f is non-constant, by Lemma 7.10. The statement implies that P _f is an affine linear isomorphism of one-dimensional complex affine spaces. It suffices to prove the statement for a dense subset in moduli, since the condition of being affine linear is closed. We may thus assume that Pic(S) is cyclic generated by $\mathcal{L}$. Then $H^{0}(\mid \mathcal{L}^{d}\mid,\mathcal{A}^{0})$ is trivial, by Lemma 7.5.

Set $\varGamma:= c_{1}(\mathcal{L})^{\perp }$. Note that $\mathit{NS}(S) = \mathbb{Z}c_{1}(\mathcal{L})$ and Γ has finite index in $H^{2}(S, \mathbb{Z})/\mathit{NS}(S)$. Let

be the composition of the projection $\varGamma \rightarrow H^{0,2}(S)$ with the isomorphisms

of Lemma 7.3. Then e is injective and its image is dense in

, by Lemma 5.4.

Given an element

, we get a marked pair (M _x , η _x ), as above. M _H (u) will be denoted by M ₀, it being the fiber of f over the origin in

. We associate next to an element γ ∈ Γ a canonical isomorphism

$$\displaystyle{h_{\gamma }: M_{0} \rightarrow M_{e(\gamma )}.}$$

Let

be the function given in (7.9), which was used in the construction of the family f. Let $\tilde{\sigma }:=\{\tilde{\sigma } _{\mathit{ij}}\}$ be the co-cycle used in that construction. Let a be the 1-co-cycle given by $a_{\mathit{ij}}:=\exp (\tau (e(\gamma ))\tilde{\sigma }_{\mathit{ij}})$. Then M _e(γ) is the Tate-Shafarevich twist of M ₀ with respect to the co-cycle a. The 1-co-cycle a is a co-boundary in $Z^{1}(\{U_{i}\},\mathcal{A}^{0})$, by Lemma 7.5 and the definition of Γ. Thus, there exists a 0-co-chain h: = { h _i } in $C^{0}(\{U_{i}\},\mathcal{A}^{0})$, satisfying δ h = a. The co-chain h is unique, since $H^{0}(\mathcal{A}^{0})$ is trivial, by our assumption on S. The co-chain h determines the isomorphism $h_{\gamma }: M_{0} \rightarrow M_{e(\gamma )}$ (Lemma 7.6).

We define next a monodromy representation associated to the family f. Denote by $h_{\gamma _{{\ast}}}: H^{2}(M_{0}, \mathbb{Z}) \rightarrow H^{2}(M_{e(\gamma )}, \mathbb{Z})$ the isomorphism induced by h _γ . Let

$$\displaystyle{\mu \:\ \varGamma \rightarrow \mathit{Mon}^{2}(M_{ 0})}$$

be given by the composition $\mu _{\gamma }:=\eta _{ 0}^{-1} \circ \eta _{e(\gamma )} \circ h_{\gamma _{{\ast}}}$ of the parallel-transport operator $\eta _{0}^{-1} \circ \eta _{e(\gamma )}$ and the isomorphism $h_{\gamma _{{\ast}}}$.

Claim 7.12.

The map μ is a group homomorphism.

Proof.

Let γ ₁, γ ₂ be elements of Γ and set $\gamma _{3}:=\gamma _{1} +\gamma _{2}$. Let the topological space B be the quotient of

obtained by identifying the four points 0, e(γ ₁), e(γ ₂), e(γ ₃). The family f descends to a family $\bar{f}: \overline{\mathcal{M}}\rightarrow B$ by identifying the fiber $M_{e(\gamma _{i})}$ with M ₀ via the isomorphisms $h_{\gamma _{i}}$, 1 ≤ i ≤ 3. Then $\mu _{\gamma _{i}}$ is the monodromy operator corresponding to any loop in B, which is the image of some continuous path from 0 to e(γ _i ) in

. Let $\bar{0} \in B$ be the image of

. The statement now follows from the fact that the monodromy representation of $\pi _{1}(B,\bar{0})$ in $H^{2}(M_{0}, \mathbb{Z})$ is a group homomorphism. □ 

The image of

via the period map is contained in the fiber of q, since the differential of the morphism q ∘ P _f vanishes, by Lemma 7.10. It follows that the variation of Hodge structures of the local system $R^{2}f_{{\ast}}\mathbb{Z}$ over

is the pullback of the one over the fiber of q via the period map P _f . Let η be the trivialization of $R^{2}f_{{\ast}}\mathbb{Z}$ given in Eq. (7.10). Given a point

, set $\alpha _{x}:=\eta _{ x}^{-1}(\alpha )$. Then $\alpha _{x} =\pi _{ x}^{{\ast}}(c_{1}(\mathcal{O}_{\mid \mathcal{L}^{d}\mid }(1)))$ and the sub-quotient variation of Hodge structures $\alpha _{x}^{\perp }/\mathbb{Z}\alpha _{x}$ is trivial.

The vertical tangent sheaf $T_{\pi _{x}}$ is naturally isomorphic to $T_{\pi _{0}}$, as we saw in the last paragraph of the proof of Lemma 7.10. The 2-form w _x induces an isomorphism $\pi _{x_{{\ast}}}T_{\pi _{x}}\stackrel{w_{x}}{\rightarrow }T^{{\ast}}\mid \mathcal{L}^{d}\mid$, by Lemma 7.9. We get the composite isomorphism $\pi _{0_{{\ast}}}T_{\pi _{0}}\mathop{\cong}\pi _{x_{{\ast}}}T_{\pi _{x}}\stackrel{w_{x}}{\rightarrow }T^{{\ast}}\mid \mathcal{L}^{d}\mid.$ Let w _x be the unique holomorphic 2-form, for which the composite isomorphism is equal to $\pi _{0_{{\ast}}}T_{\pi _{0}}\stackrel{w_{0}}{\rightarrow }T^{{\ast}}\mid \mathcal{L}^{d}\mid.$ Such a form w _x exists, since the endomorphism algebra of $T^{{\ast}}\mid \mathcal{L}^{d}\mid$ is one dimensional.

We show next that the class of w _x is the (2, 0) part of the flat deformation of the class of w ₀ in the local system $R^{2}f_{{\ast}}\mathbb{C}$. It suffices to prove the local version of that statement. Let x ₀ be a point of

. There is a differentiable trivialization of

, over an open analytic neighborhood U of x ₀, and a C ^∞ family of complex structures J _x , x ∈ U, such that $(M_{x_{0}},J_{x})$ is biholomorphic to M _x . Furthermore, the complex structures $J_{x_{0}}$ and J _x restrict to the same complex structure on each fiber of $\pi _{x_{0}}$ and $\pi _{x_{0}}$ is holomorphic with respect to both. Both complex structures induce the same complex structure on $\mathrm{Hom}\left (T_{\pi _{x_{ 0}}},\pi _{x_{0}}^{{\ast}}T_{\mathbb{R}}^{{\ast}}\mid \mathcal{L}^{d}\mid \right )$ and the two forms $w_{x_{0}}$ and w _x induce the same section in the complexification of that bundle. Hence, the difference $w_{x_{0}} - w_{x}$ is a closed 2-form in $\pi _{x_{0}}^{{\ast}}\wedge ^{2}T_{\mathbb{R}}^{{\ast}}\mid \mathcal{L}^{d}\mid \otimes _{\mathbb{R}}\mathbb{C}$. Being closed, the latter 2-form must be the pull-back of a closed 2-form θ on $\mid \mathcal{L}^{d}\mid$, since fibers of $\pi _{x_{0}}$ are connected. Now the cohomology class of $\pi _{x_{0}}^{{\ast}}\theta$ is of type (1, 1) with respect to all complex structures, since $H^{1,1}(\mid \mathcal{L}^{d}\mid ) = H^{2}(\mid \mathcal{L}^{d}\mid, \mathbb{C})$. Hence, the class of w _x is the (2, 0) part of the class of $w_{x_{0}}$ with respect to the complex structure J _x .

There exists a constant $c_{x} \in \mathbb{C}$, such that the equality

$$\displaystyle{\eta _{x}(w_{x}) =\eta _{0}(w_{0}) + c_{x}\alpha }$$

holds in $\varLambda _{\mathbb{C}}$, by the characterization of ω _x in the above paragraph. The function

defined above is equivalent to the period map P _f and is thus holomorphic and its derivative is no-where vanishing, by Lemma 7.10. If x = e(γ), we get $\eta _{0}^{-1}\eta _{e(\gamma )}(w_{e(\gamma )}) = w_{0} + c_{e(\gamma )}\alpha _{0}$, Now $h_{\gamma }(w_{0}) = w_{e(\gamma )}$, by definition of w _x ,

, and the construction of h _γ . We get the equality

$$\displaystyle{ \mu _{\gamma }(w_{0}) = w_{0} + c_{e(\gamma )}\alpha _{0}. }$$

(7.11)

The composition $c \circ e:\varGamma \rightarrow \mathbb{C}$ is a group homomorphism,

$$\displaystyle{c(e(\gamma _{1}) + e(\gamma _{2})) = c(e(\gamma _{1})) + c(e(\gamma _{2})),}$$

by Eq. (7.11) and Claim 7.12. The image e(Γ) is dense in

and so e(Γ) × e(Γ) is dense in

. We conclude that c is a group homomorphism, $c(x_{1} + x_{2}) = c(x_{1}) + c(x_{2})$, for all

. Continuity of c implies that it is a linear transformation of real vector spaces. Indeed, given x ₁, x ₂ in

, $c(\mathit{ax}_{1} + \mathit{bx}_{2}) = \mathit{ac}(x_{1}) + \mathit{bc}(x_{2})$, for all $a,b \in \mathbb{Z}$, hence also for all $a,b \in \mathbb{Q}$, and continuity implies that the equality holds also for all $a,b \in \mathbb{R}$. The map c is holomorphic, hence it is a linear transformation of one-dimensional complex vector spaces, which is an isomorphism, since c is non-constant. This completes the proof of Theorem 7.11. □ 

Let X be an irreducible holomorphic symplectic manifold of K3^[n]-type and $\pi: X \rightarrow \mathbb{P}^{n}$ a Lagrangian fibration. Set $\alpha:=\pi ^{{\ast}}c_{1}(\mathcal{O}_{\mathbb{P}^{n}}(1))$. Let d be the divisibility of (α, •). Let $(S,\mathcal{L})$ be the semi-polarized K3 surface associated to (X, α) in Diagram (5.4) and χ the Euler characteristic of the Mukai vector u in that diagram. Choose a u-generic polarization H on S.

Theorem 7.13.

Assume that X is non-special and $(S,\mathcal{L})$ satisfies Assumption  7.1 . Then X is bimeromorphic to a Tate-Shafarevich twist of the Lagrangian fibration $M_{H}(0,\mathcal{L}^{d},\chi ) \rightarrow \mid \mathcal{L}^{d}\mid$ .

Proof.

Fix a marking $\eta: H^{2}(X, \mathbb{Z}) \rightarrow \varLambda$. Starting with the period of (X, η), Theorem 7.11 exhibits a marked triple $(X^{{\prime}},\alpha ^{{\prime}},\eta ^{{\prime}})$, with $\eta ^{{\prime}}(\alpha ^{{\prime}}) =\eta (\alpha )$, in the same connected component $\mathfrak{M}_{\eta (\alpha )^{\perp }}^{+}$ as the triple (X, α, η), such that the class α ^′ is semi-ample as well and the periods P(X, η) and $P(X^{{\prime}},\eta ^{{\prime}})$ are equal. Furthermore, the Lagrangian fibration $\pi ^{{\prime}}: X^{{\prime}}\rightarrow \mid \mathcal{L}^{d}\mid$ induced by α ^′ is a Tate-Shafarevich twist of $\pi _{0}: M_{H}(0,\mathcal{L}^{d},\chi ) \rightarrow \mid \mathcal{L}^{d}\mid$. Step 1 of the proof of Theorem 1.3 yields a bimeromorphic map

, which is shown in Step 2 of that proof to satisfy f ^∗(α ^′) = α (see Eq. (6.1)). □ 

Proof (of Theorem 1.5).

The condition that NS(X) ∩α ^⊥ is cyclic generated by α implies that the semi-polarized K3 surface $(S,\mathcal{L})$, associated to (X, α), has a cyclic Picard group generated by $\mathcal{L}$. Assumption 7.1 thus holds, by Remark 7.2. Theorem 1.5 thus follows from Theorem 7.13. □