Abstract
In this paper we study holomorphic foliations with singularities having a homogeneous transverse structure of projective model (i.e., \(\mathrm{I\!P}SL(2,\mathbb {C})\) model). Our basic situation is the case of a foliation with singularities \(\mathcal F\) on a complex analytic space M of dimension two and the structure exists in the complement of some analytic subset \(S \subset M\) of codimension one. The main case occurs, as we shall see, when the analytic set is invariant by the foliation. We address both, the local and the global cases. This means two basic situations: (i) M is a projective surface (like \(M=\mathbb {C}P (2)\) or \(\overline{\mathbb {C}} \times \overline{\mathbb {C}}\)) and (ii) \(M=(\mathbb {C}^2,0)\) which means the case of germs of foliations at the origin \(0 \in \mathbb {C}^2\), having an isolated singularity at the origin. Our focus is the extension of the structure in a suitable sense. After performing a characterization of the existence of the structure in terms of suitable triples of differential forms, we consider the problem of extension of such structures to the analytic invariant set for germs of foliations and for foliations in complex projective spaces. Basic examples of this situation are given by logarithmic foliations and Riccati foliations. We also study the holonomy of such invariant sets, as a consequence of a strict link between this holonomy and the monodromy of a projective structure. These holonomy groups are proved to be solvable. Our final aim is the classification of such object under some mild conditions on the singularities they exhibit. In this work we perform this classification in the case where the singularities of the foliation are supposed to be non-dicritical and non-degenerate (more precisely, generalized curves). This case, we will see, corresponds to the transversely affine case and therefore to the class of logarithmic foliations. The more general case, which has to do with Riccati foliations, is dealt with by some extension results we prove and evoking results from Loray-Touzet-Vitorio.
Access provided by CONRICYT-eBooks. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Foliations and Transverse Structure
The Riccati differential equation
where \((x,y) \in \mathbb {C}^2\) and p, a, b, c are complex polynomials is well-known to be a basic model for complex foliations, on projective surfaces, with projective transverse structure outside an invariant algebraic curve. Similarly the Bernoulli equation
stands for a model with an affine structure outside of an algebraic invariant curve [8, 27]. In this work we develop the study and classification of transversely projective holomorphic foliations. More precisely, we study codimension one holomorphic foliations with singularities, under the hypothesis of the existence of a projective transverse structure off some analytic codimension one subset.
Recall that a foliation (holomorphic of codimension one, with singularities) is transversely projective if the corresponding non-singular foliation is given by an atlas of local submersions with projective relations, i.e., two such submersions \(y:U\rightarrow {\overline{\mathbb {C}}}\) and \({\tilde{y}} :{\tilde{U}} \rightarrow {\overline{\mathbb {C}}}\) are related by \({\tilde{y}} = \frac{a y + b }{ cy + d}\) for some \(a,b,c,d \in \mathbb {C}\) locally constant and satisfying \(ad - bc=1\). This is a particular case of foliation having a homogeneous transverse structure (cf. [4]) and in the holomorphic framework it is natural to consider the case where the foliation exhibits singularities and the transverse structure is defined in the complement of some analytic subset of codimension one [27]. This situation has two main examples given by the class of logarithmic foliations, i.e., foliations defined by simple poles closed meromorphic one-forms; and by the class of Riccati foliations, i.e., foliations induced by Riccati differential equations.
1.1 Holomorphic Foliations
The basic concepts of differentiable manifolds (as tangent space, tangent bundle, etc.) can be introduced in the complex holomorphic setting. This is also the case of the concept of foliation:
Definition 1
(holomorphic foliation) A holomorphic foliation \({\mathcal {F}}\) of (complex) dimension k on a complex manifold M is given by a holomorphic atlas \(\{\varphi _j:U_j\subset M\rightarrow V_j\subset {\mathbb {C}}^n\}_{j\in J}\) with the compatibility property: Given any intersection \(U_i\cap U_j\ne \emptyset \) the change of coordinates \(\varphi _j\circ \varphi _i^{-1}\) preserves the horizontal fibration on \({\mathbb {C}}^n\simeq {\mathbb {C}}^k\times \mathbb {C}^{n-k}\).
Examples of such foliations are, like in the “real” case, given by non-singular holomorphic vector-fields, holomorphic submersions, holomorphic fibrations and locally free holomorphic complex Lie group actions on complex manifolds.
Remark 1
-
(i)
As in the “real” case, the study of holomorphic foliations may be very useful in the classification theory of complex manifolds.
-
(ii)
In a certain sense, the “holomorphic case” is closer to the “algebraic case” than the case of real foliations.
1.2 Holomorphic Foliations with Singularities
One of the most common compactifications of the complex affine space \({\mathbb {C}}^n\) is the complex projective space \({\mathbb {C}} P(n)\). It is well-known that any foliation (holomorphic) of codimension \(k\ge 1\) on \({\mathbb {C}} P(n)\) must have some singularity (in other words, \({\mathbb {C}} P(n)\), for \(n\ge 2\), exhibits no holomorphic foliation in the sense we have considered up to now, cf. [2].) Thus one may consider such objects: singular (holomorphic) foliations as part of the zoology. Let us illustrate this concept through some examples:
Example 1
(Polynomial vector fields on \({\mathbb {C}}^2\)) Given affine coordinates \((x,y)\in \mathbb {C}^2\), let \(X = P(x,y)(\partial /\partial x) + Q(x,y) (\partial /\partial y) = (P, Q)\) be a polynomial vector field (with isolated singularities) on \({\mathbb {C}}^2\). We have an ordinary differential equation:
The local solutions are given by Picard’s Theorem (the existence and uniqueness theorem of ordinary differential equations):
Gluing the images of these unique local solutions, we can introduce the orbits of X on \({\mathbb {C}}^2\). The orbits are immersed Riemann surfaces on \({\mathbb {C}}^2\), which are locally given by the solutions of X.
Now we may be interested in what occurs these orbits in “a neighborhood of the infinity”. We may for instance compactify \({\mathbb {C}}^2\) as the projective plane \({\mathbb {C}} P(2)={\mathbb {C}}^2\cup L_\infty \), \(L_\infty \cong {\mathbb {C}} P(1)\).
-
1.
What happens to X in a neighborhood of \(L_\infty \)?
-
2.
Is it still possible to consider its orbits around \(L_\infty \)?
We may rewrite X as the coordinate system \((u, v)=(1/x,y/x)\): \(X(u, v) = \frac{1}{u^m} Y(u,v)\), \(m\in {\mathrm{I\!N}}\cup \setminus {0}\) where Y is a polynomial vector field, also with isolated singularities. The exterior product of X and Y is zero in common domain \(U: X \wedge Y = 0\). Thus, orbits of Y (or X) are orbits of X (or Y), respectively in U. Then the orbits of X extend to the (u, v)-plane as the corresponding orbits of Y along \(L_\infty \). In this same way, we may consider the extension of the orbits to the \((r,s)=(x/y,1/y)\) coordinate system. These extensions are called leaves of a foliation induced by X on \({\mathbb {C}} P (2)\). We obtain this way: A decomposition of \({\mathbb {C}} P (2)\) into immersed complex curves which are locally arrayed, as the orbits (solutions) of a complex vector field. This is a holomorphic foliation \({\mathcal {F}}\) with singularities of dimension one on \({\mathbb {C}} P(2)\).
Remark 2
(singularities are defined by differential forms) Assume that we have a holomorphic non-singular foliation \({\mathcal {F}}_0\) on \(U\setminus \{0\}\), \(0\in {\mathbb {C}}^2\), \(U\cap sing({\mathcal {F}})=\setminus {0}\). Choose local coordinates (x, y) centered at 0 and define a meromorphic function \(f:U\setminus \{0\} \rightarrow \overline{\mathbb {C}}\), \(p\in U \setminus \{0\}\), as \(f(p) =\) the inclination of the tangent to the leaf \(L_p\) of \({\mathcal {F}}_0\). By Hartogs’ Extension Theorem [18, 34] f extends to a meromorphic function \(f:U \rightarrow \overline{\mathbb {C}}\). We may write \(f(x,y) = \tfrac{a(x,y)}{b(x,y)}\), \(a,b\in \mathcal O(U)\) and define
that is,

Therefore, \({\mathcal {F}}\) is defined by a holomorphic 1-form \(\omega = a(x,y)\;dy - b(x,y)\;dx\) in U.
The above remark also motivates the following definition:
Definition 2
(holomorphic foliation with singularities) Let M be a complex manifold. A singular holomorphic foliation of codimension one \({\mathcal {F}}\) on M is given by an open cover \(M=\bigcup _{j\in J}U_j\) and holomorphic integrable 1-forms \(\omega _j \in \bigwedge ^1(U_j)\) such that if \(U_j \cap U_j \ne \emptyset \), then \(\omega _i = g_{ij}\omega _j\) in \(U_i\cap U_j\), for some \(g_{ij}\in \mathcal O^{*}(U_i\cap U_j)\). We put \( sing({\mathcal {F}})\cap U_j =\{p\in U_j; \, \omega _j(p)=0\}\) to obtain \( sing({\mathcal {F}}) \subset M\), a well-defined analytic subset of M, called singular set of \({\mathcal {F}}\). The open subset \(M \setminus sing({\mathcal {F}})\subset M\) is foliated by a holomorphic codimension one (non-singular) foliation \({\mathcal {F}}_0\). By definition the leaves of \({\mathcal {F}}\) are the leaves of \({\mathcal {F}}_0\).
Remark 3
We may always assume that \( sing({\mathcal {F}})\subset M\) has codimension \(\ge 2\). If \((f_j = 0)\) is an equation of codimension one component of \( sing({\mathcal {F}}) \cap U_j\), then we get \(\omega _j = f_j^n \bar{\omega }_j\) where \(\bar{\omega }_j\) is a holomorphic 1-form and \( sing(\bar{\omega }_j) \) does not contain \((f_j =0)\).
Remark 4
(Convention) Let M be a complex manifold. From now on, in the absence of a specific mention, by foliation on M we shall mean a codimension one holomorphic foliation with singularities. We shall also assume that the singular set \( sing({\mathcal {F}})\subset M\) has codimension \(\ge 2\). In particular, if M has dimension two then \( sing({\mathcal {F}})\) is a discrete set of points of M.
Example 2
Let \(f:M\rightarrow \overline{\mathbb {C}}\) be a meromorphic function on the complex manifold M. Then \(\omega = df\) defines a holomorphic foliation of codimension one with singularities on M. The leaves are the connected components of the levels \(\{f =\text{ c }\}, c \in \overline{\mathbb {C}}\).
Example 3
Let G be a complex Lie group and \(\varphi :G\times M\rightarrow M\) a holomorphic action of G on M. The action is foliated if all its orbits have a same fixed dimension. In this case there exists a holomorphic non-singular foliation \({\mathcal {F}}\) on M, whose leaves are orbits of \(\varphi \). However, usually, actions are not foliated, though they may define singular holomorphic foliations. For instance, an action \(\varphi \) of \(G=({\mathbb {C}},+)\) on M, \(\varphi :{\mathbb {C}}\times M \rightarrow M\) is a holomorphic flows. We have a holomorphic complete vector field \(X= \tfrac{\partial \phi }{\partial t}|_{t=0}\) on M. The singular set of X may be assumed to be of codimension \(\ge 2\) and we obtain a holomorphic singular foliation of dimension one \({\mathcal {F}}\) on M whose leaves are orbits of X, or equivalently, of \(\varphi \).
Problem 1
Study and classify actions of complex Lie groups G on a given compact complex M, in terms of the corresponding foliation.
The general problem above may be therefore regarded under the stand-point of singular holomorphic foliations theory.
Example 4
(Darboux foliations) Let M be a complex manifold and let \(f_j: M\rightarrow \overline{\mathbb {C}}\) be meromorphic functions and \(\lambda _j\in {\mathbb {C}}^*\) complex numbers, \(j=1,\dots ,r\). The meromorphic integrable 1-form \(\omega =(\prod \limits _{j=1}^r f_j) \sum \limits _{i=1}^{r} \lambda _i \frac{df_i}{f_i}\) defines a Darboux foliation \({\mathcal {F}} = {\mathcal {F}}(\omega )\) on M. The foliation \({\mathcal {F}}\) has \(f = \prod \limits _{j=1}^{r} f_j^{\lambda _j}\) as a logarithmic first integral.
Example 5
(Riccati foliations) A Riccati Foliation on \( \overline{\mathbb {C}}\times \overline{\mathbb {C}}\) is given in some affine chart \((x,y)\in \mathbb {C}\times \mathbb {C}\) by a polynomial one-form \(\omega =p(x)dy - (y^2c(x) - yb(x) -a(x))dx\). This will be thoroughly studied in the next section.
The concept of holonomy in the singular case Let now \({\mathcal {F}}\) be a holomorphic foliation (with isolated singularities) on a complex manifold M. Given a leaf \(L_0\) of \({\mathcal {F}}\) we choose any base point \(p\in L_0\subset M \setminus sing({\mathcal {F}})\) and a transverse disc \(\varSigma _p\subset M\) to \({\mathcal {F}}\) centered at p. Denote by \(Diff(\varSigma _p,p)\) the group of germs of complex diffeomorphisms of \(\varSigma _p\) with a fixed point at p. The holonomy group of the leaf \(L_0\) with respect to the disc \(\varSigma _p\) and to the base point p is the image of the representation \(Hol:\pi _1(L_0,p) \rightarrow Diff(\varSigma _p,p)\) obtained by lifting closed paths in \(L_0\) with base point p, to paths in the leaves of \({\mathcal {F}}\), starting at points \(z\in \varSigma _p\), by means of a transverse fibration to \({\mathcal {F}}\) containing the disc \(\varSigma _p\) [6, 17]. Given a point \(z \in \varSigma _p\) we denote the leaf through z by \(L_z\). Given a closed path \(\gamma \in \pi _1(L_0,p)\) we denote by \({\tilde{\gamma }}_z\) its lift to the leaf \(L_z\) and starting (the lifted path) at the point z. Then the image of the corresponding holonomy map is \(h_{[\gamma ]}(z)={\tilde{\gamma }}_z(1)\), i.e., the final point of the lifted path \({\tilde{\gamma }}_z\). This defines a diffeomorphism germ map \(h_{[\gamma ]} :(\varSigma _p, p) \rightarrow (\varSigma _p,p)\) and also a group homomorphism \(Hol :\pi _1(L_0,p) \rightarrow Diff(\varSigma _p,p)\). The image \(Hol({\mathcal {F}},L_0,\varSigma _p,p)\subset Diff(\varSigma _p,p)\) of such homomorphism is called the holonomy group of the leaf \(L_0\) with respect to \(\varSigma _p\) and p. By considering any parametrization \(z:(\varSigma _p,p) \rightarrow (D,0)\) we may identify (in a non-canonical way) the holonomy group with a subgroup of \(Diff(\mathbb {C},0)\). It is clear from the construction that the maps in the holonomy group preserves the leaves of the foliation.
Separatrices and local holonomies Fix now a germ \({\mathcal {F}}\) of holomorphic foliation with a singularity at the origin \(0\in \mathbb {C}^2\). Choose a representative \({\mathcal {F}}(U)\) for \({\mathcal {F}}\), defined in an open neighborhood U of the origin. A leaf of \(\mathcal {F}(U)\) accumulating only at 0 is closed off 0, thus by Remmert–Stein extension theorem [19] it is contained in an irreducible analytic curve through 0. Such a curve is called a local separatrix of \(\mathcal {F}\) through 0. A separatrix is therefore the union of a leaf of \({\mathcal {F}}|_U\) which is closed off the singular point, and the singular point \(0\in {\mathbb {C}}^2\). By Newton–Puiseux parametrization theorem, if U is small enough, there is an analytic injective map \(f :D \rightarrow U\) from the unit disk \(D \subset {\mathbb {C}}\) into the separatrix, mapping the origin to \(0\in {\mathbb {C}}^2\), and non-singular outside the origin \(0 \in D\). Therefore the leaf contained in a separatrix, locally has the topology of a punctured disk. In particular, given a separatrix \(\varGamma \) we may choose a loop \(\gamma \in \varGamma \setminus \{0\}\) generating the (local) fundamental group \(\pi _{1}(\varGamma \setminus \{0\})\). The corresponding holonomy map \(h_{\gamma }\) is defined in terms of a germ of complex diffeomorphism at the origin of a local disc \(\varSigma \) transverse to \(\mathcal {F}\) and centered at a non-singular point \(q\in \varGamma \setminus \{0\}\). This map is well-defined up to conjugacy by germs of holomorphic diffeomorphisms, and is generically referred to as local holonomy of the separatrix \(\varGamma \) with respect to the singularity \(0\in \mathbb {C}^2\).
1.3 Irreducible Singularities, Separatrices and Reduction of Singularities
Let \(\omega = a(x,y) dx+ b(x,y) dy\) be a holomorphic one-form defined in a neighborhood \(0\in U\in {\mathbb {C}}^2\). We say that \(0\in {\mathbb {C}}^2\) is a singular point of \(\omega \) if \(a(0,0)=b(0,0)=0\), and a non-singular point otherwise. We say that \(0\in {\mathbb {C}}^2\) is an irreducible singular point of \(\omega \) if the eigenvalues \(\lambda _1, \lambda _2\) of the linear part of the corresponding dual vector field \(X= -b(x,y)\tfrac{\partial }{\partial x} + a(x,y)\tfrac{\partial }{\partial y}\) at \(0\in {\mathbb {C}}^2\) satisfy one of the following conditions:
-
(1)
\(\lambda _1.\lambda _2\ne 0\) and \(\lambda _1/\lambda _2\notin {\mathbb {Q}_+}\)
-
(2)
either \(\lambda _1\ne 0\) and \(\lambda _2= 0\), or vice-versa.
In case (1) there are two invariant curves tangent to the eigenvectors corresponding to \(\lambda _1\) and \(\lambda _2\). In case (2) there is an invariant curve tangent at \(0\in {\mathbb {C}}^2\) to the eigenspace corresponding to \(\lambda _1\). These curves are called separatrices of the foliation.
Suppose that \(0\in {\mathbb {C}}^2\) is either a non-singular point or an irreducible singularity of a foliation \(\mathcal F\). Then in suitable local coordinates (x, y) in a neighborhood \(0\in U \in {\mathbb {C}}^2\) of the origin, we have the following local normal forms for the one-forms defining this foliation [7]:
- (Reg):
-
\(dy=0\), whenever \(0\in {\mathbb {C}}^2\) is a non-singular point of \(\mathcal F\).
and whenever \(0\in {\mathbb {C}}^2\) is an irreducible singularity of \(\tilde{\mathcal {F}}\), then either
- (Irr.1):
-
\(xdy - \lambda ydx + \omega _2(x,y) = 0\) where \(\lambda \in {\mathbb {C}}\backslash \mathbb {Q}_+\), \(\omega _2(x,y)\) is a holomorphic one-form with a zero of order \(\ge 2\) at (0, 0). This is called non-degenerate singularity. Such a singularity is resonant if \(\lambda \in \mathbb {Q}_-\) and hyperbolic if \(\lambda \notin \mathrm{I\!R}\), or
- (Irr.2):
-
\(y^{t+1}dx - [x(1+\lambda y^t) + A(x,y)]dy {=} 0\) , where \(\lambda \in {\mathbb {C}}\), \(t \in \mathrm{I\!N}{=} \{1,2,3,\dots \}\) and A(x, y) is a holomorphic function with a zero of order \(\ge t+2\) at (0, 0). This is called saddle-node singularity. The strong manifold or strong separatrix of the saddle-node is given by \(\{y=0\}\). If the singularity admits another separatrix then it is necessarily smooth and transverse to the strong manifold, it can be taken as the other coordinate axis and will be called central manifold of the saddle-node. This class of irreducible singularity is thoroughly studied in [22].
Therefore, for a suitable choice of the coordinates, we have \(\{y=0\} \subset sep(\mathcal F,U) \subset \{xy=0\}\), where \( sep(\mathcal F,U)\) denotes the union of separatrices of \(\mathcal F\) through \(0\in {\mathbb {C}}^2\).
An irreducible singularity \(xdy - \lambda ydx + \ldots =0\) is in the Poincaré domain if \(\lambda \notin \mathrm{I\!R}_-\) and it is in the Siegel domain otherwise. For singularities in the Poincaré domain, the non-resonance condition (\(\lambda \notin \mathbb {Q}\)) actually implies, by Poincaré linearization theorem, that the singularity is analytically linearizable (cf. [16]). For singularities in the Siegel domain, this question is quite more delicate [23]).
Given a foliation \({\mathcal {F}}\) of dimension one on a complex surface M with finite singular set \( sing({\mathcal {F}})\), the Theorem of reduction of singularities of Seidenberg reads as follows:
Theorem 1
([31]) There is a proper holomorphic map \(\pi :\widetilde{M} \rightarrow M\) which is a finite composition of quadratic blowing-up’s at the singular points of \({\mathcal {F}}\) in M such that the pull-back foliation \(\widetilde{\mathcal {F}}:= \pi ^* {\mathcal {F}}\) of \({\mathcal {F}}\) by \(\pi \) satisfies:
-
(a)
\( sing (\tilde{\mathcal {F}}) \subset \pi ^{-1} ( sing( {\mathcal {F}}))\), and
-
(b)
Any singularity \({\tilde{p}} \in sing( {\tilde{\mathcal {F}}})\) is irreducible.
Indeed, we can say more:
We call \({\tilde{\mathcal {F}}}\) the desingularization or reduction of singularities of \({\mathcal {F}}\). Moreover, the exceptional divisor \(E=\pi ^{-1}(sing({\mathcal {F}}))\subset \) \(\widetilde{M}\) of the reduction \(\pi \) can be written as \(E=\bigcup _{j=1}^m \mathrm{I\!P}_j\), where each \(\mathrm{I\!P}_j\) is diffeomorphic to an embedded projective line \({\mathbb {C}} P(1)\) introduced as a divisor of the successive blowing-up’s. The \(\mathrm{I\!P}_j\) are called components of the divisor E. A singularity \(q\in sing( {\mathcal {F}})\) is non-dicritical if \(\pi ^{-1}(q)\) is invariant by \({\tilde{\mathcal {F}}}\). Any two components \(\mathrm{I\!P}_i\) and \(\mathrm{I\!P}_j\), \(i\ne j\), intersect (transversely) at most one point, which is called a corner. Moreover, there are no triple intersection points. Any non-invariant component of the exceptional divisor is transverse to the lifted foliation \({\tilde{\mathcal {F}}}\) at every point. Given any analytic curve \(\varLambda \subset M\) we denote by \({\tilde{\varLambda }}:= \overline{\pi ^{-1}(\varLambda \setminus sing({\mathcal {F}}))}\subset \tilde{M}\) the strict transform of \(\varLambda \).
As seen above, a separatrix of \({\mathcal {F}}\) at \(0\in {\mathbb {C}}^2\) is the germ at \(0\in {\mathbb {C}}^2\) of an irreducible analytic curve, containing the singular point, which is invariant by \({\mathcal {F}}\). By the reduction of singularities (Theorem 1) we conclude that a separatrix \(\varGamma \) of \({\mathcal {F}}\) is the projection \(\varGamma =\pi ({\tilde{\varGamma }})\) of a curve \({\tilde{\varGamma }}\) invariant by \(\tilde{\mathcal {F}}\) and transverse to the exceptional divisor \(\pi ^{-1}(0)\). A singularity is called dicritical if it exhibits infinitely many separatrices. We shall say that a separatrix \(\varGamma \) is a dicritical separatrix if \({\tilde{\varGamma }}\) meets the exceptional divisor only at non-singular points. Equivalently, \(\varGamma =\pi ({\tilde{\varGamma }})\) is non-dicritical if \({\tilde{\varGamma }}\) is a separatrix of some singularity of \({\tilde{\mathcal {F}}}\). A non-dicritical separatrix is geometrically characterized by the fact that it is isolated in the set of separatrices. Indeed, notice that a neighborhood of some projective line in a finite sequence of blowing-ups starting at the origin corresponds to what we call sector with vertex at the origin. Thus, from the Resolution theorem (Theorem 1) a dicritical separatrix is always one which is contained in the interior of a “sector of separatrices”. Given a representative for the germ \({\mathcal {F}}\) in a neighborhood U of the singularity, we shall denote by \(\mathcal ND(sep({\mathcal {F}},U))\subset U\) the analytic set which is the union of the non-dicritical separatrices of \({\mathcal {F}}\) in U.
Definition 3
(generalized curve - [10] p. 144) A germ of a foliation singularity at the origin \(0\in {\mathbb {C}}^2\) is a generalized curve if (i) it is non-dicritical and (ii) it exhibits no saddle-node in its reduction by blow-ups.
Generalized curves play an important role in the zoology of the singularities of holomorphic foliations. They are those whose desingularization/reduction of singularities is like the one of a holomorphic function \(f:\mathbb {C}^2, 0 \rightarrow \mathbb {C},0\) [10]. In this work we will consider a slightly more general concept which is the following:
Definition 4
((non-resonant) extended generalized curve) A germ of a foliation singularity at the origin \(0\in {\mathbb {C}}^2\) will be called an extended generalized curve if the singularity exhibits no saddle-node in its reduction by blow-ups. This includes the case of dicritical singularities. An extended generalized curve singularity is called non-resonant if each connected component of the invariant part of exceptional divisor contains some non-resonant singularity.
2 Foliations with Projective Transverse Structure
2.1 Transversely Homogeneous Foliations
A (transversely) holomorphic foliation \({\mathcal {F}}\) on a smooth manifold M has a holomorphic homogeneous transverse strucutre if there are a complex Lie group G, a connected closed subgroup \(H < G\) such that \({\mathcal {F}}\) admits an atlas of submersions \(y_j:U_j \subset M \rightarrow G/H\) satisfying \(y_i = g_{ij}\circ y_j\) for some locally constant map \(g_{ij}:U_i \cap U_j \rightarrow G\) for each \(U_i \cap U_j \ne \emptyset \). In other words, the transversely holomorphic atlas of submersions for \({\mathcal {F}}\) has transiction maps given by left translations on G and submersions taking values on the homogeneous space G / H. We shall say that \({\mathcal {F}}\) is transversely homogeneous of model G / H. Some important properties of transversely homogeneous holomorphic foliations are listed below:
-
1.
Any transversely homogeneous holomorphic foliation is a transversely holomorphic foliation with a holomorphic homogeneous transverse structure.
-
2.
Given a foliation \({\mathcal {F}}\) on M as in (1) with model G / H then any real submanifold \(M \subset M\) transverse to \({\mathcal {F}}\) is equipped with a transversely holomorphic foliation \({\mathcal {F}}_1 = {\mathcal {F}}|_M\) with holomorphic homogeneous transverse structure of model G / H.
-
3.
Let \(F = G/H\) be an homogeneous space of a complex Lie group G (\(H\triangleleft G\) is a closed Lie subgroup). Any homomorphism representation \(\varphi :\pi _1(N) \rightarrow Aut(F)\) gives rise to a transversely holomorphic foliation \({\mathcal {F}}_\varphi \) on \(({\widetilde{N}\times F})/{\varphi } = M_\varphi \) which is holomorphically transversely homogeneous of model G / H.
-
4.
For the case \(G=\mathrm{I\!P}SL(2,\mathbb {C})\) and \(H\subset G\) is the affine group \(H=Aff(\mathbb {C})\) (isotropy group of the point at infinity \(\infty \in \mathbb {C}P^1\)), we have that the quotient \(G/H\simeq \mathbb {C}P^1\) is the Riemann sphere and the foliations with this transverse model are called transversely projective.
More precisely we have, for the non-singular case:
Definition 5
(transversely projective foliation: non-singular) A codimension one non-singular holomorphic foliation \({\mathcal {F}}\) on a manifold M is called transversely projective if there is an open cover \(\bigcup \limits _{j\in J} U_j = M\) such that in each \(U_j\) the foliation is given by a submersion \(f_j:U_j \rightarrow \overline{\mathbb {C}}\) and if \(U_i \cap U_j \ne \emptyset \) then we have \(f_i = f_{ij}\circ f_j\) in \(U_i \cap U_j\) where \(f_{ij}:U_i \cap U_j \rightarrow \mathrm{I\!P}SL(2,{\mathbb {C}})\) is locally constant. Thus, on each intersection \(U_i \cap U_j \ne \emptyset \), we have \(f_i = \frac{a_{ij}f_j+b_{ij}}{c_{ij}f_j+d_{ij}}\) for some locally constant functions \(a_{ij}, b_{ij}, c_{ij}, d_{ij}\) with \(a_{ij}d_{ij} - b_{ij}c_{ij} = 1\). The data \(\mathcal P = \{U_j, f_j, f_{ij}, j \in J\}\) is called a projective transverse structure for \({\mathcal {F}}\).
Basic references for transversely affine and transversely projective foliations (in the non-singular case) are found in [17].
-
(5)
Based on the Rieman-Koebe uniformization theorem we have:
Proposition 1
([27] Theorem 6.1 p. 203).) Let \({\mathcal {F}}\) be a transversely homogeneous holomorphic foliation of codimension one on \(M^n\). Then \({\mathcal {F}}\) is transversely projective foliation on \(M^n\).
Proof
We know that G / H is a simply-connected complex manifold of dimension one. By the Riemann-Koebe Uniformization theorem we have a conformal equivalence \(G/H \equiv \overline{\mathbb {C}}, \mathbb {C}\) or D the unitary disc. This implies that either \(G\subset Aut(\overline{\mathbb {C}})=\mathrm{I\!P}SL(2,\mathbb {C}), G\subset Aut(\mathbb {C})=Aff(\mathbb {C})\) or \(G\subset Aut(D)\cong \mathrm{I\!P}SL(2,\mathrm{I\!R})\). The proposition follows.
Let \({\mathcal {F}}\) be a codimension \(\ell \) foliation on a manifold M. If \({\mathcal {F}}\) admits a Lie group transverse structure of model G, or a G -transverse structure for short, then we shall call \({\mathcal {F}}\) a G -foliation or, simply, Lie foliation. The characterization of G-foliations in terms of differential forms is given below. Let \(\{\omega _1,\ldots ,\omega _\ell \}\) be a basis of the Lie algebra of G. Then we have \(d\omega _k = \sum \limits _{i<j} c_{ij} ^k \omega _i \wedge \omega _j\) for a family constants \(\{c_{ij}^k\}\) called the structure constants of the Lie algebra in the given basis.
Theorem 2
(Darboux-Lie, [17]) Let G be a complex Lie group of dimension \(\ell \). Let \(\{\omega _1,\ldots ,\omega _\ell \}\) be a basis of the Lie algebra of G with structure constants \(\{c_{ij}^k\}\). Suppose that a complex manifold \(V^m\) of dimension \(m \ge \ell \) admits a system of one-forms \(\varOmega _1,\ldots ,\varOmega _\ell \) in M such that:
-
(i)
\(\{\varOmega _1,\ldots ,\varOmega _\ell \}\) is a rank \(\ell \) integrable system which defines \({\mathcal {F}}\).
-
(ii)
\(d\varOmega _k =\sum \limits _{i<j} c_{ij}^k \varOmega _i \wedge \varOmega _j\).
Then:
-
(iii)
For each point \(p\in M\) there is a neighborhood \(p\in U_p \subseteq M\) equipped with a submersion \(f_p:U_p \rightarrow G\) which defines \({\mathcal {F}}\) in \(U_p\) such that \(f_p^* (\omega _j)=\varOmega _j\) in \(U_p\), for all \(j\in \{1,\ldots ,q\}\).
-
(iv)
If \(U_p \cap U_q \ne \emptyset \) then in the intersection we have \(f_q = L_{g_{pq}}(f_p)\) for some locally constant left translation \(L_{g_{pq}}\) in G.
-
(v)
If M is simply-connected we can take \(U_p = M\).
2.2 Transversely Projective Foliations with Singularities
Let M be a complex manifold. As already stated, if no specific mention is made, by foliation on M we shall mean a codimension one holomorphic foliation with singularities and \(\dim _\mathbb {C}M \ge 2\).
Definition 6
(transversely projective: singular) A foliation \({\mathcal {F}}\) on M is called transversely projective if the underlying “non-singular” foliation \({\mathcal {F}}_0=:{\mathcal {F}}\big |_{M\setminus sing({\mathcal {F}})}\) is transversely projective. This means that there is an open cover \(\bigcup \limits _{j\in J} U_j = M\setminus sing({\mathcal {F}})\) such that in each \(U_j\) the foliation is given by a submersion \(f_j:U_j \rightarrow \overline{\mathbb {C}}\) and if \(U_i \cap U_j \ne \emptyset \) then we have \(f_i = f_{ij}\circ f_j\) in \(U_i \cap U_j\) where \(f_{ij}:U_i \cap U_j \rightarrow \mathrm{I\!P}SL(2,{\mathbb {C}})\) is locally constant. Thus, on each intersection \(U_i \cap U_j \ne \emptyset \), we have \(f_i = \frac{a_{ij}f_j+b_{ij}}{c_{ij}f_j+d_{ij}}\) for some locally constant functions \(a_{ij}, b_{ij}, c_{ij}, d_{ij}\) with \(a_{ij}d_{ij} - b_{ij}c_{ij} = 1\).
As observed in [27] the singularities of a foliation admitting a projective transverse structure are all of type \(df=0\) for some local meromorphic function (indeed, if \(\varDelta \subset \mathbb {C}^n\) is a polydisc centered at the origin then \(\varDelta \setminus \{0\}\) is simply-connected for \(n \ge 2\)). In this work we will be considering foliations which are transversely projective in the complement of codimension one invariant divisors. Such divisors may, a priori, exhibit singularities which do not admit meromorphic first integrals.
2.3 Riccati Foliations
Example 6
(Riccati Foliations) The Riccati differential equation
where \((x,y) \in \mathbb {C}^2\) and p, a, b, c are complex polynomials has been proved to be an important model for complex foliations, on projective surfaces. In the particular case when \(c\equiv 0\), it as an important example of a foliation with affine transverse structure outside an algebraic invariant set [8, 27].
Fix affine coordinates \((x,y) \in \mathbb {C}^2\) and consider a polynomial one-form \(\varOmega = p(x)dy - \big (a(x)y^2 + b(x)y + c(x)\big )dx\) on \(\mathbb {C}^2\). Then \(\varOmega \) defines a Riccati foliation \({\mathcal {R}}\) on \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) as follows: if we change coordinates via \(u = \frac{1}{x}\), \(v = \frac{1}{y}\) then we obtain \(\varOmega (x,v) = p(x)dv + \big (a(x) + b(x)v + c(x)v^2\big ) dx\). Similarly for \(\varOmega (u,y) = u^{-n} [{\tilde{p}}(u)\,dy - \big ({\tilde{a}}(u)y^2 + {\tilde{b}}(u)y + \tilde{c}(u)\big )du]\) and \(\varOmega (u,v) = u^{-n} [{\tilde{p}}(u)\, dv- \big ({\tilde{a}}(u) + {\tilde{b}}(u)v + {\tilde{c}}(u)v^2\big )du]\). The similarity of these four expressions shows that \(\varOmega \) defines a holomorphic foliation \({\mathcal {R}}\) with isolated singularities on \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) and having a geometry as follows (see Fig. 1):
(i) \({\mathcal {R}}\) is transverse to the fibers \(\{a\} \times \overline{\mathbb {C}}\) except for invariant fibers which are given in \(\mathbb {C}^2\) by \(\{p(x)=0\}\).
(ii) If \(S = \bigcup \limits _{j=1}^r \{a_j\} \times \overline{\mathbb {C}}\) is the set of invariant fibers then \({\mathcal {R}}\) is transversely projective in \((\overline{\mathbb {C}}\times \overline{\mathbb {C}})\backslash S\). Indeed, \({\mathcal {R}}|_{(\overline{\mathbb {C}}\times \overline{\mathbb {C}})\backslash S}\) is conjugate to the suspension of a representation \(\varphi :\pi _1 (\overline{\mathbb {C}}\backslash \bigcup \limits _{j=1}^r \{a_j\}) \rightarrow \mathrm{I\!P}SL(2,\mathbb {C})\).
(iii) For a generic choice of the coefficients \(a(x), b(x), c(x), p(x) \in \mathbb {C}[x]\) the singularities of \({\mathcal {R}}\) on \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) are hyperbolic, S is the only algebraic invariant set and therefore for each singularity \(q\in sing({\mathcal {R}}) \subset S\) there is a local separatrix of \({\mathcal {R}}\) transverse to S passing through q.
Now we consider the canonical way of passing from \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) to \(\mathbb {C}P(2)\) by a map \(\sigma :\overline{\mathbb {C}}\times \overline{\mathbb {C}}\rightarrow \mathbb {C}P(2)\) obtained as a sequence of birational maps as follows: first blow-up a point, for example the origin, of \(\mathbb {C}^2 \subset \overline{\mathbb {C}}\times \overline{\mathbb {C}}\) then blow-down two suitable projective lines of self-intersection equals \(-1\) as indicated in Fig. 1. Following this process step by step we conclude that the foliation \({\mathcal {F}} = \sigma _*({\mathcal {R}}) = (\sigma ^{-1})^*({\mathcal {R}})\) induced by \({\mathcal {R}}\) on \(\mathbb {C}P(2)\) has the following characteristics:
(i’) \({\mathcal {F}}\) is transversely projective in \(\mathbb {C}P(2)\backslash S\) where \(S \subset \mathbb {C}P(2)\) is the union of a finite number of projective lines of the form \(\bigcup \limits _{j=1}^r \overline{\{x=a_j\}} \subset \mathbb {C}P(2)\) in a suitable affine chart \((x,y) \in \mathbb {C}^2 \subset \mathbb {C}P(2)\).
(ii’) For a generic choice of the coefficients of \(\varOmega \), the singularities of \({\mathcal {F}}\) in S are hyperbolic except for one single dicritical singularity \(q_\infty :(x=\infty , y=0) \in \mathbb {C}P(2)\) which after one blow-up gives a non-singular foliation transverse to the projective line except for a single tangency point. This singularity will be called a radial type singularity. The foliation \({\mathcal {F}}\) also has two other nonhyperbolic singularities, belonging to the line at infinity \(L_\infty = \mathbb {C}P(2) \setminus \mathbb {C}^2\), which is invariant, one linearizable with holomorphic first integral and the other dicritical of radial type, admitting a meromorphic first integral. Also, in general, \(S\cup L_\infty \) is the only algebraic invariant set and \( sing({\mathcal {F}}) \subset S\cup L_\infty \).
(iii’) Finally, we stress that on \(\mathbb {C}P(2)\) the foliation \({\mathcal {F}}\) is transversely projective in a neighborhood of \(L_\infty \setminus (L_\infty \cap sing({\mathcal {F}}))\).
In this work we shall focus on the problem of extension of the structure to the analytic set, as well as on the consequences of this extension. The very basic result relating transversely homogeneous foliations and suitable systems of differential forms is the classic Darboux-Lie theorem [4, 17, 27].
Example 7
(pull-backs) Let \({\mathcal {F}}\) be a transversely projective foliation on M. Let \(\pi :N\rightarrow M\) be a holomorphic map transverse to \({\mathcal {F}}\), then the pull-back foliation \(\pi ^*({\mathcal {F}})\) is transversely projective in N. This can be used to construct examples of foliations on projective manifolds, which are transversely projective outside of some algebraic invariant curve. Take for instance a rational map \(\pi :M \rightarrow \overline{\mathbb {C}}\times \overline{\mathbb {C}} \) where M is a non-singular projective manifold. Given a Riccati foliation \({\mathcal {R}}\) on \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) the pull-back \({\mathcal {F}}:=\pi ^*({\mathcal {R}})\) is then a foliation on M which is transversely projective outside of some algebraic \(C\subset M\) of codimension \(\ge 1\). As we will see, we can assume that C is invariant by \({\mathcal {F}}\), otherwise the projective structure extends to some component of C.
Example 8
(suspensions of subgroups of \(\mathrm{I\!P}SL(2,\mathbb {C})\)) A well known way of constructing transversely homogeneous foliations on fibered spaces, having a prescribed holonomy group is the suspension of a foliation by a group of biholomorphisms. This construction is briefly described below: Let \(G\subset Diff(N)\) be a finitely generated group of biholomorphisms of a complex manifold N. We can regard G as the image of a representation \(h:\pi _1(M) \rightarrow Diff(N)\) of the fundamental group of a complex (connected) manifold M. Considering the universal holomorphic covering of M, \(\pi :\widetilde{M} \rightarrow M\) we have a natural free action \(\pi _1:\pi _1(M)\times \widetilde{M} \rightarrow \widetilde{M}\), i.e., \(\pi _1(M) \subset Diff(\widetilde{M})\) in a natural way. Using this we define an action \(H:\pi _1(M)\times \widetilde{M}\times N \rightarrow \widetilde{M}\times N\) in the natural way: \(H = (\pi _1,h)\). The quotient manifold \(\frac{\widetilde{M}\times N}{H} = M_h\) is called the suspension manifold of the representation h. The group G appears as the global holonomy of a natural foliation \({\mathcal {F}}_h\) on \(M_h\) (see [17]), this foliation is called suspension foliation of G. When G is (isomorphic to) a finitely generated subgroup of \(\mathrm{I\!P}SL(2,\mathbb {C})\) the suspension foliation is transversely projective in \(M_h\).
2.4 Development of a Transversely Projective Foliation
We recall the notion of development of a transversely projective foliation, first mentioned in the Introduction, already adapting it to our current framework. Let \(\mathcal G\) be a (non-singular) holomorphic foliation on a complex manifold N. Suppose that \(\mathcal G\) is transversely projective in N. There is a Galoisian (i.e., a transitive) covering \(\pi :P \rightarrow N\) where \(\pi \) is holomorphic, a homomorphism \(h:\pi _1(N) \rightarrow \mathrm{I\!P}SL(2,{\mathbb {C}})\) and a holomorphic submersion \(\varPhi :P \rightarrow {{\mathbb {C}} P}^1\) such that:
-
(i)
\(\varPhi \) is h-equivariant. This means that for any homotopy class \([\gamma ]\in \pi _1(N)\), we have
$$ h([\gamma ]) (\varPhi (x)) = \varPhi (\widetilde{[\gamma ]}(x)), \, \forall x \in M{\setminus }S $$where by \(\widetilde{[\gamma ]}:P \rightarrow P\) we denote the covering map induced by \([\gamma ]\) in the Galoisian covering \(p:P \rightarrow N\).
-
(ii)
\(\pi ^*\big (\mathcal G\big |_{N}\big )\) is the foliation defined by the submersion \(\varPhi \).
In the above construction of the development, we may take P as the universal covering \(\pi :\widetilde{N}\rightarrow N\) of N. We shall refer to the submersion \(\varTheta :\widetilde{N} \rightarrow {{\mathbb {C}}P^1}\) as a multiform first integral of \(\mathcal G\) given by the projective structure in N. Given a homotopy class \([\gamma ] \in \pi _1(M{\setminus }S)\), the corresponding monodromy map is the image \(h([\gamma ])\subset \mathrm{I\!P}SL(2,{\mathbb {C}})\).
Definition 7
The global monodromy of the foliation, with respect to this development, is the image \(\text {Mon}(\mathcal G)=h(\pi _1(N))\subset \mathrm{I\!P}SL(2,{\mathbb {C}})\).
Remark 5
Some remarks about the above construction are: The construction of the development in [17] requires the foliation to be non-singular. Assume now that \({\mathcal {F}}\) is a foliation with singular set of codimension \(\ge 2\) on a complex manifold M. Then \(N=M\setminus sing({\mathcal {F}})\) is a complex manifold and \(\mathcal G:= {\mathcal {F}}\big |_{N}\) is non-singular. By definition \({\mathcal {F}}\) is transversely projective if and only if \(\mathcal G\) is transversely projective. Moreover, since \( sing({\mathcal {F}})\subset M\) has real codimension \(\ge 4\), we conclude that there is a natural isomorphism \(\pi _1(N)\cong \pi _1(M)\). In particular, we can assume in the above construction that \(M=N\), i.e., the notion of development above introduced can be introduced for foliations with singularities. Finally, thanks to Hartogs’ extension theorem [18], any holomorphic map from \(M\backslash sing({\mathcal {F}}) \) to \({\mathbb {C}}P^1\) extends uniquely to a holomorphic map from M to \({\mathbb {C}}P^1\).
2.5 Holonomy Groups of Transversely Projective Foliations
In what follows we consider the following situation. Let \({\mathcal {F}}\) be a holomorphic foliation on a complex surface M, \(\varLambda \subset M\) a closed analytic invariant subset of pure dimension one (a curve) and assume that \({\mathcal {F}}\) is transversely projective in \(M\backslash \varLambda \). We will follow original ideas from [26] in the same vein as in [28].
Monodromy: Using the notion of development we can introduce the notion of monodromy of the projective transverse structure of \({\mathcal {F}}\big |_{M\setminus \varLambda }\) as follows:
Fix a base point \(m_0 \in M{\setminus }\varLambda \) and a local determination \(f_{m_0}\) of the submersion \(\varPhi \) in a small ball \(B_{m_0}\) centered at \(m_0\) (we have the following commutative diagram)
Notice that \(p^{-1}(B_{m_0}) =\bigcup \limits _{\alpha \in \mathcal A} U_\alpha , \, p\big |_{U_\alpha }:U_\alpha \rightarrow B_{m_0}\) is a biholomorphism for each \(\alpha \in \mathcal A\).
By construction, the total space of the covering \(p:P \rightarrow M \backslash \varLambda \) is obtained by analytic continuation of \(f_{m_0}\) along all the elements in \(\pi _1(M{\setminus }\varLambda , m_0)\).
The fiber \(p^{-1}(m_0)\) is the set of all local determinations \(f_{m_0}\) at \(m_0\). We can, by the general theory of transitive covering spaces, identify the group Aut(P, p) of deck transformations of \(p:P \rightarrow M{\setminus }\varLambda \) to the quotient \(\pi _1(M{\setminus }\varLambda ;m_0)\big / p_\#\pi _1(P;f_{m_0})\). This is the monodromy group of \({\mathcal {F}}\big |_{M{\setminus }\varLambda }\) which will be denoted by \(\text {Mon}({\mathcal {F}},\varLambda )\).
The monodromy map is the natural projection
Our first remark is the following:
Lemma 1
The monodromy group \(\text {Mon}({\mathcal {F}},\varLambda )\) is naturally isomorphic to a subgroup of \(\mathrm{I\!P}SL(2,{\mathbb {C}})\).
Proof
This is clear since \({\mathcal {F}}\big |_{M\backslash \varLambda }\) is transversely projective on \(M\backslash \varLambda \).
Holonomy In what follows we consider the following situation. Let \({\mathcal {F}}\) be a holomorphic foliation on a complex surface M, \(\varLambda \subset M\) a closed analytic invariant subset of pure dimension one (a curve) and assume that \({\mathcal {F}}\) is transversely projective in \(M\backslash \varLambda \). Let \(S\subset \varLambda \) be an irreducible component of \(\varLambda \). We suppose that each singular point in S is irreducible and exhibits at most one separatrix transverse to S.
Here we keep on following arguments originally in [26] and mimed in [28]. We proceed to study the holonomy of each irreducible component of M. It is enough to assume that M is the union of a smooth compact curve S and local analytic separatrices \( sep({\mathcal {F}},S)\) of \({\mathcal {F}}\) transverse to S; \(M = S \cup sep({\mathcal {F}},S)\), all of them smooth invariant and without triple points. We suppose that \( sing({\mathcal {F}}) \cap S \ne \emptyset \), each singular point in S is irreducible and, if it admits two separatrices then one is transverse to S). In this case we can consider a \(C^{\infty }\) retraction \(r:W \rightarrow S\) from some tubular neighborhood W of S on M onto S such that, \(\forall \,m \in S\) the fiber \(r^{-1}(m)\) is either a disc transverse to \({\mathcal {F}}\) or a local branch of \( sep({\mathcal {F}},S)\) at \(m \in sing({\mathcal {F}})\). We set \(V = W \backslash (M \cap W)\) to obtain a \(C^\infty \) fibration \(r\big |_V :V \rightarrow S\backslash sing({\mathcal {F}})\) by punctured discs over \(S\backslash sing({\mathcal {F}})\). Since \(\pi _2(S\backslash sing({\mathcal {F}})) = 0\) the homotopy exact sequence of the above fibration gives the exact sequence

where \(\tilde{m}_0 \in V\) is a base point and \(m_0 \in S\backslash sing({\mathcal {F}})\) is its projection and \(\tau =(r\big |_V)_\#\).
Now we consider the restriction of the covering space P to V; indeed for our purposes we may assume that \(W = M\) and \(V = M{\setminus }\varLambda \) so that we are just considering the space P itself. Let \(\rho \) be the monodromy map
Denote by \(\text {Mon}({\mathcal {F}},S)\) the quotient of \(\text {Mon}({\mathcal {F}},V)\) by the (normal) subgroup  . Then there is a unique morphism \([\rho ]\) such that the diagram commutes:
. Then there is a unique morphism \([\rho ]\) such that the diagram commutes:

The morphism \([\rho ]\) is the monodromy of \({\mathcal {F}}\big |_V\) seen as follows: given any element \([\gamma ] \in \pi _1(S\backslash sing({\mathcal {F}});m_0)\) the monodromy \([\rho ]([\gamma ])\) is the analytic continuation of the local first integral \(f_{m_0}\) along \(\gamma \) and its holonomy lifting. This gives:
Lemma 2
There exists a surjective group homomorphism \(\alpha :Hol({\mathcal {F}},S) \longrightarrow \text {Mon}({\mathcal {F}},S)\) such that the diagram commutes
where \(Hol:\pi _1(S\backslash sing({\mathcal {F}})) \longrightarrow Hol({\mathcal {F}};S)\) is the holonomy morphism of the leaf \(S\backslash sing({\mathcal {F}})\) of \({\mathcal {F}}\), and \([\rho ]:\pi _1(S\backslash sing({\mathcal {F}})) \longrightarrow \text {Mon}({\mathcal {F}};S)\) is as above.
The kernel of \(\alpha \) is the subgroup \(Ker(\alpha ) < Hol({\mathcal {F}};S)\) of those diffeomorphisms keeping fixed any element \(\ell (z)\) of the fiber of \(r\big |_V:V \rightarrow S\backslash sing({\mathcal {F}})\) over \(m_o \in S\backslash sing({\mathcal {F}})\). The invariance group of \(\ell \), \(Inv(\ell ,z)\), defined as follows \(Inv(\ell ,z) = \big \{h \in Diff({\mathbb {C}},0); \ell \circ h \equiv \ell \big \}\), where \(Diff(\mathbb {C},0)\) denotes the group of germs of complex diffeomorphisms fixing the origin \(0\in \mathbb {C}\). Therefore \(Ker(\alpha )\) is a subgroup of the invariance group \(Inv(\ell ,z)\), in the sense that if \(p_\ell :V_\ell \rightarrow D^*\) is the covering space of the punctured disc \(D^* = D\backslash \{0\}\) associated to \(\ell \) then \(\ell \circ h \equiv \ell \) means that \(\forall \, m \in D^*\), \(\forall \,\ell _m \in p_\ell ^{-1}(m)\), \(\exists \,\ell _{h(m)} \in p_\ell ^{-1}(h(m))\), \(\ell _{h(m)} \circ h = \ell _m\).
In particular, to any element \(h \in Inv(\ell ,z)\) there is associated a pair \(({\tilde{h}},h)\) where \({\tilde{h}}\) is the lifting of h to the covering space \(V_\ell \) defined by \({\tilde{h}}:\ell _m \mapsto \ell _{h(m)}\).
Another lemma we need is:
Lemma 3
Let \(0 \rightarrow G \rightarrow H \rightarrow K \rightarrow 0\) be an exact sequence of groups. Then H is solvable if, and only if, G and K are solvable.
From the above discussion we have an exact sequence
We claim that \(Inv(\ell ,z)\) is solvable. Indeed, suppose the contrary. By Nakai’s Density Lemma [25] the orbits of a non-solvable subgroup of \(Diff({\mathbb {C}},0)\) are locally dense in a neighborhood \(\varGamma \) of the origin. Let therefore \(m\in \varGamma \) be a point and \(\varGamma _m \subset \varGamma \setminus \{0\}\) be a small sector with vertex at the origin, such that the orbit of m in \(\varGamma _m\) is dense in \(\varGamma _m\). Denote by \(\ell _{\varGamma _m}\) a local determination of \(\ell \) in \(\varGamma _m\). Then \(\ell _{\varGamma _m}\) is constant along each orbit of \(Inv(\ell ,z)\) in \(\varGamma _m\) and the orbit of m is dense in \(\varGamma _m\) so that \(\ell _{\varGamma _m}\) is constant in \(\varGamma _m\). By analytic continuation \(\ell \) and the first integral \(\varPhi \) are constant yielding a contradiction. Thus the group \(Inv(\ell ,z)\) is solvable and therefore embeds in \(\mathrm{I\!P}SL(2,{\mathbb {C}})\). Hence \(Hol({\mathcal {F}},S)\big /Ker(\alpha ) \simeq \text {Mon}({\mathcal {F}},S)\) embeds in \(\mathrm{I\!P}SL(2,{\mathbb {C}})\) but \(Hol({\mathcal {F}},S)\) embeds in \(Diff({\mathbb {C}},0)\), as well as \(Ker(\alpha )\) embeds in \(Inv(\ell )\) which is a subgroup of \(Diff({\mathbb {C}},0)\) and therefore \(Hol({\mathcal {F}},S)\big /Ker(\alpha )\) is isomorphic to a subgroup of \(\mathrm{I\!P}SL(2,{\mathbb {C}})\) with a fixed point. This implies that indeed, \(Hol({\mathcal {F}},S)\big /Ker(\alpha )\) is solvable and conjugate to a subgroup of \(Aff({\mathbb {C}},0)\). Therefore \(\text {Mon}({\mathcal {F}},S)\) is solvable and by Lemma 3 the holonomy group \(Hol({\mathcal {F}},S)\) is solvable.
Summarizing the above discussion we have:
Theorem 3
Let \({\mathcal {F}}\) be a holomorphic foliation on a complex surface M, \(\varLambda \subset M\) a closed analytic invariant curve and assume that \({\mathcal {F}}\) is transversely projective in \(M\backslash \varLambda \). Let \(S\subset \varLambda \) be an irreducible component of \(\varLambda \). We suppose that each singular point in S is irreducible and exhibits a single separatrix transverse to S. Then the holonomy group \(Hol({\mathcal {F}},S)\) of the leaf \(S\backslash ( sing({\mathcal {F}}) \cap S)\) of \({\mathcal {F}}\) is a solvable group.
2.6 Transversely Affine Foliations
A particular case of transversely projective foliations is described below. As above, we consider a codimension-one holomorphic foliation \({\mathcal {F}}\) on a complex manifold \(M^n\), \(n \ge 2\), with singular set \( sing({\mathcal {F}}) \subset M\) of codimension \(\ge 2\). We say that \({\mathcal {F}}\) is transversely affine in an open subset \(U \subset M\) if there exists an open cover \(\{U_{\alpha }\}_{\alpha \in A}\) of \(U\backslash sing({\mathcal {F}})\) such that there are holomorphic submersions \(y_{\alpha }:U_{\alpha } \rightarrow {\mathbb {C}}\) such that \({\mathcal {F}}\big |_{U_{\alpha }}\) is given by \(dy_{\alpha } = 0\), and for each \(U_{\alpha } \cap U_{\beta } \ne \emptyset \) we have \(y_{\beta } = a_{\alpha \beta }\,y_{\alpha } + b_{\alpha \beta }\) for some affine map \((z\mapsto a_{\alpha \beta }\,z + b_{\alpha \beta })\). Transversely affine foliations have been studied by several authors, in the real case [17, 32] and in the holomorphic case [3, 14, 27]. Examples of such complex foliations are logarithmic foliations and Bernoulli foliations as well as rational pull-backs of such foliations [8, 27]. For all of these, the foliation is transversely affine outside of some algebraic invariant curve \(S\subset {\mathbb {C}} P(2)\). In [27] we find that a foliation \({\mathcal {F}}\) on \(M={\mathbb {C}} P(2)\) which is transversely affine outside some algebraic invariant curve \(S \subset {\mathbb {C}} P(2)\) is a logarithmic foliation under some mild conditions on \( sing({\mathcal {F}}) \cap S\). Relaxing slightly the hypothesis on \( sing({\mathcal {F}}) \cap S\) we may prove that \({\mathcal {F}}\) admits a Liouvillian first integral as follows: Let \(\omega \) be a polynomial one-form which defines \({\mathcal {F}}\) in some affine space \({\mathbb {C}}^2 \subset {\mathbb {C}} P(2)\), then \(\omega \) admits a one-form \(\eta \) which is rational, with simple poles and such that \(d\omega = \eta \wedge \omega \). We call the form \(\eta \) a generalized integrating factor for \(\omega \). The Liouvillian first integral for \({\mathcal {F}}\) is \(F = \int \frac{\omega }{e^{\int \eta }}\) [8, 33]. Using [8] one may therefore conclude that, under some suitable hyperbolicity hypotheses, either \({\mathcal {F}}\) is given by a closed rational one-form on \({\mathbb {C}} P(2)\), or it is a rational pull-back of a Bernoulli foliation as follows \({\mathcal {R}}\): \(p(x)dy - (y^2a(x)+yb(x))dx = 0\).
We separate the following useful definition:
Definition 8
(generalized integrating factor) Let \(\varOmega \) be a meromorphic one-form on a complex manifold M. A meromorphic one-form \(\eta \) in M is called a meromorphic generalized integrating factor for \(\varOmega \) if we have: (1) \(d \varOmega = \eta \wedge \varOmega \) and (2) \(d \eta =0\). If this is the case then \(\varOmega \) is integrable and defines a foliation \({\mathcal {F}}\) (holomorphic, of codimension one, with singularities) on M. We shall say that \(\eta \) is a generalized integrating factor for the foliation \({\mathcal {F}}\).
3 Projective Structures and Differential Forms
3.1 Projective Triples
The very basic result relating transversely homogeneous foliations and suitable systems of differential forms is the classical Darboux-Lie theorem [4, 17, 27]. In the case of projective transverse structure this can be stated as:
Proposition 2
([27], Proposition 1.1 p. 190) Assume that \({\mathcal {F}}\) is given by an integrable holomorphic one-form \(\varOmega \) on M and suppose that there exists a holomorphic one-form \(\eta \) on M such that \(\text {(Proj.1)} d\varOmega = \eta \wedge \varOmega \). Then \({\mathcal {F}}\) is transversely projective on M if and only if there exists a holomorphic one-form \(\xi \) on M such that \(\text {(Proj.2)} d\eta = \varOmega \wedge \xi \) and \(\text {(Proj.3)}d\xi = \xi \wedge \eta \).
The proof is found below.
3.2 Examples
Example 9
Let \(\alpha \) be a closed meromorphic one-form on M and let \(f:M \rightarrow \overline{\mathbb {C}}\) be a meromorphic function. Define \((\varOmega ,\eta ,\xi )\) by: \(\varOmega = df - f^2\alpha ,\quad \eta = 2f\alpha \) and \(\xi = 2\alpha .\) Then \((\varOmega ,\eta ,\xi )\) is a projective triple and therefore \(\varOmega \) defines a holomorphic foliation on M, transversely projective in the complement of the analytic invariant codimension one set \(S \subset M\), \(S = (\alpha )_\infty \cup (f)_\infty \). The same conclusion holds for \(\varOmega _\lambda = \varOmega + \lambda \alpha \), where \(\lambda \in \mathbb {C}\). The foliation \({\mathcal {F}}(\varOmega _\lambda )\) is also transversely affine in some smaller open set of the form \(M\backslash S^\prime \) where \(S^\prime \supset S\), \(S^\prime = S \cup (f^2-\lambda =0)\). (In fact \(\frac{\varOmega _ \lambda }{f^2-\lambda } = \frac{df}{f^2-\lambda } - \alpha \) is closed and holomorphic in \(M\backslash S^\prime \)).
Example 10
Let \(h:M\rightarrow {\mathbb {C}^*}\) be holomorphic such that \(d\xi = - \frac{dh}{2h} \wedge \xi \) where \(\xi \) is holomorphic (we can write this condition as \(d(\sqrt{h}.\xi )=0)\). Let F be any holomorphic function and write (for \(\lambda \in \mathbb {C}\)) \(\varOmega = F\cdot \left( \frac{dF}{F} - \frac{1}{2} \frac{dh}{h}\right) - \left( \frac{F^2}{2} - \frac{\lambda }{2}h\right) .\xi ,\, \eta = \frac{1}{2} \frac{dh}{h} + F\cdot \xi .\) The triple \((\varOmega ,\eta ,\xi )\) satisfies the conditions of Proposition 2 and then \({\mathcal {F}} = {\mathcal {F}}(\varOmega )\) is a transversely projective foliation on M.
3.3 Proof of Proposition 2
Let us now give a proof for Proposition 2. We start with a remark about its need.
Remark 6
Proposition 2 is stated (for the real non-singular case) with an idea of its proof, in [17] (see Proposition 3.20, pp. 262). However, it seems that the suggested proof uses some triviality hypothesis on principal fiber-bundles of structural group \(Aff(\mathbb {C})\), over the manifold M (see [17] Proposition 3.6 pp. 249–250). In our case this is replaced by the existence of the form \(\eta \) in the statement. On the other hand, since some of its elements will be useful later, we supply a proof for Proposition 2.
We will use the two following lemmas whose proofs are straightforward consequences of Darboux-Lie theorem, Theorem 2, therefore left to the reader:
Lemma 4
Let \(x,y,\widetilde{x},\widetilde{y}:U\subset \mathbb {C}^n\rightarrow \overline{\mathbb {C}}\) be meromorphic functions satisfying:
-
(i)
\(ydx-xdy = \widetilde{y} d\widetilde{x} - \widetilde{x} d\widetilde{y}\);
-
(ii)
\(\frac{\widetilde{x}}{\widetilde{y}} = \frac{ax+by}{cx+dy}\), \(\begin{pmatrix} a &{}b\\ c &{}d\end{pmatrix} \in \mathrm{I\!P}SL(2,\mathbb {C})\).
Then \(\widetilde{x} = \varepsilon .(ax+by)\) and \(\widetilde{y} = \varepsilon .(cx+dy)\) for some \(\varepsilon \in \mathbb {C}\), \(\varepsilon ^2 = 1\).
Lemma 5
Let \(x,y,\widetilde{x}, \widetilde{y}:U \subset \mathbb {C}^n \rightarrow \overline{\mathbb {C}}\) be meromorphic functions satisfying \(\widetilde{x} = ax+by\), \(\widetilde{y} = cx+dy\) for some \(\begin{pmatrix} a &{}b\\ c &{}d\end{pmatrix} \in \mathrm{I\!P}SL(2,\mathbb {C})\). Then \(xdy-ydx = \widetilde{x} d\widetilde{y} - \widetilde{y} d\widetilde{x}\).
Proof
(Proof of Proposition 2) Suppose \({\mathcal {F}}\) is transversely projective in \(M^n\), say, \(\{f_i:U_i \rightarrow \mathbb {C}\}\) is a projective transverse structure for \({\mathcal {F}}\) in \(M\backslash sing({\mathcal {F}})\). In each \(U_i\) we have \(\varOmega = -g_i\,df_i\) for some holomorphic  . In each \(U_i \cap U_j \ne \phi \) we have: \(g_i\,df_i = g_j\,df_j\) and \( (1) \, f_i = \frac{a_{ij}f_j + b_{ij}}{c_{ij}f_j+d_{ij}}\) as in Definition 6. Since \(d\varOmega = d(-g_i\,df_i) = \frac{dg_i}{g_i} \wedge \varOmega \) we have \(\eta = \frac{dg_i}{g_i} - h_i\varOmega \) for some holomorphic \(h_i\) in \(U_i\). We define \(x_i,y_i,u_i,v_i:U_i \rightarrow \mathbb {C}\) in the following way: \( (2) \, y_i^2 \,{=}\, g_i, \quad \frac{x_i}{y_i} \,{=}\, f_i, \quad h_i \,{=}\, \frac{2v_i}{y_i}\text {and}x_iv_i-y_iu_i = 1. \) Thus we have: \(\varOmega = x_i\,dy_i - y_i\,dx_i\) and \((3)\, \eta = 2(v_i\,dx_i - u_i\,dy_i)\). This motivates us to define local models (see [17] Sect. 3.18 pp. 261): \(\xi _i = 2(v_i\,du_i - u_i\,dv_i) \quad \text {in}\quad U_i.\) It is easy to check that we have \(d\xi _i = \xi _i \wedge \eta , \quad d\eta = \varOmega \wedge \xi _i \quad \text {in}\quad U_i.\) We can assume that \(dx_i\) and \(dy_i\) are independent for all \(i \in I\). In fact \(dx_i \wedge dy_i = 0 \Rightarrow d\varOmega \big |_{U_i} = 2 \,dx_i\wedge dy_i = 0 \Rightarrow d\varOmega = 0\) in M (we can assume M to be connected) \(\Rightarrow \) we have \(0 = d\varOmega = \eta \wedge \varOmega \) so that \(\eta = h\varOmega \) for some holomorphic function \(h:M \rightarrow \mathbb {C}\Rightarrow \) we can choose \(\xi = \frac{h^2\varOmega }{2} + h\eta + dh\) which satisfies the relations \(d\eta = \varOmega \wedge \xi \) and \(d\xi = \xi \wedge \eta \).
. In each \(U_i \cap U_j \ne \phi \) we have: \(g_i\,df_i = g_j\,df_j\) and \( (1) \, f_i = \frac{a_{ij}f_j + b_{ij}}{c_{ij}f_j+d_{ij}}\) as in Definition 6. Since \(d\varOmega = d(-g_i\,df_i) = \frac{dg_i}{g_i} \wedge \varOmega \) we have \(\eta = \frac{dg_i}{g_i} - h_i\varOmega \) for some holomorphic \(h_i\) in \(U_i\). We define \(x_i,y_i,u_i,v_i:U_i \rightarrow \mathbb {C}\) in the following way: \( (2) \, y_i^2 \,{=}\, g_i, \quad \frac{x_i}{y_i} \,{=}\, f_i, \quad h_i \,{=}\, \frac{2v_i}{y_i}\text {and}x_iv_i-y_iu_i = 1. \) Thus we have: \(\varOmega = x_i\,dy_i - y_i\,dx_i\) and \((3)\, \eta = 2(v_i\,dx_i - u_i\,dy_i)\). This motivates us to define local models (see [17] Sect. 3.18 pp. 261): \(\xi _i = 2(v_i\,du_i - u_i\,dv_i) \quad \text {in}\quad U_i.\) It is easy to check that we have \(d\xi _i = \xi _i \wedge \eta , \quad d\eta = \varOmega \wedge \xi _i \quad \text {in}\quad U_i.\) We can assume that \(dx_i\) and \(dy_i\) are independent for all \(i \in I\). In fact \(dx_i \wedge dy_i = 0 \Rightarrow d\varOmega \big |_{U_i} = 2 \,dx_i\wedge dy_i = 0 \Rightarrow d\varOmega = 0\) in M (we can assume M to be connected) \(\Rightarrow \) we have \(0 = d\varOmega = \eta \wedge \varOmega \) so that \(\eta = h\varOmega \) for some holomorphic function \(h:M \rightarrow \mathbb {C}\Rightarrow \) we can choose \(\xi = \frac{h^2\varOmega }{2} + h\eta + dh\) which satisfies the relations \(d\eta = \varOmega \wedge \xi \) and \(d\xi = \xi \wedge \eta \).
Claim
(1) We have \(\xi _i=\xi _j\) in each \(U_i \cap U_j \ne \phi \) and therefore the \(\xi _i\)’s can be glued into a holomorphic one-form \(\xi \) in \(M\backslash sing({\mathcal {F}})\) satisfying the conditions of the statement.
Proof
From (1) and (2) we obtain \(\frac{x_i}{y_i} = \frac{a_{ij}x_j+b_{ij}y_j}{c_{ij}x_j + d_{ij}y_j}\). Therefore according to Lemma 4 we have \((4)\, x_i = \varepsilon .(a_{ij}x_j + b_{ij}x_j),\, y_i = \varepsilon .(c_{ij}x_j + d_{ij}y_j)\, \varepsilon ^2 = 1.\) Using (3) and (4) we obtain: \((a_{ij}v_i - c_{ij}u_i)dx_j + (b_{ij}v_i - d_{ij}u_i)dy_j = \varepsilon .(v_j\,dx_j - u_j\,dy_j)\) and therefore: \((5) \, v_j =\epsilon ( a_{ij}\,v_i - c_{ij}\,u_i), \, \,u_j = \epsilon (-b_{ij}\,v_i + d_{ij}\,u_j)\). It follows form (5) and Lemma 5 that \(v_i\,du_i - u_i\,dv_i = v_j\,du_j - u_j\,dv_j\) which proves the claim.
Claim
(2) We have \(\xi = \xi _i = h_i^2 \frac{\varOmega }{2} + h_i\eta + dh_i\) in each \(U_i\).
Proof
We have \(h_i^2\varOmega = \frac{4v_i^2}{y_i^2}\,(x_i\,dy_i - y_i\,dx_i)\), \(h_i\eta = \frac{4v_i}{y_i}\,(v_i\,dx_i - u_i\,dy_i)\), \(dh_i = 2d\left( \frac{v_i}{y_i}\right) \). Hence \(\frac{h_i^2\varOmega }{4} + \frac{h_i\eta }{2} + \frac{dh_i}{2} = \frac{v_i^2}{y_i}\,dx_i - \frac{v_i}{y_i^2}\,(x_iv_i-1)dy_i + \frac{dv_i}{y_i}\).
On the other hand a straightforward calculation shows that \(\frac{\xi _i}{2} = v_i\,du_i - u_i\,dv_i = \frac{v_i^2}{y_i}\,dx_i - \frac{v_i}{y_i}(x_iv_i-1)dy_i + \frac{dv_i}{y_i}\,.\) And thus Claim 2 is proved.
Since \(codim\, sing({\mathcal {F}}) \ge 2\) it follows that \(\xi \) extends holomorphically to M. This proves the first part. Now we assume that \((\varOmega ,\eta ,\xi )\) is holomorphic as in the statement of the proposition:
Claim
(3) Given any \(p \in M\backslash sing({\mathcal {F}})\) there exist holomorphic \(x,y,u,v:U \rightarrow \mathbb {C}\) defined in an open neighborhood \(U\ni p\) such that: \(\varOmega = xdy-ydx\), \(\eta = 2(vdx-udy)\) and \(\xi = 2(vdu-udv)\).
Proof
This claim is a consequence of Darboux’s Theorem (see [17] pp. 230), but we can give an alternative proof as follows: We write locally \(\varOmega = -gdf = xdy-ydx\) and \(\eta = \frac{dg}{g} - h\varOmega = 2(vdx-udy)\) as in the proof of the first part. Using Claim 2 above and the last part of Proposition 3 below we obtain locally \(\xi = \frac{h^2\varOmega }{2} + h\eta + dh + \ell .\varOmega \); for some holomorphic function \(\ell \) satisfying \(\frac{d\ell }{-2\ell } \wedge \varOmega = d\varOmega \). This last equality implies that \(d(\sqrt{\ell }.\varOmega ) = 0\) and then \(\ell = \frac{r(f)}{g^2}\) for some holomorphic function r(z). Now we look for holomorphic functions \(\widetilde{f}\), \(\widetilde{g}\) and \(\widetilde{h}\) satisfying: \(\varOmega = -\widetilde{g} d\widetilde{f}, \quad \eta = \frac{d\widetilde{g}}{\widetilde{g}} - \widetilde{h}\varOmega \) and \(\xi = \frac{\widetilde{h}^2\varOmega }{2} + \widetilde{h}\eta + d\widetilde{h}\). We try \(\widetilde{f} = U(f)\) for some holomorphic non-vanishing U(z). Using \(\varOmega = gdf = -\widetilde{g} d\widetilde{f}\) we get \(\widetilde{g} = \frac{g}{U^\prime (f)}\). Using \(\eta = \frac{dg}{g} - d\varOmega = \frac{d\widetilde{g}}{\widetilde{g}} - \widetilde{h}\varOmega \) we get \(\widetilde{h} = h- \frac{U^{\prime \prime }}{gU^\prime }\). Using \(\xi = \frac{h^2\varOmega }{2} + h\eta + dh + \ell \varOmega = \frac{\widetilde{h}^2\varOmega }{2} + \widetilde{h}\eta + d\widetilde{h}\) we get \(d\left( \frac{U^{\prime \prime }(f)}{U^\prime (f)}\right) = r(f)df\).
Therefore it is possible to write \(\varOmega \), \(\eta \) and \(\xi \) as in the statement of the claim: define \(x = \widetilde{f} y\), \(y = \sqrt{\widetilde{g}}\), \(v = \frac{\widetilde{h}y}{2}\) and \(u = \frac{xv-1}{y}\) as in the first part of the proof. This proves Claim 3.
Using Claim 3 we prove that \({\mathcal {F}}\) is transversely projective in \(M\backslash sing({\mathcal {F}})\), that is in M. The last part of Proposition 2 can be proved using the relation stated above between the projective structure and the local trivializations for \(\varOmega \), \(\eta \) and \(\xi \). For instance we prove the following.
Claim
(4) The triples \((\varOmega ,\eta ,\xi )\) and \((f\varOmega , \eta + \frac{df}{f}, \frac{1}{f}\,\xi )\) define the same projective structure for \({\mathcal {F}}\), for any holomorphic \(f:M \rightarrow \mathbb {C}^*\).
Proof
Using the notation of the first part we define \(\hat{x}_i = \sqrt{f}.\,x_i\), \(\hat{y}_i = \sqrt{f}.\,y_i\), \(\hat{u}_i = \frac{1}{\sqrt{f}}\,.\,u_i\) and \(\hat{v}_i = \frac{1}{\sqrt{f}}\,.\,v_i\). Then: \(f\varOmega = \hat{x}_i\,d\hat{y}_i - \hat{y}_i\,d\hat{x}_i\), \(\eta +\frac{df}{f} = 2(\hat{v}_i\,d\hat{x}_i - \hat{u}_i\,d\hat{y}_i)\) and \(\frac{1}{f}\,\xi = 2(\hat{v}_i\,d\hat{u}_i - \hat{u}_i\,d\hat{v}_i)\). Furthermore we have \(\frac{\hat{x}_i}{\hat{y}_i} = \frac{x_i}{y_i} = \frac{a_{ij}x_j + b_{ij}y_j}{c_{ij}x_j + d_{ij}y_j} = \frac{a_{ij}\hat{x}_j + b_{ij}\hat{y}_j}{c_{ij}\hat{x}_j + d_{ij}\hat{y}_j},\) and this proves the claim and finishes the holomorphic part of the proof.
Now we only have to observe that if \((\varOmega , \eta \)) is a pair of meromorphic one-forms and if \({\mathcal {F}}\) is transversely projective in M, then the same steps of the first part of the proof apply to construct a meromorphic one-form \(\xi \) satisfying the relations of the statement.
Let \({\mathcal {F}}\) be a codimension one holomorphic foliation with singular set \( sing({\mathcal {F}})\) of codimension \(\ge 2\) on a complex manifold M. As mentioned in the Introduction, the existence of a projective transverse structure for \({\mathcal {F}}\) is equivalent to the existence of suitable triples of differential forms (cf. Proposition 2, see also [27] Sect. 3, page 193):
This motivates the following definition:
Definition 9
(projective triple) Given holomorphic one-forms (respectively, meromorphic one-forms) \(\varOmega \), \(\eta \) and \(\xi \) on M we shall say that \((\varOmega ,\eta , \xi )\) is a holomorphic projective triple (respectively, a meromorphic projective triple) if they satisfy relations (Proj.1), (Proj.2) and (Proj.3) above. The foliation \({\mathcal {F}}^\perp \) defined by the one-form \(\xi \) is called transverse foliation corresponding to the projective triple. If \(\eta \) is not identically zero then \({\mathcal {F}}^\perp \) is really a foliation on M which is transverse to \({\mathcal {F}}\) outside of a proper analytic subset.
The following definition will play a fundamental role in the last section of this work.
Definition 10
(moderate growth (transversely projective foliations)) A foliation \({\mathcal {F}}\) on M will be called transversely projective of moderate growth if it admits a meromorphic projective triple \((\varOmega , \eta , \xi )\) defined in M. This means that \({\mathcal {F}}\) is transversely projective in some the complementar of some analytic subset \(\varLambda \subset M\) of codimension one.
The termonilogy foliation with moderate growth has already been introduced in [35]. With the above definitions, and the notation of Proposition 2, this last says that \({\mathcal {F}}\) is transversely projective on M if and only if the holomorphic pair (\(\varOmega \), \(\eta \)) may be completed to a holomorphic projective triple. Moreover, a foliation \({\mathcal {F}}\) which is transversely projective of moderate growth exhibits a projective transverse structure \(\mathcal P\) in the complement of some codimension divisor \(D\subset M\) (D contained in the polar set of the projective triple). One question then is whether the projective transverse structure \(\mathcal P\) extends to the divisor D. The other question, apparently simpler, is whether the foliation \({\mathcal {F}}\) is actually projective of moderate growth. According to [27] we may perform modifications in a projective triple as follows:
Proposition 3
([27]) Let M be a connected complex manifold.
-
(i)
Given a meromorphic projective triple \((\varOmega , \eta , \xi )\) and meromorphic functions g, h on M we can define a new meromorphic projective triple as follows:
(Mod.1) \(\varOmega ^\prime = g\,\varOmega \)
(Mod.2) \(\eta ^\prime = \eta + \frac{dg}{g} + h\,\varOmega \)
(Mod.3) \(\xi ^\prime = \frac{1}{g}\,\big (\xi - dh - h\eta - \frac{h^2}{2}\,\varOmega \big )\)
-
(ii)
Two holomorphic projective triples \((\varOmega ,\eta ,\xi )\) and \((\varOmega ^\prime , \eta ^\prime , \xi ^\prime )\) define the same projective transverse structure for a given foliation \({\mathcal {F}}\) if and only if we have (Mod.1), (Mod.2) and (Mod.3) for some holomorphic functions g, h with g non-vanishing.
-
(iii)
Let \((\varOmega ,\eta ,\xi )\) and \((\varOmega , \eta , \xi ^\prime )\) be meromorphic projective triples. Then \(\xi ^\prime = \xi +F\,\varOmega \) for some meromorphic function F in M with \(d\,\varOmega = -\frac{1}{2}\, \frac{dF}{F} \wedge \varOmega \).
This last proposition implies that suitable meromorphic projective triples also define projective transverse structures. We can rewrite condition (iii) on F as \(d(\sqrt{F} \,\varOmega ) = 0\). This implies that if the projective triples \((\varOmega , \eta , \xi )\) and \((\varOmega , \eta , \xi ^\prime )\) are not identical then the foliation defined by \(\varOmega \) is transversely affine outside the codimension one analytical invariant subset \(S=\{F=0\}\cup \{F=\infty \}\) [27].
This approach is useful because of the following proposition:
Proposition 4
([27] Theorem 4.1 p. 197) Let \({\mathcal {F}}\) be a foliation on M where M is either an open polydisc \(M\subset {\mathbb {C}}^m\) or a projective manifold over \(\mathbb {C}\) of dimension \(m \ge 2\). Assume that \({\mathcal {F}}\) admits a meromorphic projective triple \((\varOmega , \eta , \xi )\) defined in M. If \(\xi \) admits a meromorphic first integral in U then \({\mathcal {F}}\) is a meromorphic pull-back of a Riccati foliation.
Proof
By hypothesis, \(\xi \) defines a foliation which admits a meromorphic first integral. Since we are either on a projective manifold or in a polydisc centered at the origin, we can write \(\xi = g\,dR\) for some meromorphic functions g and R (these functions are rational in the case of a projective surface). Then we may replace the meromorphic triple \((\varOmega , \eta ,\xi )\) by \((\varOmega ^\prime ,\eta ^\prime ,\xi ^\prime )\) where \(\varOmega ^\prime = g\varOmega \), \(\eta ^\prime = \eta + \frac{dg}{g}\) and \(\xi ^\prime = \frac{1}{g}\,\xi = dR\). The relations \(d\varOmega ^\prime = \eta ^\prime \wedge \xi ^\prime \), \(d\eta ^\prime = \varOmega ^\prime \wedge \xi ^\prime \), \(d\xi ^\prime = \xi \wedge \eta ^\prime \) imply that \(\eta ^\prime = HdR\) for some meromorphic function H. Now we define \(\omega := \frac{H^2}{2}\,\xi ^\prime - H\eta ^\prime + dH = \frac{1}{2}\, H^2dR + dH\) one-form such that \(d\omega = -HdH \wedge dR\). On the other hand \(\eta ^\prime \wedge \omega = HdR \wedge dH = -HdH \wedge dR\). Thus \(d\omega = \eta ^\prime \wedge \omega \). We also have \(d\eta ^\prime = dH \wedge dR = (-\frac{1}{2}\, H^2dR + dH) \wedge dR = \omega \wedge \xi ^\prime \). The meromorphic triple \((\omega ,\eta ^\prime ,\xi ^\prime )\) satisfies the projective relations \(d\omega = \eta ^\prime \wedge \omega \), \(d\eta ^\prime = \omega \wedge \xi ^\prime \), \(d\xi ^\prime = \xi ^\prime \wedge \eta ^\prime \) and therefore by Proposition 3 (iii) we conclude that \(\varOmega ^\prime = \omega + F.\xi ^\prime \) for some meromorphic function F such that \(d\xi ^\prime = \xi ^\prime \wedge \frac{1}{2}\frac{dF}{F}\,\cdot \) This implies \(dF \wedge dR \equiv 0\). By the classical Stein Factorization theorem we may assume from the beginning that R has connected fibers and therefore \(dF \wedge dR \equiv 0\) implies \(F = \varphi (R)\) for some one-variable meromorphic function \(\varphi (z) \in {\mathbb {C}}(z)\). In the case where M is a projective manifold all the meromorphic objects are rational and therefore \(\varphi (z)\) is also a rational function. We obtain therefore \(\varOmega ^\prime = -\frac{1}{2}\, H^2dR + dH + \varphi (R)dR = = dH - (\frac{1}{2}\, H^2 - \varphi (R))dR.\) If we define a meromorphic map \(\sigma :M\rightarrow \overline{\mathbb {C}}\times \overline{\mathbb {C}}\) by \(\sigma (p) = \big (R(p), H(p)\big )\) then clearly \(\varOmega ' = \sigma ^*(dy-(\frac{1}{2}\, y^2 - \varphi (x))dx)\) and therefore \({\mathcal {F}}\) is the pull-back \({\mathcal {F}} = \sigma ^*({\mathcal {R}})\) of the Riccati foliation \({\mathcal {R}}\) given on \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) by the meromorphic (rational if M is a projective manifold) one-form \(\varOmega _\varphi :=dy -(\frac{1}{2}\, y^2 - \varphi (x))dx\).
Definition 11
A meromorphic projective triple \((\varOmega ', \eta ', \xi ')\) is geometric if it can be written locally as in (Mod.1), (Mod.2) and (Mod.3) for some (locally defined) holomorphic projective triple \((\varOmega , \eta , \xi )\) and some (locally defined) meromorphic functions g, h.
As an immediate consequence we obtain:
Proposition 5
A geometric projective triple \((\varOmega ^\prime , \eta ^\prime , \xi ^\prime )\) defines a transversely projective foliation \({\mathcal {F}}\) given by \(\varOmega ^\prime \) on M.
Example 11
(Riccati Foliations - revisited) Fix affine coordinates \((x,y) \in {\mathbb {C}}^2\) and consider a polynomial one-form \(\varOmega = p(x)dy - (y^2\,c(x)-yb(x)-a(x))dx\). Then \(\varOmega \) defines a Riccati foliation \({\mathcal {R}}\) on \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) as seen in Example 6 above. Now we study the Lie Algebra associated to this example. Put \(\eta = 2\frac{dy}{y} + \frac{p^\prime +b}{p}\,dx + \frac{2a}{yp}\,dx \, \text {and} \, \xi = \frac{-2a}{y^2p^2}\,dx.\) Then \((\varOmega ,\eta ,\xi )\) satisfies the projective relations stated in Proposition 2. This shows that \({\mathcal {F}}\) is transversely projective in \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) minus the algebraic subset \(\overline{\{x \in {\mathbb {C}} \mid p(x)=0\}\times {\mathbb {C}}} \cup \overline{{\mathbb {C}}\times \{y=0\}}\). But since in the case \(a(x)\not \equiv 0\), only the subset \(S = \{p(x)=0\}\times \overline{\mathbb {C}}\) is \({\mathcal {F}}\) invariant it follows that the transverse projective structure extends to \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\backslash S\). Indeed according to Proposition 3 if we define \(g = \frac{-1}{p(x)y}\) then \(\eta ^\prime = \eta + 2g\varOmega = \frac{p^\prime -b+2yc}{p}\,dx \,\text {and} \, \xi ^\prime = \xi - 2dg-2g\eta - 2g^2\varOmega = \frac{2c}{p^2}\,dx\); define a triple \((\varOmega ,\eta ^\prime ,\xi ^\prime )\) holomorphic in \((\overline{\mathbb {C}}\times \overline{\mathbb {C}})\setminus S\) which gives a projective structure for \({\mathcal {F}}\) in this affine set. This projective structure coincides with the one given in \((\overline{\mathbb {C}}\times \overline{\mathbb {C}})\setminus (S\cup \overline{\mathbb {C}}\times \{y=0\})\) by \((\varOmega ,\eta ,\xi )\). The one-form \(\eta \) is closed if and only if \(a\equiv 0\). Therefore \({\mathcal {F}}\) is transversely affine in \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\backslash (S\cup \overline{\mathbb {C}}\times \{\overline{y=0\}})\) if the projective line \(\{y=0\}\) is invariant. The forms \((\varOmega , \eta ^\prime , \xi ^\prime )\) define a rational projective triple and the projective transverse structure of the foliation \({\mathcal {F}}^{\perp }\) defined by \(\xi \) extends from \({\mathbb {C}}^2\backslash S\) to \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\). Indeed, \({\mathcal {F}}_\xi \) admits a rational first integral. We will see this is a general fact, under suitable hypothesis on the singularities of the foliation \({\mathcal {F}}\) on \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\), admitting a projective transverse structure in the complementary of an algebraic one dimensional invariant subset \(S \subset \overline{\mathbb {C}}\times \overline{\mathbb {C}}\).
Remark 7
(Ricatti versus logarithmic) In general, Ricatti foliations are not given by closed one-forms, hence are not logarithmic foliations.
3.4 Germs of Foliations and Foliations on Projective Surfaces
Let \({\mathcal {F}}\) be a holomorphic foliation aaa of codimension one on \({{\mathbb {C}} P}^2\) having singular set \( sing({\mathcal {F}}) \subset {{\mathbb {C}} P}^2\). As it is well-known we can assume that \( sing({\mathcal {F}})\) is of codimension \(\ge 2\) and \({\mathcal {F}}\) is given in any affine space \({\mathbb {C}}^2 \subset {{\mathbb {C}} P}^2\) with coordinates (x, y), by a polynomial one-form \(\varOmega (x,y) = A(x,y)dx + B(x,y)dy\) with \( sing({\mathcal {F}}) \cap {\mathbb {C}}^2 = sing(\varOmega )\). In particular \( sing({\mathcal {F}}) \subset {{\mathbb {C}} P}^2\) is a nonempty finite set of points. Given any algebraic subset \(S\subset {{\mathbb {C}} P}^2\) of dimension one we can therefore always obtain a meromorphic (rational) one-form \(\varOmega \) on \({{\mathbb {C}} P}^2\) such that \(\varOmega \) defines \({\mathcal {F}}\), \((\varOmega )_\infty \) is non-invariant and in general position (indeed, we can assume that \((\varOmega )_\infty \) is any projective line in \(\mathbb {C}P(2)\)). Also if we take \(\eta _0 = \frac{B_x}{B}\,dx + \frac{A_y}{A}\,dy\) then we obtain a rational one-form such that \(d\varOmega = \eta _0 \wedge \varOmega \) and with polar set given by \((\eta _0)_\infty = \{(x,y) \in {\mathbb {C}}^2 : A(x,y) = 0\} \cup \{(x,y) \in {\mathbb {C}}^2 : B(x,y) = 0\} \cup (\varOmega )_\infty \,.\) In particular, \((\eta _0)_\infty \cap {\mathbb {C}}^2\) has order one and the “residue" of \(\eta _0\) along any component T of \((\varOmega )_\infty \) equals \(-k\) where k is the order of T as a set of poles of \(\varOmega \). Any rational one-form \(\eta \) such that \(d\varOmega = \eta \wedge \varOmega \) writes \(\eta = \eta _0 + h\varOmega \) for some rational function h. We obtain in this way one-forms \(\eta \) with appropriately located set of poles, with respect to \({\mathcal {F}}\), and applying Propositions 2 and 3 we obtain:
Proposition 6
(foliations on projective spaces) Let \({\mathcal {F}}\) be a holomorphic foliation on \(\mathbb {C}P(2)\). Assume that \({\mathcal {F}}\) is transversely projective in \(\mathbb {C}P(2)\backslash S\) for some algebraic subset S of dimension one. Then \({\mathcal {F}}\) has a projective triple \((\varOmega , \eta , \xi )\) on \(\mathbb {C}P(2) \setminus S\) where \(\varOmega \) and \(\eta \) are rational one-forms and \(\xi \) is meromorphic on \(\mathbb {C}P(2) \backslash S\). In particular \(\xi \) defines a transverse foliation \({\mathcal {F}}^{\perp }\) to \({\mathcal {F}}\) on \(\mathbb {C}P(2) \backslash S\) having a projective transverse structure.
The same holds, with a very similar proof, for germs of foliations at the origin \(0\in {\mathbb {C}} ^2\) where the curve S is replaced by a finite set of local branches of separatrices of the foliation through the singularity. More precisely:
Proposition 7
(germs of foliations) Let \({\mathcal {F}}\) be a germ of a holomorphic foliation with a singularity at the origin \(0\in \mathbb {C}^2\). Assume that \({\mathcal {F}}\) is transversely projective in the complement of an analytic subset \(S\subset sep({\mathcal {F}},0)\) of the set of separatrices through the origin. Then, for a sufficiently small bidisc \(0\in M\subset \mathbb {C}^2\) the germ \({\mathcal {F}}\) has a projective triple \((\varOmega , \eta , \xi )\) where \(\varOmega \) is a holomorphic one-form in M, the form \(\eta \) is meromorphic in M and \(\xi \) is meromorphic in \({M\setminus }S\).
Remark 8
(Generalizations for algebraic projective manifolds) Let us consider \(M^2\) a non-singular algebraic projective surface. Let \({\mathcal {F}}\) be a foliation on \(M^2\). Since we can define in a natural way, polynomial and rational functions on \(M^2\) we can define in a natural way algebraic leaves of \({\mathcal {F}}\). Let \(S\subset M\) be an algebraic curve, i.e., a pure codimension one analytic subset. The condition that \(M\backslash S\) is affine is equivalent to say that it is a Stein manifold. This does not hold in general, very much depending on the curve \(S\subset M\). Any meromorphic function on a projective surface is a rational function. A foliation \({\mathcal {F}}\) on M is therefore given by a rational one-form \(\varOmega \) on M admitting a rational one-form \(\eta \) such that \(d\varOmega = \eta \wedge \varOmega \). We have then natural versions of Propositions 2, 3 and 6 to this situation.
4 Extension of Projective Triples
In this section we address the following basic problem. Let \({\mathcal {F}}\) be a foliation on a complex manifold M with a projective transverse structure in \({M\setminus }S\) for some codimension one analytic subset \(S\subset M\). Under which conditions does the projective structure \(\mathcal P\) extends to S ?. A more appropriate question may be as follows: suppose that the projective transverse structure \(\mathcal P\) on \(M \setminus S\) is given by a projective triple \((\varOmega , \eta , \xi )\) with (as it is natural to assume), \(\varOmega \) and \(\eta \) meromorphic in M. Under which conditions does the one-form \(\xi \) admits a meromorphic extension to S ? We shall focus on two main cases.
-
(1)
The local case, where M is a neighborhood of the origin \(0 \in \mathbb {C}^2\). In this case we regard \({\mathcal {F}}\) as a germ of a foliation at the origin \(0 \in \mathbb {C}^2\) and consider S as a subset of its set of separatrices.
-
(2)
The projective case, where M is a projective surface. In this case the objects are rational once they are meromorphic in M and \(S\subset M\) is an algebraic curve.
4.1 Algebraic Leaves and Local Separatrices
Given a foliation \({\mathcal {F}}\) on a projective surface M, by an algebraic leaf of \({\mathcal {F}}\) we mean a leaf L of the foliation which is contained in an algebraic curve in M. Thanks to the Identity Principle and to Remmert–Stein extension theorem, a leaf L of \({\mathcal {F}}\) is algebraic if and only if it accumulates only at singular points of \({\mathcal {F}}\). In this case the algebraic curve consists of the leaf and such accumulation points. The following remark will be useful:
Lemma 6
([30] Lemma 7.5 (iii)) Let \({\mathcal {F}}\) and \({\mathcal {F}}_1\) be distinct foliations on a projective surface M. If a leaf L of \({\mathcal {F}}\) is also a leaf of \({\mathcal {F}}_1\) then this leaf is algebraic.
Proof
We choose affine coordinates \((x,y) \in M\) and polynomial equations for \({\mathcal {F}}\) and \({\mathcal {F}}_1\) in these coordinates, say: \({{\mathcal {F}}}\) is given by \(\frac{dy}{dx} = \frac{P(x,y)}{Q(x,y)}\) and \( {{\mathcal {F}}}_1\) by \(\frac{dy}{dx} = \frac{P_1(x,y)}{Q_1(x,y)}\) where P, Q and \(P_1,Q_1\) are relatively prime polynomials. Suppose \((x(z), y(z)),\,\,z\in V\subset \mathbb {C}\) is a common solution of the foliations \({\mathcal {F}}\) and \({{\mathcal {F}}}_1\) on M. Then we have
so that \((PQ_1 - P_1 Q)(x(z),y(z)) = 0\). By hypothesis \(PQ_1 - P_1 Q\not \equiv 0\) so that L satisfies the non-trivial algebraic equation \(PQ_1 - P_1 Q=0\). It follows that L is algebraic.
The following statement is about transversely projective foliations with moderate growth (cf. Definition 10). It is a compilation of some results above and a preparatory step for the final conclusion:
Theorem 4
Let \({\mathcal {F}}\) be a foliation on a projective surface M, with a projective transverse structure outside of an algebraic subset \(S\subset M\) of dimension one. Let \((\varOmega , \eta , \xi )\) be a rational projective triple defining the projective transverse structure outside of the curve S. We have the following possibilities:
-
1.
S contains all the non-dicritical separatrices of \({\mathcal {F}}\) in S.
-
2.
There is some singularity \(p\in sing({\mathcal {F}}) \cap S\) and a (non-dicritical) separatrix \(\varGamma \) of \({\mathcal {F}}\) through p, which is not contained in S. In this case we have the following possibilities:
-
(a)
The leaf containing \(\varGamma \) is not algebraic and \({\mathcal {F}}^\perp \)-invariant. In this case \({\mathcal {F}}^\perp \) coincides with \({\mathcal {F}}\), \(\eta \) is closed and \({\mathcal {F}}\) admits a rational generalized integrating factor.
-
(b)
The leaf containing \(\varGamma \) is not algebraic and is not \({\mathcal {F}}^\perp \) invariant.
-
(c)
The leaf containing \(\varGamma \) is algebraic. In this case \({\mathcal {F}}\) is transversely affine in \(M \setminus (S \cup A)\) for some algebraic invariant curve \(A\subset M\) not contained in S.
-
(a)
Proof
We perform the resolution of singularities for \({\mathcal {F}}\) in S and obtain a projective surface \(\tilde{M}\) and a resolution morphism \(\sigma :\tilde{M} \rightarrow M\), a divisor \(E=\sigma ^{-1}(S)=D\cup \tilde{S}\), where D is the exceptional divisor and \(\tilde{S}\) is the strict transform of S, equipped with a pull-back foliation \({\tilde{\mathcal {F}}}=\sigma ^*({\mathcal {F}})\) with irreducible singularities in E. The foliation \({\tilde{\mathcal {F}}}\) is transversely projective in \(\tilde{M} \setminus E\). By Lemma 10 the projective transverse structure of \({\tilde{\mathcal {F}}}\) extends to the non-invariant part of D so that, for our purposes we may assume that D is \({\tilde{\mathcal {F}}}\)-invariant, though not necessarily connected. If S contains all the non-dicritical separatrices of \({\mathcal {F}}\) in S then we are in case (1).
Thus, from now on we suppose that there is a singular point \(\tilde{q}\in \tilde{S}\cap sing({\tilde{\mathcal {F}}})\) such that \({\tilde{\mathcal {F}}}\) exhibits some local separatrix \({\tilde{\varGamma }}\) through \(\tilde{q}\) which is not contained in E. Denote by \({\tilde{\mathcal {F}}}^\perp =\sigma ^*({\mathcal {F}}^\perp )\) the inverse image of \({\mathcal {F}}^\perp ={\mathcal {F}}_\xi \) on \(\widetilde{M}\). Assume that the leaf \(\tilde{A}\) of \({\tilde{\mathcal {F}}}\) containing \({\tilde{\varGamma }}\) is not algebraic. In this case its projection \(A=\sigma (\tilde{A})\) onto M is not algebraic. We have two possibilities. If \({\tilde{\varGamma }}\) is \({\mathcal {F}}_\xi \)-invariant then by, Lemma 6, \({\mathcal {F}}\) coincides with \({\mathcal {F}}^\perp \) and we are in case (2)(a) in the statement. The second possibility is that \({\tilde{\varGamma }}\) is not \({\tilde{\mathcal {F}}}\)-invariant. This corresponds to case (2)(b) in the statement.
Assume now that \(\tilde{A}\supset {\tilde{\varGamma }}\) is an algebraic leaf of \(\tilde{\mathcal {F}}\) not contained in E. This algebraic leaf projects onto an algebraic leaf A of \({\mathcal {F}}\), not contained in S. The projective transverse structure of \({\mathcal {F}}\) has A as a set of fixed points and therefore \({\mathcal {F}}\) is transversely affine in \(M \setminus (S\cup A)\) what corresponds to case (2) (c) in the statement.
Thought the above statement already gives some information, it remains to study the last case, 2(c) above. We must explore the consequences of the existence of a non-dicritical separatrix which is not contained in the curve S, in the final description of the foliation. This is done in what follows. In few words, for the case of extended generalized curves, this allows to extend the projective triple, more precisely, the one-form \(\xi \) extends to the irreducible component of S that contains this separatrix.
4.2 Extension of Projective Triples (irreducible Case)
Our main extension result for projective triples is so far the following:
Theorem 5
Let \({\mathcal {F}}\) be a holomorphic foliation (respectively a germ of a holomorphic foliation) on a projective surface U (respectively at the origin of \({\mathbb {C}}^2\)). Assume that \({\mathcal {F}}\) is transversely projective in \(U\setminus S\) where \(S \subset U\) is an algebraic invariant curve in the projective surface (respectively a finite union of local branches of non-dicritical separatrices of \({\mathcal {F}}\) through the origin and U is a bidisc centered at the origin \(0 \in \mathbb {C}^2\), where \({\mathcal {F}}\) has a representative). Suppose that the singularities of \({\mathcal {F}}\) in S are non-resonant extended generalized curves. Then \({\mathcal {F}}\) admits a meromorphic projective triple (respectively a germ of a meromorphic projective triple) \((\varOmega , \eta , \xi )\) defined in U (respectively at the origin), which defines the projective transverse structure in \(U\setminus S\) (respectively in the complement of S).
In this section we pave the way to the proof of Theorem 5.
We recall the following fundamental result from [35]:
Theorem 6
(Touzet, [35] Theorem II.3.1 p. 821) A non-degenerate non-resonant singularity \(xdy - \lambda y dx + \varOmega _2(x,y)=0, \, \lambda \in {\mathbb {C}} \setminus \mathbb {Q}_+\), is analytically linearizable if and only if the corresponding foliation \({\mathcal {F}}\) is transversely projective in \(U\setminus sep({\mathcal {F}},U)\) for some neighborhood U of the singularity.
One other tool is discussed below. Let \({\mathcal {F}}\) be a germ of an irreducible singularity at the origin \(0 \in \mathbb {C}^2\), assumed to be of resonant type or of saddle-node type. According to [35], Theorem II.4.2, the foliation admits a meromorphic projective triple in a neighborhood U of the singularity if and only if in a neighborhood of the singularity \({\mathcal {F}}\) is the pull-back of a Riccati foliation on \(\overline{\mathbb {C}} \times \overline{\mathbb {C}}\) by a meromorphic map. The proof of this theorem is based in the study and classification of the Martinet-Ramis cocycles of the singularity expressed in terms of some classifying holonomy map of a separatrix of the singularity. For a resonant singularity any of the two separatrices has a classifying holonomy and for a saddle-node it is necessary to consider the strong manifold holonomy map. Thus we conclude that the proof given in [35] actually shows that:
Lemma 7
([35], Theorem II.4.2) Let \({\mathcal {F}}\) be a germ of an irreducible singularity at the origin \(0 \in \mathbb {C}^2\), assumed to be of resonant type or of saddle-node type. The germ \({\mathcal {F}}\) is the pull-back of a Riccati foliation on \(\overline{\mathbb {C}} \times \overline{\mathbb {C}}\) by a meromorphic map if and only if there exists a meromorphic projective triple \((\varOmega ^\prime , \eta ^\prime , \xi ^\prime )\) in a neighborhood \(U_0\) of a separatrix \(S \subset sep({\mathcal {F}},U)\) provided that S is the strong separatrix if the origin is a saddle-node.
As a further motivation for our approach we mention two results which are proved in [9]. Such results imply the existence of a globally defined projective triple, parting from a geometric projective triple, in a situation similar to the one we are dealing with:
Proposition 8
([9]) Let \(\mathcal F\) be a holomorphic foliation in a neighborhood V of the origin \(0 \in {\mathbb {C}}^2\) given by the holomorphic one-form \(\varOmega \) admitting a meromorphic one-form \(\eta \) in V with \(d\varOmega = \eta \wedge \varOmega \). Suppose that \(\mathcal F\) has an irreducible non-degenerate singularity at the origin and is transversely projective in \(U\setminus sep(\mathcal F,U)\) for some neighborhood \(U\subset V\) of the origin where \(\mathcal F\) has an expression in irreducible normal form. Let be given a holomorphic one-form \(\xi \) defined in \(U \setminus sep(\mathcal F,U)\) such that \((\varOmega ,\eta ,\xi )\) is a geometric projective triple in \(U \setminus sep(\mathcal F,U)\). Then \(\xi \) extends as a meromorphic one-form to U. provided that, if the singularity is resonant, \(\xi \) extends as a meromorphic one-form to \(S^* = S-\{0\}\), for some separatrix \(S\subset sep(\mathcal F,U)\).
This proposition or the Globalization theorem in [9] give for the non-dicritical case:
Proposition 9
(extension conditions) Let \({\mathcal {F}}\) be a holomorphic foliation defined in a neighborhood V of \(0 \in {\mathbb {C}}^2\) with an isolated non-dicritical singularity at the origin. Suppose that \({\mathcal {F}}\) is transversely projective in \(U\setminus sep({\mathcal {F}},U)\) for some neighborhood \(U\subset V\) of the origin where \({\mathcal {F}}\) is given by a holomorphic one-form \(\varOmega \) admitting a meromorphic one-form \(\eta \) such that \(d\varOmega = \eta \wedge \varOmega \) in U. Let \(\xi \) be a meromorphic one-form defined in \(U \setminus sep({\mathcal {F}},U)\) such that \((\varOmega ,\eta ,\xi )\) is a geometric projective triple. Let \(\pi :{\tilde{U}} \rightarrow U\) be the reduction morphism of the singularity and denote by \(({\tilde{\varOmega }},\tilde{\eta }, \tilde{\xi })\) the pull-back by \(\pi \) of the triple \((\varOmega , \eta , \xi )\). Then the one-form \(\xi \) extends to U provided that:
- (Ext.1):
-
At any non-resonant irreducible singularity of the foliation, the form \(\tilde{\xi }\) admits a meromorphic extension (from a neighborhood of the singularity minus its separatrices) to a neighborhood of the singularity.
- (Ext.2):
-
At any resonant irreducible singularity of the foliation, the one-form \(\tilde{\xi }\) admits a meromorphic extension (from a neighborhood of an annulus contained in one of the separatrices and around the singularity) to a neighborhood of the singularity.
The (extension) conditions of the proposition above are satisfied in our current situation, as we will see below (cf. Proposition 10).
We shall reprove and extend these results by considering meromorphic triples, but which are not assumed to be geometric projective triples along the separatrices.
Remark 9
The above additional assumption (that \(\xi \) can be chosen holomorphic off the set of separatrices) is not restrictive. Indeed, in the sequel (in the paper), the foliation is assumed to be transversely projective off the set of local separatrices. Since \(\varOmega \) is defined meromorphic in a neighborhood of the singularity, we can assume that it is holomorphic otherwise we replace it conveniently (see also Lemma 11). Thus, if we write the one-form \(\varOmega =A(x,y) dx + B(x,y) dy\) with A, B holomorphic with an isolated common zero at the origin, then we can choose \(\eta =\frac{B_x}{B}dx + \frac{A_y}{A}dy\). The polar set of \(\eta \) is contained in the curves \(\{A=0\}\) and \(\{B=0\}\). So we can assume in the case of a non-degenerate non-resonant singularity that the poles of \(\eta \) are contained in the separatrices, which are the coordinate axes in suitable coordinates. Under this hypothesis, the hypothesis of existence of a projective transverse structure off the separatrices gives a holomorphic one-form \(\xi \) in the complement of the separatrices, such that \(\varOmega , \eta , \xi \) is a (holomorphic) geometric projective triple off the axes.
Next we show that the (extension) conditions in Proposition 9 are satisfied and that we can apply some of these techniques also in the dicritical case. In order to do this we remake the basic steps with the necessary changes. The starting point is the non-resonant case considered below:
Proposition 10
(non-resonant case) Suppose that the origin is a nondegenerate nonresonant singularity. Assume that \({\mathcal {F}}\) is transversely projective on \(U\setminus sep({\mathcal {F}},U)\). Let \(\eta \) be a meromorphic one-form on U and \(\xi \) be a meromorphic one-form on \(U\setminus sep({\mathcal {F}},U)\) such that on \(U \setminus sep({\mathcal {F}},U)\) the one-forms \(\varOmega , \eta , \xi \) define a projective triple. Then \(\xi \) extends as a meromorphic one-form to U.
Before going into the proof we state a lemma:
Lemma 8
(non-resonant case) Let \(\ell \) be a meromorphic function in \(U^*= U\setminus \{xy=0\}\) such that \(d\varOmega = -\frac{1}{2}\,\frac{d\ell }{\ell } \wedge \varOmega \) where \(\varOmega = g(xdy-\lambda ydx)\) for some holomorphic non-vanishing function g in U and \(\lambda \in \mathbb {C}\setminus \mathbb {Q}\). Then \(\ell = {\tilde{c}}.(gxy)^{-2}\) for some constant \({\tilde{c}} \in \mathbb {C}\).
Proof
Fix a complex number \(a\in \mathbb {C}\) and introduce the one-form \(\eta _0 = \frac{d(xyg)}{xyg} + a(\frac{dy}{y} - \lambda \frac{dx}{x})\) in U. Since \(\frac{\varOmega }{gxy}= \frac{dy}{y} - \lambda \frac{dx}{x}\) is closed it follows that \(d\varOmega = \eta _0 \wedge \varOmega \). Thus the one-form \(\varTheta := -\frac{1}{2}\,\frac{d\ell }{\ell } - \eta _0\) is closed meromorphic in \(U^*\) and satisfies \(\varTheta \wedge \varOmega = d \varOmega - d \varOmega = 0\). This implies that \(\varTheta \wedge (\frac{dy}{y} - \lambda \frac{dx}{x}) =0\) in \(U^*\) and therefore we have \(\varTheta =h. (\frac{dy}{y} - \lambda \frac{dx}{x})\) for some meromorphic function h in \(U^*\). Taking exterior derivatives we conclude that \(dh\wedge ( \frac{dy}{y} - \lambda \frac{dx}{x})=0\) in \(U^*\) and therefore h is a meromorphic first integral for \(\varOmega \) in \(U^*\). Since \(\lambda \notin \mathbb {Q}\) we must have \(h=c\), a constant: indeed, write  in Laurent series in a small bidisc around the origin. Then from \(dh\wedge ( \frac{dy}{y} - \lambda \frac{dx}{x})=0\) we obtain
in Laurent series in a small bidisc around the origin. Then from \(dh\wedge ( \frac{dy}{y} - \lambda \frac{dx}{x})=0\) we obtain  and since \(\lambda \notin \mathbb {Q}\) this implies that \(\lambda _{ij}=0, \, \forall (i,j) \ne (0,0)\).
and since \(\lambda \notin \mathbb {Q}\) this implies that \(\lambda _{ij}=0, \, \forall (i,j) \ne (0,0)\).
This already shows that the one-form \(\varTheta \) always extends as a meromorphic one-form with simple poles to U and therefore the function \(\ell \) extends as a meromorphic function to U. The residue of \(\varTheta \) along the axis \(\{y=0\}\) is given by \(Res _{\{y=0\}} \varTheta = -Res _{\{y=0\}} \frac{1}{2}\frac{d\ell }{\ell } - Res _{\{y=0\}} \eta _0= - \frac{1}{2} k - (1+a)\) where \(k\in \mathrm{I\!N}\) is the order of \(\{y=0\}\) as a set of zeroes of \(\ell \) or minus the order of \(\{y=0\}\) as a set of poles of \(\ell \). Thus by a suitable choice of a we can assume that \(Res _{\{y=0\}} \varTheta =0\) and therefore by the expression \(\varTheta =c (\frac{dy}{y} - \lambda \frac{dx}{x})\) we conclude that, for such a choice of a, we have \(0=\varTheta = -\frac{1}{2}\,\frac{d\ell }{\ell } - \eta _0\) and thus \( -\frac{1}{2}\,\frac{d\ell }{\ell } = \frac{dx}{x} + \frac{dy}{y} + \frac{dg}{g} + a(\frac{dy}{y} - \lambda \frac{dx}{x})\) and therefore, comparing residues along the axes \(\{y=0\}\) and \(\{x=0\}\) we obtain that \(1+a\in \mathbb {Q}\) and \( 1 - a\lambda \in \mathbb {Q}\). Since \(\lambda \notin \mathbb {Q}\) the only possibility is \(a=0\). This proves that indeed \(-\frac{1}{2}\,\frac{d\ell }{\ell } = \frac{dx}{x} + \frac{dy}{y} + \frac{dg}{g}\) in U and integrating this last expression we obtain \(\ell = {\tilde{c}} (gxy)^{-2}\) for some constant \({\tilde{c}} \in \mathbb {C}\). This proves the lemma.
Now we can prove Proposition 10.
Proof
(Proof of Proposition 10) By hypothesis the foliation is given in suitable local coordinates around the origin by \(xdy - \lambda ydx + \varOmega _ 2(x,y) = 0\) where \(\lambda \in \mathbb {C}\backslash \mathbb {Q}\), \(\varOmega _ 2(x,y)\) is a holomorphic one-form of order \(\ge 2\) at \(0\in \mathbb {C}^2\).
Claim
The singularity is analytically linearizable.
Indeed, if \(\lambda \notin \mathrm{I\!R}_-\) then the singularity is in the Poincaré domain with no resonance and by Poincaré-Linearization Theorem the singularity is analytically linearizable. Assume now that \(\lambda \in \mathrm{I\!R}_-\backslash \mathbb {Q}_-\). In this case the singularity is in the Siegel domain and, a priori, it is not clear that the singularity is linearizable. Nevertheless, by hypothesis \({\mathcal {F}}\) is transversely projective in \(U^* = U\setminus sep({\mathcal {F}},U)\) and by Theorem 6 the singularity \(p \in sing({\mathcal {F}})\) is analytically linearizable. This proves the claim.
Therefore we can suppose that \(\varOmega \big |_U = g(xdy-\lambda ydx)\) for some holomorphic non-vanishing function g in U. We define \(\eta _0 = \frac{dg}{g} + \frac{dx}{x} + \frac{dy}{y}\) in U. Then \(\eta _0\) is meromorphic and satisfies \(d\varOmega = \eta _0 \wedge \varOmega \) so that \(\eta = \eta _0 + h\varOmega \) for some meromorphic function h in U. We also take \(\xi _0 = 0\) so that \(d\eta _0 = 0 = \varOmega \wedge \xi _0\) and \(d\xi _0 = 0 = \xi _0 \wedge \eta \). The triple \((\varOmega ,\eta _0,\xi _0)\) is a meromorphic projective triple in U so that according to Proposition 3 we can define a meromorphic projective triple \((\varOmega ,\eta ,\xi _1)\) in U by setting \(\xi _1 = \xi _0 - dh - h\eta _0 - \frac{h^2}{2}\,\varOmega = -dh - h\eta _0 - \frac{h^2}{2}\,\varOmega \). Then we have by Proposition 3 (iii) that \(\xi = \xi _1 + \ell .\varOmega \) for some meromorphic function \(\ell \) in \(U^*\) such that \(d\varOmega = -\frac{1}{2}\,\frac{d\ell }{\ell } \wedge \varOmega \).
By Lemma 8 above we have \(\ell ={\tilde{c}} .(gxy)^{-2}\) in \(U^*\) and therefore \(\xi \) extends to U as \(\xi = \xi _1 + {\tilde{c}}. (gxy)^{-2}\) in \(U^*\). This proves the lemma.
Now we deal with the second extension condition (Ext. 2) in Proposition 9. The first step is:
Lemma 9
(resonant case) Let \({\mathcal {F}}\) be a germ of a holomorphic foliation with a resonant irreducible (non-degenerate) singularity at the origin \(0\in \mathbb {C}^2\) and let \(0\in U\subset \mathbb {C}^2\) be a bidisc centered at the origin where \({\mathcal {F}}\) is defined by a holomorphic one-form \(\varOmega \). Denote by \( sep({\mathcal {F}},U)\) the set of local separatrices of \({\mathcal {F}}\) through the origin in U. Let \(\ell \) be a meromorphic function in \(U\setminus sep({\mathcal {F}},U)\) such that \(d\,\varOmega = -\frac{1}{2}\, \frac{d\ell }{\ell } \wedge \varOmega \). Then \(\ell \) extends as a meromorphic function to U provided that \(\ell \) admits a meromorphic extension to (a neighborhood of) \(S^*=S\setminus \{0\}\) for some separatrix \(S\subset sep({\mathcal {F}},U)\). Indeed, we have the following possibilities for \({\mathcal {F}}\) in suitable coordinates in a neighborhood of the origin:
-
(i)
\({\mathcal {F}}\) is analytically linearizable, i.e., analytically conjugate to the form \(xdy - \lambda ydx=0\) for some \(\lambda \in \mathbb {C}\setminus \{0\}\).
-
(ii)
\({\mathcal {F}}\) is a non-linearizable resonance analytically conjugate to the normal form: \(\varOmega _ {n,m} = n y\,dx + m x(1 + \frac{\sqrt{-1}}{2\pi }\, x^ny^m)dy=0\) where \(n,m\in \mathrm{I\!N}\).
In all cases S is given by \(\{y=0\}\) and the function \(\ell \) extends as meromorphic function to a neighborhood of the origin.
Proof
We define the one-form \(\eta =-\frac{1}{2}\, \frac{d\ell }{\ell }\). Then \(\eta \) is a closed meromorphic one-form in \(U\setminus [ sep({\mathcal {F}},U)\setminus S]\) such that \(d\varOmega = \eta \wedge \varOmega \), moreover the polar set of \(\eta \) is contained in S and has order at most one. If \(\eta \) is holomorphic in \(U\setminus [ sep({\mathcal {F}},U)\setminus S]\) then the foliation \({\mathcal {F}}\) is transversely affine in \(U\setminus [ sep({\mathcal {F}},U)\setminus S]\) and therefore the holonomy map of the leaf \(L_0= S\setminus \{0\}\) is linearizable. Since the origin is irreducible and S is not a central manifold the conjugacy class of this holonomy map classifies the foliation up to analytic conjugation. Thus the singularity is itself linearizable. Assume now that \((\eta )_\infty \ne \emptyset .\) In this case we have the residue of \(\eta \) along S given by \(Res _{S}\eta = -\frac{1}{2} \, k\) where k is either the order of S as zero of \(\ell \) or minus the order of S as pole of \(\ell \). We have two possibilities:
(a) If \(-\frac{1}{2} \, k \notin \{2,3,\ldots \}\) then by [27], Lemma 3.1, the holonomy map of the leaf \(L_0\) is analytically linearizable and the same holds for the singularity.
(b) If \(-\frac{1}{2} \, k = t +1\ge 2\) for some \(t\in \mathrm{I\!N}\) then by [27], Lemma 3.1, the holonomy map of \(L_0\) is conjugate to a map of the form \(h(z)= \frac{\alpha z}{(1+ \beta z^t)^{\frac{1}{t}}}\), i.e., this is a finite ramified covering of an homography. Suppose that the singularity is nondegenerate say \(\varOmega = xdy - \lambda ydx +...\). If \(\lambda \notin \mathbb {Q}\) then the map h(z) is analytically linearizable and therefore, again, the singularity is linearizable. Suppose now that the map h is not analytically linearizable. Then we must have \(\lambda = -\frac{n}{m}\) for some \(n,m \in \mathrm{I\!N}\), \(< n,m> = 1\) and the holonomy h is analytically conjugate to the corresponding holonomy of the germ of singularity \( \varOmega _ {n,m} = n y\,dx + m x(1 + \frac{\sqrt{-1}}{2\pi }\, x^ny^m)dy\); such a singularity is called a non-linearizable resonant saddle. As it is well-known, in the Siegel domain and in particular in the class of resonant singularities, the analytical classification of the holonomy implies the analytical classification of the singularity. More precisely, by [23, 24] we may assume that \({\mathcal {F}}\) is of the form \(\varOmega _ {n,m} = 0\) in the variables \((x,y) \in U\). So far we have proved that the following are the possibilities for the singularities:
-
(1)
The singularity is analytically linearizable, this is the case if it is not a resonance.
-
(2)
The singularity is analytically conjugated to \(\varOmega _{n,m}\) if it is resonant and not analytically linearizable.
Let us now use these two models in order to conclude the extension of \(\ell \) to U.
Case 1. In the linearizable case we can write \(S: \{y=0\}\) and \(\varOmega = g(xdy - \lambda ydx)\) for some holomorphic non-vanishing function g in U. If we introduce \(\eta _0 = \frac{d(gxy)}{gxy}\) then we have \(d\varOmega = \eta _0 \wedge \varOmega \) and therefore \((\eta - \eta _0 ) \wedge \varOmega =0\) so that \((\eta - \eta _0 )\wedge (\frac{dy}{y} - \lambda \frac{dx}{x})=0\) and then \(\eta = \eta _0 + F.(\frac{dy}{y} - \lambda \frac{dx}{x})=0\) for some meromorphic function F in \(U_0:= U\setminus [ sep({\mathcal {F}},U)\setminus S]\). Since \(\eta \) and \(\eta _0\) are closed we conclude that \(d(F.(\frac{dy}{y} - \lambda \frac{dx}{x}))=0\) in \(U_0\). Write now  in Laurent series in a small bidisc around the origin. We obtain from the last equation that
in Laurent series in a small bidisc around the origin. We obtain from the last equation that  . If \(\lambda \notin \mathbb {Q}\) this implies that \(F=F_{00}\) is constant. Assume now that \(\lambda = -\frac{n}{m} \in \mathbb {Q}_-\). Then we have \(\varOmega \wedge d(x^ny^m)=0\) and also \(F=\varphi (x^ny^m)\) for some function
. If \(\lambda \notin \mathbb {Q}\) this implies that \(F=F_{00}\) is constant. Assume now that \(\lambda = -\frac{n}{m} \in \mathbb {Q}_-\). Then we have \(\varOmega \wedge d(x^ny^m)=0\) and also \(F=\varphi (x^ny^m)\) for some function  defined in a punctured disc around the origin. Nevertheless, the function F is meromorphic along the axis \(\{y=0\}\) and therefore \(\varphi \) admits a meromorphic extension to the origin \(0 \in \mathbb {C}\) and thus F extends as a meromorphic function \(F=\varphi (x^n y^m)\) to a neighborhood of the origin.
defined in a punctured disc around the origin. Nevertheless, the function F is meromorphic along the axis \(\{y=0\}\) and therefore \(\varphi \) admits a meromorphic extension to the origin \(0 \in \mathbb {C}\) and thus F extends as a meromorphic function \(F=\varphi (x^n y^m)\) to a neighborhood of the origin.
Case 2. In the non-linearizable (resonant) case we can write \(S : \{y=0\}\) and \(\varOmega = g\, \varOmega _ {n,m} =g( n y\,dx + m x(1 + \frac{\sqrt{-1}}{2\pi }\, x^ny^m)dy)\) for some holomorphic non-vanishing function g on U. Define \(\eta _0 = \frac{d(gx^{n+1} y^{m+1})}{gx^{n+1} y^{m+1}}\). As above we conclude that \(\eta = \eta _0 + F. (n \frac{dx}{x^{n+1}y^m} + m \frac{dy}{x^n y^{m+1}} + \frac{m \sqrt{-1}}{2 \pi } \frac{dy}{y})\) for some meromorphic function F in \(U_0\) such that \(dF\wedge (n \frac{dx}{x^{n+1}y^m} + m \frac{dy}{x^n y^{m+1}} + \frac{m \sqrt{-1}}{2 \pi } \frac{dy}{y})=0\). In other words, F is a meromorphic first integral in \(U_0\) for the foliation \({\mathcal {F}}\). This implies that F is constant. In order to see this it is enough to use Laurent series as above. Alternatively one can argue as follows. If F is not constant then the holonomy map h of the leaf \(L_0\subset S\) leaves invariant a nonconstant meromorphic map (the restriction of the first integral F to a small transverse disc to S). This implies that h is a map with finite orbits and indeed h is periodic. Nevertheless this is never the case of the holonomy map of the separatrix \(\{y=0\}\) of the foliation \(\varOmega _{n,m}\). Thus the only possibility is that F is constant.
Summarizing the above discussion, we have proved that in all cases \(\eta = \eta _0 + F.\omega \) for some meromorphic function F in U and some meromorphic closed one-form \(\omega \) in U. Moreover, F is constant except in the resonant case. This shows that \(\eta =-\frac{1}{2}\frac{d\ell }{\ell }\) admits a meromorphic extension to U and therefore also \(\ell \) admits a extends meromorphic extension to U. The lemma is proved.
The remaining step for the irreducible resonant case is the following:
Proposition 11
(resonant case) Let \({\mathcal {F}}\) be a germ of a holomorphic foliation with a resonant (irreducible) singularity at the origin \(0\in \mathbb {C}^2\) and let \(0\in U\subset \mathbb {C}^2\) be a bidisc centered at the origin where \({\mathcal {F}}\) is defined by a holomorphic one-form \(\varOmega \). Fix a separatrix \(S \subset sep({\mathcal {F}},U)\). Let \(\eta \) be a meromorphic one-form in U and \(\xi \) be a meromorphic one-form in \((U \setminus sep({\mathcal {F}},U))\cup S\) such that in \(U \setminus sep({\mathcal {F}},U)\) the one-forms \(\varOmega , \eta , \xi \) define a projective triple. Then \(\xi \) extends as a meromorphic one-form to U.
Proof
By hypothesis we are in the resonant case, i.e., \(\varOmega = g(xdy - \lambda ydx +\ldots )\) with \(\lambda = - \frac{n}{m} \in \mathbb {Q}_-\). Suppose first that the singularity is not analytically linearizable. As we have seen in Lemma 7, \({\mathcal {F}}\) is the pull-back of a Riccati foliation on \(\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) by some meromorphic map \(\sigma :U \rightarrow \overline{\mathbb {C}}\times \overline{\mathbb {C}}\) provided that there is a meromorphic projective triple \((\varOmega ^\prime , \eta ^\prime , \xi ^\prime )\) in a neighborhood W of a separatrix \(S \subset sep({\mathcal {F}},U)\). From our hypothesis such a projective triple is given by the restrictions of \(\varOmega \) and \(\eta \) to \(U\setminus [ sep({\mathcal {F}},U)\setminus S]\) and by the one-form \(\xi \). Thus we conclude that \({\mathcal {F}}\) is a meromorphic pull-back of a Riccati foliation and in particular there is a one-form \(\xi ^\prime \) defined in a neighborhood \({\tilde{U}}\) of the origin such that \((\varOmega , \eta , \xi ^\prime )\) is a projective triple in this neighborhood. This implies that \(\xi = \xi ^\prime + \ell . \varOmega \) in \({\tilde{U}}\) for some meromorphic function \(\ell \) in \({\tilde{U}}\) such that \(d\varOmega = - \frac{1}{2} \frac{d\ell }{\ell }\) in \({\tilde{U}}\). Now we have two possibilities. Either \(\xi =\xi ^\prime \) in \({\tilde{U}}\) or \(\ell \not \equiv 0\). In the first case \(\xi \) extends meromorphically to U as \(\xi =\xi ^\prime \). In the second case we apply Lemma 9 above in order to conclude that the singularity is analytically normalizable and \(\ell \) extends as a meromorphic function to U. Suppose now that the singularity is resonant analytically linearizable and \({\mathcal {F}}\) is given in U by \(\varOmega = g\big (xdy + \frac{n}{m}\,ydx\big )\) where \(n,m \in \mathrm{I\!N}\) and g is a meromorphic function in U. In this case as above we define \(\eta _0 = \frac{dg}{g} + \frac{dx}{x} + \frac{dy}{y}\), write \(\eta = \eta _0 + h\varOmega \) and define \(\xi _0=0\), \(\xi _1 = \xi _0-dh-h\eta _0 - \frac{h^2}{2}\,\varOmega = -dh - h\eta _0 - \frac{h^2}{2}\,\varOmega \). Now we have \(\xi = \xi _1 + \ell \varOmega \) for some meromorphic function \(\ell \) in \(U^*\). In this case we have from \(d\ell = -\frac{1}{2}\,\frac{d\ell }{\ell } \wedge \varOmega \) that \(\ell (gxy)^2 = [\varphi (x^ny^m)]^2\) for some meromorphic function \(\varphi (z)\) defined in a punctured neighborhood of the origin \(0 \in \mathbb {C}\). In particular we conclude that since \(\xi \) extends meromorphically to some separatrix \(\{x=0\}\) or \(\{y=0\}\) then it extends meromorphically to U.
Thus \(\xi \) extends as a meromorphic one-form to U in all cases proving the desired result.
Remark 10
Propositions 6, 10 and 11 already prove Theorem 5 in the case of a germ of a foliation with an irreducible singularity at the origin.
4.3 Extension to Non-invariant Divisors
Since we are considering the possibility of existence of non-invariant components in the exceptional divisor, we shall be able to extend the projective triple to such components. This is done by means of the following lemma regarding the non-invariant case:
Lemma 10
(non-invariant divisor, [9]) Let be given a holomorphic foliation \({\mathcal {F}}\) on a complex surface M. Suppose that \({\mathcal {F}}\) is given by a meromorphic integrable one-form \(\varOmega \) which admits a meromorphic one-form \(\eta \) on M such that \(d \varOmega = \eta \wedge \varOmega \). If \({\mathcal {F}}\) is transversely projective in \({M\setminus }S\) for some non-invariant irreducible analytic subset \(S \subset M\) of codimension one then \({\mathcal {F}}\) is transversely projective in M. Indeed, the projective transverse structure for \({\mathcal {F}}\) in \({M\setminus }S\) extends to M as a projective transverse structure for \({\mathcal {F}}\). In particular, if \(\xi \) is a meromorphic one-form in \(M\setminus U\) such that \((\varOmega ,\eta ,\xi )\) is a projective triple on \({M\setminus }S\), then \(\xi \) admits a meromorphic extension to S.
Proof
Our argumentation is local, i.e., we consider a small neighborhood U of a generic point \(q\in S\) where \({\mathcal {F}}\) is transverse to S. Thus, since S is not invariant by \({\mathcal {F}}\), performing changes as \(\varOmega ^\prime = g_1 \varOmega \) and \(\eta ^\prime = \eta + \frac{dg_1}{g_1}\) we can assume that \(\varOmega \) and \(\eta \) have poles in general position with respect to S in U. The existence of a projective transverse structure for \({\mathcal {F}}\) in \({M\setminus }S\) then gives a meromorphic one-form \(\xi \) in \(M \setminus S\) such \((\varOmega , \eta , \xi )\) is a geometric projective triple in \(M \setminus S\). For U small enough we can assume that for suitable local coordinates \((x,y)\in U\) we have \(S \cap U = \{x=0\}\) and also
for some holomorphic function \(g, h :U \rightarrow {\mathbb {C}}\) with 1 / g also holomorphic in U. Then we have
where
Thus, \(\sqrt{\ell } g = \varphi (y)\) for some meromorphic function \(\varphi (y)\) defined for \(x \ne 0\) and therefore for \(x=0\). This shows that \(\xi \) extends to U as a holomorphic one-form and then the projective structure extends to U. This shows that the transverse structure extends to S.
4.4 Extended Generalized Curves
Let us consider the general case, where we allow singularities which are not irreducible, but belong to the the class of (non-resonant) generalized curve. For this type of singularity we have the following extension result:
Proposition 12
(extension - generalized curve) Let \(\mathcal F\) be a germ of a non-resonant (and non-dicritical) generalized curve at the origin \(0\in {\mathbb {C}}^2\). Suppose that \( {\mathcal {F}}\) is transversely projective in \(U\setminus sep(\mathcal {\mathcal {F}},U)\), for some bidisc U centered at the origin, and let \((\varOmega , \eta , \xi )\) be a meromorphic projective triple in \(U\setminus sep({\mathcal {F}}, U)\) with \(\varOmega \) holomorphic in U, \(\eta \) meromorphic in U and \(\xi \) meromorphic in \(U\setminus sep({\mathcal {F}},U)\). Then the one-form \(\xi \) extends to U as a meromorphic one-form.
Proof
Let \(\pi :{\tilde{U}} \rightarrow U\) be the reduction morphism of the singularity and denote by \(({\tilde{\varOmega }},\tilde{\eta }, \tilde{\xi })\) the pull-back by \(\pi \) of the triple \((\varOmega , \eta , \xi )\). Because the singularity is non-dicritical, the exceptional divisor \(E=\pi ^{-1}(0)=\bigcup \limits _{j=1}^r \mathrm{I\!P}_j\) in the reduction process is connected and invariant. By the non-resonance hypothesis, this divisor contains some non-resonant singularity say \(p_0 \in \mathrm{I\!P}_{j_0}\). Thanks to Hartogs’ extension theorem, the one-form \(\tilde{\xi }\) also extends to the irreducible component \(\mathrm{I\!P}_{j_0}\) minus the singularities of the lifted foliation. Now according to Propositions 10 and 11, the form \(\tilde{\xi }\) also extends to all the components \(\mathrm{I\!P}_j\) intersecting \(\mathrm{I\!P}_{j_0}\). The same argument and the connectedness of E show that the projective triple \(({\tilde{\varOmega }}, \tilde{\eta }, \tilde{\xi })\) extends to a neighborhood of the exceptional divisor.
We will prove a more general case in what follows. In a natural extension of the arguments in the proof of Proposition 12 we obtain the following result which is Theorem 5 in the local case.
Proposition 13
(extension - extended generalized curve) Let \(\mathcal F\) be a germ of a holomorphic foliation at the origin \(0\in {\mathbb {C}}^2\). Suppose that for some small bidisc U centered at the origin, the representative of \( {\mathcal {F}}\) is transversely projective in \(U\setminus S\) where \(S\subset \mathcal ND( sep({\mathcal {F}},U))\subset sep(\mathcal {\mathcal {F}},U)\) is a (finite) union of local branches, all of them corresponding to non-dicritical separatrices. Assume that the singularity \(0\in S\) is a non-resonant extended generalized curve. Then \({\mathcal {F}}\) admits in U a meromorphic projective triple. Indeed, let \((\varOmega , \eta , \xi )\) be a meromorphic triple in \(U\setminus sep({\mathcal {F}}, U)\) with \(\varOmega \) holomorphic in U, \(\eta \) meromorphic in U and \(\xi \) meromorphic in \(U\setminus sep({\mathcal {F}},U)\). Then the one-form \(\xi \) extends to U as a meromorphic one-form.
Proof
(Proof of Theorem 5) The proof is similar to the one given for the case of generalized curve (Proposition 12). The existence of a meromorphic projective triple \((\varOmega , \eta , \xi )\) with \(\varOmega , \eta \) meromorphic in U and \(\xi \) in \(U\setminus S\) is granted by Proposition 6. Notice that by hypothesis each branch \(S_j\) in S is a non-dicritical separatrix and therefore it meets the exceptional divisor in some singular point \({\tilde{p}}_j\in sing({\tilde{\mathcal {F}}})\) of an invariant component \(\mathrm{I\!P}(S_j)\). We have \(S_j \cap \mathrm{I\!P}(S_j)=\{{\tilde{p}}_j\}\), where we still denote by \(S_j\) the strict transform of \(S_j\).
By the non-resonance hypothesis the component \(\mathrm{I\!P}(S_j)\) belongs to a connected component \(E(S_j)\) of the invariant part of E, which contains some non-resonant singularity \(\tilde{q}_j\in E(S_j)\cap sing({\tilde{\mathcal {F}}})\). Therefore, by the same arguments in the proof of Proposition 11 we conclude that third form of the pull-back projective triple \(({\tilde{\varOmega }}, \tilde{\eta }, \tilde{\xi })\) extends as a meromorphic one-form to this component each connected component of the invariant part of the exceptional divisor E obtained in the reduction of the singularity. The extension of \(\tilde{\xi }\) to the non-invariant components of the exceptional divisor is granted by Lemma 10. If a connected component \(E_i\) of the invariant part of E does not contain a singularity belonging to a branch of S, still it contains some non-resonant singularity and the extension to \(E_i\) is assured as above. Thus Theorem 5 is proved in the local situation. The global case, i.e., the case of foliations on projective surfaces, is proved in the same way.
For the case of projective surfaces we promptly have:
Theorem 7
Let \({\mathcal {F}}\) be a holomorphic foliation by curves on a projective manifold M. Assume that \({\mathcal {F}}\) is transversely projective in \({M\setminus }S\) where \(S \subset M\) is an algebraic curve. Suppose that the singularities of \({\mathcal {F}}\) in S are non-resonant extended generalized curves. Then \({\mathcal {F}}\) admits a rational projective triple \((\varOmega , \eta , \xi )\), which defines the projective structure for \({\mathcal {F}}\) in \(M\setminus S\).
4.5 Extension of Projective Structures \(\mathcal P\)
In this section we investigate the extension not only of meromorphic projective triples but, of projective transverse structures (generically denoted by \(\mathcal P\)) to a codimension one divisor. According to Lemma 10 we may assume that the divisor is invariant by the foliation.
Proposition 14
(extension through a point) Let \((\varOmega , \eta , \xi )\) be a meromorphic projective triple on a complex surface \(M^2\), and \(S \subset M\) an irreducible analytic subset of dimension one. Suppose that the triple defines a projective transverse structure \(\mathcal P\) outside S. If there is a point \(q\in S\) and a neighborhood \(q\in U\subset M\) to which the projective structure \(\mathcal P\) extends, then this projective structure extends to M.
Proof
According to the preceding lemma, we may assume that S is \({\mathcal {F}}\)-invariant. We consider the local case where the foliation \({\mathcal {F}}\) is given by a holomorphic one-form \(\varOmega \) in an open subset \(W\subset {\mathbb {C}}^n\) with isolated zeros and admitting a meromorphic one-form \(\eta \) on W satisfying \(d\varOmega = \eta \wedge \varOmega \). We can assume that \(\varOmega \) and \(\eta \) have poles in general position with respect to S.
For \(U\subset W\) small enough we can find a holomorphic submersion \(y :U \rightarrow {\mathbb {C}}\) and meromorphic functions \(g, \, h\) in U such that
where
Thus, \(\sqrt{\ell } g = \varphi (y)\) for some meromorphic function \(\varphi (z)\) and therefore \(\ell = \frac{\varphi ^2(y)}{g ^2}\). Hence we have
We investigate under which conditions we can write
for some suitable meromorphic functions \({\tilde{g}}, {\tilde{h}}, {\tilde{y}}\).
Imposing the above equations we obtain
We shall refer to equations in (1) as main equations. From \(g dy = {\tilde{g}} d {\tilde{y}} \) we obtain \(g = r(y) {\tilde{g}}\) for some meromorphic function r(y). This implies \(d {\tilde{y}} = r(y) dy\) and then \(\frac{dg}{g} + h dy = \frac{d{\tilde{g}} }{{\tilde{g}}} + \frac{r^\prime (y)}{r(y)} dy + h dy\) so that replacing in the second main equation we obtain \(\frac{d{\tilde{g}} }{{\tilde{g}}} + {\tilde{h}} d {\tilde{y}} = \frac{d{\tilde{g}} }{{\tilde{g}}} + \frac{r^\prime (y)}{r(y)} dy + h dy\) and then \(\frac{r^\prime (y)}{r(y)} dy + h dy = {\tilde{h}} d{\tilde{y}} = {\tilde{h}} r(y) dy\). This last equation rewrites
and the final form
Let us turn our attention to the third main equation. From this we obtain
Then
This last equation is equivalent to
Let us put
Then equation (4) rewrites
So, the original question is reduced to find conditions under which the equation above has a holomorphic solution. This is the case, for instance if \(\varphi \) is holomorphic. Now we need to return to equation \(\frac{r^\prime (y)}{r(y)}= s(y)\) and study its solutions. It is clear from integration that there is a holomorphic solution, which must be given by \(r(y) = e^{\int s(y)dy}\), if and only if the given data s(y) is either holomorphic or meromorphic with a simple pole and integral positive residue at \(y=0\).
First case. If s(y) has a simple pole at \(y=0\). We may assume for simplicity that \(s(y)= a/y\) for some \( a\in {\mathbb {C}}^*\). In this case from the differential equation \(s^\prime - s^2 /2 = - \varphi ^2\) we obtain \(\varphi =\frac{\sqrt{2a - a^2}}{y}\). Integrating \(r(y)=e^{\int s(y)dy}\) we obtain \(r(y)=y^a\). Since \(r(y)=g/{\tilde{g}}\) we have that r(y) is holomorphic without zeros. In particular we cannot have \(a\ne 0\), contradiction.
Second case. If s(y) has a pole of order \(m+1 \ge 2\) at \(y=0\). In this case we can assume that \(s(y)=a/y^{m+1}\) for some \(m \ge 1\) and integration gives \(r(y)=e^{-\frac{a}{m y^m}}\) which is not meromorphic at the origin, contradiction.
Third case. If s(y) is holomorphic at \(y=0\). In this case we write \(s(y)=ay ^m\) for some \(m \ge 0\). We obtain \(r(y)= e^{\frac{a}{m+1} y^{m+1}}\) which is holomorphic and non-vanishing.
Let us now finish the proof. Because the projective structure extends to U the equation (1) has a holomorphic solution and this implies that \(\varphi (y)\) is holomorphic according to the above considerations. As a consequence the one-form \(\xi \) is also holomorphic in U and therefore admits a holomorphic extension to \(S\setminus [(\varOmega )_\infty \cup (\eta )_\infty ]\). Hence, the projective structure extends to \(S\setminus [(\varOmega )_\infty \cup (\eta )_\infty ]\) and then to S.
The next lemma shows that once we have fixed the forms \(\varOmega \) and \(\eta \) associated to a transverse projective structure, then we may replace the third form \(\xi \) without changing the invariant set S to which we wish to extend the structure.
Lemma 11
Let \((\varOmega , \eta , \xi )\) be a meromorphic projective triple in a complex surface M. Assume that the triple defines a projective transverse structure for \({\mathcal {F}}\) in \({M\setminus }S\) for some invariant codimension one analytic subset \(S\subset M\). Let \(\xi ^\prime \) be a meromorphic one-form in M such that \((\varOmega , \eta , \xi ^\prime )\) is also a projective triple. Then S is \(\xi \)-invariant if and only if it is \(\xi ^\prime \)-invariant.
Proof
We fix a local coordinate system \((x,y)\in U\) centered at a point \(p\in M\) such that \({\mathcal {F}}\) is given in these coordinates by \(\varOmega =g dy\) and S by \(\{y=0\}\). We may write \(\xi ^\prime = \xi + \ell \varOmega \) where \(d(\sqrt{\ell } \varOmega )=0\). Then we have \(\ell = \frac{\varphi ^ 2(y)}{g}\) for some meromorphic function \(\varphi (z)\). Assume by contradiction that S is not \(\xi \)-invariant but S is \(\xi ^\prime \)-invariant. We may assume that the polar set of \(\xi \) has no irreducible component contained in S and therefore \(\varphi (y)\) and g have no poles on \(\{y=0\}\). Write \(\xi ^\prime = Adx + B dy\) with holomorphic coefficients \(A(x,y), \, B(x,y)\). Since S is \(\xi ^\prime \)-invariant we have \(A(x,y)=y \, A_1(x,y)\) for some holomorphic function \(A_1(x,y)\). Then from \(\xi ^\prime = \xi + \ell \varOmega \) we get \(\xi = y A_1(x,y) dx + ( B (x,y) - \frac{\varphi ^2(y)}{g})dy\). Since \(A_1\) and \( B (x,y) - \frac{\varphi ^2(y)}{g}\) have no poles in \(\{y=0\}\) we conclude from the above expression that S is \(\xi \)-invariant, contradiction.
5 Classification of Transversely Projective Foliations
5.1 Classification of Transversely Projective Foliations: Non-dicritical Case
We consider now an application of the above study to the classification of foliations with projective transverse structure. Nevertheless, because of the non-dicriticalness hypothesis on the singularities, we will still be dealing with the affine case (see Remark 11 (i)). The (dicritical) projective non-affine case will be dealt with later on in this work. We point out that the non-dicriticity hypothesis excludes the “pure” transversely projective case, i.e., the case where the structure is not transversely affine in some other “affine” subset. We prove:
Theorem 8
Let \({\mathcal {F}}\) be a germ of a (non-dicritical) holomorphic foliation at the origin \(0 \in {\mathbb {C}}^2\). Suppose that:
-
(i)
\({\mathcal {F}}\) is a germ of a non-resonant generalized curve and can be reduced with a single blow-up.
-
(ii)
\({\mathcal {F}}\) is transversely projective outside of the set \( sep({\mathcal {F}},0)\) of local separatrices of \({\mathcal {F}}\) through 0.
Then \({\mathcal {F}}\) admits a generalized integrating factor. In particular, \({\mathcal {F}}\) is transversely affine in some neighborhood of the origin minus its set of local separatrices \( sep({\mathcal {F}},0)\).
As for the global case we have:
Theorem 9
Let \({\mathcal {F}}\) be a foliation on a compact projective surface M. Assume that \({\mathcal {F}}\) is transversely projective in the complement of an algebraic invariant curve \(S \subset M\). Suppose that for some smooth irreducible component \(S_0\subset S\) we have:
-
(i)
The singularities of \({\mathcal {F}}\) in \(S_0\) are irreducible and non-degenerate, one of which is non-resonant.
-
(ii)
\({M\setminus }S_0\) is a Stein manifold.
Then \({\mathcal {F}}\) admits a rational generalized integrating factor. In particular \({\mathcal {F}}\) is transversely affine in an open subset \(M \setminus C\) for some algebraic curve \(C\subset M\).
We point-out that, since the singularities in \(S_0\) are irreducible non-degenerate, usually the non-resonance hypothesis appearing in Theorem 8 is automatic. Indeed, for instance for the case of the projective plane \(M=\mathbb {C}P(2)\) this is a consequence of the Index theorem [7] and of the special geometry of \(\mathbb {C}P(2)\). Actually, we can state:
Theorem 10
Let \({\mathcal {F}}\) be a foliation on the projective plane \(\mathbb {C}P(2)\), which is transversely projective in the complement of an algebraic curve \(S \subset \mathbb {C}P(2)\). Suppose that for some smooth irreducible component \(S_0 \subset S\) the singularities of \({\mathcal {F}}\) in \(S_0\) are irreducible and non-degenerate. Then \({\mathcal {F}}\) admits a rational generalized integrating factor. In particular \({\mathcal {F}}\) is transversely affine in an open subset \(M \setminus C\) for some algebraic curve \(S \subset C\subset \mathbb {C}P(2)\).
As we see from Examples 6 and 11 the general Riccati case appears when we allow the curve S to have some dicritical singularities.
Let us pave the way to the proof of Theorems 8 and 9. Let \(G\subset Diff(\mathbb {C},0)\) be a solvable subgroup of germs of complex diffeomorphisms fixing the origin \(0 \in \mathbb {C}\). We recall that [13] if the group of commutators [G, G] is not cyclic (in particular G is solvable not abelian) then G is analytically conjugate to a subgroup of \(\mathrm{I\!H}_k = \big \{z \mapsto \frac{az}{\root k \of {1+bz^k}}; a \in \mathbb {C}\setminus \{0\}, b \in \mathbb {C}\big \}\) for some \(k \in \mathrm{I\!N}\). This is the case if G (is solvable and) contains some non-resonant element. Using this we can state the following well-known technical result.
Lemma 12
Let \(G < Diff({\mathbb {C}},0)\) be a solvable subgroup of germs of holomorphic diffeomorphisms fixing the origin \(0 \in {\mathbb {C}}\) containing some non-resonant element \(f \in G\) of the form \(f(z) = e^{2\pi i\lambda }\,z +\dots \) with \(\lambda \in {\mathbb {C}}\backslash \mathbb {Q}\). We have the following possibilities:
-
(i)
G is abelian. In this case G admits a formal meromorphic invariant one-form.
-
(ii)
If G is not abelian then f is analytically linearizable in a coordinate that also embeds G into some \(\mathrm{I\!H}_k\).
Proof
(i) is in [13]. Indeed, it is well-known that G admits a formal invariant holomorphic vector field say \(\hat{M}\) with an isolated singularity at the origin \(0\in \mathbb {C}\). Such a vector field can be written \(\hat{M}(z)= \frac{y^{k+1}}{1 + \lambda y^k} \frac{\partial }{\partial y}\), for some \(k \in \mathrm{I\!N}\) and some \(\lambda \in \mathbb {C}\). Moreover, according to [13] (see also [5, 28, 29]), because this group contains some non-resonant element, this vector field is indeed analytic. Now we take the corresponding dual one-form \(\hat{\omega }= \frac{\lambda y^k + 1}{y ^{k+1}} dy\). Since \(\hat{M}\) is invariant by the maps in G the same holds for \(\hat{\omega }\). This proves (i).
Now we prove (ii). Since G contains a non-resonant element we can, as already observed above, choose a holomorphic coordinate \(z \in (\mathbb {C},0)\) which embeds G as a subgroup of the group \(\mathrm{I\!H}_k\) for some \(k \in \mathrm{I\!N}\). Given then a non-resonant map \(f \in G\) we can write \(f(z) = \frac{e^{2\pi i\lambda }\,z}{\root k \of {1+bz^k}}\) for some \(k \in \mathrm{I\!N}\), \(b \in {\mathbb {C}}\). Since \(\lambda \in {\mathbb {C}}\backslash \mathbb {Q}\) the homography \(H(z) = \frac{e^{2\pi i\lambda }\,z}{1+bz}\) is conjugate by another homography to its linear part \(z \mapsto e^{2\pi i\lambda }\,z\) and therefore f is analytically linearizable in a coordinate that also embeds G into \(\mathrm{I\!H}_k\).
Proof
(Proof of Theorem 8) Let \({\mathcal {F}}\) be defined in an open bidisc \(0 \in U \subset {\mathbb {C}}^2\) by the holomorphic one-form \(\varOmega \). Put \(\widetilde{\mathcal {F}} = \pi ^*({\mathcal {F}})\) in \(\widetilde{U} = \pi ^{-1}(U)\) where \(\pi :\widetilde{{\mathbb {C}}}_0^2 \rightarrow {\mathbb {C}}^2\) is the blow-up of \({\mathbb {C}}^2\) at \(0 \in {\mathbb {C}}^2\). Let also \({\tilde{\varOmega }}=\pi ^*(\varOmega )\) be the lift of \(\varOmega \) to \({\tilde{U}}\). The exceptional divisor \(S = \pi ^{-1}(0)\) is a compact invariant curve (a projective line). Each singularity of \({\tilde{\mathcal {F}}}\) in S is irreducible and exhibits a separatrix transverse to S. This set of separatrices (of \({\tilde{\mathcal {F}}}\) transverse to S) is \( sep(\widetilde{\mathcal {F}},S) = \overline{\pi ^{-1}( sep({\mathcal {F}},0)\backslash \{0\})} = \overline{\pi ^{-1}( sep({\mathcal {F}},0))\backslash S}\) in \(\widetilde{U}\). Now, because of (ii) the pull-back foliation \(\widetilde{\mathcal {F}}\) is transversely projective in \(\widetilde{U} \backslash \widetilde{M}\) where \(\widetilde{M} = S \cup sep(\widetilde{\mathcal {F}},S)\). According to Theorem 3 this implies that the holonomy group \(Hol(\widetilde{\mathcal {F}},S)\) of the leaf \(S\backslash sing(\widetilde{\mathcal {F}})\) of \(\widetilde{\mathcal {F}}\) is solvable. We have two cases to consider:
Case 1. The group \(Hol(\widetilde{\mathcal {F}},S)\) is abelian.
Because this holonomy group is analytically conjugate to an abelian subgroup of \(Diff(\mathbb {C},0)\), it follows from Lemma 12 (i) that there exists a meromorphic integrating factor \({\tilde{h}}\) for \({\tilde{\varOmega }}\), defined over the open curve \(S_0= S\backslash \text {sing}(\tilde{\mathcal {F}})\). By this we mean a meromorphic function \({\tilde{h}}\) defined in a neighborhood of \(S_0\) such that the form \(\frac{1}{{\tilde{h}}} {\tilde{\varOmega }}\) is closed. Moreover, according to [5, 28, 29], because of the hypothesis on the singularities in S, this integrating factor extends as a meromorphic integrating factor for \({\tilde{\varOmega }}\) in a neighborhood of S. Therefore, the foliation \({\tilde{\mathcal {F}}}\) is defined by a closed meromorphic one-form \(\tilde{\omega }= \frac{1}{{\tilde{h}}} {\tilde{\varOmega }}\) in a neighborhood of S.
Case 2. The holonomy group \(Hol(\widetilde{\mathcal {F}},S)\) is solvable but not abelian. By the non-resonance hypothesis this group contains some element of the form \(f(z) = e^{2\pi i\lambda }\,z +\dots \) with \(\lambda \in {\mathbb {C}}\backslash \mathbb {Q}\). By Lemma 12 this map f is analytically linearizable and in the same analytic coordinate that embeds the holonomy group in the group
According to Sect. 5 in [27] (see also [8, 28]), this implies that the foliation is transversely affine in the complement of its set of separatrices, admits a so called closed logarithmic derivative which is a closed meromorphic one-form \(\tilde{\eta }_0\), with simple poles defined in a small neighborhood of the origin. The form \(\tilde{\eta }_0\) satisfies
Now we can “project” the one-form \(\tilde{\eta }_0\) via the blow-up map \(\pi :\widetilde{{\mathbb {C}}}_0^2 \rightarrow {\mathbb {C}}^2\) onto a one-form \(\eta _0\) defined in a punctured neighborhood of the origin. This one-form satisfies \(\tilde{\eta }_0 = \pi ^*(\eta _0)\) and, by classical Hartogs’ extension theorem [18] it extends (to the origin) as a meromorphic one-form in a neighborhood of the origin. It is clear that \(\eta _0\) is closed and satisfies \(d \varOmega = \eta _0 \wedge \varOmega \). This proves Theorem 8.
In the same line of reasoning we can prove Theorem 10:
Proof
(Proof of Theorem 10) We know that \({\mathcal {F}}\) is given by a rational one-form \(\varOmega \) on \(\mathbb {C}P(2)\). We shall prove that \(\varOmega \) admits a rational generalized integrating factor \(\eta \) on \(\mathbb {C}P(2)\). This is partially done as in the proof of Theorem 8. Nevertheless, in order to mimic the proof of Theorem 8 we must prove:
Claim
Some singularity in \(S_0\) is non-resonant.
Proof
(Proof of Claim 5.1) Recall that an irreducible non-degenerate singularity can be written in the form \(xdy - \lambda y dx + h.o.t.=0\), where \(\lambda \in \mathbb {C}\setminus \mathbb {Q}_+\) and \(\{xy=0\}\) is the set of local separatrices. If we fix the separatrix \(\{y=0\}\) then the Index of the singularity with respect to this separatrix is given by \(\lambda \). With respect to the other separatrix the index is \({1}/{\lambda }\). By the Index theorem [7] the sum of all indexes of singularities in \(S_0\) with respect to the local branches of S is equal to a (natural) positive number, the self-intersection number of \(S_0\) in the projective plane \(\mathbb {C}P(2)\). This implies that not all indexes are rational negative. Since by definition the index of an irreducible singularity is never a positive rational number, this implies that some singularity has a non-rational index. This singularity is clearly non-resonant.
By the above claim, the holonomy group of (the leaf contained in) \(S_0\) contains some non-resonant germ. From the proof of Theorem 8 there is a meromorphic generalized integrating factor \(\eta \) defined in some neighborhood V of \(S_0\) in \(\mathbb {C}P(2)\). Since \(\mathbb {C}P(2) \setminus S_0\) is a Stein surface [34], by a theorem of Levi (see [11, 34]), we can conclude that the one-form \(\eta \) extends as a meromorphic one-form to \(\mathbb {C}P(2)\) (see [10] for similar extension arguments). Finally, the extended one-form \(\eta \) must be rational because we are on a projective manifold. As in [27] the existence of \(\eta \) implies the final part of the statement.
Proof
(Proof of Theorem 9) As for the proof of Theorem 9 very few remains to say. Indeed, the proof of Theorem 10 gives all the steps. The hypotheses (i) and (ii) are then necessary since we cannot prove a version of Claim 5.1 in this case.
Remark 11
-
(1)
Theorems 8 and 10 above show that in order to capture the generic foliations in the class of Riccati foliations it is necessary to allow dicritical singularities or curves containing all of its separatrices.
-
(2)
Theorem 8 completes an example given in [35] of a germ \({\mathcal {F}}\) satisfying (i) and (ii) but which is not a meromorphic pull-back of a Riccati foliation on an algebraic surface. Indeed, the construction given in [35] exhibits \({\mathcal {F}}\) having as projective holonomy group G, i.e., the holonomy group \(G=Hol(\widetilde{\mathcal {F}}, D)\), where D is the exceptional divisor of the blow-up, a non-abelian solvable group conjugate to a subgroup of \(\mathrm{I\!H}_1 = \big \{z \mapsto \frac{\lambda z}{1+\mu z}\big \}\).
-
(3)
In [35] it is also given an example of a foliation \({\mathcal {H}}\) on a rational surface Y such that \({\mathcal {H}}\) is transversely projective on \(Y\backslash M\) for some algebraic curve \(M \subset Y\) and such that \({\mathcal {H}}\) is not birationally equivalent to a Riccati foliation on \(\overline{\mathbb {C}} \times \overline{\mathbb {C}}\).
5.2 Logarithmic Foliations, Separatrices and Invariant Curves
Let us recall that a logarithmic foliation on a projective surface M is one given by a closed rational one-form \(\beta \) with simple poles. If \(M=\overline{\mathbb {C}}\times \overline{\mathbb {C}}\) or \(\mathbb {C}P(2)\) then a logarithmic foliation is given by a rational one-form \(\beta \) as follows: \(\beta =\sum \limits _{j=1}^r \lambda _j \frac{df_j}{f_j}\), where the \(f_j\) are rational functions on V and \(\lambda _j \in {\mathbb {C}}\setminus \{0\}\).
In [20] the author gives the following nice characterization of logarithmic foliations:
Theorem 11
(cf. [20], Theorem A) Let \({\mathcal {F}}\) be a holomorphic foliation on a compact algebraic surface M and let S be a compact curve invariant by \({\mathcal {F}}\). Assume that one of the following conditions holds:
-
(i)
Pic(M) is isomorphic to
 .
. -
(ii)
Pic(M) is torsion free, \(H^1(M, \mathbb {C}) = 0\), \(S^2 > 0\) and \(\sum \limits _{p\in sing({\mathcal {F}})- S} BB_p ({\mathcal {F}}) \ge 0\).
Also assume that every local separatrix of \({\mathcal {F}}\) through any \(p \subset sing({\mathcal {F}})\cap S\) is a local branch of S and that every singularity of \({\mathcal {F}}\) in S is a generalized curve. Then \({\mathcal {F}}\) is a logarithmic foliation.
Here, by \(BB_p ({\mathcal {F}})\) we mean the Baum-Bott index associated to the Chern number \(c_1^2\) of the normal sheaf of the foliation [1]. Also, \(Pic(M)=H^1(M,\mathcal O_M ^*)\) is the Picard group of M, while \(S^2\) denotes the self-intersection number of S. We point-out that  for the case of projective spaces \(M=\mathbb {C}P(m), m \ge 2\). Regarding condition (ii), the part \(H^1(M, \mathbb {C}) = 0\), \(S^2 > 0\) is verified for the case of projective spaces.
for the case of projective spaces \(M=\mathbb {C}P(m), m \ge 2\). Regarding condition (ii), the part \(H^1(M, \mathbb {C}) = 0\), \(S^2 > 0\) is verified for the case of projective spaces.
As a particular case we have:
Corollary 1
Let \({\mathcal {F}}\) be a holomorphic foliation on \(\mathbb {C}P(2)\) and let \(S\subset \mathbb {C}P(2)\) be an invariant algebraic curve by \({\mathcal {F}}\). Assume that: (i) every local separatrix of \({\mathcal {F}}\) through any \(p \subset sing({\mathcal {F}})\cap S\) is a local branch of S and that (ii) every singularity of \({\mathcal {F}}\) in S is a (non-dicritical) generalized curve. Then \({\mathcal {F}}\) is a logarithmic foliation.
As for the last inequality in Theorem 11 (ii) we have:
The condition \(\sum \limits _{p\in sing({\mathcal {F}})- S} BB_p ({\mathcal {F}}) \ge 0\) holds if each singularity of \({\mathcal {F}}\) in \(M \setminus S\) is linearly of Morse type (i.e. \({\mathcal {F}}\) is locally given by the holomorphic one-form \(d(xy) + h.o.t.\)). This condition also holds when \({\mathcal {F}}\) a has local holomorphic first integral around each point of M which is not in S. In particular we have:
Lemma 13
Let \({\mathcal {F}}\) be a holomorphic foliation on a compact algebraic surface M and let S be an invariant compact curve by \({\mathcal {F}}\). If \({\mathcal {F}}\) is transversely projective in \({M\setminus }S\) and the singularities in \({M\setminus }S\) are all non-dicritical then \(\sum \limits _{p\in sing({\mathcal {F}})- S} BB_p ({\mathcal {F}}) \ge O\).
Proof
Since \({\mathcal {F}}\) is transversely projective in \(M \setminus S\), any singularity \(p\in sing({\mathcal {F}}) \cap {M\setminus }S\) admits a meromorphic first integral. Because this singularity is non-dicritical, there is a holomorphic first integral. The conclusion follows from what we remarked above.
From this lemma and Theorem 11 and also Theorem 5 we promptly obtain:
Corollary 2
Let \({\mathcal {F}}\) be a holomorphic foliation on a compact algebraic surface M and let S be an invariant compact curve by \({\mathcal {F}}\). Suppose that \({\mathcal {F}}\) is transversely projective in \({M\setminus }S\) and that every singularity of \({\mathcal {F}}\) in S is a generalized curve. Assume that one of the following conditions hold:
-
(i)
Pic(M) is isomorphic to
 .
. -
(ii)
Pic(M) is torsion free, \(H^1(M, \mathbb {C}) = 0\), \(S^2 > 0\) and the singularities off S are non-dicritical.
There are two possibilities:
-
(a)
Every local separatrix of \({\mathcal {F}}\) through any \(p \subset sing({\mathcal {F}})\cap S\) is a local branch of S. In this case \({\mathcal {F}}\) is a logarithmic foliation.
-
(b)
There is a singular point \(p\in S\) exhibiting a separatrix \(\varGamma _p\) not contained in S. In this case \({\mathcal {F}}\) admits a rational projective triple \((\varOmega , \eta , \xi )\), defined on M.
Let \({\mathcal {F}}\) be a holomorphic foliation on \(\mathbb {C}P(2)\) of degree m, then \(\sum \limits _{p\in sing({\mathcal {F}})} BB_p ({\mathcal {F}}) = (m + 2)^ 2\ge 4\). The author proves the following extension of the second part of Theorem 1 in [12] to compact complex surfaces (cf. [20] Proposition 3.1):
Proposition 15
([20] Proposition 3.1) Let \({\mathcal {F}}\) be a holomorphic foliation on a compact algebraic surface M with \(H^1(M, \mathbb {C}) = 0\) and  . Let S be an invariant compact curve with only nodal type singularities.
. Let S be an invariant compact curve with only nodal type singularities.
If \(\sum \limits _{p\in sing({\mathcal {F}})- S} BB_p ({\mathcal {F}})< S^2\), then \({\mathcal {F}}\) is logarithmic.
By taking a look at the proof given in [20] we conclude that the conclusion of Theorem 11 holds for a foliation \({\mathcal {F}}\) on the complex projective plane \(\mathbb {C}P(2)\) having an invariant algebraic curve S such that each singularity of \({\mathcal {F}}\) in S is an extended generalized curve (cf. Definition 4) and if S contains each non-dicritical separatrix of each singularity of \({\mathcal {F}}\) in S.
Corollary 3
([20], Corollary 3.1) Let \({\mathcal {F}}\) be a holomorphic foliation on a compact algebraic surface M with \(H^1(M, \mathbb {C}) = 0\) and  . Let \(S\subset M\) be an invariant compact curve with only nodal type singularities. If \( sing({\mathcal {F}})\cap S = sing(S)\) and the singularities of \({\mathcal {F}}\) in S are non-degenerated, then \({\mathcal {F}}\) is a logarithmic foliation.
. Let \(S\subset M\) be an invariant compact curve with only nodal type singularities. If \( sing({\mathcal {F}})\cap S = sing(S)\) and the singularities of \({\mathcal {F}}\) in S are non-degenerated, then \({\mathcal {F}}\) is a logarithmic foliation.
5.2.1 Logarithmic Case and Moderate Growth
Theorem 12
Let \({\mathcal {F}}\) be a foliation on a projective surface M such that Pic(M) is isomorphic to  . Assume that \({\mathcal {F}}\) is transversely projective in \({M\setminus }S\) for some algebraic curve \(S \subset M\) and that the singularities of \({\mathcal {F}}\) in S are (non-dicritical) non-resonant generalized curves. Then \({\mathcal {F}}\) is a logarithmic foliation or it is transversely projective of moderate growth.
. Assume that \({\mathcal {F}}\) is transversely projective in \({M\setminus }S\) for some algebraic curve \(S \subset M\) and that the singularities of \({\mathcal {F}}\) in S are (non-dicritical) non-resonant generalized curves. Then \({\mathcal {F}}\) is a logarithmic foliation or it is transversely projective of moderate growth.
Proof
(Proof of Theorem 12) We will follow the notation in the proof of Theorem 4. Because the singularities of \({\mathcal {F}}\) are non-dicritical, the resolution divisor \(E=D\cup \tilde{S}\) is invariant by \({\tilde{\mathcal {F}}}\). Moreover, each connected component \(S^j\) of S originates a connected component of the resolution divisor. Therefore, for sake of simplicity of notation, let us assume that the singularities of \({\mathcal {F}}\) are already irreducible in M, i.e., S and E exhibit the same number of connected components. If we denote by \(\sigma :\widetilde{M} \rightarrow M\) the resolution morphism for the singularities of \({\mathcal {F}}\) in S, then \(\sigma \big |_{\widetilde{{M\setminus }S}}:\widetilde{M\setminus S} \rightarrow M \setminus S\) is a diffeomorphism, in particular the fundamental groups \(\pi _1(\widetilde{{M\setminus }S})\) and \(\pi _1({M\setminus }S)\) are isomorphic.
We have the following possibilities:
-
1.
S contains all the separatrices of \({\mathcal {F}}\) in S.
-
2.
There is a singularity of \({\mathcal {F}}\), say \(q\in S\), exhibiting a separatrix \(\varGamma \) which is not contained in S.
In case (1), since the singularities are assumed to be generalized curves we may apply Theorem 11 and conclude that \({\mathcal {F}}\) is a logarithmic foliation.
Assume that we are in case (2). Then by Theorem 5 and other results in Sect. 4.5 we conclude that the projective structure in \(M \setminus S\) defines a projective triple that extends to S. We have therefore a rational projective triple for \({\mathcal {F}}\) in M, i.e., \({\mathcal {F}}\) is transversely projective of moderate growth.
Clearly a logarithmic foliation is of moderate growth. Therefore we obtain:
Corollary 4
Let \({\mathcal {F}}\) be a foliation on \(M=\mathbb {C}P(2)\). Assume that \({\mathcal {F}}\) is transversely projective in \(\mathbb {C}P(2)\setminus S\) for some algebraic curve \(S \subset \mathbb {C}P(2)\) and that the singularities of \({\mathcal {F}}\) in S are (non-dicritical) non-resonant generalized curves. Then \({\mathcal {F}}\) is transversely projective of moderate growth.
5.3 Classification of Projective Foliations: Moderate Growth On Projective Manifolds
In [21] we find the following definition of transversely projective foliation on a smooth projective manifold. Let M be a smooth projective manifold over \(\mathbb {C}\).A (holomorphic singular) codimension one foliation \({\mathcal {F}}\) on M.The foliation is said to be transversely projective if given a non zero rational 1-form \(\omega \) defining \({\mathcal {F}}\) (and therefore satisfying the Frobenius integrability condition \(\omega \wedge d \omega = 0\) ) we have that there are rational 1-forms \(\alpha \) and \(\beta \) on M such that the \(sl_2\) -connection on the rank 2 trivial vector bundle defined by \(\varDelta = d + \begin{pmatrix} \alpha &{} \, \beta \\ \omega &{} \, - \alpha \end{pmatrix}\) is flat.
Let us compare the above definition with the one we have been using so far in this work. Indeed, compared to Definitions 6 and 6 there is a difference, quite easy to explain. In the above definition, we already assume that the foliation admits a rational projective triple, i.e., a projective triple meromorphic defined everywhere in the manifold M. This is not necessarily the case if we just start with a foliation which is (according to our definition Definition 6) transversely projective in \({M\setminus }S\) for some algebraic curve \(S\subset M\). Nevertheless, often we cannot extend the projective transverse structure to the curve S (for instance, in the case of Riccati foliations or logarithmic foliations). Thus what is considered in [21] are what we have called transversely projective foliations with moderate growth (cf. Definition 9). projective structure in \({M\setminus }S\).
The authors also introduce the following notion:
Definition 12
([21]) A Riccati foliation over a projective manifold M consists of a pair \((\pi :P \rightarrow M;H) = (P;H)\) where \(\pi :P \rightarrow M\) is a locally trivial \(\mathrm{I\!P}^1\) fiber bundle in the Zariski topology, this means that P is the projectivization of the total space of a rank two vector bundle E, and H is a codimension one foliation on P which is transverse to a general fiber of \(\pi \). In the case of a clear context, the \(\mathrm{I\!P}^1\)-bundle P is omitted from the notation. Then H is called a Riccati foliation. The foliation H is defined by the projectivization of horizontal sections of a (non unique) at meromorphic connection r on E. The connection r is uniquely determined by H and its trace on \(\det (E)\). We say that the Riccati foliation H is non-singular if it lifts to a meromorphic connection r with at worst non-singular singularities (see [15]), and irnon-singular if not. It is said that a Riccati foliation (P; H) over M factors through a projective manifold \(M^\prime \) if there exists a Riccati foliation \((\pi ^\prime :P^\prime \rightarrow M^\prime , H ^\prime )\) over \(M^\prime \), and rational maps \(\phi :M \rightarrow M ^\prime \) and \(\varPhi :P \rightarrow P ^\prime \), such that \(\pi ^\prime \circ \varPhi = \phi \circ \pi \), and \(\varPhi \) has degree one when restricted to a general fiber of P, and \(H = \varPhi ^*H ^\prime \).
Using the notion above, alternatively, in [21] the authors state that a foliation \(\mathcal F\) on M is transversely projective if there exists a triple \(\mathcal P = (P;H; \sigma )\) satisfying
-
1.
(P; H) is a Riccati foliation over M; and
-
2.
\(\sigma : M \rightarrow P\) is a rational section generically transverse to H such that \({\mathcal {F}}= \sigma ^*H\).
After making the conversion between the notions of transversely projective foliation in [21] and the one we consider in our work, we can state the main classification result of [21] as follows:
Theorem 13
(cf. [21], Theorem D) Let \(\mathcal F\) be a codimension one transversely projective foliation of moderate growth on a projective manifold M. Then at least one of the following assertions holds true.
-
1.
There exists a generically finite Galois morphism \(f :Y \rightarrow M\) such that \(f^*{\mathcal {F}}\) is defined by a closed rational one-form.
-
2.
There exists a rational map \(f :M \rightarrow S\) to a ruled surface S, and a Riccati foliation \({\mathcal {R}}\) on S such that \({\mathcal {F}} = f^*R\).
-
3.
The transverse projective structure for \({\mathcal {F}}\) has at worst non-singular singularities, and the monodromy representation of \({\mathcal {F}}\) factors through one of the tautological representations of a polydisk Shimura modular orbifold \({\mathcal {H}}\).
Combining this result and Theorem 7 we promptly obtain:
Theorem 14
Let \({\mathcal {F}}\) be a holomorphic foliation by curves on a projective manifold M. Assume that \({\mathcal {F}}\) is transversely projective in \({M\setminus }S\) where \(S \subset M\) is an algebraic curve. Suppose that the singularities of \({\mathcal {F}}\) in S are non-resonant extended generalized curves. Then at least one of the following assertions holds true.
-
1.
There exists a generically finite Galois morphism \(f :Y \rightarrow M\) such that \(f^*{\mathcal {F}}\) is defined by a closed rational one-form.
-
2.
There exists a rational map \(f :M \rightarrow S\) to a ruled surface S, and a Riccati foliation \({\mathcal {R}}\) on S such that \({\mathcal {F}} = f^*R\).
-
3.
The transverse projective structure for \({\mathcal {F}}\) has at worst non-singular singularities, and the monodromy representation of \({\mathcal {F}}\) factors through one of the tautological representations of a polydisk Shimura modular orbifold \({\mathcal {H}}\).
References
Baum, P., Bott, R.: On the zeros of meromorphic vector fields, Essais en l’honeur de G. De Rham, 29–47 (1970)
Baum, P., Bott, R.: Singularities of holomorphic foliations. J. Differ. Geom. 7, 279–342 (1972)
Berthier, M., Touzet, F.: Sur l’intégration des équations différentielles holomorphes réduites en dimension deux. Bol. Soc. Bras. Mat. 30(3), 247–286 (1999)
Blumenthal, R.: Transversely homogeneous foliations. Ann. Inst. Fourier t. 29(4), 143–158 (1979)
Camacho, C., Scárdua, B.: Foliations on complex projective spaces with algebraic limit sets. Géométrie complexe et systèmes dynamiques (Orsay, Astérisque 261, 57–88 (2000); Soc. Math. France, Paris (2000)
Camacho, C., Lins Neto, A.: Geometric Theory of Foliations. Birkhauser Inc, Boston (1985)
Camacho, C., Sad, P.: Invariant varieties through singularities of holomorphic vector fields. Ann. Math. 115, 579–595 (1982)
Camacho, C., Scárdua, B.: Holomorphic foliations with Liouvillian first integrals. Ergod. Theory Dyn. Syst. 21, 717–756 (2001)
Camacho, C., Scárdua, B.: Extension theorems for analytic objects associated to foliations. Bulletin des Sciences Mathmatiques (Paris. 1885) 136, 54–71 (2012). https://doi.org/10.1016/j.bulsci.2011.04.005
Camacho, C., Lins Neto, A., Sad, P.: Topological invariants and equidesingularization for holomorphic vector fields. J. of Differ. Geom. 20(1), 143–174 (1984)
Camacho, C., Lins Neto, A., Sad, P.: Foliations with algebraic limit sets. Ann. Math. 136, 429–446 (1992)
Cerveau, D., Lins Neto, A.: Holomorphic foliations in \(C P^ 2\) having an invariant algebraic curve. Ann. Inst. Fourier, Grenoble 41(4), 883–903 (1991)
Cerveau, D., Moussu, R.: Groupes d’automorphismes de \(({\mathbb{C}},0)\) et équations différentielles \(ydy+\cdots =0\). Bull. Soc. Math. Fr. 116, 459–488 (1988)
Cerveau, D., Sad, P.: Liouvillian integration and Bernoulli foliations. Trans. Am. Math. Soc. 350(8), 3065–3081 (1998)
Deligne, P.: Lecture Notes in Mathematics. Équations différentielles à points singuliers réguliers, vol. 163. Springer, Berlin (1970)
Dulac, H.: Solutions d’un système de équations différentiale dans le voisinage des valeus singulières. Bull. Soc. Math. Fr. 40, 324–383 (1912)
Godbillon, C.: Progress in Mathematics. Feuilletages. Études géométriques. With a preface by G. Reeb, vol. 98. Birkhäuser, Basel (1991)
Gunning, R.C.: Introduction to holomorphic functions of several variables. Function Theory. Wadsworth & Brooks/Cole Advanced Books & Software, vol. I. Pacific Grove, CA (1990)
Gunning, R.C.: Introduction to holomorphic functions of several variables. Local Theory. The Wadsworth & Brooks/Cole Mathematics Series. Wadsworth & Brooks/Cole Advanced Books & Software, vol. II. Monterey, CA (1990)
Licanic, S.: Logarithmic foliations on compact algebraic surfaces. Bol. Soc. Brasil. Mat. (N.S.) 31(1), 113–125 (2000)
Loray, F., Touzet, F., Vitrio, J.: Representations of quasiprojective groups, flat connections and transversely projective foliations (2015). arXiv:1402.1382 [math.AG]
Martinet, J., Ramis, J.-P.: Problème de modules pour des équations différentielles non lineaires du premier ordre. Publ. Math. Inst. Hautes Études Scientifiques 55, 63–124 (1982)
Martinet, J., Ramis, J.-P.: Classification analytique des équations différentielles nonlineaires resonnants du premier ordre. Ann. Sc. Ec. Norm. Sup. 16, 571–621 (1983)
Mattei, J.F., Moussu, R.: Holonomie et intégrales premières. Ann. Sci. École Norm. Sup. 13(4), 469–523 (1980)
Nakai, I.: Separatrices for nonsolvable dynamics on \({\mathbb{C}},0\). Ann. Inst. Fourier (Grenoble) 44, 569–599 (1994)
Nicolau, M., Paul, E.: A geometric proof of a Galois differential theory theorem. In: Mozo Fernandez, J. (ed.) Ecuaciones diferenciales y singularidades, Universidad de Valladolid, pp. 277–290 (1997)
Scárdua, B.: Transversely affine and transversely projective foliations. Ann. Sc. École Norm. Sup. 4\(^{e}\) sériet 30, 169–204 (1997)
Scárdua, B.: Integration of complex differential equations. J. Dyn. Control Syst. 1(5), 1–50 (1999)
Scárdua, B.: Complex vector fields having orbits with bounded geometry. Tohoku Math. J. (2) 54(3), 367–392 (2002)
Scárdua, B.: Differential algebra and Liouvillian first integrals of foliations. J. Pure Appl. Algebra 215(5), 764–788 (2011)
Seidenberg, A.: Reduction of singularities of the differential equation \(Ady=Bdx\). Am. J. Math. 90, 248–269 (1968)
Seke, B.: Sur les structures transversalement affines des feuilletages de codimension un. Ann. Inst. Fourier, Grenoble 30(1), 1–29 (1980)
Singer, M.F.: Liouvillian first integrals of differential equations. Trans. Am. Math. Soc. 333(2), 673–688 (1992)
Siu, Y.: Techniques of Extension of Analytic Objects. Marcel Dekker, N.Y. (1974)
Touzet, F.: Sur les feuilletages holomorphes transversalement projectifs. Ann. Inst. Fourier 53(3), 815–846 (2003)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Scárdua, B. (2018). On Singular Holomorphic Foliations with Projective Transverse Structure. In: Araújo dos Santos, R., Menegon Neto, A., Mond, D., Saia, M., Snoussi, J. (eds) Singularities and Foliations. Geometry, Topology and Applications. NBMS BMMS 2015 2015. Springer Proceedings in Mathematics & Statistics, vol 222. Springer, Cham. https://doi.org/10.1007/978-3-319-73639-6_6
Download citation
DOI: https://doi.org/10.1007/978-3-319-73639-6_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-73638-9
Online ISBN: 978-3-319-73639-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



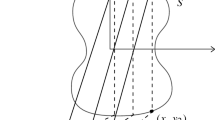


 .
. .
.