Numerical Analysis of the Conjugate Convection in an Open Cavity with and Without an Obstruction Inside

Abstract

Conjugate mixed convection due to the steady state heat transfer and the incoming fluid dynamics inside a two-dimensional square cavity is studied numerically for a Reynolds number of 400. The boundary of the left side of the cavity is a hot thick wall. The other three sides are bounded by adiabatic walls. In order to investigate the effect of a solid body on the conjugate heat transfer, a circular obstruction is placed at the centre of the cavity. The fluid inlets are at the lateral lower left wall, and the exits are located at the lateral upper right wall. The analysis is carried out for different ratios between the solid and fluid thermal conductivities. The governing equations of continuity, momentum and energy for incompressible flow are solved by the finite element method combined with the splitting operator scheme. The temperature field, the streamlines, the velocity and the pressure field are studied, and the axial velocity profiles are analysed as a function of the transversal position. It is observed that an obstruction placed inside the cavity plays a major role on vortex formation and on the thermal behaviour of the flow inside the cavity.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The numerical simulation of the conjugate convection in an open cavity with and without obstruction is an important issue in many technological processes. Manca et al. (2003) investigated the mixed convection in a U-shaped cavity, and evaluated its thermal performance in terms of the heated wall position. Mahmoudi et al. (2010) numerically examined the effect of the inlet and the outlet locations on the mixed convection flow and on the temperature field in a vented square cavity. Rahman et al. (2011) analysed the mixed convection in a ventilated square enclosure with a heat generating circular block. Mariani and Coelho (2007) presented the simulation of natural convection due to the temperature difference between the left and the right walls, and an internal local heat source in open cavities. Mamun et al. (2010) studied the effect of a heated hollow cylinder on mixed convection in a ventilated cavity. Radhakrishnan et al. (2007) reported experimental and numerical investigation of mixed convection from a heat generating element in a ventilated cavity. Varol et al. (2008) investigated the conjugate natural convection in enclosures via entropy generation. The main aim of this numerical investigation is to study the effect of the thermal conductivity of a finite thickness wall on the thermal behaviour in an open cavity with and without an obstruction. The analysis is carried out for the laminar regime and for the case when the buoyancy effect is outweighed by forced convection.

2 Problem Formulation

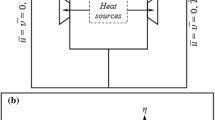
This work presents 2D numerical simulations inside an open square cavity $(H/W= 1)$ with and without an obstruction placed at the centre of the cavity, H is the height and W is the width of the cavity. The fluid, with a thermal conductivity k, enters at the left lower side wall and leaves the cavity at the right upper side wall, see Fig. 1. The thickness of the left wall, with thermal conductivity $k_{s},\, \text {is}\, {0.05}\,{\text {W}}$. Different ratios $k_{s}/k$ are investigated. The blockage ratio of the solid is fixed to $d/W=0.2,$ where d is the diameter of the obstruction. The Reynolds number $(Re=U_{m}W/\nu )$, based on the velocity of the inlet flow $U_{m}$ and the width W of the cavity, studied in this investigation was $Re=400$ for a Richardson number of $Ri=0.01$ and a Prandtl number of $Pr=\nu /\alpha =10.0$, where $\nu$ is the kinematic viscosity and $\alpha$ is the thermal diffusivity. The entrance and exit of the cavity was fixed to 0.25 W.

Fig. 1

Geometry of the cavity

The governing equations for a non-isothermal incompressible steady state flow are given as:

$$\begin{aligned} - \frac{1}{{\mathrm{{Re}}}}\Delta \vec {u} + \vec {u} \cdot \nabla \vec {u}+\nabla p = RiT\vec {J}\,\mathrm{{in}}\,\Omega , \end{aligned}$$

(1)

$$\begin{aligned} \nabla \cdot \vec {u} = 0\,\mathrm{{in}}\,\Omega , \end{aligned}$$

(2)

$$\begin{aligned} \frac{1}{{Pe}}\Delta T + \vec {u} \cdot \nabla T = 0\,in\,\Omega , \end{aligned}$$

(3)

For the solid cylinder, the energy equation is

$$\begin{aligned} \Delta T_{s} = 0\,\mathrm{{in}}\,\Omega , \end{aligned}$$

(4)

In the above equations $\Delta$ is the laplacian operator, $\vec {u}=(u_1 ,u_2 )$ is the velocity vector, being $u_{1} y \, u_{2}$ the horizontal and vertical velocity components, respectively; $\nu$ is the kinematic viscosity,  p is the pressure,  T  is the temperature,  $T_{s}$ is the temperature of the solid and $\vec {J}$ is the vertical unitary vector. In the governing equations, the Richardson number, the Reynolds number and the Peclet number are defined as follows:

$$\begin{aligned} Ri = {{g\beta h\left( {T_{h} - T_{c} } \right) } / U^{2} _{m} },\,\,\,\mathrm{{Re}} = {{U_{w} h} / \nu },\,\,\,Pe = \mathrm{{Re}}\,\mathrm{{Pr}} , \end{aligned}$$

(5)

where $g$ is the gravity, $\beta$ is the compressibility coefficient, $T_{h}$ is the hot temperature, $T_{c}$ is the cold temperature. No slip boundary conditions $(u_{1}=u_{2}=0)$ were established in all the walls of the cavity, and adiabatic walls $(\partial T/\partial n=0)$ were supposed except in the left wall where the heating takes place. The temperature of the inlet flow was fixed to $T=T_{c,}$ while the isothermal left wall was fixed to $T=T_{h}$. The non-dimensional values of this temperature were $T_{c}=0$ and $T_{h}=1$. The boundary conditions of the inlet flow were $u_{1}=U_{m}$, and $u_{2}=0$. On the outlet flow $\partial u/\partial n=0$ was imposed. The governing equations were solved with the finite element method combined with the operator splitting scheme, see Glowinski (2003). The convergence analysis was done for three different meshes with resolution of 4,500, 15,800 and 18,700 elements. An analysis of the temperature profiles on the middle horizontal and vertical lines indicates that the largest difference between the results of the meshes of 4,500 and 15,800 elements was 10%, while the maximum difference of the results between the meshes of 15,800 and 18700 was 1.02%. The analysis was also done for the velocity components. For all cases, the worst relative error between the meshes of 15800 and 18700 was less than 1.0%. All the simulations presented in this paper were performed for a cavity with 18,700 elements.

Fig. 2

Velocity fields and streamlines for $k_{s}/k={\textit{1.0}}.$ Left: without obstruction. Right: with obstruction

3 Results

Figure 2 shows the velocity field and streamlines, for $Re=400, Ri=0.01,$ $Pr=10 \;\text {and} \,k_{s}/k=1.0$. The left panel shows the behaviour of the fluid inside the cavity without an obstruction. For this case, three vortices can be observed along the diagonal perpendicular to the one that connects the inlet with the outlet. One of the vortices is anti-clockwise, big and strong, located at the central superior region of the cavity. At the upper left corner, a clockwise weak vortex appears, and at the inferior right corner another clockwise vortex emerges from the impingement of the fluid with the corner. The inlet jet emerges horizontally from the flow entrances of the cavity, but as it moves forwards, its horizontal component is decreased and the vertical component is increased. The right panel shows the behaviour of the fluid inside the cavity with a centred obstruction. For this case, the flow is characterized by four vortices, the clockwise vortex at the lower right corner remains, while three vortices appear around the obstruction as a consequence of the interaction of the solid with the flow that moves from the inlet to the outlet of the cavity. Two anti-clockwise vortices can be appreciated, one near the entrance and another near the exit of the cavity. Both are driven by the jet of fluid that crosses the cavity. The third vortex around the obstruction rotates clockwise and is driven by the motion of the other two vortices. The top panel of Fig. 3 shows the isotherms for the cases without obstruction. The contours tend to concentrate at the left wall of the cavity. The heat of the hot wall flows to the right upper part of the cavity due to the main stream of the fluid. As expected, high temperature occurs near the left wall. Farther, the contours are distorted and follow the main stream direction towards the outlet of the cavity. For low values of the thermal conductivity ratio $(k_{s}/k=0.1)$ the temperature contours remain undisturbed near of the left hot wall. As the thermal conductivity ratio $(k_{s}/k=5)$ is increased, the thermal boundary layer detaches from the lower part of the hot wall and a thermal plume moves toward the exit of the cavity due to the motion of inlet flow. This behaviour is intensified for $k_{s}/k=100$. For this case, the flux of heat reaches the central part of the cavity. The bottom panel of Fig. 3 shows the isotherms for the case when the obstruction inside the cavity has the same thermal conductivity as the fluid. This explains the behaviour of the isotherms through the obstruction, which are not affected by the boundary of the circular solid. The interaction of the solid with the flow distorts the temperature contours towards the central part of the cavity even for lower values of the thermal conductivity ratio $(k_{s}/k=0.1)$. As the ratio is increased to $k_{s}/k=5$ and $k_{s}/k=100$ the distortion of the isotherms towards the centre of the cavity are increased. When a solid is present inside the cavity, its interaction with the flow generates thermal boundary layer separation not only from the lower part of the hot wall, but also from the upper part of the hot wall, This phenomenon increases the flux of heat from the left hot wall towards the fluid.

Fig. 3

Isotherms. Top: without obstruction. Bottom: with obstruction. Left: $k_{s}/k=0.1$. Middle: $k_{s}/k=5.0$. Right: $k_{s}/k=100$

Figure 4 shows the temperature profiles in the interior surface of the left hot wall for the cavity without obstruction (see left panel) and the cavity with obstruction (see right panel) for different values of the thermal conductivity ratio. For both cases the temperature is increased as the $k_{s}/k$ ratio increases. The maximum temperature value, for a given $k_{s}/k$ ratio, is reached at the upper part of the left interior wall. For $k_{s}/k\le 1.0$ the temperature of the lower part of the interior left wall is $T\approx 0$. However, for $k_{s}/k\ge 10.0$ the temperature of the lower part of the interior left wall is $T>0.5$. For low values of $k_{s}/k$ the maximum temperatures are higher with, than without the solid blockage. For large values of $k_{s}/k$ the temperatures tend to be uniform and the maximum temperature is $T\approx 1.0$.

Fig. 4

Left wall interior temperature. Left: without obstruction. Right: with obstruction

Fig. 5

Middle vertical line temperature. Left: without obstruction. Right: with obstruction

Fig. 6

Velocity profile for $k_{s}/k={\textit{1.0}}$. Left: Horizontal component on $x=0.5$. Right: Vertical component on $y=0.5$

Figure 5 shows the temperature profiles on the middle vertical line. The left panel shows the behaviour of the temperature without the effect of the obstruction. The temperature starts to increase, reaches a maximum value about $y=0.43$ and then deceases. The larger the $k_{s}/k$ ratio the greater the temperature values. The right panel shows the effect of the obstruction on the temperature behaviour, which is more complex and is characterized by the increase of the temperature up to a maximum value of about $y=0.63$. Beyond this value, the temperature starts to decrease to a minimum and then increases again. Given a $k_{s}/k$ ratio for a particular vertical coordinate, the temperatures are higher when the obstruction is present. Figure 6 shows the horizontal velocity profiles on the middle vertical line (left panel) and the vertical velocity profile on the middle horizontal line (right panel) for the cavity with and without an obstruction. On the middle vertical line, it can be seen, for the flow without obstruction, that the fluid is accelerated as the vertical coordinate is increased, its horizontal velocity reaches a maximum at about $y=0.22$, then the velocity decreases and changes its direction to generate the main vortical motion. The effect of the obstruction is insignificant near the bottom wall. On the obstruction the velocity becomes zero and above of the obstruction surface the horizontal velocity decays. On the middle horizontal line, it can be seen, that without obstruction, the flow goes downwards as the horizontal coordinate is increased, then starts to move upwards and reaches a maximum at about $y=0.78$, then the velocity decreases toward the right wall. When the obstruction is present the vertical velocity near of the left wall becomes zero and after the obstruction the vertical velocity also reaches a maximum value.

4 Conclusions

We have presented in this work results of a finite element simulation of the flow inside an open cavity with and without a centre solid obstruction for different values of the ratio between the thermal conductivities of the solid and the fluid. The streamline patterns reveal that for a square cavity without obstruction three vortices are formed along the diagonal perpendicular to the line between the inlet and the outlet of the cavity. When the circular obstruction is placed at the centre of the cavity, the flow becomes more complex. Four vortices appear inside the cavity, three of them around the obstruction. The isotherms reveal that the presence of the obstruction intensifies the distortion of the thermal plume towards the centre and the exit of the cavity. So far, this study is limited to $Re=400, Ri=0.01 \,\text {and} \,Pr=10$. The fluid dynamics for other values is the subject of on-going research, but it is useful to understand the thermal behaviour of the flow inside an open cavity with and without an obstruction in applications like the cooling of electronic and electrical devices, thermal design of building, greenhouse design and refrigeration.