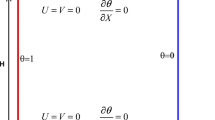Study of Natural Convection Heat Transfer in a Closed Wall with Thermal Conditions

Abstract

In this study, conjugate natural convection in a square cavity filled with fluids under steady-state condition is numerically investigated with the finite element method. The left side wall is considered as hot wall, and the right wall is considered to be cold. The top and bottom walls are assumed to be adiabatic. Different boundary conditions are introduced on the walls, and a thorough investigation is done in the present study. Numerical simulations have been done for different parameters of Grashof number (10³–10⁷) and Prandtl number. The graph of Nusselt number versus Grashof number and Nusselt number versus Prandtl number is plotted. It is observed that the buoyant forces developed in the cavity due to thermally induced density gradients vary as the value of acceleration due to gravity (g) differs, due to the change in temperature and stream function.

1 Introduction

Laminar, steady, natural convection flow was analyzed for a square closed cavity. Natural/free convection in square enclosures has been the spotlight in heat transfer analysis for more than a decade. Moreover, convection in a closed cavity with different boundary conditions is a paradigm for many practical applications like heat exchangers, cryogenic storage, furnace design, solar panels, and others.

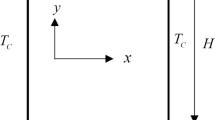
The main purpose of this study is to examine natural/free convection in a closed cavity (square) with zero wall thickness. The configuration is shown in Fig. 1. The cavity is filled with fluids (air and water) with bottom and top walls perfectly insulated while the right and cold walls are differentially cooled and heated.

Fig. 1

Geometry of the enclosure with all walls having zero thickness

The objective of this paper is to report the heat transfer characteristics in enclosures exposed to uniform, linearly varying temperatures at the right and left walls while the horizontal walls are perfectly adiabatic. The left wall is maintained at a temperature of 305 K, and the right wall is at 295 K. Heat transfer characteristics have been studied for Grashof numbers varying from 10³ to 10⁷. The cavity shown in Fig. 1 is elected for simulating natural convective heat transfer attributes.

1.1 Motivation

As shown in the literature survey, problems has been examined by Catton [1], Ostrach [2], and Hoogendoorn [3]. A cumulative study on the effects of temperature boundary conditions on free convection inside square cavities has been studied by Basak, Roy, and Balakrishnan [4].

November and Nansteel [5] and Valencia and Frederick [6] studied the natural convection in rectangular cavities where the bottom and top walls are heated and cooled differentially. Further, the case of cooling from top and heating on one side has been studied by Aydin [7], who also explored the effect of aspect ratio for rectangular cavities.

In the open literature, a definite analysis of free convection in cavities was dealt with by Ostrach [2]. Aydin and Yang [7] studied natural convection in a rectangular cavity, with one side heated and top wall cooled. The effect of sinusoidal temperature variation on the top wall in a square enclosure was studied by Sarris et al. [8]. Xia and Murthy [9] recognized that considerable attempts had been made to perceive how natural convection develops in closed enclosures. These studies made by various researchers triggered us to take up this problem and to add more value to it

1.2 Reason of Study

The natural convection in enclosures has engaged a great deal of consideration from researchers because of its wide range of applications. Researchers are conducting experiments in the same field by changing the heated plate and incorporating various boundary conditions. This natural convection in cavities has been classical, a standard problem for numerous industrial and technological applications like solar panels, nuclear reactors, electronic components, etc.

In Fig. 1, a square cavity is repleted with a fluid of Pr = 0.7 and Pr = 10. The left wall is kept hot at a temperature of about 305 K, and the right wall is kept cold at a temperature of 295 K.

The top wall and bottom wall are well insulated to study the heat transfer properties of different fluids with the variation of Grashof number (10³–10⁷).

2 Mathematical Formulation

A cavity, as demonstrated in Fig. 1, is chosen for simulating heat transfer characteristics and free convective flow. The enclosure of length (L) has a hot left wall with hot sinusoidally varying temperatures T_h, and the right cold wall is at consistent temperature T_c while the top surface and bottom surface are perfectly insulated. The gravitational force is acting in the downward direction. Due to the density gradient that arises due to the change in the thermal conditions, a buoyant flow is thus developed. Therefore, heat is transferred from a wall at a higher temperature to the wall at a lower temperature.

The equations that govern the natural convective flow are conservation of energy, mass, and momentum [4] which are penned as:

Continuity:

$$ \frac{\partial u}{\partial x}\, + \,\frac{\partial v}{\partial y} = 0$$

(1)

X-momentum:

$$ u\frac{\partial u}{\partial x}\, + \,v\frac{\partial u}{\partial y}\, = \, - \frac{1}{\rho }\frac{\partial p}{\partial x}\, + \,\gamma \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) $$

(2)

Y-momentum:

$$ u\frac{\partial v}{\partial x}\, + \,v\frac{\partial v}{\partial y}\, = \, - \frac{1}{\rho }\frac{\partial p}{\partial y}\, + \,\gamma \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right)\, + \,g\beta (T - T_{c} ) $$

(3)

Energy:

$$ u\frac{\partial T}{\partial x}\, + \,v\frac{\partial T}{\partial y}\, = \,\alpha \,\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) $$

(4)

The changes in variables are shown as follows:

$$ \theta = \,\frac{{T - T_{c} }}{{T_{h} - T_{c} }}\quad \Pr = \frac{v}{\alpha }\quad Ra = \frac{{g\beta (T_{{_{h} }} - T_{c} )L^{3} \Pr }}{{v^{2} }} $$

(5)

In this examination, the geometry has been designed and discretized the use of Gambit 2.2.3, while to simulate the natural convection of fluid in cavities, Fluent 6.2.16 CFD software is used. The consequence of distinct temperature boundary conditions at the left surface with constant temperature and top adiabatic walls is studied for different Grashof numbers. It was observed that at the corner of the bottom wall, their was a finite discontinuity in the temperature distribution during uniform temperature bottom wall boundary condition.

3 Stream Function and Nusselt Number

3.1 Stream Function

The stream function Ψ, which is realized from x and y components of the velocity, is used to study the fluid motion. For two-dimensional flows, the below equations shows the relationship among velocity component (u, v) and stream function Ψ;

$$ u\, = \,\frac{\partial \psi }{\partial y}\quad {\text{and}}\quad v\, = \, - \frac{\partial \psi }{\partial x} $$

(6)

This can be further simplified to a single equation and can be re-written as:

$$ \frac{{\partial^{2} \psi }}{{\partial x^{2} }}\, + \,\frac{{\partial^{2} \psi }}{{\partial y^{2} }}\, = \,\frac{\partial u}{\partial y} - \frac{\partial u}{\partial x} $$

(7)

Hence, from the stream function equation shown above, we can infer that anti-clockwise circulation is denoted by a positive sign of Ψ, whereas the clockwise circulation is denoted by a negative sign of Ψ.

3.2 Nusselt Number

The temperature profiles are fitted with quadratic, bi-quadratic, and cubic polynomials in order to determine the local Nusselt number and their gradients at the walls. It has been noted that for all the polynomials considered, the temperature gradients at the surface are almost the same. Therefore, only a quadratic polynomial is fitted in the temperature profiles for deriving the local gradients at the walls, which are intern used to calculate the local heat transfer coefficients. By this, the local Nusselt number is calculated. The average Nusselt number for each side is calculated by integrating the local Nusselt number over each side. The equations for the same are shown below:

$$ \overline{{{\text{Nu}}_{\text{b}} }} \, = \,\int\limits_{0}^{L} {{\text{Nu}}_{\text{b}} } dx $$

(8)

$$ \overline{{{\text{Nu}}_{\text{s}} }} \, = \,\int\limits_{0}^{H} {{\text{Nu}}_{\text{s}} } dy $$

(9)

4 Numerical Procedure

In the current study, the set of governing equations for natural convection has been converted to the algebraic equation by integrating over the control volume. The coupled system of governing equations is determined by Pressure-Implicit with Splitting of Operators (PISO). ADI has been employed to sequentially solve these sets of algebraic equations. The formulation of the convection contribution to the coefficients in the finite-volume equations has been studied using second-order upwind differential scheme. Central differencing is formulated to discretize the diffusion terms. The computation is continued till all the residuals reach 10⁻⁵ using the FLUENT 6.2.16.

5 Results and Discussion

A 41 × 41 grid point domain is used for all computations in the present study. Before the simulations, a grid refinement analysis has been conducted to estimate the optimum mesh size. It can be observed that the selected grid size provides a grid-independent solution. Hence, the simulations are all performed with a 41 × 41 spaced grid system. To determine the accuracy of this numerical procedure, the results obtained with the 41 × 41 grid-sized square cavity were compared and are in agreement with the work of Tanmay Basak a, S. Roy b, A.R. Balakrishnan for Ra = 10³–10⁷. Computations are carried out for Grashof number ranging from 10³ to 10⁷ and Pr = 0.7 and Pr = 10 with invariably heating of the left vertical wall while maintaining bottom and top walls at a well-insulated condition. In particular, the left wall needs special attention. As the mesh distribution at the corners is reduced, the Nusselt number is likely to increase. The Nusselt number for finite-volume and finite-difference method is calculated using various interpolation. This has been neglected in the current study.

In the current study, the calculations have been made for domains with different grid sizes (21 × 21, 31 × 31, 41 × 41 and 61 × 61) as well as Biasing Ratios (BR). Figure 2a shows the convergence of the average (mean) Nusselt number at the heated surface with grid refinement for Ra = 10⁵ of Lo et al. (2004). The grid 41 × 41 biasing ratio (BR) of 2 (the ratio of the maximum cell to the minimum cell is 2, thus making cells finer near the wall) gave results identical to that of 61 × 61 uniform mesh.

Fig. 2

Convergence of average Nusselt number with (a) grid refinement (b) Lo et al

A 41 × 41grid with BR = 2 is used in all further calculations. However, in the present case, the study has been made for Grashof number ranging from Gr = 10³–10⁷. The average Nusselt numbers are computed by the present methodology for the same values. Figure 2b shows the graph of local Nusselt number versus the Rayleigh numbers and hence can be inferred that local Nusselt number is directly proportional to the Rayleigh number for given Prandtl number (Fig. 3).

Fig. 3

Comparison of local nusselt number with rayleigh number for given prandtl number

Figure 4a and b shows the temperature plot and stream function for the square cavity for Grashof number varied from 10³ to 10⁹, respectively. It is clearly visible from the isotherm plot that the maximum non-dimensional temperature is present at the top of the cavity, whereas the minimum non-dimensional temperature is present at the bottom. The stream function plot shows that a lower magnitude of stream function will occupy the extreme ends of the cavity, whereas the stream function with a higher magnitude will occupy the center of the cavity. Figures 4a and b shows the temperature plot and stream function for the square cavity for Grashof number 10⁹, respectively. The magnitude of stream function increases, and also, the area occupied by the stream function with a higher magnitude is more compared to the case of Grashof number 10⁸. The thermal boundary layer is thinner compared to the case of Grashof number 10⁹.

Fig. 4

showing the stream function and temperature profile for conductivity ratio K = 5, Pr = 0.7, Rayleigh number 10³–10⁹

In Fig. 5, modest variation in local Nusselt number is noticed up to Rayleigh number 10³ owing to conduction pre-eminence and significantly varied from Rayleigh number 10⁴–10⁷ due to convection pre-eminence in the characteristics of heat transfer.

Fig. 5

showing the variation in local Nusselt number versus Rayleigh Number for different values of Prandtl number (17,7,0.7)

In Fig. 6, it is noted that the heat transfer rate decreases to a minimum value and later increases with distance for different Rayleigh numbers.

Fig. 6

showing the variation of temperature and heat flux

6 Conclusions

The main intention of the existing study is to analyze the transfer of heat in a square enclosure containing air and water during free convection. For obtaining continuous solutions with regard to isotherms and stream functions, finite element analysis was used for extensive magnitudes of Grashof number varying from 10³ to 10⁷.

The convection equations of fluids (air and water) along with continuity, energy, and momentum equations have been solved using finite element analysis.

In Fig. 6, it is observed that as the magnitude of Grashof number reaches higher values, the temperature lines tend to constrict against the left hot wall which intern increases the rate of transfer of heat at the corners of the hot wall. The heat transfer gradually decreases to a minimum value at the center.

This examination shows that the temperature distribution remains uniform for a broad spectrum of parameters. Under uniform heating conditions, because of the temperature difference among the vertical walls, the fluid flows toward the wall from the center of gravity in a clockwise direction.

The variations in Nusselt number with changes in the magnitude of Grashof number is shown in Fig. 7a and b.

Fig. 7

Variation of average Nusselt number with Grashof number for (a) Pr = 0.7 (b) Pr = 10

The present study can be accounted for various real-time applications like solar panels, heat exchangers, and others with cavities filled with different types of fluids.