1 Introduction

Natural convection in a cavity with discrete heat sources on the surface of an inner shape has attracted attention of researchers because of many engineering applications, for example, heat exchangers, electronic equipment cooling, melting of glass and so on [1,2,3]. It is noteworthy that natural convection occurs in nature without any external forces such as fan, pump, or a suction device, it is therefore considered to be the most promising heat transfer process. Apart from this, the engineering applications based on natural convection have longer durability, but require low maintenance cost.

Chen and Chen [4] considered heat sources on the bottom and left walls of a cavity. The effects of the length and strength of the heat source and the Rayleigh number are discussed with streamlines, isotherms as well as Nusselt number. Aminossadati and Ghasemi [5] investigated natural convection of a nanofluid taking into account two pairs of heat sources and sinks in a square cavity. Khanafer et al. [3] studied the influence of a porous fin mounted on the hot wall in a partially heated cavity. The results illustrate the effects of the Rayleigh number, Darcy number and fin on the natural convection heat transfer and flow field. Mirzaie and Lakzian [6] investigated heat transfer characteristics taking heat sources on the inner cylinder and heat sinks on the outer cylinder.

Incropera et al. [7] conducted an experiment to study convective heat transfer resulting from heat sources mounted to one wall of a rectangular channel. Heindel et al. [8] carried out the two- and three-dimensional numerical simulations and performed an experiment to examine conjugate natural convection for discrete heat sources in a cavity. An excellent agreement between the experiment and the three-dimensional numerical solutions was determined. However, the two-dimensional numerical predictions yield a discrepancy with the experiment in the average surface temperature of the heat sources. Moreover, Heindel et al. [9] studied the conjugate effects of conduction and natural convection resulting from an array of heat sources fixed in one vertical wall of a cavity. The temperature of the opposite vertical wall and the horizontal walls is assumed to be constant and thermally insulated. It is reported that for higher modified Rayleigh number the cavity flow demonstrates boundary layer characteristics along the vertical walls.

Hsu and Wang [10] investigated mixed convection heat transfer due to discrete heat sources on a vertical board hinged on the bottom of a cavity. As a practical application, Sarris et al. [11] considered the effect of local heat source on the glass-melting process. They found that the strength of streamlines and the fluid temperature are considerably enhanced by the length of the tank and the heat source.

Bazylak et al. [12] numerically examined the heat transfer considering an array of distributed heat sources on the bottom wall of a horizontal enclosure. A detailed analysis has been performed to reveal the optimal heat transfer rates and the inception of instability owing to the change of the length and spacing of the sources and the ratio of the width to the height of the enclosure.

Sheremet et al. [13] numerically investigated the influence of corner heater on the natural convection flow of a nanofluid in a wavy open porous tall cavity. Daniels and Punpocha [14] studied two-dimensional flow in a porous cavity due to differential heating of the upper surface and other adiabatic sidewalls. Deng [15] investigated the fluid flow and heat transfer taking into account the influence of the sources and sinks on the vertical sidewalls in a two-dimensional square cavity. Oztop et al. [16] investigated the heat transfer and flow characteristics in the presence of heat sources in a wavy-walled cavity. The vertical walls of the cavity are assumed to be differentially heated while the top and bottom wavy walls are thermally insulated. Chamkha and Ismael [17] examined the combined effect of natural convection and conduction heat transfer resulting from a triangular solid wall in a square cavity embedded in nanofluids filled porous matrix. Mahmoodi and Sebdani [18] conducted numerical simulation to study heat transfer and flow field inside a square cavity in the presence of an adiabatic square body at its center. Oztop and Bilgen [19] examined heat transfer in a square cavity having a heat generating fluid. The vertical walls are kept at uniform but different temperatures and horizontal walls are insulated while an isothermal partition is attached to the bottom wall. On the other hand, Sankar et al. [20] considered a vertical annulus embedded with a fluid-filled porous medium. The inner wall of it is assumed to be discrete heating and the outer wall is uniformly cooled. Sojoudi et al. [21] investigated natural convection heat transfer and flow properties in an attic shaped triangular cavity considering differentially heated inclined walls and a heat source in the middle of the right half of the bottom surface. Later, Sojoudi et al. [22] also studied unsteady flow and heat transfer of air due to differentially heating from inclined walls and a heat source at the bottom wall in a triangular cavity.

Sankar and Do [2] analyzed the natural convection flow and heat transfer in a vertical annulus. Two discrete heat sources have been mounted on the inner wall of the cavity. The top and bottom walls are assumed to be adiabatic and the outer wall is maintained at surrounding temperature. Results revealed that the heat transfer is comparatively higher for the bottom heat source than from the top heat source. Sankar et al. [23] also considered the heat and solute sources on the inner wall in a vertical annulus, which is placed in a fluid-saturated porous medium. It is found that the position of heat and solute sources has a strong influence on the flow field and the heat and mass transfers.

The above literature review revealed that the natural convective heat transfer and flow field strongly depend on the heat sources in a system. The aim of this study is to analyze the natural convection flow and heat transfer resulting from heat sources fixed on the inner square cylinder. The appropriate governing equations of the problem have been formulated using coordinate transformations. We solve the resulting equations using finite difference method. Results are presented in terms of the streamlines and isotherms and the local Nusselt number.

2 Model formalisms

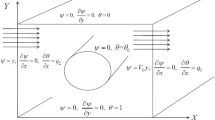
We assume a two-dimensional, laminar, natural convection flow in a cavity with an inner rectangular cylinder. Multi-heat sources of trapezoidal type are considered on the inner square cylinder. The temperature of the heat sources is assumed to be higher than the surrounding temperature of the cavity. Moreover, the walls of the inner square cylinder excluding the heat sources are thermally insulated. The physical domain with boundary conditions and the computational domain are presented in Fig. 1a, b, respectively.

Fig. 1
figure 1

a Physical domain with heat sources on the inner square cylinder. b Computational domain with heat sources

Full size image

The dimensionless stream function-vorticity equations in rectangular coordinate are [24, 25]:

$$\omega = - \left( {\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial y^{2} }}} \right)$$
(1)
$$\frac{\partial \omega }{\partial t} + \frac{\partial \psi }{\partial y}\frac{\partial \omega }{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial \omega }{\partial y} = \Pr \left( {\frac{{\partial^{2} \omega }}{{\partial x^{2} }} + \frac{{\partial^{2} \omega }}{{\partial y^{2} }}} \right) + \Pr Ra\frac{\partial T}{\partial x}$$
(2)
$$\frac{\partial T}{\partial t} + \frac{\partial \psi }{\partial y}\frac{\partial T}{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial T}{\partial y} = \frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}.$$
(3)

Equations (1)–(4) are made dimensionless defining the variables and constants as

$$t = \frac{\alpha }{{h^{2} }}\bar{t},\;x = \frac{{\bar{x}}}{h},\;y = \frac{{\bar{y}}}{h},\;l = \frac{{\bar{l}}}{h},\;b = \frac{{\bar{b}}}{h},\;u = \frac{h}{\alpha }\bar{u},\;v = \frac{h}{\alpha }\bar{v},\;w = \frac{{y_{0} }}{h},\;T = \frac{{\bar{T} - T_{0} }}{{T_{h} - T_{0} }}$$
(4)

where \(\bar{u}\) and \(\bar{v}\) are the velocity components along \(\bar{x}\)- and \(\bar{y}\)-directions, \(\bar{t}\) is the time, \(\bar{l}\) and h are the length and height of the outer square cylinder, \(\bar{T}\) is the fluid temperature, \(\bar{b}\) and y0 are the breadth and width of the heat sources and α is the thermal diffusivity.

In addition, Pr = ν/α is the Prandtl number and Ra = gβ(Th− T0)h3/(να) is the Rayleigh number, where ν is the kinematic viscosity of the fluid, g is the acceleration due to gravity, β is the volumetric expansion coefficient, Th is the temperature of the heat source and T0 is the temperature of the ambient.

The stream function ψ is defined by

$$u = \frac{\partial \psi }{\partial y},\quad v = - \frac{\partial \psi }{\partial x}$$
(5)

and the vorticity ω is given by

$$\omega = \frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}.$$
(6)

The rectangular domain is transformed to the physical domain defining the relations

$$x\left( {\xi ,\eta } \right) = \left\{ {r_{i} + \left( {r_{o} - r_{i} } \right)\eta } \right\}\sin \xi ,\;y\left( {\xi ,\eta } \right) = - \left\{ {r_{i} + \left( {r_{o} - r_{i} } \right)\eta } \right\}\cos \xi ,$$
(7)

where

$$r_{i} = \left[ {\left( {2\cos \xi } \right)^{200} + \left( {2\sin \xi } \right)^{200} } \right]^{{\frac{1}{200}}} \;{\text{and}}\;r_{o} = \left[ {\left( {\cos \xi } \right)^{200} + \left( {\sin \xi } \right)^{200} } \right]^{{\frac{1}{200}}} .$$

Here ri and ro are the radius of the inner and outer cylinders. So, the computational domain is in the (ξ, η) plane with 0 ≤ ξ ≤ 2π and 0 ≤ η ≤ 1.

Using the relations (7) in (1)–(3), we obtain

$$\nabla^{2} \psi = - J\omega ,$$
(8)
$$\frac{\partial \omega }{\partial t} + \frac{1}{J}\left( {U\frac{\partial \omega }{\partial \xi } + V\frac{\partial \omega }{\partial \eta }} \right) = \nabla^{2} \omega + \frac{1}{J}\Pr Ra\left( {y_{\eta } T_{\xi } - y_{\xi } T_{\eta } } \right),$$
(9)
$$\frac{\partial T}{\partial t} + \frac{1}{J}\left( {U\frac{\partial T}{\partial \xi } + V\frac{\partial T}{\partial \eta }} \right) = \nabla^{2} T,$$
(10)

where

$$\begin{aligned} U & = \frac{\partial \psi }{\partial \eta } = uy_{\eta } - vx_{\eta } ,\;V = - \frac{\partial \psi }{\partial \xi } = vx_{\xi } - uy_{\xi } ,\;J = x_{\xi } y_{\eta } - x_{\eta } y_{\xi } , \\ \nabla^{2} & \equiv A\frac{{\partial^{2} }}{{\partial \xi^{2} }} + 2B\frac{{\partial^{2} }}{\partial \eta \partial \xi } + C\frac{{\partial^{2} }}{{\partial \eta^{2} }} + H\frac{\partial }{\partial \xi } + G\frac{\partial }{\partial \eta },\;A = \frac{1}{J}\left( {x_{\eta }^{2} + y_{\eta }^{2} } \right), \\ B & = - \frac{1}{J}\left( {x_{\xi } x_{\eta } + y_{\xi } y_{\eta } } \right),\,\;C = \frac{1}{J}\left( {x_{\xi }^{2} + y_{\xi }^{2} } \right),\;G = B_{\xi } + C_{\eta } ,\;H = A_{\xi } + B_{\eta } . \\ \end{aligned}$$

The boundary conditions are

$$\begin{aligned} \psi & = \frac{\partial \psi }{\partial \eta } = 0,\,\,T = 0\;{\text{at}}\;\eta = 1 \\ \frac{{\partial^{2} \psi }}{{\partial \xi^{2} }} & = \frac{\partial T}{\partial \xi } = 0\;{\text{at}}\; \, \xi = 0,2\pi \\ \end{aligned}$$
(11)
$$\begin{aligned} \psi & = \frac{\partial \psi }{\partial \eta } = 0,\;\frac{\partial T}{\partial \eta } = 0\;{\text{ at}}\; \, \eta = 0, \, \;0 \le \xi < \xi_{1} , \, \; \, \xi_{2i} \le \xi < \xi_{2i + 1} \, \;{\text{and}}\; \, \xi_{{2n_{hs} }} < \xi \le 2\pi \\ T & = 1 \, \,{\text{for}}\, \, \xi_{2i - 1} \le \xi \le \xi_{2i} \;{\text{ and}}\; \, 0 \le \eta \le w. \\ \end{aligned}$$
(12)

The heat transfer is important from a physical point of view and it is defined by the Nusselt number, Nu, as

$$Nu = \frac{{\bar{h}q}}{\kappa },$$
(13)

where κ is the thermal conductivity of the fluid and q is the local heat transfer coefficient,

$$q = \pm \frac{\kappa }{{\left( {T_{h} - T_{0} } \right)}}\left( {\frac{{\partial \bar{T}}}{\partial n}} \right)_{{y = y_{0} ,h}} .$$
(14)

where ∂T̅/∂n is the normal gradient of the temperature to the top of the heat sources and outer cylinder.

From the relations (4), (7), (13) and (14), the heat transfers at the top of the heat source, Nuhs, and the outer cylinder, Nuo, are

$$Nu_{hs} = \left[ {\frac{{\left( {x_{\xi }^{2} + y_{\xi }^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{J}\left( {\frac{\partial T}{\partial \eta }} \right)} \right]_{\eta = w} \;{\text{and}}\;Nu_{o} = - \left[ {\frac{{\left( {x_{\xi }^{2} + y_{\xi }^{2} } \right)^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}{J}\left( {\frac{\partial T}{\partial \eta }} \right)} \right]_{\eta = 1} .$$
(15)

3 Numerical method

The system of Eqs. (8)–(10) with boundary conditions (11) and (12) is solved using implicit finite difference method. The convection terms are discretized using central difference approximation while central difference is used for the diffusion terms. The equations have been integrated over the whole domain. We first determine the stream function, ψ, from Eq. (8) utilizing successive-over relaxation (SOR) method with an accuracy of 10−6. The relaxation parameter, Ω, is assumed to be

$$\Omega = 2\left( {\frac{{1 - \sqrt {1 - \chi } }}{\chi }} \right)$$
(16)

where

$$\chi = \frac{1}{4}\left[ {\cos \left( {\frac{\pi }{m - 1}} \right) + \cos \left( {\frac{\pi }{n - 1}} \right)} \right]^{2}$$
(17)

A grid independent test is carried out to determine the variations of solutions with different mesh sizes. The average Nusselt number at the outer cylinder is thus shown in Table 1 taking mesh sizes of (m × n) = 200 × 20, 400 × 40, 600 × 60, 800 × 80 and 1000 × 100 where m and n are the numbers of grids in ξ and η directions, respectively. We then evaluate the absolute error in the average Nusselt number according to the formula:

$${\text{Absolute}}\;{\text{error}} = \left| {W_{k} - W_{k - 1} } \right|,$$
(18)

where k = 1, 2, 3, 4, 5 and W denotes the Nusselt number at top of the heat source and the outer cylinder. It is noted that the absolute error in the average Nusselt number for 400 × 40 grids is evaluated with reference to the value for 200 × 20 grids. It is seen from Table 1 that the absolute error decreases with the increase of the number of grids. It validates that the solutions of the present problem is independent of the number of grids. On the other hand, the absolute error in the average Nusselt number for mesh sizes 800 × 80 and 1000 × 100 is less than 5%. In this regard, the mesh size 800 × 80 is considered as a standard mesh throughout the entire computation.

Table 1 Variations of the Nusselt number at the top of the heat source and the outer cylinder when w = 0.1, b = 24°, τ = 0.2, Pr = 0.7 and Ra = 10,000
Full size table

Now a comparison is made between the present solutions and those of Hasanaoui et al. [26] for Ra = 100,000. Figures 2 shows streamlines and isotherms corresponding to a heat source of breadth 0.5 placed at the center of the bottom surface. It is clear from Fig. 2 that the present solutions yield a good agreement with the solutions of Hasanaoui et al. [26].

Fig. 2
figure 2

Comparison of a streamlines and b isotherms obtained by the present method and Hasanaoui et al. [26]

Full size image

4 Results and discussions

Numerical simulation has been carried out to investigate how the flow patterns and local Nusselt number are affected by the width and breadth of a heat source, number of heat sources and Rayleigh number. Here we consider three heat sources at ξ = 90°, 180° and 270°, breadth, b = 24°, width, w = 0.10 and Ra = 10,000 except these are not mentioned elsewhere.

Figures 3 and 4 exhibit the effect of the number of heat sources on the streamlines and isotherms, respectively. For increasing the number of heat sources, the intensity of the streamlines is increased and the structure of the isotherms is drastically changed. When the number of heat sources is 2 and 4, there are two vortices in each half about the vertical centerline of the cavity—one is a major vortex and another is a minor vortex. However, for nhs = 3 there is only one vortex in each half of the cavity. The major vortex consists of one, two and three eddies corresponding to the number of heat sources 2, 3 and 4, respectively. One thing is to be noted that when nhs = 2 and 4, no heat source is considered on the top horizontal surface of the inner square cylinder. For this reason, two minor vortices are generated on the top of the inner square cylinder.

Fig. 3
figure 3

Dimensionless streamlines with change of width of a heat source

Full size image
Fig. 4
figure 4

Dimensionless isotherms with change of width of a heat source

Full size image

The variations of the streamlines and isotherms with the change of the width of the heat sources are shown in Figs. 5 and 6, respectively. Results show that an increase in the width of the heat sources boosts the intensity of streamlines. There are two vortices in the physical domain. Also, the momentum and thermal boundary layers are found to increase with the increase in the width of the heat sources. Figure 6 clearly shows that there are three inner thermal boundary layers around the heat sources. For width w = 0.05 and 0.10, each of the vortices consists of two eyes, but they contain three eddies for w = 0.15. It is noticeable that when the width of the heat sources is relatively high, two vortices are generated on both sides of a heat source. It indicates that there exists a strong buoyancy force in the vertical direction of the top surface of a heat source so that the inner fluid particles of each vortex revolve within itself.

Fig. 5
figure 5

Dimensionless streamlines with change of width of a heat source

Full size image
Fig. 6
figure 6

Dimensionless isotherms with change of width of a heat source

Full size image

Figures 7 and 8 demonstrate the influence of the breadth of the heat sources on the streamlines and isotherms, respectively. Due to the increase of the breadth of the heat sources the strength of the streamlines augments. It is evident from the figures that the size of the vortices and the thermal boundary layer are increased for increasing the breadth of the heat sources. When the breadth of the heat sources is b = 48°, the vortices have three eyes. Among them, two eyes are generated on both sides of the vertical heat sources while the other is seen in one side of the heat source mounted on the top horizontal wall of the inner cylinder. The fact is that a high temperature zone is produced at the top of the heat sources and it obstructs the warmer fluid particles to move in the upward direction. Consequently, they rotate in the inner region of the vortex.

Fig. 7
figure 7

Dimensionless streamlines with change of breadth of a heat source

Full size image
Fig. 8
figure 8

Dimensionless isotherms with change of breadth of a heat source

Full size image

The effect of the Rayleigh number on the streamlines and isotherms is illustrated in Figs. 9 and 10, respectively. Increasing the Rayleigh number significantly enhances the intensity of the streamlines and pushes the isotherms in the upward direction. As a consequence, the heat plumes are elongated for larger Rayleigh number. These findings are similar to the results obtained by Hasanaoui et al. [26]. The new characteristics are that the eyes go far from each other owing to the increase of the Rayleigh number. When the Rayleigh number is Ra = 10,000 and 20,000, there is only one vortex in each half about the vertical centerline of the cavity. For a large Rayleigh number Ra = 50,000, there are three vortices in each half of the cavity. The reason is that higher Rayleigh number leads to strong buoyancy effect and thereby warmer fluids move swiftly. That is why, there occur three vortices as each strong heat plume results in two vortices on both sides of it.

Fig. 9
figure 9

Dimensionless streamlines with change of Rayleigh number

Full size image
Fig. 10
figure 10

Dimensionless isotherms with change of Rayleigh number

Full size image

Figure 11 depicts the effect of the width of a heat source on the Nusselt number at the top of a heat source and at the outer walls of the cavity. Increasing the width of a heat source diminishes the minimum value of the Nusselt number at the top of a heat source, but increases the Nusselt number at the outer walls of the cavity. It is clear from Fig. 11a that the heat transfer at the top of a heat source mounted on the right vertical wall first decreases and then increases with the increase of the angular distance. For larger width of a heat source, the Nusselt number on the bottom edge decreases whereas it increases on the top edge. It can be comprehended from the flow patterns shown in Figs. 5 and 6 that when the width of a heat source is higher, the colder fluid particles come close to the edges. In addition, for a heat source of width w = 0.15 a local minimum is observed across from the heat sources on the vertical walls.

Fig. 11
figure 11

Nusselt number a at the top of a heat source and b at the outer walls of the cavity with change of width of a heat source

Full size image

The influence of the breadth of the heat source on the Nusselt number at the top of a heat source and the outer walls of the cavity is illustrated in Fig. 12. Results reveal that the minimum value of the Nusselt number at the top of a heat source decreases with the increase of the breadth of a heat source. It is seen from Fig. 12a that the local maximum values occur at the both edges of a heat source and these are found to be higher for larger breadth of a heat source. Moreover, there is a minimum value in the middle of the heat source. This is due to the fact that the heat plumes arise on both sides of the edges and these are wider and bigger for an elongated heat source. Figure 12b shows that the Nusselt number at the outer walls of the cavity demonstrates higher values owing to the increase of the breadth of a heat source. Also, when the breadth of a heat source is b = 48° there occurs a local minimum nearly at the center of a heat source on the vertical wall.

Fig. 12
figure 12

Nusselt number a at the top of a heat source and b at the outer walls of the cavity with change of breadth of a heat source

Full size image

Figure 13 exhibits the effect of the Rayleigh number on the Nusselt number at the top of a heat source and at the outer walls of the cavity. Numerical calculation has been carried out taking b = 24°, w = 0.10, Ra = 10,000 and three heat sources at ξ = 90°, 180° and 270°. It is found that the heat transfer substantially increases upon increasing the Rayleigh number. This conforms to the result of Hasanaoui et al. [26]. Figure 13a shows that for increasing the angular distance the Nusselt number at the top of a heat source placed at ξ = 90° first decreases and then increases. For this reason, it is higher on both ends of a heat source and the maximum value is at the lower end (i.e., ξ = 78°). Specifically, in case of the heat sources at the vertical walls, the Nusselt number for the heat source at ξ = 90° is relatively larger at the lower edge than the upper edge (i.e., ξ = 102°). But the reverse characteristic is observed for the heat source at ξ = 270°. On the contrary, it is evident from Fig. 13b that the Nusselt number at the outer walls of the cavity attains its maximum at ξ = 180°, that is, at the middle of the heat source placed on the top horizontal wall. Moreover, there exist local maxima across the top edges (i.e., ξ = 102° and 258°) of the heat sources on the vertical walls. The reason is that the buoyancy force induces the fluid particles in the upward direction so that colder fluid particles move upward near the heat sources on the vertical walls. Consequently, a heat plume occurs on the top edge of each of the heat sources on the vertical walls and in the middle of the heat source placed on the top horizontal wall. It gives rise to higher temperature gradients and thereby the largest Nusselt number at the center of a plume.

Fig. 13
figure 13

Nusselt number a at the top of a heat source and b at the outer walls of the cavity with change of Rayleigh number

Full size image

5 Conclusions

In this study, natural convection flow and heat transfer characteristics in an annulus bounded by two concentric square cylinders are studied. We consider multiple trapezoidal heat sources on the inner square cylinder. A mathematical model suitable for the present problem is developed using suitable coordinate transformations. With the increase of the number of the heat sources, width and breadth of the heat sources and Rayleigh number, the strength of the streamlines is found to increase. A distinct characteristic is recognized for higher breadth or width of the heat sources and Rayleigh number. In these cases, two vortices are generated on both sides of a heat source. For a relatively high Rayleigh number, three vortices are observed in each half of the cavity. With increasing the width and breadth of the heat sources, the Nusselt number at the top of the heat sources diminishes, but the Nusselt number at the outer walls of the cavity increases. Contrary to this, the heat transfer is increased owing to the increase of the Rayleigh number.