Keywords

1 Introduction

Three-way decision (3WD) [17, 18] mainly deals with uncertain and incomplete information. 3WD gives the noncommitment decision when the information is inadequate [14, 21, 23]. In traditional 3WD model [17], the corresponding losses for taking different actions are calculated by Bayesian minimum loss, but the decision-makers’ psychological risk attitudes are ignored. Prospect theory points out the “bounded rational” behavior of decision makers, which expresses that people will be risk-averse toward gains and risk chase toward losses [9]. In recent years, prospect theory has been introduced into 3WD to represent the psychological risk attitudes, the achievements include 3WD based on various prospect theories [11, 12, 22] and prospect theory-based 3WD in diverse fuzzy environment [15, 20].

Gu et al. [3] presented a prospect theory-based decision framework under intuitionistic fuzzy environment, Liang et al. [6] studied 3WD in Pythagorean fuzzy environment, they all focused on dealing with discrete uncertain information rather than continuous uncertain information. In practice, there is more continuous uncertain data in real life and the discretization of it will lead to the loss of information. Then, Wang et al. [12] presented the 3WD based on third-generation prospect theory, which transformed Z-numbers into triangular fuzzy numbers to describe decision information. Triangular fuzzy number can describe continuous uncertain data but it neglect the distribution of uncertainty, which results in an insufficiently detailed depiction of uncertainty.

To against the above issues, we observed that normal fuzzy numbers can describe the uncertain continuous information subjected to normal distribution. There are many things that obey normal distribution in human activities and natural environment [16]. For instance, the score of students and the service life of products both obey normal distribution. Therefore, we proposed normal fuzzy prospect theory-based three-way decision (NFP3WD) by describing decision information with normal fuzzy numbers. In addition, previous TOPSIS methods of calculating conditional probability neglected the risk attitudes of decision-makers. To this end, we propose a normal fuzzy ideal solution method to compute conditional probability under normal fuzzy environment without class label. The contributions of this work are expressed as follows:

  • We proposed normal fuzzy prospect theory-based three-way decision method (NFP3WD) to handle continuous uncertain information with normal distribution.

  • A normal fuzzy ideal solution based on TOPSIS and prospect theory is proposed to compute conditional probability, which includes the risk attitudes of decision-makers.

The rest of this paper is set out as follows. In Sect. 2, we review some fundamental concepts and notations of normal fuzzy numbers, 3WD, and prospect theory. Section 3 proposes a normal fuzzy prospect theory-based three-way decision method. In Sect. 4, we propose a normal fuzzy ideal solution based on TOPSIS and prospect theory. In Sect. 5, we give an illustrative example, then some comparative analyzes are carried out, which verify the effectiveness and superiority of our proposed method. Section 6 summarizes our study.

2 Preliminaries

2.1 Normal Fuzzy Numbers

Definition 1

[7, 13] Suppose \(\tilde{A} \) is a fuzzy number, if \(\tilde{A} \) has the following membership function:

$$\begin{aligned} \tilde{A} (x)=exp\left\{ -\frac{(x-a)^2}{\sigma ^{2} } \right\} ,x,a\in R,\sigma >0, \end{aligned}$$
(1)

then, \(\tilde{A}\) is a normal fuzzy number, represented as \(\tilde{A}=(a,\sigma ^{2})\), and R is a set of real numbers, a is the mean of \( \tilde{A} \) and \(\sigma ^{2}\) denotes variance of \(\tilde{A}\). Obviously, when \(\sigma =0\), the normal fuzzy number \(\tilde{A}=(a,\sigma ^{2})\) degenerates to real number a.

Definition 2

[5, 8] \(E(\tilde{A})\) is the expectation of normal fuzzy number \(\tilde{A}\), which is defined as:

$$\begin{aligned} E(\tilde{A} )=\frac{\int _{-\infty }^{+\infty } x\tilde{A}(x)dx}{\int _{-\infty }^{+\infty } \tilde{A}(x)dx}. \end{aligned}$$
(2)

when \(\tilde{A}=(a,\sigma ^{2})\), \(E(\tilde{A})=a\).

Definition 3

[5, 8] Suppose normal fuzzy numbers \(\tilde{A}=(a,\sigma _{a} ^{2})\), \(\tilde{B}=(b,\sigma _{b} ^{2})\), we can derive:

  1. (1)

    if \(a>b\), then \(\tilde{A}>\tilde{B}\);

  2. (2)

    if \(a=b\), then, when \(\sigma _{a}=\sigma _{b}\), \(\tilde{A}=\tilde{B}\); when \(\sigma _{a}<\sigma _{b}\), \(\tilde{A}>\tilde{B}\);

  3. (3)

    if \(a<b\), then \(\tilde{A}<\tilde{B}\).

Definition 4

[2] Suppose normal fuzzy numbers \(\tilde{A}=(a,\sigma _{a} ^{2})\), \(\tilde{B}=(b,\sigma _{b} ^{2})\), the distance between \(\tilde{A}\) and \(\tilde{B}\) is defined as:

$$\begin{aligned} d(\tilde{A} ,\tilde{B} )=\sqrt{(a-b)^2+\frac{1}{2} (\sigma _{a}^{2} -\sigma _{b}^{2} )^2}. \end{aligned}$$
(3)

2.2 Three-Way Decision

3WD theory divides a universe into three parts reasonably and takes effective strategies to deal with each part [19]. The two states \( \varOmega = \left\{ C,\lnot C\right\} \) in 3WD indicate that an object x is in a decision class C or not, respectively. There are three actions \(\mathcal {A}=\left\{ a_{P}, a_{B}, a_{N}\right\} \) in 3WD. Taking action \( a_{P}\) denotes that we accept x belongs to C and classify x to positive region POS(C); taking action \( a_{B}\) denotes that we classify x into boundary region BND(C); and taking action \( a_{N}\) denotes that we reject x belongs to C and classify x into negative region NEG(C).

Table 1. Loss function matrix.
Full size table

Table 1 shows the different loss functions. When an object \(x \in C\), the losses for taking actions \(a_{i}\) \((i=P,B,N)\) are \(\lambda _{iP}\), respectively. When \(x \notin C\), the losses for taking actions \(a_{i}\) are \(\lambda _{iN}\), respectively. Assume that Pr(C|x) and \( Pr (\lnot C| x ) \) represent conditional probability of \(x \in C\) and \(x \notin C\), respectively. Then, based on Bayesian process, the expected losses for taking three different actions can be calculated [17], and the decision rules are based on the minimum loss. The decision rules are simplified as comparing decision thresholds and conditional probability as follows:

$$\begin{aligned} \begin{aligned} &If\ Pr ( C| x )\ge \alpha , then\ x\in POS(C);\\ &If\ \beta < Pr ( C| x )< \alpha , then\ x\in BND(C);\\ &If\ Pr ( C| x )\le \beta , then\ x\in NEG(C).\\ \end{aligned} \end{aligned}$$
(4)

2.3 Prospect Theory

Prospect theory, proposed by Kahneman and Tversky [4], describes decision makers’ behaviors under uncertainty and risk. Prospect theory integrates decision makers’ value perception factor into the decision process, and the risk attitudes of decision makers are evaluated by value function and weight function.

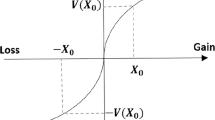
The value function describes decision makers’ risk attitudes toward gains and losses, which is an asymmetric S-shaped function. Different decision-makers may have different reference points, and that may lead to different judgments of gains and losses. Decision makers show risk aversion toward gains and risk-chasing toward losses. The value function is shown as follows [10]:

$$\begin{aligned} v(\varDelta z_{k})={\left\{ \begin{array}{ll} (\varDelta z_{k} )^{\mu }, &{}\varDelta z_{k} \ge 0 \\ -\theta (-\varDelta z_{k})^{\upsilon } , &{}\varDelta z_{k} < 0 \end{array}\right. }, \end{aligned}$$
(5)

where \( \varDelta z_{k}=z_{k}-z_{r} \), \( \varDelta z_{k} \) measures the \(k\text {-}th\) difference between reference point \( z_{r} \) and the \(k\text {-}th\) outcome \( z_{k} \). When \( \varDelta z_{k} \ge 0 \), the observed outcome is considered as a gain relative to the reference point. Conversely, if \( \varDelta z_{k} < 0 \), it is perceived as a loss.

Prospect theory holds that decision-makers always over-weight small probabilities and under-weight large probabilities [10]. Weight function \( w_{k} \) is a nonlinear transformation of the probability, the weight function given by Tversky and Kahneman [10] is shown as follows:

$$\begin{aligned} w_{k} ={\left\{ \begin{array}{ll} w^{+} (p(\varDelta z_{k}))=\frac{p(\varDelta z_{k})^{\sigma }}{(p(\varDelta z_{k})^{\sigma }+(1-p(\varDelta z_{k}))^{\sigma })^{1/\sigma } }\\ w^{-} (p(\varDelta z_{k}))=\frac{p(\varDelta z_{k})^{\delta }}{(p(\varDelta z_{k})^{\delta }+(1-p(\varDelta z_{k}))^{\delta })^{1/\delta } }\\ \end{array}\right. }, \end{aligned}$$
(6)

where \( w_{k}\) represents the decision weight, and \(p(\varDelta z_{k})\) denotes the actual probability of \( \varDelta z_{k} \). The influence degree of overweighting and underweighting to gains and losses are represented through parameters \(\sigma \) and \(\delta \), respectively, and they satisfy \( 0<\sigma , \delta <1 \).

Prospect theory holds that people prefer the maximum prospect value [11]. Suppose n denotes the number of outcomes, then, the prospect value function is shown as follows:

$$\begin{aligned} V=\sum _{k=1}^{n} w_{k}v(\varDelta z_{k} ). \end{aligned}$$
(7)

3 A Normal Fuzzy Prospect Theory-Based Three-Way Decision Method (NFP3WD)

In this section, we represent the decision information with normal fuzzy numbers and propose the NFP3WD method.

Since prospect theory seeks the maximum prospect value instead of the minimum loss, the losses in 3WD are replaced by outcomes in NFP3WD. The outcome denotes the final state of wealth for taking different actions in different states. In NFP3WD, the outcome matrix is described by normal fuzzy numbers, as shown in Table 2, where \(\tilde{Z}_{ij}=(a_{ij},\sigma _{ij} ^{2})\) \((i=P, B, N; j=P, N)\) indicates the normal fuzzy outcomes incurred for taking action i in state j.

Table 2. Normal fuzzy outcome matrix.
Full size table

Suppose \(\tilde{Z}_{r}=(a_{r},\sigma _{r} ^{2})\) represents the normal fuzzy reference point of the \( r\text {-}th \) decision maker, if \(\tilde{Z}_{ij} \ge \tilde{Z}_{r}\), the outcome \(\tilde{Z}_{ij}\) is perceived as a gain. Conversely, if \(\tilde{Z}_{ij} < \tilde{Z}_{r}\), it is perceived as a loss. According to Definition 4, the distance between \(\tilde{Z}_{ij}\) and \(\tilde{Z}_{r}\) is represented by \(d_{ij}\) \((i=P,B,N; j=P,N)\), which can be computed as follows:

$$\begin{aligned} \begin{aligned} d_{ij} = d(\tilde{Z}_{ij}, \tilde{Z}_{r})=\sqrt{(a_{ij}-a_{r})^2+\frac{1}{2} (\sigma _{ij}^{2} -\sigma _{r}^{2})^2},\ (i=P,B,N; j=P,N).\\ \end{aligned} \end{aligned}$$
(8)

Based on prospect theory, individuals tend to risk aversion to gains and risk chasing toward losses, they tend to be more sensitive to losses compared to gains, which are described by the value function. With the distance \(d_{ij}\) between normal fuzzy outcome and reference point obtained as well as the gains and losses judged, the value functions \(\tilde{v}_{ij}\) \((i=P, B, N;\) \(j=P, N)\) for taking different actions in different states are computed based on Eq. (5), shown as follows:

$$\begin{aligned} \begin{aligned} &\tilde{v}_{ij}={\left\{ \begin{array}{ll} \ \ \ \ (d _{ij} )^{\mu }, &{}\tilde{Z}_{ij}\ge \tilde{Z}_{r} \\ -\theta (d_{ij})^{\upsilon } , &{}\tilde{Z}_{ij}< \tilde{Z}_{r} \end{array}\right. }, \\ \end{aligned} \end{aligned}$$
(9)

where \(\mu \), \(\upsilon \) and \(\theta \) are suggested to set \(\mu =\upsilon = 0.88\), \(\theta =2.25\) after many psychological experiments [4]. The value function matrix is shown in Table 3.

In this table, the values \(\tilde{v}_{PP}\), \(\tilde{v}_{BP}\), and \(\tilde{v}_{NP}\) represent the value function associated with actions \(a_{P}\), \(a_{B}\), and \(a_{N}\) respectively, when \(x\in C\). Similarly, the values \(\tilde{v}_{PN}\), \(\tilde{v}_{BN}\), and \(\tilde{v}_{NN}\) represent the value function associated with actions \(a_{P}\), \(a_{B}\), and \(a_{N}\) respectively, when \(x\notin C\).

Table 3. Value function matrix.
Full size table

Next, in the 3WD theory, the conditional probability Pr(C|x) denotes the probability of \(x\in C\). \(Pr(C|x)+Pr(\lnot C|x)\) \(=1\). Prospect theory suggests that the probability should be extended to weight functions for gains and losses. The two different weight functions: \(w_{i}(Pr(C|x))\) \((i=P,B,N)\) corresponding to gains and \(w_{i}(Pr(\lnot C|x))\) \((i=P,B,N)\) corresponding to losses are presented as follows:

$$\begin{aligned} \begin{aligned} &w_{i}(Pr(C|x)) ={\left\{ \begin{array}{ll} w^{+}_{i}(Pr(C|x)),\ \tilde{Z}_{iP}\ge \tilde{Z}_{r} \\ w^{-}_{i}(Pr(C|x)),\ \tilde{Z}_{iP}< \tilde{Z}_{r} \end{array}\right. }, \\ &w_{i}(Pr(\lnot C|x)) ={\left\{ \begin{array}{ll} w^{+}_{i}(1-Pr(C|x)),\ \tilde{Z}_{iN}\ge \tilde{Z}_{r} \\ w^{-}_{i}(1-Pr(C|x)),\ \tilde{Z}_{iN}< \tilde{Z}_{r} \end{array}\right. }. \end{aligned} \end{aligned}$$
(10)

In fact, the weight functions are nonlinear transformations of conditional probabilities. Based on Eq. (6), the detailed calculation of weight function \(w_{i}(Pr(C|x))\) for Pr(C|x) and \(w_{i}(Pr(\lnot C|x))\) for \(Pr(\lnot C|x)\) are presented as follows:

$$\begin{aligned} \begin{aligned} &w_{i}(Pr(C|x))\!=\!{\left\{ \begin{array}{ll} \frac{Pr(C|x)^{\sigma }}{((Pr(C|x))^{\sigma }+(1-Pr(C|x))^{\sigma })^{1/\sigma } },&{}\tilde{Z}_{iP}\ge \tilde{Z}_{r}\\ \frac{Pr(C|x)^{\delta }}{((Pr(C|x))^{\delta }+(1-Pr(C|x))^{\delta })^{1/\delta } },&{}\tilde{Z}_{iP}< \tilde{Z}_{r}\\ \end{array}\right. }, i=P,B,N, \\ &w_{i}(Pr(\lnot C|x))={\left\{ \begin{array}{ll} \frac{(1-Pr( C|x))^{\sigma }}{((1-Pr( C|x))^{\sigma }+(Pr( C|x))^{\sigma })^{1/\sigma } },&{}\tilde{Z}_{iN}\ge \tilde{Z}_{r}\\ \frac{(1-Pr( C|x))^{\delta }}{((1-Pr( C|x))^{\delta }+(Pr(C|x))^{\delta })^{1/\delta } },&{}\tilde{Z}_{iN}< \tilde{Z}_{r}\\ \end{array}\right. }, i=P,B,N, \end{aligned} \end{aligned}$$
(11)

where the parameters are suggested to set \(\sigma =0.61\) and \(\delta =0.69\) by Tversky and Kahneman [4] and the settings are extensively used in the studies corresponding to prospect theory.

Subsequently, with value functions and weight functions obtained, based on Eq. (7), the prospect value \(\tilde{V}(a_{i}|x)\) \((i=P, B, N)\) of taking actions \(a_{P}\), \(a_{B}\), and \(a_{N}\) are calculated as follows:

$$\begin{aligned} \begin{aligned} &\tilde{V}(a_{P}|x)=\tilde{v} _{PP}w_{P}(Pr(C|x))+\tilde{v} _{PN}w_{P}(Pr(\lnot C|x));\\ &\tilde{V}(a_{B}|x)=\tilde{v} _{BP}w_{B}(Pr(C|x))+\tilde{v} _{BN}w_{B}(Pr(\lnot C|x));\\ &\tilde{V}(a_{N}|x)=\tilde{v} _{NP}w_{N}(Pr(C|x))+\tilde{v} _{NN}w_{N}(Pr(\lnot C|x)). \end{aligned} \end{aligned}$$
(12)

Then, the decision rules based on the maximum prospect value are shown as follows:

$$ \begin{aligned} \begin{aligned} &\ If\ \tilde{V}(a_{P}|x)\ge \tilde{V}(a_{B}|x)\ \& \ \tilde{V}(a_{P}|x)\ge \tilde{V}(a_{N}|x), \ then\ x\in POS(C);\\ &\ If\ \tilde{V}(a_{B}|x)\ge \tilde{V}(a_{P}|x)\ \& \ \tilde{V}(a_{B}|x)\ge \tilde{V}(a_{N}|x), \ then\ x\in BND(C);\\ &\ If\ \tilde{V}(a_{N}|x)\ge \tilde{V}(a_{P}|x)\ \& \ \tilde{V}(a_{N}|x)\ge \tilde{V}(a_{B}|x), \ then\ x\in NEG(C).\\ \end{aligned} \end{aligned}$$
(13)

In general, the decision rule of three-way decision is simplified to the comparison of decision thresholds and conditional probability Pr(C|x). Wang et al. [11] have proved that the decision thresholds \(\alpha \), \(\beta \) and \(\gamma \) exist and are unique in prospect theory-based three-way decisions. Similarly, the decision thresholds \(\alpha \), \(\beta \) and \(\gamma \) also exist and are unique in our NFP3WD.

Suppose \(\alpha \), \(\beta \) and \(\gamma \) are the intersections between \(\tilde{V}(a_{P}|x)\) and \(\tilde{V}(a_{B}|x)\), \(\tilde{V}(a_{B}|x)\) and \(\tilde{V}(a_{N}|x)\), \(\tilde{V}(a_{P}|x)\) and \(\tilde{V}(a_{N}|x)\), respectively. Let \(\tilde{V}_{1}=\tilde{V}(a_{P}|x)-\tilde{V}(a_{B}|x)\), \(\tilde{V}_{2}=\tilde{V}(a_{B}|x)-\tilde{V}(a_{N}|x)\) and \(\tilde{V}_{3}=\tilde{V}(a_{P}|x)-\tilde{V}(a_{N}|x)\). Then, \(\alpha \), \(\beta \) and \(\gamma \) are the zero points of \(\tilde{V}_{1}\), \(\tilde{V}_{2}\) and \(\tilde{V}_{3}\), respectively. If \(\alpha > \beta \), the decision rules are:

$$\begin{aligned} \begin{aligned} &\ If\ Pr(C|x)\ge \alpha ,then \ x\in POS(C);\\ &\ If\ \beta <Pr(C|x)< \alpha \ ,then \ x\in BND(C);\\ &\ If\ Pr(C|x)\le \beta ,then \ x\in NEG(C).\\ \end{aligned} \end{aligned}$$
(14)

Otherwise, the decision rules are:

$$\begin{aligned} \begin{aligned} &\ If\ Pr(C|x)\ge \gamma ,then \ x\in POS(C);\\ &\ If\ Pr(C|x)< \gamma ,then \ x\in NEG(C).\\ \end{aligned} \end{aligned}$$
(15)

4 The Normal Fuzzy Ideal Solutions for NFP3WD

For the information system without class label, the TOPSIS method can calculate the conditional probability [6]. However, traditional TOPSIS method does not consider the psychological risk attitudes. Therefore, we integrated prospect theory with TOPSIS to design a method to compute conditional probability of normal fuzzy system without class label.

Suppose \(IS=(U, AT, V, f)\) is a normal fuzzy information system without class label, where \(U= \left\{ o_{1},o_{2},\cdots , o_{m} \right\} \) represents the universe with m objects, \(AT= \left\{ g_{1},g_{2},\cdots , g_{n} \right\} \) denotes the attribute set of normal fuzzy information system. Then, the weights of attributes are expressed as \(\omega = \left\{ \omega _{1},\omega _{2},\cdots , \omega _{n} \right\} ^{T}\), where \(\omega _{q}\) \((q=1,\cdots ,n)\) represents the weight of attribute \(g_{q}\) and satisfies \(0\le \omega _{q}\le 1 \), \(\sum _{q=1}^{n} \omega _{q}=1\). In our normal fuzzy information system, let \(\tilde{A}_{pq}=(a_{pq},\sigma _{pq}^{2})\) \((p=1,\cdots ,m; q=1,\cdots ,n.)\) represents the value of the \(q\text {-}th \) attribute of the \(p\text {-}th \) object. The detailed normal fuzzy information system is shown in Table 4.

Table 4. Normal fuzzy information system.
Full size table

In Table 4, assume that all the attributes in normal fuzzy information system are positive attributes. To eliminate the dimensional effect of attributes, we perform the following transformation to standardize the values of the attributes:

$$\begin{aligned} \tilde{a}_{pq}=\frac{a_{pq}}{\max _{ 1\le p\le m } {\left\{ {a}_{pq} \right\} }} ,\tilde{\sigma }_{pq}^2=\frac{\sigma _{pq}^2}{\max _{ 1\le p\le m } {\left\{ {\sigma }_{pq}^2 \right\} }}\cdot \frac{\sigma _{pq}^2}{a_{pq}}. \end{aligned}$$
(16)

The standardized attribute value is expressed as \(\tilde{B}_{pq}=(\tilde{a}_{pq},\tilde{\sigma }_{pq}^2)\). In general, TOPSIS chooses the maximum attribute value as the positive ideal solution and the minimum attribute value as the negative ideal solution. In NFP3WD, we determine the two ideal solutions of each attribute by the mean and variance of the normal fuzzy number. More specifically, the maximum mean and the minimum variance of each attribute are selected to constitute the positive ideal solution \(\tilde{B}_{q}^{+}\). And the minimum mean and the maximum variance of each attribute are selected to construct the negative ideal solution \(\tilde{B}_{q}^{-}\). Then, the positive ideal solution is expressed as \(o^{+}= \left\{ \tilde{B}_{1}^{+},\tilde{B}_{2}^{+},\cdots , \tilde{B}_{n}^{+} \right\} \) and the negative ideal solution is expressed as \(o^{-}= \left\{ \tilde{B}_{1}^{-},\tilde{B}_{2}^{-},\cdots , \tilde{B}_{n}^{-} \right\} \), where

$$\begin{aligned} \begin{aligned} \tilde{B}_{q}^{+}=(\tilde{a}_{q}^{+},\tilde{\sigma }_{q}^{2+}), \ \tilde{a}_{q}^{+}=max_{ 1\le p\le m } \tilde{a}_{pq}, \ \tilde{\sigma }_{q}^{2+}=min_{ 1\le p\le m }\tilde{\sigma }_{pq}^{2},\\ \tilde{B}_{q}^{-}=(\tilde{a}_{q}^{-},\tilde{\sigma }_{q}^{2-}),\ \tilde{a}_{q}^{-}=min_{ 1\le p\le m } \tilde{a}_{pq},\ \tilde{\sigma }_{q}^{2-}=max_{ 1\le p\le m }\tilde{\sigma }_{pq}^{2}.\\ \end{aligned} \end{aligned}$$
(17)

In the TOPSIS method, with the ideal solutions obtained, the distance between object \(o_{p}\) and \(o^{+}\) as well as the distance between \(o_{p}\) and \(o^{-}\) can be computed. Then, the conditional probability of the object \(o_{p}\) belonging to C can be calculated based on the above distances.

Based on Eq. (3), the distance \(d_{pq}^{+}=d(\tilde{B}_{pq} ,\tilde{B}_{q}^{+})\) between \(\tilde{B}_{pq}\) and \(\tilde{B}_{q}^{+}\), and the distance \(d_{pq}^{-}=d(\tilde{B}_{pq} ,\tilde{B}_{q}^{-})\) between \(\tilde{B}_{pq}\) and \(\tilde{B}_{q}^{-}\) are calculated as follows:

$$\begin{aligned} \begin{aligned} &d_{pq}^{+}=d(\tilde{B}_{pq} ,\tilde{B}_{q}^{+})=\sqrt{(\tilde{a}_{pq}-\tilde{a}_{q}^{+})^2+\frac{1}{2} (\tilde{\sigma } _{pq}^{2} -\tilde{\sigma }_{q}^{2+})^2},\\ &d_{pq}^{-}=d(\tilde{B}_{pq} ,\tilde{B}_{q}^{-})=\sqrt{(\tilde{a}_{pq}-\tilde{a}_{q}^{-})^2+\frac{1}{2} (\tilde{\sigma } _{pq}^{2} -\tilde{\sigma }_{q}^{2-})^2}.\\ \end{aligned} \end{aligned}$$
(18)

However, the distances calculated in TOPSIS do not include the risk attitudes. In prospect theory, value functions are utilized to represent the risk attitudes toward gains and losses. Thus, we utilize the value functions of the original distances as the new distances between objects and ideal solutions.

Algorithm 1
figure a

Decision process of NFP3WD with normal fuzzy ideal solution.

Full size image

According to prospect theory, let \(o^{+}= \left\{ \tilde{B}_{1}^{+},\tilde{B}_{2}^{+},\cdots , \tilde{B}_{n}^{+} \right\} \) be the positive reference point of decision maker and \(o^{-}= \left\{ \tilde{B}_{1}^{-},\tilde{B}_{2}^{-},\cdots , \tilde{B}_{n}^{-} \right\} \) be the negative reference point of decision maker. For attribute \(g_{q}\), let \(\tilde{B}_{q}^{+}\) and \(\tilde{B}_{q}^{-}\) be the positive reference point and negative reference point, respectively. Compared to \(\tilde{B}_{q}^{+}\), \(g_{q}\) represents a loss, and people will show risk chasing toward it conversely, \(g_{q}\) represents a gain in contrast to \(\tilde{B}_{q}^{-}\), and people will show risk averse toward it.

Then, the value functions of original distance \(d_{pq}^{+}\) and \(d_{pq}^{-}\) are calculated to represent the new distances that take into account decision-maker’s risk attitude. Because all attributes in our normal fuzzy information system are positive attributes, we know that all \(\tilde{B}_{pq}\le \tilde{B}_{q}^{+}\) and all \(\tilde{B}_{pq}\ge \tilde{B}_{q}^{-}\). Thus, the value functions are computed as follows:

$$\begin{aligned} \begin{aligned} &\tilde{v}_{pq}^{+}=-\theta (d_{pq}^{+})^{\upsilon },\ \ \tilde{v}_{pq}^{-}=(d_{pq}^{-})^{\mu }, \end{aligned} \end{aligned}$$
(19)

where \(\tilde{v}_{pq}^{+}\) denotes the value function of \(d_{pq}^{+}\), and \(\tilde{v}_{pq}^{+}\le 0\); \(\tilde{v}_{pq}^{-}\) denotes the value function of \(d_{pq}^{-}\), and \(\tilde{v}_{pq}^{-}\ge 0\).

Fig. 1.
figure 1

Decision procedure of NFP3WD with normal fuzzy ideal solution.

Full size image

Since each attribute in our information system has different weights, the new distance between object \(o_{p}\) and \(o^{+}\), as well as the new distance between object \(o_{p}\) and \(o^{-}\) are calculated as follows:

$$\begin{aligned} \begin{aligned} \tilde{v}_{p}^{+}=\sum _{q=1}^{n} \omega _{q}\tilde{v}_{pq}^{+},\ \ \tilde{v}_{p}^{-}=\sum _{q=1}^{n} \omega _{q}\tilde{v}_{pq}^{-}, \end{aligned} \end{aligned}$$
(20)

where \(\tilde{v}_{p}^{+}\) denotes the new distance between object \(o_{p}\) and the positive ideal solution \(o^{+}\); \(\tilde{v}_{p}^{-}\) denotes the new distance between \(o_{p}\) and the negative ideal solution \(o^{-}\).

Since the relative closeness of \(o_{p}\) to \(o^{+}\) is a good reflection of the conditional probability [1, 6]. Thus, we compute the conditional probability by relative closeness as follows:

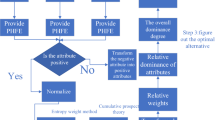
$$\begin{aligned} Pr(C|o_{p})=RC(o_{p})=\frac{\tilde{v}_{p}^{-} }{\left| \tilde{v}_{p}^{+} \right| +\tilde{v}_{p}^{-} }. \end{aligned}$$
(21)

The whole decision process of NFP3WD with normal fuzzy ideal solution is shown in Fig. 1. Algorithm 1 describes the pseudocode of our proposed methods. In Algorithm 1, the decision thresholds are calculated through steps 1 to 5, conditional probability is calculated through steps 6 to 11, and step 12 obtains the decision results.

5 Illustrative Example

In this section, we apply our proposed methods to make decisions about investment projects.

5.1 Background Description

There are six investment projects represented as \(U= \{ o_{1} \), \( o_{2} \), \( o_{3} \), \( o_{4} \), \( o_{5} \), \( o_{6} \} \). These investment projects have four attributes represented as \(AT=\{g_ {1}\), \(g_ {2}\), \(g_ {3}\), \(g_ {4} \}\), denote the “Safety”, “Efficiency” , “Marketing environment” and “Team capability” of investment projects. All four attributes are positive and their weights are \(\omega = \{ 0.1\), 0.4, 0.2, 0.3 \( \} ^{T}\). The attribute values are described by normal fuzzy numbers, the normal fuzzy information system of the six investment projects is shown in Table 5.

Table 5. Normal fuzzy information system.
Full size table

The normal fuzzy outcome matrix of investment projects is shown in Table 6. There are 10 investors denoted as \(E= \{e_{1}\), \( e_{2} \), \( e_{3} \), \( e_{4} \), \( e_{5} \), \( e_{6} \), \( e_{7} \), \( e_{8} \), \( e_{9} \), \( e_{10}\) \(\}\). Each investor has different expectations for the outcome of an investment project, which can be denoted by reference points. The normal fuzzy reference points for 10 investors are shown in Table 7.

Table 6. Normal fuzzy outcome matrix.
Full size table
Table 7. Normal fuzzy reference points.
Full size table

In this example, we need to give the actions that each investor should take for each project. Investors are usually bounded-rational when making decisions. Therefore, the above decision-making problem can be solved using our NFP3WD method and normal fuzzy ideal solution method.

5.2 Decision Processes and Decision Results

Based on steps 1 to 5 in Algorithm 1, the decision thresholds are obtained as shown in Table 8.

Table 8. Decision thresholds of NFP3WD.
Full size table
Fig. 2.
figure 2

Decision thresholds of NFP3WD

Full size image

The figure depicted in Fig. 2 illustrates the changes in decision thresholds as the reference points undergo variation, the reference point of investor increase from \(e_{1}\) to \(e_{10}\). By Fig. 2, it can be observed that variations in reference points significantly affect \(\alpha \) and \(\beta \), but have little impact on \(\gamma \). As the reference point increases, \(\alpha \) initially increases and then decreases, while \(\beta \) initially decreases and then increases. On the other hand, \(\gamma \) remains relatively stable throughout the variations in reference points.

Then, conditional probabilities of six investment projects are calculated according to steps 6 to 11 in Algorithm 1, as shown in Table 9.

Table 9. Conditional probabilities of projects.
Full size table

The decision results by step 12 of Algorithm 1 are presented in Table 10. Through Table 10, the decision results will change with the variation of normal fuzzy reference point \(\tilde{Z}_{r}=(a_{r},\sigma _{r}^{2})\). In addition, with the increase of normal fuzzy reference points, BND(C) becomes larger first and then gets smaller, while POS(C) and NEG(C) are on the contrary. This variation trend is the same as in the P3WD method [11].

Table 10. Decision results of investment projects.
Full size table

5.3 Comparative Analysis

We compare our NFP3WD method with traditional 3WD model [17] and P3WD model [11] by calculating the decision thresholds of investment projects in Sect. 5 using these three methods. The traditional 3WD model [17] makes decisions based on minimum loss, and the loss matrix is represented by crisp numbers. P3WD model [11] incorporates decision-makers risk attitudes using prospect theory, but its outcome matrix is still represented by crisp numbers rather than fuzzy numbers. The calculated decision thresholds of the three methods are shown in Fig. 3.

Fig. 3.
figure 3

Decision thresholds of three models.

Full size image

From Fig. 3, we find that the decision threshold does not change within the ten investors in traditional 3WD model. In the P3WD model, when decision-makers have the same expectation \(a_{r}\) in reference points, the corresponding values of decision thresholds do not change with the change of \(\sigma _{r}^{2}\) in the reference points. While in our NFP3WD method, the decision threshold changes with both the variations of \(a_{r}\) and \(\sigma _{r}^{2}\) in normal fuzzy reference points. These results indicate that our NFP3WD method performs better on considering decision-makers’ uncertain preferences.

In addition, our NFP3WD method can handle the continuous uncertain decision information with normal distribution. More, our normal fuzzy ideal solution method combined TOPSIS and prospect theory, which takes into account decision-makers’ risk attitudes. The comparison of our proposed method with other methods is shown in Table 11.

Table 11. The comparative analysis with other methods.
Full size table

6 Conclusion

In this paper, we present a normal fuzzy prospect theory-based three-way decision method, in which we utilize normal fuzzy numbers subjected to normal distribution to represent the continuous uncertain decision information. The other is that we design a normal fuzzy ideal solution method to estimate conditional probability in normal fuzzy information system without class label, which considers the risk attitudes of decision-makers. In the end, an illustrative example and comparative analysis verify the effectiveness and superiority of our proposed methods.