1 Introduction

Decision-making is the combination of data analysis and information fusion in order to choose an optimal decision alternative which results in desired outcomes. Data analysis is the process of transforming and modelling the raw data with the goal of discovering useful information for decision-making. Information fusion is the process of combining (or merging) the entire discovered information with the goal of providing knowledge about decision space to a decision-maker [1]. Decision-making can be either normative or descriptive; former provides rational decision as outcome, whereas, latter provides knowledge about decision space to a decision-maker. In domains like medical diagnosis, military activities, stock prediction and others, decision-makers need knowledge about the situation (decision space) which aids them in choosing an optimal decision. Knowledge-based systems like recommendation systems [2], decision support systems [3], information systems [4], expert systems [5] and many others [6] are designed and developed to aid humans in various tasks. Among them, Decision Support System (DSS) based on decision theory mainly focuses on analysing the pieces of evidence (or attribute-value pairs) with respect to decision alternatives (or class labels) to support decision-makers with comprehensive knowledge in decision-making tasks. A huge attention is given to model information uncertainty because it has a significant impact on the knowledge provided by a DSS [7]. In recent years, many theories such as fuzzy set theory [8], probability theory and its extensions [9], possibility theory [10], Z-number theory [11] and others [12], among which a few date back to 1940s, are re-explored to enhance decision-making under uncertainty. Among all these theories, Dempster Shafer (DS) Theory [13, 14], an extension of probability theory, has many advantages in modelling uncertainty and fusing information. Dempster Shafer Theory (DST), well-known as evidence theory or the theory of belief functions can be viewed as a two-step process: first, computation of the basic probabilities for pieces of evidence using Basic Probability Assignment (BPA) or mass function; and second, computation of the fusion probabilities for decision alternatives using DS Combination rule. The major advantage with DST is that it considers the powerset of decision alternatives while computing both the basic probabilities and fusion probabilities. This supports a decision-maker in attaining knowledge about all the possible combinations of decision alternatives. However, there exists some open issues in DST; first is basic probability computation, and second is conflicting evidence combination. Though numerous solutions have been proposed to resolve these open issues, there is no generalised method so far. The necessities and the possible approaches to resolve both the open issues are detailed in the following subsections.

1.1 Basic probabilities computation

The choice of a mass function plays a pivotal role in the computation of basic probabilities. A BPA matrix is formed by considering the pieces of evidence as columns and elements in the powerset of decision alternatives as rows. A mass function computes the basic probabilities for each piece of evidence with respect to each subset of decision alternatives. These probability values constitute the BPA matrix. Basic probabilities can be computed by subjective or objective methods. Subjective methods include interviews, scenario walkthroughs, and discussion sessions with domain experts, to obtain basic probabilities [15]. But domain experts may not be available all the time to share the knowledge. Moreover, deviations in the perspectives of different domain experts increases the vagueness and ambiguity in the process. By considering these drawbacks, many studies in literature focus on objective methods to obtain basic probabilities rather than subjective methods. Objective methods apply statistical analysis [16], clustering techniques [17], and fuzzy arithmetic approaches [18], on the domain relevant datasets, to obtain basic probabilities. Objective methods are preferred over subjective methods because of the convenience in fetching the information from datasets rather than obtaining subjective knowledge. Therefore, this work focuses on exploring objective methods to compute the basic probabilities.

In objective methods, a target model is developed for each attribute with respect to each subset of class labels based on the training dataset. Basic probabilities are computed for each piece of evidence in a test instance by considering the corresponding target models. In a training dataset, if the attribute-values are either categorical or discrete, then the target models are developed based on statistical methods. If the attribute-values are continuous, then different authors propose different methods, such as clustering algorithms [17], distance measures [19], fuzzy membership functions [20], and hybrid approaches [21] to generate the target models. In recent times, many authors prefer to use fuzzy set theory to generate the target model in case of continuous-valued attributes. Fuzzy sets are characterized by fuzzy membership functions; commonly used membership functions include triangular, trapezoidal, gaussian and sigmoid [22]; among these triangular membership function (trimf) is widely applied due to its feasibility and simplicity. Oftentimes the datasets consist of different types of values for different attributes. Therefore, this work considers confidence measure to develop the target model in case of categorical (discrete-valued) type attributes, and triangular fuzzy number in case of numerical (continuous-valued) type attributes. The trimf-based target model considers the minimum, mean and maximum value as the lower, intermediate and upper values of the fuzzy set characterized by a trimf.

1.2 Conflicting evidence combination

According to Zadeh’s example [23], if a piece of evidence is assigned zero as the basic probability to a decision alternative, and there exist another piece of evidence which is assigned a basic probability greater than zero to that element then the evidence is said to be conflicting [24]. This scenario is often possible in real-time because few pieces of evidence are completely unrelated to decision alternatives whereas few other pieces of evidence are more related to them. In such cases, the information fusion process considers remaining basic probabilities and assigns fusion probabilities appropriately; but when DS combination rule is applied to fuse the conflicting pieces of evidence, it provides counter-intuitive fusion probabilities. Many authors follow any of the two solutions to handle conflicting pieces of evidence; that is either modifying the combination rule, or ensuring that the basic probabilities are greater than zero. Modifying the combination rule may not be a good choice because it may lose its mathematical properties. Ensuring that the basic probabilities are greater than zero may contradict domain knowledge [25]. For example, in medical diagnosis, a symptom can be no way related to a disease and therefore its basic probability is zero. If the basic probability is updated to greater than zero, then it states that there exists a relation between the symptom and the disease. This means that updating the belief probabilities may contradict domain knowledge. Therefore, this work prefers to replace the combination rule with Multi Criteria Decision Making (MCDM) methods to assign fusion probabilities to decision alternatives [26]. The major difference between the MCDM methods and DS combination rule is that the combination rule considers the basic probabilities associated with all the supersets and subsets of a decision alternative to compute its fusion probability, whereas, MCDM methods only consider the basic probabilities associated with a decision alternative. This does not mean that the MCDM methods consider the combination classes as separate classes. Even in MCDM methods, the basic probabilities of combination classes are computed by considering the uncertain instances; the only difference lies in the computation of fusion probabilities. MCDM methods consider each attribute-value pair in a test instance as a criterion and the basic probabilities associated with them as criterion-values. The weight for each criterion is computed based on Jousselme Evidence Distance (JED). As the distance between the criteria increases, the criterion-weight decreases. Both basic probabilities and criterion-weights are considered for assigning fusion probability to each element in the powerset of decision alternatives.

1.3 Prospects evaluation

DSS developed based on the optimal MCDM method provides interpretable knowledge about the decision space along with a rational decision alternative (one with highest fusion probability) to aid decision-makers. If the rational decision does not match with the decision-makers’ expected decision alternative, then decision-makers will utilise that knowledge to choose a decision alternative according to their utilities and prospects [27]. Most of decision-makers desire to choose an optimal decision with less cognitive effort. But it is strenuous to analyse the outcomes of decision alternatives based on the fusion probabilities. Therefore, this work considers prospect theory to analyse the outcomes associated with decision alternatives.

According to prospect theory, the outcome associated with each decision alternative can be either gain or loss [28]. Different decision-makers will have different attitudes towards gains and losses associated with decision alternatives. In general, decision-makers are risk-averse towards gains and risk-seeking towards losses and more sensitive towards losses than gains. Moreover, decision-makers often exhibit irrational behaviour while making decisions. These variations in the attitudes and in the thought-process has a significant impact on the final optimal decision alternative chosen by them. Therefore, this work considers the risk attitude of a decision-maker as a reference point to compute the gain-loss value associated with decision alternatives.

The main contribution of this paper is a DSS framework which provides interpretable knowledge about decision alternatives. The key approaches used in this framework are as follows:

  • A method to compute the basic probabilities is chosen based on the type of attribute-values. Triangular fuzzy number is used for continuous-valued attributes and confidence measure is used for all remaining types of attribute-values.

  • MCDM methods to assign fusion probabilities to decision alternatives instead of evidence combination rules.

  • Prospect theory-based value function to compute the gain-loss value of each decision alternative for generating the preference order.

Remainder of this paper is organised as follows; Section 2: overview of preliminaries; Section 3: details about the proposed DSS; Section 4: rigorous experimental analysis on publicly available datasets; and Section 5: conclusion and outlook.

2 Preliminaries

This section presents the commonly used definitions and notations in evidence theory including JED, prospect theory and the triangular fuzzy model.

2.1 Evidence theory

Consider a dataset, D, with N distinct attribute-value pairs referred as pieces of evidence, and M distinct class labels referred as elements in Frame of Discernment (FoD). BPA matrix is formed by considering the pieces of evidence as rows and elements in the powerset of FoD as columns. Mass function assigns a basic probability value to each piece of evidence with respect to each element in the powerset of FoD. These values constitute the BPA matrix as shown below.

$$ \text{FoD,} {\Theta}=\{\theta_{1},\theta_{2},...,\theta_{M}\} $$
$$ \wp{({\Theta})}=\{\{\emptyset\},\{\theta_{1}\},\{\theta_{2}\},...,\{\theta_{1},\theta_{2}\},...,{\Theta}\} $$
$$ \begin{array}{@{}rcl@{}} \begin{bmatrix} BPA & \{\theta_{1}\} & \{\theta_{2}\} & {\cdots} & \{\theta_{1},\theta_{2}\} & {\cdots} & {\Theta} \\ e_{1} & P_{e_{1},\{\theta_{1}\}} & P_{e_{1},\{\theta_{2}\}} & {\cdots} & P_{e_{1},\{\theta_{1},\theta_{2}\}} & {\cdots} & P_{e_{1},{\Theta}} \\ e_{2} & P_{e_{2},\{\theta_{1}\}} & P_{e_{2},\{\theta_{2}\}} & {\cdots} & P_{e_{2},\{\theta_{1},\theta_{2}\}} &{\cdots} & P_{e_{2},{\Theta}} \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} & \vdots\\ e_{N} & P_{e_{N},\{\theta_{1}\}} & P_{e_{N},\{\theta_{2}\}} & {\cdots} & P_{e_{N},\{\theta_{1},\theta_{2}\}} & {\cdots} & P_{e_{N},{\Theta}} \end{bmatrix} \end{array} $$

This work assumes that the FoD is complete and therefore assigns zero as the basic probability to null set in the powerset of FoD. The sum of the basic probabilities \((P_{e_{i},\theta _{1}}\) to \(P_{e_{i},{\Theta }})\) associated with a piece of evidence (ei) is equal to one. The belief structure of a piece of evidence, \(m_{e_{i}}\), is formed by considering the corresponding belief probabilities and column names in the BPA matrix.

$$ m_{e_{i}}=\{\{\theta_{1}\}:P_{e_{i}\theta_{1}} ; \{\theta_{2}\}:P_{e_{i}\theta_{2}} ; ... ; \{\theta_{1},\theta_{2}\}:P_{e_{i}\{\theta_{1},\theta_{2}\}} ; .... ; {\Theta}:P_{e_{i}{\Theta}}\} $$

DST, being an extension of Bayesian probability theory, the only difference in the belief structure of a piece of evidence is that DST considers and assigns basic probabilities to all the elements in the powerset of FoD whereas Bayesian assigns to only elements in FoD [29]. Due to this extension, DST can model the uncertainty in information better than the probability theory. However, choosing an appropriate mass function to assign basic probabilities which can represent the uncertainty precisely is still an open issue. DS combination rule presented in (1) combines the belief structure of distinct pieces of evidence for assigning the fusion probabilities to each element in the powerset of FoD [13, 14].

$$ {e_{1}} \oplus {e_{2}} = f_{e(2),\theta} = \begin{cases} 0 & \text{If } \theta = \emptyset\\ \frac{1}{1-k} {\sum}_{A \cap B = \theta} P_{e_{1}A} P_{e_{2}B} & \text{If } \theta \in \wp{({\Theta})}, \theta \neq \emptyset \end{cases} $$
(1)
$$ \text{Normalisation factor, }k = \underset{A \cap B = \emptyset}{\sum} P_{e_{1}A} P_{e_{2}B} $$

In (1), fe(2),𝜃, is the fusion probability assigned to 𝜃 by combining the pieces of evidence (e1 and e2).

2.2 Jousselme evidence distance

JED is used to measure the distance between the belief structures of pieces of evidence [30]. While computing the distance, it considers the commonality among the elements in the powerset of FoD to which the basic probabilities are assigned in a belief structure.

$$ J(e_{i},e_{j})=\sqrt{\frac{1}{2}(m_{e_{i}}-m_{e_{j}})D(m_{e_{i}}-m_{e_{j}})^{T}} $$
(2)

In (2), \(m_{e_{i}}\) and \(m_{e_{j}}\) are the two belief structures associated with ei and ej respectively. D is a Jaccard similarity matrix formed by considering the elements in the powerset of FoD as rows and columns. Each element, \(D(A_{i},A_{j})=\frac {|A_{i} \cap A_{j}|}{|A_{i} \cup A_{j}|}\). The coefficient, \(\frac {1}{2}\) is used to normalise and to ensure that the distance ranges from zero to one. The success of the JED lies in D.

2.3 Prospect theory

Daniel Kahneman and Amos Tversky proposed prospect theory in 1979 to describe the thought process of humans while choosing among decision alternatives based on the corresponding fusion probabilities [28]. Prospect theory states that the decision-makers choose decision alternatives based on their attitude towards gains and losses rather than the fusion probabilities. It models these features and characteristics by considering the value function and weight function. The former considers the difference between the decision alternative’s fusion probability and reference point, and the latter considers decision-weights to over weight the lower fusion probabilities and under weight the high and moderate fusion probabilities. The value function determines whether choosing an alternative is a gain or a loss. The reference point, which ranges from zero to one, is directly provided by decision-makers and it reflects their attitude towards gains and losses. It is subjected to change depending on the decision-maker’s expectations and attitudes. An asymmetric S-shaped curve as shown in Fig. 1 represents the value function.

$$ v({a_{i}})= \begin{cases} ({\Delta} a_{i})^{\alpha} & \text{If } {\Delta} a_{i} \geq 0 \\ - \beta ({\Delta} a_{i})^ \gamma & \text{If } {\Delta} a_{i} < 0 \end{cases} $$
(3)
Fig. 1
figure 1

Value function from prospect theory

Full size image

In (3), ai is the decision alternative, zi is the fusion probability of ai, zr is the reference point provided by a decision-maker, and Δai = zi − zr. Δai ≥ 0 can be viewed as a gain whereas Δai < 0 can be viewed as a loss. The parameters α and γ are considered as the risk-attitude coefficients. The parameter, β reflects the sensitivity of decision-maker towards gains or losses. Both α and γ ranges from zero to one whereas β is always greater than one. Authors like Abdellaoui et al. [31], Bleichrodt et al. [32], Booij et al. [33], Tversky et al. [34], Wakker et al. [35], Wang et al. [36] and others [37] have conducted various physiological experiments and determined the values for α,β and γ. In this work, we consider α = 0.89,β = 2.29, and γ = 0.92 as suggested by Tversky and Kahneman [34] and used by Wang et al. [36] in his works.

2.4 Triangular fuzzy model

Zadeh proposed the fuzzy set theory in 1965 as an extension of traditional set theory to handle the uncertainty in information [23]. Each linguistic variable has fuzzy sets that are characterized by membership functions. The membership function associates each element of the variable with a value in the interval, [0,1]. In this work, each linguistic variable (attribute), X, is associated with M fuzzy sets, where M is the number of elements in FoD (classes in D). The fuzzy sets are characterised using triangular membership function as shown in Fig. 2.

Fig. 2
figure 2

Triangular fuzzy membership function (trimf)

Full size image

In Fig. 2, x is the value associated with attribute ai, and class label cj, in dataset D. The lower bound (trimf.a) is the minimum possible value that ai can take with respect to cj, whereas the upper bound (trimf.c) is the maximum possible value that ai can take with respect to cj, and the intermediate value (trimf.b) is the average of all the possible values that ai can take with respect to cj. The fuzzy membership value for each attribute-value pair (piece of evidence), μ(x) or μ(ei), is computed using (4). It represents the degree to which the attribute is supporting to a class.

$$ \mu(x)=\begin{cases} 0 & \text{If } x<a \\ \frac{x-a}{b-a} & \text{If } a \leq x \leq b \\ \frac{c-x}{c-b} & \text{If } b < x \leq c \\ 0 & \text{If } x>c \\ \end{cases} $$
(4)

In (4), x represents the attribute-value which needs to be fuzzified. The parameters, trimf.a,trimf.b, and trimf.c are the lower bound, intermediate value, and upper bound of x respectively.

2.5 Related works

This subsection presents an overview of the recent works in decision-making, evidence theory, and prospect theory. A decision-making model consists of four methods, namely, basic probabilities computation, evidence-weight computation, evidence combination, and gain-loss analysis. Basic probability computation considers target models to assign values to pieces of evidence, evidence-weight computation considers either uncertainty measure or distance measure to assign weight to evidence, evidence combination considers combinational operator to assign fusion probabilities to decision alternatives, and finally, gain-loss analysis considers value function to decide whether choosing an alternative is a gain or a loss to a decision-maker. Table 1 presents the summary of recent works in decision- making.

Table 1 Summary of recent works in decision-making
Full size table

Based on the information provided in Table 1, there is no framework in literature which applies MCDM methods instead of evidence combination rules to rank the alternatives. Therefore, this work proposes a decision-making framework which applies MCDM methods to combine the basic probabilities and weights of evidence for ranking alternatives. Moreover, the proposed framework includes prospect theory to analyse the gains and losses associated with the ranking order provided by an optimal MCDM method.

3 Proposed method

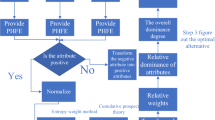
This section focuses on the framework of the proposed DSS presented in Fig. 3. Consider a dataset, D, with x samples, n attributes, and m distinct classes. p% of x in D are considered as training samples and the remaining (1 − p)% of x are testing samples. Each training sample is the combination of attribute-value pairs and a class label, whereas, each testing sample consists of only attribute-value pairs.

Fig. 3
figure 3

Framework of the proposed DSS

Full size image

The proposed DSS can be viewed as a five-step process; first, generating the target models based on the training samples, second, assigning basic probabilities to each attribute-value pair in a test instance, third, computing weights for each piece of evidence or criterion, fourth, computing fusion probabilities for each subset of decision alternatives based on the MCDM methods, and finally analysing the gains and losses associated with each decision alternative with reference to decision-maker’s attitude towards risk in decision-making. The goal of the proposed DSS is to provide descriptive knowledge about decision space along with rational decision.

3.1 Generation of target models

A target model matrix is formed by considering the distinct attributes as columns and elements in the powerset of class labels as rows. Each cell in target model matrix consists of a target model which is developed for the corresponding attribute in a column and subset of classes in a row. Each attribute in training dataset can have either categorical (nominal and ordinal) or numeric values (discrete and continuous). If the attribute-values are either categorical or discrete, then each unique attribute-value pair is considered to generate the target models, whereas, if the attribute-values are continuous, then its range is considered. For example, consider a dataset consists of ‘Gender’ as one of the attributes. In general, ‘Gender’ attribute will be discrete in nature with ‘Male’ and ‘Female’ as attribute-values. If the statistical methods are applied on the ‘Gender’ attribute then the target model for ‘Gender=Male’ is p whereas the target model for ‘Gender=Female’ is 1 − p where p is the probability. When the test instance arrives with ‘Gender’ as one of the piece of evidence, then the probability, p or 1 − p is directly considered as the basic probability depending on the value associated with that piece of evidence. Assume that the triangular fuzzy model which best suits for continuous-values attributes is chosen as a mass function to develop the target model for categorical and discrete-valued attributes. For convenience, ‘Male’ is noted as ‘0’ and ‘Female’ is noted as ‘1’. The target model for an attribute which is developed based on the triangular fuzzy number consists of minimum, intermediate, and maximum values. Intermediate value in the target model of an attribute is the mean of all the values associated with that attribute. If the triangular fuzzy number is applied on the ‘Gender’ attribute, then the target model will have (0,x,1) as minimum, intermediate and maximum values respectively. When a testing sample arrives with ‘Gender’ is equal to ‘0’, then it is equal to minimum value and results in zero as the basic probability, whereas, if the ‘Gender’ is equal to ‘1’ then it is equal to maximum value and results in zero as the basic probability. Therefore, when a triangular fuzzy model is applied on categorical attributes like ‘Gender’, the basic probability will be always equal to zero. While combining all the pieces of evidence, the piece of evidence with zero as the basic probability does not contribute to the fusion probabilities associated with decision alternatives. Though, the ‘Gender’ attribute is providing some information, applying an incorrect target model is causing the information loss. Hence, the target models must be developed appropriately so that they do not lead to information loss.

In order to overcome the difficulty with generating the appropriate target models, this work chooses the method to develop target models based on the type of the attribute-values. In case of either categorical or discrete-valued attributes, confidence measure is applied, whereas in case of continuous-valued attributes, triangular fuzzy number is applied to generate the target models. Algorithm 1 presents the development of target models for both categorical and numerical type of attributes.

figure c

3.2 Assignment of basic probabilities

The target models for all the attributes with respect to each subset of classes are developed based on training samples in Section 3.1. Algorithm 2 presents the computation of basic probabilities from corresponding target models. Each attribute-value pair in a test instance will have corresponding row of target models in target model matrix. An attribute is unavailable in target model matrix only when there is no such attribute in entire training samples. But, this is a rare case because both the training and testing samples are split from same dataset and therefore contains same number of attributes. If the attribute is unavailable in target model matrix, then this work temporarily ignores that attribute-value pair and considers the next attribute-value pair in a test instance. If the attribute is available in target model matrix, then basic probabilities are computed with respect to each subset of classes by considering the corresponding target models. Target models are developed either by using triangular fuzzy model or by using confidence measure. If the target model is developed based on the triangular fuzzy number then the basic probabilities are computed using (4). If the target model is developed based on the confidence measure, the confidence value corresponding to the attribute-value is directly chosen as the basic probability. Likewise, basic probabilities are computed for each attribute-value pair in a test instance with respect to each element in the powerset of class labels. The basic probabilities associated with each attribute are normalised so that their sum is equal to one.

figure d

3.3 Computation of criterion-weight

A standard which provides a basis or information to decide among alternatives is known as criterion. This work considers each attribute-value pair as a criterion instead of considering generic criteria like risk, reliability, cost and others. Attribute-value pairs can be considered as criteria because the basic probabilities associated them provide information to decide among alternatives. The criterion-weight is computed based on the distance from remaining criteria. As the distance between the criteria increases, criterion-weight decreases. For example, if two pieces of evidence are in favour of two distinct decision alternatives then the distance between them increases. Since, both the pieces of evidence are in favour of different decision alternatives, they are not providing any information for choosing one among those alternatives. Hence, their criterion-weight decreases. This work considers JED measure to compute the distance among criteria. The advantage with JED is that it considers the commonality between the subsets of decision alternatives along with basic probability to compute the distance. Since, the powerset of decision alternatives are considered while computing the basic probabilities, Jousselme is the preferable distance measure.

$$ \begin{array}{@{}rcl@{}} \begin{bmatrix} Weight Matrix & e_{1} & e_{2} & {\cdots} & e_{n} \\ e_{1} & 0 & 1-J(e_{1},e_{2}) & {\cdots} & 1-J(e_{1},e_{n}) \\ e_{2} & 1-J(e_{1},e_{2}) & 0 & {\cdots} & 1-J(e_{2},e_{n}) \\ {\vdots} & {\vdots} & {\vdots} & {\vdots} & \vdots\\ e_{n} & 1-J(e_{n},e_{1}) & 1-J(e_{n},e_{2}) & {\cdots} & 0 \end{bmatrix} \end{array} $$

where, J(ei,ej) is the jousselme distance between ei and ej. Each element is subtracted from one because the criterion-weight which is computed using (5) decreases with increase in the distance.

$$ \text{Criterion-weight}(Cw_{e_{i}})= \underset{j \in n /e_{i}}{\sum} (1-J(e_{i},e_{j})) \text{ if } e_{i} \neq e_{j} $$
(5)

3.4 Multi-criteria decision-making

This work experiments on various MCDM methods like Simple Additive Weighting (SAW), Multiplicative Exponential Weighting (MEW), Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), modified TOPSIS (mTOPSIS), Weighted Sum Method (WSM), VIKOR, and Preference Ranking Organisation Method for Enriching Evaluation (PROMETHEE-V) to choose an optimal method which results in intuitive fusion probabilities [26]. These MCDM methods rank the decision alternatives based on the fusion probabilities. Distinct MCDM methods compute fusion probabilities in distinct ways.

  1. 1.

    SAW: The fusion probability of each alternative is the sum of the weighted basic probabilities of pieces of evidence.

    $$ \text{Fusion probability }z_{j}=\sum\limits_{i=1}^{n} Cw_{e_{i}}BPA_{e_{i},c_{j}} $$
  2. 2.

    MEW: The fusion probability of each alternative is the exponential sum of the weighted basic probabilities of pieces of evidence.

    $$ z_{j}=\prod\limits_{i=1}^{n} BPA_{e_{i},c_{j}}^{Cw_{e_{i}}} $$
  3. 3.

    TOPSIS: The fusion probability of each alternative is computed based on positive ideal solution (j+) and negative ideal solution (j−).

    $$ z_{j}= \frac{(S_{j})^{-}}{(S_{j})^{+}+(S_{j})^{-}} $$
    $$ (S_{j})^{+}=\sqrt{\sum\limits_{i=1}^{n} (N_{ij}-j^{+})^{2}} \text{ ; } (S_{j})^{-}=\sqrt{\sum\limits_{i=1}^{n} (N_{ij}-j^{-})^{2}} $$

    where \(N_{ij}=BPA_{e_{i},c_{j}}Cw_{e_{i}}\).

  4. 4.

    modified TOPSIS: Fusion probabilities are computed similar to TOPSIS. But, the computation of (Sj)+ and (Sj)− are different.

    $$ z_{j}= \frac{(S_{j})^{-}}{(S_{j})^{+}+(S_{j})^{-}} $$
    $$ (S_{j})^{+}=\sqrt{\sum\limits_{i=1}^{n} Cw_{e_{i}}(d_{e_{i},c_{j}}^{+})^{2}} \text{ ; } (S_{j})^{-}=\sqrt{\sum\limits_{i=1}^{n} Cw_{e_{i}}(d_{e_{i},c_{j}}^{-})^{2}} $$

    where, \(d_{e_{i},c_{j}}^{+}=j^{+}-BPA_{e_{i},c_{j}}\) and \(d_{e_{i},c_{j}}^{-}=BPA_{e_{i},c_{j}}-j^{-}\)

  5. 5.

    WSM: Fusion probability of each alternative is maximum among the weighted sum of basic probabilities.

    $$ z_{j}=\max {\sum}_{i=1}^{n} Cw_{e_{i}}BPA_{e_{i},c_{j}} $$
  6. 6.

    VIKOR: Fusion probability of an alternative is computed based on ideal solutions (i+,i−) and distance measures.

    $$ z_{j}=v \frac{S_{j}-S^{+}}{S^{-}-S^{+}}+(1-v)\frac{R_{j}-R^{+}}{R^{-}-R^{+}} $$
    $$ S_{j}= \sum\limits_{i=1}^{n} \frac{Cw_{e_{i}}(i^{+}-BPA_{e_{i},c_{j}})}{i^{+}-i^{-}} $$
    $$ R_{j}= \max_{i} \frac{Cw_{e_{i}}(i^{+}-BPA_{e_{i},c_{j}})}{i^{+}-i^{-}} $$

    where v is the user-defined value, S+,S− and R+,R− are the best, worst solutions computed using Manhattan distance and Chebyshev distance respectively.

  7. 7.

    PROMETHEE-V: This method focuses on pair-wise comparison of alternatives to find the best suitable alternative rather than computing fusion probabilities. The proposed system considers V-shape as the preference function to rank the alternatives. The in-depth mathematical details about preference functions in PROMETHEE can be found in [26].

The decision alternative with high fusion probability is considered as the highest rank whereas the decision alternative with least fusion probability is considered as the lowest rank. The optimal MCDM method is chosen based on the accuracy and intuitiveness of fusion probabilities. Fusion probabilities are said to be intuitive when they support decision-maker in attaining gains.

3.5 Computation of prospects

The proposed DSS which is developed based on the MCDM method is capable enough to provide rational decision alternative and the interpretable knowledge about decision space to aid decision-makers in decision-making tasks. However, it may be difficult to a decision-maker to analyse the outcomes associated with decision alternatives based on the fusion probabilities. Therefore, this work considers value function from prospect theory to compute the gains and losses associated with decision alternatives. These gains and losses along with fusion probabilities aid decision-maker in choosing an optimal decision alternative. No two decision-makers will have same attitude towards risk associated with gains or losses. The value function from prospect theory considers the attitude of a decision-maker as a reference point. The degree of deviation is measured by computing the difference between the reference point and the fusion probability. This deviation decides whether the decision-maker will get gain or loss by choosing the corresponding decision alternative. If the difference is greater than zero, then the decision-maker will gain by choosing the corresponding decision alternative. If the difference is less than zero, then the decision-maker incur a loss by choosing the corresponding decision alternative. The difference is substituted in the value function to compute the gain or loss value. These gain or loss values of all the decision alternatives are provided to a decision-maker as an additional knowledge. Algorithm 3 presents the computation of gains and losses from fusion probabilities. Most of the existing works consider the decision-making scenario as a classification problem [49]. Classification is the process of learning patterns from training samples in order to predict the category of a query sample. These classification algorithms come under normative decision-making where the focus is on providing a rational prediction with less, or sometimes even without any information related to other decision alternatives. However, decision-makers in domains like healthcare needs reasoning and knowledge about decision alternatives in terms of fusion probabilities and gain-loss values as outcomes rather than meagre prediction for optimal decision-making. Therefore the proposed DSS follows descriptive decision-making where the focus is on generating the preference order of decision alternatives with appropriate reasoning. The following section presents a series of experiments on ten datasets from University of California, Irvine (UCI) repository [51] to analyse the outcomes of the proposed DSS which is developed based on the descriptive decision-making model.

figure e

4 Experimental methods and observations

The proposed DSS considers each attribute-value pair in a test instance as criterion to generate the preference order of decision alternatives. MCDM methods like SAW, MEW, TOPSIS, mTOPSIS, WSM, VIKOR, and PROMETHEE-V are applied to analyse each possible combination of decision alternatives with respect to each criterion. As a result, MCDM methods assign fusion probabilities for decision alternatives to generate the preference order. Each decision-maker will have distinct attitudes towards risk involved in decision-making. These variations in the attitudes would have a significant impact on the preference order. The prospect theory based value function computes the losses and gains associated with each decision alternative. The preference order is re-arranged based on the gains and losses associated with decision alternatives. DSS is developed using the following tools and packages: Python and RStudio are used to perform experiments on datasets and to visualize the results. NumPy and Pandas libraries in python are used to perform the logical and mathematical operations on datasets. FuzzyNumbers package in RStudio is used to stimulate the triangular fuzzy membership functions. MCDM and pymcdm packages in python are used to implement the MCDM methods. Sklearn and Matplotlib packages in python are used to compute the evaluation metrics and to plot the ROC curves.

4.1 Results and analysis

This section focuses on presenting a series of experiments on both life sciences (medical) and miscellaneous datasets from the UCI repository to evaluate the performance of proposed DSS. Table 2 presents the overview of UCI datasets that are considered in this work. 80% of the samples in a dataset are considered for generating the target models, and the remaining 20% of samples for evaluating the MCDM methods.

Table 2 Overview of the UCI datasets
Full size table

Since the focus of this work is more on medical decision-making, each subsection details the efficiency and rationality of the proposed DSS on each of the medical datasets.

4.1.1 Diabetes dataset

The diabetes dataset consists of two classes and eight attributes [52]. Each attribute has a different range of continuous values. Figure 4 presents the triangular fuzzy target models for all the attributes in diabetes dataset. Consider a test instance which belongs to class_0 for decision-making. Basic probabilities for each piece of evidence in a test instance are computed based on the corresponding target models. Table 3 presents the basic probabilities for each piece of evidence in a test instance. The weight of each piece of evidence is computed based on JED. The list of MCDM methods which are detailed in Section 3.4 are applied on the basic probabilities along with corresponding weights to assign a fusion probability to each element in the powerset of decision alternatives. Other than the modified TOPSIS method, the remaining methods such as SAW, MEW, TOPSIS, WSM, VIKOR, and PROMETHEE-V assign first rank to class_0 for a test instance with 0.3379, 0.3367, 0.5028, 0.5023, 0.5, and 0.0589 as fusion probabilities respectively.

Fig. 4
figure 4

Fuzzy target models for continuous-valued attributes in diabetes dataset

Full size image
Table 3 Basic probabilities for a test instance in diabetes dataset
Full size table

If the decision-maker intends to know the gains and losses associated with fusion probabilities, then the reference point has to be provided. There can be three possibilities for a reference point, i.e., less than 0.5, 0.5, and greater than 0.5 based on the risk attitude of a decision-maker. If the decision-maker is not willing to provide a reference point then this work considers 0.25, 0.5, 0.75 as three reference points and computes the gains and losses. Table 4 presents the gains and losses of fusion probabilities assigned to class_0 by various MCDM methods. Consider x to be a reference point; deviation between the fusion probabilities and x increases with increase in x. If the deviation is positive, then the decision-maker will gain by choosing the corresponding decision alternative, whereas, if the deviation is negative, then the decision-maker will incur loss by choosing the decision alternative. In general, decision-makers are more sensitive towards losses than gains. Therefore, no-gain is more preferred than the minimal amount of loss. Since, most of the fusion probabilities in Table 4 are less than 0.6, either 0.25 or 0.5 is the preferred reference point. Choosing the reference point greater than the fusion probability results in a loss. For a test instance from this dataset, VIKOR method assigns high gain value, i.e., 0.2911 with respect to 0.25 as the reference point compared to other MCDM methods.

Table 4 Prospect values for a test instance in diabetes dataset
Full size table

Figure 5 presents the fusion probabilities by MCDM methods such as SAW, MEW, TOPSIS, and VIKOR for all the test instances. From Fig. 5, it can be observed that the VIKOR method and TOPSIS method provide high fusion probabilities compared to other MCDM methods. Assigning high fusion probability to a test instance increases the confidence in decision-maker while choosing the decision alternative. Moreover, increase in the fusion probability increases the gain value of a decision alternative.

Fig. 5
figure 5

Fusion probabilities by MCDM methods for diabetes dataset

Full size image

4.1.2 Liver disorders dataset

The liver disorders dataset consists of two classes and ten attributes. Among the ten attributes, a2 is the only discrete-valued attribute. Remaining nine attributes has different range of continuous values. Figure 6 presents the triangular fuzzy target models for the nine continuous-valued attributes in liver disorders dataset. Confidence measure is applied on a2 to generate the target models with respect to elements in the powerset of decision alternatives.

Fig. 6
figure 6

Fuzzy target models for continuous-valued attributes in liver disorders dataset

Full size image

Consider a test instance which belongs to class_1 for decision-making based on the MCDM methods. Table 5 presents the basic probabilities for each piece of evidence in a test instance which are computed by considering the corresponding target models.

Table 5 Basic probabilities for a test instance in liver disorders dataset
Full size table

The weight of each piece of evidence in Table 5 is computed based on the JED. MCDM methods listed in Section 3.4 are applied on the basic probabilities and the weights of pieces of evidence to assign fusion probabilities for elements in the powerset of decision alternatives. None of the MCDM methods assign high fusion probability to class_1 other than VIKOR method. Hence VIKOR assigns first rank to class_1 for a test instance with 0.5652 as the fusion probability. Since the fusion probability is greater than 0.5, the reference point which is less than or equal to 0.5 results in gain to a decision-maker. Decrease in the reference point increases the deviation which in turn increases the gain value. Figure 7 presents the fusion probabilities assigned by MCDM methods to all test instances. It can be observed from Fig. 7 that both VIKOR and TOPSIS methods assign high fusion probabilities to testing instances compared to SAW and MEW.

Fig. 7
figure 7

Fusion probabilities by MCDM methods for liver disorders dataset

Full size image

4.1.3 Cleveland-heart disease dataset

The C-heart disease dataset consists of two classes and thirteen attributes. Among 13 attributes, a2, a3, a6, a7, a9, a11, a12, and a13 are discrete-valued whereas the remaining five (a1, a4, a5, a8, and a10) are continuous-valued attributes. Since the dataset is a mixture of discrete and continuous-valued attributes, the target models are developed based on the confidence measure and the triangular fuzzy method respectively. Figure 8 presents the target models for each continuous-valued attribute with respect to each subset of classes.

Fig. 8
figure 8

Fuzzy target models for continuous-valued attributes in C-heart disease dataset

Full size image

Consider a test instance which belongs to class_0 for decision-making based on the MCDM methods. Table 6 presents the basic probabilities for each piece of evidence in a test instance. All the seven MCDM methods such as SAW, MEW, TOPSIS, mTOPSIS, WSM, VIKOR, and PROMETHEE-V assign 0.5177, 0.4802, 0.8001, 0.7946, 0.7904, 1, and 0.5561 as fusion probabilities to class_0 for a test instance respectively. Therefore, all MCDM methods assign first rank to class_0 for a test instance. If the VIKOR method is chosen as optimal, then the decision-maker will get gain irrespective of the reference point. Even in case of TOPSIS and WSM methods, decision-maker will get gain for reference point equal to less that 0.75. Figure 9 presents the fusion probabilities assigned by distinct MCDM methods for testing samples. VIKOR method assigns a fusion probability equal to 1 to almost all test instances of class_1. However, it assigns minimal fusion probabilities to test instances of class_0. Though TOPSIS method has not assigned high fusion probabilities like VIKOR, it almost assigns considerable fusion probabilities to all the testing instances.

Table 6 Basic probabilities for a test instance in C-heart disease dataset
Full size table
Fig. 9
figure 9

Fusion probabilities by MCDM methods for C-heart disease dataset

Full size image

4.1.4 Hepatitis dataset

The hepatitis dataset consists of two classes and nineteen attributes. Among 19 attributes, a2 to a13, and a19 are discrete-valued whereas the remaining six (a1, a14, a15, a16, a17 and a18) are continuous-valued attributes. Figure 10 presents the target models for continuous-valued attributes with respect to each subset of classes. Consider a test instance which belongs to class_0 for decision-making. Table 7 presents the basic probabilities for each piece of evidence in a test instance.

Fig. 10
figure 10

Fuzzy target models for continuous-valued attributes in hepatitis dataset

Full size image
Table 7 Basic probabilities for a test instance in hepatitis dataset
Full size table

The MCDM methods such as SAW, MEW, TOPSIS, mTOPSIS, WSM, VIKOR, and PROMETHEE-V assign 0.6358, 0.5941, 0.8885, 0.8738, 0.9434, 1, and 0.7467 as fusion probabilities to class_0 for a test instance respectively. Hence, all the MCDM methods identify the decision alternative for a test instance correctly.

Decision-maker will get gain by considering the fusion probability of VIKOR method irrespective of the reference point value. Assume that the decision-maker is providing 0.75 as the reference point; decision-maker will get gain for the fusion probabilities provided by MEW, TOPSIS, mTOPSIS, WSM, and VIKOR methods. If the reference point is equal to or less than 0.5, decision-maker will get gain for any of the MCDM methods. Figure 11 presents the fusion probabilities assigned by MCDM method to all the testing samples which belong to class_0. Due to class imbalance, there are only four testing samples which belong to class_1 in hepatitis dataset. Only MEW method predicts three out of four testing samples of class_1 correctly.

Fig. 11
figure 11

Fusion probabilities by MCDM methods for hepatitis dataset

Full size image

4.1.5 Wisconsin-breast cancer dataset

The Wisconsin-breast cancer dataset consists of two classes and thirty attributes. Each attribute has a different range of continuous values. Consider a test instance which belongs to class_1 for decision-making. Target models are developed for continuous-valued attributes based on the triangular fuzzy method. Table 8 presents the basic probabilities for each piece of evidence in a test instance. MCDM methods are applied on the basic probabilities and the weights of pieces of evidence to assign fusion probabilities to elements in the powerset of decision alternatives. MCDM methods such as SAW, TOPSIS, mTOPSIS, VIKOR and PROMETHEE-V, other than MEW and WSM, assign first rank to class_1 for a test instance. Figure 12 presents the fusion probabilities assigned by MCDM methods to all the testing samples. Though, VIKOR assigns fusion probability equal to 1 to most of the samples in class_1, it assigns low fusion probabilities to few testing samples which belong to class_1. Comparatively, TOPSIS provides intuitive fusion probabilities for all the test instances.

Table 8 Basic probabilities for a test instance in W-breast cancer dataset
Full size table
Fig. 12
figure 12

Fusion probabilities by MCDM methods for W-breast cancer dataset

Full size image

4.1.6 Miscellaneous benchmark datasets

Though the focus is on medical decision-making, this work considers five miscellaneous datasets to evaluate the performance of proposed DSS. Figure 13 presents the fusion probabilities assigned by MCDM methods to the corresponding class labels. It can be observed from Fig. 13 that both TOPSIS and VIKOR methods assign high fusion probabilities compared to SAW and MEW. If the fusion probability of a test instance is greater than the reference point, then the decision-maker will get gain in choosing the corresponding decision alternative. In case, if the decision-maker is ideal towards risk in decision-making, then 0.5 is considered as the reference point. In most of the cases, TOPSIS and VIKOR assign a fusion probability greater than 0.5 which gives gain to a decision- maker.

Fig. 13
figure 13

Fusion probabilities by MCDM methods for non-medical dataset

Full size image

4.2 Observations and findings

DSS developed based on the MCDM methods provide both rational decision alternative and knowledge about decision space to aid the decision-maker in decision-making. The subset with high fusion probability is considered as a rational decision. Rational decisions are compared with actual decisions to evaluate the performance of MCDM methods. This section focuses on observing and analysing the performance of MCDM methods on testing instances to find the optimal MCDM method.

Table 9 presents the accuracy of MCDM methods on testing instances. It is quite difficult to choose an optimal MCDM method from Table 9 because few methods achieve high accuracy for few datasets whereas few other methods for remaining datasets. Tables 10 and 11 presents the accuracy of individual classes in testing instances. This work considers the combination of both the classes just to represent uncertainty in the attribute-values in terms of basic probabilities.

Table 9 Accuracy of MCDM methods on UCI datasets
Full size table
Table 10 Accuracy of MCDM methods on class_0
Full size table
Table 11 Accuracy of MCDM methods on class_1
Full size table

Among all the MCDM methods, TOPSIS achieves high accuracy for most of the datasets compared to VIKOR and PROMETHEE-V in Tables 10 and 11. Table 12 presents the area under curve values, and Fig. 14 presents the corresponding receiver operating characteristic curves.

Table 12 AUC values of MCDM methods on UCI datasets
Full size table
Fig. 14
figure 14

ROC plots for MCDM methods on UCI datasets

Full size image

The fusion probabilities assigned by the MCDM methods are also considered along with accuracy and AUC values to evaluate the performance of proposed DSS. Though VIKOR method assigns high fusion probabilities compared to TOPSIS method for most of the datasets, TOPSIS maintains the consistency in assigning the fusion probabilities. By considering both the interpretability of MCDM methods in terms of basic probabilities, evidence weights and fusion probability, and performance of the MCDM methods in terms of accuracy and ROC curves, it can be concluded that the TOPSIS is the optimal method for decision-making.

4.3 Comparative analysis

In this section, performance of the chosen optimal method, TOPSIS, is compared with seven state-of-art classifiers like nearest mean classifier (NMC) [53], k-nearest neighbours (k NN) [54], support vector machine (SVM) [55], SVM with radial basis kernel (SVMRBF) [55], decision tree (DT) [56], Naïve Bayes (NB) [57], multilayer perceptron (MLP) [58], and four different combination methods based on DST like k NN-DST [59], normal distribution based classifier (NDBC) [60], evidential calibration (Evi-Calib) [61], and weighted fuzzy Dempster–Shafer framework (WFDSF) [62]. Table 13 presents the accuracies of various methods along with proposed method on five UCI datasets. It can be inferred from Table 13 that the proposed method achieves accuracy of above average for four among five datasets. Though the accuracy of proposed method on C-heart disease dataset is below average, it is capable enough to predict most of the class_1 testing instances which can be inferred from Table 11. The overall accuracy of C-heart disease dataset is not as high as desired because of uncertainty in the testing instances of class_0.

Table 13 Comparison of accuracies over five UCI datasets
Full size table

When there is uncertainty in attribute-values, there will be no significant difference among the basic probabilities associated with different classes. This leads to assigning almost equal fusion probabilities to distinct classes. Though the class with high fusion probability is considered for computing accuracy, the fusion probabilities associated with all the elements in the powerset of class labels are given to a decision-maker. The choice of a final decision alternative which results in desired outcomes depends on the decision-maker’s attitude towards risk and uncertainty. The ranking order of alternatives is subjecting to change depending on the reference point provided by a decision-maker. The change in the ranking order may increase or decrease the accuracy of the model. Therefore, the superiority of the proposed decision-making framework lies in its capability of providing fully interpretable knowledge to a decision-maker in terms of fusion probabilities, attribute-weights, loss-gain values of possible alternatives and their combinations. Providing knowledge instead of a rational decision alternative gives choice to a decision-maker for deciding an optimal alternative.

4.4 Practical implications

When a system is developed, measuring its performance and comparing it with existing approaches are mandatory, but achieving good results on publicly available datasets alone is not sufficient for its adoption in practice. Thus, this subsection presents detail analysis on the implications which needs to be considered when the proposed interpretable system is used for providing support in real-time decision-making scenarios.

In domains like healthcare, a sequence of actions is performed manually for making a diagnostic decision. Though the proposed system aids the decision-makers involved in diagnosis with interpretable knowledge and evidential reasoning, decision-experts are partially not in favour of adopting support systems in clinical practice due to following implications:

Information quality: The proposed interpretable system needs historical data to compute the basic probability of a decision alternative with respect to each piece of evidence. In case of real-time scenarios, the data may be unclean, inconsistent, ambiguous and noisy. Basic probabilities which are computed based on the information extracted from such data may not be appropriate. Gathering huge volumes of clean, subject-oriented and relevant data may improve the basic probabilities, but it is not always feasible. Though the proposed system is capable enough to compute basic probabilities with partial information, the system’s outcomes may not be reliable for critical instances.

System capability: Once the proposed interpretable system is developed based on the past data, it should be able to refine the basic probabilities of alternatives based on current information too. In some cases, information keeps evolving and may have new additional features. Since the proposed system is maintaining the basic probability assignment matrix, the new features are considered as new columns and the corresponding probabilities are computed. But considering all the new features without background analysis may significantly impact on the complexity, reliability, and the clinical relevance of the system.

Domain Relevance: When a new query is given to the proposed system, the probability of each alternative with respect to each piece of evidence, weight of evidence, fusion probability of alternatives, and prospect of each alternative for three reference points are provided to a decision-maker as knowledge about the decision space. In case, if the decision-maker (user) is not convinced with the provided knowledge, then he can provide reference for prospects, and weights for evidence to modify the outcomes. But providing subjective reference-values and weight-values may be difficult for a decision-maker.

Knowledge Representation: Different decision-maker will follow different procedures to make an optimal decision. The proposed system aids decision-makers with knowledge about decision alternatives; but if the system is not able to customise the knowledge according to the decision-maker’s cognition, then decision-maker may not be benefited. Along with outcome-customisation, it is desirable that the system is socio-technical for an enhanced user-experience.

User satisfaction: Decision-making model’s interpretability increases decision-makers’ trust on the system. But, if the decision-maker is not able to choose an optimal decision with the support of system’s knowledge, then he may not be willing to use the system further. This may create an aversion in medical-experts from using decision support systems.

Though there are many more practical implications with the usage of DSS, it is beyond the scope of this work to explore the exhaustive list of all practical implications. Interested readers can refer to [64, 65].

5 Conclusion

This work presents a framework for developing a decision support system which provides interpretable knowledge along with rational decision to aid decision-makers in decision-making tasks. The two open issues: basic probabilities computation, and conflicting evidence combination are addressed by choosing a mass function based on the data type of attribute-values, and replacing the evidence combination rule with MCDM methods respectively. Though the combination of class labels do not appear explicitly in data, it needs to be considered as it plays an essential role in modelling uncertainty, and assigning basic probabilities. None of the MCDM methods assign a high rank to combination class for any test instance because of minimal basic probabilities compared to individual classes. A series of experiments on UCI classification datasets are conducted to choose an optimal MCDM method based on results of performance metrics, and intuitiveness of fusion probabilities. Among seven distinct MCDM methods, TOPSIS is chosen as an optimal MCDM method and it is incorporated as a descriptive decision-making model in the proposed DSS. Basic probabilities of pieces of evidence along with their weights, and fusion probabilities of subsets of decision alternatives along with gains and losses are provided to a decision-maker as an interpretable knowledge about decision space. The ranking order of decision alternatives are subject to change depending on the decision-maker’s attitude towards risk. But, sometimes decision-makers may not be confident enough to provide, or may not be willing to reveal their risk attitude. Computing reference point in such scenarios may be challenging. An objective approach which can compute reference point from the previous decisions made by the decision-maker, and that which can customise preference order of alternatives may aid the decision-maker in such scenarios. In future, the concepts discussed and the framework presented in this work can be extended to multi-class decision-making to verify the effectiveness of a DSS based on descriptive decision-making model. Extensions of this work can possibly be the application of this framework in evidence based medicine, risk management systems, utility based analysis and in many such areas of engineering and management.