Methods for Determination and Calculation of Deflections of the Vertical

Abstract

This Chapter is devoted to determination of deflections of the vertical (DOV). A general overview of DOV determination methods on a moving base is provided. The methods addressed include the gravimetric method, astrogeodetic method, and inertial-geodetic method. Also considered are gravity gradiometry, satellite or aircraft altimetry, satellite-to-satellite tracking and other satellite missions using the Earth’s gravity models, as well as combinations of these methods. The automated zenith telescope developed by Concern CSRI Elektropribor, which determines DOV components by field observations of the near-zenith part of the stellar sky, is described. Findings from field studies are presented proving the efficiency of the proposed technical solutions. The integrated system comprising a precision inertial measurement unit and a GNSS compass developed by Concern CSRI Elektropribor is presented.

I. Chelpanov–Deceased

FormalPara Introduction

This chapter is devoted to the methods for determining and calculating deflections of the vertical. It includes three sections.

Section 3.1 presents a general overview of the methods used to determine deflections of the vertical (DOV) on a moving base. Special attention is given to the gravimetric method, which is based on gravity anomaly measurements, the astrogeodetic method, involving comparison of astronomical and geodetic coordinates, and its version, the inertial-geodetic method. Also considered are gravity gradiometry, based on measuring the second derivatives of gravity potential, satellite or aircraft altimetry, based on trajectory altitude measurements, satellite-to-satellite tracking and other satellite missions using the Earth’s gravity models, as well as combinations of these methods (for example, astrogravimetric method). The classification criteria for DOV determination methods are proposed, and their comparative qualitative analysis is carried out.

Section 3.2 is devoted to the determination of DOV components by the astrogeodetic method. The focus here is on the description of an automated zenith telescope developed by Concern CSRI Elektropribor, intended for real-time determination of DOV components by field observations of the near-zenith part of the stellar sky. The principle of operation, basic parameters of the components, algorithms for processing the observation results and accuracy characteristics of the zenith telescope are discussed. The results of field studies are presented proving the efficiency of the proposed technical solutions and processing algorithms, and the suitability of the automated zenith telescope for high-precision DOV determination.

And finally, Sect. 3.3 describes the inertial-geodetic method for DOV determination. The general idea and features of the method are discussed, with special attention given to the potential for its implementation in high latitudes. The proposed solution is creation of a specialized integrated system comprising a precision inertial measurement unit and a GNSS compass, which is a two-antenna receiving system with a 6 m long antenna baseline. Algorithms for the problem solution are described. The accuracy of the integrated system is estimated based on the simulation and the results of sea trials of the GNSS compass developed by Concern CSRI Elektropribor.

3.1 DOV Determination on a Moving Base

Both high-precision navigation and geodetic surveying require the knowledge of the Earth’s gravity field (EGF) parameters. These parameters traditionally include quasi-geoid height ζ, gravity anomaly Δg (GA), and DOV. Deflections of the vertical provide more detailed information on the Earth’s figure and nonuniform mass distribution under its surface, help to solve reduction problems of higher geodesy and improve the positioning accuracy achieved by high-precision marine navigation instruments.

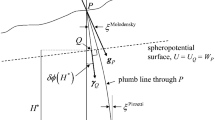
Due to the complicated nature of the Earth’s surface and its internal structure, the direction of the actual gravity vector (vertical) does not coincide with the direction of the normal gravity vector at the points of the Earth’s physical surface. This difference is referred to as the deflection of the vertical, or plumb line deflection. A distinction is made between astrogeodetic and gravimetric DOVs (Ogorodova 2006). Deflections of the vertical are usually specified by a set of two deflection angles in the meridian plane ξ and the plane of prime vertical η, respectively (Shimbirev 1975).

DOV values close to the Earth’s surface are within several angular seconds and may come up to one angular minute. For high-precision navigation, it is required to measure the DOV components with errors not exceeding 0.5–1 arcsec. This is feasible on a fixed base, but causes significant technical difficulties onboard moving vehicles (Peshekhonov et al. 1989; Anuchin 1992).

Currently, a wide variety of methods aided with specialized hardware have been developed to determine DOV. To study and comparatively estimate these methods, their specific use on a moving base should be taken into account. Then it should be remembered that all DOV measurements are taken by indirect methods, and the values are calculated in real time or during postprocessing. It is very important to provide stable operating conditions for the measuring equipment and to apply various error reduction methods, both hardware and software.

For the analysis and combination and optimization synthesis of various algorithms while developing the software and well-founded schemes and engineering solutions, diverse DOV determination methods should be represented in the form of classification diagrams based on the selected criteria. Consideration of possible designs of measurement systems with account for various combinations of classification criteria allows covering a wide range of design and technical solutions, as well as stimulating the development of new options using new combinations of components.

This Section gives a comparative analysis of various methods for DOV determination on a moving base taking into account the selected classification criteria.

3.1.1 Basic Methods for DOV Determination

In higher geodesy, the methods for studying the Earth’s figure and gravitational field are traditionally classified into geometric and physical (gravimetric) ones, which are subdivided in accordance with the characteristics of the measured quantities (Shimbirev 1975; Torge 2001; Ogorodova 2006). In geometric methods, primary measurements are measurements of lengths and angles, whereas in gravimetric methods, they are gravity measurements. DOV determination methods can also be divided into physical and geometric methods. However, when determining DOV on a moving base (satellites, airplanes, ships, etc.), other features should be taken into account such as the vehicle’s dynamic performance, information processing algorithms used, etc.

The main available methods to determine DOV include

• gravimetric method based on gravity anomaly measurements;

• astrogeodetic method based on the comparison of astronomical and geodetic coordinates;

• inertial-geodetic method based on the use of output signals of a precision inertial navigation system (INS) and GNSS;

• gravity gradiometry method based on the measurement of second derivatives of the geopotential;

• satellite or aircraft altimetry method based on measuring the altitude of the trajectory of a moving vehicle;

• method using EGF global models based on satellite-to-satellite tracking, as well as combinations of these methods (e.g., astrogravimetric method). In addition to the above listed, the collocation method may also be mentioned based on the use of known correlations between various EGF components.

The gravimetric method based on the acquisition and processing of data arrays on gravity anomalies is one of the main methods for determining DOV at sea. A gravimetric survey was first carried out by F. A. Vening-Meinesz in 1923 onboard a submarine. This method is traditionally practiced in the Russian Federation for trajectory or aerial surveys (Bolshakov 1997; Drobyshev et al. 2006; Nepoklonov 2010; Koneshov et al. 2015, 2016b). It is based on the numerical solution of the Laplace equation for the disturbing gravity potential in explicit form and requires postprocessing of large arrays of primary measurement data. DOV values are obtained by applying Vening-Meinesz’ formulas (3.1.1) given in Table 3.1 to the gravimetric survey data. The initial data for DOV calculation are the measured gravity anomaly values Δg with their corresponding geodetic coordinates B, L. Airborne gravimetry is more efficient as compared to marine measurements, although the observed wavelength of the measured gravity anomalies is somewhat longer and the dependencies are more smoothed.

Table 3.1 Analytical dependencies of DOV parameters on measured parameters for various methods

The astrogeodetic method is based on measuring astronomical and geodetic coordinates at given points along a path or over an area (Peshekhonov et al. 1995; Kudrys 2009; Hirt et al. 2010; Tsodokova et al. 2014). The angles generated by the systems measuring the astronomical coordinates are continuously compared with the readings of geodetic instruments: formula (3.1.2) in Table 3.1. As for the accurate measurement of geodetic coordinates on a moving base, there is virtually no alternative to the GNSS. Astronomical coordinates can be measured by precision systems such as an astronavigation system, or a zenith telescope. These systems implement the astronomic positioning method.

This method has some limitations, for example, when applied at sea, the required accuracy can only be provided at very low speeds (the vessel drift cannot exceed 2 km over the measurement time of about 20 min); another requirement is that near-zenith stars be continuously observed, hence, the sky should be only slightly cloudy and the system should be highly sensitive to faint stars (Vasiliev et al. 1991a). To ensure the desired DOV accuracy, the spatial angular stabilization of the astronomical system is required. Therefore, the best results can be obtained on an inherently non-mobile platform (such as drifting ice) (Troitskii 1994). This ensures the high accuracy of angular measurements and determination of the geodetic zenith with minimal error.

The advantage of the astronavigation system and zenith telescope is that the errors in modeling the inertial frame are limited and practically do not depend on the duration of continuous operation. Their key strong point consists in the ability to determine the full DOV values.

The inertial-geodetic method utilizes a precision INS and rests on the dependence of errors in its output navigation parameters on the anomalies. This method is described in detail in (Schultz and Winokur 1969; Nesenyuk et al. 1980; Dmitriev 1997; Li and Jekeli 2008; Timochkin 2013), and in Sect. 3.3. Analysis and consideration of the INS error, actually a methodical one, makes it principally possible to directly determine DOV increments with respect to the reference value at a reference point by filtering or smoothing using the differences in the INS and GNSS measurements. It is important that the INS should be a precision one so that in constructing the inertial vertical, the methodical errors caused by the disagreement between the actual EGF and its calculated model used in INS algorithms prevail over instrumental errors of inertial sensors—gyroscopes and accelerometers (Emel’yantsev et al. 2015). In contrast to the astronavigation system, the inertial coordinate system in the INS is based on the readings of gyroscopes and accelerometers, and the errors in the inertial frame simulation are determined by the gyro drift. It should be noted that due to the accumulation of the INS longitude error, the full DOV value in the prime vertical plane cannot be determined during the correction even with perfectly known longitude, i.e., this component is not completely observable (Emel’yantsev et al. 2015).

On the other hand, the advantage of INS as compared to astronavigation system is its independence from weather conditions and time of day. In principle, the inertial-geodetic method can be considered as a type of astrogeodetic method where the astronomical coordinates are generated using a precision INS (Dmitriev 1991; Emel’yantsev et al. 2015). It should be emphasized that, unlike the conventional astrogeodetic method, in the inertial-geodetic method the INS generates both astronomical coordinates and their derivatives.

DOV determination by gravity gradiometry uses a device measuring all the components of the tensor of the geopotential second derivatives, the so-called full tensor gradiometer (FTG). This method involves the implementation of an algorithm where the readings of gyroscopes, accelerometers, and FTGs are integrated in real time to determine the vehicle position and gravity vector increments along the motion path with account for the base angular position (Peshekhonov et al. 1989; Evstifeev 2017). To provide for accurate operation of such a system during DOV determination, it is critically important to ensure accurate angular stabilization of the FTG in the Earth-fixed coordinate system and to know the initial conditions of the integration, which are specified by other methods and means. To measure DOV accurate to about 1 arcsec, the permissible FTG error should be 1 Eo, and the error in FTG spacial angular stabilization should be max 1 arcsec without using analytical methods to calculate the stabilizer errors (Staroseltsev 1995; Semenov 2012). The material relating to gravity gradiometers is presented in more detail in Sect. 5.2.

Altimetry method of DOV determination is based on the application of quasi-geoid height models. The accuracy of the method depends on the accuracy of determining the coordinates of the vehicle (satellite or airplane) and the accuracy of measuring the altitude above the Earth’s surface and the sea level. DOV values are determined using the G. Moritz formulas—formulas (3.1.4) in Table 3.1 (Moritz 1980). The observed wavelength of anomalies determined by the altimetry method is within the range between 30 and 300 km (LaCoste et al. 1982; Watts et al. 1984; Medvedev et al. 2010).

The use of global EGF models based on the results of satellite missions has provided an enormous amount of data about the EGF. The data received from the CHAMP, GRACE, and GOCE satellite missions were used to derive global models of the EGF anomalies that actually can be used to calculate and display the distribution of DOV components all over the Earth’s surface (Jekeli 1999; Hirt 2010; Koneshov et al. 2012; Karpik et al. 2015). It would take several tens or even hundreds of years to solve this global problem by gravimetric or other methods. In this sense, methods based on satellite data are beyond competition. The CHAMP and GRACE missions use satellite-to-satellite tracking. In the CHAMP mission, in the high-low satellite mode the low-orbit satellites are tracked from high-orbit satellites, thus allowing the gravity vector to be measured as the first derivative of the geopotential. In this case, DOV parameters can be determined by the gravimetric method.

The satellite-to-satellite tracking in low-low mode was implemented in the GRACE project employing two twin satellites separated by 220 km at the orbit altitude of about 500 km. The distance between satellites is determined with very high accuracy (about 10 μm) using a precise K-band microwave ranging system (Albertella et al. 2002; Kima and Tapley 2002). Each of the satellites within the system is also tracked from high-orbit satellites. In this system, differences between gravitational accelerations are calculated on a long base as if it were a giant gradiometer measuring some components of the tensor of the geopotential second derivatives. The data obtained for determining DOV smoothed parameters are more informative than in the previous case.

In GOCE mission, an FTG was installed in a satellite. It was designed as a set of three pairs of orthogonal high-precision accelerometers with three sensitive axes spaced 50 cm apart. This resulted in significant progress in determining the distribution of the EGF anomaly parameters (Albertella et al. 2002).

Using global EGF models based on satellite data to determine the DOV variability in a local area (with a short resolvable wavelength) is limited because of rather high speeds and altitudes of satellites above the Earth’s surface. Lower orbits are impracticable for satellites due to atmospheric drag.

Global EGF models constructed by the mission data can be found in Sect. 6.1.

Table 3.1 gives the analytical equations used to calculate DOV by the results of direct measurements of other physical quantities using the above methods.

Potential accuracies of DOV determination methods are determined based on the measured parameters and performance of modern equipment.

3.1.2 Features of DOV Determination on a Moving Base

Specific features of DOV determination on a moving base are as follows:

• the need to measure small physical forces and accelerations against the background of large noise, mostly formed by the forces of inertia;

• impossibility, in most cases, to stop a vehicle to make corrections;

• high accuracy requirements for measuring the system orientation angles or compensation for angle variation;

• high speeds of the vehicle relative to the Earth’s surface and large distance between the measuring equipment and the Earth (in case of airborne or satellite measurements);

• the need to strictly follow the programmed linear paths during motion to reduce disturbing effects on the instrumentation during turns;

• the need to occasionally update measurements and introduce corrections at preformed zero (reference) points to obtain the corrected DOV values.

The observed DOV variability along the path can be conventionally defined by the wavelengths of anomalies. That is, the shorter the wavelength of the anomaly measureable by a certain method, the more accurately the DOV variability is determined. For example, at a high altitude above the Earth’s surface and at a high speed, the instrumentation smoothes short waves while neglecting minor DOV variations. In accordance with the available information, Fig. 3.1 clearly compares the capabilities of various methods to determine the DOV depending on the wavelength of the gravitational field anomalies and the achievable measurement error (Peshekhonov et al. 1989; Anuchin 1992; Li et al. 2001; Albertella et al. 2002; Seeber 2003; Volgyesi 2005; Tse and Baki Iz 2006; Hirt and Seeber 2008; Ceylan 2009; Featherstone and Lichti 2009; Kudrys 2009; Hirt 2010; Jekeli 2011, 2012; Smith et al. 2013; Guo et al. 2014; Rezo et al. 2014; Šprlák and Novák 2014; Koneshov et al. 2014, 2016a). In DOV determination, the minimum observable wavelength and measurement error are different depending on the kind of vehicle.

Fig. 3.1

Capabilities of different DOV determination methods

The advance in modern technology has opened up new possibilities that make researchers reconsider the application and feasibility of various methods for DOV determination.

It was shown that DOV can be measured onboard accurate to 1 arcmin if the errors of the applied gravity gradiometers, accelerometers, and gyroscopes do not exceed 1 Eo, 2 ⋅ 10^–5 ms⁻² (2 μg), 5 ⋅ 10^–4°/h, respectively (Peshekhonov et al. 1989). As for the inertial-geodetic method, the positioning error of geodetic measurements should not exceed 5–10 m. It was noted that such accuracies were unattainable in 1989 (Peshekhonov et al. 1989).

The new results obtained in modern engineering include the following:

• 1. GPS and GLONASS positioning accuracy (using open channels) is 1–2 m; it is expected to be improved to a few tens of centimeters (Revnivykh 2012; Mikhailov 2014).

• 2. High-precision gyroscopes such as electrostatic gyroscopes and systems based on them have been developed. It has become feasible to design strapdown INS on fiber-optic gyroscopes with drifts of about 1 nm per month (2 ⋅ 10⁻⁵°/h) (Peshekhonov 2003, 2011; Paturel et al. 2014).

• 3. Prototypes of gravity gradiometers, operating and keeping high accuracy on a moving base, have been developed. The studies starting from the 1970–1980s resulted in the creation of devices that have successfully passed the tests aboard satellites, planes, and vessels (Gerber 1978; Murphy 2004; Mumaw 2004; Richeson 2008; DiFrancesco et al. 2009; Soroka 2010; Rummel et al. 2011; McBarnet 2013). Currently available are Lockheed Martin, Bell Geospace, and ARKeX FTGs, with errors of about 1–5 Eo, used aboard aircraft and vessels mainly for mineral exploration (DiFrancesco et al. 2009). Studies were conducted to design cryogenic gravity gradiometers with drifts of about 0.02–1 Eo (DiFrancesco 2007; Richeson 2008; Soroka 2010; Carraz et al. 2014). The FTG used in the GOCE space mission was configured as a set of three pairs of orthogonal high-precision electrostatic accelerometers with noise levels of about 0.003 Eo/√Hz in the measurement range of 0.005–0.1 Hz (Rummel et al. 2011). The current state of development of gravity gradiometers is described in Sect. 5.2.

• 4. Mechanical PIGA-type accelerometers with a drift stability of 0.1–1 μg have been developed, and accelerometers based on cold atom interferometry with a resolution of 10^–5 μg are emerging (Yole Development Report 2012).

• 5. New generation gravity sensors have been created, including those on cold atoms, for mobile gravimeters. Their sensitivity thresholds are about a few hundredths of fractions of mGal. The accuracies of modern gravity sensors are comparable with those of ground-based devices, which allows their unrestricted application in marine and airborne gravimetric surveys to improve both the accuracy and spatial resolution of surveys (Krasnov et al. 2014; Peshekhonov et al. 2015; Forsberg et al. 2015; Menoret et al. 2016; Zahzam et al. 2016). The principal feasibility of using absolute gravimeters on a moving base has been validated (Peshekhonov et al. 2016; Vitushkin 2015). More details on the state of development of gravimetric instruments, including absolute gravimeters, can be found in Chap. 1.

• 6. CHAMP, GRACE, and GOCE satellite missions have been implemented (Sugaipova 2015) and global models of the Earth’s gravitational field have been refined based on the mission data. This made it possible to generate geopotential models with the maximum number of spherical harmonics and to obtain digital models of average DOV values for standard geographical 5 × 5 arcmin trapezoids. DOV errors using EGM2008 model (up to degree 2190) are on average about 1–2 arcsec, which can be compared with DOV accuracy by the astrogeodetic method (Rummel et al. 2002; Nepoklonov 2009; Pavlis 2010; Koneshov et al. 2013). Global EGF models based on the data obtained in satellite missions can be found in Sect. 6.1.

Thus, the modern instrument engineering creates a potential to determine DOV parameters on a moving base with sufficiently high accuracy.

3.1.3 Classification Criteria of DOV Determination Methods

The methods to determine the parameters of EGF anomalies at sea using INS were classified based on individual criteria by Anuchin (1992): the methods are divided into direct, integral, indirect, and combined. In accordance with the terminology accepted in Russian metrology (RMG 29-2013), direct methods directly determine the required physical quantities, and in indirect methods the results of direct measurements of the quantities functionally related to the sought quantity are mathematically transformed to determine it.

The analysis of the existing methods shows that it is impossible to directly measure DOV as angles between the normal to the ellipsoid and the vertical direction (determination of astrogeodetic DOV) or angles between the directions of the vectors of the real and normal gravity fields (determination of gravimetric DOV).

All DOV measurements are performed by indirect methods with subsequent calculation of the sought values. Even the idea of the geometric method measuring DOV as an angular misalignment between the two coordinate systems (Maslov 1983) requires the separate construction of the geodetic and astronomic verticals using different instruments; therefore, it cannot be considered a direct method.

Analysis of the available methods for determining DOV on a moving base as a set of techniques helps to define the following important classification criteria that seriously affect the structure and composition of a measurement system and are used by the authors as the basic criteria for classification schemes:

• 1. Real-time or a posteriori DOV determination procedures.

• 2. Methods to improve the DOV determination accuracy.

• 3. Conditions of the practical application of DOV determination methods.

The first of the main classification criteria is the DOV determination procedure. Based on the measurement processing method, such procedures can be reasonably divided into those providing real-time calculations directly during the vehicle motion and those allowing only posteriori calculation of the sought DOV parameters using the postprocessing of full data arrays (Fig. 3.2).

Fig. 3.2

Classification of DOV determination methods based on measurement processing procedure

Strictly speaking, the algorithms used to determine DOV in real time can also be used a posteriori. However, since the real-time operation is one of the most important factors in determining DOV, this criterion is represented as a separate subdivision in this classification.

Figure 3.2 shows the collocation procedure not described above (Moritz 1980; Volfson 1997). This method has not found wide use, however, it is included in the classification criteria to provide a comprehensive overview of available procedures. The collocation method uses covariance relations between different components of the measured and estimated processes (Moritz 1980). It determines DOV components based on primary data from type 1 or type 2 gravitational variometers without direct measurements of the vertical gradient, which considerably simplifies the hardware implementation of such a measurement system (Volfson 1997; Bouman 2012).

Another significant classification criterion concerns the methods to improve the DOV determination accuracy (Fig. 3.3). These methods are grouped as instrumental, algorithmic, and combined methods. Instrumental methods employ the systems protecting the equipment against various external effects (forces and moments of inertia in translational motion, vibrations and angular oscillations of the platform, electromagnetic fields, and temperature) or decreasing these effects. For example, the thermal stabilization system protects equipment from variations of the ambient temperature and maintains the preset operating temperature. The spatial shock-absorbing system reduces the effect of vibration acceleration. It is necessary to have an angular stabilization system that allows keeping the angular position of the measuring device in a specified coordinate system with small errors. ARKeX demonstrates an FTG on shock absorbers with a thermal insulation protector on its website (ARKeX 2013).

Fig. 3.3

Classification of DOV determination methods based on accuracy improving methods

Algorithmic methods refer to the methods of data processing. The principles of signal processing influence the selection of procedures for processing data arrays and the possibility of obtaining results in real time or a posteriori. The filters and algorithms used are chosen empirically, or their structures and characteristics are determined by applying various optimization procedures. If at least plausible descriptions of the properties of useful signals and noise as random processes are available, optimization for steady-state (stationary) modes is carried out in real time based on spectral densities by Wiener method (Chelpanov et al. 1978; Dmitriev 1991; Loparev and Yashnikova 2012; Stepanov 2012) (using local approximation procedures); and for non-stationary modes, including the initial stages (with account for deterministic components), by Kalman method (Dmitriev 1991; Loparev et al. 2012a, b; Loparev and Yashnikova 2012; Stepanov 2012; Stepanov et al. 2014; Sokolov et al. 2016).

The combined methods utilize various measuring devices and algorithmic methods to obtain more comprehensive information on DOV components in different wavelength ranges. In Zheleznyak and Koneshov (2007), it was noted that marine and airborne surveys are required to determine DOV in the short-wavelength ranges, and satellite altimetry data are needed for long-wavelength measurements. For marine measurements, the best results in determining DOV over the entire wavelength range are provided by an integrated system including INS, GNSS, astronavigation system, and a velocity sensor (Anuchin 1992).

When considering general classification criteria of DOV determination methods, the conditions for their implementation should be taken into account (Fig. 3.4). One of the key criteria is the type of platform on which measurements are taken. They are grouped as follows:

Fig. 3.4

Classification of DOV determination methods based on implementation conditions

• slow-moving platforms (e.g., drifting ice) characterized by low speeds and very low accelerations;

• ground-based vehicles, which can be stopped at certain points for observation and data correction (a conventionally mobile platform);

• marine vehicles characterized by large linear and angular accelerations; or a submarine with much smaller accelerations;

• aircraft (airplanes, helicopters, dirigibles) best suited for inaccessible mountainous areas. They have high linear speeds and accelerations due to atmospheric turbulence;

• space vehicles with low accelerations and lack of gravity, but very distant from the Earth’s surface.

An interrelated classification criterion partly determined by the type of the vehicle covers a variety of typical levels of external factors directly affecting the DOV measuring equipment after all protection measures have been taken. These factors include inertial forces (vibration, impacts, overloading due to turning cycles) not compensated by the shock absorption system, the temperature, the altitude above the Earth’s surface (the readings should be reduced), and the environment (air, water, vacuum). All these factors require consideration and special analysis before starting the design of instrumentation.

The last criterion determines the type of the geometric set of points of the measurement area where DOV values are determined. This is essential for selecting a DOV determination method. For example, astronomic methods are most effective for measurements at a point (or isolated points); inertial methods using INS should preferably be used for trajectory measurements during the vehicle motion (if a model is used to specify DOV variability along the motion path); gravimetric methods are applied in aerial measurements to achieve the desired DOV accuracy.

3.1.4 Qualitative Comparative Analysis of the Methods

A method for determining DOV on a moving base is selected based on the problem statement, requirements for the measured parameters, and availability of high-precision equipment. The requirements for the measured parameters usually include the achievable DOV accuracy, resolvable wavelength, and the ability to determine relative or absolute values.

For long-wavelength measurements, there exist global DOV maps based on the data obtained in the space missions mentioned above. For wavelengths over 10 km, mainly global models obtained by satellite missions or airborne gradiometry can be used. Short-wavelength real-time measurements should be taken by gravity gradiometry or astrogeodetic methods.

Implementation of a particular method depends on the performance of the instrumentation. DOV determination systems should be designed with account for the technological potential and feasibility of creating or using systems to improve the accuracy.

Zenith telescope or astronavigation system on a moving platform is able to determine DOV absolute values, but this requires the development of a precision gyroscopic stabilization system, which is a nontrivial problem taking into consideration the dimensions of the zenith telescope. Besides, such a system would require a comfortable environment for its operation: small motion angles and scattered clouds.

Using the inertial-geodetic method to determine relative DOV values requires an INS with high-accuracy gyroscopes. To set the initial conditions of INS operation, it is required to determine exact astronomical coordinates, for example, using astronomical measuring instruments. In addition, to determine DOV by the inertial-geodetic method with the use of Kalman filtering, it is necessary to specify a preliminary statistical mathematical model of the gravity field along the motion path (Anuchin 1992; Staroseltsev and Yashnikova 2016).

Despite all of its advantages, gravity gradiometry requires unique instrumentation such as FTG. It should be noted that it took about 30–40 years to design FTGs able to operate on a moving base. Only a small number of companies owning or having rights to use this technology can apply this method. To be able to use an FTG on a moving base, it is necessary to ensure high-precision gyro stabilization and apply all possible, both hardware and algorithmic, means of improving the accuracy.

3.1.5 Conclusion

Various methods to determine DOV on a moving base have been considered, and the potential for their hardware implementation has been estimated. It is shown that the comparative analysis of these methods requires that their specific application on a moving base be taken into account. Then it should be remembered that all DOV measurements are taken by indirect methods, and DOV values are calculated in real time or during postprocessing. It is very important to provide stable operating conditions for the measuring equipment and to apply various error reduction methods, both hardware and software.

A structured system of classification criteria of DOV determination methods is proposed. The following three main classification criteria are selected: procedures for real-time or a posteriori DOV determination; methods for improving DOV accuracy, including instrumental, algorithmic, and combined ones; conditions for the practical application of DOV determination methods. A comparative qualitative analysis of the methods and fundamental solutions that implement various requirements for the instruments being developed has been carried out.

3.2 DOV Determination with the Use of an Automated Zenith Telescope

As mentioned in Sect. 3.1, DOV components can be determined with high precision by various methods. However, the methods based on the use of gravimetric or satellite data make it possible to determine DOV components with a specified error only if a significant amount of work was done previously and there is a detailed survey of the area of interest. In poorly studied areas, as well as in the case of more stringent requirements for the accuracy of determining DOV components, the astro-geodetic method based on a comparison of the astronomical and geodetic coordinates can be used (Table 3.1). Modern satellite equipment allows geodetic coordinates to be determined with accuracy of a few centimeters. Thus, DOV determination accuracy is limited by the error in determining astronomical coordinates, the reduction of which is an urgent task.

This section considers the basic principles of determining astronomical coordinates and DOV components by observing stars, as well as the instruments used to solve this problem in Russian and international geodetic astronomy. The emphasis is placed on the automated zenith telescope (AZT), the main parameters of its components and the algorithms for processing the observation results; also discussed is estimation of the AZT accuracy characteristics.

3.2.1 General Principles of Determining Astronomical Coordinates in Geodetic Astronomy

Astronomical latitude φ and the local sidereal time s at observation time T at some point on the Earth’s surface can be determined if the zenith position on the celestial sphere is determined for this time and this point. Indeed, declination of the zenith is numerically equal to the observer’s latitude δ_Z = φ, and its right ascension to the local sidereal time α_Z = s (Fig. 3.5).

Fig. 3.5

Determination of the zenith position on the celestial sphere. P_n is the celestial north pole; P_s is the celestial south pole; ϒ is the vernal equinox; N is the north point; S is the south point; Z is the zenith (P_nZS is the celestial meridian); t is the horary angle; α is the right ascension; δ is the declination; A is the azimuth; z is the zenith distance

At any given moment of time T, the position of the zenith on the celestial sphere Z (α_Z, δ_Z) can be defined by

• zenith distances of at least two stars with known equatorial coordinates (α₁, δ₁) and (α₂, δ₂);

• the intersection of at least two verticals passing through these stars, i.e., azimuths of stars A₁ and A₂.

Thus, depending on the measurands, the methods for determining astronomical coordinates are divided into two main groups: zenithal and azimuthal.

In the zenithal methods, the time and latitude of the instrument position are determined from the measured zenith distances of stars or the differences in the zenith distances of stars, or from observations of groups of stars at the same zenith distance.

Azimuthal methods of astronomical determinations make it possible to determine the time and latitude based on the azimuths of two stars or using the measured differences in azimuths of stars or from observations of groups of stars in the same vertical (Uralov 1980).

As is known, the longitude of a point relative to the initial meridian is numerically equal to the difference between the local times of the same kind (Kulikov 1969) determined simultaneously (or with reference to the same moment) both at the observation point and at the point located at the first meridian, i.e.,

$$\uplambda = s - S = m\rm{ - }{\text{UT1,}}$$

where

s is the local sidereal time;

S is the Greenwich sidereal time;

m is the local mean solar time;

UT1 is the mean Greenwich meridian universal time (Brumberg et al. 2004).

Thus, the problem of determining the longitude of a point consists in

• determining the local time s or m at a time T based on the measurements of the zenith distances of the stars or their azimuths;

• determining the time of the first meridian S or UT1 at the same moment of time T, for example, using the transmission of exact time signals over a radio link.

In geodetic astronomy, the horizontal coordinates of stars (A, z) are considered measurable, the equatorial coordinates of stars (α, δ) are considered known, and the geographical coordinates of point (φ, λ) are considered determinable. The relations between the determinable, known, and measurable parameters are obtained through the solution of the parallactic triangle (Kulikov 1969). The formulas for the relations of parameters used in the zenithal and azimuthal methods of astronomical determinations take the following form, respectively:

$$\cos z = \sin \upvarphi \sin \updelta + \cos \upvarphi \cos \updelta \cos t;$$

(3.2.1)

$${\text{ctg}}\,A = \sin \upvarphi \,{\text{ctg}}\;t - {\text{tg}}\;\updelta \cos \upvarphi /\sin t.$$

(3.2.2)

In (3.2.1) and (3.2.2), t is the horary angle (t = s − α).

From the above description of methods for determining astronomical coordinates, it is possible to formulate the following problems to be solved using astronomical equipment:

• measurement of zenith distances of stars and horizontal directions to stars;

• recording of moments of these measurements in a given time measurement system;

• recording of moments of the passage of stars through specified ertical circles or almucantar (a small circle of the celestial sphere whose plane is parallel to the plane of the horizon (Kulikov 1969)).

In Russia, astronomical field observations are conducted with the use of measuring systems that are capable of providing solutions to the above problems. Such systems consist of the following interrelated parts:

• an astronomical tube used as a sighting device. It turns around two mutually perpendicular axes; the vertical axis is set in the direction of the plumb line using levels;

• divided circles connected with the axes of rotation, vertical and horizontal, with readout devices;

• devices for pointing at a star, allowing for simultaneous measurement of small angular distances within the field of view and recording the moments of observations of stars—eyepiece micrometers (conventional, contact, photoelectric ones);

• astronomical clock that serves as a scale for measuring time when recording the moments of star observations;

• chronographs—devices for recording observation results;

• radio receiving equipment connected to the clock and the chronograph used to receive the time signals transmitted by time service radio stations.

The first three parts of the system are combined in one unit—the astronomical instrument, which has a communication channel with the clock and the recording devices.

The following astronomical instruments have been used in Russia for high-precision astronomical determinations of latitude and longitude: AU 2/10 (USSR, since the 1930s), Wild T-4 (Wild, Switzerland, since the 1940s, Fig. 3.6), DKM3-A (Kern-Aarau, Switzerland), AU01 (Russia, TsNIIGAiK, since the mid-1980s) (Rukovodstvo 1984).

Fig. 3.6

Wild T-4 astronomical instrument

When conducting high-precision astronomical determinations of coordinates using astronomical instruments (with visual recording of objects), it is necessary to take into account the influence of various components of the instrumental error: collimation error, tilting of the horizontal axis, lateral flexure of the telescope tube, errors in the pivot shapes, etc. (Uralov 1980; Rukovodstvo 1984). With this aim in view, the instrument is thoroughly examined before observations. For the above reasons, the requirements for the observers’ qualifications are higher, and the duration of observations significantly increases (as a rule, to ensure high precision in determining astronomical coordinates, observations are conducted for three months).

In addition, the fact that the readings of the chronometer or the clock may be perceived by ear at the moments of star sighting, explains the observer’s significant personal error, as well as a great random error of observations. To reduce the influence of these factors, as well as to improve performance, semi-automatic and automatic methods are used for star observation using special devices, primarily photodetector devices (e.g., CCD and CMOS image sensors) as radiation detectors. CCD- and CMOS image sensors make it possible to ensure observation of faint objects, as well as a digital representation of the observation material, which allows the results to be processed using a computer directly in the observation process, which improves both the performance and accuracy of determinations. Reference of observations to the precise time scale can also be carried out automatically using GNSS receivers.

Thus, the use of automated devices significantly improves the accuracy and efficiency of determining astronomical coordinates and, as a consequence, DOV components.

Work on the creation of such automated devices has been carried out over the past three decades. In the 1990s, a prototype of an automated prismatic astrolabe was created at Concern CSRI Elektropribor (Vasiliev et al. 1991b).

Digital zenith telescopes were created in a number of European universities (Hannover, Zurich) to quickly determine DOV components. They allow obtaining values with an accuracy of 0.2–0.3 arcsec and higher within less than an hour of observation (Hirt and Bürki 2002; Hirt et al. 2010). Work on creating such devices is also under way in Austria (Gerstbach and Pichler 2003), Turkey (Halicioglu et al. 2012), China (Tian et al. 2014).

In 2017 Concern CSRI Elektropribor completed the development of the prototype of an AZT designed for quick determination (about an hour) of DOV components from observations of the circumzenithal area of the stellar sky in the field of view. This Section describes the principle of operation of this device, the main parameters of its component parts, and the algorithms for processing observation results.

3.2.2 Description of the AZT and Its Principle of Operation

The AZT is an optoelectronic system, the sight axis of which is directed to the zenith. The objective connected to the camera and inclination sensors is mounted on a platform that can turn around a vertical axis (Fig. 3.7). A precise leveling mechanism is provided for horizontal leveling.

Fig. 3.7

AZT functional diagram

The AZT consists of an optoelectronic device, control device, and a power supply system containing a power supply device, battery packs, and chargers.

A general view of the AZT is presented in Fig. 3.8.

Fig. 3.8

General view of the AZT: 1—optoelectronic device; 2—control device; 3—power supply device; 4—battery pack; 5—charger; 6—tripod; 7—package

The optoelectronic device is intended

• to form images of stars in the field of view of the objective and record them in the plane of the digital camera photodetector;

• to determine the geodetic coordinates (latitude and longitude) of the observation point;

• to form the UTC scale based on the GNSS data;

• to determine the astronomical coordinates of the observation point.

The optoelectronic device includes

• a catadioptric objective with the pupil diameter of 200 mm, the angular field of view 1.1 × 1.5°, and the relative aperture ratio of 1:6;

• a digital camera built on the basis of a thermally stabilized 20-megapixel CMOS image sensor (the size of the image sensor’s sensitive area is 36.8 × 24.6 mm (5120 × 3840 pixels));

• GNSS receiver;

• guidance module;

• leveling system;

• inclination sensors.

The control device contains computational units of functional parts combined by exchange channels into a uniform information and control system. It is intended.

• to control AZT components (guidance drives, leveling drives, inclination sensors);

• to organize information exchange between the AZT components;

• to process observation data;

• to present the observation data on the display and record them to storage media.

The power supply device and battery packs provide the equipment with a stabilized voltage of autonomous power supply for 6 h.

During operation, the AZT is installed at a required point, whereupon its component parts are assembled. The AZT is controlled by the operator through the control device. The activation command initiates the preparation mode—leveling of the optoelectronic device platform. Next, the mode of DOV component determination is switched on, after which (within an hour) the values of astronomical and geodetic coordinates, as well as DOV components are displayed on the control device.

As shown in Sect. 3.1, the DOV components are determined using the following relations:

$$\begin{aligned} \upxi & = \upvarphi - B; \\ \upeta & = (\uplambda - L)\cos \upvarphi , \\ \end{aligned}$$

(3.2.3)

where

ξ is the DOV projection on the meridian plane;

η is the DOV projection on the prime vertical plane;

B, L are the geodetic coordinates of the location (latitude and longitude);

φ, λ are the astronomical coordinates of the location.

The astronomical coordinates are determined by measuring the direction to stars with known equatorial coordinates (the right ascension α, the declination δ) using the equivalence of astronomical coordinates (φ, λ) of the observation point (AZT location) and equatorial coordinates of stars located directly in the zenith (Fig. 3.9). This equivalence is due to the validity of the following relations:

$$\begin{gathered} \upvarphi = \updelta ; \hfill \\ \uplambda = \upalpha - \uptheta , \hfill \\ \end{gathered}$$

(3.2.4)

Fig. 3.9

Equivalence of astronomical and equatorial coordinates

where θ is the Greenwich apparent sidereal time (the horary angle of the vernal equinox relative to the Greenwich meridian, Fig. 3.9) (Abakumov 1996; Avanesov et al. 2013; Brumberg et al. 2004).

It should be emphasized that the probability of finding stars directly at the zenith point is extremely small; therefore, the purpose of observation is to record a sequence of frames with star images in the circumzenithal area (within the field of view) using a photodetector; to measure the coordinates of the energy centers of all stars in each frame, identify them, and determine the equatorial coordinates of the zenith point. Concurrently with the frames recording, also fixed is the time needed to calculate θ.

3.2.3 Algorithm for Determining DOV Components Using the AZT and Error Analysis

A block diagram of the algorithm for determining DOV components is shown in Fig. 3.10.

Fig. 3.10

Block diagram of the algorithm for determining DOV components

After obtaining an image of the stellar sky, it is necessary to select areas containing images of objects, which is done with the help of a binary mask (Fig. 3.11a). To form it, the image is first filtered in order to eliminate the influence of background heterogeneity. In AZTs, this procedure is done with the use of a median filter (Andreev 2005). Then, related areas are identified using threshold filtering (Fig. 3.11a).

Fig. 3.11

Binary mask (a) and the identified objects (b)

Objects are identified along the borders of the binary mask areas in the original image (Fig. 3.11b). The identified objects represent groups of photodetector elements, whose output signal values are used to determine the coordinates of the star image energy centers.

For highly accurate determination of astronomical coordinates, it is necessary to measure the star image position in the photodetector plane with an accuracy of hundredths of the decomposition element (pixel) of the photodetector, i.e., with subpixel resolution. This problem can be solved by different processing methods: for example, the weighted average method, the least squares method, the extreme correlation method, etc. (Berezin et al. 2004; Gonzalez et al. 2004; Mantsvetov et al. 2006; Yakushenkov and Solomatin 1986; Gaivoronsky et al. 2013). However, the weighted average method was chosen for the AZT being developed as the easiest one to implement.

Further, in order to reduce the time and amount of calculations needed to identify stars, it is necessary to determine the working area in the star catalogue based on the geodetic coordinates of the observation point and the image recording time.

Since the Earth rotates and the celestial sphere is stationary, it is necessary to know the Earth orientation relative to the celestial sphere for each moment of image recording, for which purpose Greenwich apparent sidereal time θ is used. The latter corresponds to the angle between the Greenwich meridian and the vernal equinox (see Fig. 3.9). The moment of frame recording is tied to the time recorded by a GNSS receiver. Next, GNSS time is converted to the Greenwich apparent sidereal time (Brumberg et al. 2004; Kovalevsky 2004).

Equatorial coordinates of stars are determined from the star catalogue in the identified workspace. The AZT prototype makes use of a catalogue specially developed by the Institute of Applied Astronomy of the Russian Academy of Sciences. This catalogue contains information about stars whose equatorial coordinates are known with high accuracy. But it is also possible to use such catalogues as Hipparcos, Tycho, UCAC4 (Tsvetkov 2005a, b).

Star catalogues give the data for a certain epoch of observation (as a rule, it is J2000) and represent mean equatorial coordinates. To convert to the current values of the equatorial coordinates of objects, a reduction is made taking into account the proper motions of the stars, precession and nutation parameters, annual aberration, etc. (Brumberg et al. 2004; Astronomicheskii Ezhegodnik 2008). Next, an array is formed containing the equatorial coordinates of the stars (currently in the field of view) reduced to the observation epoch.

Thus, the initial data for the star identification algorithm are coordinates x*, y* of the energy centers of the object images in the photodetector plane and the equatorial coordinates of the stars currently in the field of view reduced to the observation epoch. To solve the identification problem, it is necessary to compare the objects in two areas (those in the image and from the catalogue). In AZT, this problem is solved using the method based on the combination of two algorithms: the algorithms for similar triangles and interstellar angular distances (Gaivoronsky et al. 2015).

Finally, an array is formed in which the coordinates of the stars in the image are compared with the equatorial coordinates of the stars from the catalogue. The next step in the algorithm for determining astronomical coordinates is transformation of the rectangular coordinates of the star image energy centers into the equatorial coordinates. First, spherical coordinates of stars are transformed to the so-called standard coordinates (Blazhko 1979). This transformation is performed by a conical projection from the center of the celestial sphere to the point with coordinates (α₀, δ₀). This point corresponds to the intersection of the AZT sight axis with the celestial sphere (Fig. 3.12a).

Fig. 3.12

Transformation of star coordinates: a is the transformation of equatorial coordinates of stars into standard coordinates; b is the transformation of rectangular coordinates determined in the photodetector plane into standard coordinates

In the tangent plane, axes ζ and μ are tangent to the parallel and the celestial meridian, respectively. Axis ζ is directed towards the increase of the right ascensions and axis μ, to the north. This local system is called a standard coordinate system (Kovalevsky 2004). The transformation of equatorial coordinates of stars into standard coordinates is called the central projection; it is performed using the following expressions (Blazhko 1979):

$$\upzeta^{\ast} = \frac{ctg\updelta^{\ast}\sin (\upalpha^{\ast} - \upalpha_0 )}{{\sin \updelta_0 + ctg\updelta^{\ast}\cos \updelta_0 \cos (\upalpha^{\ast} - \upalpha_0 )}};\upmu^{\ast} = \frac{\cos \updelta_0 - ctg\updelta^{\ast}\sin \updelta_0 \cos (\upalpha^{\ast} - \upalpha_0 )}{{\sin \updelta_0 + ctg\updelta^{\ast}\cos \updelta_0 \cos (\upalpha^{\ast} - \upalpha_0 )}},$$

where

α*, δ* are the equatorial coordinates of the star;

α₀, δ₀ are the equatorial coordinates of the point corresponding to the intersection of the telescope sight axis with the celestial sphere (Fig. 3.12a):

$$\upalpha_{0 } = L + \uptheta ;\;\updelta_{0 } = B.$$

Standard coordinates, in turn, are connected by the polynomial transformation with the coordinates of the star image energy centers determined in the photodetector plane. If there are no image distortions, a linear (affine) transformation is used, which is written as follows:

$$\begin{aligned} \upzeta^{\ast} & = A_0 + A_1 x^{\ast} + A_2 y^{\ast}, \\ \upmu^{\ast} & = B_0 + B_1 x^{\ast} + B_2 y^{\ast}, \\ \end{aligned}$$

(3.2.5)

where

x*, y* are the coordinates of the star image energy center;

A₀, B₀ are the origin of the coordinate system x, y in the coordinate system ζ, μ (Fig. 3.12b).

Under the condition that the x-, y-axes are orthogonal, the transformation parameters are described as follows (Kiselev 1989):

$$\begin{aligned} A_0 & = - M_x \cdot x_0 \cdot \cos \upgamma + M_y \cdot y_0 \sin \upgamma ; \\ A_1 & = M_x \cdot \cos \upgamma ; \\ A_2 & = - M_y \cdot \sin \upgamma ; \\ B_0 & = - M_x \cdot x_0 \cdot \sin \upgamma - M_y \cdot y_0 \cos \upgamma ; \\ B_1 & = M_x \cdot \sin \upgamma ; \\ B_2 & = M_y \cdot \cos \upgamma , \\ \end{aligned}$$

where

x₀, y₀ are the coordinate origin ζ, μ in the coordinate system x, y (Fig. 3.12b);

γ is the angle between the axes +x and +ζ (Blazhko 1979);

M_x, M_y are image scales on the x-axis and y-axis, respectively:

$$M_x = \frac{m_\upzeta }{{m_x }};\begin{array}{*{20}c} {M_y = \displaystyle{\frac{m_\upmu }{{m_y }}}} \\ \end{array} .$$

The transformation parameters A₀, A₁, A₂, B₀, B₁, B₂ are determined for each image from measurements, representing a set of formulas (3.2.5) for all identified stars. This problem is solved by the least-squares method or the generalized least-squares method (Stepanov 2010; Motorin and Tsodokova 2016).

To compensate for the tilt of the objective’s sight axis relative to the axis of rotation of the optoelectronic device and eliminate the influence of the offset of the inclination sensors, observations are made in two diametrically opposite positions (I and II), with the instrument turning by 180°.

Figure 3.13 shows a block diagram of the algorithm for determining the astronomical coordinates of the point corresponding to the intersection of the axis of rotation of the optoelectronic device with the celestial sphere. To determine the astronomical coordinates (φ_Z, λ_Z), it is necessary to transform rectangular coordinates in the photodetector plane into standard coordinates using expressions (3.2.5) and the transformation parameters A₀, A₁, A₂, B₀, B₁, B₂ obtained at the previous stage. After that, it is necessary to determine the equatorial coordinates using the following formulas (Blazhko 1979):

$$\upalpha = \upalpha_0 + arctg\left( {\frac{\upzeta }{\cos \updelta_0 - \upmu \sin \updelta_0 }} \right);\updelta = arctg\left( {\frac{{\left( {\upmu + tg\updelta_0 } \right)\cos (\upalpha - \upalpha_0 )}}{1 - \upmu tg\updelta_0 }} \right).$$

Fig. 3.13

Block diagram of the algorithm for determining the astronomical coordinates of the point corresponding to the intersection of the axis of rotation of the optoelectronic device with the celestial sphere

Further, the astronomical coordinates are determined, with regard to the Greenwich apparent sidereal time, in accordance with (3.2.4).

The final astronomical coordinates of the point corresponding to the intersection of the axis of rotation of the optoelectronic device with the celestial sphere are obtained by averaging the astronomical coordinates determined in two diametrically opposite positions:

$$\upvarphi_Z = \frac{{\upvarphi_I + \upvarphi_{II} }}{2};\uplambda_Z = \frac{{\uplambda_I + \uplambda_{II} }}{2}.$$

After obtaining astronomical coordinates based on the observation data in two positions, it is necessary to make a correction for the tilt relative to the horizon according to the inclination sensors:

$$\Delta \upvarphi_n = n_\upvarphi ;\;\Delta \uplambda_n = n_\uplambda \sec \upvarphi_Z .$$

Here,

$$\begin{aligned} n_\upvarphi & = n_1 \cos (A_{ph} ) - n_2 \sin (A_{ph} ), \\ n_\uplambda & = n_1 \sin (A_{ph} ) + n_2 \cos (A_{ph} ), \\ \end{aligned}$$

where n₁, n₂ are data of the 1st and 2nd inclination sensors, respectively, calculated according to the expressions:

$$n_1 = \frac{{n_{1I} - n_{1II} }}{2};n_2 = \frac{{n_{2I} - n_{2II} }}{2},$$

where n_1I, n_1II are the data of the 1st sensor in the I and II positions, respectively; n_2I, n_2II are the data of the 2nd sensor in the I and II positions, respectively; A_ph is the azimuth of the photodetector row (Fig. 3.14):

$$A_{ph} = \frac{3\uppi }{2} - \upgamma .$$

Fig. 3.14

The azimuth of the photodetector row

In addition, it is necessary to compensate for the offset of the instantaneous pole relative to the mean pole:

$$\begin{aligned} \Delta \upvarphi_p & = - x_p \cos L + y_p \sin L; \\ \Delta \uplambda_p & = - (x_p \sin L + y_p \cos L) \cdot tgB, \\ \end{aligned}$$

where (x_p, y_p) is the offset of the instantaneous pole relative to the mean pole (Brumberg et al. 2004) (x_p, y_p = const).

Thus, the values of astronomical coordinates are calculated using the formulas:

$$\upvarphi = \upvarphi_Z + \Delta \upvarphi_n + \Delta \upvarphi_p ;\;\uplambda = \uplambda_Z + \Delta \uplambda_n + \Delta \uplambda_p .$$

Further, DOV components are determined using expressions (3.2.3), taking into account the geodetic coordinates obtained with GNSS equipment.

The error in determining DOV components with AZT depends on the accuracy of determining the geodetic and astronomical coordinates. The error in determining geodetic coordinates is determined by the characteristics of the GNSS receiver and is at a level of 2–3 m (≤0.1arcsec). The error of astronomical coordinates, in turn, depends on

• error in the image fix to the time scale;

• error in determining the equatorial coordinates of stars;

• error due to an inaccurate choice of the point corresponding to the intersection of the sight axis of the celestial sphere;

• error in determining the coordinates of the star image energy centers in the photodetector plane;

• error in the rotation of the optoelectronic device around the vertical axis;

• error of inclination sensors;

• error in determining the offset of the instantaneous pole relative to the mean pole.

The error in determining the coordinates of the star image energy centers in the photodetector plane and the error of the inclination sensors have the greatest influence on the accuracy of determining DOV components. According to preliminary estimates obtained by computer simulation, the error in determining DOV components using AZT does not exceed 0.3 arcsec.

3.2.4 Field Studies of the AZT Prototype

The AZT prototype was created to test and checkout the developed data processing algorithms (Fig. 3.15).

Fig. 3.15

The AZT prototype: 1—objective; 2—digital camera; 3—inclination sensors

The AZT prototype contained the following equipment:

• a Meade LX-90-ACF (USA) catadioptric objective with a 2000 mm focal length and 200 mm entrance pupil diameter;

• a CMOS 20-megapixel camera JAI SP-20000-PMCL (JAI Ltd. Japan) built on a CMOS image sensor; the size of the sensitive area of the image sensor is 32.77 × 24.58 mm (5120 × 3840 pixels); the pixel size is 6.4 × 6.4 μm. The camera allows synchronization of the image by an external pulse with accuracy of 25 μs;

• JAVAD ALPHA GPS/GLONASS receiver (to generate a second marker fixed to the UTC scale and determine geodetic coordinates);

• Wyler Zerotronic Type 3 inclination sensors with the angle measurement range of ±0.5°.

The AZT prototype provided for a series of stellar sky images in two diametrically opposite positions. Observations were carried out at one point on different dates. Processing of the observation data was carried out using the developed algorithms.

The following results were obtained after processing the data of all observation series: the values of the DOV components determined in the field studies are close to the real values; the RMSD between the series does not exceed 1 arcsec, which is an acceptable result for the prototype, given the unequal effect of temperature fields on different structural elements, as well as changes in illumination because the observations were conducted in urban conditions.

3.2.5 Conclusion

A description is given of the AZT developed at Concern CSRI Elektropribor, JSC. The telescope is intended to determine DOV components in real time from field observations of the ircumzenithal area of the stellar sky.

The AZT principle of operation, the main parameters of its component parts, as well as the algorithms for processing the observation data have been discussed, and the telescope accuracy characteristics are given.

The results of the AZT prototype field studies clearly show the effectiveness of the proposed technical solutions and algorithms for processing observation data, as well as the feasibility of using the AZT under consideration to determine DOV with high accuracy.

3.3 Inertial Geodetic Method for DOV Determination

As mentioned in Sect. 3.1, the idea of the inertial geodetic method is based on using data from a precision INS and a GNSS receiver (Nash and Jordan 1978; Anuchin et al. 1982; Peshekhonov et al. 1989; Dmitriev 1997; Salychev et al. 1999; Nassar, 2003; Li and Jekeli, 2008). At the same time, unlike the classical astrogeodetic method, the INS used in the implementation of the inertial geodetic method produces not only astronomical coordinates but also their derivatives. This makes it possible to solve the DOV estimation problem using differential measurements, based on external information on the components of the linear speed vector and the acceleration of the vehicle in the local navigation frame. Section 3.3 is devoted to the features of the inertial geodetic method. In this case, it is assumed that a strapdown inertial measurement unit (SIMU) acts as an INS.

3.3.1 Inertial Geodetic Method Using Positional and Velocity Measurements

When DOV is determined using the inertial geodetic method, in general, the following velocity and positional differential measurements can be used (taking into account the features of the satellite navigation equipment in determining navigation parameters, including synchronization of velocity measurements) (Emel’yantsev and Stepanov 2016):

$$\begin{aligned} z_{V_j } \left( {t_{k + 1} } \right) & = \left[ {\nabla S_{j\_INS} \left( {t_{k + 1} } \right) - \nabla S_{j\_GNSS} \left( {t_{k + 1} } \right)} \right]/Tz,\quad (j = E,N,H), \\ z_\upvarphi (t_{k + 1} ) & = \upvarphi_{INS} (t_{k + 1} ) - \upvarphi_{GNSS} (t_{k + 1} ), \\ z_\uplambda (t_{k + 1} ) & = \uplambda_{INS} (t_{k + 1} ) - \uplambda_{GNSS} (t_{k + 1} ), \\ z_h (t_{k + 1} ) & = h_{INS} (t_{k + 1} ) - h_{GNSS} (t_{k + 1} ), \\ \end{aligned}$$

where

• $\nabla S_{j\_GNSS} \left( {t_{k + 1} } \right)$ are the increments of the Cartesian coordinates of a vehicle in projections onto the geographic axes measured in a GNSS receiver with a discreteness of $Tz = t_{k + 1} - t_k$ (for most modern GNSS receivers, interval Tz is in the range between 0.1 and 1 s);

  $\nabla S_{j\_INS} \left( {t_{k + 1} } \right) = \int_{t_k }^{t_{k + 1} } {V_{j\_pr} (\uptau )} d\uptau$ are the increments of Cartesian coordinates on the interval $Tz$ calculated according to the INS data on the vehicle speed.

Taking into account the data synchronization of the INS and the GNSS receiver, we can write:

$$z_{V_j } \left( {t_{k + 1} } \right) = \Delta V_j (t_{k + 1} ) + \upnu_{V_j } \left( {t_{k + 1} } \right),$$

(3.3.1)

where

$\Delta V_j$ is the error of the linear-speed vector components produced by the INS;

$\upnu_{V_j } \left( {t_{k + 1} } \right) = - \left[ {\Delta V_j \left( {t_{k + 1} } \right) - \Delta V_j \left( {t_k + Tz/2} \right)} \right] - \updelta \nabla S_{j\_GNSS} \left( {t_{k + 1} } \right)/Tz$ is the reduced noise. Here, $\updelta \nabla S_{j\_GNSS} \left( {t_{k + 1} } \right)/Tz$ is the error of the linear-speed vector components. While deducing the above expression, the following should be borne in mind. In the GNSS receiver, the speed is generated as an integral of the phase in the Doppler channel over the time interval Tz. Thus, in practice, it can be assumed that the obtained speed corresponds to its average value on the interval Tz. To ensure synchronization during the formation of differential measurements, the components of the INS speed are generated in a similar way. To form measurements, it is important to go to the current time for determining the speed by the INS and its error while taking into account the difference in speed errors related to the middle of the interval Tz and the time it is finished and attributing this difference to the measurement noise. It should also be noted that, since the difference in the errors of the INS speed components generated by INS within the interval Tz is small, the fact that the measurements correlate with their errors can be neglected.

For positional measurements, the following is true:

$$\begin{aligned} z_\upvarphi (t_{k + 1} ) & = \Delta \upvarphi - \updelta \upvarphi_{GNSS} , \\ z_\uplambda (t_{k + 1} ) & = \Delta \uplambda - \frac{1}{\cos \upvarphi }\updelta W_{GNSS} , \\ z_h (t_{k + 1} ) & = \Delta h - \updelta h_{GNSS} , \\ \end{aligned}$$

(3.3.2)

where $\Delta \upvarphi ,\updelta \upvarphi_{GNSS}$, $\Delta \uplambda ,\updelta W_{GNSS} = \updelta \uplambda_{GNSS} \cos \upvarphi$, $\Delta h,\updelta h_{GNSS}$ are the errors of the INS and GNSS (in the differential mode), correspondingly, with respect to the observer’s coordinates.

Assume that speed measurements (3.3.1) are used to effectively damp the natural (Schuler and diurnal) variations of SIMU errors. Then, according to the analytical solutions given in Emel’yantsev and Stepanov (2016), in the conditions of a quasi-stationary vehicle (i.e., at stops, when it is not required to get information about the change in the DOV), at some i-th point of the route for smoothed time values of positional measurements (3.3.2), we will have the following:

$$\tilde{z}_{\upvarphi i} = - \frac{1}{\Omega }( - \Delta \overline{\upomega }_{bH} \cos \upvarphi_i + \Delta \overline{\upomega }_{bN} \sin \upvarphi_i ) + \frac{{\Delta \overline{a}_{bN} }}{g} - \upxi_i - \updelta \tilde{\upvarphi }_{GNSS} ,$$

(3.3.3)

$$\begin{aligned} \tilde{z}_{\uplambda i} \cos \upvarphi_i & = - \tilde{\upalpha }_* (t_k )\cos \upvarphi_i + (\Delta \overline{\upomega }_{bH} \sin \upvarphi_i + \Delta \overline{\upomega }_{bN} \cos \upvarphi_i )\cos \upvarphi_i \cdot \Delta t \\ & \quad - \frac{1}{\Omega }\Delta \overline{\upomega }_{bE} \sin \upvarphi_i + \frac{{\Delta \overline{a}_{bE} }}{g} + \upeta_i - \updelta \tilde{W}_{GNSS} , \\ \end{aligned}$$

(3.3.4)

where $\tilde{\upalpha }_\ast (t_k )$ is the smoothed value of the SIMU error in longitude accumulated due to the gyroscope drifts; $\Delta t = t - t_k$, where $t_k$ is the moment of the last SIMU correction in longitude; $\Delta \overline{\upomega }_{bj}$, $\Delta \overline{a}_{bj}$ ($j = E,N,H$) are low-frequency components of the gyroscope drifts and accelerometer errors in projections onto the geographical axes due to instability of their zeros with respect to the values during the calibration time; $\Omega$ is the angular velocity of the diurnal rotation of the Earth; $g$ is the value of the normal gravity acceleration at the equator; $\upxi_i ,\upeta_i$ are the values of DOV components at the observer’s meridian and in the prime vertical plane, respectively; $\updelta \tilde{\upvarphi }_{GNSS} ,\updelta \tilde{W}_{GNSS}$ is the level of the smoothed noise of the GNSS receiver.

Note that in the case of the SIMU longitudinal correction generated by the GNSS, the expression for error $\tilde{\upalpha }_\ast (t_k )$, according to Emel’yantsev and Stepanov (2016), can be written as:

$$- \tilde{\upalpha }_* (t_k )\cos \upvarphi = \frac{1}{\Omega }\Delta \overline{\upomega }_{bE} (t_k )\sin \upvarphi_i - \frac{{\Delta \overline{a}_{bE} (t_k )}}{g} - \upeta (t_k ).$$

(3.3.5)

It is also pertinent to note that due to the presence of the term $\tilde{\upalpha }_\ast (t_k )$, i.e., accumulation of the INS error in longitude, it is impossible to determine the total value of the DOV component $\upeta$ in the prime vertical plane during the correction, even if the longitude is known exactly. That is, with the specified scope of measurements, the DOV component $\upeta$ cannot be observed fully. For a quasi-stationary vehicle, the frequency of longitudinal corrections does not affect the accuracy of DOV estimation. A similar situation takes place during motion, since the errors in (3.3.5) are not separated. They can be separated due to maneuvering, which is undesirable for DOV estimation because this dramatically complicates the description of the DOV model and causes difficulties in estimation (separation of DOV spectra and drifts of gyroscopes and accelerometers, which will be discussed later).

Substituting (3.3.5) into Eq. (3.3.4), we derive:

$$\begin{aligned} \tilde{z}_{\uplambda i} \cos \upvarphi_i & = (\Delta \overline{\upomega }_{bH} \sin \upvarphi_i + \Delta \overline{\upomega }_{bN} \cos \upvarphi_i )\cos \upvarphi_i \cdot \Delta t \\ & \quad - \frac{1}{\Omega }\Delta \tilde{\upomega }_{bE} \sin \upvarphi_i + \frac{{\Delta \tilde{a}_{bE} }}{g} + \nabla \upeta_i - \updelta \tilde{W}_{GNSS} , \\ \end{aligned}$$

(3.3.6)

where $\nabla \upeta_i = \upeta_i - \upeta (t_k )$ is the increment of the DOV component $\upeta$ with respect to the SIMU update point; $\Delta \tilde{\upomega }_{bE}$, $\Delta \tilde{a}_{bE}$ are the variations of the corresponding errors over the interval $\Delta t = t - t_k$.

According to (3.3.3), (3.3.6), the DOV estimates at the i-th route point are calculated as follows:

$$\begin{aligned} \hat{\upxi }_i & = - \tilde{z}_{\upvarphi i} , \\ \nabla \hat{\upeta }_i & = \tilde{z}_{\uplambda i} \cos \upvarphi_i , \\ \end{aligned}$$

(3.3.7)

and the errors of their determination are described by the following expressions:

$$\begin{aligned} \updelta \tilde{\upxi }_{gi} & = \frac{1}{\Omega }( - \Delta \overline{\upomega }_{bH} \cos \upvarphi_i + \Delta \overline{\upomega }_{bN} \sin \upvarphi_i ) - \frac{{\Delta \overline{a}_{bN} }}{g} + \updelta \tilde{\upvarphi }_{GNSS} , \\ \updelta \nabla \tilde{\upeta }_i & = (\Delta \overline{\upomega }_{bH} \sin \upvarphi_i + \Delta \overline{\upomega }_{bN} \cos \upvarphi_i )\cos \upvarphi_i \Delta t - \frac{1}{\Omega }\Delta \tilde{\upomega }_{bE} \sin \upvarphi_i \\ & \quad + \frac{{\Delta \tilde{a}_{bE} }}{g} - \updelta \tilde{W}_{GNSS} . \\ \end{aligned}$$

(3.3.8)

Assume that bias instabilities of the SIMU’s gyroscopes and accelerometers are at a level of $\Delta \tilde{\upomega } \le 3 \cdot 10^{ - 5}$°/h, $\Delta a \le 10^{ - 5}$ m/s². The level of smoothed values $\updelta \tilde{\upvarphi }_{GNSS}$, $\updelta \tilde{W}_{GNSS}$ of the GNSS receiver noise does not exceed 3 m. Then in middle latitudes, approximately, we have $\tilde{\upxi }_i$ ≤ 0.6 arcsec, $\nabla \tilde{\upeta }_i$ ≤ 0.7 arcsec. Note that the time between SIMU longitudinal corrections should not exceed 3 h, which characterizes the allowable interval between the reference points for $\upeta$.

It should be noted that to improve the accuracy of DOV determination, it is advisable to carry out initial measurements both on forward and reverse courses. In this case, SIMU gyroscope drifts and accelerometer errors will be autocompensated in the axes of the local navigation frame with the North, East and Earth ellipsoid orthogonal axes with the origin at the point of the navigation solution (Groves 2013), which results in a sharp decrease in the accumulated error in coordinates and, accordingly, increase in the accuracy of DOV determination. Assuming that their variation has a low-frequency character, their effect, as well as the effect of misalignment between the sensitive axes of the gyro and accelerometer, can be critically mitigated.

When the problem of DOV estimation is solved by the inertial geodetic method while the vehicle is moving, it is required to take into account the DOV variation along the motion path using, in particular, the corresponding statistical models, for example, those given in Nash and Jordan (1978). However, it should be taken into consideration that the accuracy of DOV determination can be improved only if there is a significant difference between the spectra of gyro drifts and accelerometer errors and the DOV spectrum in the process of the vehicle motion. In addition, the inconsistency of the calculated DOV models used in the filtering problem with their real changes in the survey area may result in additional errors in their estimation.

As follows from the above reasoning, when DOV are determined by the inertial geodetic method using data even from a precise INS, it is necessary to have reference points of exact DOV values, which is a significant disadvantage of this method.

3.3.2 Using ZUPT Technology

Another variant of the method under consideration is based on the use of differential velocity and acceleration measurements only. For land vehicles, it is implemented using so-called ZUPT corrections (zero velocity update). In marine and airborne gravimetry, this method can also make use of GNSS data (Dmitriev 1997; Mangold 1995; Salychev et al. 1999; Nassar 2003; Li and Jekeli 2008).

It was mentioned above that the use of differential position measurements provides observability of only the DOV full meridional component. It should be emphasized that in this case, when using ZUPT velocity measurements, it is only possible to measure the increments of both DOV components along the motion path, which follows from the specific features of the formation of differential measurements as increments of the value to be analyzed at a given time interval (see (3.3.13), (3.3.15)).

The initial information for DOV estimation during ZUPT corrections (INS) is a measurement, for example, for component $\upxi$:

$$z_\upxi = \Delta \tilde{\dot{V}}_N ,$$

which represents the output signal of the corresponding “horizontal” accelerometer smoothed over time $\tilde{T}$ of a stop (here, $\Delta V_N$ is the INS error in the north component of the linear speed vector). For SIMU, this is the projection of the data from the triad of accelerometers on the axis $N$. According to Dmitriev (1997), this measurement for the ($i - 1$)-th stop can be represented as follows:

$$z_{\upxi (i - 1)} = g\tilde{\upbeta }_{(i - 1)} + \Delta \overline{a}_{bN(i - 1)} - g\upxi_{(i - 1)} ,$$

(3.3.9)

where $\tilde{\upbeta }_{(i - 1)}$ is the ($i - 1$)-th stopping time-averaged error of the vertical construction, determined mainly by its Schuler oscillations; $\Delta \overline{a}_{bN(i - 1)}$ is the zero drift of the “horizontal” accelerometer taking into account the assumption that the accelerometer noises are effectively smoothed over interval $\tilde{T}$.

The variability of error $\upbeta (t)$ in the $i$-th interval of motion is described by two equations for the northern channel of the vertical analogue (Anuchin and Emel’yantsev 2003). Reduce them to the form (Dmitriev 1997), given that the interval of motion between stops is $T$$< <$$2\uppi /\upnu$:

$$\ddot{\upbeta } + \upnu^2 \upbeta = \Delta \tilde{\upomega }_{m_2 } - \frac{1}{R}(\Delta \overline{a}_{bN} - \dot{V}_E \Delta K + \dot{V}_N \Delta M_a ) + \upnu^2 \upxi ,$$

(3.3.10)

where, according to Emel’yantsev and Stepanov (2016), $\Delta \tilde{\upomega }_{m_2 } = - \Omega \uptau_\ast (t_0 ) + \Delta \upomega_{bm_2 }$ is the equivalent drift of the gyro unit around the eastern axis (here, $\Omega$ is the angular velocity of the Earth diurnal rotation; $\uptau_\ast$ is the SIMU error in the construction of the celestial axis in a plane orthogonal to the plane of the observer’s meridian); $\upnu$ is the Schuler frequency; $\Delta M_a$ is the accuracy of the accelerometer scale factor; $\Delta K$ is the INS heading error.

At the stop, provided that $\Delta V_N (t_0 ) = 0$, from (3.3.9) it follows:

$$\upbeta (t_0 ) = \tilde{\upbeta }_{(i - 1)} = - \frac{1}{g}\Delta \overline{a}_{bN(i - 1)} + \upxi_{(i - 1)} ,\dot{\upbeta }(t_0 ) = \Delta \tilde{\upomega }_{m_2 i} .$$

(3.3.11)

Following (Dmitriev 1997), assume that the INS operation time includes intervals of motion with a length $T$ and stops with a length $\tilde{T}$. The vehicle acceleration on each interval [0, $T$] can be described by the following model:

$$\dot{V}(t) = V\updelta (t) - V\updelta (T - t),$$

(3.3.12)

where $\updelta (t)$ is a delta function. This model defines a uniform motion on the interval [0, $T$] with an instantaneous stop and the speed acceleration to a value equal to V.

The solution to Eq. (3.3.10) for $t = T$ of the beginning of the i-th stop, taking into account (3.3.12), and for $t_0 = 0$, $\upnu$ << 1, has the form:

$$\begin{aligned} \upbeta (T) & = \tilde{\upbeta }_{(i - 1)} + \Delta \tilde{\upomega }_{m_2 i} T - \frac{1}{R}( - \Delta K \cdot S_E + \Delta M_a S_N ) \\ & \quad - \upnu^2 \int\limits_0^T {\left[ {\frac{1}{g}\Delta a_{bN} (\uptau ) - \upxi (\uptau )} \right]} \left( {T - \uptau } \right)d\uptau , \\ \end{aligned}$$

(3.3.13)

where $S_E$, $S_N$ are the lengths of the path traveled by the vehicle on the $i$-th section of the motion path in geographic axes; $\Delta a_{bN} (\uptau ),\upxi (\uptau )$ refer to time $\Delta a_{bN}$ and spatial $\upxi$ variability on the intervals $T$ and $S$.

Based on the solutions given in (Dmitriev 1997; Emel’yantsev and Stepanov 2016), it can be shown that, when using a medium accuracy-grade SIMU ($\Delta \tilde{\upomega } \le 5 \cdot 10^{ - 3}$°/h, $\Delta a \le 3 \cdot 10^{ - 5}$ m/s², $\Delta M_a \le 10^{ - 5}$) and the lengths of intervals between vehicle stops $T$ = 2…5 min, formula (3.4.13), with regard to smoothing during formation of measurements (3.3.9), can be presented in the following form:

$$\tilde{\upbeta }_i = \tilde{\upbeta }_{(i - 1)} + \Delta \tilde{\upomega }_{m_2 i} T + \Delta_i ,$$

(3.3.14)

where error $\Delta_i$ does not exceed 0.1 arcsec (Markley and Crassidis 2014).

By analogy with (3.3.9), taking into account (3.3.14), measurement $z_\upxi$ for the i-th stop is represented as follows:

$$\begin{aligned} z_{\upxi i} & = g\tilde{\upbeta }_i + \Delta \overline{a}_{bNi} - g\upxi_i \\ & = - g\nabla \upxi_i + \Delta \overline{a}_{bNi} - \Delta \overline{a}_{bN(i - 1)} + g\Delta \tilde{\upomega }_{m_2 i} T + g\Delta_i , \\ \end{aligned}$$

(3.3.15)

where $\nabla \upxi_i = \upxi_i - \upxi_{(i - 1)}$.

Then, the following formula is used to obtain the estimate of increment $\upxi$:

$$\updelta \hat{\upxi }_i = - z_{\upxi i} /g;$$

(3.3.16)

at the same time, the error in estimating increment $\upxi$ is defined as follows:

$$\updelta \nabla \tilde{\upxi }_i = - \left( {\frac{{\Delta \overline{a}_{bNi} - \Delta \overline{a}_{bN(i - 1)} }}{g} + \Delta \tilde{\upomega }_{m_2 i} T + \Delta_i } \right).$$

(3.3.17)

For the error in determining increment $\upxi$ relative to the reference point, we have:

$$\updelta \nabla \tilde{\upxi }_i = \sum_{j = 1}^i {\updelta \nabla \tilde{\upxi }_j } = - \left[ {\frac{{\Delta \overline{a}_{bN} (t_i ) - \Delta \overline{a}_{bN} (t_0 )}}{g} + \sum_{j = 1}^i {\Delta \tilde{\upomega }_{m_2 j} T} + \sum_{j = 1}^i {\Delta_j } } \right].$$

(3.3.18)

The analysis of (3.3.18) shows that the accuracy of determining DOV increments relative to the reference point with the use of the ZUPT INS correction is affected only by the instability of accelerometer biases, while the error of their initial calibration does not play a significant role. At the same time, calibration errors of the gyro drifts and their time instability are fully reflected in the errors of DOV estimation.

The effect of the gyroscope drift can be reduced by processing a sequence of measurements of the type (3.3.15) generated at stops with the aim to filter relatively high-frequency signals $\nabla \upxi_i$, $\nabla \upeta_i$ against the background of slowly varying sequences $\Delta \tilde{\upomega }_i T$. For this purpose, it is necessary to develop appropriate statistical models of DOV and gyro drifts. This makes it possible to obtain (Dmitriev 1997) DOV determination errors of about $\upsigma_{\tilde{\upxi }(\tilde{\upeta })} \le$ 1 arcsec using the data from the INS of the considered accuracy grade over the interval $T_\Sigma$ = 1 h. Obviously, a significant increase in the accuracy of DOV determination $\upsigma_{\tilde{\upxi }(\tilde{\upeta })}$ << 1 arcsec can be achieved if the DOV values are known exactly not only at the starting point but also at the end $t = T_\Sigma$ point of the route.

3.3.3 DOV Determination in High Latitudes

Consider a possible variation of the inertial geodetic method which can be used to determine the full DOV while maintaining the accuracy of DOV determination in high latitudes. For this purpose, it is proposed to additionally include a specially designed precision GNSS compass with an antenna baseline from 6 to 10 m into the integrated system and replace the differential measurement of longitude with the corresponding heading measurement:

$$z_K (t_{k + 1} ) = K_{INS} (t_{k + 1} ) - K_{GNSS} (t_{k + 1} ) = \Delta K - \updelta K_{GNSS} ,$$

(3.3.19)

where $\updelta K_{GNSS}$ are the errors of the multi-antenna GNSS receiver that are determined mostly by phase measurement noise provided that the reference frames of the SIMU and GNSS antenna module of the receiving equipment are matched in azimuth. Note that the error level of $\updelta K_{GNSS}$ does not practically depend on the latitude of the vehicle location.

Assume that in this case as well, velocity measurements (3.3.5) are used to damp the natural variations of SIMU errors. Then, according to the solutions given in (Emel’yantsev and Stepanov 2016), in the conditions of a quasi-stationary vehicle at an i-th route point, the heading measurements (3.3.19) smoothed on the final time interval can be represented as follows:

$$\tilde{z}_{Ki} \cos \upvarphi_i = - \frac{1}{\Omega }\Delta \overline{\upomega }_{bE} + \sin \upvarphi_i \frac{{\Delta \overline{a}_{bE} }}{g} + \sin \upvarphi_i \cdot \upeta_i - \updelta \tilde{K}_{GNSS} \cos \upvarphi_i .$$

(3.3.20)

From Eqs. (3.3.3) and (3.3.20), it follows that $\hat{\upxi }_i = - \tilde{z}_{\upvarphi i}$, $\hat{\upeta }_i = \tilde{z}_{Ki} ctg\upvarphi_i$, where for the DOV estimation errors, we have:

$$\begin{aligned} \updelta \tilde{\upxi }_i & = \frac{1}{\Omega }( - \Delta \overline{\upomega }_{bH} \cos \upvarphi_i + \Delta \overline{\upomega }_{bN} \sin \upvarphi_i ) - \frac{{\Delta \overline{a}_{bN} }}{g} + \updelta \tilde{\upvarphi }_{GNSS} , \\ \updelta \tilde{\upeta }_i & = - \frac{1}{\Omega \sin \upvarphi_i }\Delta \overline{\upomega }_{bE} + \frac{{\Delta \overline{a}_{bE} }}{g} - \updelta \tilde{K}_{GNSS} ctg\upvarphi_i . \\ \end{aligned}$$

(3.3.21)

From the solutions obtained, it follows that the proposed method makes it possible to estimate the total values of DOV components, so that there is no need in making reference points at sea, and also the fact that the effect of errors $\updelta K_{GNSS}$ in heading measurements on the accuracy of DOV determination is significantly reduced because the level of these errors does not depend on the latitude.

With the accepted values of SIMU and GNSS receiver errors in position coordinates, as well as the level of the smoothed noise of the precision GNSS compass (which includes the errors in matching the reference frames of the SIMU and GNSS antenna module) of the order of $\updelta \tilde{K}_{GNSS}$ = 5 arcsec at a latitude of 80°, we have $\tilde{\upxi }_i \le 0.6$ arcsec, $\tilde{\upeta }_i \le 1.06$ arcsec.

3.3.4 Simulation Results

To study the errors of the integrated system in solving the problem under consideration, a simulation model of the SIMU operation was used with discrete recursive algorithms similar to the model given in (Emel’yantsev and Stepanov 2016).

To form the virtual units of SIMU gyros and accelerometers, the following values of the parameters of their error models projected on the axes $x_b y_b z_b$ of the measurement unit were used.

Gyro errors:

• $\Delta M_{gx} ,\,\,\Delta M_{gy} ,\,\,\Delta M_{gz}$—instability of scale factors—random values with RMSE of $10^{ - 5}$%;

• $\Delta \overline{\upomega }_{xb} ,\,\,\Delta \overline{\upomega }_{yb} ,\;\Delta \overline{\upomega }_{zb}$—systematic error components of the gyroscopes characterizing gyro bias stability from run to run—random values with an RMSE of $3 \cdot 10^{ - 5}$°/h;

• $\Delta \upomega_{xb} ,\,\,\Delta \upomega_{yb} ,\,\,\Delta \upomega_{zb}$—gyro random error components characterizing in-run bias stability—the first-order Markov processes $\upsigma 1_g = \, 10^{ - 5}$°/h, $\upmu_g$ = 1/20 h^–1;

• the gyro fluctuation error components—discrete white noise with an RMSE of $\upsigma 2_g = \, 10^{ - 3}$°/h at a frequency of 100 Hz.

Errors of linear accelerometers:

• $\Delta M_{ax} ,\,\,\Delta M_{ay} ,\,\,\Delta M_{az}$—instability of scale factors—random values with an RMSE of $10^{ - 4}$%;

• $\Delta \overline{a}_{xb,} \,\Delta \overline{a}_{yb,} \,\Delta \overline{a}_{zb}$—bias stability from run to run—random values with an RMSE of $10^{ - 5}$ m/s²;

• $\Delta a_{xb,} \,\Delta a_{yb,} \,\Delta a_{zb}$—in-run bias stability—first-order Markov processes $\upsigma 1_a = 3 \cdot 10^{ - 6}$ m/s², $\upmu_a = 1/1 \, h^{ - 1}$;

• fluctuation error components—discrete white noise at the operating frequency with an RMSE of $\upsigma 2_a = \, 10^{ - 4}$ m/s² at a frequency of 100 Hz.

DOV components were represented by Markov processes similar to those in (Nash and Jordan 1978), with $\upsigma_\upxi = \upsigma_\upeta$ = 5 arcsec, $d$ = 20 nm.

The GNSS errors:

• velocity errors —discrete white noise $\upsigma_{V_{GNSS} }$ = 0.01 m/s at 10 Hz;

• position errors—discrete white noise $\upsigma_{S_{GNSS} }$ = 3 m at 10 Hz;

• heading errors—deviation $\updelta \overline{K}_{GNSS}$ = 5 arcsec and discrete white noise $\upsigma_{\updelta K_{GNSS} }$ = 3 arcmin at 10 Hz.

As is known, the majority of currently available GNSS compasses have an accuracy of about 0.2°·1/L (1σ), where 1/L is the ratio of the 1-m antenna baseline to the length L of the antenna baseline. This level of errors is primarily due to the noise of phase measurements generated in the GNSS receiver [Novatel].

To set the level of errors of the specialized GNSS compass with an antenna baseline of about 6 m shown in Fig. 3.16, the results of the sea trials of the Vega GNSS compass (developed at the CSRI Elektropribor) with an about 19 m-long antenna baseline were used (Emel’yantsev et al. 2011). From this research, it follows that the heading fluctuation errors of the stable course were about 3 arcmin (1σ). The angular offset in the heading error is due to the misalignment in the reference frames of the GNSS compass and FOG-based IMU-120 (IXblue, France) used as a reference SIMU.

Fig. 3.16

Heading error (arcmin) of Vega GNSS compass as compared with IMU-120

In the simulation, it is assumed that the reference frames of the precision SIMU and the GNSS compass antenna module are matched with an accuracy of 5 arcsec before going to sea at a point with known DOV components, and that in the process of DOV determination, the position of antenna phase centers is periodically updated, for example, using the procedure described in (Blazhnov et al. 2014).

The following differential measurements are used:

$$\begin{aligned} z_{V_j } \left( {t_{k + 1} } \right) & = [\nabla S_{j\_INS} \left( {t_{k + 1} } \right) - \nabla S_{j\_GNSS} \left( {t_{k + 1} } \right)]/Tz,\quad (j = E,N,H), \\ z_\upvarphi (t_{k + 1} ) & = \upvarphi_{INS} (t_{k + 1} ) - \upvarphi_{GNSS} (t_{k + 1} ), \\ z_\uplambda (t_{k + 1} ) & = \uplambda_{INS} (t_{k + 1} ) - \uplambda_{GNSS} (t_{k + 1} ), \\ z_h (t_{k + 1} ) & = h_{INS} (t_{k + 1} ) - h_{GNSS} (t_{k + 1} ), \\ z_K (t_{k + 1} ) & = K_{INS} (t_{k + 1} ) - K_{GNSS} (t_{k + 1} ). \\ \end{aligned}$$

(3.3.22)

These measurements were processed using the Kalman filter with feedback at each measurement epoch.

The following approximations were used to describe the error model of the integrated system:

• gyro $\Delta \overline{\upomega }_i$ and accelerometer $\Delta \overline{a}_i (i = x_b ,y_b ,z_b )$ run-to-run and in-run bias stability were approximated by the relevant Wiener processes;

• the DOV components $\upxi_i$, $\upeta_i$ at the i-th point of the path were described by random values with known variances.

Under the assumptions made, the state vector of the simulation model of the system is represented as follows:

$$\begin{aligned} x^T = & \left[ {\begin{array}{*{20}l} \upalpha \hfill & \upbeta \hfill & \upgamma \hfill & {\Delta V_E } \hfill & {\Delta V_N } \hfill & {\Delta V_H } \hfill & {\Delta \upvarphi } \hfill & {\Delta \uplambda } \hfill & {\Delta h} \hfill & {\Delta \overline{\upomega }_{xb} } \hfill & {\Delta \overline{\upomega }_{yb} } \hfill \\ \end{array} } \right. \\ & \quad \left. {\begin{array}{*{20}l} {\Delta \overline{\upomega }_{zb} } \hfill & {\Delta \overline{a}_{xb} } \hfill & {\Delta \overline{a}_{yb} } \hfill & {\Delta \overline{a}_{zb} } \hfill & \upxi \hfill & \upeta \hfill \\ \end{array} } \right], \\ \end{aligned}$$

and the dynamics matrix $F = \left[ {f_{i,j} } \right],\left( {i,j = \overline{1,17}} \right)$ is similar to the models given in (Emel’yantsev and Stepanov 2016), taking into account the assumptions made.

The measurement matrix $H_{k + 1}$ corresponds to Eq. (3.3.22), whose non-zero elements are the following:

$$H_{1,4} = 1;H_{2,5} = 1;H_{3,6} = 1;H_{4,7} = 1;H_{5,9} = 1;H_{6,1} = 1.$$

(3.3.23)

The simulation was carried out with the following initial data:

• characteristics of the Earth and gravitational field:

  $R = {6371000}$ (m) is the mean radius of the Earth;

  $\Omega = {7.2921151467} \cdot {10}^{ - 5}$ (rad/s); $S_{gr} (t_0 )$ = 0;

  $\upmu_g = {3.98603} \cdot {10}^{{14}}$ (m³/s²) is the gravitational constant of the Earth;

  ε = 2.634 ⋅ 10²⁵(m⁵/s²) and χ = 6.773 ⋅ 10³⁶(m⁷/s²) are the coefficients of the gravity potential decomposition;

• φ = 80°; $V_o = 0$ m/s; K = 0° or K = 180°, pitching angles are small.

The simulation results are presented in Fig. 3.17:

Fig. 3.17

Errors (arcsec) in DOV estimates at K = 0° (a) and at K = 180° (b)

From the above data, it follows that averaged errors in DOV determination at the $i$-th point of the path obtained on the forward and reverse courses are ≤0.1  arcsec for $\tilde{\upxi }_i$ and ≤0.75 arcsec for $\tilde{\upeta }_i$.

In conclusion, it should be noted that a precision multi-antenna satellite orientation system with two antenna baselines, the one that determines the vehicle’s pitching angles, may be an alternative to a GNSS compass. In this case, differential measurements formed on the basis of pitching angles can be used instead of heading measurements. This will completely eliminate the need to use positional measurements (3.3.2) and significantly reduce the accuracy requirements for the SIMU gyroscopes. The proposed version of the method also allows determining the full DOV values in different regions of the World Ocean with no limitations on the observer’s latitude.

3.4 Conclusion

Features of the inertial geodetic method for DOV determination have been considered.

It is noted that the use of only velocity and positional differential measurements cannot provide full observability of DOV components since it allows determining only one—the full value—of the DOV component, in the plane of the observer’s meridian. As for ZUPT technology, it does not allow determination of full DOV components.

A modified inertial geodetic method, proposed and considered in this section, makes it possible to determine full DOV components in all latitudes, including high latitudes. The modified method is implemented through the use of a precision INS and a specialized GNSS compass with an antenna baseline of about 6 m.

It is shown that in order to achieve an acceptable accuracy in DOV determination, it is necessary to ensure the accuracy of determining the heading angle of about 6 arcsec. It should be noted that the error in determining the heading angle also includes the error in matching the reference frames of the INS and the antenna module of the GNSS compass. Such matching must be carried out with an error of no more than 6 arcsec every time before the vessel leaves the port at a point with known DOV value, and also periodically in the process of DOV determination to precisely determine the position of the phase centers of the GNSS compass receiving antennas.