Introduction

Heights are the basic geographical information for the study of marine geophysics, geodesy and oceanography. The local mean sea level (LMSL) estimated from the long-term tidal data is often selected as the national or regional height datum (Rapp 1994). The height datum is commonly connected to many leveling benchmarks to build and maintain the national or regional height reference frame with the precise leveling method. So the orthometric or normal heights (NHs) are traditionally referenced to LMSL. Differences among different local height datums may be >2 m because of the effect of sea surface topography (Rummel and Teunissen 1988). Because continent and island are separated by sea, there are often different height datums on continent and island, which makes one country or region owning islands have different height reference frames and not unify the corresponding geographical information. Therefore many geodetic scientists pay more attention to the height datum unification and height transfer (Amos and Featherstone 2009; Zhang et al. 2009; Nahavandchi and Soltanpour 2006; Ardalan and Safari 2005; Jekeli 2003; Hipkin 2002; Burša et al. 1999, 2001; Featherstone 2000; Grafarend and Ardalan 1999; Pan and Sjöberg 1998; Rapp 1995; Rummel and Ilk 1995; Sanso and Usai 1995; Heck and Rummel 1990; Colombo 1980).

NH connection across sea can be made to unify the height datum of continent and island using methods of precise leveling, trigonometric leveling, hydrostatic leveling, oceanic dynamics, GPS/leveling, and/or geopotential difference (Xu et al. 2009). The precise leveling method is not used to connect heights through the long distance across sea, which makes the distance difference between forward sight and backward sight very large. The height difference estimated with the trigonometric method includes errors caused from the no parallelism of levels, the vertical refractive index difference, the deflection of the vertical (DOV) and the precise target sighting (Guo et al. 2011; Li et al. 2007). One connecting pipe full of homogeneous liquid which should have much high quality and no air pocket to hold the hydrostatic balance is used to transfer height across sea based on the hydrostatic balance theory with the hydrostatic leveling method (Madsen and Tscherning 1990). The hydrostatic balance is seriously affected by the air pressure difference, the temperature difference and the liquid density difference (Li and Jiang 2001). LMSL differs from the geoid/quasigeoid since there exist the sea surface slope and the sea surface topography (Xu and Rummel 1991; Rummel and Teunissen 1988). The long-term tidal data should be elaborately processed to calculate LMSLs (Ekman 1999) to connect height with the oceanic dynamic leveling method which needs more oceanic data to remove the effect of the sea surface slope and the dynamic oceanic topography (Guo et al. 2010a). A local continent geoid/quasigeoid model fitted with GPS/leveling data can be extrapolated to near islands to connect height across sea. On the one hand, the precision for the mathematical local geoid/quasigeoid model is only up to level of decimeter or centimeter (Guo et al. 2005). On the other hand, the extrapolating algorithm also gives new errors and the premise for the method requires GPS/leveling benchmarks on continent and unknown points on island belonging to the same local geoid/quasigeoid. The geopotential difference method is also used to connect height across sea (Xu et al. 2009). The geodetic boundary problem can be solved to determine the geopotential difference to unify the height datum (Zhang et al. 2009; Ardalan and Grafarend 2004; Rapp 1997; Sanso and Usai 1995; Heck and Rummel 1990; Rummel and Teunissen 1988; Colombo 1980). But the method needs more gravity data over the large area which will take long time and be more expensive.

Based on the astronomical leveling principle, the height anomaly difference of two stations can be calculated when DOVs along the route connecting these two stations across sea are known. When we again know the ellipsoidal height difference, we can estimate the NH difference based on the relationship of ellipsoidal height and NH. So a route connection method of NH is put forward to transfer height datum through the long distance across sea in the paper. Ship-borne global navigation satellite system (GNSS) technique is used to measure distances and ellipsoidal heights along the ship track across sea. Ship-borne gravimeter is used to measure oceanic gravity data along the ship route. DOVs along the route can be estimated from the ship-borne gravity data with the least squares collocation (LSC) method based on EGM2008 (Pavlis et al. 2008, 2012) and DTU10MSS (Andersen 2010). Meantime geodetic coordinates and DOVs of end stations of the connecting route on continent and island are precisely measured with GNSS and astro-geodetic techniques. So precisions of DOVs on the route across sea can be further improved with the measured DOVs on land and island. Finally the NH difference between continent and island can be precisely estimated from data of sea surface height (SSH), gravity, and DOV on the ship track across sea.

Height anomaly difference

DOV indicates the slope degree of geoid with respect to the referenced ellipsoid (Guan and Ning 1981; Moritz 1980; Heiskanen and Moritz 1967). So the height anomaly difference can be computed with DOVs, gravity and geodetic data to unify NH datum across sea.

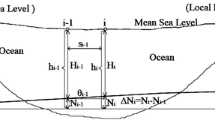
Figure 1 shows two stations A and B on the ground surface where A is very close to B. The ellipsoid and geoid/quasigeoid can be approximated to be planes near A in this case. So \( BB^{{\prime }} = {\text{d}}H \) is the ellipsoidal height difference between A and B, and \( AB^{{\prime }} = {\text{d}}l \) is the projected component of AB. \( \angle B^{{\prime \prime }} AB^{{\prime }} \) is the projected component θ of DOV on station A along the direction AB, that is

$$ \theta = \xi \cos \alpha + \eta \sin \alpha $$
(1)

where ξ and η are the meridian and the prime vertical components of DOV on station A respectively, and α is the azimuth of AB. So from Fig. 1 we can obtain

$$ {\text{d}}H = {\text{d}}h - \tan \theta {\text{d}}l \approx {\text{d}}h - \theta {\text{d}}l $$
(2)

where dh is the leveling height difference and θ is very small. Here the negative sign in the right side indicates that the height is positive upward.

Fig. 1
figure 1

Height anomaly difference. AB′ parallels to the ellipsoid and is perpendicular to BB′. AB″ locates in the level passing station A

Full size image

Based on the relationship of ellipsoidal height H and NH H γ, that is, H = H γ + ζ, we can rewrite Eq. (2) as

$$ {\text{d}}\zeta = - ({\text{d}}H^{\gamma } - {\text{d}}h) - \theta {\text{d}}l $$
(3)

where ζ is the height anomaly. Based on the astro-geodetic theory (Guan and Ning 1981; Heiskanen and Moritz 1967), we all know that \( {\text{d}}H^{\gamma } - {\text{d}}h = \frac{g - \gamma }{{\bar{\gamma }}}{\text{d}}h \) for the level ellipsoid. So we can get

$$ {\text{d}}\zeta = - \theta {\text{d}}l - \frac{g - \gamma }{{\bar{\gamma }}}{\text{d}}h $$
(4)

where g is the actual gravity, γ is the normal gravity, and \( \bar{\gamma } \) is the averaged normal gravity. Integrating Eq. (4), we can get the height anomaly difference Δζ AB between stations A and B as

$$ \Delta \zeta_{AB} = \zeta_{B} - \zeta_{A} = - \int\limits_{A}^{B} {\theta {\text{d}}l - \int\limits_{A}^{B} {\frac{g - \gamma }{{\bar{\gamma }}}{\text{d}}h} } $$
(5)

DOV in Eq. (5) is on the ground instead of geoid. Because g − γ is the surface gravity anomaly and \( \bar{\gamma } \) is the mean normal gravity, the second term in the right side of Eq. (5) is tiny. This term cannot be neglected when line AB is long.

In general, we cannot know the analytical expressions of θ and g in Eq. (5). So Eq. (5) can only be solved with the numerical discrete integration, that is

$$ \Delta \zeta_{AB} = \sum\limits_{i = 1}^{n} {\Delta \zeta_{i} } = - \sum\limits_{i = 1}^{n} {\left( {\theta_{i} l_{i} + \frac{{g_{i} - \gamma_{i} }}{{\bar{\gamma }_{i} }}\Delta h_{i} } \right)} $$
(6)

where Δh i is the height difference of segment i with the spirit leveling method and n is the divided segment number for track AB. We cannot directly make the spirit leveling on ship over sea so that Δh i is unknown. Geoid approximately accords with quasigeoid on seas. We can get Δh i  = ΔH i  − Δζ i for one short measuring segment over sea. So Eq. (6) can be rewritten as

$$ \begin{aligned} \Delta \zeta_{AB} & = - \sum\limits_{i = 1}^{n} {\left( {1 - \frac{{g_{i} - \gamma_{i} }}{{\bar{\gamma }_{i} }}} \right)^{ - 1} \left( {\theta_{i} l_{i} + \frac{{g_{i} - \gamma_{i} }}{{\bar{\gamma }_{i} }}\Delta H_{i} } \right)} \\ & = \sum\limits_{i = 1}^{n} {\Delta H_{i} } - \sum\limits_{i = 1}^{n} {\left( {1 - \frac{{g_{i} - \gamma_{i} }}{{\bar{\gamma }_{i} }}} \right)^{ - 1} (\theta_{i} l_{i} + \Delta H_{i} )} \\ \end{aligned} $$
(7)

where ΔH i is the ellipsoidal height difference determined with GNSS technique for segment i along the ship route.

NH difference and its accuracy analysis

The ellipsoidal height H A and NH H γ A of station A on continent can be precisely determined with GNSS technique and the spirit leveling method respectively, and the ellipsoidal height H B of station B on island can be precisely measured with GNSS technique. But NH H γ B of B is unknown. Referencing Eq. (7), the NH difference ΔH γ AB between stations A and B is

$$ \begin{aligned} \Delta H_{AB}^{\gamma } & = H_{B}^{\gamma } - H_{A}^{\gamma } = (H_{B} - H_{A} ) - \Delta \zeta_{AB} \\ & = \Delta H_{AB} - \sum\limits_{i = 1}^{n} {\Delta H_{i} } + \sum\limits_{i = 1}^{n} {\left( {1 - \frac{{g_{i} - \gamma_{i} }}{{\bar{\gamma }_{i} }}} \right)^{ - 1} (\theta_{i} l_{i} + \Delta H_{i} )} \\ & = \sum\limits_{i = 1}^{n} {\left( {1 - \frac{{g_{i} - \gamma_{i} }}{{\bar{\gamma }_{i} }}} \right)^{ - 1} (\theta_{i} l_{i} + \Delta H_{i} )} \\ \end{aligned} $$
(8)

where ΔH AB  = H B  − H A , and theoretically \( \Delta H_{AB} = \sum\nolimits_{i = 1}^{n} {\Delta H_{i} } \) is one check condition.

We can use the ship-borne gravimetry and GNSS techniques to measure gravity data and ellipsoidal heights along the ship route from A to B across sea. So data of gravity, distance and ellipsoidal height difference in Eq. (8) can be collected or calculated. The normal gravity can be precisely computed based on the physical geodesy theory (Guan and Ning 1981; Heiskanen and Moritz 1967). DOV can be estimated from the ship-borne gravity data with LSC based on EGM2008 to degree 2160 (Pavlis et al. 2008, 2012). So Eq. (8) can be solved to get the NH difference and then NH of station B is \( H_{B}^{\gamma } = H_{A}^{\gamma } + \Delta H_{AB}^{\gamma }. \)

The height-connection route is divided into n segments in the numerical discrete integration (8) and we suppose that measurements of all segments are independent. Based on the error propagation theory, from Eq. (8) we can get the precision expression of ΔH γ AB as

$$ m_{{\Delta H_{AB}^{\gamma } }}^{2} = \sum\limits_{i = 1}^{n} {\left[ {\left( {1 - \frac{{g_{i} - \gamma_{i} }}{{\bar{\gamma }_{i} }}} \right)^{ - 2} \left( {\theta_{i}^{2} m_{{l_{i} }}^{2} + l_{i}^{2} m_{\theta i}^{2} + m_{{\Delta H_{i} }}^{2} } \right) + \frac{{m_{{g_{i} }}^{2} }}{{\bar{\gamma }_{i}^{2} }}\left( {1 - \frac{{g_{i} - \gamma_{i} }}{{\bar{\gamma }_{i} }}} \right)^{ - 4} (\theta_{i} l_{i} + \Delta H_{i} )^{2} } \right]} $$
(9)

where \( m_{{\Delta H_{AB}^{\gamma } }} \), m l , m θ , mΔ H , and m g are precisions of NH difference, distance, DOV component, ellipsoidal height difference, and ship-borne gravity, respectively.

For example, there is a height-connection route over sea whose distance is up to 100 km. In general, DOVs over sea do not exceed 20″, the ellipsoidal height differences are <5 m, the gravity anomalies are <200 mGal, and the normal gravity is about 980 Gal (Guan and Ning 1981; Guo et al. 2013). Tables 1 and 2 list precisions of NH differences corresponding to different segment distances and accuracies of DOVs.

Table 1 Precisions of NH differences under conditions of γ = 980 Gal, g − γ = 200 mGal, θ = 20″, ΔH = 5 m, m l  = 0.2 m, mΔ H  = 50 mm and m g  = 10 mGal (unit in mm)
Full size table
Table 2 Precisions of NH differences under conditions of γ = 980 Gal, g − γ = 200 mGal, θ = 20″, ΔH = 5 m, m l  = 0.2 m, mΔ H  = 10 mm and m g  = 10 mGal (unit in mm)
Full size table

When the length of each segment is <10 km, error of ellipsoidal height difference is the main ingredient to affect the precision of NH connection across sea, listed in Table 1. It is not notable to improve the precision of NH difference in some sort with more precise DOVs. For example, when the accuracy of DOV for the segment of 1 km is changed from 2″ to 0.1″, the precision of height difference is meliorated to 50.1 cm from 50.9 cm whose improving rate is only 1.02. When the each segment length is equal to or >10 km, the ameliorative accuracy of DOV can efficiently improve the precision of estimated NH difference. Here the error of DOV for the segment of 50 km becomes the main error to affect the height connection across sea. For example, the precision of DOV is meliorated from 2″ to 0.1″, the accuracy of NH difference is ameliorated to 7.9 cm from 68.9 cm whose improving rate is 98.77, listed in Table 1.

From Table 2, we can find that it is not obvious to improve the accuracy of NH difference when the precision of DOV for the segment of ~5 km is improved. For example, the precision of DOV for segment of 1 km is changed from 2.0″ to 0.1″, the precision of NH difference is only improved to 10.0 cm from 13.9 cm whose improving rate is 1.39. When the length of segment is >5 km, the improvement of precision of DOV can efficiently raise the precision of NH difference. For example, the precision of DOV for the segment of 25 km is changed from 2.0″ to 0.1″, the precision of estimated NH difference is improved to 3.1 cm from 48.5 cm with the improving rate of 10.46.

From Tables 1 and 2, we can find that the error of ellipsoidal height difference is the main factor to affect the estimated NH difference when the segment length is <10 km for the connecting route of 100 km across sea. Errors of estimated NH differences for segments of 25, 50 and 100 km are mainly caused from the errors of DOVs. For example, when precision of DOV is 1″, the precision of NH difference is only improved to 48.5 cm from 48.8 cm as the precision of ellipsoidal height difference is improved to 1 cm from 5 cm. Shorter the length of segment is, more seriously the precision of ellipsoidal height difference affects the NH difference and more faintly the precision of DOV affects the NH difference. When the length of segment is equal to or <10 km, the estimated NH difference is mainly caused from the error of ellipsoidal height difference. For example, when the precision of DOV is 1″, the precision of NH difference is improved to 11.1 cm from 50.2 cm as the precision of ellipsoidal height difference is improved to 1 cm from 5 cm.

How to determine optimally the segment length is one important problem to calculate precisely the NH difference from Eq. (8). Precisions of ship-borne gravity and distance seldom affect the precision of NH difference, generally <1 mm (Guo et al. 2013). So neglecting errors of measured gravity and distance, the precision of NH difference can be optimal when

$$ lm_{\theta } = m_{\Delta H} $$
(10)

So

$$ l = \frac{{m_{\Delta H} }}{{m_{\theta } }} $$
(11)

Based on Eq. (11), Table 3 lists the optimal segment length relative to precisions of ellipsoidal height difference and DOVs. The precision of ellipsoidal height difference over sea with the ship-borne GNSS technique can be better than 5.0 cm, and the precision of DOV can be up to 1″. So the lengths of segment along the route over sea may be about 10 km.

Table 3 Segment lengths for different precisions of ellipsoidal height and DOV (unit in km)
Full size table

SSHs and DOVs measured with ship-borne gravimetry and GNSS along the route over sea

Equation (8) is used to calculate the NH difference across sea when the gravity anomalies, DOVs and ellipsoidal height differences along the route are known. Here we adopted the ship-borne gravimetry and GNSS technique to precisely measure these data along the ship track.

One ship-borne gravimeter can be fixed in the gyro system on the ship to precisely measure the ocean gravity anomalies with the resolution of 1–2 km. The mean squared error of ship-borne gravity generally is about 3 mGal by analysis of crossover coincident values (Huang et al. 2005). To reduce the gravimetric error caused from the ship locations with large uncertainties, the post processing of ship-borne double-frequency GNSS data is made to estimate precisely ship positions, which can make the gravimetric error better than 0.5 mGal. To lessen the error of space reduction of gravity anomalies, the height of the gravimeter above the sea surface should be exactly determined. One pose meter should be fixed on the ship to measure the roll, yaw and pitch. The heights between gravimeter and sea surface at the prow, poop, larborad and starboard are precisely measured, respectively. The ship draft model with respect to consuming oil value should be built. So the height-caused gravimetric error is better than 0.2 mGal. Ship-borne GNSS technique is used to calculate the ship speed with the kinematic post-processing method to reduce the Eötvös effect to better than 0.5 mGal. Gravity base sites at the pier are built and the gravimeter grid value which is used to correct the ship-borne measurements can be calculated through the associated measurement and comparison to the gravities on the base sites. In order to reduce noises caused by wave and wind, the residuals between ship-borne gravimetry data and the modeled data from the Earth gravity field model like EGM2008 to degree 2160 (Pavlis et al. 2008, 2012) are filtered with the Gaussian filter. The precision of ship-borne gravimetry data can be further improved by the colinear adjustment method.

The ellipsoidal height H a of ship-borne GNSS antenna can be precisely determined with the kinematic positioning method under the condition of approximately constant ship speed and stable sea state by the ship-borne GNSS receiver and antenna. The vertical distances between GNSS antenna and sea surface at the prow, poop, larborad, and starboard are measured on the regular basis and interval. The ship draft model with respect to consuming oil value should be built. The ellipsoidal height of GNSS antenna and the vertical distances to the sea surface should be corrected by the ship attitudes. So the vertical distance H s between the GNSS antenna and the sea surface can be calculated to get SSH as

$$ SSH = H_{a} - H_{s} $$
(12)

In order to further improve the precision of SSHs, differences between the SSHs measured by the ship-borne GNSS technique and those from the mean SSH model like DTU10MSS (Andersen 2010) should be filtered to remove errors caused from wind and wave by the Gaussian filter with the window of 45 s. The colinear adjustment can improve precisions of SSHs better than 5.0 cm and those of ellipsoidal height differences better than 3.5 cm (Guo et al. 2013).

The remove-restore technique is used to calculate the precise DOVs along the ship route. The residual between the ship-borne gravity anomaly Δg and the modeled gravity anomaly Δg ′ determined from EGM2008 to degree 2160 (Pavlis et al. 2012) is computed, that is, δg = Δg − Δg ′. The residual DOV corresponding to Δg can be estimated with LSC (Guo et al. 2010b)

$$ \delta \xi = C_{\xi g} (C_{gg} + n_{gg} )^{ - 1} \delta g $$
(13)
$$ \delta \eta = C_{\eta g} (C_{gg} + n_{gg} )^{ - 1} \delta g $$
(14)

where Δξ and Δη are the residual meridian and the prime vertical components of DOV, C ξg and C ηg are the covariance matrices between the meridian component and the residual gravity anomaly, and the prime vertical component and the residual gravity anomaly, respectively; C gg is the variance matrix of the residual gravity anomaly; and n gg is the noise matrix of the residual gravity anomaly.

The residual DOV estimated from (13) and (14) adds the modeled DOV (ξ ′ and η ′) estimated from the Earth’s gravity field model EGM2008 to degree 2160 (Pavlis et al. 2012) to get the final DOV along the ship track, that is

$$ \xi = \xi^{\prime } + \Delta \xi ,\eta = \eta^{\prime } + \Delta \eta $$
(15)

We all know that it is very difficult even or impossible to implement the traditional astro-geodetic surveying on the ship over sea to get precise DOVs. There are two points A and B on the shore and the island coast, respectively. We can precisely measure their meridian and prime vertical components of DOVs with the traditional astro-geodetic method, that is, ξ 0 A , η 0 A , ξ 0 B , and η 0 B , respectively. There is a ship route over sea from A to B along which DOVs are calculated with Eq. (15). So we can get the ship-borne DOVs ξ A , η A , ξ B , and η B , respectively. The differences between the astro-geodetic and the ship-borne DOVs are

$$ \Delta \xi_{A} = \xi_{A}^{0} - \xi_{A} ,\quad \Delta \eta_{A} = \eta_{A}^{0} - \eta_{A} ,\quad \Delta \xi_{B} = \xi_{B}^{0} - \xi_{B} ,\quad \Delta \eta_{B} = \eta_{B}^{0} - \eta_{B} $$
(16)

Supposing that the differences between the astro-geodetic and the ship-borne DOVs along the route are linear, we can get the linear model

$$ \Delta \xi = a_{10} + a_{11} l,\quad \Delta \eta = a_{20} + a_{21} l $$
(17)

where a 10 = Δξ A , \( a_{11} = \frac{{\Delta \xi_{B} - \Delta \xi_{A} }}{{l_{AB} }} \), a 20 = Δη A , \( a_{21} = \frac{{\Delta \eta_{B} - \Delta \eta_{A} }}{{l_{AB} }} \), and l is the distance of interesting point to station A.

Components of DOV of point i along the connecting route determined with the ship-borne technique are ξ i and η i , and the distance of point i to station A is l Ai . Corrected components calculated by Eq. (17) are Δξ i  = a 10 + a 11 l Ai and Δη i  = a 20 + a 21 l Ai . Then the improved components of DOV of point i are

$$ \xi_{i}^{0} = \xi_{i} + \Delta \xi_{i} = \xi_{i} + a_{10} + a_{11} l_{Ai} ,\quad \eta_{i}^{0} = \eta_{i} + \Delta \eta_{i} = \eta_{i} + a_{20} + a_{21} l_{Ai} $$
(18)

The ship-borne gravimetry is made along the connecting route and DOV is estimated from the ship-borne gravity data with LSC (Guo et al. 2010b). The astro-geodetic surveying is made on the continent and the island to improve the accuracies of DOVs. So the accuracies of DOVs along the ship track over sea can be better than 1″ (Guo et al. 2013).

Practical cases of NH connection across sea

We selected several practical cases to test the new method to connect NH along the ship route across sea. We select stations NZ, SLZ, TD, L84 and L82 located on Qingdao coastal sea, and THS and SQ on Penglai coastal sea, China, seeing Fig. 2. Stations NZ, SLZ, L84, L82 and THS are located on the mainland. Station TD is located on Tuo Island and SQ is located on Nanchangshan Island. To check the estimated results of route height connection, the trigonometric leveling method is used to precisely determine NH differences both between THS and SQ, and NZ and TD, and the spirit leveling method is used to determine the NH differences both between NZ and SLZ, and THS and NZ.

Fig. 2
figure 2

NH connection test along the route across sea. Circles stand for stations of corresponding names or points along the ship track

Full size image

Table 4 lists closure errors for all close loops in the height connecting cases, that is, NZ–SLZ–TD–NZ, L82–NZ–TD–L82 and L84–TD–NZ–SLZ–L84. The errors for NZ–SLZ–TD–NZ are coincident for segments of 4, 2, and 1 km. When the segment length is 2 km, the errors for L82–NZ–TD–L82 and L84–TD–NZ–SLZ–L84 are smallest.

Table 4 Closed errors for close loops (unit in mm)
Full size table

Table 5 lists errors for several loops comparing with the practical measurements in the connecting case, that is, NZ–TD, NZ–SLZ, and THS–SQ. In order to validate the height connecting accuracy with the new method, loops NZ–TD and THS–SQ were measured with the trigonometric leveling method, and the loop NZ–SLZ was observed with the precise spirit leveling method over land. Here error means the difference between the measured NH difference and the estimated NH difference with the method put forward in the paper. When the segment length is 1 km, the error for loop NZ–TD is smallest. When the segment length is 4 km, the errors for loops NZ–SLZ and THS–SQ are best.

Table 5 Errors for three loops comparing with practical measurements (unit in mm)
Full size table

We also made a route connection of NH through the long distance more than 500 km across sea. Table 6 lists errors for different segments comparing with practical leveling measurements in the connecting case, that is, NZ–THS. The distance of the route across sea is 510.53 km, seeing Fig. 2. Here segment length is set to 20, 10 and 5 km, respectively. Loop NZ–THS was precisely measured with the spirit leveling method over the mainland. When the segment length is 5 km, the error of loop NZ–THS is smallest.

Table 6 Errors for loop NZ-TH comparing with practical leveling result
Full size table

Another index to evaluate the precision of the connecting NH is the full root-mean-square error (FRMSE) of height difference per kilometer (Guo et al. 2013) as

$$ w = \pm \sqrt {\frac{1}{M}\left[ \frac{WW}{L} \right]} $$
(19)

where w is FRMSE per kilometer, W is the loop error in mm, L is the loop distance in km, and M is the number of loops. Substituting data listed in Table 4 for Eq. (19), we calculated FRMSEs per 1 km for segmentations of 4, 2, and 1 km to be 2.68, 2.62 and 2.76 mm, respectively. Considering errors listed in Tables 4 and 5, FRMSEs per 1 km for segmentations of 4, 2, and 1 km estimated with Eq. (19) are 7.41, 7.26 and 7.21 mm, respectively.

Conclusions

Based on the astro-geodetic principle, a new NH connection method along a long-distance ship route across sea is put forward in the paper. Algorithms to calculate the NH difference from data of ship-borne gravity, SSH, distance and DOV along the ship track across sea were concluded based on the astronomical leveling theory. The ship-borne gravimetry is used to collect precise oceanic gravity data whose precisions are improved by the colinear adjustment and the Gaussian filter to remove the effects of sea wind and wave. The precision of ship-borne gravity data can be better than 3 mGal. The ship-borne GNSS technique is utilized to measure precise SSHs whose precisions are also ameliorated by the colinear adjustment and the Gaussian filter. The precision of ship-borne SSHs can be better than 5 cm and that of SSH differences better than 3.5 cm. DOVs along the connecting route can be estimated from the ship-borne gravity data with LSC. DOVs on ends of the route also can be precisely measured with the traditional astro-geodetic method up to precision of 0.3″. Supposing that differences between the astro-geodetic and the gravity-derived DOV are linear, we used one linear model to improve the precisions of gravity-derived DOVs. In this study, one precise Earth gravity field model like EGM2008 to degree 2160 (Pavlis et al. 2012) and one precise SSH model like DTU10MSS (Andersen 2010) are referenced to process the ship-borne gravity and SSHs with the remove-restore technique. So the precision of DOV along the ship track across sea can be better than 1″.

Errors of DOVs and SSH differences seriously affect precisions of connecting NHs along the route across sea. Errors of ship-borne gravity and distance have little effects on the height connecting precision. The segment distance also affects precisions of connecting NH. We deduced the equation to calculate the optimal segment distance based on the principle of equal impacts from errors of DOV and SSH difference. The precision of connecting NH is optimal under condition that the segment distance is about 5–10 km.

We selected the coast in Shandong Peninsula, China, as the tentative area for connecting NH with the new method. The practical precision of connecting NH can be up to 7.2 mm/km from Eq. (19). For the connecting route of more than 500 km over sea, the precision of connecting height is up to 309.9 mm comparing with the spirit leveling method. How to improve precisions of DOVs and SSH differences should be further studied to get more precise connecting NH along the ship track across sea.