1 Introduction

Determination of the deflection of the vertical (DOV) has deep roots in geodesy going back to traditional horizontal control that required correcting astronomically observed latitude and longitude in order to obtain corresponding geodetic coordinates. In addition, horizontal angles (and azimuths) measured by transit or theodolite require correction (Laplace’s condition) in the transformation to angles turned about the ellipsoid normal. Conversely, a comparison of astronomically observed latitude and longitude (or azimuth) and geodetic quantities obtained from a triangulation network were used to derive the DOV components (Heiskanen and Moritz 1967, p. 197–9). Concern for the deflection of the plumb line already entered geodesy in the eighteenth century when the Earth’s shape, whether flattened at the equator or at the poles, was hotly debated. P. Bouguer on a deciding expedition to Ecuador to determine an arc length (for comparison with the length of an equal latitudinal increment determined at high latitude) questioned the accuracy of astronomically observed positions due to the predicted large deflection caused by the mountainous terrain. Finally convinced of the observational accuracy, the conclusion led to a rejection of the predicted deflection and the first ideas of isostatic compensation (Watts 2001, p. 6). Even today with global navigation satellite systems, such as GPS, providing the majority of geodetic control, DOVs still play an important, albeit less prominent, role. Being closely related to the horizontal components of the gravity vector in a local coordinate system they are needed to compensate inertial navigation and guidance systems that do not directly sense the influence of gravitation. The DOV also plays a supporting role, though merely as a stepping stone, in transforming satellite altimetry to the gravity anomaly on the ocean surface (Sandwell and Smith 1997, Appendix B).

While the historical geodetic determination of the DOV is primarily of a geometric nature, more modern determinations are usually done from a geophysical or gravimetric perspective. The most famous is the Vening–Meinesz formulation that convolves surface gravity anomalies with a Green’s function (Heiskanen and Moritz 1967, p. 114; Hofmann-Wellenhof and Moritz 2005, p. 119). Yet even today the astrogeodetic method is still pursued with very accurate portable astrolabes (Hirt and Bürki 2002). Besides the Vening–Meinesz integral method, other gravimetric methods have been used in the past. For example, Rose and Nash (1972) used the horizontal accelerometers of an inertial navigation system (INS) to infer the DOV and, among others, Jekeli and Kwon (1999) demonstrated vector gravimetry with an airborne INS and GPS.

Another gravimetric method to determine the DOV is by gravity gradiometry and the earliest such results came from torsion balance observations reported by K. Oltay of the Eötvös Geophysical Research Institute, Budapest, in the 1920s (Heiland 1940, p. 169). Other determinations were made by Badekas and Mueller (1968) with torsion balance data obtained in southwestern Ohio, USA. Also Herring (1978, 1979) investigated the feasibility of such determinations and Völgyesi (1977, 2005) carried out DOV computations from extensive torsion balance data in Hungary. The first airborne gradiometer test in the 1980s (Jekeli 1988) also stimulated a number of attempts to study and determine the deflection of the vertical from such data (Heller and MacNichol 1983; Arabelos and Tziavos 1992; Jekeli 1993). Although these latter results were not particularly fruitful, the concept of gradiometry for determination of the deflection of the vertical remains interesting for applications in inertial navigation and guidance (e.g., Jekeli 2006), as well as in geophysics (Sun and Zhou 2012).

Obtaining the horizontal components of gravity, and hence the deflections of the vertical, from gravity gradients along a survey line is not complicated, being essentially an along-track integration. The complications arise if the measured gradients are not the required individual elements of the gravity gradient tensor and because the line integration turns any data error into more systematic errors; e.g., white noise turns into a random walk, and a measurement bias turns into a trend error. It is the objective of this paper to demonstrate some of these complications with airborne gravity gradiometry data and to show, at the same time that, by suitable processing methods, these data yield a DOV map that improves previously available models. Also, of particular interest is the comparative capability of single-instrument and full-tensor gradiometers in estimating the DOV components.

2 Mathematical theory

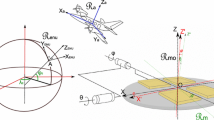
The deflection of the vertical (DOV) is the angle between the true vertical, as defined by the direction of Earth’s gravity vector, e.g., in terms of astronomic coordinates of latitude and longitude, \(\varPhi , \varLambda \), of a point, and either a geometrically or a physically defined reference direction. The corresponding geometric definition of the reference direction is given by the geodetic coordinates associated with a particular ellipsoid that approximates the Earth. The DOV is then of the Helmert, or also, astrogeodetic type. An alternative reference definition is the direction of normal gravity. The DOV is then of the Molodensky type, where the normal gravity vector is defined at the point where the normal and actual gravity potentials are equal (Fig. 1). If the geometric ellipsoid and the normal ellipsoid are identical in size, shape, location, and orientation, then for points on the geoid the Helmert and Molodensky DOVs are the same and are also known as the Pizzetti DOV (Jekeli 1999).

It can be shown that the south-to-north and west-to-east components, \(\xi \) and \(\eta \), respectively, of the Helmert DOV at a point, P, are given (Pick et al. 1973, p. 432) by

$$\begin{aligned} \xi ^{\mathrm{Helmert}}= & {} \varPhi -\phi +\frac{1}{2}\eta ^{2}\tan \phi +3{\mathrm{rd}}\hbox {-order terms}, \end{aligned}$$
(1)
$$\begin{aligned} \eta ^{\mathrm{Helmert}}= & {} \left( {\varLambda -\lambda } \right) \cos \phi +3{\mathrm{rd}}\hbox {-order terms}, \end{aligned}$$
(2)

where \(\phi , \lambda \) are the geodetic coordinates of P. The Molodensky DOV components differ from these by the curvature of the normal plumb line, which is given (Heiskanen and Moritz 1967, p.196; Hofmann-Wellenhof and Moritz 2005, p.233) by

$$\begin{aligned} \delta \xi _{\mathrm{norm.curv.}} =-\delta \phi \left( {H^{*}} \right) \simeq 0.17H^{*}\sin 2\phi \hbox { (arcsec)}, \end{aligned}$$
(3)

where \(H^{*}\) is the normal height of P with respect to the quasigeoid in units of km (or, of Q with respect to the ellipsoid; see Fig. 1). Since there is no curvature of the normal plumb line out of the meridian plane, one has the simple relationship between the geometric and physical types of DOV,

$$\begin{aligned} \xi ^{\mathrm{Molodensky}}= & {} \xi ^{\mathrm{Helmert}}-\delta \phi \left( {H^{*}} \right) , \end{aligned}$$
(4)
$$\begin{aligned} \eta ^{\mathrm{Molodensky}}= & {} \eta ^{\mathrm{Helmert}}. \end{aligned}$$
(5)

Here the curvature of the normal plumb line between the points, P and Q, is neglected since their separation nominally is only of order of about 30 m. The normal curvature effect can reach a significant fraction of an arcsecond, or more, for heights greater than several kilometers (which is the case, in particular, for points at aircraft altitude).

Fig. 1
figure 1

Deflection of the vertical (south-to-north component, \(\xi \)) according to various definitions. The normal gravity potential is U and the actual gravity potential is W. See the main text for an explanation of the other symbols

Full size image

If the geometric ellipsoid (geodetic datum) and the ellipsoid of the reference gravity field are not identical, standard formulas exist to transform deflections of the vertical from one to the other geometric reference directions (e.g., Heiskanen and Moritz 1967, p. 207).

The Molodensky definition comes close to the meaning of the DOV as determined by gravimetric methods. In linear approximation it can be shown (Jekeli 1999) that the Molodensky DOV components are also

$$\begin{aligned} \xi ^{\mathrm{Molodensky}}( P)= & {} \xi ^{\mathrm{grav}}( P )=-\frac{1}{\gamma _Q }\frac{1}{M_P +h_P }\left. {\frac{\partial T}{\partial \phi }} \right| _P , \end{aligned}$$
(6)
$$\begin{aligned} \eta ^{\mathrm{Molodensky}}( P)= & {} \eta ^{\mathrm{grav}}(P)\nonumber \\= & {} -\frac{1}{\gamma _Q }\frac{1}{\left( {N_P +h_P } \right) \cos \phi _P }\left. {\frac{\partial T}{\partial \lambda }} \right| _P , \end{aligned}$$
(7)

where \(T=W-U\) is the disturbing potential, N, M are the principal radii of curvature of the ellipsoid, h is the geodetic height (along the ellipsoid perpendicular), and \(\gamma \) is the magnitude of normal gravity. The linear approximation neglects terms of the order of the squared DOV components. Inasmuch as \(\xi \) and \(\eta \) have typical orders of magnitude of \(10^{\prime \prime }\), the linear approximation generally is in error by less than a milliarcsecond.

In local areas, defined by a Cartesian coordinate system, x, y, z, say, north-east-down, one can make a further planar approximation that replaces (6) and (7) with

$$\begin{aligned} \xi ^{\mathrm{grav}}(P)= & {} -\frac{1}{\gamma _Q }\left. {\frac{\partial T}{\partial x}} \right| _P, \end{aligned}$$
(8)
$$\begin{aligned} \eta ^{\mathrm{grav}}(P)= & {} -\frac{1}{\gamma _Q }\left. {\frac{\partial T}{\partial y}} \right| _P. \end{aligned}$$
(9)

This local planar approximation of the DOV, and also for the gravity gradients, essentially neglects the curvature of the ellipsoid (or, approximately, the sphere), as well as the local convergence of meridians and is adequate for present purposes (Appendix). Indeed, the difference between using spherical and planar coordinates is found to be completely negligible using the gradient data at hand (Sect. 3). In this paper only the Molodensky, or gravimetric, DOV is considered; and, a transformation to the Helmert DOV can be made using (4) (and (5).

With the availability of horizontal gravity gradient measurements, a determination of the DOV is feasible that is more direct than the classical Vening–Meinesz approach. In the local Cartesian coordinate system, let the gravity gradient disturbances be

$$\begin{aligned} {\varvec{\Gamma }}= & {} {\varvec{\nabla }} ( {\varvec{\nabla }} T )^{\mathrm{T}}=\left( {{\begin{array}{lll} {\frac{\partial ^{2}T}{\partial x^{2}}}&{}\quad {\frac{\partial ^{2}T}{\partial x\partial y}}&{}\quad {\frac{\partial ^{2}T}{\partial x\partial z}} \\ {\frac{\partial ^{2}T}{\partial y\partial x}}&{}\quad {\frac{\partial ^{2}T}{\partial y^{2}}}&{}\quad {\frac{\partial ^{2}T}{\partial y\partial z}} \\ {\frac{\partial ^{2}T}{\partial z\partial x}}&{}\quad {\frac{\partial ^{2}T}{\partial z\partial y}}&{}\quad {\frac{\partial ^{2}T}{\partial z^{2}}} \\ \end{array} }} \right) \nonumber \\= & {} \left( {{\begin{array}{lll} {\varGamma _{{ xx}} }&{}\quad {\varGamma _{{ xy}} }&{}\quad {\varGamma _{{ xz}} } \\ {\varGamma _{yx} }&{}\quad {\varGamma _{{ yy}} }&{}\quad {\varGamma _{{ yz}} } \\ {\varGamma _{zx} }&{}\quad {\varGamma _{zy} }&{}\quad {\varGamma _{zz} } \\ \end{array} }} \right) . \end{aligned}$$
(10)

In free space, the disturbing potential is twice differentiable and satisfies Laplace’s equation,

$$\begin{aligned} \frac{\partial ^{2}T}{\partial x^{2}}+\frac{\partial ^{2}T}{\partial y^{2}}+\frac{\partial ^{2}T}{\partial z^{2}}=0; \end{aligned}$$
(11)

hence, the gradient tensor, \({\varvec{\Gamma }}\), is traceless. It is also symmetric because the gradients are independent of the order of partial differentiation of T.

The total differentials of the horizontal partial derivatives of T are

$$\begin{aligned} \mathrm{d}\left( {\frac{\partial T}{\partial x}} \right)= & {} \frac{\partial ^{2}T}{\partial x^{2}}\mathrm{d}x+\frac{\partial ^{2}T}{\partial x\partial y}\mathrm{d}y+\frac{\partial ^{2}T}{\partial x\partial z}\mathrm{d}z, \end{aligned}$$
(12)
$$\begin{aligned} \mathrm{d}\left( {\frac{\partial T}{\partial y}} \right)= & {} \frac{\partial ^{2}T}{\partial y\partial x}\mathrm{d}x+\frac{\partial ^{2}T}{\partial y^{2}}\mathrm{d}y+\frac{\partial ^{2}T}{\partial y\partial z}\mathrm{d}z. \end{aligned}$$
(13)

Substituting from (8) through (10) and integrating (12) and (13), one has the line integrals for the DOV components in planar approximation,

$$\begin{aligned} \left\{ {{\begin{array}{l} {\xi ( P)} \\ {\eta (P)} \\ \end{array} }} \right\}= & {} \left\{ {{\begin{array}{l} {\xi ({P_0 })} \\ {\eta ({P_0 })} \\ \end{array} }} \right\} -\frac{1}{\gamma }{\mathop {\int }\limits _{P_0}^P} {\left\{ {{\begin{array}{l} {\varGamma _{{ xx}} } \\ {\varGamma _{yx} } \\ \end{array} }} \right\} \mathrm{d}x} -\frac{1}{\gamma }{\mathop {\int }\limits _{P_0}^P} {\left\{ {{\begin{array}{l} {\varGamma _{{ xy}} } \\ {\varGamma _{{ yy}} } \\ \end{array} }} \right\} \mathrm{d}y} \nonumber \\&-\frac{1}{\gamma }{\mathop {\int }\limits _{P_0}^P} {\left\{ {{\begin{array}{l} {\varGamma _{{ xz}} } \\ {\varGamma _{{ yz}} } \\ \end{array} }} \right\} \mathrm{d}z} . \end{aligned}$$
(14)

Therefore, a discrete set of gradient tensor elements along a trajectory can be numerically integrated to obtain the DOV components along that trajectory, provided that components at the initial point are known. For example, with the trapezoidal rule for numerical integration applied to a set of gradients, \(\varGamma _{{ xx}}^{(j)}\), \(\varGamma _{{ xy}}^{(j)}\), \(\varGamma _{{ xz}}^{(j)}\), \(\varGamma _{{ yy}}^{(j)}\), \(\varGamma _{{ yz}}^{(j)}\), \(j=0,\ldots , J-1\), one has

$$\begin{aligned} \left\{ {{\begin{array}{l} {\xi \left( {P_{J-1} } \right) } \\ {\eta \left( {P_{J-1} } \right) } \\ \end{array} }} \right\}\simeq & {} \left\{ {{\begin{array}{l} {\xi \left( {P_0 } \right) } \\ {\eta \left( {P_0 } \right) } \\ \end{array} }} \right\} \nonumber \\&-\frac{1}{2\gamma }\sum _{j=0}^{J-2} {\left\{ {{\begin{array}{l} {\varGamma _{{ xx}}^{\left( j \right) } +\varGamma _{{ xx}}^{\left( {j+1} \right) } } \\ {\varGamma _{{ xy}}^{\left( j \right) } +\varGamma _{{ xy}}^{\left( {j+1} \right) } } \\ \end{array} }} \right\} \Delta x_{j,j+1} } \nonumber \\&-\frac{1}{2\gamma }\sum _{j=0}^{J-2} {\left\{ {{\begin{array}{l} {\varGamma _{{ xy}}^{\left( j \right) } +\varGamma _{{ xy}}^{\left( {j+1} \right) } } \\ {\varGamma _{{ yy}}^{\left( j \right) } +\varGamma _{{ yy}}^{\left( {j+1} \right) } } \\ \end{array} }} \right\} \Delta y_{j,j+1} } \nonumber \\&-\frac{1}{2\gamma }\sum _{j=0}^{J-2} {\left\{ {{\begin{array}{l} {\varGamma _{{ xz}}^{\left( j \right) } +\varGamma _{{ xz}}^{\left( {j+1} \right) } } \\ {\varGamma _{{ yz}}^{\left( j \right) } +\varGamma _{{ yz}}^{\left( {j+1} \right) } } \\ \end{array} }} \right\} \Delta z_{j,j+1} }\nonumber \\ \end{aligned}$$
(15)

where \(\Delta x_{j,j+1} =x_{j+1} -x_j\), \(\Delta y_{j,j+1} =y_{j+1} -y_j\), \(\Delta z_{j,j+1} =z_{j+1} -z_j\). In the local Cartesian north-east-down coordinate system, the coordinates, x and y, are associated, for example, with northings and eastings of a UTM projection, while heights, h, are typically given as positive upwards, hence, \(z=-h\).

If only a single-gradiometer instrument is available (and leveled), which consists of only two pairs of accelerometers, such as the Lockheed Martin gravity gradiometer instrument [formerly, the Bell Aerospace gravity gradiometer, (Jekeli 1988)], then the measurements are two gradients, \(\varGamma _\Delta ={( {\varGamma _{{ yy}} -\varGamma _{{ xx}} } )}/2\) and \(\varGamma _{{ xy}}\), being the two components of the differential curvature of the gravity field (Heiland 1940, p. 174). Even neglecting the vertical gradient along a nearly horizontal trajectory, it is not possible to simply integrate these in order to obtain the DOV components. It is possible, however, by using two essentially parallel trajectories. This was the idea described by Badekas and Mueller (1968) in processing torsion balance data, exactly of this type, for the DOV determination in southwestern Ohio.

Consider a single pair of points, \(P_j\) and \(P_{j+1}\), for which the DOV component differences are, from (15) (based on the trapezoidal method of numerical integration),

$$\begin{aligned} \left\{ {{\begin{array}{l} {\Delta \xi _{j,j+1} } \\ {\Delta \eta _{j,j+1} } \\ \end{array} }} \right\}= & {} -\frac{1}{2\gamma }\left( \left\{ {{\begin{array}{l} {\varGamma _{{ xx}}^{\left( j \right) } +\varGamma _{{ xx}}^{\left( {j+1} \right) } } \\ {\varGamma _{{ xy}}^{\left( j \right) } +\varGamma _{{ xy}}^{\left( {j+1} \right) } } \\ \end{array} }} \right\} \Delta x_{j,j+1}\right. \nonumber \\&+\left\{ {{\begin{array}{l} {\varGamma _{{ xy}}^{\left( j \right) } +\varGamma _{{ xy}}^{\left( {j+1} \right) } } \\ {\varGamma _{{ yy}}^{\left( j \right) } +\varGamma _{{ yy}}^{\left( {j+1} \right) } } \\ \end{array} }} \right\} \Delta y_{j,j+1} \nonumber \\&\left. +\left\{ {{\begin{array}{l} {\varGamma _{{ xz}}^{\left( j \right) } +\varGamma _{{ xz}}^{\left( {j+1} \right) } } \\ {\varGamma _{{ yz}}^{\left( j \right) } +\varGamma _{{ yz}}^{\left( {j+1} \right) } } \\ \end{array} }} \right\} \Delta z_{j,j+1} \right) . \end{aligned}$$
(16)

Defining the azimuth, \(\alpha _{j,j+1}\), of \(P_{j+1}\) at \(P_j\) (Fig. 2), and the distance, \(\Delta s_{j,j+1}\), between them, one has

$$\begin{aligned}&\Delta x_{j,j+1} =\Delta s_{j,j+1} \cos \alpha _{j,j+1} , \nonumber \\&\Delta y_{j,j+1} =\Delta s_{j,j+1} \sin \alpha _{j,j+1}. \end{aligned}$$
(17)

Substituting these into (16), and assuming that \(\Delta z_{j,j+1} =0\), it is easy to see that

$$\begin{aligned}&\left\{ {{\begin{array}{l} {\Delta \xi _{j,j+1} } \\ {\Delta \eta _{j,j+1} } \\ \end{array} }} \right\} =-\frac{\Delta s_{j,j+1} }{2\gamma }\left\{ {{\begin{array}{l} {\left( {\varGamma _{{ xx}}^{\left( {j+1} \right) } +\varGamma _{{ xx}}^{\left( j \right) } } \right) \cos \alpha _{j,j+1} +\left( {\varGamma _{{ xy}}^{\left( {j+1} \right) } +\varGamma _{{ xy}}^{\left( j \right) } } \right) \sin \alpha _{j,j+1} } \\ {\left( {\varGamma _{{ xy}}^{\left( {j+1} \right) } +\varGamma _{{ xy}}^{\left( j \right) } } \right) \cos \alpha _{j,j+1} +\left( {\varGamma _{{ yy}}^{\left( {j+1} \right) } +\varGamma _{{ yy}}^{\left( j \right) } } \right) \sin \alpha _{j,j+1} } \\ \end{array} }} \right\} , \end{aligned}$$
(18)

which, when appropriately combined, leads to

$$\begin{aligned}&\Delta \xi _{j,j+1} \sin \alpha _{j,j+1} -\Delta \eta _{j,j+1} \cos \alpha _{j,j+1} \nonumber \\&\quad =\frac{\Delta s_{j,j+1} }{2\gamma }\left( \left( {\varGamma _\Delta ^{\left( j \right) } +\varGamma _\Delta ^{\left( {j+1} \right) } } \right) \sin 2\alpha _{j,j+1}\right. \nonumber \\&\qquad \left. +\left( \varGamma _{{ xy}}^{\left( j \right) } +\varGamma _{{ xy}}^{\left( {j+1} \right) } \right) \cos 2\alpha _{j,j+1} \right) \end{aligned}$$
(19)
Fig. 2
figure 2

Geometry of coordinates with x, y as northing and easting, respectively

Full size image

Equation (19) does not separate the differences, \(\Delta \xi _{j,j+1} =\xi _{j+1} -\xi _j\) and \(\Delta \eta _{j,j+1} =\eta _{j+1} -\eta _j\). But for three distinct points, \(P_{j-2}\), \(P_{j-1}\), \(P_j\), there are two constraints on the DOV differences—the sums of the three corresponding differences must vanish,

$$\begin{aligned} \Delta \xi _{j-2,j-1} +\Delta \xi _{j-1,j} +\Delta \xi _{j,j-2}= & {} 0,\nonumber \\ \quad \Delta \eta _{j-2,j-1} +\Delta \eta _{j-1,j} +\Delta \eta _{j,j-2}= & {} 0. \end{aligned}$$
(20)

Equation (19) is ineffectual in providing information on one of the DOV components if the azimuth is an integer multiple of \(\pi /2\). If \(\alpha _{j,j+1} =0^{\circ },180^{\circ }\), then (19) provides no information on \(\Delta \xi _{j,j+1}\); and, if \(\alpha _{j,j+1} =90^{\circ },270^{\circ }\), then (19) provides no information on \(\Delta \eta _{j,j+1}\). Also, a singularity arises if the three points, \(P_{j-2}\), \(P_{j-1}\), \(P_j\), are co-linear, and solution instability results for nearly co-linear triplets.

Nevertheless, in general, a pair of parallel tracks of gradients, \(\varGamma _\Delta ={( {\varGamma _{{ yy}} -\varGamma _{{ xx}} } )}/2\) and \(\varGamma _{{ xy}}\), can lead to estimates of the DOV components. Consider roughly parallel tracks of K observation points each (assume no azimuth degeneracies), as in Fig. 3. For the first two tracks there are 4K unknown DOV components, \(\xi \), \(\eta \), and an equal number (4K) of observations, \(\varGamma _\Delta \) and \(\varGamma _{{ xy}}\). Per track, there are \(K-1\) along-track connections (equations) of the form (19), and K cross-track connections between the tracks, for a total number of only \(3K-2\) equations. Clearly the constraints (20) are needed and can be incorporated by adding \(K-1\) diagonal connections, as shown in Fig. 3, again in the form of Eq. (19). Still, these final \(4K-3\) equations require at least three additional constraints to solve for all the DOV components. For example, one could include observations of the DOV components at the two endpoints of one of the tracks.

Fig. 3
figure 3

Geometry of a \(J\times K\) grid of gradient observations, \(\varGamma _\Delta \) and \(\varGamma _{{ xy}}\)

Full size image

Each additional track of points adds 2K unknowns and 2K observations, but only \(2K-1\) additional along-track and cross-track connections. Thus, without further external DOV control, additional diagonal connections are needed to supply the necessary constraints. But, it is noted that diagonal connections do not provide extra observational information, only geometric stability. On the other hand, one cannot add arbitrarily more diagonal connections because having too many such constraints simply means that observations are used multiple times, which is not permitted from an estimation viewpoint. Indeed, let “derived observations”, defined by the right-hand side of (19),

$$\begin{aligned} G_{j_1 ,j_2 }= & {} \frac{\Delta s_{j_1 ,j_2 } }{2\gamma }\left( \left( {\varGamma _\Delta ^{\left( {j_1 } \right) } +\varGamma _\Delta ^{\left( {j_2 } \right) } } \right) \sin 2\alpha _{j_1 ,j_2 } \right. \nonumber \\&\quad \left. +\left( {\varGamma _{{ xy}}^{\left( {j_1 } \right) } +\varGamma _{{ xy}}^{\left( {j_2 } \right) } } \right) \cos 2\alpha _{j_1 ,j_2 } \right) , \end{aligned}$$
(21)

be collected in the vector, G; and, let the actual observations, \(\varGamma _\Delta \) and \(\varGamma _{{ xy}}\), constitute the vector, y. For two tracks triangulated as in Fig. 3, the total number of derived observations in G is less than the total number in y. If the error dispersion matrix of y is non-singular then so is that of G. However, as soon as the size of G is greater than the size of y, its error dispersion matrix becomes singular, indicative of perfect error correlations between, or multiple uses of observations, \(\varGamma _\Delta \) and \(\varGamma _{{ xy}}\). Thus, one must carefully trade between geometric stability (i.e., DOV estimability) and observational independence. Performing a Delaunay triangulation, having O(3JK) sides, on a spatial distribution of JK points with observations of \(\varGamma _\Delta \) and \(\varGamma _{{ xy}}\) and treating quantities, \(G_{j_1 ,j_2}\), corresponding to all sides as observations is technically not correct. The exceptions include a single triangulated pair of tracks, as done by Badekas and Mueller (1968), or including vertical gradients, \(\varGamma _{{ xz}}\), \(\varGamma _{{ yz}}\) (also available with torsion balance measurements). The other, theoretically untenable, option is to use the \(G_{j_1 ,j_2}\) as true observations (and neglect their correlation). In this respect, the actual data processing performed by Völgyesi (2005) for the triangulation of the spatial distribution of torsion balance data over a \(25\hbox { km}\times 30\hbox { km}\) test area is not clear in his documentation.

In flat terrain, or in an aerial survey, the vertical gradients provide much less local information to the DOV estimation than the horizontal gradients. This is obvious from Eq. (15) which shows that the contribution of \(\varGamma _{{ xz}}\) and \(\varGamma _{{ yz}}\) depends on \(\Delta z\). In addition, the relationship between the vertical gradients alone and the DOV components is analogous to the relationship between gravity anomalies and the geoid undulation (i.e, the former is just the horizontal derivative of the latter). This means that the estimation of DOV components from vertical gradients only requires a global, at least a regional, distribution of data, just as Stokes’s integral for the geoid undulation requires such a distribution of gravity anomalies. Again, there is minimal DOV information from the vertical gradients along a track.

3 Parkfield data

The theory of Sect. 2 is tested on an airborne gradiometer data set that was collected in a 10 km by 10 km area over the San Andreas Fault near Parkfield, California, by Bell Geospace, Inc., in 2004 (Bell Geospace 2004) using a full-tensor gradiometer (FTG). Both free-air and terrain-corrected gradients are provided. From these data one can also simulate measurements of a single-gradiometer instrument that measures only \(\varGamma _\Delta \) and \(\varGamma _{{ xy}}\).

The airborne data points, shown in Fig. 4, have an average spacing of \(63\pm 5\,\hbox { m}\) along roughly straight tracks. There are 49 survey tracks, labeled L11 through L491 from north-west to south-east, that are approximately 200 m apart. In addition, there are 10 cross tracks, labeled T10 through T100, from south-west to north-east, that are spaced approximately 1 km apart. The flight altitudes above the ellipsoid were designed to follow the general terrain and resulted in altitudes increasing from about 840 m in the west corner to about 1350 m in the east corner of the survey area (Fig. 5). The differences in elevations between survey tracks and cross-tracks at their intersections, however, are practically negligible with a mean value of 1.5 m and a standard deviation of 13.6 m.

Fig. 4
figure 4

Airborne gravity gradiometer data points in the Parkfield, CA, area along survey tracks, L11 through L491, and cross tracks, T10 through T100

Full size image
Fig. 5
figure 5

Altitude profiles of the survey tracks and cross tracks in the Parkfield survey area

Full size image

The tensor elements were pre-processed by Bell Geospace to remove internal biases and trends, as well as other inconsistencies, using proprietary algorithms and filters. The resulting gradients are given in a local, left-handed, east-north-down coordinate system. For consistency with the notation of Sect. 2 (Fig. 2), these gradients are transformed to the north-east-down coordinate system. The pre-processing essentially yields gravity gradient disturbances with respect to a high-degree reference field, which, however, is unknown since it is embedded in the removal of internal biases and trends. Locally these data describe the short-wavelength features of the gradient field. The statistical means and standard deviations of the gradients and their cross-over discrepancies at the points of intersection of the survey and cross-tracks are listed in Table 1. The cross-over discrepancies have a mean value close to zero and are relatively much smaller than the magnitudes of the gradients, thus indicating a reasonably large signal-to-noise ratio, as well as internal signal consistency over the survey area. In calculating these discrepancies, the vertical differences of the order of 14 m between the survey and cross-tracks are neglected. The statistics of the data, themselves, are given only formally, since the data are not random, but have large systematic components due to the geologic nature of the San Andreas fault. Bell Geospace does not provide an uncertainty of their data, and one may use the cross-over discrepancies as a conservative measure of the data error. The average of the standard deviations in Table 1 (last column), \(\sigma _\varGamma =6.5\hbox { E}\), is used where needed in the subsequent data processing.

Table 1 Statistics of the free-air gravity gradients along the Parkfield survey tracks and their discrepancies with respect to corresponding gradients on the cross-tracks. Subscripts, x, y, z, refer to the north-east-down coordinate system (the units are \(1\,\hbox { E}\equiv 1\) Eötvös \(=10^{-9}\,\hbox { s}^{-2}\))
Full size table

A “truth” model is required in order to assess the quality of the DOV components estimated from the gravity gradient data as described in Sect. 2. The astrogeodetic DOVs available in the region (Jekeli 1999), with stated accuracy of \(0.2^{\prime \prime }\)–\(0.4^{\prime \prime }\), are rather sparse as shown in Fig. 6 and fall entirely outside the gravity gradient survey area.

Fig. 6
figure 6

Astrogeodetic stations (crosses) near the Parkfield survey area (parallelogram)

Full size image
Fig. 7
figure 7

Contributions to the DOV components, \(\xi \) (left) and \(\eta \) (right), along the survey track, L51, of the Parkfield gravity gradient survey and comparison to the USDOV2012 values. All values are referenced to the initial point

Full size image

On the other hand, the National Geodetic Survey has computed a high-resolution DOV model, USDOV2012, from their gravimetric geoid model, USGG2012, which is based on \(1^{\prime }\times 1^{\prime }\) gravity data for the conterminous US and the long-wavelength GOCO03S satellite geopotential model (Mayer-Gürr et al. 2012). A comparison of the USDOV2012 values to the astrogeodetic DOVs near the Parkfield survey area yields the following statistics, mean, \(\mu \), and standard deviation, \(\sigma \), for the differences, \(\Delta \xi =\xi _{\mathrm{astro}} -\xi _{\mathrm{USDOV2012}}\), \(\Delta \eta =\eta _{\mathrm{astro}} -\eta _{\mathrm{USDOV2012}}\),

$$\begin{aligned}&\mu _{\Delta \xi } =0.58^{\prime \prime }, \quad \mu _{\Delta \eta } =0.11^{\prime \prime } \hbox { and } \sigma _{\Delta \xi } =1.65^{\prime \prime },\nonumber \\&\sigma _{\Delta \eta } =1.02^{\prime \prime }. \end{aligned}$$
(22)

It is noted that the Parkfield astrogeodetic DOVs refer to the WGS84 datum, which is consistent with the normal field implied by the USDOV2012 values. The astrogeodetic deflection components, \(\xi \), are corrected for the normal plumb line curvature (3), although the effect (\(\hbox {mean of absolute}~\hbox {values} = 0.04^{\prime \prime }\)) is significantly below the stated accuracy of the astrogeodetic values and does not affect the comparison. Assuming the astrogeodetic values are closer to the truth, the accuracy of the USDOV2012 model is of the order of \(1.0^{\prime \prime }\)–\(1.7^{\prime \prime }\) in this area. On the other hand, this model has much higher spatial resolution than the astrogeodetic data, and serves as a reasonable substitute for truth when calibrating systematic errors and assessing the gradient-integrated DOVs.

4 DOV estimation

4.1 Full-tensor gradiometer data

Much can be learned from the Parkfield data set by investigating the integration of the gradients along a single track, e.g., the survey track, L51. Applying Eq. (15) and setting the integration constants to zero (\(\xi ( {P_0 } )=0\), \(\eta ( {P_0 } )=0\)), the estimated DOV components along this track are shown in Fig. 7. The maximum along-track contributions to \(\xi \) and \(\eta \) from the vertical gradients, \(\varGamma _{{ xz}}\) and \(\varGamma _{{ yz}}\), are \(0.23^{\prime \prime }\) and \(0.06^{\prime \prime }\), respectively, for a total vertical distance travelled of about 110 m. The relative contributions to the deflections along the other tracks are similar. Thus, as expected, the main contributors to the DOVs along a dominantly horizontal track are the horizontal gradients.

Integrated gradient errors tend to accumulate rather than average out and the DOV estimates have expected trend errors when compared to the USDOV2012 values (Fig. 7). Despite these systematic errors the DOV estimates appear to contain slightly higher resolution structure than implied by the USDOV2012 model, which is limited by the resolution of the gravity input data. The gradient data used in this case are free-air gradients; and; terrain corrections, commonly applied for ground surveys, do not improve the estimation. In fact, the resulting DOV estimates are expectedly smoother and tend to annihilate their short-wavelength features, as demonstrated in Fig. 8. All subsequent results are thus based on the free-air gradients.

Fig. 8
figure 8

Comparison of DOV components estimated from free-air gradients and terrain-corrected gradients (assumed mass density, \(2670\,\hbox { kg/m}^{3})\) with USDOV2012 values

Full size image

Trend errors can be calibrated with truth data at both ends of the track. They can also be calibrated to a large extent by adjusting the cross-over discrepancies of the DOV components at the multiple intersections of the 59 Parkfield tracks. The methodology developed by Serpas (2003) is adopted for each component separately. The model for the estimated component, \(\xi \), on the survey track, s, is

$$\begin{aligned}&\xi _s \left( j \right) =\xi _s^{\mathrm{true}} \left( j \right) +b_{\xi , s} +m_{\xi , s} d_s \left( j \right) +\varepsilon _{\xi , s} \left( j \right) ,\nonumber \\&\quad j=0,\ldots , n_s -1; \end{aligned}$$
(23)

and, on the cross-track, c, it is

$$\begin{aligned}&\xi _c \left( k \right) =\xi _c^{\mathrm{true}} \left( k \right) +b_{\xi ,c} +m_{\xi ,c} d_c \left( k \right) +\varepsilon _{\xi ,c} \left( k \right) ,\nonumber \\&\quad k=0,\ldots ,n_c -1. \end{aligned}$$
(24)

Here \(\xi _s^{\mathrm{true}}\) and \(\xi _c^{\mathrm{true}}\) represent the true values of \(\xi \), while \(b_{\xi , s}\) and \(b_{\xi ,c}\) are biases for the corresponding tracks, and, \(m_{\xi ,s}\) and \(m_{\xi ,c}\) are corresponding trend parameters. The distances,

$$\begin{aligned} d_s \left( j \right)= & {} \sqrt{\left( {x_j^{\left( s \right) } -x_0^{\left( s \right) } } \right) ^{2}+\left( {y_j^{\left( s \right) } -y_0^{\left( s \right) } } \right) ^{2}}, \nonumber \\ d_c \left( k \right)= & {} \sqrt{\left( {x_k^{\left( c \right) } -x_0^{\left( c \right) } } \right) ^{2}+\left( {y_k^{\left( c \right) } -y_0^{\left( c \right) } } \right) ^{2}}, \end{aligned}$$
(25)

are computed on the assumption that the tracks are essentially straight lines. The random errors in \(\xi \) are denoted by \(\varepsilon _{\xi ,s}\) and \(\varepsilon _{\xi ,c}\). A similar formulation holds for the west-east DOV component, \(\eta \).

The points of intersection of the survey and cross-tracks are represented by \(j_c\) and \(k_s\). The actual coordinates of these points and the corresponding gradient-integrated values of \(\xi \) for each track are derived by linear interpolation. The height difference of the tracks at a point of their horizontal intersection is neglected (see Fig. 4). Since the true values, \(\xi _s^{\mathrm{true}} ( {j_c } )\) and \(\xi _c^{\mathrm{true}} ( {k_s })\), are the same, subtracting (24) from (23) at these points yields

$$\begin{aligned} \Delta \xi \left( {j_c, k_s } \right)= & {} b_{\xi ,s} -b_{\xi ,c} +m_{\xi ,s} d_s \left( {j_c } \right) \nonumber \\&-m_{\xi ,c} d_c \left( {k_s } \right) +\Delta \varepsilon _\xi \left( {j_c,k_s } \right) , \end{aligned}$$
(26)

for \(s=1,\ldots , J\), \(c=1,\ldots , K\), where J is the number of survey tracks and K is the number of cross-tracks. The left side constitutes a set of observations and the right side a set of parameters and observation errors. The distances, \(d_s ( {j_c } )\) and \(d_c ( {k_s })\), are known quantities. There are JK intersection points, hence JK observations for J survey tracks intersected by K cross-tracks; and, the total number of parameters is \(2( {J+K})\). If \(K=2\), then there is a datum defect, or rank deficiency, of 4. That is, the configuration for the \(\xi \)-profiles constructed from the survey tracks and 2 cross-tracks is floating with 4 degrees of freedom, e.g., the two biases and two trends of the cross-tracks. Adding another cross track with its own bias and trend does not constrain the configuration in any absolute way, and so, regardless of the number of cross-tracks, the rank deficiency is always 4.

For the purpose of reducing the cross-over discrepancies for all tracks the first and last cross-track profiles, T10 and T100, are fitted to the USDOV2012 model in terms of a bias and a trend (Fig. 9). The four parameters, \(b_{\xi ,1}\), \(m_{\xi ,1}\), \(b_{\xi ,K}\), \(m_{\xi ,K}\), for these tracks are then assumed known and used in the corresponding equations (26) (that is, for \(c=1\) and \(c=K\)). The system of equations then has full rank and the remaining parameters may be solved and applied, thus minimizing the cross-over discrepancies over the entire set of intersecting tracks.

Fig. 9
figure 9

Comparison of USDOV2012 deflections (\(\xi \) on the left, \(\eta \) on the right) and gradient-integrated deflections on cross-tracks T10 (top) and T100 (bottom) of the Parkfield survey, before and after adjustment with respect to USDOV2012 in terms of bias and trend error

Full size image
Table 2 Statistics (mean \({\vert }\) standard deviation) of DOV cross-over discrepancies and differences (all points) with respect to the USDOV2012 model
Full size table

The model represented by (26) is linear and has the compact form,

$$\begin{aligned} {{\varvec{l}}}=\mathbf{A}{{\varvec{p}}}+{\varvec{\varepsilon }} , \end{aligned}$$
(27)

where \({{\varvec{l}}}\) is the vector of observed cross-over discrepancies, \({{\varvec{p}}}\) is the vector of unknown biases and slopes, \(\mathbf{A}\) is the corresponding design matrix, and \({\varvec{\varepsilon }}\) is the random error in the observations. For the case at hand, there are \(JK=490\) observations and \(2( {J+K} )-4=114\) unknown parameters (and \(\mathrm{rank}( A)=114)\). It is assumed that the random errors in the gradient-integrated DOVs are independent and have identical statistical distributions, meaning that all observations are given equal weight. Therefore, the least-squares solution for the parameters is

$$\begin{aligned} \hat{{{{\varvec{p}}}}}=\left( {\mathbf{A}^{\mathrm{T}}{} \mathbf{A}} \right) ^{-1}{} \mathbf{A}^{\mathrm{T}}{{\varvec{l}}}. \end{aligned}$$
(28)

The estimated parameters are then applied to the gradient-integrated component, \(\xi \), according to (24). An identical procedure is implemented for the other DOV component, \(\eta \).

The statistics, mean and standard deviation, for the cross-over discrepancies of the gradient-integrated DOV components before and after the cross-over adjustment are shown in Table 2, which also includes the overall statistical comparison to the USDOV2012 model after the adjustment. Figure 10 compares the USDOV2012 model to the cross-over-adjusted, gradient-integrated DOVs. Each of these surface plots was generated by first linearly interpolating the values at the track points onto a \(100\times 100\) grid. There is considerably more structure, presumably induced by geology, in the gradient-integrated DOVs than in the USDOV2012 model. The small systematic linear features aligned with the cross-tracks are artifacts of the imperfect cross-over adjustment. In order to reduce these one might consider more elaborate cross-over adjustments for additional parameters besides bias and trend.

Fig. 10
figure 10

Surface plots of the USDOV2012 deflection components (top) and Parkfield gradient-integrated deflection components (after cross-over adjustment) (bottom)

Full size image

4.2 Single-instrument gradiometer data

If only a single-gradiometer instrument is available, measuring the components, \(\varGamma _\Delta ={( {\varGamma _{{ yy}} -\varGamma _{{ xx}} })}/2\) and \(\varGamma _{{ xy}}\), then DOV components can be estimated using multiple parallel tracks, as developed in Sect. 2 for a \(J\times K\) grid of data points. The model (19) is augmented with observables of the DOV components, specifically the USDOV2012 values, at the two ends of a specified track of data and is written in the form,

$$\begin{aligned} {{\varvec{f}}}\left( {{{\varvec{y}}},{\varvec{\chi }}} \right) =\mathbf{B}{{\varvec{y}}}+\mathbf{H}{\varvec{\chi }} =\mathbf{0}, \end{aligned}$$
(29)

where the \(\textit{2JK}\times 1\) vector of parameters is

$$\begin{aligned} {\varvec{\chi }} =\left( {{\begin{array}{lllllllllll} {\xi _{1,1} }&{} {\eta _{1,1} }&{} \cdots &{} {\xi _{1,K} }&{} {\eta _{1,K} }&{} \vert \cdots \vert &{} {\xi _{J,1} }&{} {\eta _{J,1} }&{} \cdots &{} {\xi _{J,K} }&{} {\eta _{J,K} } \\ \end{array} }} \right) ^{\mathrm{T}};\nonumber \\ \end{aligned}$$
(30)

and, the \(( {2JK+n_{\mathrm{dov}} })\times 1\) vector of observables is

$$\begin{aligned} {{\varvec{y}}}= & {} \left( {\varGamma _\Delta ^{\left( {1,1} \right) } }~ {\varGamma _{{ xy}}^{\left( {1,1} \right) } }~ \cdots ~ {\varGamma _\Delta ^{\left( {1,K} \right) } }~ {\varGamma _{{ xy}}^{\left( {1,K} \right) } }~ \vert \cdots \vert ~ {\varGamma _\Delta ^{\left( {J,1} \right) } }~ {\varGamma _{{ xy}}^{\left( {J,1} \right) } }\right. \nonumber \\&\left. \cdots ~ {\varGamma _\Delta ^{\left( {J,K} \right) } }~ {\varGamma _{{ xy}}^{\left( {J,K} \right) } }~ \vert {\varvec{y}_{\mathrm{dov}}^{\mathrm{T}} } \right) ^{\mathrm{T}}, \end{aligned}$$
(31)

where the \(n_{\mathrm{dov}} \times 1\) vector, \(\varvec{y}_{\mathrm{dov}}\), comprises the observed DOV components. Matrices \(\mathbf{B}\) and \(\mathbf{H}\) can be inferred from (19). It is assumed that in addition to the \(J( {K-1} )\) along-track and \(( {J-1})K\) cross-track connections between points, only \(J+K-3\) diagonal connections are made so that the number of equations in (29) and the row dimension of \(\mathbf{B}\) and \(\mathbf{H}\) is \(2JK-3+n_{\mathrm{dov}}\).

Fig. 11
figure 11

Estimates of \(\xi \) (left) and \(\eta \) (right) using the model (29) obtained from three tracks, L11, L21, and L31. The apparent grouping of estimates, \(\xi _{\mathrm{L11}}\), \(\xi _{\mathrm{L21}}\), or \(\xi _{\mathrm{L21}}\), \(\xi _{\mathrm{L31}}\), and \(\eta _{\mathrm{L11}}\), \(\eta _{\mathrm{L21}}\), or \(\eta _{\mathrm{L21}}\), \(\eta _{\mathrm{L31}}\), in each case results from the triangulation either of tracks L11 and L21 or of tracks L21 and L31. The average of \(\xi _{\mathrm{L21}}\) from these two groups is denoted \(\xi _{\mathrm{avg}}\), and the FTG-integrated estimate is denoted \(\xi _{\mathrm{FTG}}\); likewise, for the west-east deflection component, \(\eta \)

Full size image
Fig. 12
figure 12

Estimates of \(\xi \) (left) and \(\eta \) (right) using the model (29) applied to three tracks, L21, L31, and L41. The alternative estimates of \(\xi _{\mathrm{L31}}\) and \(\eta _{\mathrm{L31}}\) in each case result from the triangulation either of tracks L21 and L31 or of tracks L31 and L41. The average of \(\xi _{\mathrm{L31}}\) from these is denoted \(\xi _{\mathrm{avg}}\), and the FTG-integrated estimate is denoted \(\xi _{\mathrm{FTG}}\); likewise, for the west-east deflection component, \(\eta \)

Full size image

The least-squares solution for the parameters is given by

$$\begin{aligned} \hat{{{\varvec{\chi }}}}={\varvec{\chi }}_0 -\left( {\mathbf{H}^{\mathrm{T}}{} \mathbf{M}^{-1}{} \mathbf{H}} \right) ^{-1}{} \mathbf{H}^{\mathrm{T}}\mathbf{M}^{-1}{{\varvec{W}}}, \end{aligned}$$
(32)

where, with weight matrix, \(\mathbf{P}\), for the observations,

$$\begin{aligned} \mathbf{M}=\mathbf{BP}^{-1}{} \mathbf{B}^{\mathrm{T}}, \quad {{\varvec{W}}}={{\varvec{f}}}\left( {\tilde{{{\varvec{y}}}},{\varvec{\chi }}_0 } \right) , \end{aligned}$$
(33)

and \(\tilde{{{\varvec{y}}}}\) is the vector of actual observations, while \({\varvec{\chi }}_{0}\) is the vector of initial parameters (\({\varvec{\chi }}_0 =\mathbf{0}\)). It is assumed that the variances of the gradient observations, \(\varGamma _\Delta \) and \(\varGamma _{{ xy}} \), are the same, \(\sigma _\varGamma ^2 =( {5.5\hbox { E}})^{2}\), agreeing roughly with the cross-over discrepancies listed in Table 1; that the variances for the DOV component observations have the same value, \(\sigma _{\mathrm{dov}}^2 =( {1.4^{\prime \prime }})^{2}\), agreeing roughly with the values obtained from the comparison of USDOV2012 and astrogeodetic DOVs; and, that all observations are uncorrelated. Hence, the weight matrix is diagonal.

The number of data points on the Parkfield gradiometry survey tracks, all nominally 10 km in length, varies from 149 to 193. Thus, to satisfy the simplifying assumptions of the data grid (Fig. 3), all survey tracks are decimated to 149 points. With \(J=49\) this implies a row dimension for \(\mathbf{B}\) greater than 14,599. Although \(\mathbf{B}\) and \(\mathbf{H}\) are sparse, and \(\mathbf{P}\) is diagonal, neither \(\mathbf{M}\) nor \(\mathbf{H}^{\mathrm{T}}\mathbf{M}^{-1}{} \mathbf{H}\) is block diagonal, and maximizing efficiency in terms of computer storage and computational speed is a challenge. On the other hand, tests show that the DOV estimation depends strongly on the chosen diagonal connections, leading to the alternative of sequentially processing only a minimal number of survey (or, cross) tracks.

For example, the estimates of \(\xi \) and \(\eta \) from gradients on three tracks L11, L21, and L31 can be obtained with a triangulation either between tracks L11 and L21 or between L21 and L31. Figure 11 shows that the estimates differ significantly. The average of the two estimates on L21, in this case, is close to the FTG-integrated value (with the bias and trend relative to the USDOV2012 endpoint values removed). The diagonal connections give more weight to the observations on the triangulated pair of tracks and thereby bias the estimates on neighboring tracks. On the other hand, the short-wavelength structure of the DOV signal appears common in both estimates.

Table 3 Statistics (mean \({\vert }\) standard deviation) of differences between \(\varGamma _\Delta ,\varGamma _{{ xy}}\)-derived DOVs and the USDOV2012 model (all points)
Full size table
Fig. 13
figure 13

Surface plots of the Parkfield triangulated-gradient-derived deflection components, \(\xi \) on the left and \(\eta \) on the right (after cross-over adjustment)

Full size image

For some other tracks, the estimates from alternative triangulations are closer, but differ more significantly in their average from the FTG-integrated values (again, with the bias and trend relative to the USDOV2012 endpoint values removed), as shown in Fig. 12. And, again, the short-wavelength DOV signal is evident and common to both. Whether from a triplet of adjacent tracks or merely a pair of tracks, the DOV estimates on the tracks that are triangulated differ only at the level of milliarcseconds. Therefore, the final estimates from the horizontal gradients, \(\varGamma _\Delta \) and \(\varGamma _{{ xy}}\), are obtained from pair-wise triangulated tracks and averaged (without weights) on the tracks that have two estimates. This procedure also uses gradient data more than once without considering their correlation, but at least from a numerical perspective it is a viable method to solve for the roughly 18,000 unknown DOV components on the 59 survey and cross-tracks.

The independently sequential least-squares estimation of \(\xi \) and \(\eta \) for triangulated pairs of tracks, L11&L21, L21&L31, ..., T10&T20, T20&T30, ..., requires observed DOV values in each case at the endpoints of one track, for which the USDOV2012 values are used. The resulting averaged estimates are cross-over adjusted, as in the case of the FTG-integrated DOV estimates, in an attempt to calibrate the biases and trend errors in the estimates on individual tracks. As before, the bias and trend error control is provided by USDOV2012 values on cross-tracks T10 and T100 (very similar results are obtained using T20 and T90). Table 3 summarizes the statistics of their final differences with respect to the USDOV2012 model. Clearly, there is some improvement by performing the cross-over adjustment, but the overall estimation compared to USDOV2012 is significantly worse than the FTG-integrated DOV estimation (see Table 2). Indeed, corresponding spatial visualizations (Fig. 13) exhibit a highly striped pattern in both along-track and cross-track directions from which no geologic structure is discernible. The most apparent reason is the disagreement between the triangulated-gradient estimates and the FTG-integrated estimates, illustrated, for example, in Fig. 12. This should not necessarily be a surprise since data of the type, \({( {\varGamma _{{ yy}} -\varGamma _{{ xx}} } )}/2\), are not equivalent to individual data, \(\varGamma _{{ xx}}\) and \(\varGamma _{{ yy}}\). Separating the terms of the difference, \(\varGamma _\Delta \), is accomplished heuristically by using two parallel tracks, but not without error; and these errors accumulate and propagate systematically to the DOV estimates. This error is likely greater for the more widely spaced cross-tracks than the survey tracks. Another contributing factor is the possible distortion in the bias and trend error calibration resulting from the required end-matching of each pair of triangulated tracks, as indicated in Figs. 11 and 12. This track-by-track fit to USDOV2012 endpoint values, in addition to the cross-over adjustment, creates excessive control that prevents representation of the short-wavelength features in two-dimensions, although they appear in the profiles.

5 Conclusion

The otherwise straightforward estimation of deflections of the vertical from gravity gradients on survey lines is subject to systematic error due to the numerical integration. This requires adequate control to calibrate bias and trend errors. A calibration method is tested for a regular set of intersecting lines of airborne gravity gradient data over a local 10 km square area. Using full-tensor gradient data and minimal error control, including a cross-over adjustment of the DOV estimates, the agreement between the resulting deflections and a longer-wavelength model, USDOV2012, is at the level of 0.6–\(0.9\,\hbox {arcsec}\). However, rather than representing estimation error, this level of discrepancy ostensibly embodies true short-wavelength signal. Processing single-instrument gradients, \(\varGamma _\Delta ={( {\varGamma _{{ yy}} -\varGamma _{{ xx}} } )}/2\) and \(\varGamma _{{ xy}}\), using pair-wise triangulations of parallel data tracks does not yield nearly the same level of agreement with USDOV2012. This may be attributed primarily to a lack of adequate data, as the DOV estimates from FTG and single-instrument data along a single track can differ significantly.