1 Introduction

Guaranteeing safety of civil structures and their occupants against earthquakes has been a major concern of researchers and engineers for many years. A contemporary approach for obtaining satisfactory level of safety is to use structural control in order to grant to buildings the ability to bear such unwanted dynamic phenomena [9]. Generally speaking, physical realization of structural control is done by actuators that apply forces to the vibrating structure in real time. There are many types of such actuators, and each one imposes different design constraints on the control law [1, 13, 15, 18]. A famous type of devices, known to be effective in many applications, is the controlled hydraulic damper . It is a type of semi-active device [9, 11] whose operation principle resembles that of viscous fluid damper [3]. The difference though is the presence of a valves system that dictates the flow of the fluid through the hydraulic damper’s orifices [13]. The valves are adjusted electromechanically, leading to different damping’s properties. Closing the valve increases the damping and vice versa when it opens. Incorporation of such dampers into a controller allows it to adjust the damping to a preferred value during the structure’s dynamic response in real time. This kind of devices has been implemented in several full-scale structures [10, 13, 14].

Many control devices manifest highly nonlinear behavior. The problem is that taking into account such nonlinear complexities during the controller design can establish a significant hurdle for the control designer. A work-around solution is to separate between the system’s and the damper’s dynamics [21]. This allows for the nonlinear properties of the device to be considered separately from the system’s controller. The latter is designed to generate control signals, mostly optimal by some sense, that are tracked by the device’s controller. A dilemma that naturally emerges in such situation is what to do when the system’s controller instructs a signal which is not feasible by the device’s limitations. A simple and popular approach in such a case is to use arbitrary clipping [14, 16, 17, 22]. However, the arbitrary clipping of the control trajectory distorts it and therefore raises a theoretical question on its contribution to the controlled plant. This issue spurs formulation of optimal control designs that can account for semi-active devices’ limitations and reduce the need of arbitrary clipping [4,5,6,7,8]. The present study suggests a new method for the computation of optimal feedback for a plant controlled by multiple semi-active controlled hydraulic dampers and subjected to external, a priori known deterministic excitation input.

2 Background

2.1 The Plant Model

The characteristics of civil structures, in conjunction with common engineering assumptions, allow to model them by linear approaches, such as dynamic linear models. Consider a model of an excited structure with lumped masses, linear damping, linear stiffness, and a controller comprised of multiple actuators. The equations of motion in the structure’s degrees of freedom (DOFs) are given by the following second-order initial value problem [19]:

(1)

This is a linear time invariant (LTI ) model, in which M > 0, C d ≥ 0, and K > 0 are symmetric mass, damping, and stiffness matrices, respectively,Footnote 1 \({\mathbf {z}}:\mathbb {R}\rightarrow \mathbb {R}^{n_z}\) is a smooth vector function, which represents the DOF displacements, \({\mathbf {w}}:\mathbb {R}\rightarrow \mathbb {R}^{n_w}\) is a vector function of the control forces that are generated by the actuators, \(\boldsymbol {\Psi }\in \mathbb {R}^{n_z\times n_w}\) is an input matrix that describes how the control force inputs affect the structure’s DOF, and \({\mathbf {e}}:\mathbb {R}\rightarrow \mathbb {R}^{n_z}\) is a vector function that describes the external excitation force inputs. Here, z(t) is the intersection of z at t. That is, here, z(t) is used to signify a specific vector in \(\mathbb {R}^{n_z}\), obtained at a given t, whereas z refers to the entire trajectory over ]0, t f[.

When dealing control theory, state-space representation is much more convenient than (1). Hence, transforming it to the state-space form yields

(2)

where

n = 2n z.

Let the control devices, embedded in the structure, be semi-active . Even though such actuators have many advantages, which is why they garner attention from many researchers, they impose some constraints on the synthesized control. Basically, the semi-active dampers set limits on the control force—w i, as follows:

  1. 1.

    w i is always opposed to the relative velocity of the damper’s anchors. This assures that the damper only consumes mechanical energy from the structure.

  2. 2.

    Physical considerations inhibit the device from generating a control force when the relative velocity in the damper is zero. In other words, w i must vanish when there is no motion in the damper.

  3. 3.

    For some semi-active dampers, there is some minimal amount of damping that the device provides during its motion, even in off-state, i.e., when no damping effort is exerted.

In addition to these three semi-active constraints, which are related to the traits of semi-active dampers, many practical implementations require the control force to be bounded.

In order to include these constraints in a control problem, they should be quantified. Assume that the relative velocity of the damper’s anchors can be represented as linear combination of the state variables, i.e., as c i x for some \({\mathbf {c}}_i^T\in \mathbb {R}^{n}\), and that a linear viscous damping is valid to the given problem [20]. Then, the above limitations are expressed by the following constraints:

  1. C1:

    w i(t)c i x(t) ≤ 0

  2. C2:

    c i x(t) = 0 → w i(t) = 0

  3. C3:

    |w i(t)|≥ w i,min(t, x(t)) ≥ 0

  4. C4:

    w i,max ≥|w i(t)|

for all t ∈ [0, t f] and for some \(w_{i,min}:\mathbb {R}\times \mathbb {R}^n\rightarrow [0,w_{i,max}]\). Note that the lower bound must satisfy w i,min(t, x(t)) = 0 whenever c i x(t) = 0; otherwise C2 and C3 might contradict.

In this work, constraints C1–C4 are adapted to the traits of a certain type of controlled hydraulic dampers. A control design must account for these constraints, especially when the optimal control design is sought. Otherwise, the design’s relevancy to a constrained problem is dubious. The problem is that the inclusion of such constraints into optimal control design problem can turn it into a very nontrivial problem. A method that can be used to tackle such a problem is explained below.

2.2 Krotov’s Method: A Global Method of Successive Improvements of Control

Krotov’s method is aimed at numerically solving optimal control problems. However, its utilization depends on the successful formulation of a function’s sequence with special properties. If such a sequence can be found, it allows to compute a candidate optimum of the addressed optimal control problem. This subsection describes elements from Krotov’s theory, relevant to the addressed problem.

Let

(3)

be a state equation, \(\mathcal {u}\subseteq \{\mathbb {R}\rightarrow \mathbb {R}^{n_u}\}\) be the set of admissible control trajectories, and \(\mathcal {x}\subseteq \{\mathbb {R}\rightarrow \mathbb {R}^{n}\}\) be the set of state trajectories that are reachable from \(\mathcal {u}\) and x(0). The term admissible process refers to the state and control trajectories \(({\mathbf {x}}\in \mathcal {x},{\mathbf {u}}\in \mathcal {u})\) which satisfy (3). The goal is to find an admissible process that minimizes the following performance index:

$$\displaystyle \begin{aligned} J({\mathbf{x}},{\mathbf{u}}) = \int\limits_0^{t_f} l(t,{\mathbf{x}}(t),{\mathbf{u}}(t)) \mathrm{d}\, t + l_f({\mathbf{x}}(t)){} \end{aligned} $$
(4)

Definition 1 (Improving Sequence)

Let {(x k, u k)} be a sequence of admissible processes, and assume that \(\inf _{\substack {{\mathbf {x}}\in \mathcal {x}\\{\mathbf {u}}\in \mathcal {u}}} J({\mathbf {x}},{\mathbf {u}})\) exists. If

$$\displaystyle \begin{aligned} J({\mathbf{x}}_k,{\mathbf{u}}_k)\geq J({\mathbf{x}}_{k+1},{\mathbf{u}}_{k+1}) {} \end{aligned} $$
(5)

for all k = 1, 2, … and

$$\displaystyle \begin{aligned} \lim_{k\rightarrow \infty} J({\mathbf{x}}_k,{\mathbf{u}}_k) = \inf_{\substack{{\mathbf{x}}\in\mathcal{x}\\{\mathbf{u}}\in\mathcal{u}}} J({\mathbf{x}},{\mathbf{u}}) \end{aligned} $$
(6)

then {(x k, u k)} is said to be an improving sequence .

Such a sequence is the outcome of Krotov’s method . In order to obtain the improving sequence, the method successively improves admissible processes, as follows [12].

Theorem 1

Let (x k, u k) be a given admissible process and q be some smooth function, and define s and s f as

(7)
(8)

where \(\boldsymbol {\upxi }\in \mathbb {R}^n\) and \(\boldsymbol {\upnu }\in \mathbb {R}^{n_u}\) are some vectors.

If q grants to s and s f the next property:

$$\displaystyle \begin{aligned} s(t,{\mathbf{x}}_k(t),{\mathbf{u}}_k(t)) =& \max_{\boldsymbol{\upxi}\in \mathcal{x}(t)} s(t,\boldsymbol{\upxi},{\mathbf{u}}_k(t))\\ s_{f}({\mathbf{x}}_{k}(t_f)) =& \max_{\boldsymbol{\upxi}\in\mathcal{x}(t_f)} s_{f}(\boldsymbol{\upxi}) \end{aligned} $$
(9)

and if \(\hat {\mathbf {u}}\) is a control feedback which satisfies

(10)

then x k+1 , which solves

(11)

and the control trajectory \({\mathbf {u}}_{k+1}(t)=\hat {\mathbf {u}}(t,{\mathbf {x}}_{k+1}(t))\) satisfy (5).

It follows from this theorem that if for a prescribed (x k, u k), one can find q such that (9) holds, then it is possible to find an improved admissible process—(x k+1, u k+1). Such q is denoted as improving function . Solving this problem over and over yields an improving sequence and hence leads to the solution of the optimization problem. In his work, Krotov showed that if, at some point, the processes stop changing, then the obtained process satisfies Pontryagin’s minimum principle .

Generally speaking, the iterative procedure is summarized in the following algorithm. Its initialization requires to compute some initial admissible process—(x 0, u 0). Afterward, the following steps are iterated for k = {0, 1, 2, …} until convergence is attained:

  1. 1.

    Find q k that grants s k and s f,k the next property:

    $$\displaystyle \begin{aligned} s_k(t,{\mathbf{x}}_k(t),{\mathbf{u}}_k(t)) =& \max_{\boldsymbol{\upxi}\in\mathcal{x}(t)} s_k(t,\boldsymbol{\upxi},{\mathbf{u}}_k(t))\\ s_{f,k}({\mathbf{x}}_k(t_f)) =& \max_{\boldsymbol{\upxi}\in\mathcal{x}(t_f)} s_{f,k}(\boldsymbol{\upxi}) \end{aligned} $$

    at a given (x k, u k) and for all t in [0, t f]. Here, s k and s f,k are the functions obtained by substituting q k into (7) and (8).

  2. 2.

    Find a minimizing feedback

    $$\displaystyle \begin{aligned} \hat{\mathbf{u}}_{k+1}(t,{\mathbf{x}}(t)) = \arg\min_{\boldsymbol{\upnu}\in\mathcal{u}(t)} s_k(t,{\mathbf{x}}(t),\boldsymbol{\upnu}) \end{aligned} $$

    for all t in [0, t f]

  3. 3.

    Propagate into the next improved state and control processes, by solving

    $$\displaystyle \begin{aligned} \dot{\mathbf{x}}_{k+1}(t) =& {\mathbf{f}}{\big(}t,{\mathbf{x}}_{k+1}(t),\hat{\mathbf{u}}_{k+1}(t,{\mathbf{x}}_{k+1}(t)){\big)} \end{aligned} $$

    and setting

    $$\displaystyle \begin{aligned} {\mathbf{u}}_{k+1}(t) =& \hat{\mathbf{u}}_{k+1}(t,{\mathbf{x}}_{k+1}(t)) \end{aligned} $$

As it can be seen from the above, the use of Krotov’s method requires to formulate a sequence of improving functions —{q k}. In general, the search for these improving functions can be a significant challenge. As of this writing, there is no known unified method for their formulation, and they usually differ from one optimal control problem to another.

3 Main Results

Consider a structure equipped with a set of controlled hydraulic dampers and subjected to an a priori known external excitation—\({\mathbf {g}}:\mathbb {R}\rightarrow \mathbb {R}^n\). It is assumed that the control forces follow a linear viscous damping law and that each device features merely two control phases—on or off. In many works, (2) is used for modeling such a system in conjunction with a set of limitations, reflecting the constraints induced by the nature of the semi-active dampers . In this study, however, a bilinear representation is used, allowing to account for the system’s dynamics and constraints C1–C4. It will be shown that the alternative representation is equivalent to that based on (2).

Consider the bilinear state-space equation :

(12)

where n u = n w; \({\mathbf {c}}_i^T\in \mathbb {R}^{n}\) is constructed such that c i x is the relative velocity of the damper’s anchors, positive when the damper elongates, and u i is a control trajectory that satisfies \(u_i(t) \in \mathcal {u}_i(t,{\mathbf {x}})\), where \(\mathcal {u}_i({\mathbf {x}})\) is the set of control trajectories, which are admissible in the i-th device . \(\mathcal {u}_i(t,{\mathbf {x}})\) is the set of admissible values at some time—t. It is defined by

$$\displaystyle \begin{aligned} \mathcal{u}_i(t,{\mathbf{x}}) = \left\{\begin{array}{cl} \{d_i,D_i\}, \qquad & D_i|{\mathbf{c}}_i{\mathbf{x}}(t)|\leq w_{i,max} \\ d_i, & \text{otherwise}\end{array}\right. {} \end{aligned} $$
(13)

Here, D i ≥ d i ≥ 0 are the damper’s on/off gains. Physically, they are the maximal and minimal viscous damping coefficients of the i-th control device, respectively. When the valve is opened, the device provides a minimal damping force—w i,min(t, x(t)) = d i|c i x(t)|.

The following proposition shows that the suggested representation accords to a model, governed by (2) with constraints C1–C4.

Proposition 1

If (x, u) is an admissible process by means of (12) and (13), and if d i|c i x(t)| < w i,max is met, then \(({\mathbf {x}},(-u_i{\mathbf {c}}_i{\mathbf {x}})_{i=1}^{n_u})\) is an admissible process by means of (2) with constraints C1–C4.

Proof

Let (x, u) be an admissible process by means of (12) and (13), and let

(14)

It follows that

$$\displaystyle \begin{aligned} \hat w_i({\mathbf{x}}(t),t){\mathbf{c}}_i{\mathbf{x}}(t) &= -u_i(t)({\mathbf{c}}_i{\mathbf{x}}(t))^2\leq 0 \end{aligned} $$
(15)

i.e., C1 is satisfied. The compliance of \(\hat w_i\) with C2 is straightforward from its definition. C3 is satisfied because

$$\displaystyle \begin{aligned} |\hat w_i({\mathbf{x}}(t),t)| &= u_i(t)|{\mathbf{c}}_i{\mathbf{x}}(t)| \geq d_i|{\mathbf{c}}_i{\mathbf{x}}(t)| = w_{i,min}(t,{\mathbf{x}}(t)) \end{aligned} $$

C4 is satisfied by the hypothesis. Hence, \(({\mathbf {x}},{\hat {\mathbf {w}}}({\mathbf {x}}))\) is admissible by means of (2) with constraints C1–C4. □

Therefore, assuming that the problem is defined with large enough w i,max, representations (2) and (12) are interchangeable.

The next definition formally states the addressed optimal control problem.

Definition 2 (CBQR)

The continuous-time bilinear quadratic regulator (CBQR) control problem is a search for an optimal and admissible process (x ∗, u ∗) that minimizes the quadratic performance index :

$$\displaystyle \begin{aligned} J({\mathbf{x}},{\mathbf{u}}) =& \frac{1}{2}\int\limits_0^{t_f} {\mathbf{x}}(t)^T{\mathbf{Q}}{\mathbf{x}}(t) + \sum_{i=1}^{n_u} u_i(t)^2 r_i \mathrm{d}\, t + \frac{1}{2}{\mathbf{x}}(t)^T{\mathbf{H}}{\mathbf{x}}(t) {} \end{aligned} $$
(16)

where \(0\leq {\mathbf {Q}},{\mathbf {H}}\in \mathbb {R}^{n\times n}\), and r i > 0 for i = 1, …, n u. An admissible process is a pair (x, u) which satisfies (12) and \(u_i\in \mathcal {u}_i({\mathbf {x}})\) for i = 1, …, n u.

From physical viewpoint, the performance index weighs the states’ response against the time-varying damping gains. Smaller values of \((r_i)_{i=1}^{n_u}\) will produce a control law which tends to produce more frequent closed-valve pulses.

The CBQR problem will be solved here by Krotov’s method. To this end, a class of improving functions and minimizing feedback , which suit to the CBQR problem are formulated in the next lemmas.

Lemma 1

Let \(q(t,\boldsymbol {\upxi }) = \frac {1}{2}\boldsymbol {\upxi }^T{\mathbf {P}}(t)\boldsymbol {\upxi } + {\mathbf {p}}(t)^T\boldsymbol {\upxi }\) , where \(\boldsymbol {\upxi }\in \mathbb {R}^n\), \({\mathbf {P}}:\mathbb {R}\rightarrow \mathbb {R}^{n\times n}\) is a continuous, piecewise smooth and symmetric, matrix function, and \({\mathbf {p}}:\mathbb {R}\rightarrow \mathbb {R}^{n}\) is a continuous and piecewise smooth, vector function.

Let . The vector of control laws, \((\hat u_i)_{i=1}^{n_u}\) , which minimizes s(t, x(t), u(t)) over \(\{{\mathbf {u}}(t)\in \mathcal {u}(t,{\mathbf {x}})\}\) , is given by

$$\displaystyle \begin{aligned} \hat u_i(t,{\mathbf{x}}(t)) &=\left\{\begin{array}{cl}d_i, & D_i|{\mathbf{c}}_i{\mathbf{x}}(t)|>w_{i,max} \\ \arg \min\limits_{\nu_i\in\{d_i,D_i\}} \left(\nu_i - v_i(t,{\mathbf{x}}(t)) \right)^2, & \mathit{\text{otherwise}} \end{array}\right. {} \end{aligned} $$
(17)

Proof

The partial derivatives of q are

$$\displaystyle \begin{aligned} q_t(t,\boldsymbol{\upxi}) = \frac{1}{2}\boldsymbol{\upxi}^T\dot{\mathbf{P}}(t)\boldsymbol{\upxi} + \dot {\mathbf{p}}(t)^T\boldsymbol{\upxi};\quad q_{\mathbf{x}}(t,\boldsymbol{\upxi}) = \boldsymbol{\upxi}^T{\mathbf{P}}(t) + {\mathbf{p}}(t)^T \end{aligned} $$
(18)

Let \(\boldsymbol {\upnu }\in \mathbb {R}^{n_u}\). By explicitly writing (7) and rearranging, we obtain

(19)
(20)

where v i was defined in the lemma. Completing the squares leads to

where \(f_2:\mathbb {R}\times \mathbb {R}^n\rightarrow \mathbb {R}\) is some function that is independent of ν i. It follows that a minimum of s(t, x(t), ν) over \(\{\boldsymbol {\upnu }|\boldsymbol {\upnu }\in \mathcal {u}(t,{\mathbf {x}})\}\) is the minimum of the quadratic sum with relation to each \(\{\nu _i|\nu _i\in \mathcal {u}_i(t,{\mathbf {x}})\}\), independently. Thereby, the admissible minimum is attained at \(\nu _i=\arg \min _{\nu _i\in \mathcal {u}_i(t,{\mathbf {x}})} \left (\nu _i - v_i(t,{\mathbf {x}}(t)) \right )^2\) for each device. This fact is reflected by (17).

Lemma 2

Let (x k, u k) be a given admissible process, and let P k and p k be the solutions of

(21)

and

$$\displaystyle \begin{aligned} \dot {\mathbf{p}}_k(t) = & - \left({\mathbf{A}}-{\mathbf{B}}\,{\mathbf{diag}}({\mathbf{u}}_k(t)){\mathbf{C}}\right)^T{\mathbf{p}}_k(t) -{\mathbf{P}}_k(t){\mathbf{g}}(t) ;\qquad {\mathbf{p}}_k(t_f)={\mathbf{0}} {} \end{aligned} $$
(22)

then

$$\displaystyle \begin{aligned} q_k(t,\boldsymbol{\upxi}) =& \frac{1}{2}\boldsymbol{\upxi}^T{\mathbf{P}}_k(t)\boldsymbol{\upxi} + {\mathbf{p}}_k(t)^T\boldsymbol{\upxi} \end{aligned} $$

grants s k and s f,k the property:

$$\displaystyle \begin{aligned} s_k(t,{\mathbf{x}}_k(t),{\mathbf{u}}_k(t)) =& \max_{\boldsymbol{\upxi}\in\mathcal{x}(t)} s_k(t,\boldsymbol{\upxi},{\mathbf{u}}_k(t))\\{} s_{f,k}({\mathbf{x}}_k(t_f)) =& \max_{\boldsymbol{\upxi}\in\mathcal{x}(t_f)} s_{f,k}(\boldsymbol{\upxi}) \end{aligned} $$

and thus is an improving function .

Proof

Substituting q k into (8) yields

$$\displaystyle \begin{aligned} &s_{f,k}({\mathbf{x}}(t_f)) = \frac{1}{2}{\mathbf{x}}(t_f)^T{\mathbf{H}}{\mathbf{x}}(t_f) - \left(\frac{1}{2}{\mathbf{x}}(t_f)^T{\mathbf{P}}_k(t_f){\mathbf{x}}(t_f) + {\mathbf{p}}_k(t_f)^T{\mathbf{x}}(t_f)\right) = 0 \end{aligned} $$

for all \({\mathbf {x}}(t_f)\in \mathcal {x}(t_f)\). Hence, s f,k(x(t f)) ≤ s f,k(x k(t f)).

By substituting v i into (20) and then reordering terms, s k(t, x(t), u k(t)) becomes

$$\displaystyle \begin{aligned} s_k(t,{\mathbf{x}}(t),{\mathbf{u}}_k(t)&) =\frac{1}{2}{\mathbf{x}}(t)^T \left(\dot{\mathbf{P}}_k(t) + {\mathbf{P}}_k(t)\left({\mathbf{A}}-{\mathbf{B}}\,{\mathbf{diag}}({\mathbf{u}}_k(t)){\mathbf{C}}\right) \right.\\ &\left. + \left({\mathbf{A}}-{\mathbf{B}}\,{\mathbf{diag}}({\mathbf{u}}_k(t)){\mathbf{C}}\right)^T{\mathbf{P}}_k(t) + {\mathbf{Q}} \right){\mathbf{x}}(t)\\ &+{\mathbf{x}}(t)^T\left( \dot {\mathbf{p}}_k(t) + \left({\mathbf{A}}-{\mathbf{B}}\,{\mathbf{diag}}({\mathbf{u}}_k(t)){\mathbf{C}}\right)^T{\mathbf{p}}_k(t) +{\mathbf{P}}_k(t){\mathbf{g}}(t)\right) \\ & +{\mathbf{p}}_k(t)^T{\mathbf{g}}(t) +\frac{1}{2}\sum_{i=1}^{n_u} u_{i,k}(t)^2 r_i \end{aligned} $$

As \(\dot {\mathbf {P}}_k(t)\) and \(\dot {\mathbf {p}}_k(t)\) satisfy (21) and (22), we have

$$\displaystyle \begin{aligned} s_k(t,{\mathbf{x}}(t),{\mathbf{u}}_k(t)) = & \frac{1}{2}{\mathbf{x}}(t)^T {\mathbf{0}}{\mathbf{x}}(t) + {\mathbf{x}}(t)^T {\mathbf{0}} +{\mathbf{p}}_k(t)^T{\mathbf{g}}(t) \\ = & {\mathbf{p}}_k(t)^T{\mathbf{g}}(t) +\frac{1}{2}\sum_{i=1}^{n_u} u_{i,k}(t)^2 r_i \end{aligned} $$

Since s k(t, x(t), u k(t)) = s k(t, x k(t), u k(t)), it is obvious that

$$\displaystyle \begin{aligned} s_k(t,{\mathbf{x}}(t),{\mathbf{u}}_k(t))) \leq s_k(t,{\mathbf{x}}_k(t),{\mathbf{u}}_k(t)) \end{aligned} $$

for all x(t).

It can be seen that, if g = 0, then p k(t) = 0, and the problem reduces to the free vibrations case that is described in [2].

By putting together Sect. 2.2 and the above two lemmas, the sequences {q k} and {(x k, u k)} can be computed where the second one is an improving sequence . As J is nonnegative, it has an infimum and {(x k, u k)} gets arbitrarily close to a candidate optimum .

The resulting algorithm is summarized in Algorithm 1. Its output is an arbitrary approximation for P ∗ and p ∗, which define the optimal control law. It should be noted that, seemingly, the use of absolute value in step (8) of the iterations stage is theoretically unnecessary. However, it is needed due to practical considerations. Sometimes, numerical computation errors may cause the algorithm to lose its monotonicity when J starts converging.

Algorithm 1 CBQR: Algorithm for successive improvement of control process

4 Numerical Example

This section demonstrates the seismic response of a controlled structure whose control trajectories are calculated by the suggested method. The simulations were carried out numerically by MATLAB computational framework.

The model that is used here is the same one suggested by Spencer et al. [19] as a control benchmark problem for seismically excited buildings, except for slight modifications. Here, its response was simulated to El-Centro horizontal ground acceleration input [3]. Peak ground acceleration was set to 0.3 g.

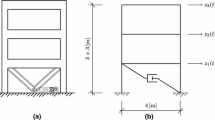
Nine controlled on/off hydraulic dampers are assumed to be embedded in the structure. The model’s and the control devices’ configuration are shown in Fig. 1. In this figure, z i is the i-th DOF and w i is the control force in the adjacent device. The devices are numbered from 1 to 9 in an increasing order, starting from the device mounted in the first floor.

Fig. 1
figure 1

Evaluation model and dampers configuration

Full size image

State-space model was formulated according to (2). The external excitation is \({\mathbf {e}}=\boldsymbol {\upgamma }^T\ddot z_g\), where \(\boldsymbol {\upgamma }=\begin {bmatrix}1&1&\ldots &1\end {bmatrix}^T\in \mathbb {R}^{21}\)and \(\ddot z_g\) is the earthquake input.

The response of three cases was analyzed:

Case 1::

There are no control devices.

Case 2::

The control law is the clipped optimal control law [13].

Case 3::

The control law is a CBQR one.

The clipped optimal control logic, which was used in case 1, is based on the prevalent LQR control law. The clipping logic is described in previous studies [13].

In accordance with (14), each control force w i is associated with an equivalent damping gain—u i. Identical properties were set for all the devices. The on/off gains were defined as D = 5 × 106 kg∕s and d = 2 × 105 kg∕s. The maximal allowable control force was set to w max = 20 × 103 kN.

The i-th rows in the observation matrix \({\mathbf {C}}\in \mathbb {R}^{9\times 42}\) are c i. The state weighting matrix Q for cases 1 and 2 was chosen such that

$$\displaystyle \begin{aligned} {\mathbf{x}}(t)^T{\mathbf{Q}}{\mathbf{x}}(t) = 5\times10^{18}\left(z_1(t)^2 + z_2(t)^2 + \sum_{i=3}^{21} (z_i(t)-z_{i-1}(t))^2 \right) \end{aligned} $$

Such a weighting accounts for the inter-story drifts in the structure, which is a common evaluation quantity in seismic practice [19]. It can be obtained here by letting Q = 5 × 1018 N T N, where \({\mathbf {N}}\in \mathbb {R}^{n\times n}\) is defined by (N)i,i = 1 for 1 ≤ i ≤ 21, (N)i+1,i = −1 for 2 ≤ i ≤ 20, and (N)i,j = 0 in the other elements. Unlike the states’ weighting, which has the same meaning in cases 1 and 2, the control weighting for case 1 has different interpretation than that of case 2. In the LQR method, which underpins case 1, the control weighting relates to the control forces, whereas in case 2 the CBQR control weighting relates to the equivalent damping gains. It means that case 1 and case 2 have completely different design goals. Hence, in order to create a common comparison basis, case 1 control weighting was chosen such that the Euclidean norm \(\|(u_i^{c1})_{i=1}^{n_u}\|\) will be approximately the same as \(\|(u_i^{c2})_{i=1}^{n_u}\|\). To this end, \((r_i^{c1})_{i=1}^{9}=(1,1,\ldots ,1)\times 4.7\times 10^{5}\) and \((r_i^{c2})_{i=1}^{9}=(1,1,\ldots ,1)\times 10^{-4}\) were set for cases 1 and 2, respectively.

The initial state vector was set to zero.

Figure 2 shows the progress of the performance index during 9 design iterations. A dramatic improvement can be seen after the first iteration. Practically, the algorithm converged after the second one. Figure 3 shows the inter-story drifts of the 10th floor during the first 10 s of the response. It can be seen that cases 2 and 3 present pretty close performance with a slight advantage in favor of case 3. The peak inter-story drifts throughout the building are given in Fig. 4. It can be seen that case 3 attained additional improvement, compared to case 2. The control policies of cases 2 and 3 resulted with different control signals. Figure 5 shows the first 10 s of the control signal u 1, synthesized by each control law for the first device, located in the first floor. The variations in the signal express the valve’s open/close commands in this device, generated in effort to regulate the vibrations. Figure 6 shows the form of control force w 1, generated during the first 10 s in the same device. The sharp changes reflect moments when the valve’s state was switched in the device.

Fig. 2
figure 2

Performance index values in each iteration

Full size image
Fig. 3
figure 3

Inter-story drifts in the 10th floor

Full size image
Fig. 4
figure 4

Peak inter-story drifts throughout the structure

Full size image
Fig. 5
figure 5

Control signal u 1 in (a) case 2 and (b) case 3

Full size image
Fig. 6
figure 6

Control force w 1

Full size image