1 Introduction

Bilinear differential equations are simple and at the same time effective nonlinear dynamic models that appear in some linearizations of nonlinear systems at a common fixed point [1], and in many practical modern control problems [2]. Despite their nonlinearity, their properties are close to those of linear systems and therefore they can be treated by several techniques and procedures from linear systems theory [3].

Optimal control of bilinear models has been addressed by several researchers. In [4], a bilinear-quadratic optimal control problem was defined for a homogeneous bilinear system, unconstrained control forces and a quadratic performance index. An iterative scheme, that produces a linear control law, was derived by using Pontryagin’s minimum principle and the successive approximations approach.

The use of Adomian decomposition method for the solution of the time-varying bilinear quadratic, optimal unconstrained control problem was suggested in [5]. According to this method, the bilinear model is represented by a convergent sequence of linear ones. Then, the solution of a bilinear quadratic problem is represented as a convergent sequence of LQR solutions. The optimal tracking problem is considered to illustrate the theory.

An optimal control law for a tracking problem related to a bilinear system and a quadratic performance index was suggested in [6]. The theoretical framework was constructed by using Lagrange’s multipliers, and an iterative algorithm was proposed for its solution.

In [7], the bilinear quadratic optimal unconstrained control problem is solved by construction of Hamiltonian equations, which leads to the common two-point boundary value problem for the state and co-state. The computation of the initial co-state is done successively by solving two first-order quasi-linear partial differential equations, which are derived in the paper.

The present paper introduces a method for solving a constrained optimal control problem for a single input bilinear system and a quadratic performance index. Emphasis is placed on semi-active control of mechanical vibrations in structures. As a first step, it is shown that a bilinear model with a single, constrained control input, can be used for describing a semi-active controlled plant. Next, Krotov’s method is used to derive an algorithm for the computation of an optimal feedback that obeys the constraints. As it will be described hereinafter, the main novelty in this study is the formulation of the sequence of Krotov functions that suits the addressed problem and allows for Krotov’s method to be used for its solution. The required computational steps are arranged as an algorithm and the outlines of the proofs for convergence and the optimality of the solution are given. The efficiency of the suggested method is demonstrated by numerical example.

2 Bilinear Models for Semi-Active Structural Control

The state-space model of a free vibrating linear structure, equipped with a set of actuators is governed by [8]:

$$\begin{aligned} {\dot{{\mathbf {x}}}}(t)&= {\mathbf {A}}{\mathbf {x}}(t)+{\mathbf {B}}{\mathbf {w}}(t) ;\quad {\mathbf {x}}(0)\in \mathbb {R}^n ;\quad t\in ]0,t_f[ ;\quad {\mathbf {x}}(t) = \begin{bmatrix}{\mathbf {z}}(t)\\{\dot{{\mathbf {z}}}}(t)\end{bmatrix}\\ {\mathbf {A}}:=&\begin{bmatrix} {\mathbf {0}}&{\mathbf {I}}\\ -{\mathbf {M}}^{-1}{\mathbf {K}}&-{\mathbf {M}}^{-1}{\mathbf {C}}_d\end{bmatrix} \in \mathbb {R}^{n\times n} \\ {\mathbf {B}}&= \begin{bmatrix}{\mathbf {b}}_1&\ldots&{\mathbf {b}}_{n_w}\end{bmatrix} :=\begin{bmatrix} {\mathbf {0}}\\ {\mathbf {M}}^{-1}{\varvec{\varPhi }}\end{bmatrix} \in \mathbb {R}^{n\times n_w} \end{aligned}$$

where \({\mathbf {M}}>0\), \({\mathbf {C}}_d\ge 0\) and \({\mathbf {K}}>0\) are \(n_z\times n_z\) mass, damping and stiffness matrices, respectively;Footnote 1 \(n_z\) is the number of dynamic degrees of freedom (DOF); \(n_w\) is the number of control forces applied to the plant; \({\mathbf {z}}:[0,t_f]\rightarrow \mathbb {R}^{n_z}\) is a smooth vector function, which represents the DOF displacements; \({\mathbf {w}}:[0,t_f]\rightarrow \mathbb {R}^{n_w}\) is a vector function of the control forces and \({\varvec{\varPhi }}\in \mathbb {R}^{n_z\times n_w}\) is an input matrix that describes how the force inputs affects the structure’s DOF. This model is well-known and is widely used in many structural control problems.

A proper control law, which is used for the computation of \({\mathbf {w}}\), must take into account different constraints that originate in the physical control implementation strategy. It is common to classify structural control into four strategies. One of them is the semi-active control [9], it uses inherently dissipative controllers for improving the stability of a dynamic system. It differs from active ones since it is incapable of adding energy to the plant, i.e., it cannot excite the plant. It also differs from passive control since the control law can adapt to the response in real time. While semi-active controllers are restricted to systematic mechanical energy dissipation [10], semi-active actuators have a more severe restriction. These devices are characterized by local energy dissipation, in other words, the work done by the actuator can only be negative.

An intuitive approach that can be used as a semi-active control law is the clipped optimal control. According to which, the controller design is usually done by some known optimal method and by ignoring the actuator constraints. Later, when the control forces are applied, the control commands are arbitrarily clipped whenever the physical constraints are violated. This approach was used for semi-active control by many researchers (e.g., [11,12,13,14,15,16]). However, although it has the benefit of being simple, clipped optimal control distorts the control signal and therefore raises a question on the theoretical justification of the clipped signal. Here, we suggest an alternative which is based on bilinear models and that is known to minimize a defined performance index.

For several types of semi-active actuators, such as magneto-rheological dampers (MRD), pneumatic actuators [17], electromagnetic friction dampers [18], and semi-active viscous dampers [8], the generated force is always opposed to some linear combination of the plant states [19]. That constraint can be modeled conveniently by using a bilinear form.

For example, a variable viscous damper [8] is a type of semi-active actuator, in which the damping gain is controlled by real-time adjustment of the mounting angle between two passive viscous dampers. The produced force is governed by

$$\begin{aligned} w(t) = -u(t) \dot{z}_d(t)=-u(t) {\mathbf {c}}{\mathbf {x}}(t) \end{aligned}$$

where the viscous damping gain \(u:[0,t_f]\rightarrow [0,\infty [\) is a nonnegative, continuous function; \(\dot{z}_d:[0,t_f]\rightarrow \mathbb {R}\) is the damper velocity which can be written as a linear combination of the states- \(\dot{z}_d(t)={\mathbf {c}}{\mathbf {x}}(t)\), where \({\mathbf {c}}\in \mathbb {R}^n\) is a row vector that produces the suitable linear combination.

Another example for bilinear control force representation are MRDs. According Bingham’s constitutive model, the MRD force is the sum of two components [20]: viscous damping force and a controllable yield force- \(w^y\). While the damping coefficient can be designed by linear viscous design methods [21], a control law should be found for \(w^y\). Since \(w^y\) is always opposed to the damper velocity, it can also be represented in the form \(w^y(t) = -u(t) \dot{z}_d(t)\). only that here \(u:[0,t_f]\rightarrow [0,\infty [\) is a nonnegative, unnecessarily continuous, function. Note that from the physical viewpoint, that representation can be interpreted as an equivalent variable viscous damper. Hence, both the variable viscous damper force and the MRD force can be represented as a bilinear feedback:

$$\begin{aligned} w({\mathbf {x}}(t),u(t)) = -u(t) {\mathbf {c}}{\mathbf {x}}(t) \end{aligned}$$
(1)

By virtue of the above, the state-space equation of a plant configured with \(n_w\) semi-active actuators, can be written as:

$$\begin{aligned} {\dot{{\mathbf {x}}}}(t)&= {\mathbf {A}}{\mathbf {x}}(t)+\sum _{i=1}^{n_w}{\mathbf {b}}_i w_i({\mathbf {x}}(t),u_i(t)) ={\mathbf {A}}{\mathbf {x}}(t)-\sum _{i=1}^{n_u}u_i(t){\mathbf {b}}_i {\mathbf {c}}_i{\mathbf {x}}(t) \end{aligned}$$
(2)

where \({\mathbf {c}}_i\) are defined with correspondence to the semi-active actuator type and \((u_i)_{i=1}^{n_u}\) is a vector of control input signals. Here, \(n_w=n_u\) based on an assumption that each actuator is controlled by single control signal.

It should be noted that unlike the optimal constrained control problem, defined in [19], in the bilinear semi-active representation, the constraint which requires \(w({\mathbf {x}}(t),u(t))\ne 0\) when \({\mathbf {c}}{\mathbf {x}}(t)=0\), is satisfied intrinsically.

3 Krotov’s Method

While the use of first-order variational calculus or Pontryagin’s minimum principle is fairly common in optimal control and its applications, for many problems these theorems provide merely necessary conditions [22], and as a result, the calculated solution is at most a candidate local optimum. Starting in the sixties, new results on sufficient conditions for global optimum of optimal control problems were published by V. F. Krotov [23]. These results were used in this paper for solving the addressed problem.

Before starting with the main derivations of this paper, the following two theorems should be introduced. They are based on the theory provided by Krotov and are written in a form which is more suitable to the addressed problem.

Let \(\mathscr {U}\) be a collection of admissible control signals and \(\mathscr {X}\) a linear space of state vector functions. The term admissible process refers to the pair \(({\mathbf {x}},{\mathbf {u}})\), where \({\mathbf {u}}\in \mathscr {U}\), \({\mathbf {x}}\in \mathscr {X}\) and they both satisfy the states equation

$$\begin{aligned} {\dot{{\mathbf {x}}}}(t) = {\mathbf {f}}({\mathbf {x}}(t),{\mathbf {u}}(t),t) ;\quad {\mathbf {x}}(0)\in \mathbb {R}^n,\,t\in ]0,t_f[ \end{aligned}$$
(3)

The notation \(\mathscr {X}(t)=\{{\mathbf {x}}(t)|{\mathbf {x}}\in \mathscr {X}\}\subset \mathbb {R}^n\) means an intersection of \(\mathscr {X}\) at a given t. For instance, \(\mathscr {X}(t_f)\) is a set of all the terminal states of the processes in \(\mathscr {X}\).

The function \(q:\mathbb {R}^n\times [0,t_f]\rightarrow \mathbb {R}\) is a piecewise smooth function, denoted as Krotov function [2, 23, 24]. Each q is related with some equivalent formulation of performance index, as follows.

Theorem 3.1

Consider a performance index:

$$\begin{aligned} J({\mathbf {x}},{\mathbf {u}})&= l_f({\mathbf {x}}(t_f)) + \int \limits _0^{t_f} l({\mathbf {x}}(t),{\mathbf {u}}(t),t) \mathrm {d}\,t \end{aligned}$$

where \(l_f:\mathbb {R}^n\rightarrow \mathbb {R}\) and \(l:\mathbb {R}^n\times \mathbb {R}^{n_u}\times [0,t_f]\rightarrow \mathbb {R}\) are continuous.

Let q be a Krotov function. Let \(q_t\) and \(q_{\mathbf {x}}\) denote its partial derivatives. For each q there is an equivalent representation of \(J({\mathbf {x}},{\mathbf {u}})\):

$$\begin{aligned} J_{eq}({\mathbf {x}},{\mathbf {u}})&= s_f({\mathbf {x}}(t_f)) + q({\mathbf {x}}_0,0) + \int \limits _0^{t_f} s({\mathbf {x}}(t),{\mathbf {u}}(t),t) \mathrm {d}\,t \equiv J({\mathbf {x}},{\mathbf {u}}) \end{aligned}$$
(4)

where

$$\begin{aligned} s({\mathbf {x}}(t),{\mathbf {u}}(t),t) :=&q_t({\mathbf {x}}(t),t) + q_{\mathbf {x}}({\mathbf {x}}(t),t) {\mathbf {f}}({\mathbf {x}}(t),{\mathbf {u}}(t),t) + l({\mathbf {x}}(t),{\mathbf {u}}(t),t) \end{aligned}$$
(5a)
$$\begin{aligned} s_f({\mathbf {x}}(t_f)) :=&l_f({\mathbf {x}}(t_f)) - q({\mathbf {x}}(t_f),t_f) \end{aligned}$$
(5b)

Proof

See section 2.3 in [24]. \(\square \)

The equivalent formulation of J leads to the sufficient condition for a global optimal admissible process, which is given in the following theorem.

Theorem 3.2

Let s and \(s_f\) (Eqs. (5a) and (5b)) be related with some Krotov function - q. Let \(({\mathbf {x}}^*,{\mathbf {u}}^*)\) be an admissible process. If:

$$\begin{aligned} \begin{aligned} s({\mathbf {x}}^*(t),{\mathbf {u}}^*(t),t)&= \min _{{\mathbf {x}}\in \mathscr {X}(t),{\mathbf {u}}\in \mathscr {U}(t)} s({\mathbf {x}},{\mathbf {u}},t) \; \forall t\in [0,t_f[ \\ s_f({\mathbf {x}}(t_f))&= \min _{{\mathbf {x}}\in \mathscr {X}(t_f)} s_f({\mathbf {x}}) \end{aligned} \end{aligned}$$
(6)

then \(({\mathbf {x}}^*,{\mathbf {u}}^*)\) is an optimal process.

Proof

Assume that Eq. (6) holds. Thus:

$$\begin{aligned} J_{eq}({\mathbf {x}},{\mathbf {u}})-J_{eq}({\mathbf {x}}^*,{\mathbf {u}}^*) =&s_f({\mathbf {x}}(t_f))-s_f({\mathbf {x}}^*(t_f)) \\&+ \int \limits _0^{t_f} s({\mathbf {x}}(t),{\mathbf {u}}(t),t)-s({\mathbf {x}}^*(t),{\mathbf {u}}^*(t),t) \mathrm {d}\,t \end{aligned}$$

By the hypothesis, for any admissible process \(({\mathbf {x}},{\mathbf {u}})\) we have

$$\begin{aligned} s_f({\mathbf {x}}(t_f))-s_f({\mathbf {x}}^*(t_f)) \ge 0 ;\quad s({\mathbf {x}}(t),{\mathbf {u}}(t),t)-s({\mathbf {x}}^*(t),{\mathbf {u}}^*(t),t) \mathrm {d}\,t \ge 0, \end{aligned}$$

which assures that \(J_{eq}({\mathbf {x}},{\mathbf {u}})-J_{eq}({\mathbf {x}}^*,{\mathbf {u}}^*) = J({\mathbf {x}},{\mathbf {u}})-J({\mathbf {x}}^*,{\mathbf {u}}^*) \ge 0\). Therefore \(({\mathbf {x}}^*,{\mathbf {u}}^*)\) is optimal. \(\square \)

Remark 3.1

  • An optimum derived by this theorem is global since the minimization problem defined in Eq. (6) is global [23].

  • Although theorem 3.2 provides a hint for finding a global optimum, the main problem remains—the existence and formulation of a suitable Krotov function. Note that a similar approach is used in Lyapunov’s method of stability.

  • Note that the equivalence \(J({\mathbf {x}},{\mathbf {u}}) = J_{eq}(q,{\mathbf {x}},{\mathbf {u}})\) holds if \({\mathbf {x}}\) and \({\mathbf {u}}\) satisfy the state equation (Eq. (3)). Otherwise, Eq. (4) might be false.

  • Since q is not unique, the equivalent representation \(J_{eq}\), s and \(s_f\), are also nonunique.

  • In many publications, such as [23], s is written with an opposite sign before l, which turns some of the minimization problems into maximization problems. Though, there is no intrinsic difference between these two formulations.

Theorems 3.1 and 3.2 provide not only a sufficient condition for global optimality but also lay the foundation for novel algorithms for the solution of optimal control problems [23], one of them is known as Krotov’s method. According to this method, the solution is not direct but a sequential one. It yields a convergent sequence of admissible processes whose limit is \(({\mathbf {x}}^*,{\mathbf {u}}^*)\) (theorem 3.2) [24]. Such a sequence of processes is called an optimizing sequence. The approach was used successfully for optimal control of bilinear systems in quantum-mechanics [2], and oscillations damping [25].

The method initializes with some admissible process \(({\mathbf {x}}_0,{\mathbf {u}}_0)\). An improved admissible process \(({\mathbf {x}}_1,{\mathbf {u}}_1)\) is computed in the following manner:

  1. 1.

    Formulate \(q_0\) such that \(s_0\) and \(s_{f0}\) will satisfy:

    $$\begin{aligned} s_0({\mathbf {x}}_0(t),{\mathbf {u}}_0(t),t)&= \max _{{\mathbf {x}}\in \mathscr {X}(t)} s_0({\mathbf {x}},{\mathbf {u}}_0(t),t) \; \forall t\in [0,t_f[ \\ s_{f0}({\mathbf {x}}_0(t_f))&= \max _{{\mathbf {x}}\in \mathscr {X}(t_f)} s_{f0}({\mathbf {x}}) \end{aligned}$$
  2. 2.

    Formulate a mapping \(\hat{{\mathbf {u}}}_0:\mathbb {R}^n\times [0,t_f]\rightarrow \mathbb {R}^{n_u}\) such that

    $$\begin{aligned} {\hat{{\mathbf {u}}}}_0({\mathbf {x}}(t),t) = \arg \min _{{\mathbf {u}}\in \mathscr {U}(t)} s_0({\mathbf {x}}(t),{\mathbf {u}},t) \; \forall {\mathbf {x}}\in \mathscr {X}, t\in [0,t_f] \end{aligned}$$
  3. 3.

    Solve \({\dot{{\mathbf {x}}}}_1(t) = {\mathbf {f}}({\mathbf {x}}_1(t),\hat{{\mathbf {u}}}_0({\mathbf {x}}_1(t),t),t)\), for the given \({\mathbf {x}}(0)\), and set \({\mathbf {u}}_1(t)={\hat{{\mathbf {u}}}}_0({\mathbf {x}}_1(t),t)\) for all \(t\in [0,t_f]\).

\(({\mathbf {x}}_2,{\mathbf {u}}_2)\) is computed by starting over from \(({\mathbf {x}}_1,{\mathbf {u}}_1)\), formulation of \(q_1\) and \({\hat{{\mathbf {u}}}}_1\), and so on.

As in Lyapunov’s method, the use of Krotov’s method is not straightforward. It requires the formulation of a suitable sequence of Krotov functions, \(\{q_k\}\), such that \(s_k\) and \(s_{fk}\) will satisfy the aforementioned min/max problem. If a sequence of such functions can be found, it allows the computation of a global optimum for the given optimal control problem. However, the search for such a Krotov function is a significant challenge that should be overcome in order to use this method. The difficulty is that there is no known unified approach for formulating Krotov functions and they usually differ from one optimal control problem to another. In this work, a suitable sequence of Krotov functions was found for the following constrained bilinear quadratic regulator problem.

4 Optimal Control Problem and Solution—Main Results

The constrained bilinear quadratic regulator (CBQR) problem is defined as follows.

Definition 4.1

(CBQR) Let \(\mathscr {U}=\{u:[0,t_f]\rightarrow [0,\infty [\}\) be a collection of admissible control signals. Let the state-space \(\mathscr {X}\) be a linear space of continuous and piecewise smooth vector functions \({\mathbf {x}}:[0,t_f]\rightarrow \mathbb {R}^n\).

It is desirable to find an optimal and admissible process \(({\mathbf {x}}^*,u^*)\) that satisfies the bilinear states equation:

$$\begin{aligned} {\dot{{\mathbf {x}}}}(t)&= [{\mathbf {A}}-u(t){\mathbf {b}}{\mathbf {c}}]{\mathbf {x}}(t) ;\quad {\mathbf {x}}(0)\in \mathbb {R}^n,\,t\in ]0,t_f[ \end{aligned}$$
(7)

and minimizes quadratic performance index:

$$\begin{aligned} J({\mathbf {x}},u)&= \frac{1}{2}\int \limits _0^{t_f} {\mathbf {x}}(t)^T{\mathbf {Q}}{\mathbf {x}}(t) +r u^2(t) \mathrm {d}\,t \end{aligned}$$

where \({\mathbf {A}}\in \mathbb {R}^{n\times n}\); \({\mathbf {c}},{\mathbf {b}}\in \mathbb {R}^n\) where \({\mathbf {b}}\) is a column vector and \({\mathbf {c}}\) is a row vector; \(0\le {\mathbf {Q}}\in \mathbb {R}^{n\times n}\); \(r>0\).

The following theorems define the optimal control law and the sequence of q which are needed for applying Krotov’s method for the CBQR problem. Two notations will be used in order to distinguish between the control signal and the control law. The first will be denoted as u and the second as \({\hat{u}}\).

Theorem 4.1

Let the Krotov function be

$$\begin{aligned} q({\mathbf {x}}(t),t) = 0.5{\mathbf {x}}(t)^T{\mathbf {P}}(t){\mathbf {x}}(t);\quad {\mathbf {P}}(t_f) = {\mathbf {0}}\end{aligned}$$

where \({\mathbf {P}}:[0,t_f]\rightarrow \mathbb {R}^{n\times n}\) is a symmetric matrix function, smooth above \(]0,t_f[\); and let \({\mathbf {x}}\) be a given process. Then, there exists a unique control law that minimizes \(s({\mathbf {x}}(t),u(t),t)\) and it is defined by:

$$\begin{aligned} {\hat{u}}({\mathbf {x}}(t),t) = \max \left\{ \frac{{\mathbf {x}}(t)^T{\mathbf {P}}(t){\mathbf {b}}{\mathbf {c}}{\mathbf {x}}(t)}{r},0 \right\} \end{aligned}$$
(8)

Proof

The partial derivatives of q are:

$$\begin{aligned} q_{\mathbf {x}}({\mathbf {x}}(t),t)&= {\mathbf {x}}(t)^T{\mathbf {P}}(t) ;\quad q_t({\mathbf {x}}(t),t) = 0.5{\mathbf {x}}(t)^T{\dot{{\mathbf {P}}}}(t){\mathbf {x}}(t) \end{aligned}$$

Substituting in Eqs. (5a) and (5b) yields:

$$\begin{aligned} s_f({\mathbf {x}}(t_f))&= 0 \nonumber \\ s({\mathbf {x}}(t),u(t),t)&= 0.5{\mathbf {x}}(t)^T{\dot{{\mathbf {P}}}}(t){\mathbf {x}}(t) + {\mathbf {x}}(t)^T{\mathbf {P}}(t)\left[ {\mathbf {A}}- u(t){\mathbf {b}}{\mathbf {c}}\right] {\mathbf {x}}(t)\nonumber \\&\quad + 0.5{\mathbf {x}}(t)^T{\mathbf {Q}}{\mathbf {x}}(t)+ 0.5u^2(t) r\nonumber \\&= 0.5{\mathbf {x}}(t)^T\left\{ {\dot{{\mathbf {P}}}}(t) + {\mathbf {P}}(t)\left[ {\mathbf {A}}- u(t){\mathbf {b}}{\mathbf {c}}\right] \right. \nonumber \\&\quad \left. + \left[ {\mathbf {A}}^T - u(t){\mathbf {c}}^T {\mathbf {b}}^T\right] {\mathbf {P}}(t) +{\mathbf {Q}}\right\} {\mathbf {x}}(t) + 0.5u^2(t) r \end{aligned}$$
(9)

Completing the square leads to:

$$\begin{aligned} s({\mathbf {x}}(t)&,u(t),t) = 0.5{\mathbf {x}}(t)^T[{\dot{{\mathbf {P}}}}(t) + {\mathbf {P}}(t){\mathbf {A}}+ {\mathbf {A}}^T{\mathbf {P}}(t) + {\mathbf {Q}}\\&\quad \quad \quad \quad \quad -({\mathbf {c}}{\mathbf {x}}(t))^2 {\mathbf {P}}(t){\mathbf {b}}{\mathbf {b}}^T{\mathbf {P}}(t)/r]{\mathbf {x}}(t) +0.5r [u(t) - {\mathbf {x}}(t)^T{\mathbf {P}}(t){\mathbf {b}}{\mathbf {c}}{\mathbf {x}}(t)/r]^2 \\&\quad \quad \quad \quad = f_2({\mathbf {x}}(t),t) {+}0.5r [u(t) {-} v({\mathbf {x}}(t),t)]^2 ; \quad v({\mathbf {x}}(t),t) {:=} \frac{{\mathbf {x}}(t)^T{\mathbf {P}}(t){\mathbf {b}}{\mathbf {c}}{\mathbf {x}}(t)}{r} \end{aligned}$$

where \(f_2\) is independent of u. It is obvious that for minimization of \(s({\mathbf {x}}(t),u(t),t)\) it is best to choose \(u(t)=v({\mathbf {x}}(t),t)\), however, this choice is admissible only if \(v({\mathbf {x}}(t),t)\ge 0\). For \(v({\mathbf {x}}(t),t) < 0 \), the admissible minimization is given by \(u(t)=0\). That result is summarized in Eq. (8). \(\square \)

Theorem 4.2

Let \(({\mathbf {x}}_k,u_k)\) be a given process and let \({\mathbf {P}}_k(t)\) be the solution of:

$$\begin{aligned} \begin{aligned} {\dot{{\mathbf {P}}}}_k(t)&= - {\mathbf {P}}_k(t)[{\mathbf {A}}- u_k(t) {\mathbf {b}}{\mathbf {c}}] - [{\mathbf {A}}^T - u_k(t){\mathbf {c}}^T {\mathbf {b}}^T]{\mathbf {P}}_k(t) - {\mathbf {Q}}\\ {\mathbf {P}}_k(t_f)&= {\mathbf {0}};\quad t\in ]0,t_f[ \end{aligned} \end{aligned}$$
(10)

Then, the Krotov function

$$\begin{aligned} q_k({\mathbf {x}}(t),t)&= 0.5{\mathbf {x}}(t)^T{\mathbf {P}}_k(t){\mathbf {x}}(t) \end{aligned}$$

satisfies

$$\begin{aligned} s_k({\mathbf {x}}_k(t),u_k(t),t) = \max _{{\mathbf {x}}\in \mathscr {X}(t)} s_k({\mathbf {x}},u_k(t),t) \end{aligned}$$
(11)

Proof

According to Eq. (9), \(s_k({\mathbf {x}}(t),u_k(t),t)\) will be

$$\begin{aligned} s_k({\mathbf {x}}(t),u_k(t),t)&=\,0.5{\mathbf {x}}(t)^T\left( {\dot{{\mathbf {P}}}}_k(t) + {\mathbf {P}}_k(t)[{\mathbf {A}}- u_k(t){\mathbf {b}}{\mathbf {c}}] \right. \\&\qquad \left. \phantom {{\dot{{\mathbf {P}}}}} + [{\mathbf {A}}^T - u_k(t){\mathbf {c}}^T {\mathbf {b}}^T]{\mathbf {P}}_k(t) +{\mathbf {Q}}\right) {\mathbf {x}}(t) + 0.5 u_k^2(t) r_i \end{aligned}$$

Substitution of \({\dot{{\mathbf {P}}}}_k(t)\) from Eq. (10) yields

$$\begin{aligned} s_k({\mathbf {x}}(t),u_k(t),t) =\;&0.5{\mathbf {x}}(t)^T [{\mathbf {0}}]{\mathbf {x}}(t) +0.5 u_k^2(t) r_i = 0.5 u_k^2(t) r_i \end{aligned}$$

Since \(s_k({\mathbf {x}}(t),u_k(t),t) = s_k({\mathbf {x}}_k(t),u_k(t),t)\), it is obvious that

$$\begin{aligned} s_k({\mathbf {x}}(t),u_k(t),t) \le s_k({\mathbf {x}}_k(t),u_k(t),t) ;\quad \forall t\in [0,t_f],\, {\mathbf {x}}\in \mathscr {X}\end{aligned}$$

\(\square \)

Fig. 1
figure 1

An a illustration and b dynamic scheme of the evaluated model

Full size image

The dependency of Krotov’s method on a Krotov function makes it somewhat abstract. The last two theorems turn it into a concrete solution method for the addressed CBQR problem. Theorem 4.2 provides a suitable Krotov function (step 1 in Krotov’s method), and theorem 4.1 define the corresponding control law (step 2 in Krotov’s method). The resulting algorithm is summarized in Fig. 1. It computes two sequences, \(\{q_k\}\) and \(\{({\mathbf {x}}_k,u_k)\}\), where the latter is an optimizing sequence. Its output is an “arbitrary close” approximation for the optimal \({\mathbf {P}}\), which defines the control law (Eq. (8)). As J has an infimum, the convergence of \(\{({\mathbf {x}}_k,u_k)\}\) to the optimal process \(({\mathbf {x}}^*,u^*)\), is guaranteed. It should be noted that the use of absolute value in line 8 of the algorithm is theoretically unnecessary. Though, due to numerical computation errors, the algorithm might lose its monotonicity when it gets closer to the optimum without it.

figure a

5 Numerical Example

To demonstrate the efficiency of the CBQR control design, a dynamic model of a typical 3 floor free vibrating reinforced concrete frame was analyzed. The control force was applied through a single variable viscous damper installed at the first floor. The model is represented as a plane frame whose dynamic scheme is presented in Fig. 1. All computations were carried out using original routines written in MATLAB framework.

The mass, damping, and stiffness matrices as well as the control force distribution vector are:

$$\begin{aligned} {\mathbf {M}}&= \begin{bmatrix} 25.2&0.246&-0.0591\\ 0.246&25.2&0.168\\ -0.0591&0.168&25.5 \end{bmatrix}\times 10^{3} ;\quad {\mathbf {C}}_d=\begin{bmatrix} 160&-68.6&6.75\\ -68.6&152&-60.3\\ 6.75&-60.3&82.7 \end{bmatrix}\times 10^{3} \\ {\mathbf {K}}&= \begin{bmatrix} 80.2&-42.1&4.17\\ -42.1&75.5&-37\\ 4.17&-37&32.6 \end{bmatrix}\times 10^{6};\quad {\varvec{\phi }}= \begin{bmatrix} 0.982 \\ 0.0092 \\ -0.000875\end{bmatrix} \end{aligned}$$

\({\mathbf {K}}\), \({\mathbf {M}}\) and \({\varvec{\phi }}\) were computed by suitable Ritz transformations. \({\mathbf {C}}_d\) is a Rayleigh proportional damping matrix and \({\mathbf {c}}=\begin{bmatrix}{\mathbf {0}}&{\varvec{\phi }}^T\end{bmatrix}\). The states and control weighting matrices are:

$$\begin{aligned} {\mathbf {Q}}= \begin{bmatrix} 6&-3&0&0&0&0\\ -3&6&-3&0&0&0\\ 0&-3&3&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0 \end{bmatrix}\times 10^{15} ;\quad r=1 \end{aligned}$$
(12)

The initial state was chosen to be- \({\mathbf {x}}(0)=\begin{bmatrix}0\,&0\,&0\,&0.4\,&0.4\,&0.4\end{bmatrix}^T\).

The following cases were considered:

  • Case A: Uncontrolled structure.

  • Case B: LQR controlled structure.

  • Case C: CBQR controlled structure.

The LQR control weights were chosen such that the mechanical energy dissipated in each actuator, for cases B and C, would be equal. Ten iterations were carried out. The performance index improvement for each iteration is illustrated in Fig. 2. As it is evident from the figure, convergence was achieved after two iterations, and the change in J is monotonic. As a matter of fact, some small nonmonotonic variations were observed after the 5th iteration. However, their absolute value was decreasing consistently and they returned to be monotonic whenever the sample time was reduced.

Fig. 2
figure 2

Performance index values for each iteration

Full size image

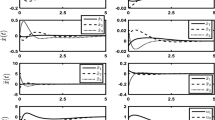
The CBQR control signal is given in Fig. 3. Its continuous form should be noted. For many semi-active control design approaches, e.g., bang–bang control [3] or clipped optimal control [13], u is not continuous and rapidly varying. From a practical viewpoint, smoothness is an advantage of the CBQR as rapid changes might be unwanted and sometimes impossible for control realization. The roof displacements for cases A to C are presented in Fig. 4. It can be seen that better performance was achieved in case B. The reason is that, unlike case C, in case B no constraints were imposed on the control signal and therefore additional improvement was gained. However, its realizability under semi-active constraints is questionable.

Fig. 3
figure 3

CBQR control signal

Full size image
Fig. 4
figure 4

Roof displacements

Full size image

Figure 5 illustrates the correspondence between the actuator control force and velocity for case B. Figure 6 does the same for case C. It is observed that for case B there are intervals in which the computed control force is required to have the same sign as the actuator velocity. This is physically impossible for many semi-active actuators. On the other hand, the control force for case C is always opposed to the actuator velocity.

Fig. 5
figure 5

Case B—Normalized control force versus actuator velocity

Full size image
Fig. 6
figure 6

Case C—Normalized control force versus actuator velocity

Full size image

6 Conclusions

In this study a CBQR problem was defined, i.e., a constrained optimal control problem of a single input, free vibrating bilinear system and a quadratic performance index. It was shown that the CBQR problem is a mathematical formulation of a common semi-active control design problem which appears in structural control. The plant model that was used is general and is suitable for many structural control problems. The problem was solved by Krotov’s method, which is also known as the “global method of successive improvements of control.” Since the use of Krotov’s method requires a sequence of Krotov functions that corresponds to the properties of the addressed optimal control problem, a new type of Krotov function that suits the CBQR problem was formulated.

The computational steps were organized as an algorithm, which requires the states equation and a differential Lyapunov equation to be solved in each iteration. A proof outline for the algorithm convergence is provided.

The method was used for semi-active control design of a stable, free vibrating plant with a single control input. It was shown that the physical constraint related to semi-active actuator force can be relaxed by using CBQR as a control design tool, without the need of any arbitrary signal clipping. Its efficiency was demonstrated in a numerical example. It was demonstrated that the CBQR control signal is continuous, which is an advantage since from a practical viewpoint, rapid changes might be unwanted (and sometimes impossible) for control realization. The improvement in the controlled plant response is evident from the simulation results.