1 Introduction

A promising approach for the suppression of unwanted dynamic phenomena in civil structures, known as structural control, attracts growing attention in the last decades [1]. Generally speaking, physical realization of structural control is done by actuators which apply forces to the vibrating structure in real time. There are many types of such actuators; one can see, for example, [2,3,4,5]. However, each type imposes different design constraints on the control law. Semi-active dampers are type of actuators, whose physical properties ensure that they will only dissipate mechanical energy from the structure [6]. Additionally, they can change their dissipative properties according to external control commands by just a small power source [1]. These properties ensure the stability of the controlled structure and allow the controller to operate in case of external power outage.

The control design for a structure with semi-active dampers was addressed in many studies. A strategy for practical semi-active controller design was described in [7]. It allows for the nonlinear properties of semi-active dampers to be considered separately from the plant controller. Due to its simplicity, clipped optimal control is very popular for plant controller design [8,9,10,11]. However, the arbitrary clipping of the control trajectory distorts it and therefore raises a theoretical question on its contribution to the controlled plant. The synthesis of truly optimal controller for a structure with semi-active dampers, which is also theoretically justified, was addressed in very few studies. Recently, new results have been published in this area [12,13,14]. The present study suggests a new method for the computation of optimal feedback for a plant controlled by multiple semi-active control devices and subjected to an external, a priori known deterministic disturbance input. It is an extension of the results reported for a free vibration single input [12] and the free vibrating multi-input [13].

2 Background

2.1 The Plant Model

Consider a model of an excited structure with lumped masses, linear damping, linear stiffness and a controller comprised of multiple actuators. The equations of motion in its degrees of freedom (DOFs) are given by the following second-order initial value problem [15]:

$$\begin{aligned} {\mathbf {M}}\ddot{\mathbf {z}}(t) + {\mathbf {C}}_d \dot{\mathbf {z}}(t) + {\mathbf {K}}{\mathbf {z}}(t) = {\varvec{{\Psi }}}{\mathbf {w}}(t)+{\mathbf {e}}(t) ;\quad {\mathbf {z}}(0), \dot{\mathbf {z}}(0), \forall t\in ]0,t_f[ \end{aligned}$$
(1)

This is a linear time-invariant (LTI) model, in which \({\mathbf {M}}>0\), \({\mathbf {C}}_d\ge 0\) and \({\mathbf {K}}>0\) are symmetric mass, damping and stiffness matrices, respectively;Footnote 1\({\mathbf {z}}:\mathbb {R}\rightarrow \mathbb {R}^{n_z}\) is a smooth vector function, which represents the DOF displacements; \({\mathbf {w}}:\mathbb {R}\rightarrow \mathbb {R}^{n_w}\) is vector function of the control forces which are generated by the actuators; \({\varvec{{\Psi }}}\in \mathbb {R}^{n_z\times n_w}\) is an input matrix that describes how the control force inputs affect the structure’s DOF; \({\mathbf {e}}:\mathbb {R}\rightarrow \mathbb {R}^{n_z}\) is a vector function that describes the external disturbance force inputs.

The state-space form of (1) is

$$\begin{aligned} \dot{\mathbf {x}}(t) = {\mathbf {A}}{\mathbf {x}}(t)+{\mathbf {B}}{\mathbf {w}}(t) + {\mathbf {g}}(t); \quad {\mathbf {x}}(0), \forall t\in ]0,t_f[ \end{aligned}$$
(2)

where

$$\begin{aligned}&{\mathbf {x}}(t) :=\begin{bmatrix}{\mathbf {z}}(t)\\\dot{\mathbf {z}}(t)\end{bmatrix}; \quad {\mathbf {A}}:=\begin{bmatrix} {\mathbf {0}}&{\mathbf {I}}\\ -{\mathbf {M}}^{-1}{\mathbf {K}}&-{\mathbf {M}}^{-1}{\mathbf {C}}_d\end{bmatrix} \in \mathbb {R}^{n\times n}\\&{\mathbf {B}}:=\begin{bmatrix} {\mathbf {0}}\\ {\mathbf {M}}^{-1}{\varvec{{\Psi }}}\end{bmatrix} \in \mathbb {R}^{n\times n_w}; \quad {\mathbf {g}}(t) :=\begin{bmatrix}{\mathbf {0}}\\ {\mathbf {e}}(t) \end{bmatrix} \end{aligned}$$

\(n=2n_z\).

The semi-active dampers set limits on \(w_i\) as follows:

  1. 1.

    \(w_i\) is always opposed to the relative velocity of the damper anchors. That assures that the damper will only consume mechanical energy from the structure.

  2. 2.

    \(w_i\) must vanish when there is no motion in the damper. That is, physical considerations does not allow control force generation when the relative velocity in the damper is zero.

  3. 3.

    For some semi-active dampers, when there is motion in the damper there is some minimal amount of damping that it provides, even in off-state, i.e., when no control command is given.

When the relative velocity of the damper anchors can be written as linear combination of the state elements, i.e., as \({\mathbf {c}}_i{\mathbf {x}}\) for some \({\mathbf {c}}_i^T\in \mathbb {R}^{n}\), then it follows that each w should satisfy the following constraints:

  1. C1:

    \(w_i(t){\mathbf {c}}_i{\mathbf {x}}(t)\le 0\),

  2. C2:

    \({\mathbf {c}}_i{\mathbf {x}}(t)= 0\rightarrow w_i(t)=0\),

  3. C3:

    \(|w_i(t)|\ge w_{i,\min }(t,{\mathbf {x}}(t)) \ge 0\)

for all \(t\in [0,t_f]\) and for some \(w_{i,\min }:\mathbb {R}\times \mathbb {R}^n\rightarrow [0,\infty [\). Note that the lower bound must satisfy \(w_{i,\min }(t,{\mathbf {x}}(t))=0\) whenever \({\mathbf {c}}_i{\mathbf {x}}(t)=0\). Otherwise C2 and C3 will contradict.

The control design process must take constraints C1–C3 into consideration, especially when optimal control design is sought. A method that can be used for control synthesis of such constrained optimal control problems is Krotov’s method.

2.2 Krotov’s Method: Successive Global Improvements of Control

Krotov’s method is aimed at numerical solution of optimal control problems. However, the method requires the formulation of a function sequence with special properties. If such sequence can be found, it allows the computation of a global optimum for the addressed optimal control problem. This subsection describes elements from Krotov’s results which are relevant to this study.

Let

$$\begin{aligned} \dot{\mathbf {x}}(t) = {\mathbf {f}}(t,{\mathbf {x}}(t),{\mathbf {u}}(t)); \quad {\mathbf {x}}(0), \forall t\in ]0,t_f[ \end{aligned}$$
(3)

be the state equation; \(\mathscr {U}\subseteq \{\mathbb {R}\rightarrow \mathbb {R}^{n_u}\}\) be the set of admissible control trajectories and \(\mathscr {X}\subseteq \{\mathbb {R}\rightarrow \mathbb {R}^{n}\}\) be the set of state trajectories which are reachable from \(\mathscr {U}\) and \({\mathbf {x}}(0)\). The term admissible process refers to a state and control trajectories \(({\mathbf {x}}\in \mathscr {X},{\mathbf {u}}\in \mathscr {U})\) which satisfy (3). The goal of an optimal control problem is to find an admissible process which minimizes the following performance index.

$$\begin{aligned} J({\mathbf {x}},{\mathbf {u}}) = \int \limits _0^{t_f} l(t,{\mathbf {x}}(t),{\mathbf {u}}(t)) \mathrm {d}\,t \end{aligned}$$
(4)

Definition 2.1

(Optimizing sequence) Let \(\{({\mathbf {x}}_k,{\mathbf {u}}_k)\}\) be a sequence of admissible processes and assume that \(\inf _{\begin{array}{c} {\mathbf {x}}\in \mathscr {X}\\ {\mathbf {u}}\in \mathscr {U} \end{array}} J({\mathbf {x}},{\mathbf {u}})\) exists. If

$$\begin{aligned} J({\mathbf {x}}_k,{\mathbf {u}}_k)\ge J({\mathbf {x}}_{k+1},{\mathbf {u}}_{k+1}) \end{aligned}$$
(5)

for all \(k=1,2,\ldots \) and

$$\begin{aligned} \lim _{k\rightarrow \infty } J({\mathbf {x}}_k,{\mathbf {u}}_k) = \inf _{\begin{array}{c} {\mathbf {x}}\in \mathscr {X}\\ {\mathbf {u}}\in \mathscr {U} \end{array}} J({\mathbf {x}},{\mathbf {u}}) \end{aligned}$$
(6)

then \(\{({\mathbf {x}}_k,{\mathbf {u}}_k)\}\) is said to be an optimizing sequence.

Krotov’s method is aimed at the computation of such sequence, and it does so by successive improvements of admissible processes as follows [16].

Theorem 2.1

Let \(({\mathbf {x}}_k,{\mathbf {u}}_k)\) be a given admissible process, \(q_k\) be some smooth function and define s and \(s_f\) as:

$$\begin{aligned} s(t,{\varvec{\xi }},{\varvec{\nu }})&:=q_t(t,{\varvec{\xi }}) + q_{\mathbf {x}}(t,{\varvec{\xi }}) {\mathbf {f}}(t,{\varvec{\xi }},{\varvec{\nu }}) + l(t,{\varvec{\xi }},{\varvec{\nu }}) \end{aligned}$$
(7)
$$\begin{aligned} s_f({\varvec{\xi }})&:=l_f({\varvec{\xi }}) - q(t_f,{\varvec{\xi }}) \end{aligned}$$
(8)

where \({\varvec{\xi }}\in \mathbb {R}^n\), \({\varvec{\nu }}\in \mathbb {R}^{n_u}\) are some vectors.

If \(({\mathbf {x}}_k,{\mathbf {u}}_k)\) is the solution to the following maximization problem:

$$\begin{aligned} s_k(t,{\mathbf {x}}_k(t),{\mathbf {u}}_k(t))&= \max _{{\varvec{\xi }}\in \mathscr {X}(t)} s_k(t,{\varvec{\xi }},{\mathbf {u}}_k(t))\nonumber \\ s_{f,k}({\mathbf {x}}_{k}(t_f))&= \max _{{\varvec{\xi }}\in \mathscr {X}(t_f)} s_{f,k}({\varvec{\xi }}) \end{aligned}$$
(9)

and if \(\hat{\mathbf {u}}_{k+1}\) is a control feedback which satisfies

$$\begin{aligned} \hat{\mathbf {u}}_{k+1}(t,{\varvec{\xi }}) = \arg \min _{{\varvec{\nu }}\in \mathscr {U}(t)} s_k(t,{\varvec{\xi }},{\varvec{\nu }}) ;\quad \forall t\in [0,t_f] \end{aligned}$$
(10)

then \({\mathbf {x}}_{k+1}\) which solves

$$\begin{aligned} \dot{\mathbf {x}}_{k+1}(t) = {\mathbf {f}}(t,{\mathbf {x}}_{k+1}(t),\hat{\mathbf {u}}_{k+1}(t,{\mathbf {x}}_{k+1}(t))) ;\quad {\mathbf {x}}_{k+1}(0) = {\mathbf {x}}(0), \forall t\in ]0,t_f[ \end{aligned}$$
(11)

and the control trajectory \({\mathbf {u}}_{k+1}(t)=\hat{\mathbf {u}}_{k+1}(t,{\mathbf {x}}_{k+1}(t))\) satisfy (5).

It follows from this theorem that if for given \(({\mathbf {x}}_k,{\mathbf {u}}_k)\) one can find \(q_k\) such that (9) holds, then it is possible to find an improved process—\(({\mathbf {x}}_{k+1},{\mathbf {u}}_{k+1})\). Such \(q_k\) is denoted as improving function. Solving this problem over and over yields an optimizing sequence and hence leads to the solution of the optimization problem.

The iterations are summarized in the following algorithm. Its initialization requires the computation of some initial admissible process—\(({\mathbf {x}}_0,{\mathbf {u}}_0)\). Afterward, the following steps are iterated for \(k=\{0,1,2,\ldots \}\) until convergence is reached:

  1. 1.

    Find \(q_k\) that solves

    $$\begin{aligned} s_k(t,{\mathbf {x}}_k(t),{\mathbf {u}}_k(t))&= \max _{{\varvec{\xi }}\in \mathscr {X}(t)} s_k(t,{\varvec{\xi }},{\mathbf {u}}_k(t))\\ s_{f,k}({\mathbf {x}}_k(t_f))&= \max _{{\varvec{\xi }}\in \mathscr {X}(t_f)} s_{f,k}({\varvec{\xi }}) \end{aligned}$$

    for a given \(({\mathbf {x}}_k,{\mathbf {u}}_k)\) and for all t in \([0,t_f]\). Here \(s_k\) and \(s_{f,k}\) are the functionals obtained by substitution of \(q_k\) into (7) and (8).

  2. 2.

    Find an optimal feedback

    $$\begin{aligned} \hat{\mathbf {u}}_{k+1}(t,{\mathbf {x}}(t)) = \arg \min _{{\varvec{\nu }}\in \mathscr {U}(t)} s_k(t,{\mathbf {x}}(t),{\varvec{\nu }}) \end{aligned}$$

    for all t in \([0,t_f]\)

  3. 3.

    Propagate into the next, improved state and control processes, by solving

    $$\begin{aligned} \dot{\mathbf {x}}_{k+1}(t) = {\mathbf {f}}{\big (}t,{\mathbf {x}}_{k+1}(t),\hat{\mathbf {u}}_{k+1}(t,{\mathbf {x}}_{k+1}(t)){\big )} \end{aligned}$$

    and setting

    $$\begin{aligned} {\mathbf {u}}_{k+1}(t) = \hat{\mathbf {u}}_{k+1}(t,{\mathbf {x}}_{k+1}(t)) \end{aligned}$$

As it can be seen from the above, the use of Krotov’s method requires formulation of a suitable sequence—\(\{q_k\}\). However, the search for these improving functions is a significant challenge. As of this writing, there is no known unified approach for the formulation of these functions and they usually differ from one optimal control problem to another.

3 Main Results

Consider a structure which is controlled by a set of semi-active dampers and subjected to an a priori known external excitation—\({\mathbf {g}}:\mathbb {R}\rightarrow \mathbb {R}^n\). The state-space equation of such structure is given in (2), and constraints C1–C3 are induced on the control forces due to the semi-active nature of the dampers. However, here, an alternative representation will be used. It will be shown that the alternative representation is equivalent to the first one.

Consider the bilinear state-space equation:

$$\begin{aligned} \dot{\mathbf {x}}(t) = \left( {\mathbf {A}}- \sum _{i=1}^{n_u}{\mathbf {b}}_i u_i(t){\mathbf {c}}_i\right) {\mathbf {x}}(t) + {\mathbf {g}}(t) ;\quad {\mathbf {x}}(0), \forall t\in ]0,t_f[ \end{aligned}$$
(12)

where \(n_u=n_w\); \({\mathbf {c}}_i^T\in \mathbb {R}^{n}\) is constructed such that \({\mathbf {c}}_i{\mathbf {x}}\) is the relative velocity of the damper’s anchors; \(u_i\) is a control trajectory that satisfies

$$\begin{aligned} u(t) \in \left[ u_{i,\min }(t,{\mathbf {x}}(t)),u_{i,\max }(t,{\mathbf {x}}(t))\right] \end{aligned}$$
(13)

\(u_{i,\min },u_{i,\max }:\mathbb {R}\times \mathbb {R}^n\rightarrow \mathbb {R}\) satisfy \(u_{i,\max }(t,{\varvec{\xi }})\ge u_{i,\min }(t,{\varvec{\xi }})\ge 0\) for all \(t\in \mathbb {R}\) and \({\varvec{\xi }}\in \mathbb {R}^n\). Additionally, \(u_{i,\min }\) satisfies \(u_{i,\min }(t,{\varvec{\xi }})|{\mathbf {c}}_i{\varvec{\xi }}| = w_{i,\min }(t,{\varvec{\xi }})\).

Proposition 3.1

If \(({\mathbf {x}},{\mathbf {u}})\) is an admissible process by means of (12) and (13), then \(({\mathbf {x}},(-u_i{\mathbf {c}}_i{\mathbf {x}})_{i=1}^{n_u})\) is an admissible process by means of (2) with constraints C1–C3.

Proof

Let \(({\mathbf {x}},{\mathbf {u}})\) be an admissible process by means of (12) and (13) and let

$$\begin{aligned} \hat{w}_i({\mathbf {x}}(t),t) :=-u_i(t){\mathbf {c}}_i{\mathbf {x}}(t) \end{aligned}$$
(14)

It follows that

$$\begin{aligned} \hat{w}_i({\mathbf {x}}(t),t){\mathbf {c}}_i{\mathbf {x}}(t) = -u_i(t)({\mathbf {c}}_i{\mathbf {x}}(t))^2\le 0 \end{aligned}$$
(15)

i.e., C1 is satisfied. The compliance of \(\hat{w}_i\) with C2 is straightforward from its definition. Finally,

$$\begin{aligned} |\hat{w}_i({\mathbf {x}}(t),t)| = u_i(t)|{\mathbf {c}}_i{\mathbf {x}}(t)| \ge u_{i,\min }(t,{\mathbf {x}}(t))|{\mathbf {c}}_i{\mathbf {x}}(t)| = w_{i,\min }(t,{\mathbf {x}}(t)) \end{aligned}$$

Hence, \(({\mathbf {x}},{\hat{\mathbf {w}}}({\mathbf {x}}))\) is admissible by means of (2) with constraints C1–C3. \(\square \)

It should be noted that in addition to the semi-active constraints, many practical implementations require that the control force will not exceed some upper bound. That can be achieved by a proper definition of \(u_{i,\max }\).

Let the set of control trajectories, which are admissible in the ith semi-active damper, be denoted by \(\mathscr {U}_i({\mathbf {x}})\). Its \({\mathbf {x}}\) dependency can be clearly seen in (13). In other words, each u in \(\mathscr {U}_i({\mathbf {x}})\) satisfies (13) where \({\mathbf {c}}_i\), \(u_{i,\max }\) and \(u_{i,\min }\) follow the above-mentioned definitions.

The addressed optimal control problem is given in the next definition.

Definition 3.1

(CBQR) The constrained bilinear quadratic regulator (CBQR) control problem is a search for an optimal and admissible process \(({\mathbf {x}}^*,{\mathbf {u}}^*)\), which minimizes the quadratic performance index:

$$\begin{aligned} J({\mathbf {x}},{\mathbf {u}}) = \frac{1}{2}\int \limits _0^{t_f} {\mathbf {x}}(t)^T{\mathbf {Q}}{\mathbf {x}}(t) + \sum _{i=1}^{n_u} u_i(t)^2 r_i \mathrm {d}\,t \end{aligned}$$
(16)

where \(0\le {\mathbf {Q}}\in \mathbb {R}^{n\times n}\) and \(r_i>0\) for \(i=1,\ldots ,n_u\). An admissible process is a pair \(({\mathbf {x}},{\mathbf {u}})\) which satisfies (12) and \(u_i\in \mathscr {U}_i({\mathbf {x}})\) for \(i=1,\ldots ,n_u\).

From physical viewpoint, the performance index weighs the states response against the time-varying damping gains. Smaller values of \((r_i)_{i=1}^{n_u}\) will produce a control law which tends to generate larger gain values. This might require larger semi-active dampers, depending on the specific damper type.

The CBQR problem will be solved by Krotov’s method. To this end, a class of improving functions that suit to the CBQR problem will be formulated in the next lemmas.

Lemma 3.1

Let

$$\begin{aligned} q(t,{\varvec{\xi }}) = \frac{1}{2}{\varvec{\xi }}^T{\mathbf {P}}(t){\varvec{\xi }}+ {\mathbf {p}}(t)^T{\varvec{\xi }};\quad {\mathbf {P}}(t_f) = {\mathbf {0}};\,{\mathbf {p}}(t_f)={\mathbf {0}}\end{aligned}$$

where \({\varvec{\xi }}\in \mathbb {R}^n\); \({\mathbf {P}}:\mathbb {R}\rightarrow \mathbb {R}^{n\times n}\) is a continuous, piecewise smooth and symmetric, matrix function; and \({\mathbf {p}}:\mathbb {R}\rightarrow \mathbb {R}^{n}\) is a continuous and piecewise smooth, vector function.

Let \(v_i(t,{\varvec{\xi }}) :=\frac{{\mathbf {b}}_i^T({\mathbf {P}}(t){\varvec{\xi }}+ {\mathbf {p}}(t)){\mathbf {c}}_i{\varvec{\xi }}}{r_i}\). The vector of control laws, \((\hat{u}_i)_{i=1}^{n_u}\), which minimizes \(s(t,{\mathbf {x}}(t),{\mathbf {u}}(t))\), is given by

$$\begin{aligned} \hat{u}_i(t,{\mathbf {x}}(t))&= \arg \min _{{\varvec{\nu }}\in \mathscr {U}_i(t,{\mathbf {x}})} s(t,{\mathbf {x}}(t),{\varvec{\nu }}) \nonumber \\&=\left\{ \begin{array}{ll} u_{i,\min }(t,{\mathbf {x}}(t)), &{} \quad v_i(t,{\mathbf {x}}(t))\le u_{i,\min }(t,{\mathbf {x}}(t))\\ u_{i,\max }(t,{\mathbf {x}}(t)),&{} \quad v_i(t,{\mathbf {x}}(t))\ge u_{i,\max }(t,{\mathbf {x}}(t))\\ v_i(t,{\mathbf {x}}(t)), &{} \quad \text {otherwise} \end{array}\right. \end{aligned}$$
(17)

Proof

The partial derivatives of q are

$$\begin{aligned} q_t(t,{\varvec{\xi }}) = \frac{1}{2}{\varvec{\xi }}^T\dot{\mathbf {P}}(t){\varvec{\xi }}+ \dot{\mathbf {p}}(t)^T{\varvec{\xi }};\quad q_{\mathbf {x}}(t,{\varvec{\xi }}) = {\varvec{\xi }}^T{\mathbf {P}}(t) + {\mathbf {p}}(t)^T \end{aligned}$$
(18)

Let \({\varvec{\nu }}\in \mathbb {R}^{n_u}\). Substituting into (7) and (8) yields

$$\begin{aligned} s_f({\mathbf {x}}(t_f))&= 0 \quad \forall {\mathbf {x}}(t_f)\in \mathscr {X}(t_f) \end{aligned}$$
(19)
$$\begin{aligned} s(t,{\mathbf {x}}(t),{\varvec{\nu }})&=q_t(t,{\mathbf {x}}(t)) + q_{\mathbf {x}}(t,{\mathbf {x}}(t)) {\mathbf {f}}(t,{\mathbf {x}}(t),{\varvec{\nu }})\nonumber \\&\quad + \frac{1}{2} \left( {\mathbf {x}}(t)^T{\mathbf {Q}}{\mathbf {x}}(t)+ \sum _{i=1}^{n_u} \nu _i^2 r_i \right) \end{aligned}$$
(20)
$$\begin{aligned}&=\frac{1}{2}{\mathbf {x}}(t)^T \left( \dot{\mathbf {P}}(t) + {\mathbf {P}}(t){\mathbf {A}}+{\mathbf {A}}^T{\mathbf {P}}(t)+ {\mathbf {Q}}\right) {\mathbf {x}}(t) \nonumber \\&\quad +{\mathbf {x}}(t)^T( \dot{\mathbf {p}}(t) + {\mathbf {A}}^T{\mathbf {p}}(t) +{\mathbf {P}}(t){\mathbf {g}}(t)) +{\mathbf {p}}(t)^T{\mathbf {g}}(t) \nonumber \\&\quad + \frac{1}{2} \sum _{i=1}^{n_u} r_i \nu _i^2 -2r_i \nu _i v_i(t,{\mathbf {x}}(t)) \end{aligned}$$
(21)

where \(v_i\) was defined in the lemma. Completing the square leads to

$$\begin{aligned} s(t,{\mathbf {x}}(t),{\varvec{\nu }})&=\frac{1}{2}{\mathbf {x}}(t)^T \left( \dot{\mathbf {P}}(t) + {\mathbf {P}}(t){\mathbf {A}}+{\mathbf {A}}^T{\mathbf {P}}(t)+ {\mathbf {Q}}\right) {\mathbf {x}}(t)\\&\quad +{\mathbf {x}}(t)^T( \dot{\mathbf {p}}(t) + {\mathbf {A}}^T{\mathbf {p}}(t) +{\mathbf {P}}(t){\mathbf {g}}(t)) +{\mathbf {p}}(t)^T{\mathbf {g}}(t) \\&\quad + \frac{1}{2}\sum _{i=1}^{n_u} r_i(\nu _i - v_i(t,{\mathbf {x}}(t)))^2-r_i v_i(t,{\mathbf {x}}(t))^2\\&=f_2(t,{\mathbf {x}}(t)) + \frac{1}{2}\sum _{i=1}^{n_u} r_i\left( \nu _i - v_i(t,{\mathbf {x}}(t)) \right) ^2 \end{aligned}$$

where \(f_2:\mathbb {R}\times \mathbb {R}^n\rightarrow \mathbb {R}\) is some functional independent of \(\nu _i\). It follows that a minimum of \(s(t,{\mathbf {x}}(t),{\varvec{\nu }})\) over \(\{{\varvec{\nu }}|{\varvec{\nu }}\in \mathscr {U}(t,{\mathbf {x}})\}\) is the minimum of the quadratic sum with relation to each \(\{\nu _i|\nu _i\in \mathscr {U}_i(t,{\mathbf {x}})\}\), independently. The minimizing and admissible \(\nu _i\in \mathscr {U}_i(t,{\mathbf {x}})\) is calculated as follows:

  1. 1.

    If \(v_i(t,{\mathbf {x}}(t))\le u_{i,\min }(t,{\mathbf {x}}(t))\), the admissible minimum is attained at \(\nu _i=u_{i,\min }(t,{\mathbf {x}}(t))\).

  2. 2.

    If \(v_i(t,{\mathbf {x}}(t))\ge u_{i,\max }(t,{\mathbf {x}}(t))\), the admissible minimum is attained at \(\nu _i=u_{i,\max }(t,{\mathbf {x}}(t))\).

  3. 3.

    Otherwise the admissible minimum is attained at \(\nu _i=v_i(t,{\mathbf {x}}(t))\).

The admissible minimizing \(\hat{u}_i\) that corresponds to the admissible minimizing \(\nu _i\) is given by (17). \(\square \)

Lemma 3.2

Let \(({\mathbf {x}}_k,{\mathbf {u}}_k)\) be a given admissible process, and let \({\mathbf {P}}_k\) and \({\mathbf {p}}_k\) be the solutions of

$$\begin{aligned} \dot{\mathbf {P}}_k(t)&= - {\mathbf {P}}_k(t)({\mathbf {A}}- {\mathbf {B}}\,{\mathbf {diag}}({\mathbf {u}}_k(t)){\mathbf {C}}) \nonumber \\&\quad - ({\mathbf {A}}- {\mathbf {B}}\,{\mathbf {diag}}({\mathbf {u}}_k(t)){\mathbf {C}})^T{\mathbf {P}}_k(t) - {\mathbf {Q}};\qquad {\mathbf {P}}_k(t_f)={\mathbf {0}} \end{aligned}$$
(22)

and

$$\begin{aligned} \dot{\mathbf {p}}_k(t) = - \left( {\mathbf {A}}-{\mathbf {B}}\,{\mathbf {diag}}({\mathbf {u}}_k(t)){\mathbf {C}}\right) ^T{\mathbf {p}}_k(t) -{\mathbf {P}}_k(t){\mathbf {g}}(t) ;\qquad {\mathbf {p}}_k(t_f)={\mathbf {0}} \end{aligned}$$
(23)

then

$$\begin{aligned} q_k(t,{\mathbf {x}}(t)) = \frac{1}{2}{\mathbf {x}}(t)^T{\mathbf {P}}_k(t){\mathbf {x}}(t) + {\mathbf {p}}_k(t)^T{\mathbf {x}}(t) \end{aligned}$$

is an improving function and the related \(s_k\) satisfies

$$\begin{aligned} s_k(t,{\mathbf {x}}_k(t),{\mathbf {u}}_k(t)) = \max _{{\varvec{\xi }}\in \mathscr {X}(t)} s_k(t,{\varvec{\xi }},{\mathbf {u}}_k(t)) \end{aligned}$$
(24)

Proof

By substituting \(v_i\) into (21) and then reordering terms, \(s_k(t,{\mathbf {x}}(t),{\mathbf {u}}_k(t))\) becomes

$$\begin{aligned} s_k(t,{\mathbf {x}}(t),{\mathbf {u}}_k(t))&=\frac{1}{2}{\mathbf {x}}(t)^T \left( \dot{\mathbf {P}}_k(t) + {\mathbf {P}}_k(t)\left( {\mathbf {A}}-{\mathbf {B}}\,{\mathbf {diag}}({\mathbf {u}}_k(t)){\mathbf {C}}\right) \right. \\&\quad \left. + \left( {\mathbf {A}}-{\mathbf {B}}\,{\mathbf {diag}}({\mathbf {u}}_k(t)){\mathbf {C}}\right) ^T{\mathbf {P}}_k(t) + {\mathbf {Q}}\right) {\mathbf {x}}(t)\\&\quad +{\mathbf {x}}(t)^T\left( \dot{\mathbf {p}}_k(t) + \left( {\mathbf {A}}-{\mathbf {B}}\,{\mathbf {diag}}({\mathbf {u}}_k(t)){\mathbf {C}}\right) ^T{\mathbf {p}}_k(t) +{\mathbf {P}}_k(t){\mathbf {g}}(t)\right) \\&\quad +{\mathbf {p}}_k(t)^T{\mathbf {g}}(t) +\frac{1}{2}\sum _{i=1}^{n_u} u_{i,k}(t)^2 r_i \end{aligned}$$

As \(\dot{\mathbf {P}}_k(t)\) and \(\dot{\mathbf {p}}_k(t)\) satisfies (22) and (23), we have

$$\begin{aligned} s_k(t,{\mathbf {x}}(t),{\mathbf {u}}_k(t))&= \frac{1}{2}{\mathbf {x}}(t)^T {\mathbf {0}}{\mathbf {x}}(t) + {\mathbf {x}}(t)^T {\mathbf {0}}+{\mathbf {p}}_k(t)^T{\mathbf {g}}(t) \end{aligned}$$
(25)
$$\begin{aligned}&= {\mathbf {p}}_k(t)^T{\mathbf {g}}(t) +\frac{1}{2}\sum _{i=1}^{n_u} u_{i,k}(t)^2 r_i \end{aligned}$$
(26)

Since \(s_k(t,{\mathbf {x}}(t),{\mathbf {u}}_k(t)) = s_k(t,{\mathbf {x}}_k(t),{\mathbf {u}}_k(t))\) it is obvious that

$$\begin{aligned} s_k(t,{\mathbf {x}}(t),{\mathbf {u}}_k(t))) \le s_k(t,{\mathbf {x}}_k(t),{\mathbf {u}}_k(t)) \end{aligned}$$

for all \({\mathbf {x}}(t)\). \(\square \)

It can be seen that, if \({\mathbf {g}}={\mathbf {0}}\), then \({\mathbf {p}}_k(t) = {\mathbf {0}}\) and the problem is reduced to the free vibrations case reported in [17].

By putting together Sect. 2.2 and these two lemmas, the sequences \(\{q_k\}\) and \(\{({\mathbf {x}}_k,{\mathbf {u}}_k)\}\) can be computed where the second one is an optimizing sequence. As J is nonnegative, it has an infimum and \(\{({\mathbf {x}}_k,{\mathbf {u}}_k)\}\) gets arbitrarily close to the optimum.

The resulting algorithm is summarized in Fig. 1. Its output is an arbitrary approximation for \({\mathbf {P}}^*\) and \({\mathbf {p}}^*\), which define the optimal control law. It should be noted that even the use of absolute value in step (8) of the iterations stage is theoretically unnecessary; it is needed due to practical considerations. Sometimes, numerical computation errors may cause the algorithm to lose its monotonicity when getting closer to the optimum.

figure a

4 Numerical Example

This section demonstrates the seismic response of a controlled structure whose control trajectories are calculated by the suggested method. The simulations were carried out using original subroutines written in MATLAB.

The model follows the one suggested by Spencer et al. [15], as a control benchmark problem for seismically excited buildings, except slight modifications. Its response was simulated to artificial white noise horizontal ground acceleration input [18] with a peak acceleration of 0.3 g.

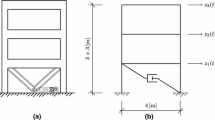
The control forces were applied through 21 control devices. The model and the control device locations are shown in Fig. 1. In this figure, \(z_i\) is the ith DOF and \(w_i\) is the control force related to the adjacent device. The devices are numbered from 1 to 21 in an increasing order starting from the device mounted in B-2.

Fig. 1
figure 1

Evaluation model and dampers configuration

Full size image

The state-space model parameters were computed according to (2). The external disturbance force input was set to \({\mathbf {e}}={\varvec{\gamma }}^T\ddot{z}_g\) where \({\varvec{\gamma }}=\begin{bmatrix}1&1&\ldots&1\end{bmatrix}^T\in \mathbb {R}^{21}\) and \(\ddot{z}_g\) is the earthquake input.

The response was analyzed for four cases:

Case 1::

There are no control devices.

Case 2::

The control devices are fluid viscous dampers.

Case 3::

The control devices are semi-active dampers which are governed by clipped LQR control law.

Case 4::

The control devices are semi-active dampers which are governed by CBQR control law.

In case 2, the control law for each damper was assumed to be linear:

$$\begin{aligned} w_i^{c2}(t) = - \tilde{u}_i {\mathbf {c}}_i{\mathbf {x}}(t) \end{aligned}$$

where \(\tilde{u}_i\) is the linear viscous gain of the ith damper and \({\mathbf {c}}_i^T\in \mathbb {R}^{42}\) is constructed such that \({\mathbf {c}}_i{\mathbf {x}}\) is the elongation velocity of the ith damper. \(\tilde{u}_i\)’s values were computed by the optimal control design method suggested in [19]. They are given in the second column of Table 1.

Table 1 Damper properties for cases 2, 3 and 4
Full size table

In case 3, a clipped LQR control law was used. The control forces were computed according to an inhomogeneous LQR control law [20] and were clipped whenever they violated the following semi-active constraints. In accordance with (14), each control force \(w_i^{c3}\) is associated with an equivalent damping gain—\(u_i^{c3}\). The lower bound of \(u_i^{c3}\) was set to \(u_{i,\min }=\min _{i\in [1,21]}\tilde{u}_i = 1.039\times 10^{5}\, \mathrm {kg/s} \), and its upper bound was set to

$$\begin{aligned} u_{i,\max }(t,{\mathbf {x}}(t)) = \left\{ \begin{array}{ll} 0, &{}\quad {\mathbf {c}}_i{\mathbf {x}}(t)=0,\\ \dfrac{\max _t |w_i^{c2}(t)|}{{\mathbf {c}}_i{\mathbf {x}}(t)}, &{}\quad \text {otherwise}\end{array}\right. \end{aligned}$$

Here \({\mathbf {c}}_i\) identical to that of case 2 and \(\max _t |w_i^{c2}(t)|\) is the peak control force value that was generated in case 2 at the ith damper. It means that the controller was designed such that the control force generated in the ith semi-active damper will not exceed the peak control force value of the corresponding viscous damper from case 2. The peak control forces values are given in the third column of Table 1.

In case 4, the semi-active control forces were also modeled as in (14) and the same constraints from case 3 were imposed. The control forces were computed by the CBQR method.

The ith rows in the observation matrix \({\mathbf {C}}\in \mathbb {R}^{21\times 42}\) is \({\mathbf {c}}_i\). The state weighting matrix \({\mathbf {Q}}\) for cases 3 and 4 was chosen such that

$$\begin{aligned} {\mathbf {x}}(t)^T{\mathbf {Q}}{\mathbf {x}}(t) = 5\times 10^{18}\sum _{i=1}^{21} d_i(t)^2 \end{aligned}$$

where \(d_i(t)\) is the inter-story drift in the ith floor. For the given model, such weighting can be achieved by letting \({\mathbf {Q}}= 5\times 10^{18}{\mathbf {N}}^T{\mathbf {N}}\) where \({\mathbf {N}}\in \mathbb {R}^{n\times n}\) is defined by \(({\mathbf {N}})_{i,i}=1\) for \(1\le i\le 21\), \(({\mathbf {N}})_{i+1,i}=-1\) for \(2\le i\le 20\) and \(({\mathbf {N}})_{i,j}=0\) in the other elements. Unlike the states weighting, which have the same meaning both in case 3 and case 4, the control weighting for case 3 has a different meaning from that of case 4. In the LQR method, which is the design basis in case 3, the control weighting relates to the control forces, whereas in case 4 the CBQR control weighting relates to the equivalent damping gains. It means that case 3 and case 4 have completely different design goals. Hence, in order to create a common comparison basis, case 3 control weighting was chosen such that the euclidean norm \(\Vert (u_i^{c3})_{i=1}^{n_u}\Vert \) will be of the same order as \(\Vert (u_i^{c4})_{i=1}^{n_u}\Vert \). As a result, \({\mathbf {R}}_{c3}={\mathbf {I}}\times 4.5\times 10^{5}\) and \((r_i^{c4})_{i=1}^{21}=(1,1,\ldots ,1)\times 10^{-4}\) were chosen for case 3 and 4, respectively.

The initial state vector was set to zero.

Figure 2 shows the progress of the performance index during nine design iterations. A dramatic monotonic improvement can be seen in the first three iterations. Some small non-monotonic variations were observed after that due to numerical computation issues. Practically, the solution converged at the third iteration. Figure 3 shows the roof displacements for each case. In case 3, the control law gained a modest improvement, comparing to case 1. On the other hand, a significant enhancement in peak roof displacement is evident in cases 2 and 4. Figure 4 shows the form of control trajectory \(u_2\) for cases 3 and 4. A logarithmic scale was used due to the extreme changes in its values. Its complex form can be clearly seen for both cases. As \(u_2\) serves as an equivalent, time-varying damping gain for the second semi-active damper it makes sense to compare it with \(\tilde{u}_2\) from case 2. In both cases, the control law generates large \(u_2\) values, compared to \(\tilde{u}_2\). Its peak values are more than 1100 times bigger than \(\tilde{u}_2\). That is because its upper bound is \(u_{2,\max }\) which is an unbounded function on its own. \(u_{2,\max }\) becomes infinite when the damper velocity reaches zero. That allows a significant increase in \(u_2\) values at such moments. Yet, even that \(u_2\) peak values are very large, compared to case 2, the peak control forces have the same magnitude of those from case 2. Figure 5 shows the form of control force \(w_2\), for cases 2, 3 and 4. Its saturation in case 4 can be seen clearly. In case 3, the control force magnitude is very low. Considering the modest improvement in the roof displacements, which are given in Fig. 3, Fig. 5 implies that the clipped optimal control fails to generate an efficient control which is equivalent to that from case 4.

Fig. 2
figure 2

Performance index values in each iteration

Full size image
Fig. 3
figure 3

Roof displacements

Full size image
Fig. 4
figure 4

Control trajectory \(u_2\)

Full size image
Fig. 5
figure 5

Control force \(w_2\)

Full size image

5 Conclusions

A new method for computing optimal semi-active feedback was formulated. It extends previously published results on CBQR control design to a case of a plant controlled by multiple semi-active control dampers and subjected to external, a priori known deterministic disturbance input. The addressed plant was modeled by a linear state-space model with constraints on the control forces reflecting the semi-active nature of the dampers. The control force was written in an equivalent bilinear form. The incorporation of this force representation led to a bilinear state-space model. The optimal control problem was defined for the above-mentioned state-space model, control force constraints and a performance index which is quadratic in the states and the equivalent damping gains. The methodology that was used for optimal control synthesis for this problem is Krotov’s method.

Krotov’s method requires the formulation of a piecewise smooth function sequence with special properties. However, the search for these functions, denoted here as improving functions, is a significant challenge due to its strong relation with the formulated problem. In this study, a new sequence of improving functions, which enables the use of Krotov’s method in this case, was formulated. Its incorporation in Krotov’s algorithm led to the suggested novel algorithm for solution of the CBQR problem for excited optimal semi-active control design. The results were demonstrated numerically by CBQR control design of controlled structure which is subjected to seismic input.

The results imply that the solution of the addressed optimal control problem has strong dependency on the excitation input. It means that an optimal control that was designed for one disturbance input will be sub-optimal for other one. Hence, the method can be used for optimal semi-active control design of problems with a priori known disturbance inputs and as a basis for control design in case of unknown disturbance inputs. For example, it can be used to evaluate how some sub-optimal solution is far from the optimal one.