Analysis of Nonlinear Behaviors in Active Magnetic Bearing-Rotor System

Abstract

The dynamic characteristics of an active magnetic bearing-rotor system were investigated by considering the nonlinearity of electromagnetic force and current saturation. This chapter used the harmonic balance method to obtain approximate solutions containing all information of static equilibrium, vibration amplitude, and phase. Based on the solutions, dynamic characteristics of the system were illustrated. It was found that there existed bifurcation behavior, and the cause lies in the static equilibrium rather than vibration amplitude. There were multiple static equilibria in the system, and non-contact support of active magnetic bearing created physical condition for the existence of nontrivial equilibria. The supercritical pitchfork bifurcation of static equilibrium with respect to excitation amplitude occurred, which made system performance deteriorate, and even threatened system stability. In the end, the analysis results were validated numerically.

1 Introduction

The active magnetic bearing (AMB)-rotor system is inherently nonlinear. During operation, most components may show nonlinear characteristics, such as the nonlinearity of electromagnetic force (the nonlinear relationship of electromagnetic force with respect to rotor displacement and currents) [1, 2], saturation nonlinearities [3], hysteresis [4], and rotor nonlinearities including the internal friction [5] and rotor crack [6]. If the operating condition is harsh, some of nonlinear factors will be prominent and exert influences on the systems.

Nonlinear factors can lead to unexpected behaviors. For example, the nonlinearity of electromagnetic force could cause jump phenomenon, period doubling, quasi-periodic motion, and chaos. The nonlinearity of electromagnetic force is common in the AMB-rotor system. Its effects have been discussed in [2, 7, 8]. Other nonlinear factors can also lead to complicated behaviors. Refs. [9, 10] considered both current saturation and nonlinearity of electromagnetic force and found supercritical pitchfork bifurcation in an AMB-rotor system. Generally, these nonlinear behaviors have negative influences. It is necessary to investigate them and thereby propose effective measures to prevent them.

The approximate analytical methods are effective and common in nonlinear analyses of AMB-rotor systems. Ref. [2] utilized the method of multiple scales to obtain analytical solutions describing dynamic characteristics in main resonance region. The jump phenomenon was found. The harmonic balance method can also be used to analyze nonlinear behaviors in main and harmonic resonance regions [11]. These analytical analyses of AMB-rotor systems usually focused on the vibration characteristics. The approximate solutions obtained only contain the vibration amplitude and phase. There were some limitations. The suspension characteristics that are also important to the system were not mentioned.

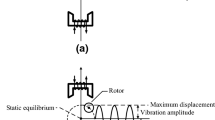
During operation of the AMB-rotor system, the rotor suspends without contact with the stator. This brings some advantages, such as no mechanical wear and low maintenance cost. But it also means that mechanical clearance between the rotor and stator is much larger than those of mechanical bearings, and the rotor can move in a relatively large physical space. The rotor may suspend steadily in different positions for different conditions. The steady suspension position of the rotor is called static equilibrium. Due to large mechanical clearance of AMBs, the static equilibrium can make contributions to the rotor displacement that is defined with respect to the reference position. In the AMB-rotor system, the rotor displacement depends on both vibration amplitude and static equilibrium. Therefore, the researches that only focused on the rotor vibration amplitude and phase [2, 7, 8, 11] cannot obtain the comprehensive dynamic characteristics. However, the effects of static equilibrium on system performance and stability were only discussed in a few researches [12], which needs to be explored further.

In this research background, this chapter analyzed both effects of rotor vibration and static equilibrium analytically. Compared with the method of multiple scales adopted in [12] that can only get static equilibrium and vibration amplitude but no vibration phase, the harmonic balance method adopted in this chapter can obtain approximate solutions including all of them. Nonlinear behaviors of the system were further investigated based on the solutions.

2 Mathematical Model

As Fig. 1 shows, an AMB-rotor system consists of the sensor, controller, power amplifier, electromagnets, and rotor. During operation, once the rotor deviates from the reference position, its displacement is measured by the sensor, and the measurement signal is transmitted to the controller. The controller gives the control command based on its control law. Thereby, the power amplifier outputs currents, which generate electromagnetic forces in the actuator to act on the rotor and return it to the reference position. By this way, AMBs can support the rotor without contact force.

Fig. 1

System diagram of AMB-rotor system

However, some nonlinear factors exist in the system. The current output from the power amplifier has extreme limits. The electromagnetic force generated in the electromagnet is inherently nonlinear. The AMB-rotor system with current saturation and nonlinear electromagnetic force has been introduced in [9, 12]. The same model is adopted in this chapter.

This chapter only focuses on the direction where unexpected behaviors happen, and the high-order actual controller is simplified into a PD controller equivalently. By considering the nonlinearity of electromagnetic force and current saturation, a single degree-of-freedom model can be obtained. To facilitate subsequent analysis, the model has been transformed into a non-dimensional one.

Under the action of PD controller, the control current can be expressed as

$$\displaystyle \begin{aligned} i=K_p y+{K_d} \dot{ y}, {} \end{aligned} $$

(1)

where y is the rotor displacement, $\dot y$ is its first derivative with respect to time, and K _p, K _d are proportional and differential gains of PD controller, respectively.

The electromagnetic force is generated by control current i and bias current i ₀ together. But limited by output capacity of power amplifier, system currents i _± in opposite electromagnets have extremum values, which are formulated in

$$\displaystyle \begin{aligned} {i_\pm}=\mathrm{med}\left( 0, {i_0} \pm i,1\right), {} \end{aligned} $$

(2)

where “med” means taking the median value among three values in the bracket and the bias current is i ₀ = 0.5.

According to [1], the electromagnetic force F can be formulated as

$$\displaystyle \begin{aligned} F={K_F}\left(\left(\frac{{i_+}}{1+ y}\right)^2-\left(\frac{ {i_-}}{1- y}\right)^2\right), {} \end{aligned} $$

(3)

where K _F is the force coefficient determined by the system structure, whose value is 0.0097.

Under the action of unbalance excitation, the motion differential equation is

$$\displaystyle \begin{aligned} \ddot {y}=-{F}+ {f}\cos\left({\Omega} {t}\right), {} \end{aligned} $$

(4)

where f is the amplitude of unbalance excitation, while Ω is the excitation frequency, namely the rotor speed.

Equations (1)–(4) make up the nonlinear model. However, the fraction expression of electromagnetic force (3) brings challenges to subsequent analysis. In order to get analytical solutions, the approximation of electromagnetic force is obtained in the possible operating region of the system. A polynomial fitting of the electromagnetic force F _f with respect to i and y is performed. The fitting model is obtained as follows:

$$\displaystyle \begin{aligned} \ddot{y}=- {F_f}+ {f}\cos\left( {\Omega} {t}\right). {} \end{aligned} $$

(5)

In this equation, the fitting electromagnetic force can be expressed as

$$\displaystyle \begin{aligned} {F_f} =\sum_{1\leq m+n \leq 11} k_{m,n}{ y}^m \dot{y}^n, {} \end{aligned} $$

(6)

where k _m,n = 0 if m + n is even number; otherwise, k _m,n are relational expressions about controller parameters K _p, K _d. The nonlinearity of electromagnetic force and current saturation are approximated by fitting electromagnetic force to this polynomial. Subsequent analysis is conducted based on polynomial model (5).

3 Analytical Analysis

The harmonic balance method is a common one of approximate analytical methods to do dynamic analyses of nonlinear systems. In this chapter, it is used to study both effects of rotor vibration and static equilibrium on dynamic characteristics of the AMB-rotor system. The solving procedure is as follows.

This chapter only focuses on the first-order approximate solution. The solution of polynomial model (5) is set as

$$\displaystyle \begin{aligned} y=C+a\cos\left( \Omega t+\phi\right), {} \end{aligned} $$

(7)

where a and ϕ are the vibration amplitude and phase, respectively, while C represents the static equilibrium. All of them need to be determined.

Substitution of (7) into (5) leads to a polynomial equation with C, a, and ϕ, which contains a constant term, a first-order harmonic term, and high-order harmonic terms. By neglecting high-order harmonic terms and collecting the similar terms according to constant term, $\cos \left ( \Omega t \right )$ and $\sin \left ( \Omega t \right )$, respectively, we can obtain three algebraic equations,

$$\displaystyle \begin{aligned} G_1\left(a,\phi,C \right) =0, {} \end{aligned} $$

(8)

$$\displaystyle \begin{aligned} G_2\left(a,\phi,C \right) =0, {} \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} G_3\left(a,\phi,C \right) =0, {} \end{aligned} $$

(10)

where $G_1\left (a,\phi ,C \right )$, $G_2\left (a,\phi ,C \right )$, and $G_3\left (a,\phi ,C \right )$ are the polynomial expressions whose coefficients depend on system parameters including K _p, K _d, and Ω.

Solving algebraic equations (8), (9), and (10), the static equilibrium C, vibration amplitude a, and vibration phase ϕ can be obtained. Then, the periodic solution y shown in (7) is determined.

The stability of periodic solutions can be analyzed by the Floquet theory.

Introduce state variables $x_1=\dot {y}$, x ₂ = y, and x ₃ =  Ωt, and transform polynomial model (5) into an autonomous one,

$$\displaystyle \begin{aligned} {\dot{\mathbf{x}}}={ \left[ \begin{array}{ccc} \dot{x_1} \\ \dot{x_2} \\ \dot{x_3} \end{array} \right ]}={\left[\begin{array}{ccc} - {F_f}\left(x_1,x_2\right)+ f \cos\left( x_3\right) \\ x_1 \\ { {\Omega}}. \end{array} \right]}=\mathbf{G}\left( \mathbf{x}\right) . {} \end{aligned} $$

(11)

Equation (11) is a periodic function whose period is $T=\frac {2\pi }{{ {\Omega }}}$. According to [13], its monodromy matrix can be calculated by

$$\displaystyle \begin{aligned} \frac{\mathrm{d} \mathbf{M}\left( t\right) }{\mathrm{d} t}&=\frac{{\partial} \mathbf{G}\left(\mathbf{x} \right) }{{\partial}{\mathbf{x}}}\big|{}_{{\mathbf{x}}_{\mathbf{0}}} \mathbf{M}\left( t \right) ,\\ \mathbf{M}\left(0 \right) &=\mathbf{I}, \end{aligned} $$

(12)

where x ₀ is the corresponding periodic solution of (11). Integrate (12) in a period T and obtain monodromy matrix $\mathbf {M}\left (T \right )$. Then, the stability of each periodic solution can be determined by eigenvalues of the monodromy matrix.

4 Results and Discussions

4.1 Supercritical Pitchfork Bifurcation

In this chapter, the system parameters are chosen as K _p = 1.904, K _d = 4.801, and Ω = 1. The approximate solutions and their stability can be obtained through above analysis procedure. It is found that the number and stability of solutions may change for different excitations. The coexistence of multiple solutions leads to nonlinear behaviors.

In the AMB-rotor system, the rotor displacement can intuitively show effects of nonlinear factors and indicate the system performance. Under the influences of nonlinearity of electromagnetic force and current saturation, the rotor displacement exhibits complicated behaviors, as shown in Fig. 2. There are three different solutions that are represented by y ₁, y ₂, and y ₃, respectively. It is the extremum values of rotor displacement that affect system performance and stability. Therefore, the maximum and minimum values are marked. During operation, the rotor can move in the range of motion limited by maximum and minimum displacements. The dotted line represents the range of motion.

Fig. 2

Rotor displacement with respect to excitation amplitude: black line—mechanical limit, red line—y ₁, blue line—y ₂, green line—y ₃, solid line—stable solution, dashed line—unstable solution, dotted line—range of motion of rotor

It can be seen that there is only one periodic solution y ₁ for small f. The maximum and minimum displacements y _1max, y _1min are symmetric around the reference position, namely the zero displacement point in Fig. 2. As f increases in a certain range, y ₁ increases nearly linearly (see y _1max). No unexpected behaviors occur. However, as f increases to a critical value, namely f = 0.156, nonlinear factors become prominent and complicated behaviors occur. The trivial solution y ₁ still exists, but its stability changes. Namely, the trivial solution y ₁ becomes unstable. In addition, two other solutions y ₂ and y ₃ appear. In this situation, three solutions coexist, but only one of the stable solutions, namely y ₂ or y ₃, can be exhibited in actual system. This is a bifurcation of rotor displacement with respect to excitation amplitude. After bifurcation, the absolute values of y _2max and y _3min are much larger than y _1max.

The bifurcation of rotor displacement will affect the system performance and stability. There are auxiliary bearings in the system, which can avoid damage to the rotor and stator during a touchdown process. But auxiliary bearings also create mechanical limits for the rotor, which are defined as the relative positions of auxiliary bearings from the reference position and marked in Fig. 2. If the rotor displacement exceeds mechanical limits, it will collide with auxiliary bearings that will lead to instability. Before bifurcation, maximum and minimum displacements y _1max, y _1min are acceptable. However, after bifurcation, difference values of y _2max or y _3min to mechanical limits become much smaller. The rotor approaches the auxiliary bearings much closer. This will weaken the capacity of resisting to a disturbance. Under the effect of disturbance, the possibility of collision between rotor and stator increases. The system performance deteriorates. As f is further increased to 0.195, y _2max and y _3min will exceed the mechanical limits and the system cannot keep stable even if there is no disturbance.

It should also be noted that unexpected behaviors appearing in the system are not only about the dynamic characteristics of vibration. After bifurcation, for y ₂ and y ₃ that can be exhibited during operation, the range of motion of the rotor is not symmetric around the reference position. It means that the static equilibrium does not coincide with the reference position all the time.

It can also be known from analytical results that all of C, a, and ϕ in solution (7) have multiple values. The static equilibrium C, vibration amplitude a, and phase ϕ are illustrated, respectively, to explain their effects on rotor displacement.

Figure 3 shows the relationship between the static equilibrium C and f. The stability of static equilibrium can be determined as follows: the static equilibria in stable periodic solutions are thought to be stable, and that in unstable periodic solution is thought to be unstable. The static equilibrium exhibits complicated characteristics. As f is small, there is only one static equilibrium, namely the stable trivial equilibrium. It coincides with the reference position. However, as f is increased to 0.156, where the bifurcation of rotor displacement occurs, both number and stability of static equilibrium change. The trivial equilibrium loses its stability. And two stable nontrivial equilibria appear. The nontrivial equilibria are symmetric around the reference position and increase gradually with the further increase of f. The relatively large mechanical clearance makes existence of nontrivial equilibria physically possible. The phenomenon is called pitchfork bifurcation. The branch solution and unstable trivial solution locate in the same side of the critical point. Therefore, the bifurcation is a supercritical one.

Fig. 3

Static equilibrium with respect to excitation amplitude: solid line—stable solution, dashed line—unstable solution

To make clear the role of rotor vibrations in nonlinear behaviors of the AMB-rotor system, the vibration amplitude a and phase ϕ are obtained and shown in Fig. 4. There is a one-to-one correspondence between a and ϕ. For small f, there is one solution for vibration amplitude and phase. However, after bifurcation point of the rotor displacement, there are two solutions for vibration amplitude and phase, while there are three solutions for rotor displacement and static equilibrium. And a ₁, ϕ ₁ are the vibration amplitudes in solution y ₁. The vibration amplitude and phase in solution y ₂ and y ₃ are the same, and they are a ₂ and ϕ ₂. It can be seen that values of a ₁ and a ₂, ϕ ₁ and ϕ ₂ have slight differences. They hardly have influences on the rotor displacement.

Fig. 4

Vibration amplitude and phase with respect to excitation amplitude: solid line—stable solution, dashed line—unstable solution

It can be concluded that the complicated behaviors reflected in the rotor displacement are caused by the bifurcation of static equilibrium. The dynamic characteristics of vibration are not complicated. Under influences of the nonlinearity of electromagnetic force and current saturation, the number and stability of static equilibrium will be different for different conditions. The relatively large mechanical clearance creates physical conditions for the existence of nontrivial equilibria. As a result, the supercritical pitchfork bifurcation of static equilibrium occurs in the AMB-rotor system.

Looking back to Fig. 2, as f is small, the bifurcation of static equilibrium has not appeared and the rotor vibrates around the trivial equilibrium. With the gradual increase of f, the static equilibrium remains zero. The maximum rotor displacement increases because the vibration amplitude increases. At this stage, the maximum rotor displacement is exactly the vibration amplitude. However, after bifurcation of static equilibrium, the trivial equilibrium loses its stability. The rotor deviates from the reference position and starts to vibrate around one of nontrivial equilibria. The maximum rotor displacement is the sum of vibration amplitude and absolute value of the static equilibrium. The supercritical pitchfork bifurcation of static equilibrium results in the fact that the maximum rotor displacement increases dramatically. Although the bifurcation of static equilibrium does not cause instability in mathematics, it can make system performance deteriorate and even lose stability during actual operation.

4.2 Numerical Validation

The analysis results obtained through harmonic balance method are validated numerically in this section.

The bifurcation of static equilibrium is also obtained through numerical method. The numerical integration can obtain the stable equilibria but no unstable equilibria. The comparison of analytical and numerical results is shown in Fig. 5. It can be seen that the analytical and numerical results are generally in agreement.

Fig. 5

Comparison of numerical and analytical results: solid line—stable analytical solution, dashed line—unstable analytical solution, circle—numerical solution, note: the same color represents same solution

To illustrate the bifurcation, the time-domain responses before and after bifurcation are shown in Fig. 6a,b, respectively. For f = 0.1, the rotor vibrates slightly around the trivial equilibrium. There is only one stable analytical solution. The numerical results and analytical solution are highly consistent. For f = 0.2, the nonlinear characteristics of the AMB-rotor system become prominent and multiple solutions coexist. There is one unstable solution and two stable solutions. In the numerical simulation, the stable solution can be exhibited, while the unstable cannot. Two time-domain responses are obtained for two different initial conditions and are consistent with two stable analytical solutions after entering the steady state. There is no numerical solution corresponding to the unstable solution.

Fig. 6

Time-domain responses: solid line—stable analytical solution, dashed line—unstable analytical solution, circle—numerical solution, note: the same color represents the same solution. (a) f = 0.1. (b) f = 0.2.

The analytical solutions obtained through harmonic balance method and their stability results are proved to be correct and accurate.

5 Conclusions

The dynamic characteristics of the AMB-rotor system were analyzed by considering the nonlinearity of electromagnetic force and current saturation. The analytical solutions containing both information of rotor vibration and suspension were obtained through the harmonic balance method, and nonlinear dynamic analysis was performed based on the solutions. It was found there might be multiple solutions for the rotor displacement. During actual operation, the rotor may vibrate around a position deviating from the reference position. The system performance deteriorates and even instability may happen. Through further analysis, it is found that the unexpected behaviors are mainly caused by a supercritical pitchfork bifurcation of the static equilibrium. In other words, the effects of nonlinear are reflected in the static equilibrium rather than vibration amplitude and phase. At last, the accuracy and stability of the solutions were validated.