Keywords

1 Introduction

The 2-D systems are found in various practical and physical processes where the information propagation occurs in two independent directions such as gas absorption and water stream heating. During the last decade, the research on 2-D systems both in practice and theory has enticed a large number of scholars due to their extensive applications [16], for example, image data processing, circuit analysis, transmission and other areas.

It has been well recognized that time-delay often occurs in practical systems, particularly in 2-D systems due to data transmission and finite speed of information processing among various parts of the system [20]. In addition, the reaction of realistic systems to external signals is seldom instantaneous and always affected by time delays. The time-delay frequently degrades the system performance and even causes the system instability [13]. Therefore, the exploration of time-delay systems stability plays a key role in applied models which has caused quite a stir in recent years.

The \(H_{\infty }\) technique introduced in [9] has been in the spotlight in recent years which attracted researchers, for example [5, 7, 8, 12, 17, 22, 23]. One of it many advantages is that it is insensitive to the exact knowledge of the statistics of the noise signals.

In this paper, 2-D systems are described by Fornasini-Marchesini (FM) second model [6, 10, 11] and based on the free-weighting matrix approach, proposed in [14, 15, 21] and by constructing a Lyapunov functional [18], a delay-dependent \(H_{\infty }\) performance analysis is reached by keeping some useful terms from the difference of Lyapunov functions.

This paper is adjusted to five sections: In Sect. 2, the problem under study is formulated. In Sect. 3, new criterion is obtained in terms of LMI, which ensure the asymptotic stability and the \(H_{\infty }\) performance of 2-D discrete systems described by the FM second model. Numerical examples are given to highlight the results in Sect. 4. Finally, some conclusions are provided in Sect. 5.

Notations: Throughout the paper, \(\mathbb {R}^{p}\) denotes the p-dimensional real Euclidean space, \(\mathbb {R}^{p\times q}\) denotes the set of all \(p\times q\) matrices. \(\mathbf{0} \) and I represent zero matrix identity matrix respectively. \(diag\{...\}\) denotes a block-diagonal matrix in symmetric block matrices or long matrix expressions. \(X^{T}\) stand for the transpose and the matrix X. \(Q >0\) \((Q < 0)\) means that Q is real symmetric and positive (negative) definite matrix. The notation ||x|| stands for the Euclidean norm of the vector x.

2 Problem Formulation

We consider the 2-D system with time-varying delays described by the following FM second model [10]:

$$\begin{aligned} x(s_{1}+1,s_{2}+1)= & {} A_{1}x(s_{1}+1,s_{2})+ A_{2}x(s_{1},s_{2}+1)+ A_{1d}x(s_{1}+1,s_{2}-d_{j})\nonumber \\+ & {} A_{2d}x(s_{1}-d_{i},s_{2}+1)+ B_{1}w(s_{1}+1,s_{2})+ B_{2}w(s_{1},s_{2}+1) \nonumber \\ z(s_{1},s_{2})= & {} Cx(s_{1},s_{2})+ Dw(s_{1},s_{2}) \end{aligned}$$
(1)

where \(x({s_{1},s_{2}})\in \mathbb {R}^{n}\) is the state vector, \(z({s_{1},s_{2}})\in \mathbb {R}^{m}\) the signal to be estimated, \(w({s_{1},s_{2}})\in \mathbb {R}^{s}\) is the disturbance input. \(A_{1}\), \(A_{2}\), \(A_{1d}\), \(A_{2d}\), \(B_{1}\), \(B_{2}\), C and D are constant matrices with appropriate dimensions, \(d_{i}\) and \(d_{j}\) are time varying delays along horizontal and vertical directions, respectively, satisfying \(\tau _{1}\le d_{j}\le \tau _{2}\) and \(\tau _{3}\le d_{i}\le \tau _{4}\) where \(\tau _{1}\), \(\tau _{2}\), \(\tau _{3}\) and \(\tau _{4}\) are known positive integers \(\tau _{v}=\tau _{2}-\tau _{1}\) and \(\tau _{h}=\tau _{4}-\tau _{3}\).

The boundary conditions for the system are specified as:

$$\begin{aligned} \left\{ \begin{array}{ll} x({s_{1},s_{2}})=\varphi _{s_{1},s_{2}},\quad \forall s_{1}\geqslant 0, s_{2}\in [-\tau _{2},0]\\ x({s_{1},s_{2}})=\psi _{s_{1},s_{2}}, \quad \forall s_{2}\geqslant 0, s_{1}\in [-\tau _{4},0]\\ \psi _{0,0}=\varphi _{0,0}. \end{array} \right. \end{aligned}$$
(2)

In what follows, the boundary conditions assumed to satisfy:

$$\begin{aligned} \mathop {\sum }\nolimits _{s_{1}=0}^{\infty }\mathop {\sum }\nolimits _{s_{2}=-\tau _{2}}^{0}\varphi _{s_{1},s_{2}}^{T} \varphi _{s_{1},s_{2}}< \infty , \quad \mathop {\sum }\nolimits _{s_{2}=0}^{\infty }\mathop {\sum }\nolimits _{s_{1}=-\tau _{4}}^{0}\psi _{s_{1},s_{2}}^{T} \psi _{s_{1},s_{2}}<\infty \end{aligned}$$

By considering the zero initial conditions, the \(H\infty \) norm of the system in (1) is given by:

$$\begin{aligned} ||G(z_{1},z_{2})||_{\infty }= & {} sup_{\tiny {w_{1},w_{2}\in [0,2\pi ]}}\sigma _{max}[G(e^{jw_{1}},e^{jw_{2}})] \end{aligned}$$

where \(\sigma _{max}\) denotes the maximum singular value of the corresponding matrix, and

$$\begin{aligned} G(z_{1},z_{2})= & {} C(z_{1}z_{2}I- A_{1}z_{1}- A_{2}z_{2}- A_{1d}z_{1}z_{2}^{-d_{j}}- A_{2d}z_{1}^{-d_{i}}z_{2})^{-1}\\&(B_{2}z_{2}+ B_{1}z_{1})+ D \end{aligned}$$

is the transfer function from the disturbance input \(w(s_{1},s_{2})\) to the output \(z(s_{1},s_{2})\) for the system in (1).

To get the main results of this paper, the following definition and lemmas are needed.

lemma1 [4] For given symmetric matrices

$$\begin{aligned}S= & {} S^{T}=\left[ \begin{array}{cc} S_{11} &{} S_{12} \\ * &{} S_{22} \end{array}\right] \end{aligned}$$

where \(S_{11}\) and \(S_{22}\) are square matrices, the following conditions are equivalent

Definition 1

[24] The 2-D system given in (1) with zero boundary conditions in (2) is said to have \(H_{\infty }\) disturbance attenuation \(\gamma \) if it is asymptotically stable and:

$$\begin{aligned} \begin{array}{c} ||z({s_{1},s_{2}})||_{2}<\gamma ||w({s_{1},s_{2}})||_{2} \end{array} \end{aligned}$$
(3)

For any nonzero \(w(s_{1},s_{2})\in {L_{2}}\{[0,\infty ),[0,\infty )\}\) where

$$\begin{aligned} z({s_{1},s_{2}})= & {} \left[ \begin{array}{cc} z^{T}({s_{1}+1,s_{2}}) &{} z^{T}({s_{1},s_{2}+1})\\ \end{array} \right] ^{T}\\ w({s_{1},s_{2}})= & {} \left[ \begin{array}{cc} w^{T}({s_{1}+1,s_{2}}) &{} w^{T}({s_{1},s_{2}+1})\\ \end{array} \right] ^{T}\\ \end{aligned}$$

3 Main Results

In this section, we consider the \(H_{\infty }\) performance analysis problem of system (1). For this case the following theorem holds.

Theorem 1

Given integers \(\tau _{1}\le d_{j}\le \tau _{2}\) and \(\tau _{3}\le d_{i}\le \tau _{4}\) and scalar \(\gamma >0\) the system (1) with time varying \(d_{i}\) and \(d_{j}\) satisfying initial conditions given in (2) is asymptotically stable for all nonzero \(w({s_{1},s_{2}})\in L_{2}\{[0,\infty ),[0,\infty )\}\) and (3) is satisfied if there exist appropriately dimensioned matrices \(P=P_{a}+P_{b}=P^{T}>0\), for \(i=1,2, j=1,2\), \(Q_{ij}=Q_{ij}^{T}>0\), \(Z_{1j}=Z_{1j}^{T}>0\), \(Z_{2j}=Z_{2j}^{T}>0\), for \(j=h,v\) \(X_{j}=\left[ \begin{array}{cc} X_{11j} &{} X_{12j}\\ * &{} X_{22j}\\ \end{array}\right] \ge 0,\)   \(Y_{j}=\left[ \begin{array}{cc} Y_{11j} &{} Y_{12j}\\ * &{} Y_{22j}\\ \end{array}\right] \ge 0,\quad \) \(N_{j}=\left[ \begin{array}{c} N_{1j}\\ N_{2j}\\ \end{array}\right] \),   \(M_{j}= \left[ \begin{array}{c} M_{1j}\\ M_{2j}\\ \end{array}\right] \),   \(S_{j}= \left[ \begin{array}{c} S_{1j}\\ S_{2j}\\ \end{array}\right] , for\quad j=1,2\) such that the following matrix inequalities hold:

$$\begin{aligned} \beta= & {} \left[ \begin{array}{ccccc} \beta _{11} &{} \beta _{12} &{} \beta _{13} &{} \beta _{14}&{}\beta _{15} \\ * &{} \beta _{22} &{} \beta _{23} &{} \beta _{24}&{}\beta _{25} \\ * &{} * &{} \beta _{33} &{} \beta _{34}&{}\beta _{35} \\ * &{} * &{} * &{} \beta _{44}&{}\beta _{45}\\ * &{} * &{} * &{} * &{}\beta _{55} \\ \end{array} \right] <0 \end{aligned}$$
(4)

and

$$\begin{aligned} \varPsi _{1j}= & {} \left[ \begin{array}{cc} Xi &{} N_{j} \\ * &{} Z_{1j}\\ \end{array}\right] \ge 0,\quad \varPsi _{2j}= \left[ \begin{array}{cc} Yi &{} M_{j} \\ * &{} Z_{2j}\\ \end{array}\right] \ge 0,\quad \varPsi _{3j}= \left[ \begin{array}{cc} Xi+Yi &{} S_{j} \\ * &{} Z_{1j}+Z_{2j}\\ \end{array}\right] \ge 0,i=h,v,j=1,2\\ \end{aligned}$$

where

$$\begin{aligned} \beta _{11}= & {} \phi ,\quad \beta _{12}=\left[ \begin{array}{cc} \sqrt{\tau _{4}}\phi _{1}^{T}Z_{11}&\sqrt{\tau _{h}}\phi _{1}^{T}Z_{21} \end{array}\right] ,\quad \beta _{13}=\left[ \begin{array}{cc} \sqrt{\tau _{2}}\phi _{2}^{T}Z_{12} &{}\sqrt{\tau _{v}}\phi _{2}^{T}Z_{22}\\ \end{array} \right] \\ \end{aligned}$$
$$\begin{aligned} \beta _{14}= & {} \left[ \begin{array}{cc} \phi _{e1}^{T} &{} \phi _{e2}^{T}\\ \end{array} \right] ,\quad \beta _{15}=\left[ \begin{array}{cc} \phi _{3}^{T}P_{a} &{} \phi _{3}^{T}P_{b}\\ \end{array} \right] ,\quad \beta _{22}=\left[ \begin{array}{cc} -Z_{11} &{} 0\\ 0 &{} -Z_{21}\end{array} \right] \\ \end{aligned}$$
$$\begin{aligned} \beta _{33}= & {} \left[ \begin{array}{cc} -Z_{12} &{} 0\\ 0 &{} -Z_{22}\\ \end{array} \right] ,\quad \beta _{44}=\left[ \begin{array}{cc} -I &{} 0\\ 0 &{} -I\\ \end{array} \right] ,\quad \beta _{55}=\left[ \begin{array}{cc} -P_{a} &{} 0\\ 0 &{} -P_{b}\\ \end{array} \right] \\ \end{aligned}$$
$$\begin{aligned} \beta _{ij}= & {} \left[ \begin{array}{cc} 0 &{} 0\\ 0 &{} 0\\ \end{array} \right] for\quad i=2,3,4\quad ,j=3,4,5 \quad and \quad i\ne j\\ \end{aligned}$$

the zero matrix is appropriately dimensioned.

$$\begin{aligned} \phi= & {} \left[ \begin{array}{ccccc} \pi _{1} &{} \pi _{2} &{} \pi _{3}&{}\pi _{4}&{}\pi _{5} \\ * &{} \pi _{6} &{} \pi _{7}&{}\pi _{8}&{}\pi _{9} \\ * &{} * &{} \pi _{10}&{}\pi _{11}&{}\pi _{12}\\ * &{} * &{} *&{}\pi _{13}&{}\pi _{14}\\ * &{} * &{} *&{}*&{}\pi _{15}\\ \end{array}\right] \\ \end{aligned}$$
$$\begin{aligned} \pi _{1}= & {} \left[ \begin{array}{cc} \phi _{v1} &{} 0\\ * &{} \phi _{h1}\\ \end{array}\right] ,\quad \pi _{2} = \left[ \begin{array}{cc} \phi _{v2} &{} 0\\ * &{} \phi _{h2}\\ \end{array}\right] ,\quad \pi _{3} = \left[ \begin{array}{cc} S_{12} &{} -M_{12}\\ 0 &{} 0\\ \end{array}\right] ,\quad \pi _{4} = \left[ \begin{array}{cc} 0 &{} 0\\ S_{11} &{} -M_{11}\\ \end{array}\right] \\ \end{aligned}$$
$$\begin{aligned} \pi _{6}= & {} \left[ \begin{array}{cc} \phi _{v3} &{} 0\\ * &{} \phi _{h3}\\ \end{array}\right] ,\quad \pi _{7} = \left[ \begin{array}{cc} S_{22} &{} M_{22}\\ 0 &{} 0\\ \end{array}\right] ,\quad \pi _{8} = \left[ \begin{array}{cc} 0 &{} 0\\ S_{21} &{} M_{21}\\ \end{array}\right] ,\quad \pi _{10}= \left[ \begin{array}{cc} -Q_{12} &{} 0\\ * &{} -Q_{22}\\ \end{array}\right] \\ \end{aligned}$$
$$\begin{aligned} \pi _{13}= & {} \left[ \begin{array}{cc} -Q_{11} &{} 0\\ * &{} -Q_{21}\\ \end{array}\right] ,\quad \pi _{15} = \left[ \begin{array}{cc} -\gamma ^{2}I &{} 0\\ 0 &{} -\gamma ^{2}I\\ \end{array}\right] ,\quad \pi _{l} = \left[ \begin{array}{cc} 0&{} 0\\ 0 &{} 0\\ \end{array}\right] ,for\quad l=5,9,11,12,14 \end{aligned}$$

with

also

$$\begin{aligned} \phi _{1}= & {} \left[ \begin{array}{cccccccccc} A_{1}&(A_{2}-I)&A_{1d}&A_{2d}&0&0&0&0&B_{1}&B_{2} \end{array} \right] \\ \phi _{2}= & {} \left[ \begin{array}{cccccccccc} (A_{1}-I)&A_{2}&A_{1d}&A_{2d}&0&0&0&0&B_{1}&B_{2} \end{array} \right] \\ \phi _{3}= & {} \left[ \begin{array}{cccccccccc} A_{1} &{} A_{2}&{} A_{1d} &{} A_{2d}&{}0&{}0&{}0&{}0 &{} B_{1} &{} B_{2}\\ \end{array} \right] \\ \phi _{e1}= & {} \left[ \begin{array}{cccccccccc} 0 &{} C&{} 0 &{} 0 &{} 0 &{} 0&{}0 &{} 0 &{} 0 &{} D\\ \end{array} \right] \\ \phi _{e2}= & {} \left[ \begin{array}{cccccccccc} C &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{}0 &{} 0 &{} D &{} 0\\ \end{array} \right] \end{aligned}$$

Proof

Let 

$$\begin{aligned} \eta _{1}(s_{1},s_{2})= & {} x(s_{1}+1,s_{2}+1)-x(s_{1},s_{2}+1) \\ \eta _{1}(s_{1},s_{2})= & {} A_{1}x(s_{1}+1,s_{2})+(A_{2}-I)x(s_{1},s_{2}+1)+A_{1d}x(s_{1}+1,s_{2}-d_{j})+A_{2d}x(s_{1}-d_{i},s_{2}+1)\nonumber \end{aligned}$$
(5)
$$\begin{aligned}+ & {} B_{1}w(s_{1}+1,s_{2})+B_{2}w(s_{1},s_{2}+1) \end{aligned}$$
(6)
$$\begin{aligned} x_{sys}(s_{1},s_{2})= & {} \left[ \begin{array}{cccc} x^{T}(s_{1}+1,s_{2})&{}x^{T}(s_{1},s_{2}+1)&{}x^{T}(s_{1}+1,s_{2}-d_{j})&{}x^{T}(s_{1}-d_{i},s_{2}+1)\\ \end{array}\right. \\&\left. ..\begin{array}{cccc} x^{T}(s_{1}+1,s_{2}-\tau _{1})&{}x^{T}(s_{1}+1,s_{2}-\tau _{2})&{}x^{T}(s_{1}-\tau _{3},s_{2}+1)&{}x^{T}(s_{1}-\tau _{4},s_{2}+1)\\ \end{array}\right. ..\\&\left. ..\begin{array}{cc} w^{T}(s_{1}+1,s_{2})&{} w^{T}(s_{1},s_{2}+1)\\ \end{array}\right] ^{T} \end{aligned}$$

\(\Rightarrow \)      \(\eta _{1}(s_{1},s_{2})=\phi _{1}x_{sys}(s_{1},s_{2})\)

The same for the vertical direction:

\(\Rightarrow \)      \(\eta _{2}(s_{1},s_{2})=\phi _{2}x_{sys}(s_{1},s_{2})\)

Choose a Lyapunov functional candidate to be

where \(P=P_{a}+P_{b}=P^{T}>0\), \(Q_{ij}=Q_{ij}^{T}>0\), i = 1, 2, j=1,2, \(Z_{1j}=Z_{1j}^{T}>0\) j = 1, 2, \(Z_{2j}=Z_{2j}^{T}>0\) j = 1, 2 are to be calculated. Defining \(\varDelta V(s_{1}+1,s_{2})=V(s_{1}+1,s_{2})-V(s_{1},s_{2})\) and \(\varDelta V(s_{1},s_{2}+1)=V(s_{1},s_{2}+1)-V(s_{1},s_{2})\) yields

figure a
figure b

From (5), we have

figure c

the same for vertical direction.

then the following equations are true for any matrices \(N_{1}\), \(N_{2}\), \(M_{1}\), \(M_{2}\), \(S_{1}\) and \(S_{2}\) with appropriate dimensions for \(\varDelta V(s_{1},s_{2}+1):\)

$$\begin{aligned} 0= & {} 2\times [x^{T}(s_{1},s_{2}+1)N_{11}+x^{T}(s_{1}-d_{i},s_{2}+1)N_{21} \nonumber \\&\times [x(s_{1},s_{2}+1)-x(s_{1}-d_{i},s_{2}+1)-\sum _{l=s_{1}-d_{i}}^{s_{1}-1}\eta _{1}(l,s_{2})] \end{aligned}$$
(7)
$$\begin{aligned} 0= & {} 2\times [x^{T}(s_{1},s_{2}+1)M_{11}+x^{T}(s_{1}-d_{i},s_{2}+1)M_{21}\nonumber \\&\times [x(s_{1}-d_{i},s_{2}+1)-x(s_{1}-\tau _{4},s_{2}+1)-\sum _{l=s_{1}-\tau _{4}}^{s_{1}-d_{i}-1}\eta _{1}(l,s_{2})] \end{aligned}$$
(8)
$$\begin{aligned} 0= & {} 2\times [x^{T}(s_{1},s_{2}+1)S_{11}+x^{T}(s_{1}-d_{i},s_{2}+1)S_{21}\nonumber \\&\times [x(s_{1}-\tau _{3},s_{2}+1)-x(s_{1}-d_{i},s_{2}+1)-\sum _{l=s_{1}-d_{i}}^{s_{1}-\tau _{3}-1}\eta _{1}(l,s_{2})] \end{aligned}$$
(9)

The same thing for \(\varDelta V(s_{1}+1,s_{2})\).

In the other hand, for any appropriately dimensioned matrices \(X_{i}=X_{i}^{T}\ge 0,\) \(Y_{i}=Y_{i}^{T}\ge 0,\) for i = h, v, the following equations are true:

$$\begin{aligned} 0= & {} \tau _{4}\xi _{1}^{T}(s_{1},s_{2})X_{h}\xi _{1}(s_{1},s_{2})-\sum _{_{l=s_{1}-d_{i}}}^{_{s_{1}-1}}\xi _{1}^{T}(s_{1},s_{2})X_{h}\xi _{1}(s_{1},s_{2})\nonumber \\- & {} \sum _{_{l=s_{1}-\tau _{4}}}^{_{s_{1}-d_{i}-1}}\xi _{1}^{T}(s_{1},s_{2})X_{h}\xi _{1}(s_{1},s_{2}) \end{aligned}$$
(10)
$$\begin{aligned} 0= & {} \tau _{h}\xi _{1}^{T}(s_{1},s_{2})Y_{h}\xi _{1}(s_{1},s_{2})-\sum _{_{l=s_{1}-d_{i}}}^{_{s_{1}-\tau _{3}-1}}\xi _{1}^{T}(s_{1},s_{2})Y_{h}\xi _{1}(s_{1},s_{2})\nonumber \\- & {} \sum _{_{l=s_{1}-\tau _{4}}}^{_{s_{1}-d_{i}-1}}\xi _{1}^{T}(s_{1},s_{2})Y_{h}\xi _{1}(s_{1},s_{2}) \end{aligned}$$
(11)
$$\begin{aligned} 0= & {} \tau _{2}\xi _{2}^{T}(s_{1},s_{2})X_{v}\xi _{2}(s_{1},s_{2})-\sum _{_{l=s_{2}-d_{j}}}^{_{s_{2}-1}}\xi _{2}^{T}(s_{1},s_{2})X_{v}\xi _{2}(s_{1},s_{2})\nonumber \\- & {} \sum _{_{l=s_{2}-\tau _{2}}}^{_{s_{2}-d_{j}-1}}\xi _{2}^{T}(s_{1},s_{2})X_{v}\xi _{2}(s_{1},s_{2}) \end{aligned}$$
(12)
$$\begin{aligned} 0= & {} \tau _{v}\xi _{2}^{T}(s_{1},s_{2})Y_{v}\xi _{2}(s_{1},s_{2})-\sum _{_{l=s_{2}-d_{j}}}^{_{s_{2}-\tau _{1}-1}}\xi _{2}^{T}(s_{1},s_{2})Y_{v}\xi _{2}(s_{1},s_{2})\nonumber \\- & {} \sum _{_{l=s_{2}-\tau _{2}}}^{_{s_{2}-d_{j}-1}}\xi _{2}^{T}(s_{1},s_{2})Y_{v}\xi _{2}(s_{1},s_{2}) \end{aligned}$$
(13)
$$\begin{aligned} \xi _{1}(s_{1},s_{2})= & {} \left[ \begin{array}{cc} x^{T}(s_{1},s_{2}+1)&x^{T}(s_{1}-d_{i},s_{2}+1) \end{array}\right] ^{T}\\ \xi _{2}(s_{1},s_{2})= & {} \left[ \begin{array}{cc} x^{T}(s_{1}+1,s_{2})&x^{T}(s_{1}+1,s_{2}-d_{j}) \end{array}\right] ^{T}\\ \end{aligned}$$

Then, if the terms of the right side of the Eqs. (7)–(13) are added to \(\varDelta V(s_{1},s_{2})=\varDelta V(s_{1}+1,s_{2})+V(s_{1},s_{2}+1)\), we have:

figure d

thus  if  \(\varPsi _{1j}, \varPsi _{2j}\ge 0, \varPsi _{3j}\ge 0 \; for \; j=1,2\)  and

$$\begin{aligned}&(\phi +\phi _{1}^{T}(\tau _{4}Z_{11}+\tau _{h}Z_{21})\phi _{1} +\phi _{2}^{T}(\tau _{2}Z_{12}+\tau _{v}Z_{22})\phi _{2}+\phi _{e1}^{T}\phi _{e1} +\phi _{e2}^{T}\phi _{e2}+\phi _{3}^{T}(P_{a}+P_{b})\phi _{3})<0 \end{aligned}$$

which is equivalent to (4) by schur compliments, then

$$\begin{aligned} \varDelta V(s_{1},s_{2})+z^{T}(s_{1},s_{2})z(s_{1},s_{2})-\gamma ^{2}w^{T}(s_{1},s_{2})w(s_{1},s_{2})<0 \end{aligned}$$

This ensures that (3) holds under zero-initial conditions for all nonzero \(w({s_{1},s_{2}})\in L_{2}\{[0,\infty ),[0,\infty )\}\) and a specified \(\gamma >0\) following the similar line in [25]. On the other hand, (4) entails that the following matrix inequality (14) holds, which guarantees \(\varDelta V(s_{1},s_{2})<0\), such that the system (1) with \(w({s_{1},s_{2}})=0\) is asymptotically stable.

$$\begin{aligned} \beta= & {} \left[ \begin{array}{cccc} \beta _{11} &{} \beta _{12} &{} \beta _{13} &{}\beta _{15} \\ * &{} \beta _{22} &{} \beta _{23} &{}\beta _{25} \\ * &{} * &{} \beta _{33} &{}\beta _{35} \\ * &{} * &{} * &{}\beta _{55} \\ \end{array} \right] <0 \end{aligned}$$
(14)

where

$$\begin{aligned} \phi= & {} \left[ \begin{array}{cccc} \pi _{1} &{} \pi _{2} &{} \pi _{3}&{}\pi _{4} \\ * &{} \pi _{6} &{} \pi _{7}&{}\pi _{8} \\ * &{} * &{} \pi _{10}&{}\pi _{11}\\ * &{} * &{} *&{}\pi _{13}\\ \end{array}\right] \\ \end{aligned}$$

This completes the proof.   \(\square \)

Remarque:

The terms \(\sum _{l=s_{1}-\bar{h_{1}}}^{s_{1}-d_{i}-1}\eta _{1}^{T}(l,s_{2})Z_{s_{1}}\eta _{1}(l,s_{2})\) and \(\sum _{l=s_{2}-\bar{h_{2}}}^{s_{2}-d_{j}-1}\eta _{2}^{T}(s_{1},l)Z_{s_{2}}\eta _{2}(s_{1},l)\) are kept in Theorem 1 to overcome the conservativeness. On the other hand, \(\tau _{2}\) and \(\tau _{4}\) are split into two parts like \(d_{j}\) and \(\tau _{2}-d_{j}\), \(d_{i}\) and \(\tau _{4}-d_{i}\), for vertical and horizontal direction, respectively, in order to prove Theorem 1 thus showing the benefits of the suggested method.

Fig. 1.
figure 1

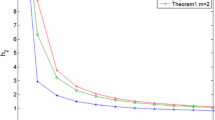
Transfer function (Example 1).

Full size image

4 Numerical Example

In this section, we will give a numerical example to illustrate the applicability of the proposed result.

Example 1

[19] Denote the design of 2-D delay-dependent \( H_ {\infty } \) performance and filter for a stationary random field in image processing where the disturbances are a random process (noise), using LMI approach proposed in (4), the 2-D system can be converted to the 2-D FM model system (1) with the ensuing parameters:

$$\begin{aligned} A_{1}=\left[ \begin{array}{cc} 0.3 &{} 0 \\ 0 &{} 0 \\ \end{array}\right] ,\quad A_{2}=\left[ \begin{array}{cc} 0 &{} 0 \\ 1 &{} 0.2\\ \end{array}\right] ,\quad A_{1d}=\left[ \begin{array}{cc} 0 &{} -0.03\\ -0.08 &{} 0\\ \end{array} \right] ,\quad A_{2d}=\left[ \begin{array}{cc} -0.03 &{} 0\\ 0 &{} 0\\ \end{array} \right] \end{aligned}$$
$$\begin{aligned} B_{1}= & {} \left[ \begin{array}{cc} 1 &{} 0\\ 0 &{} 0\\ \end{array}\right] ,\quad B_{2}=\left[ \begin{array}{cc} 0 &{} 0 \\ 0 &{} 0 \\ \end{array}\right] ,\quad C=\left[ \begin{array}{cc} 3 &{} 1\\ \end{array}\right] , \quad D=\left[ \begin{array}{cc} 0&1 \end{array}\right] \end{aligned}$$

Given \(\tau _{3}=3\), \(\tau _{4}=3\), \(\tau _{1}=2\), \(\tau _{2}=2\) by solving the LMIs, the minimum \(H_{\infty }\) norm bound for this example is \(\gamma _{opt}= 6.9671\).

Fig. 1 shows the maximum singular values plot of the transfer function matrix of the system (1). In the figure, the grids denote the obtained \( H_ {\infty } \) disturbance attenuations and its maximum value is 6.3725, which is below 6.9671.

5 Conclusion

This paper has explored the problems of stability and delay-dependent \(H_{\infty }\) performance analysis for 2-D discrete systems with time varying delay described by FM second model without ignoring any terms in the derivative of lyapunov functional by considering the relationship between the delay and it upper bound. The new criteria may be extended to systems with uncertainties.