Abstract
A simple, yet versatile yield surface in the stress space is combined with a hypoplastic equation to simulate the influence of recent deformation history on the mechanical behaviour of sand. This yield surface is used to describe the intensity of anelastic flow. In the model, the state is fully described by the current stress, the void ratio and a novel back stress-like tensor. This new state variable determines the shape and size of the yield surface and accounts for recent deformation/stress history. The direction of the anelastic flow upon shearing is obtained from a generalization of the Taylor’s dilatancy rule. As a distinctive feature of the model, this dilatancy is able to reproduce the strong contractancy upon reversals observed in experiments without the need of additional state variables. The model corrects some known shortcomings of previous hypoplastic models like overshooting and the excessive accumulation of stress/strain upon strain/stress cycles of small amplitude (ratcheting). Laboratory tests are simulated to show the capabilities of the model to reproduce the soil behaviour under monotonic and cyclic loading conditions after different deformation histories.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Besides pycnotropic (density dependency) and barotropic (pressure dependency), the mechanical behaviour of soils is also historiotropic, i.e. it is strongly influenced by the loading history (stress/strain path dependency). Despite having the same density and the same pressure, samples subjected to different loading histories exhibit different mechanical responses. This well known phenomenon can be observed in the experiments of Doanh et al. [1] on loose Hostun sand. The Fig. 1 shows different stress paths obtained during undrained triaxial compression and extension tests. At the beginning of the undrained tests, the samples have the same isotropic stress \(p=100\) kPa and nearly the same void ratio \(e \approx 0.94\), but different recent histories. These recent histories were generated by first subjecting the sample to drained triaxial compression up to a certain stress ratio (marked as preloading with the numbers 1 to 10 in Fig. 1) and then reducing the stress ratio until the isotropic stress of \(p=100\) (marked with the number 1) was reached. It can be observed that loose sand may behave like dense sand (dilative behaviour) and can reach large deviatoric stresses if the undrained shearing coincides with the direction of the previous deviatoric strain/stress history. The higher the stress ratio reached during drained triaxial compression the higher the stress ratio upon subsequent undrained triaxial compression. On the contrary, a strong reduction of the maximum deviatoric stress reached during undrained triaxial extension is observed when the sample was previously subjected to drained triaxial compression.

Experiment data adapted from [1].
Undrained triaxial compression and extension tests on Hostun RF loose sand preceded by different drained triaxial preloading.
The importance of recent history is not restricted to the monotonic behaviour of loose samples. Triaxial tests reported by Ishihara und Okada [2] show the effect of preshearing (application of a shear stress before the actual test) on the cyclic behaviour of medium dense Fuji River sand. In these tests, the samples were first subjected to undrained cyclic stresses until the pore water pressure increased up to a certain value. Then, the drainage was opened, the pore water dissipated, and the initial effective pressure was reached again (reconsolidation). Finally, subsequent undrained cyclic stresses were applied to observe influence of preshearing on the development of effective stresses and strains. Ishihara und Okada found that after small preshearing, the reduction of effective pressure and the accumulation of strains in the subsequent undrained stress cycles were less than those obtained during the preshearing phase. However, “samples subjected to large preshear on one side of triaxial loading, compression or extension, became stiffer on that side, but softer on the opposite side”, [2]. Ishihara und Okada defined small and large preshearing in terms of stress (not of strain) and used the Phase Transformation Line (PTL) [3] as the boundary between small and large. Preshearing that reaches stress ratios below and above the PTL were called small and large, respectively. These experiments show also that the effects of stress histories reaching large stress ratios can be observed even after the unloading from the large shear stress to the isotropic axis (with a shear strain of approx. 0.5%) and after the reconsolidation (with a volumetric strain of approx. 0.7%).
A similar behaviour has been observed in the experiments of Wichtmann and Triantafyllidis [4] on dense Karlsruhe fine sand samples. After a preloading with stresses beyond the PTL, the accumulation of pore water pressure in the subsequent undrained cyclic test with small stress amplitudes is so strong, that the effective pressure in the sample almost vanished after few cycles. This surprising effect, by which a dense sand behaves almost like a loose sand upon undrained cyclic loading, may be attributed to the persistent influence of the stress history.
In order to describe the effects of recent stress/strain history on the mechanical behaviour of sand, we propose a constitutive model that combines the well known hypoplastic equation, [5] and [6], with a simple yield surface in stress space. The yield surface is used to compute the intensity of anelastic flow. The anelastic flow is more intense for stresses outside than for those inside the yield surface. The shape of the yield surface is determined by a novel state variable  , which can be regarded as back-stress and provides information about the recent stress loading history. The evolution of
, which can be regarded as back-stress and provides information about the recent stress loading history. The evolution of  is provided separately for its isotropic and deviatoric portions. The direction of the anelastic flow upon shearing is obtained from a generalization of the Taylor’s [7] dilatancy rule. As a distinctive feature of the model, this dilatancy is able to reproduce the strong contractancy upon reversals observed in experiments without the need of additional state variables. Furthermore, the hypoelastic stiffness is replaced by a hyperelastic one (similar as in the neohypoplastic model [8]). The model corrects some known shortcomings of previous hypoplastic models like overshooting and the excessive accumulation of stress/strain upon strain/stress cycles of small amplitude (ratcheting).
is provided separately for its isotropic and deviatoric portions. The direction of the anelastic flow upon shearing is obtained from a generalization of the Taylor’s [7] dilatancy rule. As a distinctive feature of the model, this dilatancy is able to reproduce the strong contractancy upon reversals observed in experiments without the need of additional state variables. Furthermore, the hypoelastic stiffness is replaced by a hyperelastic one (similar as in the neohypoplastic model [8]). The model corrects some known shortcomings of previous hypoplastic models like overshooting and the excessive accumulation of stress/strain upon strain/stress cycles of small amplitude (ratcheting).
After defining the notation used throughout the paper in Sect. 2, the main hypoplastic equation and the hyperelastic stiffness are described in Sects. 3 and 4, respectively. The constitutive model is designed to reproduce two observed attractors: the Limiting Compression Curve (LCC) [9] upon monotonic compressive volumetric straining and the Critical State (CS) [10] and [11] after long monotonic shearing. In the CS, plastic deviatoric flow ( with
with  ) is possible without changes in stress
) is possible without changes in stress  when a critical void ratio \(e=e_c\) is reached. To describe these attractors, two different degrees of nonlinearities and flow rules are adopted: \(Y_I\) and
when a critical void ratio \(e=e_c\) is reached. To describe these attractors, two different degrees of nonlinearities and flow rules are adopted: \(Y_I\) and  for radial compression and \(Y_D\) and
for radial compression and \(Y_D\) and  for shearing. The Sect. 5 presents a one dimensional model to simulate isotropic compression. In this simple model, loading/unloading and reloading phases are distinguished by the overconsolidation ratio, which is based on the concept of overstress. The overconsolidation ratio is a measure of how close the current stress and the yield stress are. In this simple model, the yield stress provides a mechanism to “memorize” previous stress paths. These concepts, i.e. the distinction between loading and unloading and the yield stress as a memory mechanism, are generalized in Sect. 6 to the stresses and strains in 3 dimensions (and for shear loading). For this purpose a yield surface in the stress space defined by a new state variable
for shearing. The Sect. 5 presents a one dimensional model to simulate isotropic compression. In this simple model, loading/unloading and reloading phases are distinguished by the overconsolidation ratio, which is based on the concept of overstress. The overconsolidation ratio is a measure of how close the current stress and the yield stress are. In this simple model, the yield stress provides a mechanism to “memorize” previous stress paths. These concepts, i.e. the distinction between loading and unloading and the yield stress as a memory mechanism, are generalized in Sect. 6 to the stresses and strains in 3 dimensions (and for shear loading). For this purpose a yield surface in the stress space defined by a new state variable  is introduced. A novel flow rule that depends on void ratio, stress and the direction of the strain rate is constructed from the well known Taylor’s [7] dilatancy. In Sect. 7 the results of different element tests reported in the literature are compared with the simulations computed with the model to evaluate the performance of the proposed constitutive equation. In addition, a special set of tests conducted to evidence the influence of monotonic loading on subsequent cyclic behaviour is presented and contrasted with simulation results.
is introduced. A novel flow rule that depends on void ratio, stress and the direction of the strain rate is constructed from the well known Taylor’s [7] dilatancy. In Sect. 7 the results of different element tests reported in the literature are compared with the simulations computed with the model to evaluate the performance of the proposed constitutive equation. In addition, a special set of tests conducted to evidence the influence of monotonic loading on subsequent cyclic behaviour is presented and contrasted with simulation results.
2 Notation
A fixed orthogonal Cartesian coordinate system with unit vectors  is used throughout the text. A repeated (dummy) index in a product indicates summation over this index taking values of 1, 2 and 3. A tensorial equation with one or two free indices can be seen as a system of three or nine scalar equations, respectively. We use the Notation Kronecker’s symbol \(\delta _{ij} \) and the permutation symbol \(e_{ijk}\). Vectors and second-order tensors are distinguished by bold typeface, for example
is used throughout the text. A repeated (dummy) index in a product indicates summation over this index taking values of 1, 2 and 3. A tensorial equation with one or two free indices can be seen as a system of three or nine scalar equations, respectively. We use the Notation Kronecker’s symbol \(\delta _{ij} \) and the permutation symbol \(e_{ijk}\). Vectors and second-order tensors are distinguished by bold typeface, for example  . Fourth order tensors are written in sans serif font (e.g.
. Fourth order tensors are written in sans serif font (e.g.  ). The symbol
). The symbol  denotes multiplication with one dummy index (single contraction). For instance, the scalar product of two vectors can be written as
denotes multiplication with one dummy index (single contraction). For instance, the scalar product of two vectors can be written as  . Multiplication with two dummy indices (double contraction) is denoted with a colon, for example
. Multiplication with two dummy indices (double contraction) is denoted with a colon, for example  , wherein
, wherein  reads trace of a tensor. The expression \(()_{ij}\) is an operator extracting the component (i, j) from the tensorial expression in brackets, for example
reads trace of a tensor. The expression \(()_{ij}\) is an operator extracting the component (i, j) from the tensorial expression in brackets, for example  . The tensor
. The tensor  is singular (yields zero for every skew symmetric tensor), but for symmetric argument
is singular (yields zero for every skew symmetric tensor), but for symmetric argument  ,
,  represents the identity operator, such that
represents the identity operator, such that  . A tensor raised to a power, like
. A tensor raised to a power, like  , is understood as a sequence of \(n-1\) multiplications
, is understood as a sequence of \(n-1\) multiplications  . The brackets \(\Vert ~~\Vert \) denote the Euclidean norm, i.e.
. The brackets \(\Vert ~~\Vert \) denote the Euclidean norm, i.e.  or
or  . The definition of Mc Cauley brackets reads \({<}x{>} = (x + | x|)/2 \). The deviatoric part of a tensor is denoted by an asterisk, e.g.
. The definition of Mc Cauley brackets reads \({<}x{>} = (x + | x|)/2 \). The deviatoric part of a tensor is denoted by an asterisk, e.g.  , wherein
, wherein  holds. The components of diagonal matrices (with zero off-diagonal components) are written as \(~\mathrm{diag}[~,~,~]\), for example \(~\text{1 }= ~\mathrm{diag}[1,1,1]\). The Roscoe’s invariants for the axisymmetric case \(\sigma _2 = \sigma _3\) and \(\epsilon _2 = \epsilon _3\) are then defined as
holds. The components of diagonal matrices (with zero off-diagonal components) are written as \(~\mathrm{diag}[~,~,~]\), for example \(~\text{1 }= ~\mathrm{diag}[1,1,1]\). The Roscoe’s invariants for the axisymmetric case \(\sigma _2 = \sigma _3\) and \(\epsilon _2 = \epsilon _3\) are then defined as  and \( \epsilon _q = -\frac{2}{3}(\epsilon _1 - \epsilon _3) \). The general definitions
and \( \epsilon _q = -\frac{2}{3}(\epsilon _1 - \epsilon _3) \). The general definitions  and
and  are equivalent to the ones from the axisymmetric case but may differ in sign. The isomorphic invariants for the axisymmetric case are defined as
are equivalent to the ones from the axisymmetric case but may differ in sign. The isomorphic invariants for the axisymmetric case are defined as  ,
,  ,
,  , and
, and  , with
, with  and
and  . Dyadic multiplication is written without \( \otimes \), e.g.
. Dyadic multiplication is written without \( \otimes \), e.g.  or
or  . Proportionality of tensors is denoted by tilde, e.g.
. Proportionality of tensors is denoted by tilde, e.g.  . The operator \((\sqcup )^{\rightarrow }=\sqcup /\left\| \sqcup \right\| \) normalizes the expression \(\sqcup \), for example
. The operator \((\sqcup )^{\rightarrow }=\sqcup /\left\| \sqcup \right\| \) normalizes the expression \(\sqcup \), for example  . The sign convention of general mechanics with tension positive is obeyed. Objective Zaremba-Jaumann rates are denoted with a superimposed dot, for example the rate of the Cauchy stress is
. The sign convention of general mechanics with tension positive is obeyed. Objective Zaremba-Jaumann rates are denoted with a superimposed dot, for example the rate of the Cauchy stress is  .
.
3 The Hypoplastic Equation
In the new hypoplastic model, the stress rate  is written as nonlinear function of the strain rate
is written as nonlinear function of the strain rate  as follows
as follows

where the fourth rank tensor  is the hyperelastic stiffness,
is the hyperelastic stiffness,  is the so called degree of nonlinearity and
is the so called degree of nonlinearity and  is the flow direction. In order to reproduce the influence of previous deformation paths on the current material response, we introduce a new stress-like state variable,
is the flow direction. In order to reproduce the influence of previous deformation paths on the current material response, we introduce a new stress-like state variable,  . Thus, the material state is fully determined by the current stress
. Thus, the material state is fully determined by the current stress  , the current void ratio e, and the current back-stress
, the current void ratio e, and the current back-stress  . In addition to the evolution of
. In addition to the evolution of  (1) and the evolution of the void ratio e,
(1) and the evolution of the void ratio e,

the constitutive model requires the evolution of the back-stress  , which is described in Sect. 6.7.
, which is described in Sect. 6.7.
4 Hyperelasticity
Previous hypoplastic models include an empirical dependency of the stiffness tensor  on the stress [5, 12]. To reduce excessive ratcheting of hypoplasticity, Niemunis and Herle [13] introduced a new strain-like variable (the so called intergranular strain
on the stress [5, 12]. To reduce excessive ratcheting of hypoplasticity, Niemunis and Herle [13] introduced a new strain-like variable (the so called intergranular strain  ) which is fully determined by the recent history of deformation. During changes in the strain direction (detected by the angle between
) which is fully determined by the recent history of deformation. During changes in the strain direction (detected by the angle between  and
and  ), the nonlinear part of the model (
), the nonlinear part of the model ( ) vanishes and the overall stiffness increases. Since one cannot guarantee that there exists a one-to-one function
) vanishes and the overall stiffness increases. Since one cannot guarantee that there exists a one-to-one function  , this model is called hypoelastic. Hypoelastic models have in general some disadvantages. For example, one can find a closed strain loop for which neither the stress nor the energy is recovered [6, 14]. Since the model is path dependent due to the arbitrarily included pressure dependency, energy can be either created or dissipated depending on the sense of circulation in which the closed loop is appliedFootnote 1. This may become a serious shortcoming for modeling cyclic loading. To overcome this deficiency, we replaced the hypoelastic stiffness
, this model is called hypoelastic. Hypoelastic models have in general some disadvantages. For example, one can find a closed strain loop for which neither the stress nor the energy is recovered [6, 14]. Since the model is path dependent due to the arbitrarily included pressure dependency, energy can be either created or dissipated depending on the sense of circulation in which the closed loop is appliedFootnote 1. This may become a serious shortcoming for modeling cyclic loading. To overcome this deficiency, we replaced the hypoelastic stiffness  of previous hypoplastic models [5] by a hyperelastic one
of previous hypoplastic models [5] by a hyperelastic one  .
.
We use the hyperelastic stiffness proposed for paraelasticity [15] and neohypoplasticity [16]. This stiffness is a homogeneous function of stress of order \(n \approx 0.6\),  (with \(\lambda >0\)). The complementary energy is given by
(with \(\lambda >0\)). The complementary energy is given by

where the stress invariants  and
and  are normalized \(\bar{P}=P/P_0\), \(\bar{R}=R/P_0\) by the reference pressure \(P_0\), say \(P_0\) = 1 kPa, to attain unit consistency. The constants
are normalized \(\bar{P}=P/P_0\), \(\bar{R}=R/P_0\) by the reference pressure \(P_0\), say \(P_0\) = 1 kPa, to attain unit consistency. The constants  , \(n\approx 0.6\), and \(\alpha \approx 0.1\) are material parameters. The compliance
, \(n\approx 0.6\), and \(\alpha \approx 0.1\) are material parameters. The compliance  is obtained as the second derivative of the potential with respect to the stress, i.e.
is obtained as the second derivative of the potential with respect to the stress, i.e.  . That is
. That is

wherein  represents the fourth order identity tensor \(I_{ijkl}=\left( \delta _{ik}\delta _{jl} + \delta _{il}\delta _{jk}\right) /2\) and
represents the fourth order identity tensor \(I_{ijkl}=\left( \delta _{ik}\delta _{jl} + \delta _{il}\delta _{jk}\right) /2\) and
For a given degree of homogeneity n of the stiffness with respet to the pressure, the exponent \(\alpha \) can be related to the Poisson ratio \(\nu _\mathrm{iso}\) at the isotropic stress axis (\(Q=0\)) using [15]:
The hyperelastic stiffness is obtained after the inversion of the compliance. For convenience (see Sect. 5), and in order to take into account the influence of the void ratio on the stiffness, we introduce the factor \(F(e)=(1+e)/e\). Finally, the stiffness is written as

5 Model for Isotropic Compression
Let consider the special case of isotropic compression, i.e. isotropic stress (\(Q=0\), \(P\ne 0\)) and isotropic strain rates (\(\dot{\epsilon }_Q=0, \dot{\epsilon }_P \ne 0\)). We assume that upon isotropic compression, regardless of the initial void ratio and pressure, the Limiting Compression Curve (LCC) proposed by Pestana and Whittle [9] is asymptotically reached. Furthermore, we merge the concept of LCC with the pycnotropy function \(e_i(P)\) of the hypoplastic model of Gudehus [17] and Bauer [18], which describes the loosest possible state at a given pressure P. States beyond \(e_i\), that is \(e>e_i\), are not allowed. The LCC (or \(e_i(P)\)) is described by the Bauer’s [18] formula
where the maximum allowed void ratio at zero pressure \(e_{i0}\), the so called hardness of solid phase \(h_{si}\), and the exponent \(n_{Bi}\) are material constants.
The bulk modulus \(K_i = \frac{\partial p}{\partial \epsilon _{\mathrm{vol}}} =\frac{1}{3} \frac{\partial P}{\partial \epsilon _P} \) along the LCC is obtained after solving (11) for P, replacing \(e_i\) by e, and differentiating after \(\epsilon _P\)
with \( \frac{\partial e}{\partial \epsilon _P} =-(1+e)\sqrt{3}\) from (2).
If we assume that unloading and reloading are nearly elastic processes, we can describe them using the hyperelastic stiffness given in (10). The bulk stiffness K for hyperelasticityFootnote 2 yields

The loading/unloading/reloading processes can be described by

In order to simulate these processes with the hypoplastic Eq. (1), we must find a suitable definition of Y. We start by extracting the isotropic portion of the model by multiplying both sides of (1) by \(-\vec {~\text{1 }}:\)

Since the deformation is purely volumetric  and the stress remains isotropic \(Q=0\), the flow rule must be isotropic
and the stress remains isotropic \(Q=0\), the flow rule must be isotropic  . Therefore, (15) becomes
. Therefore, (15) becomes
We propose the following expression for Y
with
and the overconsolidation Ratio \(\mathrm{OCR}\) defined as
where \(P_B\) is a state variable that resembles the preloading pressure, i.e. it accounts for previous stress loading.
The evolution of \(P_B\) upon volumetric compression must satisfy some empirical observations. In contrast to clayFootnote 3, there is no unique virgin compression line for sand. Sand samples prepared at the same initial pressure but different initial densities show different compression lines. However, for a sample prepared at a given initial density \(e_0\) and pressure \(P_0\) there is a single compression line, at which we may regard the sample state as “normal consolidated”. Along this line the pressure P and the preconsolidation pressure \(P_B\) are identical, i.e. \(\mathrm{OCR}=P_B/P=1\). Therefore, we propose the evolution of the preconsolidation pressure \(P_B\) due to volumetric compression to be
where \(n_O\) is a material constant. During volumetric compression starting from \(P_B=P\) (i.e. \(\mathrm{OCR}=1\)), Eqs. (20) and (16) become identical (hence, \(\dot{P}_B=\dot{P}\) and \(\mathrm{OCR}=1\)). Upon unloading (volumetric extension), \(\mathrm{OCR}\) increases and both \(\dot{P}_B\) and Y tend to zero. In this case the model response (16) is nearly hyperelastic. This means, both processes in (14) can be described with a single equation Eq. (15). Instead of an explicit criterion for loading and unloading, the term \(\mathrm{OCR}^{-n_O}\) provides a smooth switch between the two expressions in (14). Notice that states at which the current pressure P is larger than the preconsolidation pressure \(P_B\), that means \(\mathrm{OCR}<1\), are allowed.
Notice also that in (18) we introduced the function \(\mathrm{max}()\) because the expression \(1-\left( e_i/e\right) ^{n_O} K_i/K\) becomes negative for P smaller than
with \(\xi ={-1/(1-n-n_{Bi})}\).
6 Constitutive Model with Historiotropic Yield Surface
The notions developed for the 1-Dimensional model presented in Sect. 5 are now extended to represent more general stress states and strain paths. In particular, the 3-D model must be able to describe the asymptotic state reached upon shearing. The material behaviour observed in oedometric, isotropic, and triaxial tests should be also described by the model.
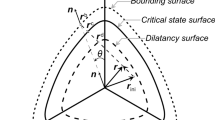
6.1 Historiotropic Yield Surface \(g=0\)
For the 1D model (see Sect. 5), the overconsolidation ratio was defined in (19) as \(\mathrm{OCR}= p_B/p\). In this case, the state variable \(p_B\) could be related to the preconsolidation pressure, e.g. the maximum pressure at which the sample has been subjected before the actual test. However, the definition of \(\mathrm{OCR}\) for the general case has to be modified in order to include the influence of the deviatoric portions of the stress  . Furthermore, it has to account for a more general definition of the preconsolidation pressure \(p_B\), i.e. the preconsolidation stress tensor
. Furthermore, it has to account for a more general definition of the preconsolidation pressure \(p_B\), i.e. the preconsolidation stress tensor 

which is a new state variable with isotropic \(-p_B ~\text{1 }\) and deviatoric  (i.e.
(i.e.  ) parts. To achieve this goal, we propose the equation
) parts. To achieve this goal, we propose the equation

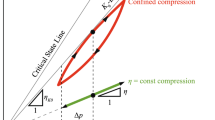
with

to define a yield surface that can be used to compute the \(\mathrm{OCR}\) in the general case, see Fig. 3. Stresses  lying on the yield surface, i.e. all stresses that satisfy (23) for a given void ratio e and preconsolidation stress
lying on the yield surface, i.e. all stresses that satisfy (23) for a given void ratio e and preconsolidation stress  , correspond to \(\mathrm{OCR}=1\). The size \(p_B\) and inclination
, correspond to \(\mathrm{OCR}=1\). The size \(p_B\) and inclination  of the yield surface with respect to the isotropic axis in the stress space is determined by the new state variable
of the yield surface with respect to the isotropic axis in the stress space is determined by the new state variable  . In (24), \(c_b \) is a material constant and the Mc Cauley brackets operator is defined as \(\left\langle \sqcup \right\rangle = \frac{1}{2}(\sqcup +\left| \sqcup \right| )\). The deviatoric tensor
. In (24), \(c_b \) is a material constant and the Mc Cauley brackets operator is defined as \(\left\langle \sqcup \right\rangle = \frac{1}{2}(\sqcup +\left| \sqcup \right| )\). The deviatoric tensor

represents the inclination of the current stress with respect to the major axis of the yield surface. Near the origin of the \(p-\)axis, the maximum opening of the yield surface is controlled by peak friction angle \(\varphi _{peak}\) via

where \(M_w\) and \(M_o\) are the maximum stress ratios (q/p) in the direction of the tensors  and
and  , respectively. The peak friction angle \(\varphi _{peak}\) is a function of the void ratio and the pressure, see Sect. 6.4.2. For a given angle \(\varphi \) and a given tensor \({\sqcup }\) we use a general expression for the slope \( M(\varphi ,\theta _{\sqcup })\) of the stress ratio on the \(p-q-\)plane. The slope M can be found as an interpolation between the two extreme values for triaxial compression \(M_c\) and triaxial extension \(M_e\) over the Lode’s angle \(\theta \) as \(M = \frac{1}{2} \left[ \left( M_c-M_e\right) \cos (3\theta ) + \left( M_c+M_e\right) \right] \) or
, respectively. The peak friction angle \(\varphi _{peak}\) is a function of the void ratio and the pressure, see Sect. 6.4.2. For a given angle \(\varphi \) and a given tensor \({\sqcup }\) we use a general expression for the slope \( M(\varphi ,\theta _{\sqcup })\) of the stress ratio on the \(p-q-\)plane. The slope M can be found as an interpolation between the two extreme values for triaxial compression \(M_c\) and triaxial extension \(M_e\) over the Lode’s angle \(\theta \) as \(M = \frac{1}{2} \left[ \left( M_c-M_e\right) \cos (3\theta ) + \left( M_c+M_e\right) \right] \) or
with \(s=\sin \varphi \) and \(c=\cos (3 \theta ) \). The Lode’s angle \(\theta _{\sqcup }\) of the tensor \(\sqcup \) is defined as
and \(\vec {\sqcup ^*} = \left( \sqcup ^*\right) ^\rightarrow \ne \left( \vec {\sqcup }\right) ^*\). For isotropic tensors, i.e. \(\left\| \sqcup ^*\right\| =0\), Eq. (28) cannot be used due to the division by zero in \(\vec {\sqcup ^*}= \sqcup ^*/\left\| \sqcup ^*\right\| \). In this case we arbitrary set \(\cos (3 \theta _{\sqcup }) = 1\). Triaxial compression and extension are especial cases of (27)

Conversely, for a given M and \(\theta \) (\(c=\cos (3 \theta )\)) we can find the mobilized angle \(\varphi \) from (27) as
Notice that the projection of the surface \(q/p-M=0\) (with M defined by (27)) onto the deviatoric plane may become concave for large friction angles. Although, alternative convex surfaces, like that from Matsuoka and Nakai [21], could be adopted, we use this concave surface because of its simplicity and because the flow rule is not associative (c.f. [22]).
Similar to the yield surface of the SANISAND model [22], the surface (23) can be thought as a conical surface with sharp apex at \(p=0\). The opening of this cone around its axis  varies from a maximal value \(M_w\) at \(p=0\) to zero at \(p/p_B=1\) (the cap of the surface), see \(\alpha \) in (24) and Fig. 4. Furthermore, the opening of the cone reduces when the inclination
varies from a maximal value \(M_w\) at \(p=0\) to zero at \(p/p_B=1\) (the cap of the surface), see \(\alpha \) in (24) and Fig. 4. Furthermore, the opening of the cone reduces when the inclination  reaches its maximum value in the direction of
reaches its maximum value in the direction of  , see \(\beta \) in (24).
, see \(\beta \) in (24).
Notice that both the maximum opening \(M_w\) of the yield surface and the maximum slope \(M_o\) of the  in the \(p-q-\)space are determined by the peak friction angle, \(\varphi _{peak}\), which is a function of the void ratio and the pressure.
in the \(p-q-\)space are determined by the peak friction angle, \(\varphi _{peak}\), which is a function of the void ratio and the pressure.
6.2 Overconsolidation Ratio \(\mathrm{OCR}\)
In Sect. 5 we used the Overconsolidation Ratio in the multiplicator \(\mathrm{OCR}^{-n_O}\) as a way to distinguish between first loading and unloading/reloading. In order to expand this idea to general stress states (and not only for the isotropic case), we combine the concept of overstress [23] with the yield surface \(g=0\). This generalization has been implemented in hypoplastic constitutive models for clay, e.g. [6] and [24]. Stress states lying on the yield surface \(g=0\) correspond to \(\mathrm{OCR}=1\). Within \((\mathrm{OCR}<1)\) the yield surface is the intensity of anelastic flow smaller than outside \((\mathrm{OCR}>1)\) the yield surface. \(\mathrm{OCR}\) is defined as
where \(p_{B+}\) is the “size” of a pseudo-yield surface on which the current stress  lies. To compute \(p_{B+}\) we proceed as follows. For a given stress
lies. To compute \(p_{B+}\) we proceed as follows. For a given stress  , void ratio e, and inclination
, void ratio e, and inclination  , we find \(p_{B+}\) from a surface \(g_{+}=0\)
, we find \(p_{B+}\) from a surface \(g_{+}=0\)

Graphical interpretation of \(p_B\) and \(p_{B+}\) used in the definition of \(\mathrm{OCR}\) (30)
The surface \(g_{+}=0\) is affine to \(g=0\), i.e. both have the same inclination  , the same opening \(\varphi _{peak}(e,p)\), but different back pressure \(p_{B+}\) (instead of \(p_B\)), see Fig. 5. Using (31) and (23) with the substitution (24) we obtain
, the same opening \(\varphi _{peak}(e,p)\), but different back pressure \(p_{B+}\) (instead of \(p_B\)), see Fig. 5. Using (31) and (23) with the substitution (24) we obtain

6.3 Generalized Taylor’s Dilatancy \(M_d\)
The dilatancy \(M_d\), which is the ratio of plastic volumetric \(\dot{\epsilon }_v^p\) to the plastic deviatoric \(\dot{\epsilon }_q^p\) strain rates, i.e. \(M_d=\dot{\epsilon }_v^p/\left| \dot{\epsilon }_q^p\right| \), is a distinctive phenomenon of granular materials and is one of the most important aspects in the description of the mechanical behaviour of soils. The accurate modeling of dilatancy becomes even more relevant for cyclic loading. The experiments of Pradhan and Tatsuoka [25] and [26] show that the dilatancy \(M_d\) is a function not only of stress \(\eta =q/p\) (like in Camclay model [10]  ), or of the void ratio (like in [27]
), or of the void ratio (like in [27]  ), but also a function of the direction of shearing
), but also a function of the direction of shearing  .
.
Consider a triaxial compression test on a dense sand sample at constant pressure. For stress ratios larger than the critical one \(\eta =q/p>M_c\), the dilatancy is positive, i.e. the volume of the sample increases with shearing. At this state we may have two different dilatancies depending on the direction of shearing. Upon continued shearing, the sample dilates, i.e. \(M_d>0\). If the direction of shearing is reversed, say from triaxial compression to triaxial extension, then the sample contracts, i.e. \(M_d<0\). To describe this dependency of dilatancy on the strain direction, Pradhan and Tatsuoka [25] use two different equations: one for triaxial compression and other for triaxial extension.
In order to describe the relation between dilatancy, stress (ratio), void ratio and strain direction, we generalize of the Taylor’s interlocking concept [7] by assuming that:
-
1.
the division of strength into a portion due to internal friction and another due to dilatancy applies also for states different to the peak.
-
2.
the dilatancy is zero at two stages: at PTL and at the critical state CS.
-
3.
the Taylor’s rule observed in simple shear test can be extended to multiaxial stress states.
We start from the concept of interloking, which was stated by Taylor [7] as follows. Consider a direct shear test on dense sample. The shear strength at the peak \(\tau _{peak}\) consists of two portions:
where \(\tau _c=\sigma \tan \varphi _c\) is the internal shear strength, with \(\varphi _c\) as the critical friction angle, and \(\tau _e\) is the portion of the shear strength related to interlocking. At the peak, the sample thickness h increases with the shearing displacement u, which represents a ratio of \({\Delta h}_{peak}\) units of height per unit of \({\Delta u}_{peak}\). The expansion of the sample is resisted by the normal stress \(\sigma \). For the occurrence of the expansion, energy must be supplied. The amount of energy \(E_e^\mathrm{used}\) used during expansion is the product of the normal force \(\sigma A\) applied on the top and bottom of the sample and the thickness increment \(\Delta h_{peak}\), i.e. \(E_e^\mathrm{used}=\sigma A \Delta h_{peak}\). The portion of the shearing stress \(\tau _e\) supplies the energy for expansion \(E_e^\mathrm{supplied}\), which is the product of the shear force \(\tau _e A\) and the shearing displacement \(\Delta u_{peak}\), i.e. \(E_e^\mathrm{supplied}= \tau _e A \Delta u_{peak}\). Setting these two energies equal, \(E_e^\mathrm{used} = E_e^\mathrm{supplied}\), we obtain
or \(\tau _e = \sigma \Delta h_{peak}/ \Delta u_{peak}\). We can therefore rewrite (33) as
Dividing the last equation by \(\sigma \) and substituting \(\tau _{peak}/\sigma \) = \(\tan \varphi _{peak}\) yields
where
and \(\psi _{peak}\) is defined as the dilatancy angle at peak state. If we assume that the relation between mobilized friction angle \(\varphi _m\) and dilatancy angle \(\psi \) given in (36) holds at any state (and not just at peak state where \( \varphi _m=\varphi _{peak}\) and \( \psi =\psi _{peak}\)), (36) becomes
Equation (38) can be interpreted as a constraint between stress and strain ratios during shearing. Notice that (38) has been obtained for constant \(\sigma \). The advantage of direct shear or constant pressure triaxial tests is that volume changes induced by pure shearing can be easily identified. On the contrary, in drained triaxial tests, for example, a constitutive relation is required to identify which portion of the volume change is due to the change of applied pressure, and which portion is due just to interlocking.
We modify now the Taylor’s rule given by (38) to incorporate two effects: the void ratio (and pressure) dependency and the strong contractancy upon reversals. Experiments of Ishihara [3] show that the dilatancy equals zero at two stages: at the critical state CS and at the Phase Transformation Line PTL. To reproduce this observation, we replace \( \tan \varphi _c\) by \(\tan \varphi _{PTL}\) in (38), where \(\varphi _{PTL}(e,p)\) is a function of void ratio and pressure, see Sect. 6.4.3. For dense sand \(e<e_c(p)\), the PTL lies below the critical state line CSL, \(\varphi _{PTL}<\varphi _{c}\). For loose sand \(e>e_c(p)\), the PTL lies above the CSL \(\varphi _{PTL}>\varphi _{c}\) and may not be reached upon undrained shearing. After long monotonic shearing, the sample approaches the critical state, at which deviatoric straining produces neither stress nor volume change. Therefore, at the critical state (where \(e=e_c\)), the PTL coincides with CSL, i.e. \(\varphi _{PTL}=\varphi _{c}\).
Experiments show also that the maximum contractancy is attained upon reversals of the strain path. We propose the factor  as a way to reproduce this observation. Incorporating this two modifications into (38), we obtain
as a way to reproduce this observation. Incorporating this two modifications into (38), we obtain

For a given mobilized friction angle \(\varphi _m>\varphi _{PTL}\), we can obtain two different dilatancies from a single Eq. (39): a positive dilatancy \(\tan \varphi _m - \tan \varphi _{ {PTL}}\) if  or a stronger contractancy \(-\tan \varphi _m - \tan \varphi _{ {PTL}}\) if the strain rate is reversed, e.g.
or a stronger contractancy \(-\tan \varphi _m - \tan \varphi _{ {PTL}}\) if the strain rate is reversed, e.g.  . Notice, however, that (39) relates three angles: \(\psi , \varphi _m\), and \(\varphi _{PTL}\). In order to generalize this equation for three dimensions, we must find a relation between the angle \(\psi \) and the volumetric and deviatoric invariants of the strain rate. Neglecting the difference between plastic and total deviatoric strain rates we can use (27), which express an angle in terms of stress invariants, to relate the dilatancy angle \(\psi \) with tensor invariants of the plastic strain rate
. Notice, however, that (39) relates three angles: \(\psi , \varphi _m\), and \(\varphi _{PTL}\). In order to generalize this equation for three dimensions, we must find a relation between the angle \(\psi \) and the volumetric and deviatoric invariants of the strain rate. Neglecting the difference between plastic and total deviatoric strain rates we can use (27), which express an angle in terms of stress invariants, to relate the dilatancy angle \(\psi \) with tensor invariants of the plastic strain rate

where \(s=\sin \psi \) and  . In hypoplasticity, the direction of the deviatoric anelastic strain has the same direction as the deviatoric stress. In (40), however, we have assumed that the plastic deviatoric shearing is parallel to
. In hypoplasticity, the direction of the deviatoric anelastic strain has the same direction as the deviatoric stress. In (40), however, we have assumed that the plastic deviatoric shearing is parallel to  . This assumption is based on the observation, that after long monotonic shearing,
. This assumption is based on the observation, that after long monotonic shearing,  and
and  become parallel, see (53). Using (40) and writing
become parallel, see (53). Using (40) and writing  , we can now formulate a flow rule for shearing as
, we can now formulate a flow rule for shearing as

Figure 6 compares the flow rule (41) with experimental results. In this simulations it has been assumed that the plastic strain rate is given by  with
with  and \(\varphi _{PTL}=\varphi _{c}=27^{\circ }\).
and \(\varphi _{PTL}=\varphi _{c}=27^{\circ }\).
6.4 Characteristic Curves
Besides the Limiting Compression Curve (LCC) defined in (11), the model requires explicit relations between the critical void ratio, the maximum friction angle, and the phase transformation line with the pressure.
6.4.1 Critical Void Ratio \(e_c(p)\)
After large monotonic shearing a sand sample approaches a state at which further isochoric shearing is possible at constant stress. This state is approached independently of the initial density or stress of the sample. At this state, the so called critical state, the material reaches a critical void \(e_c\), which is a one-to-one function of the pressure p, and a critical stress ratio M (at which the mobilized friction angle \(\varphi _m = \varphi _c\)). The critical void ratio is described by the Bauer’s formula [18]
with the constants \(e_{c0}, h_{sc},\) and \(n_{Bc}\).
Experimental results of constant pressure triaxial tests [25, 26] compared with the dilatancy given by (40) and (41) with  and \(\varphi _{PTL}=\varphi _{c}=27^{\circ }\). Conventions: \(dv_d= \varepsilon _a + 2 \varepsilon _r\), \(d\gamma = \varepsilon _a - \varepsilon _r\) where \(\varepsilon _a\) and \(\varepsilon _r\) are the axial and radial strain components (compression positive), respectively. \(d\gamma ^d\) represents the plastic portion of \(d\gamma \).
and \(\varphi _{PTL}=\varphi _{c}=27^{\circ }\). Conventions: \(dv_d= \varepsilon _a + 2 \varepsilon _r\), \(d\gamma = \varepsilon _a - \varepsilon _r\) where \(\varepsilon _a\) and \(\varepsilon _r\) are the axial and radial strain components (compression positive), respectively. \(d\gamma ^d\) represents the plastic portion of \(d\gamma \).
6.4.2 Maximum Friction Angle \(\varphi _{peak}\)
The maximum attainable stress obliquity depends on the void ratio and the pressure. Larger stress obliquities can be reached by dense sands than by looser ones, see Fig. 7. We describe the maximum stress obliquity in terms of the friction angle \(\varphi _{\mathrm{peak}}\) via
with the constant \(n_{peak}\). Notice that at the critical state \(e=e_c\) the maximum friction angle equals the critical one.
6.4.3 Friction Angle at Phase Transformation Line \(\varphi _{PTL}\)
The Phase Transformation Line (PTL) described by Ishihara et al. [3] indicates the stress ratio at which, upon monotonic shearing, the sand changes from contractive to dilative behaviour. The PTL (usually depicted in the \(p-q-\)space) is related to the friction angle \(\varphi _{PTL}\) and depends on the pressure and the void ratio
with the constant \(n_{PTL}\). Dense sands reach the PTL at lower stress ratios than loose ones, see Fig. 7. Notice that at the critical state \(e=e_c\), where unbounded shear strain is possible with no volume changes, the PTL line becomes the CSL, i.e. \(\tan \varphi _{PTL} = \tan \varphi _c\).
6.5 Intensity of Anelastic Flow
The intensity of anelastic flow Y is defined as an interpolation between two main loading cases: \(Y_D\) for shearing and \(Y_I\) for isotropic compression (see Sect. 5)
Upon shearing, the degree of nonlinearity is given by (see Fig. 8)

with

where  is the deviatoric portion of the stress
is the deviatoric portion of the stress  ,
,  is the image of the current stress
is the image of the current stress  projected onto the limiting surface \(f=0\) in the direction of
projected onto the limiting surface \(f=0\) in the direction of  , and the exponent \(n_{YD}\) is a material constant. The limiting surface \(f=0\) is an open cone in the stress space, whose opening is determined by the maximum friction angle \(\varphi _{peak}\). This surface is given by the equation
, and the exponent \(n_{YD}\) is a material constant. The limiting surface \(f=0\) is an open cone in the stress space, whose opening is determined by the maximum friction angle \(\varphi _{peak}\). This surface is given by the equation

Since  is parallel to
is parallel to  , we can find
, we can find  from (47) as
from (47) as

6.6 Flow Rule 
The flow rule  is interpolated from the two special cases: the flow rule
is interpolated from the two special cases: the flow rule  for isochoric shearing and the flow rule
for isochoric shearing and the flow rule  for radial compression
for radial compression

where \(\xi \) is a large number, say \(\xi \approx 1000\). During isochoric shearing, \(Y_D>0\) and the second term on the right-hand side of (49) vanishes. Upon radial compression,  alienates asymptotically with the current stress ratio
alienates asymptotically with the current stress ratio  and
and  tends to zero. In this case \(Y_D\) cannot be determined from (45). For this special case we define
tends to zero. In this case \(Y_D\) cannot be determined from (45). For this special case we define

where \(w_\mathrm{tol}\) is a small number, say \(w_\mathrm{tol} = 10^{-4}\), and the first term on the right hand side of (49) vanishes. Notice that a similar interpolation of the flow rule has been used in the SANISAND model [22]. In order to reproduce the asymptotic behaviour upon radial compression, i.e. those tests with  and
and  , the flow rule
, the flow rule  should be given by
should be given by

where \(c_{mI}\) is a material constant. The asymptotic value of the deviatoric portion  of the back stress
of the back stress  upon radial compression is
upon radial compression is  . At this stage
. At this stage  , the tensor
, the tensor  vanishes
vanishes  , see Sect. 6.7, and \(Y_D=0\) (50). In addition the stress path approaches a constant stress ratio, at which the directional homogeneity
, see Sect. 6.7, and \(Y_D=0\) (50). In addition the stress path approaches a constant stress ratio, at which the directional homogeneity  can be observed [6]. Using this property of the hypoplastic Eq. (1), the constant \(c_{mI}\) can be found by making the flow direction
can be observed [6]. Using this property of the hypoplastic Eq. (1), the constant \(c_{mI}\) can be found by making the flow direction  compatible with the stress
compatible with the stress  , which is reached after long oedometric compression. \(K_0\) can be computed from the empirical “Jacky” formula \(K_0=1-\sin \varphi _c\). In the asymptotic case, the direction of flow must be uniaxial, i.e.
, which is reached after long oedometric compression. \(K_0\) can be computed from the empirical “Jacky” formula \(K_0=1-\sin \varphi _c\). In the asymptotic case, the direction of flow must be uniaxial, i.e.  . Therefore, \(c_{mI}\) is
. Therefore, \(c_{mI}\) is
6.7 Evolution of the State Variable 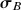
Similar as in the anisotropic viscohypoplastic model [24], the evolution of the state variable  is given in separate equations for
is given in separate equations for  and \(p_B\). For the evolution of
and \(p_B\). For the evolution of  , i.e. the inclination of the yield surface \(g=0\), we propose
, i.e. the inclination of the yield surface \(g=0\), we propose

According to this equation,  evolves upon any kind of deformation (isotropic or deviatoric). The evolution rate is controlled by the material constant \(C_2\) and is larger for stresses outside (\(\mathrm{OCR}<1\)) than for stresses inside (\(\mathrm{OCR}>1\)) the yield surface \(g=0\).
evolves upon any kind of deformation (isotropic or deviatoric). The evolution rate is controlled by the material constant \(C_2\) and is larger for stresses outside (\(\mathrm{OCR}<1\)) than for stresses inside (\(\mathrm{OCR}>1\)) the yield surface \(g=0\).  evolves in the direction given by the difference between the current stress ratio
evolves in the direction given by the difference between the current stress ratio  and
and  . To avoid numerical problems when the stress reaches the limit stress surface, and therefore
. To avoid numerical problems when the stress reaches the limit stress surface, and therefore  , the stress
, the stress  in (53) should be replaced by
in (53) should be replaced by  . After long radial compression, both
. After long radial compression, both  and
and  approach an asymptotic stress ratio and the evolution of
approach an asymptotic stress ratio and the evolution of  ceases.
ceases.
The evolution of \(p_B\), i.e. the size of the yield surface \(g=0\), consists of two portions
\(\dot{p}_{B I}\) is related to volumetric and \(\dot{p}_{B D}\) to deviatoric deformations. The evolution of \(p_B\) during isotropic compression has been discussed in Sect. 5 and is given by (20). Hence,

With this equation, \( {p}_{BI}\) increases during volumetric compression and reduces during volumetric extension. However, during volumetric extension \(\mathrm{OCR}\) increases making the reduction of \( {p}_{BI}\) negligible. Therefore, \(\dot{p}_{BI}\) can be thought to be similar to the isotropic hardening of Camclay.
In case of shear deformations, we propose an evolution equation similar to (53)

This equation allows for strong reductions of \(p_B\) during undrained cyclic loading, which resembles the material degradation observed in phenomena like cyclic mobility. Such reductions of \(p_B\) during pure deviatoric shearing can also describe the discrepancy between the compression curve and reconsolidation curves after some undrained shear cycles observed by Ishihara und Okada [2].
7 Comparison of the Model with Experimental Results
The proposed constitutive model has been implemented in a Fortran code (called UMAT – User MATerial subroutine) that is compatible with the commercial Finite Element program Abaqus. The UMAT is also compatible with the IncrementalDriver routine [28], which is an open-source code designed to verify the numerical implementation of the constitutive model and to simulate element tests.
To evaluate the performance of the model, experimental results of monotonic and cyclic triaxial tests on different sands were simulated. Furthermore, additional experiments on Karlsruhe fine sand, which were specially designed to study the influence of previous deformation histories on subsequent cyclic loading, were also simulated.
7.1 Monotonic Triaxial Tests
Figures 9, 10, and 11 compare the laboratory with the simulation results of triaxial compression tests on loose, medium dense, and dense Toyoura sand samples [29], respectively. These experiments are commonly used as benchmark for constitutive models because they account for the material response to monotonic undrained shearing over a wide range of pressures and densities. The material constants used in the simulations are listed in Table 1. Isotropic compression tests on Toyoura sand for different densities have been also simulated, Fig. 2. It can be seen that the model is able to reproduce the experimental results in an acceptable way for all pressures and densities.

Experiment data adapted from [29].
Experiment results and simulation of triaxial compression tests on Toyoura sand for dense (\(e=0.735\)) samples.
7.2 Drained and Undrained Triaxial Tests on Loose Sand
To show the influence of previous deformation history on the subsequent material response, Doanh [1] conducted a set of experiments on Hostun RF loose sand. Starting at an isotropic stress of \(p_0=100\) kPa, the samples were subjected to drained triaxial compression up to different stress ratios denoted by the dots (1 to 10) in Fig. 12, upper part, left. Then the deviatoric stress was reduced in order to reach the initial isotropic stress with \(p=100\) kPa. At this point, all samples had similar void ratios, \(e_0 \approx 0.94\). Then, undrained triaxial compression and extension tests were conducted. It can be observed that the maximum deviatoric stress upon undrained compression increases with the stress ratio attained during the preloading phase. Converserly, the maximum deviatoric stress attained in undrained extension reduces with the stress ratio reached during the preceding drained triaxial compression. This observation can be qualitatively reproduced by the proposed constitutive model, see Fig. 12, lower part, right.
7.3 Cyclic Triaxial Tests
The capabilities of the model were also tested under cyclic conditions. Figure 13 shows the simulation of undrained cyclic triaxial tests of small amplitude on Karlsruhe fine sand [4]. Starting from an isotropic stress of \(p_0=200\) kPa and \(e_0=0.952\) (\(I_{D0}=0.27\)) stress cycles of amplitude \(q^{\mathrm{ampl}}=40\) kPa were applied. It can be observed that in the experiment as well as in the simulation, the accumulation of pore water pressure (or the reduction of effective pressure) after each cycle reduces with the number of cycles. The experiment was stopped when the accumulated axial strain reached 10%. This criterion was satisfied after 72 cycles in the experiment and after 120 cycles in the simulation. However, an acceptable agreement between experiment and simulation can be observed.

Experiment data adapted from [29].
Experiment results and simulation of triaxial compression tests on Toyoura sand for medium dense (\(e=0.833\)) samples.

Experiment data adapted from [29].
Experiment results and simulation of triaxial compression tests on Toyoura sand for loose (\(e=0.907\)) samples.

Experiment data adapted from [1].
Undrained triaxial compression and extension tests on Hostun RF loose sand preceded by different drained triaxial preloading.
A cyclic undrained triaxial test with larger stress amplitude \(q^{\mathrm{ampl}}=60\) kPa was also simulated, see Fig. 14. The cyclic loading started from an isotropic stress of \(p_0=200\) kPa and an initial void ratio of \(e_0=0.726\) (\(I_{D0}=0.87\)). After about 80 cycles, the effective stress pressure reduces to nearly zero. Beyond that point, a cyclic attractor, a butterfly-shaped stress path in the \(p-q-\)space can be observed. The model simulates a stronger reduction of the effective stress than the one observed in the experiment. After 27 cycles, the accumulated axial strain was about 10% and the effective pressure became zero. However, the cyclic attractor could not be properly captured by the simulation.
7.4 Combination of Monotonic and Cyclic Loading
In a further validation attempt, experiments with cyclic loads of variable amplitude as well as combinations of monotonic and cyclic loading were simulated. Figure 15 shows the simulation of an undrained triaxial test with successive loading/unloading phases. The experiment starts from an isotropic stress of \(p_0=200\) kPa and an initial density of \(I_{D0}=0.34\). After the application of a (compressive) strain increment of \(\Delta \epsilon _1=0.05\%\), the deviatoric stress is reduced to zero. Then, successive cycles of reloading (with strain increment \(\Delta \epsilon _1=0.05\%\)) and unloading (reduction of deviatoric stress up to \(q=0\)) phases took place. As reference, the results of a purely monotonic test is depicted. In contrast to hypoplasticity [13] or the ISA model [30], where the previous deformation path is tracked by a strain-like state variable (i.e. the intergranular strain), it can be seen that the proposed model can reproduce the cyclic loading of variable amplitude without overshooting or ratcheting effects.

Experiment data adapted from [4].
Undrained cyclic triaxial tests of small stress amplitude on Karlsruhe fine sand.
A similar performance can be observed in the simulation of cyclic tests with small and large amplitudes. Figure 16 presents the simulation of a drained triaxial test with constant pressure and cycles of small and large amplitude on Toyoura sand. Figure 17 shows the simulation of an undrained triaxial test on dense Karlsruhe sand with cycles of small and large amplitude too. In both cases it can be observed that the model can “remember” the stress point from which the unloading (cycle of small amplitude) process started and that this stress point is reached again upon reloading. A stiffer and nearly elastic response during the small “unloading cycles” can be also reproduced by the model.
7.5 Cyclic Loading with Different Deformation Histories
To investigate (and/or test) the evolution equation for the novel state variable  , we conducted special tests applying the same cyclic loads, but preceded by different deformation histories on dense sand samples. The Karlsruhe fine sand can be characterized by the following parameters: \(d_{50}\) = 0.14 mm, \(C_u\) = 1.5 (\(\le \) 5, i.e. poorly graded sand), \(e_{\text {min}}\) = 0.677, \(e_{\text {max}}\) = 1.054 and \(\varrho _s\) = 2.65 g/cm\(^3\). The samples, with diameter d = 100 mm and height h = 200 mm, were prepared using either the dry pluviation or the moist tamping method. Then, the pores of the samples were fully saturated with water to allow a precise measurement of volume changes by means of a differential pressure transducer DPT that was connected to a pipette system.
, we conducted special tests applying the same cyclic loads, but preceded by different deformation histories on dense sand samples. The Karlsruhe fine sand can be characterized by the following parameters: \(d_{50}\) = 0.14 mm, \(C_u\) = 1.5 (\(\le \) 5, i.e. poorly graded sand), \(e_{\text {min}}\) = 0.677, \(e_{\text {max}}\) = 1.054 and \(\varrho _s\) = 2.65 g/cm\(^3\). The samples, with diameter d = 100 mm and height h = 200 mm, were prepared using either the dry pluviation or the moist tamping method. Then, the pores of the samples were fully saturated with water to allow a precise measurement of volume changes by means of a differential pressure transducer DPT that was connected to a pipette system.
All drained cyclic tests started from the same initial isotropic stress of \(p_0\) = 100 kPa and from nearly the same density (\(I_{D0}\approx 0.8\)). The stress controlled cyclic loading consisted of stress increments of magnitude \(l_{pq} = 40\) kPa applied successively upon 16 different stress ratios \(\eta =\Delta q/\Delta p\) in the following sequence: \( \eta = 1.125, 1.0, 0.875, \dots , -0.625\), and \(-0.750\). Each stress increment with stress ratio \(\eta _i\) (loading) was followed by another stress increment with \(-\eta _i\) (unloading) until the initial stress \(p_0=100\) kPa and \(q_0=0\) was reached. Then, the next stress increment, with \(\eta _{i+1}\) was applied. The process was repeated for each of the 16 stress increments, see Fig. 18(a), left. The resulting strains are also shown in Fig. 18(a), right.

Experiment data adapted from [4].
Undrained cyclic triaxial tests of large stress amplitude on Karlsruhe fine sand.

Experiment data adapted from [4].
Experiment results and simulation of an undrained triaxial compression test with successive loading/unloading phases on Karlsruhe fine sand.

Experiment data adapted from [25].
Combination of cycles of large and small amplitude.

Experiment data adapted from [4].
Combination of cycles of large and small amplitude.
In order to investigate the influence of previous deformation history on the cyclic behaviour of the material, sand samples were subject to undrained triaxial deformations in compression as well as in extension before the drained cyclic tests described above were conducted, see Fig. 18(b) and (c). The monotonic and cyclic components of the axial loading were applied by means of a pneumatic cylinder located below the pressure cell. The cell pressure was applied pneumatically with water in the cell. Both the vertical \(\sigma _1\) and the horizontal \(\sigma _3\) total stresses were controlled independently.
These experiments were simulated using the proposed model and the hypoplastic model with intergranular strain [13], see Fig. 19. The material constants for the proposed constitutive model and for hypoplasticity are given in Tables 1 and 2, respectively. It can be observed that in comparison with hypoplasticity, the present model is able to reproduce (qualitatively) better the influence of previous deformation on the material response to the subsequent cyclic loads. Furthermore, the mechanical behaviour of the samples during the undrained monotonic preloading and unloading phases is better captured by the proposed model than by hypoplasticity.
Test results on Karlsruhe fine sand (a) without preloading history (Test AP1) as reference test, (b) preloading history in compression area (Test AP2) and (c) preloading history in extension area (Test AP3). \(I_{D0}\) after sample preparation (air pluviation) and \(I_{D1}\) at start of drained stress paths.
Figure 20 shows the same experiments as in Fig. 18, but on samples prepared by the moist tamping method. Compared to the air pluviation, the moist tamping method produces samples that show less contractancy during the undrained preloading and unloading phases. Furthermore, the overall response of the samples prepared by the moist tamping method is stiffer than that of the samples prepared by the air pluviation method. The influence of the preparation method on the mechanical behaviour of sand cannot be captured by the proposed constitutive model.
Test results on Karlsruhe fine sand (a) without preloading history (Test MT1) as reference test, (b) preloading history in compression area (Test MT2) and (c) preloading history in extension area (Test MT3). \(I_{D0}\) after sample preparation (moist tamping) and \(I_{D1}\) at start of drained stress paths.
8 Conclusions
The present model introduces three main changes to the well known hypoplastic equation [5]: (1) a hyperelastic stiffness, (2) a yield surface to account for recent deformation history, and (3) a new state variable (a back-stress)  , which describes the size and inclination of the yield surface. These changes enable the proposed model to overcome some known shortcoming not only of hypoplastic, but also of elastoplastic constitutive models:
, which describes the size and inclination of the yield surface. These changes enable the proposed model to overcome some known shortcoming not only of hypoplastic, but also of elastoplastic constitutive models:
-
1.
In contrast to yield surfaces with a constant elastic range defined in the strain space (like in hypoplasticity with intergranluar strain [13] or in the ISA model [30]), the size of the proposed yield surface \(g=0\), which is defined in the stress space, varies with the back stress
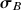 . Combined with the concept of \(\mathrm{OCR}\), this yield surface allows the simulation of cyclic loads of different amplitudes without overshooting or excessive ratcheting.
. Combined with the concept of \(\mathrm{OCR}\), this yield surface allows the simulation of cyclic loads of different amplitudes without overshooting or excessive ratcheting. -
2.
The influence of recent deformation history on the mechanical behaviour of sand can be captured with the additional state variable
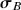 and the yield surface.
and the yield surface. -
3.
The presented model is able to simulate the degradation of the material stiffness during undrained cyclic loading without additional state variables. Advanced constitutive models like SANISAND [22], ISA [30], or Neohypoplasticity [16] require an additional state variable (the so called
 variable) to induce extra contractancy after reversals at large stress obliquities.
variable) to induce extra contractancy after reversals at large stress obliquities. -
4.
Radial compression paths with loading and unloading cycles can be also well reproduced by the proposed model.
Notes
- 1.
Clockwise (CW) or counter clockwise (CCW).
- 2.
Notice that the K can be obtained directly from the hyperelastic potential as \(K = \frac{1+e}{e}\left[ 3 \frac{\partial ^2 \bar{\psi }}{\partial P^2} \right] ^{-1}\). In this case, the potential simplifies to \(\bar{\psi }(P,R)= P_0c \bar{P}^{2-n}\) because \(P=R\) holds for \(Q=0\).
- 3.
In clay, a family of parallel virgin compression lines (in the \(e-\ln (p)-\)diagram) can be obtained by deforming the samples at different straining rates.
References
Doanh, T., Dubujet, P., Touron, G.: Exploring the undrained induced anisotropy of Hostun RF loose sand. Acta Geotech. 5, 239–256 (2010)
Ishihara, K., Okada, S.: Effects of stress history on cyclic behavior of sand. Soils Found. 18(4), 31–45 (1978)
Ishihara, K., Tatsuoka, F., Yasuda, S.: Undrained deformation and liquefaction of sand under cyclic stresses. Soils Found. 15(1), 29–44 (1975)
Wicthmann, T.: Soil behaviour under cyclic loading - experimental observations, constitutive description and applications. Heft 180, Institut für Boden und Felsmechanik, Karlsruhe Institut für Technologie (KIT) (2016)
Wolffersdorff, P.: A hypoplastic relation for granular materials with a predefined limit state surface. Mech. Cohesive-Frictional Mater. 1, 251–271 (1996)
Niemunis, A.: Extended hypoplastic models for soils. Habilitation, monografia 34, Ruhr-University Bochum (2003)
Taylor, D.: Fundamentals of Soil Mechanics. Wiley, New York (1948)
Niemunis, A., Grandas-Tavera, C.E.: Computer aided calibration, benchmarking and check-up of constitutive models for soils. Some conclusions for neohypoplasticity. In: Triatafyllidis, T. (ed.) Holistic Simulation of Geotechnical Installation Processes, vol. 82, pp. 168–192. Springer, Heidelberg (2017)
Pestana, J., Whittle, A.: Compression model for cohesionless soils. GEOT 45(4), 611–631 (1995)
Roscoe, K.H., Burland, J.B.: On the generalized stress-strain behaviour of ‘wet’ clay. In: Engineering Plasticity, pp. 535–609. Cambridge University Press, Cambridge (1968)
Schofield, A., Wroth, C.: Critical State Soil Mechanics. McGraw-Hill, London (1968)
Wu, W.: Hypoplastizität als mathematisches Modell zum mechanischen Verhalten granularer Stoffe. Veröffentlichungen des Institutes für Boden-und Felsmechanik der Universität Fridericiana in Karlsruhe, Heft Nr. 129 (1992)
Niemunis, A., Herle, I.: Hypoplastic model for cohesionless soils with elastic strain range. Mech. Cohesive-Frictional Mater. 2, 279–299 (1997)
Niemunis, A., Prada-Sarmiento, L., Grandas-Tavera, C.: Paraelasticity. AG 6(2), 67–80 (2011)
Prada Sarmiento, L.: Parelastic description of small-strain soil behaviour. Dissertation, Veröffentlichungen des Institutes für Bodenmechanik und Felsmechanik am Karlsruher Institut für Technologie, Heft 173 (2011)
Niemunis, A., Grandas Tavera, C.E., Wichtmann, T.: Peak stress obliquity in drained und undrained sands. Simulations with neohypoplasticity. In: Triatafyllidis, T. (ed.) Holistic Simulation of Geotechnical Installation Processes, pp. 85–114. Springer, Heidelberg (2015)
Gudehus, G.: A comprehensive constitutive equation for granular materials. Soils Found. 36(1), 1–12 (1996)
Bauer, E.: Calibration of a comprehensive constitutive equation for granular materials. Soils Found. 36, 13–26 (1996)
Miura, N., O-Hara, S.: Particle-crushing of a decomposed granite soil under shear stresses. Soils Found. 19(3), 1–14 (1979)
Miura, N., Murata, H., Yasufuku, N.: Stress-strain characteristics of sand in a particle-crushing region. Soils Found. 24(1), 77–89 (1984)
Matsuoka, H., Nakai, T.: Stress-strain relationship of soil based on the SMP, constitutive equations of soils. In: Specialty Session 9, Japanese Society of Soil Mechanics and Foundation Engineering, IX ICSMFE, Tokyo, pp. 153–162 (1977)
Taiebat, M., Dafalias, Y.F.: SANISAND: simple anisotropic sand plasticity model. IJNAMG 32, 915–948 (2008)
Olszak, W., Perzyna, P.: The constitutive equations of the flow theory for a nonstationary yield condition. In: Applied Mechanics, Proceedings of the 11th International Congress, pp. 545–553 (1966)
Niemunis, A., Grandas-Tavera, C., Prada-Sarmiento, L.: Anisotropic visco-hypoplasticity. Acta Geotech. 4, 293–314 (2009)
Pradhan, T., Tatsuoka, F., Sato, Y.: Experimental stress-dilatancy relations of sand subjected to cyclic loading. Soils Found. 29(1), 45–64 (1989)
Pradhan, T., Tatsuoka, F.: On stress-dilatancy equations of sand subjected to cyclic loading. Soils Found. 29(1), 65–81 (1989)
Li, X., Dafalias, Y., Wang, Z.: State dependent dilatancy in critical state constitutive modelling of sand, vol. 36, no. 4, pp. 599–611 (1999)
Niemunis, A.: IncrementalDriver (2019). http://www.pg.gda.pl/~aniem/dyd.html
Verdugo, R., Ishihara, K.: The steady state of sandy soils. Soils Found. 36(2), 81–91 (1996)
Fuentes Lacouture, W.M.: Contributions in mechanical modelling of fill materials. Dissertation, Veröffentlichungen des Institutes für Bodenmechanik und Felsmechanik am Karlsruher Institut für Technologie, Heft 179 (2014)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Grandas Tavera, C.E., Triantafyllidis, T., Knittel, L. (2020). A Constitutive Model with a Historiotropic Yield Surface for Sands. In: Triantafyllidis, T. (eds) Recent Developments of Soil Mechanics and Geotechnics in Theory and Practice. Lecture Notes in Applied and Computational Mechanics, vol 91. Springer, Cham. https://doi.org/10.1007/978-3-030-28516-6_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-28516-6_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-28515-9
Online ISBN: 978-3-030-28516-6
eBook Packages: EngineeringEngineering (R0)






 .
.




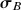



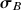 . Combined with the concept of
. Combined with the concept of 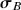 and the yield surface.
and the yield surface. variable) to induce extra contractancy after reversals at large stress obliquities.
variable) to induce extra contractancy after reversals at large stress obliquities.