Abstract
Apart from time-driven creep or relaxation, most viscoplastic models (without plastic and viscous strain separation) generate no or a very limited accumulation of strain or stress due to cyclic loading. Such pseudo-relaxation (or pseudo-creep) is either absent or dwindles too fast with increasing OCR. For example, the accumulation of the pore water pressure and eventual liquefaction due to cyclic loading cannot be adequately reproduced. The proposed combination of a viscous model and a hypoplastic model can circumvent this problem. The novel visco-hypoplasticity model presented in the paper is based on an anisotropic preconsolidation surface. It can distinguish between the undrained strength upon triaxial vertical loading and horizontal loading. The strain-induced anisotropy is described using a second-order structure tensor. The implicit time integration with the consistent Jacobian matrix is presented. For the tensorial manipulation including numerous Fréchet derivatives, a special package has been developed within the algebra program MATHEMATICA (registered trade mark of Wolfram Research Inc.). The results can be conveniently coded using a special FORTRAN 90 module for tensorial operations. Simulations of element tests from biaxial apparatus and FE calculations are also shown.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In geotechnical engineering, the stress-strain-time behaviour of clay-like soils is important for the evaluation of long-term performance of constructions. Even relatively small differential settlements occurring late (when the structure is finished and statically indeterminate) may lead to a considerable increase in internal forces and affect the serviceability.
The constitutive models for the time-dependent behaviour are developed mainly along the line of viscoplasticity. In the past decade, hypoplastic constitutive model has been established as an attractive alternative. Hypoplasticity was developed primarily for cohesionless soil. Recently, hypoplastic constitutive models have been extended to clayey soil and rockfill material [8, 24, 35, 60], and the model parameters have been determined for a large number of soils [51]. Moreover, hypoplastic constitutive models have been used to solve numerous boundary value problems, e.g. earth retaining wall [61], shallow foundation [52, 58], pile foundation [22], shear band formation [62] and site response analysis [50].
Here, a model of rheological effects for normally consolidated and lightly overconsolidated soft soils into the hypoplastic framework is discussed. Sophisticated phenomena like delayed-creep or tertiary creep for normally consolidated clays and hesitation period are not considered [10, 54]. Several authors [31, 54] have mentioned the discrepancy between laboratory and in situ measurements. This interesting anomaly is outside the scope of the present paper. Neither effects caused by cementation nor structure e.g. [10, 32, 54] are considered. The current stress, the void ratio and the anisotropy structure tensor are used as state variables. The anisotropic visco-hypoplastic model can describe creep, relaxation, rate dependence and combinations thereof. Previous works [1, 12, 28] have described the same phenomena within the critical state framework for isotropic preconsolidation surface. A similar isotropic model including an endochronic kernel was proposed by Oka [48]. A pseudo relaxation, e.g. due to undrained cyclic loading, can also be obtained with the proposed model. Similarly, as in the visco-plastic approach proposed [49], a preconsolidation surface (corresponding to overconsolidation ratio OCR = 1) is defined in the stress space. Contrary to the well-known elliptical yield surface of the modified Cam clay (MCC) model, our preconsolidation surface is anisotropic and need not lie along the hydrostatic axis. The first indications of deviations of the preconsolidation surface from the isotropic location along the hydrostatic axis were experimentally observed in the early seventies [29, 37, 38]. The first numerical implementations into elastoplasticity were attempted a decade later [5, 6, 7, 48]. Worth mentioning is also an interesting and original description of anisotropy by Dean [20] based on a novel specific length concept. Our structural tensor is constituted by stress and volumetric strain rate, however.
The preconsolidation surface is used to calculate the intensity of viscous flow and the direction of flow. The assumed associated flow rule (AFR) can be considered as a simplification compared to others [16, 67]. This surface can be surpassed by the stress path, and the stress portion protruding outside the preconsolidation surface is termed ‘overstress’. The rate of creep increases with the overstress. Similarly like [12, 13] and contrarily to [28], for example, the proposed model allows for viscous creep and also for the stress states inside the preconsolidation surface (OCR < 1) (i.e. a small creep is possible also for negative overstress). In both cases (OCR < 1 and OCR > 1), the creep rate changes very quickly, say with OCR−20, compared to the reference creep rate D r which corresponds roughly to OCR = 1. Outside the preconsolidation surface (OCR < 1) the creep rate increases, and inside (OCR > 1) it decreases compared to the reference rate. The evolution of the anisotropy is allowed only for volumetric compression (for negative rate of the void ratio, \(\dot{e}< 0),\) and its rate depends on the current stress and OCR. The description of the model (starting from the 1-d visco-hypoplastic version) and of its implicit time integration are presented. The model has been implemented in a FORTRAN 90 code according to the ABAQUS Footnote 1 user-material-subroutine conventions. The program has been verified by recalculation of element tests under various laboratory conditions, such as biaxial tests and FE calculations of punching tests.
2 Notation
The list of symbols used in this paper is presented in the Appendix. A fixed orthogonal Cartesian coordinate system with unit vectors \(\{{\bf e}_1,{\bf e}_2,{\bf e}_3 \}\) is used throughout the text. A repeated (dummy) index in a product indicates summation over this index taking values of 1, 2 and 3. A tensorial equation with one or two free indices can be seen as a system of three or nine scalar equations, respectively. We use the Kronecker’s symbol δ ij and the permutation symbol e ijk . Vectors and second-order tensors are distinguished by bold typeface, for example \({\bf N}, {\bf T}, {\bf v}.\) Fourth-order tensors are written in sans serif font (e.g. L ). The symbol · denotes multiplication with one dummy index (single contraction), for instance the scalar product of two vectors can be written as \({\bf a} \cdot {\bf b} = a_k b_k.\) Multiplication with two dummy indices (double contraction) is denoted with a colon, for example \({\bf A}:{\bf B} = \hbox{tr}({\bf A}\cdot{\bf B}^T) = A_{ij} B_{ij},\) wherein \(\hbox{tr}\;{\bf X} = X_{kk}\) reads trace of a tensor. The expression () ij is an operator extracting the component (i, j) from the tensorial expression in brackets, for example \(({\bf T}\cdot{\bf T})_{ij} = T_{ik} T_{kj}.\) The multiplication \(A_{ijklmn} B_{kl},\) with contraction over the middle indices, is abbreviated as \({\mathsf{A}} \hat{:} {\bf B}.\) We introduce the fourth-order identity tensor \(({\mathsf{J}})_{ijkl} = \delta_{ik}\delta_{jl}\) and its symmetrizing part \( {{I}}_{ijkl} = \frac{1}{2}(\delta_{ik} \delta_{jl} + \delta_{il} \delta_{jk}).\) The tensor \({\mathsf{I}}\) is singular (yields zero for every skew symmetric tensor), but for symmetric argument \({\bf X},\) I represents the identity operator, such that \({\bf X}={\mathsf{I}}:{\bf X}.\) A tensor raised to a power, like \({\bf T}^n,\) is understood as a sequence of n − 1 multiplications \({\bf T}\cdot{\bf T}\cdot \ldots {\bf T}.\) The brackets || || denote the Euclidean norm, i.e. \(||{\bf v}|| = \sqrt{v_i v_i} \) or \(|| {\bf T}|| =\sqrt{{\bf T}:{\bf T}}.\) The definition of Mc Cauley brackets reads \(<x>=(x+| x|)/2. \) The deviatoric part of a tensor is denoted by an asterisk, e.g. \({\bf T}^* = {\bf T} - \frac{1}{3} {{\bf 1}} \hbox{tr}{\bf T},\) wherein \(({\bf 1})_{ij} = \delta_{ij}\) holds. The Roscoe’s invariants for the axisymmetric case \(T_2 =T_3\) and \(D_2 =D_3\) are then defined as \(p = -{\bf 1}:{\bf T}/3 , q = -(T_1 - T_3) , D_v = - {\bf 1}:{\bf D}\) and \( D_q = -\frac{2}{3}(D_1 - D_3) .\) The general definitions \(q = \sqrt{\frac{3}{2}} ||{\bf T}^*|| \) and \(D_q = \sqrt{\frac{2}{3}}|| {\bf D}^*|| \) are equivalent to the ones from the axisymmetric case but may differ in sign. Dyadic multiplication is written without ⊗, e.g. \(({\bf a} {\bf b})_{ij} = a_i b_j\) or \(({\bf T} {\bf 1})_{ijkl} = T_{ij} \delta_{kl}.\) Proportionality of tensors is denoted by tilde, e.g. \({\bf T} \sim {\bf D}.\) The components of diagonal matrices (with zero off-diagonal components) are written as \( {\rm diag}[, , ],\) for example \({\bf 1} = {\rm diag}[1,1,1].\) The operator \((\sqcup)^{\rightarrow}=\sqcup/ || \sqcup || \) normalizes the expression \(\sqcup,\) for example \(\overset{\rightarrow}{{\bf D}} = {\bf D}/||{\bf D}|| .\) The hat symbol \(\hat\sqcup = \sqcup/\hbox{tr}\sqcup\) denotes the tensor divided by its trace, for example \(\hat{\bf T} = {\bf T}/\hbox{ tr }{\bf T}.\) The sign convention of general mechanics with tension positive is obeyed. The abbreviations \(\sqcup^{\prime} = \frac{\partial \sqcup}{\partial {\bf T}}\) and \(\sqcup^{\circ} = \frac{\partial \sqcup}{\partial \varvec{\Omega}}\) denote the derivatives of \(\sqcup\) with respect to tensorial state variables \({\bf T}\) and \(\varvec{\Omega},\) respectively. Objective Zaremba-Jaumann rates are denoted with a superimposed circle (rather than a dot), for example the Z-J rate of the Cauchy stress is \( {\mathring{\bf T}}. \)
3 One-dimensional visco-plasticity
In the 1-d oedometric model, the vertical stress is denoted by T (always negative) and the strain rate as \(D =\dot{e}/(1+e).\) Let us start from the equations commonly used in evaluation of oedometric tests for the frequently used special cases of
-
constant rate of strain (CRSN) first loading, i.e. with D = const
-
inviscid unloading or reloading
-
creep (T = const)
We have, respectively
where \( \epsilon \) is the vertical (= axial = volumetric) logarithmic strain (Hencky strain \( \epsilon=\ln(h/h_0)=\ln((1+e)/(1+e_0)) \) with h and h 0 denoting the initial and the current height of the sample, respectively). These relations need the following material constants: the [15] compression index λ, the swelling index κ and the coefficient of secondary compression ψ. The quantities \( \epsilon_0 \), T 0, t 0 are the reference values of strain, stress and time, respectively. The values T 0 and \( \epsilon_0 \) must be taken from the same “special case”, i.e. both must correspond to the primary compression line or to the same unloading-reloading branch.
This engineering description can be generalized to the following 1-d model [45]
where T B (>0) is an equivalent stress. The advantage here is that arbitrary combinations of the above processes (including relaxation) can be predicted. Note that the creep rate D vis is a function of stress T and void ratio e only. Imai [25] and Lerouiel [31] have shown the validity of this so-called hypothesis B in laboratory and in situ, respectively. The discussion between hypotheses A [36] and B [25, 31] will not be reiterated here. The material constants are the viscosity index I v and the previously mentioned coefficients λ and κ. The reference values are the creep rate (fluidity parameter) D r = 1%/h, and the reference states T B0 and e B0 on the primary compression line (or reference isotach [59]) corresponding to the creep rate D r (see Fig. 1) or to the CRSN compression with \(D={\lambda}D_r/(\lambda-\kappa).\)
The values ε0 and T 0 are needed only once to initialize the incremental process. The parameters of the engineering description can be shown [42] to be related to the parameters
of the 1-d model. These equations are obtained comparing Eqs. 1–3 with Eq. 4 for the special cases.
4 Isotropic visco-hypoplasticity
The aforementioned 1-d model was generalized [42] using hypoplasticity and OCR based on the isotropic preconsolidation surface of the modified Cam Clay Model (MCC). The decomposition of the strain rate into elastic and viscous portions \( {\bf D} = {\bf D}^e + {\bf D}^{{\rm vis}} \) was assumed. All irreversible deformations were treated collectively as a time-dependent variable \({\bf D}^{{\rm vis}}.\) The viscous strain rate \({\bf D}^{{\rm vis}} = {\bf D}^{{\rm vis}}({\bf T},e)\) was assumed to be a function of the Cauchy stress \({\bf T}\) and the void ratio e. The Norton’s power rule [46] for the intensity of viscous flow and the hypoplastic flow rule for its direction were adopted. The hypoplastic flow rule \( {\bf D}^{\rm vis} \sim {\bf m}({\bf T}) \) and the hypoelastic barotropic stiffness \({\mathsf{E}}\) were used as follows
A hyperelastic stiffness based upon complementary energy potentials [23] and similar to the model proposed by [43], is planned in a future version of this model as a replacement for the current \({\mathsf{E}}.\)
The definition of OCR has been generalized for non-isotropic stresses based on MCC preconsolidation surface. An analogous generalization based on the anisotropic preconsolidation surface will be presented in the next section, Eq. 39. The expression \(\text{OCR}^{-1/{I_v}},\) used as the function for intensity of the creep, can be shown to be analogous to the one proposed by Adachi and Oka [1, 2, 47]. Readers familiar with the old hypoplastic notation [21, 65] based on two tensorial functions
may find the following interrelations helpful:
wherein κ denotes the swelling coefficient [15] taken from \(\ln(p)-\ln(1+e)\) diagram, Fig. 1. In the above expressions for \({\mathsf{E}}\), the coefficients a and F M are defined as
with
and θ is the Lode’s angle given in Eq. 43. Note that the “hypoelastic” stiffness depends on the critical friction angle φ c .
The small-strain constitutive behaviour described with the so-called intergranular strain [44] is left out in the current anisotropic version for brevity. A future version of the model should consider the small strain stiffness effects [9,14, 26, 33, 55, 56, 42, 44]. The isotropic visco-hypoplasticity is extensively discussed in [42], and it has been used in numerous FE applications. Here, we concentrate on the anisotropic preconsolidation surface and on the implicit time integration strategy only.
5 Anisotropic model
From numerical tests [57], it can be concluded that the isotropic model [42] requires an anisotropic extension, especially for a better fit of the biaxial test results on K 0 consolidated samples [63]. This can be achieved using anisotropic functions for OCR and for the unit tensor m defining the flow rule. A well-known anisotropic effect of naturally consolidated soils manifests itself in the undrained shear tests. The undrained shear strength c u turns out to be significantly greater for triaxial compression than for extension, and this effect cannot be explained by the different inclinations of the critical state lines \( M_C = \frac{6 \sin\varphi_c}{3-\sin\varphi_c}\) and \(M_E =- \frac{6 \sin\varphi_c}{3+\sin\varphi_c},\) respectively.
The main constitutive equation of the new model takes the form similar to Eq. 7
Apart from the anisotropic functions for OCR and for the flow rule m, Eq. 13 introduces a small-term \(C_1 {\mathsf{E}}: {\bf m} || {\bf D} || \) with a material constant C 1 ≈ 0.1 or less. Upon 1-d strain cycles (so called in-phase cycles), the hypoelasticFootnote 2 linear term \({\mathsf{E}}:{\bf D}\) causes no accumulation of stress. The term \(C_1 {\mathsf{E}}: {\bf m} || {\bf D}|| \) causes accumulation dependent on m and on the length of the strain path \(\int || {\bf D}|| {\rm d} t.\) One may call it pseudo-relaxation, but since
resembles the hypoplastic nonlinear term we prefer to call \( {\bf D}^{\rm Hp} \) the hypoplastic strain and \( C_1 {\mathsf{E}}: {\bf m} || {\bf D} || \) the hypoplastic relaxation. Note that the rates \({\bf D}^{\rm vis}\) and \({\bf D}^{\rm Hp}\) are parallel, and both are functions of the current state described by stress T and the equivalent stress \({\bf T}^B\) (see the next subsection). The essential difference between \({\bf D}^{\rm vis}\) and \({\bf D}^{\rm Hp}\) is that the hypoplastic strain is driven by the magnitude of the deformation, whereas the viscous strain is driven by time t.
5.1 One-dimensional version of the novel model
The effect of the hypoplastic strain \({\bf D}^{\rm Hp}\) can be examined in one-dimensional case using \(D^{\rm Hp} = -C_1|D| .\) The anisotropy of the yield surface and of the flow are not relevant, of course.
From
one may obtain the following special cases:
-
During pure creep \(\dot{T} \equiv 0\) from the first equation of Eq. 16 follows \(D+C_1 |D| =D^{\rm vis}\) and since C 1 ≪ 1 holds, we conclude that D and D vis have the same sign (both are negative = compressive) and therefore |D| = −D. We obtain, therefore, a slightly larger value of the creep rate
$$ D = \frac{1}{{1-C_1}} D^{\rm vis} $$(17)compared to \(D =D^{\rm vis}\) in the original model Eq. 4.
-
The pure relaxation is obtained substituting D ≡ 0 into the first equation of Eq. 16. We obtain
$$ \dot{T} = - \frac{-T}{\kappa} D^{{\rm vis}} > 0 $$(18)which is identical to the relaxation rate from the original model Eq. 4.
-
Let us assume a constant compressive creep rate \( D^{\rm vis} = {\rm const}<0.\) We examine the implications of \(\dot{D}^{\rm vis} = 0.\) Judging by the second equation of Eq. 16 (for T ≠ 0 and T B ≠ 0, of course), the constant rate of creep requires
$$ \left(\frac{T}{T_B} \right)^{{\bf{\cdot}}} = 0\quad{\rm or}\quad\dot{T}/T = \dot{T}_B/T_B $$(19)In the latter form, we may substitute \(\dot{T}_B/T_B = -D/\lambda \) from the last equation of Eq. 16 and \(-\kappa \dot{T}/T = D - D^{\rm vis} + C_1 | D| \) from the first equation of Eq. 16. This leads to
$$ -\frac{1}{\kappa} \left[ D - D^{\rm vis} + C_1 | D| \right] = -D /\lambda $$(20)Assumption D > 0 would result in \( D^{\rm vis}/D =1-{\kappa /\lambda}+C_1\) which cannot be satisfied for \( D^{\rm vis}<0\) because \(1-{\kappa}/{\lambda}+C_1>0\) holds. Therefore, D must be negative and hence
$$ D = D^{\rm vis} \left[ 1 - \kappa /\lambda - C_1\right]^{-1} = {\hbox {const}} < 0 $$(21)Equation (21) shows that our initial assumption about the viscous strain \( D^{\rm vis} ={\rm const}<0\) implies a compression with a constant strain rate deformation. The rate of deformation is slightly different from \(D =D^{\rm vis} \lambda/(\lambda-\kappa) \) obtained analogously [42] from Eq. 4. The relation between the stress rate and the strain rate for such case is obtained by elimination of D vis in the first equation of Eq. 16 using Eq. 21.
$$ \dot{T} = \frac{-T}{\kappa}(D + C_1 |D| - D^{\rm vis})\quad{\rm with}\quad {D<0}$$(22)$$ \dot{T} = \frac{-T}{\kappa}(1- C_1 - \left[ 1 - \kappa /\lambda - C_1\right]) D $$(23)$$ \dot{T} = \frac{-T}{\lambda}D $$(24)After time integration, this relation can be represented by a straight line parallel to the reference isotach in the compression diagram in Fig. 1.
5.2 Anisotropic preconsolidation surface and the flow rule
The anisotropy of visco-hypoplastic model follows from the equation of the preconsolidation surface. In the new model, the preconsolidation surface has the form of an inclined ellipse in the p-q space, Fig. 2 or an ellipsoid in the principal stress space Fig. 4. The tensorial equation of the preconsolidation surface has the form
The equivalent pressure of the isotropic MCC model is replaced by the preloading stress
see Fig. 2.
Note that a simple rotation of the Cam clay preconsolidation ellipse would not satisfy the isochoric flow condition for critical state [27].
The size of the ellipse is described by the scalar state variable p B , and the obliquity is described by the deviatoric structural tensor \(\varvec{\Omega},\) similar to the model introduced by Dafalias [18]. Keeping \(\varvec{\Omega}={\bf 0},\) we enforce isotropic preconsolidation because the main diameter of the ellipse remains on the hydrostatic axis. The slope of the critical surface in the p-q diagram is described by M = M(θ) which depends on the critical friction angle and is a function of the Lode’s angle \(\theta({\bf T})\) of stress discussed further in this section (in the Drucker–Prager model M would be a material constant). The condition \(q^2 =M^2 p^2\) of critical state can be expressed in general case as
For triaxial compression, M(θ) reaches the maximum \( M_C = \frac{6 \sin\varphi_c}{3-\sin\varphi_c}.\) For triaxial extension, M(θ) reaches the minimum \(M_E = -\frac{6 \sin\varphi_c} {3+\sin\varphi_c}.\) Additionally, we introduce M Ω which denotes the critical slope for θ dictated by the current \(\varvec{\Omega}.\) In general, \(M\ne{M_{\varvec{\Omega}}}.\) The critical state is assumed to be isotropic, independent of stress T and of deformation history \(\varvec{\Omega},\) contrarily to [39, 67].
Equation (25) of the preconsolidation surface has been derived from the general equation of an ellipse
in the space of normalized Roscoe components \(\bar{p} = p/p_B\) and \(\bar{q} = q / (M p_B).\) The following requirements have been imposed:
meaning that the ellipse should pass through the points \((\bar{p}, \bar{q}) = (0,0)\) and (1, ω) having the outer normal parallel to the \(\bar{p}\hbox{-axis}\) there. Moreover, we require
meaning that on crossing with the critical state lines \(\bar{p}= \pm \bar{q}\) the ellipse \(f(\bar{p}, -\bar{p}) = 0\) should have the outer normal parallel to the \(\bar{q}\hbox{-axis}.\) These features of the preconsolidation surface are not always satisfied by models in the literature, for instance [27, 32]. All these conditions lead to the preconsolidation surface
wherein the second equation has been obtained using the definitions of \(\bar{p}\) and \(\bar{q}\) and multiplying f with (p B M)2. The tensorial form Eq. 25 results from the definition of the Roscoe’s deviatoric invariant: \(q^2 = \frac{3}{2} {\bf T}^* : {\bf T}^*, \omega^2 = \frac{3}{2} \varvec{\Omega} : \varvec{\Omega} \) and \(q \omega= \frac{3}{2} {\bf T}^* : \varvec{\Omega}\).
Analogous conditions imposed onto the preconsolidation surface \( F({\bf T} ,\varvec{\Omega},p_B)\) given in Eq. 25 and on its outer normal
are satisfied:
-
\( F({\bf 0},\varvec{\Omega},p_B) = 0 \)
-
\( F^{\prime}({\bf 0},\varvec{\Omega},p_B) \sim {\bf 1} ,\) note that \(\partial F/ \partial M = 0\) in this case
-
\( F({\bf T}^B,\varvec{\Omega},p_B) = 0, \) note that \(M={M_{\varvec{\Omega}}}\) for \({\bf T} = {\bf T}^B.\)
-
\( F^{\prime}({\bf T}^B,\varvec{\Omega},p_B) \sim {\bf 1},\) note that ∂F/∂M = 0 in this case
-
For intersection line of surfaces \(F_{\rm crit}({\bf T}) = 0 \) and \( F({\bf T},\varvec{\Omega},p_B) = 0 \) given by Eqs. 25 and 27, respectively, holds the isochoric flow rule
$$ {\bf 1}: F^{\prime}({\bf T}^B,\varvec{\Omega},p_B) = 0 $$(38)
One can easily show that the expression in square brackets in Eq. 37 multiplied with p is \(\left[ \ldots \right] p = F - F_{\rm crit},\) so the volumetric portion of the outer normal F′ must indeed vanish if F and F crit simultaneously do.
We intend to replace the hyperellipse Eq. 25 by the alternative formulation Eq. 51 in future. This function not only guarantees to satisfy the isochoric flow rule in the critical state exactly but also keeps all principal stresses negative.
Similar strain-induced anisotropic yield surfaces have been used in numerous elasto-plastic soil models (e.g. [19, 30, 64]). Contrary to the elastoplastic yield surfaces, however, the surface Eq. 25 can be surpassed by the stress path.
The preconsolidation surface Eq. 25 can be shown to be orthotropic with the orthotropy axis coinciding with the principal directions of \(\varvec{\Omega}.\) If required by experimental data, the mathematical form of Eq. 25 can be extended in future according to representation theorems. An example of such systematic approach for transversally isotropic soils is given in [11].
The overconsolidation ratio OCR describes the “distance” from the current stress \({\bf T}\) to the preconsolidation surface. Stresses inside the preconsolidation surface correspond to F < 0 and OCR > 1. Stresses outside correspond to F > 0 and OCR < 1. In the case F = 0 or equivalently OCR = 1, stresses lie on the preconsolidation surface, and the intensity of creep \(|| {\bf D}^{{\rm vis}}|| \) takes referential value \(|| {\bf D}^{{\rm vis}}|| = D_r\) which is evident from Eq. 14 for OCR=1. The corresponding creep rate is \(|| {\bf D} || = D_r/(1-C_1) \approx D_r.\)
The rate of the viscous strain rate \({\bf D}^{{\rm vis}} \) depends strongly on the distance between the current stress and the preconsolidation surface. The intensity of the viscous strain rate \({\bf D}^{{\rm vis}} \) becomes very high outside this surface and very low inside it. The generalized definition of the overconsolidation ratio is
in which p B+ is found as the parameter analogous to p B describing an ellipse having the same inclination \(\varvec{\Omega}\) as the preconsolidation surface, but passing through the current stress T rather than through the equivalent stress \({\bf T}^B\) which corresponds to the current void ratio. In other words, we determine p B+ from
using the current values \({\bf T}^*,\) p and \(\varvec{\Omega}\) (see Figs. 2, 3).
The evolution equation of \({\bf T}^B\) will be described via p B and \( \varvec{\Omega} = {\bf T}^{*B}/p^B. \) A representation of the preconsolidation surface and \(\varvec{\Omega}\) in the principal stresses space is shown in Figs. 4 and 5. In general, \(\varvec{\Omega}\) and T are not coaxial.
View of Fig. 4 from a point on the isotropic axis
The critical state surface is assumed to be described by the Matsuoka-Nakai [34] condition
where φ c is the critical friction angle. In order to make the critical stress obliquity M = q/p (with \(p=-\frac{1}{3} \hbox{tr}\,{\bf T}\) and \(q=\sqrt{\frac{3}{2}}|| {\bf T}^*||)\) consistent with the Matsuoka–Nakai criterion Eq. 41, M must depend on the Lode’s angle θ determined from
and \( \overset{\rightarrow}{{\bf T}^*}= ({{\bf T}^*})^{{\rightarrow}}. \) Unfortunately, the relation M(θ) is not straightforward. In some literature, (as in [29]), its determination is delegated to the numerical implementation. This may slow down the calculation. Given the Lode’s angle θ, the condition q = M p can be shown to be equivalent to Eq. 41 if M is the smaller positive root of the following equation
This cubic equation may be solved for M analytically. For the special case cos(3θ) = 0 or θ = 30°, the Eq. 44 becomes quadratic, and we take the positive root
We take this value also for \({\bf T} \sim {\bf 1}.\) Otherwise, the smaller positive root is
wherein H() is the Heaviside function and
The analytical expression Eq. 47 is relatively complicated, and M changes slowly with T. Therefore, in the Newton iteration procedures that follow, we will assume
The cost of computation of M′ is expected to be high compared to some marginal increase in the convergence rates.
The flow rule m needs to be defined for an arbitrary stress T and not just for stresses on the yield surface as it is the case in elastoplasticity. For this purpose, we propose the following procedure. First, the preconsolidation pressure p B+ is found from \(F({\bf T}, \varvec{\Omega}, p_{B+}) = 0\) for the current T and \(\varvec{\Omega}.\) Next, an auxiliary surface (dashed ellipse in Fig. 2) \(F_{+}({\bf T})= F({\bf T}, \varvec{\Omega}, p_{B+}) = 0\) is constructed. Finally, the direction of flow follows from
wherein p B+ and \(\varvec{\Omega}\) are constant, and the analytical expression for the Fréchet derivative \(\overset{\rightarrow}{F_{+}^{\prime}}\) is given in Eq. 72 in Sect. 6.2. In other words, we construct a hypothetical preconsolidation surface (dashed ellipse in Fig. 2) passing through the current stress T and affine to the current preconsolidation surface (solid-line ellipse in Fig. 2). Then, we calculate m as a unit outer normal to this surface (the associated flow rule with respect to \(F_{+}({\bf T}) = 0).\)
Small deviations from AFR are allowed for [40], and such a non-associated flow rule (NAFR) may be necessary in a future version of the model in order to satisfy the condition of isochoric flow direction in the critical state.
As an unpleasant consequence of the consistency of the critical stress ratio M(θ) with the Matsuoka–Nakai criterion, the preconsolidation surface becomes slightly concave near the isotropic axis, see Fig. 4 and tensile stresses (\(\hbox{tr}\,{\bf T} <0\) but one of the principal stresses may become positive) can be reached at very low pressures.
In order to remove these shortcomings, an alternative preconsolidation surface
with
and ϕmax > 9 is currently being studied (e.g. see Fig. 6). Such surfaces are smooth, have no concavity and are bounded to the compressive stresses.
Preconsolidation surface Eq. 52 based on the Matsuoka-Nakai function with ϕ(p)
5.3 Evolution of state variables \(\varvec{\Omega}\) and p B
The evolution equations of the preconsolidation stress \({\bf T}^B\) are provided separately for p B and for \(\varvec{\Omega}.\) The evolution of the structural deviatoric tensor \(\overset{\circ}{\varvec{\Omega}}\) is proposed to be
We do not follow the idea [20, 41] that relates the evolution of the anisotropy tensor \(\varvec{\Omega}\) to the plastic strain deformation alone, because it implies evolution of \(\varvec{\Omega}\) for critical state flow. The length of such process cannot influence the structure. In our opinion, the evolution of \(\varvec{\Omega}\) is possible upon contractant strain paths only, i.e. only for \(\hbox{tr}\,{\bf D} < 0,\) and for subcritical stress states (\(\hbox{tr}\,{\bf m} < 0).\) The rate of this evolution increases rapidly with decreasing OCR. Since I v ≈ 0.05, the evolution of \(\varvec{\Omega}\) is practically absent at OCR > 1.5. In this case, the multiplier \({\text{OCR}}^{-1/{I_v}}\,{\approx}\,3 {\cdot}10^{-4} \) makes \({\mathring{\varvec \Omega}}\) almost negligible. The direction of \({\mathring{\varvec \Omega}}\) is dictated by the difference between the current stress deviator \({\bf T}^*\) and \(\varvec{\Omega}\) (both appropriately scaled). The scalar multipliers at \(\varvec{\Omega}\) and \({\bf T}^*\) are chosen to reproduce the asymptotic behaviour upon radial compression tests, i.e. those with \(\hbox{tr}\,{\bf D}<0\) and \(\hat{\bf T}^* = {\text{const}}.\) The asymptotic value of the structural tensor is in such case \( \varvec{\Omega} = -(\frac{3C_{3}}{M}\hat{\bf T}^*).\) The material parameter C 3 can be easily found making the direction of flow \({\bf m}\) compatible with the uniaxial (oedometric) compression \({\bf T}_{K_0} \sim \rm{diag}[ -1,-K_0,-K_0 ]\) (with K 0 = 1 − sinφ), Fig. 7. The direction of flow should be uniaxial, i.e. \({\bf m} = \rm{diag}[-1,0,0]\) (at least in the asymptotic case).
Hence, C 3 can be expressed in terms of K 0 and \(M_C={6 \sin \varphi_c}/({3-\sin \varphi_c})\) as follows
The rate of evolution of \(\varvec{\Omega}\) can be controlled by the material constant C 2. This constant can be calibrated from triaxial results that follow a long proportional compression path with \(\hat{\bf T} = {\text {const}}\) and \(\hbox{tr}\,{\bf D}< 0,\) say following a K 0-line. Next, we unload the sample until the stress path reaches the hydrostatic axis (Fig. 8). Finally, we load the sample again in such way that the stress path follows the hydrostatic axis. Upon this hydrostatic compression, we record the deviatoric strain rate observing how much total volumetric strain is necessary for \(\varvec{\Omega}\) to take a new asymptotic position. The rotation of \(\varvec{\Omega}\) can be demonstrated experimentally as a rotation of m corresponding to the direction of irreversible strain. Such rotation has been observed [3] keeping the stress obliquity \(\hat{\bf T} = \frac{1}{3}{\bf 1}\) constant, Fig. 8.
The rate of rotation \({\mathring{\varvec \Omega}}\) of the preconsolidation surface can be indirectly measured via rotation of the flow rule m upon an isotropic stress path (Z. Mróz, personal communication, [3])
In a biaxial apparatus, the calibration of the parameter C 2 can be done using a similar principle. Once the sample has reached a proportional stress ratio, say a K 0 state, a new proportional compression strain path, with a different strain ratio, is applied until a new stress ratio is obtained (at least asymptotically). Such an experiment was carried out by [63] and is shown in Fig. 9. In absence of anisotropic effects (no rotation of preconsolidation surface, i.e. \(\varvec{\Omega}= {\bf 0}={\text{const}}),\) i.e for C 2 = 0, stress paths for proportional compression are poorly reproduced.
The preconsolidation pressure p B is a one-to-one function of the void ratio e and it satisfies the equation of the isotropic reference isotach
This equation describes the virgin isotropic compression line obtained at the referential rate
Any state (e, p) upon this referential first compression process can be chosen to be the reference state (e 0, p B0). Equation (55) is parallel to the oedometric first compression line [15] commonly used in elastoplastic models. The rate form
follows directly from time differentiation of Eq. 55 using \(\dot{e}= (1+e)\hbox{tr}\,{\bf D}.\) Equation (57) is analogous to the well-known volumetric hardening; however, the total volumetric strain rate \(\hbox{tr}\,{\bf D}\) is used instead of the plastic one \(\hbox{tr}\,{\bf D}^{\rm pl}.\) Therefore, contrary to elasto-plastic formulations, our \(\dot{p}_B\) becomes negative during isotropic unloading, Fig. 10. In elasto-plastic models, such unloading would be considered as an “elastic” process, and the preconsolidation would remain constant.
The evolution of the void ratio \(e\) is calculated from \(\dot{e}= (1+e)\hbox{tr}\,{\bf D}.\) Note, however, that we treat the preconsolidation pressure p B , and not e, as a primary state variable, although they are interrelated one-to-one via Eq. 55. The unique dependence p B (e) postulated in Eq. 55 means, in particular, that radial compressive stress paths with constant obliquity q/p and carried out at the same strain rate, say \(|| {\bf D}|| = D_r\) generate identical preconsolidation pressure p B (e). In comparison with the isotropic model, the compression lines in \(\ln(p)-\ln(1+e)\) diagram obtained from the anisotropic model for different stress ratios q/p should be closer to each other, Fig. 11.
Left: Evolution of the anisotropy \(\varvec{\Omega}\) during natural (uniaxial) consolidation. Isotropic state \(\varvec{\Omega}= {\bf 0}\) is assumed as the initial condition. The evolution of the \(\varvec{\Omega}\) can be seen via the preconsolidation stress \({\bf T}^B.\) Right: Reduction in the preconsolidation pressure p B upon unloading (\(\dot{e}>0)\) is allowed for in hypoplasticity. In elastoplastic models, reduction in the preconsolidation pressure is possible only during plastic dilatant flow
Monotonic compression lines with constant strain rate \(|| {\bf D} || = D_r\) and constant stress ratios q/p. The unique p B (e) relationship does not imply that the compression lines \(\ln p-\ln(1+e)\) become unique in the anisotropic model (right), although their distance is closer compared to the isotropic model (left)
5.4 Discussion of the model
It is well-known that for a given isochoric direction of deformation the strain rate affects the undrained strength of clayey soils [understood as \(c_u = \frac{1}{2}(T_{\rm max} - T_{\rm min})],\) but it does not affect the maximum effective stress ratio (understood as \(T_{\rm max}/T_{\rm min}).\) In undrained triaxial tests, one can observe this effect plotting the stress paths in the p-q diagram, Fig. 12. This figure illustrates two deformation paths a and b carried out in the same direction \({\bf D}_a \sim {\bf D}_b,\) but at different rates \(|| {\bf D}_a || > || {\bf D}_b||.\) Both strain rates are undrained, \( \hbox{tr}\,{\bf D}_a = \hbox{tr}\,{\bf D}_b = 0,\) and both are kept unchanged during the deformation process.
The asymptotic stationary stress state corresponds to \( {\mathring{\bf T}} = {\bf 0}.\) In this subsection, we demonstrate that both the isotropic and the anisotropic models can reproduce this behaviour and that the additional hypoplastic term \(C_1 {\bf m} || {\bf D} || \) from Eqs. 13 and 14 does not spoil it.
In the isotropic model Eq. 7 without \({\bf D}^{\rm Hp},\) the stationarity condition \( {\mathring{\bf T}} = {\bf 0} \) implies \({\bf D} = D_r {\bf m} {\text{OCR}} ^{-1/{I_v}}\) for both strain rates, and since these rates are proportional, the ensuing asymptotic states \({\bf T}_a^{\rm asy}\) and \({\bf T}_b^{\rm asy}\) must correspond to the same flow direction \({\bf m},\) but to different values of the overconsolidation ratios OCR a < OCR b (\({\bf D}_a\) is faster than \({\bf D}_b).\) Since \({\bf m}({\bf T})\) is a homogeneous stress function, i.e. \({\bf m}(\chi {\bf T}) =\chi {\bf m}({\bf T})\) for any χ > 0, the asymptotic states must be proportional \({\bf T}_a^{\rm asy} \sim {\bf T}_b^{\rm asy}.\) For a given (and constant) preconsolidation pressure common for both deformation rates inequality OCR a < OCR b implies \(|| {\bf T}_a^{\rm asy} || > || {\bf T}_b^{\rm asy} ||,\) and hence the deviatoric portion of \({\bf T}_a^{\rm asy}\) must be larger too.
The term \(C_1 {\bf m} || {\bf D} || \) in Eq. 13 does not spoil the proportionality of the asymptotic stresses discussed earlier for the isotropic model. Once again, we compare the asymptotic stresses of the same two deformation paths assuming a common initial stress and a common preconsolidation \({\bf T}^B.\) Note that \({\bf T}^B\) remains constant during any isochoric deformation. Indeed, according to Eqs. 53 and 57, neither \(\varvec{\Omega}\) nor p B may change while \(\hbox{tr}\,{\bf D} = 0.\)
In the anisotropic model Eq. 13 with \({\bf D}^{\rm Hp} \neq {\bf 0},\) the stationarity condition \( {\mathring{\bf T}} = {\bf 0}\) leads to
from which we may conclude that the required common flow rule is \({\bf m} = \overset{\rightarrow}{\bf D}_a = \overset{\rightarrow}{{\bf D}}_b.\) Recall that \({\bf D}_a\) and \({\bf D}_b\) are proportional. Hence, using the homogeneity of the flow rule (for a given and constant \({\bf T}_B)\) with respect to stress, we infer that the asymptotic stresses are proportional \({\bf T}_a^{\rm asy} \sim {\bf T}_b^{\rm asy}.\)
The asymptotic stresses \({\bf T}_a^{\rm asy}\) and \({\bf T}_b^{\rm asy}\) lie on the critical surface. Again, due to \({\text{OCR}}_a<{\text{OCR}}_b\) the stress magnitudes are different, \(|| {\bf T}_a^{\rm asy} || > || {\bf T}_b^{\rm asy} ||.\) Larger strain rates imply larger stress magnitudes and therefore larger c u , Fig. 13.
In agreement with the critical state soil mechanics, the critical state condition corresponds to \(\hbox{tr}\,{\bf D} = \hbox{tr}\,{\bf m} = 0.\) For a given preconsolidation stress \({\bf T}^B\) and for strain rates \(|| {\bf D}|| = {\text{const}}, \) it describes a unique surface in the stress space. No unique critical void ratio e(p) is postulated in this model, however. This is so due to the anisotropy and the rate dependence. The critical stress ratios (q/p)crit correspond to the Matsuoka-Nakai surface and are not influenced by \({\bf T}^B.\) In this sense, the critical stress ratio can be regarded as isotropic. The preconsolidation surface and the flow direction depend strongly on \({\bf T}^B,\) and hence they are anisotropic. Since \({\bf T}^B\) may evolve we may speak of induced anisotropy.
After a natural oedometric preconsolidation, the undrained strength c uE for triaxial extension can be even twice smaller than the strength c uC upon triaxial compression. In the isotropic models (with \(\varvec{\Omega}={\bf 0}),\) the relation (at the same void ratio e = const and at the same deformation rate \(|| {\bf D}||) \) between these strengths would be \(c_{uE}/c_{uC} = M_E/M_C = {\text{const}}.\)
Starting from the normally consolidated initial K 0-stress state (preceded by an oedometric consolidation), the deformation needed to reach the critical state upon an undrained triaxial extension is substantially larger than upon the undrained triaxial compression. In the simulation presented in Figs. 14 and 15, the deviatoric strain required to reach the critical state under triaxial extension is about 3 times larger than the one upon triaxial compression. This feature can be reproduced by the model in accordance with experiments, [63]. The observation that the active earth pressure is mobilized much faster than the passive one may be expected to be correctly reproduced in FE simulations.
Undrained stress–strain curves calculated with anisotropic visco-hypoplasticity upon triaxial compression (segment K-A) and extension (segment K-P) preceded by K 0-consolidation. The respective stress paths are shown in Fig. 14
Small closed stress cycles generate an additional accumulation of the deformation independently of creep. This effect is considered using C 1 > 0 and was absent in the previous model as demonstrated in Fig. 16.
6 Implicit integration of finite increments
The constitutive models supposed to be used in FE programs deal with finite increments of stress and strain rather than their rates. Implicit integration (Euler backward) of anisotropic soil models has also been recommended for elastoplasticity [4], using the close-projection method. Let us consider a time increment from t n to t n+1. Given the state \( \{ {\bf T}_{n}, \varvec{\Omega}_{n}, p_{B n} \} \) at the beginning of the increment, the strain increment \(\Updelta \varvec{\epsilon}\) and the time increment \({\Updelta}t=t_{n+1}-t_n, \) we must determine the values \({\bf T}_{n+1},\) \(\varvec{\Omega}_{n+1}\) and p B n+1 at the end of the increment (including the nonlinearities within this single increment).
The main difficulty in the incremental formulation of the constitutive model compared to the rate form Eqs. 7, 53 and 57 follows from the fact that the stiffness \( {\mathsf{E}},\) the preconsolidation pressure p B , the anisotropic tensor \(\varvec{\Omega}\) and the viscous strain rate \({\bf D}^{\rm vis}\) used in Eqs. 7, 53 and 57 as “given” do not remain constant upon the increment. According to the definitions Eqs. 39, 50 and 10, they change with stress, and this change of stress is unknown itself. For reasons of numerical stability of the time integration, the changes in the state variables upon the increment should be taken into account. From this point of view, it is safe to take the final values of state variables, i.e. the ones at the end of increment (further denoted with the index \(\sqcup_{n+1})\) rather than the known ones \(\sqcup_{n}\) from the beginning of the increment. The advantage of such implicit (Euler backward) time integration over the explicit (Euler forward) integration was already pointed out by Zienkiewicz [68] and Cormeau [17], and can be here demonstrated comparing two implementations of the 1-d viscoplastic model. We combine Eq. 4 into a single expression for stress increment.
The strain rate D is given as \(\dot{e}/(1+e).\) All rates are written as increments. In the explicit time integration, one uses the stiffness and the viscous rate at the beginning of the increment. Therefore, all quantities appearing on the right-hand side are known (they pertain to time t), and the calculation of T n+1 can be performed directly. In the analogous equation with implicit integration
the unknown stress T n+1 appears on both sides of equation. In some cases such equations can be resolved for T n+1 analytically, but more often the solution has to be found iteratively. Equation (59) leads to instabilities even at relatively small void ratio increments Δe = −0.003, see Fig. 17, whereas Eq. 60 works also with larger increments Δe = −0.01. Note that implicit integration improves stability but not the accuracy of the integration. Therefore, excessively large increments are not recommended. The ramp function in the creep rate with McCauley brackets may cause numerical difficulties, cf. discussion between integration algorithms for Perzyna-type and Duvuant-Lions-type creep models, [53].
Numerical results of oedometric compression calculated with λ = 0.1, κ = 0.01, T B0 = 100, e B0 = 1, D r = −0.01, I v = 0.05 starting from initial conditions T = −50 and e = 1 (corresponds to OCR = 2). The loading (compression) is applied in large increments Δe = −0.01 (implicit) or in small increments Δe = −0.003 (explicit) with Δt = 1 per increment. Despite smaller increments, the explicit integration leads to instabilities
In the 3-d model, analogously to Eq. 60, the final values of state variables should satisfy the following implicit evolution equations:
where \(\sqcup_{n+1}\) denotes the (unknown) value of \(\sqcup\) at the end of the increment. These equations are nonlinear with respect to the final values of state variables, and we have to solve these equations iteratively. Note that the strain increment is given and remains constant in this iteration.
6.1 Implicit solution for a given stain increment \(\Updelta \varvec{\epsilon} \)
The essential issue in incremental calculation of viscoplastic equations is the nonlinearity within a single increment.
The values of \({\bf T}_{n+1}, \varvec{\Omega}_{n+1}\) and p B n+1 appear on both sides of Eqs. (61–63) being hidden in the expressions \( \mathsf{E},\) m and OCR on the right-hand side. These equations will need to be solved for the unknown tensors \({\bf T}_{n+1}\) and \(\varvec{\Omega}_{n+1}.\) The third equation is also implicit, but it is sufficiently simple (linear with respect to p B n+1) to be directly solved:
We start the process of iterative search for \({\bf T}_{n+1}\) and \(\varvec{\Omega}_{n+1}\) by choosing the elastic predictor as an initial guess. In other words, we choose \({\bf T}_{n+1} = {\bf T}_n +\Updelta {\bf T}^{\rm el} \) and \( \varvec{\Omega}_{n+1} = \varvec{\Omega}_{n} \) with \(\Updelta {\bf T}^{\rm el} = \mathsf{ E}_{n} : \Updelta \varvec{\epsilon}.\) Next, this initial guess will be improved adding corrections \({\bf c}_T\) and \({\bf c}_\Omega\) to \({\bf T}_{n+1}\) and \(\varvec{\Omega}_{n+1}, \) respectively. The corrections are obtained keeping the strain increment \(\Updelta \varvec{\epsilon}\) unchanged and minimizing the errors \({\bf r}_T, {\bf r}_\Omega\) resulting from usage of approximate values of \({\bf T}_{n+1}\) and \(\varvec{\Omega}_{n+1}\) in the evolution equations upon the increment. From now on, we drop the n+1 index, so that T and \(\varvec{\Omega}\) denote the most recent approximations of \({\bf T}_{n+1}\) and \(\varvec{\Omega}_{n+1}.\) The following 12 independent components of errorsFootnote 3 (due to symmetry \(\Omega_{ij} = \Omega_{ji}\) and \(T_{ij} =T_{ji})\) may appear:
Formally, we may see these errors as functions of T and \(\varvec{\Omega}\) and our intention is that these errors vanish after corrections, i.e.
In the Newtonian iterative solution, one approximates the above equations using the first terms of Taylor expansion
wherein dash and circle denote the Fréchet derivatives with respect to T and \(\varvec{\Omega},\) see the next subsection. All derivatives are calculated using the most recent updated variables \({\bf T}, \varvec{\Omega}\) and with the final value of p B . For the Newton iteration process we may construct the system of equations
Having solved this system numerically for \({\bf c}_T\) and \({\bf c}_{\Omega},\) we add these corrections to the respective total values T, \(\varvec{\Omega}.\)
The procedure requires the inversion of an unsymmetric 12 × 12 matrix containing the derivatives of the discrepancies. This iteration process continues until the norms of \({\bf r}_T\) and \( {\bf r}_{\Omega}\) are lower than some tolerance values.
An analogous iteration at constant \(\Updelta \varvec{\epsilon}\) is known as the Return Mapping Iteration (RMI) in elasto-plastic models. It should not be mixed up with the equilibrium iteration (EI) in which the strain increment is varied until the equilibrium of stresses with external loads is reached.
6.2 Fréchet derivatives
The calculation of derivatives that appear in Eq. 68 can be tedious, and therefore we found them using an algebra program Mathematica [66] with the package nova.m developed by the first authorFootnote 4. In the RMI process, we need various tensorial derivatives and the chain rules thereof. Starting with the stiffness tensor \( \mathsf{E}\), we calculate its stress derivative as
with
We assume \(F_M^{\prime}\approx {\bf 0}\) for simplicity. The stiffness \( \mathsf{E}\) is independent of \(\varvec{\Omega}\) and hence \(\mathsf{E}^{\circ} = {\bf 0}\) holds. The flow rule m is obtained for the updated stress T from \(F_+({\bf T}, p_{B+}, \varvec{\Omega}) = 0\) keeping the updated \( \varvec{\Omega}\) constant, i.e.
with
The total change in m with stress should take into account the variability of p B+ with stress which can be calculated from
as
The correct stress derivative of m written as a function \({\bf m}({\bf T}, \varvec{\Omega}, p_{B+})\) is therefore found from the chain rule
wherein
For the calculation of m′, we also need
Analogously, the partial derivative of the flow direction m written as a function \({\bf m}({\bf T}, \varvec{\Omega}, p_{B+})\) with respect to \(\varvec{\Omega}\) should take into account the variation of p B+ with respect to \(\varvec{\Omega},\) i.e.
wherein
and
The derivatives of the overconsolidation ratio \(\hbox{OCR} =p_B/p_{B+}\) with respect to T and \(\varvec{\Omega}\) are
It is convenient to define the scalar A that describes the intensity of hypoplastic and the viscous strain rate:
Its derivatives, with respect to T and \( \varvec{\Omega}\) are
Using the above partial derivatives the error in the stress equation can be expressed as
and its derivatives with respect to T and \( \varvec{\Omega}\) are
The error in the evolution equation of \(\varvec{\Omega}\) is
and its derivatives with respect to \({\bf T}, \varvec{\Omega}\) and p B are
The errors \({\bf r}_T, {\bf r}_{\Omega}\) from Eqs. 85 and 88 as well as their derivatives \( {\bf r}_T', {\bf r}_T^{\circ}, {\bf r}_{\Omega}',{\bf r}_{\Omega}^{\circ} \) from Eqs. 86, 87, 89 and Eq. 90 enter Eq. 68. This system can be converted to the matrix form
from which the corrections \({\bf c}_T\) and \({\bf c}_\Omega\) can be calculated. Derivatives \( {\bf r}_T', {\bf r}_T^{\circ}, {\bf r}_{\Omega}',{\bf r}_{\Omega}^{\circ}\) appearing in Eq. 91 have been converted analogously in the way a 3 × 3 × 3 × 3 stiffness tensor would be converted to a 6 × 6 stiffness matrix. The errors \({\bf r}_T, {\bf r}_{\Omega} \) are both converted to “vectors” with six components analogously in the way a 3 × 3 stress tensor would be converted to a stress “vector”. The six-component correction “vectors” resulting from Eq. 91 must be converted back to 3 × 3 tensors \({\bf c}_T, {\bf c}_{\Omega}.\) However, doing this back conversion, we must treat the corrections like strains, i.e. their mixed components must be halved! A conversion of second-order tensors to 9-component “vectors” and fourth order tensors to 9 × 9 matrices is not a good idea, because the resulting 18 × 18 matrix in Eq. 91 would be not only larger but also singular. Note that the rows corresponding to mixed components, e.g. \(\sqcup_{12}\) and \(\sqcup_{21},\) would be in this case identical.
6.3 The Jacobian \({\rm d} \Updelta {\bf T} / {\rm d} \Updelta\varvec{\epsilon}\)
The Jacobian \(\mathsf{ H}={\rm d} \Updelta {\bf T} / {\rm d} \Updelta \varvec{\epsilon}\) is required for the efficient equilibrium iteration on the FE-level, in particular when the full Newton iteration strategy is used (as in Abaqus/Standard). In the implicit integration scheme, the tensor \(\mathsf{ H}\), should be calculated using the state variables \({\bf T}, \varvec{\Omega}\) and p B at the end of the increment and at the end of the RMI. In order to find \(\mathsf{ H}\) we write out the equation for stress increment in the form
It is convenient to distinguish the following subexpressions: \({\bf A}({\bf T},\Updelta \varvec{\epsilon}),\) \({\bf B}({\bf T},\varvec{\Omega},p_B, e, \Updelta \varvec{\epsilon})\) and \({\bf C}({\bf T},\varvec{\Omega},p_B,\) \( e,\Updelta \varvec{\epsilon})\) so that the Jacobian can be written as
The derivatives of A, B and C with respect to \(\Updelta \varvec{\epsilon}\) can be computed via the derivatives with respect to T and \(\varvec{\Omega}.\) For simplicity, however, we disregard the derivative \({\rm d} \varvec{\Omega} /{\rm d} \Updelta \varvec{\epsilon} \approx \mathsf{0}\) while calculating \( \mathsf{H}\). Since the stress T is one of the arguments of the functions A, B, C, it is convenient to use the unknown as yet Jacobian \( \mathsf{H}\) itself in the chain-rule calculations via T, namely \({{\rm d} \sqcup}/{{\rm d} \Updelta \varvec{\epsilon}} = \sqcup':\mathsf{ H} + \ldots\;.\) With these simplifications, we obtain
Note that \({\rm d} \Updelta {\bf T} / {\rm d} \Updelta \varvec{\epsilon} ={\rm d} {\bf T} / {\rm d} \Updelta \varvec{\epsilon} \) because \(\Updelta {\bf T} = {\bf T} - {\bf T}_n\) and the initial stress \({\bf T}_n \) is constant. Moreover, for the sake of simplicity, we assume \(\partial M / \partial {\bf T} \approx {\bf 0}.\) Hence the following approximations are obtained
The substitution of Eqs. 97 and 98 into Eq. 95 results in
wherein
Substituting Eq. 98 into Eq. 96 we obtain
wherein
The Eq. 93 can now be written as
and resolved for the Jacobian \( \mathsf{H}\)
Very few equilibrium iterations are necessary in the numerical calculation with Abaqus using this approximation of the Jacobian despite relatively large time steps.
7 Comparison with experimental results
The presented model has been implemented using the constitutive Fortran 90 routine UMAT written in accordance with the conventions of the FE Program Abaqus Standard. The same routine can be also linked with IncrementalDriver Footnote 5 to perform calculations of element tests with stress or strain or mixed control of cartesian components or combinations thereof.
In order to verify the model, the results of biaxial tests [63] on remoulded kaolin clay were simulated. The predictions were calculated with the set of material parameters shown in Table 1. Other properties of the material are: liquid limit w L = 48%, plastic limit w P = 18%, clay fraction 59% and organic content 5.6%.
7.1 Undrained shearing tests
Two sets of strain controlled tests were considered (see Fig. 18). In both cases, the kaolin powder was mixed with water and 1-d consolidated (with D 1 = −0.5%/h and D 2 = D 3 = 0) in a biaxial apparatus. In all tests, the initial state was nearly the same, i.e. T 1 = −24 kPa, T 2 = −8 kPa, T 3 = −10 kPa and e = 1.396. In the simulations, the initial value of the structure tensor \(\varvec{\Omega}\) is set to zero prior to the 1-d consolidation. For the first set of experiments, the sample was consolidated until T 1 = −672 kPa. Then, isochoric shearing was applied in compression (with D 1 = −0.354%/h, D 2 = 0.354%/h and D 3 = 0) and in extension (with D 1 = 0.354%/h, D 2 = −0.354%/h and D 3 = 0). The corresponding stress paths and stress–strain curves are presented in Figs. 19 and 20, respectively. Predictions of the new model with and without hypoplastic strain and anisotropy are also shown in Figs. 19 and 20. In the second series of experiments, the sample was uniaxially consolidated to T 1 = −800 kPa and uniaxially unloaded (with D 1 = 0.5%/h and D 2 = D 3 = 0) until a nearly isotropic stress state was reached. To such overconsolidated samples, an isochoric deformation was applied in compression and extension. The comparisons between predicted and measured data are presented in Figs. 21 and 22.
Predicted and measured stress-strain curves for undrained shear compression and extension after K 0 consolidation, see Fig. 18b
The results of the numeric calculations are generally in agreement with the laboratory data. The stress paths are well predicted by the model. The predicted shear strength of the overconsolidated samples in compression was higher than in the experiment, Fig. 22, because of the assumed homogeneity of the deformation. In the real experiment, “isochoric” shearing in the overcritical regime may lead to localization of deformation, and some local volume increase (or even cavitation in fast tests) may take place. The zero change in volume can be imposed to the whole sample but not locally.
Predicted and measured stress–strain curves for undrained shear compression and extension after K 0 consolidation and unloading, see Fig. 18c
7.2 Relaxation test
The relaxation of stress at three different stress levels under constant deformation was investigated. The kaolin powder was mixed with water and 1-d consolidated in the biaxial apparatus until a significant stress level was achieved. This stress state (T 1 = −22 kPa, T 2 = T 3 = −8 kPa) and void ratio e = 1.4 are considered as the initial state. In the simulation the tensor \(\varvec{\Omega}\) is set to zero at the initial state. In a first step, the sample was consolidated (with D 1 = 0.5%/h and \(D_2=D_3=0\)) up to T 1 = −108 kPa. In a second step, the deformation was kept constant (\(D_1=D_2=D_3=0)\) during 6 h, and the changes on stress were recorded. The whole test was strain controlled. This two steps were successively applied (with the same strain rates and relaxation times). The prediction of the model and the results from laboratory are presented in Fig. 23. A good accordance between prediction and measurement are observed not only during the K 0-consolidation steps, but also at the three relaxation phases (see Fig. 24).
Predicted and measured relaxation of stress component T 1 (of Fig. 23) at phases A, B and C (zoomed)
7.3 Proportional strain paths
Monotonic compression was performed using 4 different proportional strain paths, see Table 2 (note that D 3 = 0). After large deformation, proportional stress responses were obtained. The initial stress state and void ratio are similar to the tests of Sects. 1 and 2. The initial value of \(\varvec{\Omega}\) is also set to zero. The predictions of the stress ratios \(K_{2/1}=T_2/T_1\) and \(K_{3/1} =T_3 /T_1\) for strain ratios different from the oedometric one are close to the measurements, see Figs. 25 and 26. As the material parameter C 3 was obtained from measured values of K 0, the calculated stress ratios for oedometric compression (path IV in Table 2, Figs. 25 and 26) are considered back-calculations. Predictions using C 2 = 0 (no allowance of preconsolidation surface rotations, i.e. no anisotropy if \(\varvec{\Omega} = {\bf 0}\) at the beginning of the process) provide larger K-values compared with laboratory data.
Asymptotic values of \(K_{2/1}=T_2/T_1\) after large proportional strain paths with constant strain rates (see Table 2) versus the strain invariant \(\alpha = \sqrt{6} \overset{\rightarrow}{{\bf D}^*} \cdot \overset{\rightarrow}{{\bf D}^*} : \overset{\rightarrow}{{\bf D}^*}.\) In this case, \(K_0 = K_{2/1} =0.68\) is obtained after applying path IV
8 FE-calculation of a strip foundation
The classical plane strain problem with a rigid strip foundation is examined using the UMAT routine within the commercial FE program Abaqus. The width of the foundation is 1.0m. The size of the discretized subsoil, boundary conditions and the body forces are presented in Fig. 27. A 0.2 m punching was applied within 100 seconds. The loading is defined as a vertical displacement of the nodes under the foundation. The contact between soil and foundation is perfectly rough, i.e. the nodes under the foundation cannot move horizontally. Since the subsoil boundary conditions and body forces are symmetric with respect to the vertical axis of the foundation, we have used this symmetry in the discretization. The soil parameters given in Table 1 have been used.
Asymptotic values of \(K_{3/1}=T_3/T_1\) after large proportional strain paths with constant strain rates (see Table 2) versus the strain invariant α. \(K_0 =K_{3/1} =0.68\) is obtained after applying path IV
The undrained conditions were simulated using the bulk modulus of water K w = 500 MPa and adding the stiffness of water
to the material stiffness \( \mathsf{H}\) (Jacobian). The total stress was used in Abaqus, and the effective stress was used internally in the umat . The bulk stiffness of water was multiplied by the volume strain increments to update the pore water pressure p w . The water pressure was stored in memory as an internal state variable at each integration point. The FE mesh is shown in Fig. 28. The CPE4 elements of Abaqus have been used. Despite full integration, the volumetric locking (due to water stiffness or due to isochoric plastic flow) was eliminated by usage of a special volume strain operator that provided a constant volumetric strain in all four Gauss integration points within an element. The consolidation elements of Abaqus e.g. CPE4P or CPE8P were not used.
At first, the geometric nonlinearity (Abaqus uses Hughes-Winget algorithm) was used, but due to considerable distortion of elements (a 0.2 m punching was applied) the calculation was slowed down to over 1 h on a conventional PC. In order to enable fast comparisons, the geometric nonlinearity was switched off and as a result the 0.2 m punching took only a quarter of an hour.
The initial conditions for stress T preconsolidation pressure p B and anisotropy \(\varvec{\Omega}\) were all varied. The vertical stress component was given by the buoyant unit weight of soil \({\gamma'}=10\hbox{kN/m}^3\) and additionally increased by an equally distributed surcharge of 15 kPa, Fig. 27. The horizontal stress was calculated using the coefficient of earth pressure at rest K 0 = 1 − sinφ c , K 0 = 1.0, and K 0 = 1.3. The anisotropic structure tensor was either switched off \(\varvec{\Omega} = {\bf 0}\) or taken in the value \(\varvec{\Omega} = \varvec{\Omega}^{\rm asymp}_0 \) which results from uniaxial vertical deformation along x 2, since diag[0, −1, 0] is used in the model as the direction of sedimentation. The latter choice corresponds to natural K 0 - consolidation. The preconsolidation pressure p B was calculated multiplying p B+ from Eq. 40 (a function of T and \(\varvec{\Omega})\) with OCR = 1 or with OCR = 4. The combinations of the initial conditions and the resulting bearing capacities obtained from the FE calculation are given in Figs. 29, 30 and 31.
In each case, a limit load was reached. The vertical displacement necessary to reach the asymptotic reaction force under the foundation varied from 0.06 to 0.16 m. It is interesting to observe that the limit load related to the undrained strength c uComp at the depth of 1m corresponds approximately to the limit analysis solution \(T_{22} =(2+\pi) c_{u \rm Comp} \) by Prandtl for the isotropic preconsolidation and to about 77% of this value for the anisotropic preconsolidation.
9 Concluding remarks
The anisotropic visco-hypoplastic model presented here preserves the merits of the isotropic visco-hypoplasticity (the description of creep, relaxation and rate dependence), improves the response to cyclic loading and, of course, provides an anisotropic enhancement which can be observed in the response to triaxial (or biaxial) compression and extension paths after anisotropic K 0 consolidation. The rotation of the preconsolidation surface controlled by the state variable \(\varvec{\Omega}\) provides also a better estimation of K 0 during an oedometric compression.
Notes
Registered trade mark of a commercial FE program, http://www.simula.com.
The hyperelastic stiffness is conservative in the sense that any closed strain cycle causes a closed stress cycle and vice versa. For hypoelastic formulations, this is true for in-phase cycles only, e.g. \(\varvec{\epsilon}(t) = \sin(t) \varvec{\epsilon}^{\rm ampl}. \) The out-of-phase strain cycles, e.g. with \(\epsilon_{11} = \epsilon_{11}^{\rm ampl} \sin(t)\) and \(\epsilon_{22} = \epsilon_{22}^{\rm ampl} \sin(t+ \pi/3)\) may lead to undesired accumulation of stress. The direction of accumulation depends on the sense of rotation (
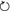 or
or  ).
).exactly 11 because Ω ii = 0.
nova.m can be downloaded from http://www.rz.uni-karlsruhe.de/~gn99/. The expression \(\frac{\partial T_{ij}}{\partial T_{kl}}(=I_{ijkl})\) can be calculated with
$$ \begin{aligned}{\tt In} \left[ {\tt 1}\right]{\tt :=Needs} \left[\tt {''Tensor`nova`''}\right]; {\tt In} \left[ {\tt 2} \right]\, {\tt :=\,fD} \left[T\left[i,j \right],T\left[ {\tt k, l} \right]\right] \\ {\tt Out} \left[2\right]:= (\backslash \left[{\tt Delta}\right] \left[ {\tt i, l} \right]\backslash \left[ {\tt Delta}\right] \left[ {\tt j, k} \right] + \backslash \left[ {\tt Delta} \right] \left[ {\tt i,k } \right]\backslash \left[ {\tt Delta} \right] \left[ {\tt j,l } \right])/{\tt 2} \end{aligned}$$The Mathematica expressions enter directly in the code using a FORTRAN-90 tensorial module. For example, the derivative of stress discrepancy with respect to stress \({\bf r}_T^{\circ}\) Eq. 86 can be coded in a single line \({\tt drTdO}= ({\tt E .xx. ((m .out. dAdO) + dmdO*A))}\) \(!{\bf r}_T^{\circ} = {\tt E} : ({\bf m} A^{\circ} + {\bf m}^{\circ} A)\) where the double contraction and the dyadic product are directly evaluated using the operators .xx. and .out., respectively.
IncrementalDriver is a program written by the first author to test constitutive routines. Its open source code can be downloaded from http://www.rz.uni-karlsruhe.de/~gn99/.
References
Adachi T, Oka F (1982) Constitutive equations for normally consolidated clay based on elasto-viscoplasticity. Soil Found 22:57–70
Adachi T, Oka F, Hirata T, Hashimoto T, Pradhan TBS, Nagaya J, Mimura M (1991) Triaxial and torsional hollow cylinder tests of sensitive natural clay and an elasto-viscoplastic constitutive model. In: Proceedings of the 10-th ECSMFE, Florence
Anandarajah A (2000) On influence of fabric anisotropy on the stress-strain behaviour of clays. Comp Geotech 27:1–17
Axelsson K, Yu Y (1988) Constitutive modelling of swedish fine grained soils. Mechanical properties and modelling of silty soils. In: Proceedings of the 2nd nordic geotechnical meeting, Oslo University, pp 14–18
Baligh MM, Whittle A (1987) Soil models and design methods. In: Geotechnical design: design methods and parameters conference, Politecnico di Torino
Banerjee PK, Kumbhojkar A, Yousif NB (1987) A generalized elasto-plastic model for anisotropically consolidated clays. In: Desai CS (ed) Constitutive laws for engineering materials: theory and applications. Elsevier, pp 495–504
Banerjee PK, Yousif NB (1986) A plasticity model for the mechanical behaviour of anisotropically consolidated clay. Int J Num Anal Meth Geomech 10:521–541
Bauer E (2009) Hypoplastic modelling of moisture-sensitive weathered rockfill materials. Acta Geotech. doi:10.1007/s11440-009-0099-y
Bellotti R, Jamiolkowski M, Lo Presti DCF, O’Neill DA (1996) Anisotropy of small strain stiffness in Ticino sand. Géotechnique 46(1):115–131
Betten J (2008) Creep mechanics. Springer, Berlin
Boehler JP, Sawczuk A (1977) On yielding of oriented solids. Acta Mech 27:185–206
Borja RI (1992) Generalized creep and stress relaxation model for clays. J Geotech Eng Div ASCE 118(11):1765–1786
Borja RI, Kavazanjian E (1985) A constitutive model for the stress–strain-time behaviour of wet clays. Géotechnique 35(3):283–298
Burland JB, Georgiannou VN (1991) Small strain stiffness under generalized stress changes. In: Proceedings of the 10th European conference soil mechanics and foundation engineering, Florence, vol 1, pp 41–44
Butterfield R (1979) A natural compression law for soils. Géotechnique 29:469–480
Callisto L, Calabresi G (1998) Mechanical behaviour of a natural soft clay. Géotechnique 48(4):495–513
Cormeau I (1975) Numerical stability in quasi-static elasto/visco-plasticity. Int J Num Meth Eng 9:109–127
Dafalias YF (1987) An anisotropic critical state clay plasticity model. In: Desai CS (ed) Constitutive laws for engineering materials: theory and applications. Elsevier, pp 513–521
Darve F, Butterfield R (1989) Geomaterials: constitutive equations and modelling. Elsevier, New York
Dean ETR (1989) Isotropic transformations models for finite axial strains events. Technical report 224, Cambridge Geotechnical Group
Gudehus G (1996) A comprehensive constitutive equation for granular materials. Soil Found 36(1):1–12
Henke S, Grabe J (2008) Numerical investigation of soil plugging inside open-ended piles with respect to the installation method. Acta Geotech 3:215–223
Houlsby GT, Puzrin AM (2006) Principles of hyperplasticity. Springer, London
Huang WX, Wu W, Sun DA, Sloan S (2006) A simple hypoplastic model for normally consolidated clay. Acta Geotech 1:15–27
Imai G, Yi-Xin Tang (1992) A constitutive equation of one-dimensional consolidation derived from inter-connected tests. Soil Found 32(2):83–96
Jardine RJ, Symes MJ, Burland JB (1984) The measurement of soil stiffness in the triaxial apparatus. Géotechnique 34:323–340
Kavvadas M (1983) A kinematic hardening constitutive model for clays. In: Proceedings of 2nd international conference constitutive laws in engineering materials, Tucson, pp 263–270
Kutter BL, Sathialingam N (1992) Elastic-viscoplastic modelling of rate-dependent behaviour of clays. Géotechnique 42(3):427–441
Larsson R (1977) Basic behaviour of Scandinavian soft clays. Technical report 4, Swedish Geotechnical Institute
Leoni M, Karstunen M, and Vermeer PA (2008) Anisotropic creep model for soft soils. Géotechnique 58(3):215–226
Leroueil S, Kabbaj M, Tavenas F (1988) Study of the validity of a XXX model in situ conditions. Soil Found 28(3):13–25
Leroueil S, Vaughan PR (1990) The general congruent effects of structure in natural soils and weak rocks. Géotechnique 40(3):467–488
Lewin PI, Burland JB (1970) Stress-probe experiments on saturated normally consolidated clay. Géotechnique 20:38–56
Matsuoka H, Nakai T (1977) Stress-strain relationship of soil based on the SMP, constitutive equations of soils. Speciality session 9, Japanese society of soil mechanics and foundation engineering, IX ICSMFE, Tokyo, pp 153–162
Mašín D, Herle I (2007) Improvement of a hypoplastic model to predict clay behaviour under undrained conditions. Acta Geotech 2(4):261–268
Mesri G, Choi YK (1985) The uniqueness of the end-of-primary (EOP) void ratio-effective stress relationship. In: Soil mechanics and foundation engineering, vol 2. Proceedings of the 11th international conference in San Francisco, USA, pp 587–590
Mitchell RJ (1970) On the yielding and mechanical strength of leda clay. Can Geotech J 7:297–312
Mitchell RJ (1972) Some deviations from isotropy in a lightly overconsolidated clay. Geotechnique 22(3):459–460
Molenkamp F, Van Ommen A (1986) Initial state for anisotropic elasto-plastic model. In: 2nd International symposium on numerical models in geomechanics, Ghent
Mróz Z (1966) On forms of constitutive laws for elastic-plastic solids. Archiwum Mechaniki Stosowanej
Mróz Z, Niemunis A (1987) On the description of deformation anisotropy of materials. In: Boehler JP (ed) Yielding, damage and failure of anisotropic solids. Proceedings of IUTAM symposium in Grenoble, France, pp 171–186
Niemunis A (2003) Extended hypoplastic models for soils, Habilitation, monografia 34, Ruhr-University Bochum
Niemunis A, Cudny M (1998) On hyperplasticity for clays. Comput Geotech 23:221–236
Niemunis A, Herle I (1997) Hypoplastic model for cohesionless soils with elastic strain range. Mech Cohes Frict Mater 2:279–299
Niemunis A, Krieg S(1996) Viscous behaviour of soil under oedometric conditions. Can Geotech J 33(1):159–168
Norton F (1929) The creep of steel at high temperatures. Mc Graw Hill, NY
Oka F, Adachi T, Okano Y (1986) Two-dimensional consolidation analysis using an elasto-viscoplastic constitutive equation. Int J Num Anal Meth Geomech 10:1–16
Oka F, Leroueil S, Tavenas F (1989) A constitutive model for natural soft clay with strain softening. Soil Found 29:54–66
Olszak W, Perzyna P (1966) The constitutive equations of the flow theory for a nonstationary yield condition. In: Applied mechanics. Proceedings of the 11th international congress, pp 545–553
Reyes DK, Rodriguez-Marek A, Lizcano A (2009) A hypoplastic model for site response analysis. Soil Dyn Earthq Eng 29(1):173–184
Rondón HA, Wichtmann T, Triantafyllidis T, Lizcano A (2007) Hypoplastic material constants for a well-graded granular material for base and subbase layers of flexible pavements. Acta Geotech 2(2):113–126
Salciarini D, Tamagnini C (2009) A hypoplastic macroelement model for shallow foundations under monotonic and cyclic loads. Acta Geotech 4(3):163–176
Schwer L (1994) A viscoplastic augmentation of the smooth cap model. In: Siriwardane HJ, Zaman MM (eds) Computer methods and advances in geomechanics, Balkema, Rotterdam, pp 671–676
Sekiguchi H (1985) Constitutive laws of soils. Macrometric approaches—static-intrinsically time dependent. In: Discussion session. Proceedings of the 11th ICSMFE, San Francisco, USA
Simpson B (1992) Retaining structures: displacement and design. Géotechnique 42(4):541–576
Stallebrass E (1990) Modelling of the effect of recent stress history on the deformation of overconsolidated soils. PhD thesis, The City University
Sturm H (2004) Modelling of biaxial tests on remoulded saturated clay with a visco-hzpoplastic constitutive law, 2004. Diplomarbeit, Institut für Boden und Felsmechanik, Universität Karlsruhe
Sturm H (2009) Numerical investigation of the stabilisation behaviour of shallow foundations under alternate loading. Acta Geotech. doi: 10.1007/s11440-09-0102-7
Suklje L (1969) Rheological aspects of soil mechanics. Wiley, London
Weifner T, Kolymbas D (2007) A hypoplastic model for clay and sand. Acta Geotech 2(2):103–112
Tejchman J, Bauer E, Tantono SF (2007) Influence of initial density of cohesionless soil on evolution of passive earth pressure. Acta Geotech 2(1):53–63
Tejchman J, Górski J (2009) Finite element study of patterns of shear zones in granular bodies during plane strain compression. Acta Geotech. doi: 10.1007/s11440-009-0103-6
Topolnicki M (1987) Observed stress–strain behaviour of remoulded saturated clay and examination of two constitutive models Heft 107, Institut für Boden und Felsmechanik, Universität Karlsruhe
Whittle AJ, Kavvadas MJ (1994) Formulation of mit-e3 constitutive model for overconsolidated clays. J Geotech Eng Div ASCE 120(1):173–198
Wolffersdorff PAv (1996) A hypoplastic relation for granular materials with a predefined limit state surface. Mech Cohes Frict Mater 1:251–271
Wolfram S (2004) The Mathematica Book, 5th edn. Wolfram Media, Inc, Champaign
Yong RN, Mohamed AO (1988) Performance prediction of anisotropic clays under loading. 114(3)
Zienkiewicz OC, Cormeau IC (1974) Visco-plasticity—plasticity and creep in elastic solids—a unified numerical solution approach. Int J Num Meth Eng 8:821–845
Acknowledgments
The financial support from the German Research Community (DFG-Anisotropy TR 218/4-3) is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding authors
List of symbols
List of symbols
1.1 The following symbols are used in this paper
- A :
-
Auxiliary variable for the intensity of viscous and hypoplastic strain rates
- A, B, C :
-
Auxiliary subexpresssions for the definition of Jacobian \( \mathsf{H}\)
- a :
-
Hypoplastic constant
- b :
-
Auxiliary term in M(θ) function
- C 1 :
-
Material constant for hypoplastic strain
- C 2 :
-
Material constant for evolution of anisotropy
- C 3 :
-
Material constant limiting anisotropy
- \({\bf c}_T\) :
-
Stress correction tensor (RMI)
- c u :
-
Undrained shear strength
- c uComp :
-
Undrained shear strength for triaxial compression
- \({\bf c}_{\Omega}\) :
-
Correction on anisotropy tensor (RMI)
- D :
-
1-d strain rate (extension > 0)
- D vis :
-
1-d viscous strain rate
- D v :
-
Roscoe’s volumetric strain rate
- D q :
-
Roscoe’s deviatoric strain rate
- D r :
-
Reference creep rate
- D :
-
Strain rate tensor
- \({\bf D}^*\) :
-
Deviatoric strain rate tensor
- \({\bf D}^{\rm e}\) :
-
Elastic strain rate tensor
- \({\bf D}^{\rm Hp}\) :
-
Hypoplastic strain rate tensor
- \({\bf D}^{\rm vis}\) :
-
Viscous strain rate tensor
- \( \mathsf{E}\) :
-
Hypoelastic stiffness tensor
- \(\hat{\mathsf{E}}\) :
-
Dimensionless hypoelastic stiffness tensor
- e :
-
Void ratio
- e 0 :
-
Reference void ratio
- e 100 :
-
Reference void ratio preconsolidation p B = 100 kPa
- \(\dot{e}\) :
-
Void ratio rate
- e B0 :
-
Void ratio on the reference isotach (1-d model)
- F :
-
Preconsolidation surface
- F + :
-
Surface affine to F passing through current stress
- F crit :
-
Critical state surface
- F M :
-
Function of the Lode angle used in hypoplasticity
- G :
-
Alternative definition of the preconsolidation surface
- H():
-
Heaviside function
- \( \mathsf{H}\) :
-
Jacobian tensor
- \( \mathsf{H}\) w :
-
Stiffness tensor of water
- h :
-
Current height of the sample
- h 0 :
-
Initial height of the sample
- h 1, h 2, h 3 :
-
Auxiliary variables for \(p_{B+}^0\)
- \( \mathsf{I}\) :
-
Fourth order symmetric identity tensor
- I v :
-
Viscosity index
- \( \mathsf{J}\) :
-
Fourth order identity tensor
- K w :
-
Bulk modulus of water
- K 0 :
-
Coefficient of earth pressure at-rest
- K 2/1, K 3/1 :
-
Stress ratios
- \( \mathsf{K}, \mathsf{N}, \mathsf{R}, \mathsf{S}, \mathsf{W}, \mathsf{Z}\) :
-
Auxiliary fourth order tensors for the definition of the Jacobian \( \mathsf{H}\)
- \(\hat{\mathsf{L}}\) :
-
Dimensionless hypoelastic stiffness used in hypoplasticity
- M :
-
Slope of the critical state line (a function of θ)
- M C :
-
Slope of the critical state line for triaxial compression
- M E :
-
Slope of the critical state line for triaxial extension
- M Ω :
-
Critical state slope for the current \(\varvec{\Omega}\)
- m :
-
Flow rule (a function of T and \(\varvec{\Omega}\))
- \(\hat{\bf N}\) :
-
Dimensionless hypoplastic relaxation tensor
- OCR:
-
Overconsolidation ratio
- p :
-
Roscoe’s mean effective stress \(p=-\hbox{tr}\;{\bf T}/3\)
- \(\bar{p},\bar{q}\) :
-
p, q Scaled so that MCC ellipse becomes a circle with a unit diameter
- p B :
-
Equivalent (preconsolidation) pressure
- p B+ :
-
pseudo equivalent (preconsolidation) pressure
- p w :
-
Pore water pressure
- Q :
-
Surcharge uniform pressure for calculation of the strip foundation
- q :
-
Roscoe’s deviatoric stress \(q=\sqrt{\frac{3}{2}}||{\bf T}^*||\)
- \({\bf r}_T\) :
-
Stress error tensor
- \({\bf r}_\Omega\) :
-
Anisotropy error tensor
- s :
-
Settlement of a footing
- T :
-
1-d stress (compression negative)
- \(\dot{T}\) :
-
1-d stress rate
- t :
-
Time
- T 0 :
-
1-d reference value of stress
- T B :
-
1-d equivalent stress(T B > 0)
- \(\dot{T}_B\) :
-
1-d equivalent stress rate
- T B0 :
-
Equivalent 1-d stress on the reference isotach
- T max :
-
Maximum principal stress
- T min :
-
Minimum principal stress
- t 0 :
-
Reference time
- T :
-
Cauchy effective stress tensor
- \({\bf T}^*\) :
-
Deviatoric stress tensor
- \({\bf T}^B\) :
-
Equivalent stress tensor
- \(\dot{\bf T}\) :
-
Stress rate tensor
- \( {\mathring{\bf T}}\) :
-
Zaremba-Jaumann stress rate
- \(\hat{\bf T}\) :
-
Dimensionless stress tensor \(\hat{\bf T}={\bf T}/\hbox{tr}\;{\bf T}\)
- \({\bf T}_{K0}\) :
-
Uniaxial compression stress
- x 1, x 2 :
-
Horizontal and vertical coordinates
- w L :
-
Liquid limit
- w P :
-
Plastic limit
- α:
-
strain invariant from [62] \(\alpha= \sqrt{6} \overset{\rightarrow}{{\bf D}^*} \cdot \overset{\rightarrow}{{\bf D}^*} : \overset{\rightarrow}{{\bf D}^*}\)
- β:
-
Auxiliary term in M(θ) function
- γ′:
-
Buoyant unit weight
- δ ij :
-
Kroenecker symbol
- \(\Updelta \sqcup\) :
-
Increment of \(\sqcup\)
- \( \epsilon \) :
-
1-d logarithmic strain
- \( \epsilon_0\) :
-
1-d reference value of logarithmic strain
- θ:
-
Lode’s angle
- λ:
-
Compression index
- κ:
-
Swelling index
- μ i :
-
Coefficients of the general equation of an ellipse
- ϕ:
-
Matsuoka-Nakai’s constant term \(\phi=\frac{9-\sin^2{\varphi_c}}{1-\sin^2{\varphi_c}}\)
- ϕ(p):
-
Matsuoka-Nakai analogous term for the alternative preconsolidation surface
- ϕmax :
-
Constant of the alternative pre- consolidation surface
- φ c :
-
Critical friction angle
- χ:
-
Positive scalar homogeneity
- Ψ:
-
Angle between the current stress state and the isotropic axis
- ψ:
-
Coefficient of secondary compression
- \(\varvec{\Omega}\) :
-
Anisotropy tensor
- ω:
-
Anisotropy of the ellipse in \(\bar{p}-\bar{q}\) space
- 1 :
-
Second order identity tensor
Rights and permissions
About this article
Cite this article
Niemunis, A., Grandas-Tavera, C.E. & Prada-Sarmiento, L.F. Anisotropic visco-hypoplasticity. Acta Geotech. 4, 293–314 (2009). https://doi.org/10.1007/s11440-009-0106-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11440-009-0106-3

































 or
or  ).
).