1 Background

The analysis of heat transfer characteristics of various fluid flows can be extremely useful in improving the performance of industrial systems. Natural convection can highly be significant, especially when moving fluid is minimally influenced by forced convection heat transfer. Natural convection has piqued the interest of scientists since it occurs in a variety of technical applications. Geothermal systems, heat exchangers, chemical catalytic reactors, fiber and granular insulation, packed beds, petroleum reservoirs, and nuclear waste dumps all use natural convection to transfer heat [1,2,3]. Mixed convection of Cu–water nanofluid inside a two-sided lid-driven cavity filled with heterogeneous porous media is optimized. The horizontal walls are adiabatic and movable, and the vertical walls are exposed to constant hot and cold temperatures. Two-phase mixture model and Darcy–Brinkman–Forchheimer relation are implemented, respectively, for the simulation of nanofluid and fluid flow through porous media [4,5,6]. In the recent decade, various researchers investigated exergy analyses and entropy generation to provide the best geometry of the heat exchanger. Using nanofluid and swirl flow devices are passive techniques for improving thermal efficiency. Exergy variations for forced convection of nanofluid through a pipe equipped with twisted tape turbulators have been simulated via finite volume method [7, 8].

The study of blood flow through a stenosed artery is very important because of the fact that the cause and development of many cardiovascular diseases are related to the nature of blood movement and the mechanical behavior of the blood vessel walls. Stenosis is defined as a partial occlusion of the blood vessels due to the accumulation of cholesterol, fats, and the abnormal growth of tissue. Cardiac catheterization (also called heart catheterization) is a diagnostic procedure that does a comprehensive examination to determine how the heart and its blood vessels function. One or more catheter is inserted through a peripheral blood vessel in the arm (antecubital artery or vein) or leg (femoral artery or vein) with X-ray guidance. This procedure gathers information such as adequacy of blood supply through the coronary arteries, blood pressure, blood flow throughout chambers of the heart, collection of blood samples, and X-rays of the heart’s ventricles or arteries [9, 10].

Analysis of natural convection is often difficult, particularly when a non-Newtonian fluid is flowing in a system. Various flows of Newtonian and non-Newtonian fluids bounded by two infinite parallel vertical plates have been studied analytically, numerically, and experimentally by numerous scholars. A numerical solution is investigated for Rivlin–Ericksen fluid natural convection flow and heat transfer between parallel plates. Nowadays, much attention is being paid to the application of nanofluids for cooling purposes [11,12,13].

Nanoparticles can significantly improve the thermal conductivity of base fluids by altering their thermophysical properties, resulting in improved heat transfer [14,15,16,17]. Chamkha [18], using continuum equations, constructed a mathematical model for a continuous two-phase non-Newtonian fluid flow over an infinite porous flat plate. Ellahi et al. [19] used series solutions to investigate the heat transfer features of a fully developed incompressible non-Newtonian fluid flow in coaxial cylinders using Reynolds and Vogel models. Youssri et al. [20, 21] presented a numerical technique for solving one- and two-dimensional partial differential heat equation and the fractional Bagley–Torvik equation with homogeneous boundary conditions by employing the tau and collocation methods. The Runge–Kutta method was used to investigate the influence of free convection flow on non-Newtonian fluid flow through a porous media along with an isothermal vertical flat plate [22]. The natural convection of a non-Newtonian nanofluid flow between two infinite parallel vertical flat plates was investigated analytically using the differential transformation approach. Domairry et al. [23] discovered that as the volume percentage of nanoparticles grows, the thickness of the momentum boundary layer increases while the thickness of the thermal boundary layer drops.

Pittman et al. [24] examined the natural convection heat transfer of a non-Newtonian fluid moving over an electrically heated vertical plate under constant surface heat flux circumstances and found that the temperature difference grows as the distance between the fluid and the plate increases. Using analytical and numerical approaches, Hatami et al. [25] examined the natural convection of a non-Newtonian nanofluid flow between two vertical flat plates. The Boussinesq approach was utilized by Ternik et al. [26] to calculate the natural convection of non-Newtonian nanofluids in a square differentially heated chamber.

The aim of this work is to investigate analytical and numerical solutions of the radiation effect on MHD flow of Rivlin–Ericksen nanofluid of grade three through porous medium with uniform heat source between two vertical flat plates. In addition, the effects of dimensionless non-Newtonian viscosity, radiation, porosity parameter, Hartmann number, Eckert number, Prandtl number, and heat source parameter on the temperature and velocity of flow between two infinitely parallel vertical flat plates are investigated. The reduced ordinary differential equations are solved using MDTM, FDM, and shooting method. This approach provides highly accurate solution estimates in a series of steps. The variation distribution of velocity and temperature with the parameters that govern the problem is presented. Furthermore, graphical and numerical results for the velocity and temperature profiles are presented and discussed for various parametric conditions. Finally, comparisons with previously published works are made and showed that the present results have high accuracy and are found to be in good agreement.

2 Mathematical formulation of the problem

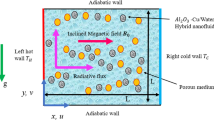
A schematic of the problem under study is shown in Fig. 1. It consists of two flat plates that can be positioned vertically. A non-Newtonian fluid is contained on two flat plates separated by 2b. At x =  + b and x = b, the walls are kept at constant temperatures T1 and T2, respectively, with T1 > T2. The fluid near the wall is caused by the temperature difference, at x =  − b to rise and at x =  + b to fall [27]. The fluid is a water-based nanofluid containing copper. The base fluid and the nanoparticles are considered to be in thermal equilibrium, with no slide between them. Table 1 lists the nanofluid’s thermophysical properties [28].

Fig. 1
figure 1

Schematic diagram of the problem under investigation

Full size image
Table 1 Thermo-physical properties of water and nanoparticles
Full size table

Radiative heat flux \(q_{{\text{r}}}\) can be calculated by using Rosseland approximation as follows [29, 30]:

$$q_{{\text{r}}} = - \frac{{4\, \sigma^{*} }}{{ 3 \,k^{*} }}\frac{{\partial T^{4} }}{\partial x},$$
(1)

where the Stephan–Boltzmann constant and the mean absorption coefficient, respectively, are represented by σ* and K*. The temperature differences in the flow are supposed to vary by the fourth power of T which can be expressed by a linear function of temperature. This can be implemented by expansion of \(T^{4}\) based on Taylor series as follows [29]:

$$T^{4} = T_{\infty }^{4} + 4 T_{\infty }^{3} \left( { T - T_{\infty } } \right) + 6 T_{\infty }^{2} \left( {T - T_{\infty } } \right)^{2} + \cdots$$
(2)

By neglecting higher-order terms of temperature in Eq. (2) against the first-degree term, the following expression is achieved [29]:

$$\left( {T^{4} \cong 4 T_{\infty }^{3} T - 3 T_{\infty }^{4} } \right)$$
(3)

Subsequently, by substituting Eq. (3) into Eq. (1), radiative heat flux is rewritten as follows [29]:

$$q_{{\text{r}}} = - \frac{{16\, T_{\infty }^{3} \sigma^{*} }}{{ 3\, k^{*} }}\frac{\partial T}{{\partial x}}$$
(4)

The effective density \(\rho_{{{\text{nf}}}}\), the effective dynamic viscosity \(\mu_{{{\text{nf}}}}\), the heat capacitance \(\left( {\rho C_{p} } \right)_{{{\text{nf}}}}\), and the thermal conductivity \(\kappa_{{{\text{nf}}}}\) of the nanofluid can be expressed by the solid volume fraction \(\varphi\) as

$$\rho_{{{\text{nf}}}} = \rho_{f} (1 - \varphi ) + \rho_{f} \varphi$$
(5)
$$\mu_{{{\text{nf}}}} = \frac{{\mu_{f} }}{{(1 - \varphi )^{2.5} }}$$
(6)
$$\left( {\rho C_{p} } \right)_{{{\text{nf}}}} = \left( {\rho C_{p} } \right)_{f} \left( {1 - \varphi } \right) + \left( {\rho C_{p} } \right)_{s} \varphi$$
(7)
$$\frac{{\kappa_{{{\text{nf}}}} }}{{\kappa_{f} }} = \frac{{\kappa_{s} + 2 \kappa_{f} - 2 \varphi \left( { \kappa_{f} - \kappa_{s} } \right)}}{{\kappa_{s} + 2 \kappa_{f} + \varphi \left( {\kappa_{f} - \kappa_{s} } \right)}}$$
(8)
$$\frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{f} }} = 1 + \frac{{3 \left( { \frac{{\sigma_{s} }}{{\sigma_{f} }} - 1} \right) \varphi }}{{\left( { \frac{{\sigma_{s} }}{{\sigma_{f} }} + 2} \right) - \left( { \frac{{\sigma_{s} }}{{\sigma_{f} }} - 1 } \right)}}$$
(9)

The Navier–Stokes and energy equations can be constructed as follows under these assumptions and using the nanofluid model presented by Maxwell Garnett (MG) model [31]:

The equation of motion is [32 and 31]:

$$\mu_{{{\text{nf}}}} \frac{{{\text{d}}^{2} u}}{{{\text{d}}x^{2} }} + 6\beta_{3} \left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right)^{2} \frac{{{\text{d}}^{2} u}}{{{\text{d}}x^{2} }} + \rho_{o} \gamma (T - T_{m} )g - \frac{{\mu_{{{\text{nf}}}} }}{{K_{{{\text{nf}}}} }}u - \sigma_{{{\text{nf}}}} \beta_{0}^{2} u = 0,$$
(10)

and the energy equation is as follows:

$$K_{{{\text{nf}}}} \frac{{{\text{d}}^{2} T}}{{{\text{d}}x^{2} }} + 2\beta_{3 } \left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right)^{4} + \mu_{{{\text{nf}}}} \left( {\frac{{{\text{d}}u}}{{{\text{d}}x}}} \right)^{2} + Q_{0} (T - T_{m} ) - \frac{{{\text{d}}q_{r} }}{{{\text{d}}x}} = 0,$$
(11)

Rajagopal [27] has demonstrated that by using the similarity variables:

$$v = \frac{u}{{u_{0} }},\;\eta = \frac{x}{b}\;{\text{and}}\;\theta = \frac{{T - T_{m} }}{{T_{1} - T_{2} }},$$
(12)

By substituting the above parameters, the Navier–Stokes equations and the energy equations can be reduced to two ordinary differential equations:

$$\frac{{{\text{d}}^{2} v}}{{{\text{d}}\eta^{2} }} + 6\delta \left( {1 - \varphi } \right)^{2.5} \left( {\frac{{{\text{d}}v}}{{{\text{d}}\eta }}} \right)^{2} \frac{{{\text{d}}^{2} v}}{{{\text{d}}\eta^{2} }} + \theta - A{\text{Ha}}^{2} \left( {1 - \varphi } \right)^{2.5} v - \frac{P}{B} v = 0,$$
(13)
$$\left( {1 + \frac{4}{{3{ }B{ }R_{d} }}} \right)\frac{{d^{2} \theta }}{{d\eta^{2} }} + 2\delta {\text{ Ec }}\Pr \left( {\frac{dv}{{d\eta }}} \right)^{4} + \left( {\frac{{{\text{Ec}}\;\Pr }}{B}} \right){ }\left( {1 - \varphi } \right)^{{ - { }2.5}} \left( {\frac{dv}{{d\eta }}} \right)^{2} + \frac{\alpha }{B}\theta = 0,$$
(14)

where A = \(\frac{{\sigma_{{{\text{nf}}}} }}{{\sigma_{f} }}\), B = \(\frac{{\kappa_{{{\text{nf}}}} }}{{\kappa_{f} }}\), \(\mu_{{{\text{nf}}}}\) = \(\frac{{\mu_{f} }}{{\left( {1 - \varphi } \right)^{2.5} }}\), \(v_{o}\) = \(\frac{{\rho_{0} \gamma gb^{2} \left( { T_{1} - T_{2} } \right)}}{{\mu_{{{\text{nf}}}} }}\),\(\delta = \frac{{\beta_{3} u_{0}^{2} }}{{\mu_{f} b^{2} }}\) is the dimensionless non-Newtonian viscosity, \(P = { }\frac{{b^{2} }}{{k_{f} }}{ }\) is the porosity parameter, \({\text{Ha}}^{2} = \frac{{\sigma_{f} \beta_{0}^{2} b^{2} }}{{ \mu_{f} }}\) is the Hartmann number,\({ }R_{d} = { }\frac{{k k^{*} }}{{4 \sigma^{* } T_{\infty }^{3} }}\) is the radiation parameter, \({\text{Ec}} = \frac{{u_{0}^{2} }}{{c_{f } \left( {T_{1 - } T_{2} } \right)}}\) is the Eckert number, \(\Pr = \frac{{\mu_{f } c_{f} }}{{k_{f} }}\) is the Prandtl number and \(\alpha = { }\frac{{Q_{0} { }b^{2} }}{{k_{f} }}{ }\) is the heat source parameter.

The following are the appropriate boundary conditions:

$$v\left( { - 1} \right) = 0,\;\theta \left( { - 1} \right) = { }\frac{1}{2},$$
(15)
$$v\left( 1 \right) = 0,\;\theta \left( 1 \right) = - { }\frac{1}{2},$$
(16)

3 Methods

3.1 Analytical method

When DTM is used for solving differential equations with the boundary conditions at infinity or problems that have highly nonlinear behavior, the outcomes were diverse solutions. Furthermore, power series are ineffective when the independent variable has large values. To address this problem, MDTM has been used for the analytical solution of differential equations, and it is discussed in this section. For this, the following nonlinear initial value problem is considered.

By applying differential transformation theorems on Eqs. (13) and (14), the following recursive relations can be obtained:

$$\begin{aligned} & \left( {k + 1} \right)\left( {k + 2} \right)V\left( {k + 2} \right) + 6\delta \left( {1 - \varphi } \right)^{2.5} \mathop \sum \limits_{{r_{2} = 0}}^{k} \mathop \sum \limits_{{r_{1} = 0}}^{{r_{2} }} \left( {r_{1} + 1} \right)\left( {r_{2} - r_{1} + 1} \right)\left( {k - r_{2} + 1} \right)\left( {k - r_{2} + 2} \right) \\ & V\left( {r_{1} + 1} \right)V\left( {r_{2} - r_{1} + 1} \right)V\left( {k - r_{2} + 2} \right) + \Theta \left( k \right) - A{\text{Ha}}^{2} \left( {1 - \varphi } \right)^{2.5} V\left( k \right) - \frac{P}{B}V\left( k \right) = 0, \\ \end{aligned}$$
(17)
$$\begin{aligned} & \left( {1 + \frac{4}{{3 B R_{d} }}} \right)\left( {k + 1} \right)\left( {k + 2} \right) \Theta \left( {k + 2} \right) + 2 \delta {\text{Ec}} \Pr \mathop \sum \limits_{{r_{3} = 0}}^{k} \mathop \sum \limits_{{r_{2} = 0}}^{{r_{3} }} \mathop \sum \limits_{{r_{1} = 0}}^{{r_{2} }} \left( {r_{1} + 1} \right)\left( {r_{2} - r_{1} + 1} \right)\left( {r_{3} - r_{2} + 1} \right) \\ & \left( {k - r_{3} + 1} \right)V\left( {r_{1} + 1} \right)V\left( {r_{2} - r_{1} + 1} \right)V\left( {r_{3} - r_{2} + 1} \right)V(k - r_{3} + 1) + \frac{{E_{c} P_{r} }}{B}\left( {1 - \varphi } \right)^{ - 2.5} \mathop \sum \limits_{r = 0}^{k} \left( {r + 1} \right)\left( {k - r + 1} \right) \\ & V\left( {r + 1} \right) V\left( {k - r + 1} \right) + \frac{\alpha }{B}\Theta \left( k \right) = 0, \\ \end{aligned}$$
(18)

where V (k) and Θ (k) are the differential transforms of u (\(\eta\)) and θ (\(\eta\)).

The boundary condition’s (15–16) differential transform is as follows:

$$V\left( 0 \right) = 0,\;\Theta (0) = \frac{1}{2},$$
(19)
$$\mathop \sum \limits_{k = 0}^{i} v\left( k \right)2^{k} = 0,\;\mathop \sum \limits_{k = 0}^{i} \Theta \left( k \right)2^{k} = - \frac{1}{2},$$
(20)

We can consider the following boundary conditions (15–16):

$$v( - 1) = 0,\;\theta ( - 1) = \frac{1}{2},$$
(21)
$$v`\left( { - 1} \right) = \lambda ,\;\theta `( - 1) = \omega ,$$
(22)

Then, differential transforms of (21–22) are given by

$$V\left( 0 \right) = 0,\;\Theta (0) = \frac{1}{2},$$
(23)
$$V\left( 1 \right) = \lambda ,\;\Theta (1) = \omega ,$$
(24)

Moreover, by substituting Eqs. (23) and (24) into Eqs. (17) and (18) and by the recursive method, we can calculate other values of V (k) and Θ (K) with the aid of Mathematica 12.3 algorithms.

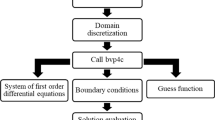
3.2 Finite difference method

The system of coupled nonlinear ordinary differential Eqs. (13–14) with boundary conditions (15–16) is solved for the flow velocity and temperature using FDM by designing MATLAB and Mathematica programs and then the present graphics are drawn by designing the Excel program. The following linearized form should be applied because of nonlinearity in this system:

$$\frac{{{\text{d}}^{2} v}}{{{\text{d}}\eta^{2} }}\left( {1 + 6\left( {1 - \varphi } \right)^{2.5} \left( {\frac{{{\text{d}}\overline{v}}}{{{\text{d}}\eta }}} \right)^{2} } \right) + \theta \left( {A{\text{Ha}}^{2} \left( {1 - \varphi } \right)^{2.5} + \frac{P}{B}} \right)v = 0,$$
(25)
$$\left( {1 + \frac{4}{{3 B R_{d} }}} \right)\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\eta^{2} }} + {\text{Ec }}\Pr \frac{{{\text{d}}v}}{{{\text{d}}\eta }}\left( {2\delta \left( {\frac{{{\text{d}}\overline{v}}}{{{\text{d}}\eta }}} \right)^{3} + \frac{{\left( {1 - \varphi } \right)^{ - 2.5} }}{B} \frac{{{\text{d}}\overline{v}}}{{{\text{d}}\eta }}} \right)^{3} + \frac{\alpha }{B}\theta = 0,$$
(26)

where bar notation denotes the iterated terms that convert Eqs. (13–14) to a linearized one.

By applying Taylor’s expansions of the dependent variables about central point for Eqs. (25–26), a system of algebraic equations [33] is obtained:

$$\frac{{{\text{d}}v_{i} }}{{{\text{d}}\eta }} = \frac{{v_{i + 1} - v_{i - 1} }}{\Delta } + o(\Delta^{2} )$$
(27)
$$\frac{{{\text{d}}^{2} v_{i} }}{{{\text{d}}\eta^{2} }} = \frac{{v_{i + 1} - 2v_{i} + v_{i - 1} }}{{\Delta^{2} }} + o(\Delta^{2} )$$
(28)
$$\frac{{{\text{d}}^{2} \theta_{i} }}{{{\text{d}}\eta^{2} }} = \frac{{\theta_{i + 1} - 2\theta_{i} + \theta_{i - 1} }}{{\Delta^{2} }} + o(\Delta^{2} )$$
(29)

where i = 1, 2, 3,…, m + 1 and m is the number of subintervals of the finite domain of solution (− 1 < \(\eta { }\) < 1).

3.3 Shooting method

Numerical solutions of the ordinary differential Eqs. (13–14) subject to Neumann boundary conditions (15) and (16) are obtained using classical Runge–Kutta method with shooting techniques and MATLAB package (ode45). The set of coupled nonlinear ordinary differential equations along with boundary conditions have been reduced to a system of simultaneous equations of the first order for the unknowns following the method of superposition in Na [34].

Equations (13)–(14) can be written as follows:

$$z_{1}^{^{\prime}} = z_{2} ,$$
(30)
$$z_{2}^{^{\prime}} = \frac{{ - z_{3} + A H_{a}^{2} \left( {1 - \varphi } \right)^{2.5} z_{1} + \frac{P}{B} z_{1} }}{{1 + 6 \delta \left( {1 - \varphi } \right)^{2.5} \left( {z_{2} } \right)^{2} }}$$
(31)
$$z_{3}^{^{\prime}} = z_{4} ,$$
(32)
$$z_{4}^{^{\prime}} = \frac{{ - 2\delta E_{c} P_{r} \left( {z_{2} } \right)^{4} - \left( {\frac{{E_{c } P_{r} }}{B}} \right) \left( {1 - \varphi } \right)^{ - 2.5} \left( {z_{2} } \right)^{2} - \frac{\alpha }{B} z_{3} }}{{\left( {1 + \frac{4}{{3 B R_{d} }}} \right)}}$$
(33)

where \(z_{1}\) = \(v\) and \(z_{3}\) = \(\theta\).

$${\text{The initial conditions are}}\;z_{1} ( - 1) = 0,\;z_{2} ( - 1) = i_{1} ,\;z_{3} ( - 1) = \frac{1}{2},\;z_{4} ( - 1) = i_{2} ,$$
(34)

where \(i_{1}\) and \(i_{2}\) are a priori unknowns that must be resolved as part of the solution.

Ode45 integrates the system of differential Eqs. (30–33) with suitable guess values for initial conditions \(i_{1}\) and \(i_{2}\). The calculated values of the velocity and temperature profiles are compared with the given boundary conditions.

4 Results

4.1 Discussion

In this paper, MDTM, FDM, and shooting method are applied successfully to find the solution of the radiation effect on MHD flow of Rivlin–Ericksen nanofluid of grade three through porous medium with uniform heat source between two vertical flat plates. Tables and graphical representation of the results are very useful to demonstrate the efficiency and accuracy of MDTM, FDM, and shooting method for the problem stated in this work. In order to ensure that the current results are accurate, we compared these results with the previously published work. The graphs (2–9) (a) and (b) show the effects of φ, δ, P, Ha, Rd, Ec, Pr, and α on V (η) and θ (η) profiles. Figures 2, 3, 4, and 5a show that an increase in φ, α, Ec, and Pr parameters leads to an increase in V (η), but Figs. 6, 7, 8, and 9a present that an increase in δ, Rd, Ha, and P parameters leads to a decrease in V (η). In addition, Figs. 2, 3, 4, and 5b show that an increase in φ, α, Ec, and Pr parameters leads to an increase in θ (η), but Figs. 6, 7, 8, and 9b present that an increase in δ, Rd, Ha, and P parameters leads to a decrease in θ (η). It can also be observed that P and Ha on θ (η) are very little, almost nonexistent (Figs. 8 and 9b).

Fig. 2
figure 2

Result of V (η) and θ (η) for various \(\varphi\) when Rd = 1, δ = 1, P = 1, Ha = 1, Ec = 1, Pr = 1, and \(\alpha\) = 1

Full size image
Fig. 3
figure 3

Result of V (η) and θ (η) for various \(\alpha\) when \(\varphi\) = 0.01, δ = 1, P = 1, Ha = 1, Ec = 1, Pr = 1, and Rd = 1

Full size image
Fig. 4
figure 4

Result of V (η) and θ (η) for various Ec when \(\varphi\) = 0.01, δ = 1, P = 1, Ha = 1, Rd = 1, Pr = 1, and \(\alpha\) = 1

Full size image
Fig. 5
figure 5

Result of V (η) and θ (η) for various Pr when \(\varphi\) = 0.01, δ = 1, P = 1, Ha =1, Ec = 1, Rd = 1, and \(\alpha\) = 1

Full size image
Fig. 6
figure 6

Result of V (η) and θ (η) for various δ when \(\varphi\) = 0.01, Rd = 1, P = 1, Ha = 1, Ec = 1, Pr = 1, and \(\alpha\) = 1

Full size image
Fig. 7
figure 7

Result of V (η) and θ (η) for various Rd when \(\varphi\) = 0.01, δ = 1, P = 1, Ha = 1, Ec = 1, Pr = 1, and \(\alpha\) = 1

Full size image
Fig. 8
figure 8

Result of V (η) and θ (η) for various Ha when \(\varphi\) = 0.01, δ = 1, P = 1, Rd = 1, Ec = 1, Pr = 1, and \(\alpha\) = 1

Full size image
Fig. 9
figure 9

Result of V (η) and θ (η) for various P when \(\varphi\) = 0.01, δ = 1, Rd =1, Ha = 1, Ec = 1, Pr = 1, and \(\alpha\) = 1

Full size image

In addition, Tables 2 and 3 show comparison between MDTM, FDM, and shooting method with GM, LSM, and CM [32]. As can be seen, this approximate analytical and numerical solution is in good agreement with the relevant solutions.

Table 2 Comparison solution by MDTM, FDM, and shooting method with GM, LSM, and CM [32] for V (η) when \(\varphi\) = 0.01, δ = 1, P = 0, Ha = 3, Rd = 2, Ec = 1, Pr = 6.2, and \(\alpha\) = 0
Full size table
Table 3 Comparison solution by MDTM, FDM, and shooting method with GM, LSM, and CM [32]) for θ (η) when \(\varphi\) = 0.01, δ = 1, P = 0, Ha = 3, Rd = 2, Ec = 1, Pr = 6.2, and \(\alpha\) = 0
Full size table

Moreover, Tables 4, 5, 6, and 7 (Nu and HPM [35]) demonstrate a comparison between MDTM, FDM, and shooting technique. This approximate analytical and numerical solution agrees well with the pertinent solutions, as can be seen.

Table 4 Comparison solution by MDTM, FDM, and shooting method with Nu and HPM [35] for V (η) when \(\varphi\) = 0.01, δ = 1, P = 0, Ha = 0, \(\frac{1}{{R_{d} }}\) = 0, Ec = 1, Pr = 6.2, and \(\alpha\) = 0
Full size table
Table 5 Comparison solution by MDTM, FDM, and shooting method with Nu and HPM [35] for V (η) when \(\varphi\) = 0.07, δ = 2, P = 0, Ha = 0, \(\frac{1}{{R_{d} }}\) = 0, Ec = 2, Pr = 6.2, and \(\alpha\) = 0
Full size table
Table 6 Comparison solution by MDTM, FDM, and shooting method with Nu and HPM [35] for θ (η) when \({ }\varphi\) = 0.01, δ = 1, P = 0, Ha = 0, \(\frac{1}{{R_{d} }}\) = 0, Ec = 1, Pr = 6.2, and \(\alpha\) = 0
Full size table
Table 7 Comparison solution by MDTM, FDM, and shooting method with Nu and HPM [35] for θ (η) when \(\varphi\) = 0.07, δ = 2, P = 0, Ha = 0, \(\frac{1}{{R_{d} }}\) = 0, Ec = 2, Pr = 6.2, and \(\alpha\) = 0
Full size table

5 Conclusions

In this paper, the radiation effect on MHD flow of Rivlin–Ericksen nanofluid of grade three through porous medium with uniform heat source between two vertical flat plates is studied analytically by MDTM and numerically by FDM and shooting method. Results in graphs and tables for the velocity and temperature profiles are presented and discussed for various parameters φ, δ, P, Ha, Rd, Ec, Pr, and α. Moreover, the results indicate the restraining effects of various parameters on velocity and temperature. Furthermore, comparisons with previously published works are made and showed that the present results have high accuracy and are found to be in good agreement. In particular, results for different parameters are summarized in the next two paragraphs.

  • It has been found that the parameters φ, α, Ec, and Pr vary directly with velocity v (η) and temperature θ (η).

  • It has been displayed that the parameters δ, P, Ha, and Rd vary inversely with velocity v (η) and temperature θ (η).