Magneto-convective Al₂O₃/Cu–Water hybrid nanofluid flow in a heated enclosure containing non-Darcy porous medium: lattice Boltzmann simulation

Abstract

The present article deals with the incompressible magnetohydrodynamic (MHD) hybrid nanofluid flow through a heated enclosure containing a non-Darcy porous medium. Employing non-Darcy-based model, the non-dimensional governing mass, energy and momentum equations associated with boundary conditions have been solved by suitable transformations and D2Q9-based Lattice Boltzmann Method via MATLAB. At fixed value of Pr, the present analysis has been done considering the variation in Hartmann number (Ha), heat generation (Q), Rayleigh number (Ra), thermal radiation (Rd), and Darcy number (Da) to numerically explore the influence of MHD nanofluid flow on considered geometry in terms of temperature contours, streamlines and Nusselt number distributions. It has been observed that the increase in the values of Ra causes the increase in the length of vortex diagonally. In addition, a linear relationship has been found between the values of Ra and the magnitude of Nusselt number. Furthermore, it has been found that the trend of local Nusselt number decreases with the increase in the values of Ha.

1 Introduction

Nowadays, the study of hydro-thermal features of hybrid nanofluid flow through a heated enclosure has received a lot of researcher’s interest due to its various applications in manufacturing devices and equipments like solar collectors, refrigerators, nuclear reaction systems, and biomedical devices, etc. Because of the extensive use of free convection in business disciplines nanofluids have been adopted as superior working fluids to normal fluids. In the year 2002, Biswas et al. [1] have investigated the heat transmission of Al₂O₃–Cu/H₂O hybrid nanofluid through an inclined enclosure. Mehryan et al. [2] studied the different phenomena of nanofluid flow characteristics over a cavity. They concluded that nanofluid's presence causes heat transfer enhancement more than base fluid's presence. Employing LBM, Sheikholeslami et al. [3] analyzed the thermal enhancement of water-nanofluids flow through a square with MHD. They revealed that the values of the mean Nusselt number enhance with the increase in the values of volume fraction of nanofluid and Ha. Bendaraa et al. [4] computationally analyzed free convection in a square cavity filled with copper–water nanofluid by solving the governing equations using finite difference approach and upwind technique. Giwa et al. [5] hybrid nanofluids have been explored as a new type of nanofluid for thermal and heat flow properties when implemented on single-particle nanofluids. However, very few experimental studies have been described in the municipal domain on the free convection of hybrid nanofluids in cavities. Bhatti et al. [6] found that computational framework. Gorla et al. [7] utilized a numerical investigation of MHD free convection flow and heat transfer in a non-Darcy porous enclosure with differential heating and a Cu–Al₂O₃–water hybrid nanofluid is conducted. They found that Finite difference techniques discretize the governing equations in a 2-dimensional space. Using MHD nanofluid flow a number of authors Al-Farhany et al. (2022); Chen & Xu et al. (2022); Nath & Murugesan et al. [8] have considered the phenomena of the improvement of thermal efficiency through different types of enclosure. Many scientists have extensively studied heat forced convection within magnetohydrodynamics. A large number of scientific papers have accumulated in the last few years on natural convection in different shaped envelopes. Mekheimer et al. [9] studied the hemodynamic effects of nanoparticles in drug delivery models. Ibrahim et al. [10] conducted an experiment to study nanofluids with free convection researched in a magnetic field for their effects on heat transmission. The studied parameters are Rayleigh number (10³–10⁶), magnetic field angle, radiation parameter (0–2), and nanoparticle size fraction (0–5%). Mliki & Abbassi et al. [11] the entropy generation investigates the natural convection of magnetic hybrid-nanofluid (Al₂O₃-Cu/H₂O) in a heated burner-shaped cavity using the Lattice Boltzmann method (LBM). As a result, calculations are obtained by plotting the shape of streamlines, isotherms and local entropy generation. Ma & Yang et al. [12] investigated that a new method called the simple and highly stable thermal lattice Boltzmann method based on the lattice Boltzmann framework was used to quadratically simulate the hybrid nanofluid natural convection and heat transfer with thermal barrier at high Rayleigh numbers. Redouane et al. [13] experimentally studied the Heat transfer of Ag/Al2O3–water hybrid in a rotating cylinder and casing with an inner wavy porous layer is performed in this study. GFEM is used to perform calculations. They analyzed heat transfer distribution in the cavity is improved as the rotational speed increases in the direction of rotation. In Liao et al. [14] correlation between non-local temperature gradient and heat flux an interval-segment derivative of Fourier's law is studied to describe it. With this innovative semi-analytical method, the necessary primary components are changed into a system of standard nonlinear equations. They discussed that changing the working fluid from water to single nanofluid or hybrid nanofluid depends on the temperature rise. In Rashad et al.[15] nanofluid is one of the most effective passive methods for improving heat transfer aimed at improving the performance of many heating systems such as engines, vehicles and nuclear reactors. In Giwa et al.[16] natural convection thermodynamic properties and properties in magnetic field of composite nanofluid in square cavities are investigated. Massoudi et al. [17] studied free convection heat transfer in a W-shaped envelope saturated with an Ag/Al₂O₃ hybrid nanofluid subjected to a uniform magnetic field and is studied computationally in two dimensions. The equations solved by the finite element method and the numerical simulation software COMSOL Multiphysics. In Mokaddes Ali et al. [18] the free convection flow and heat transfer components of a hybrid nanofluid operating in a cavity are investigated numerically. The dimensionless equations are solved by the finite element method. The heat transfer rate increases with the roughness of the cavity. Tayebi et al. [19] investigated the heat gradient between the inner and outer cylinders serves to create the buoyancy-driven flow. They also investigated the equations that are solved numerically in a dimensionless, non-primitive form using the finite volume discretization method. Bondarenko et al. [20] acknowledges the influence of a heat source and a heat conductor on free convection in a square enclosure filled with alumina–water nanofluid. They studied that this paper analyzes a passive cooling system for a heat source based on a nanofluid. Ganesh et al. [21] have performed thermo-hydraulic phenomena of Al₂O₃–H₂O nanofluid flow using finite difference method. Among all the considered barriers and based on heat transfer, they have analyzed the conclusion that the triangular type barrier is more effective than others. In Grosan et al.[22], using computational methods, we explore the effects of magnetic fields on natural convection flow and heat transfer parameters in a rectangular cavity filled with a porous material. In Miroshnichenko et al.[23] the natural convection of an al₂o₃–water nanofluid in a slanted open cavity with a heat-generating solid element has been investigated. This issue enables comprehension of a potential use of nanofluids for cooling heat-generating components in open cavities. The cavity's upper edge should be porous enough to allow nanofluid to enter. The Oberbeck–Boussinesq equations were formulated and then used to run a simulation. Hasan Sajjadi et al. [24] (MRT)-analyzed the natural convection nanofluid flow through a microcavity by a lattice Boltzmann method with double multiple relaxation time. Employing LB, Sheikholeslami et al. [3] investigated the thermal enhancement of water-nanofluids flow through a square with magnetic. They revealed that the values of the mean Nusselt number enhance with the increase in the values of volume fraction of nanoparticles and Ha. H. Sajjadi et al. [25] studied the MHD flow through an enclosure with porous media using LBM with the aid of MRT. They found that the rate of heat transfer increases with the increase in the values of Ra. Groşan et al.[26] employed the finite difference approach to get a numerical solution. When the nanoparticles' thermal conductivity is much greater than the porous medium's solid structure adding them to the fluid-saturated porous medium lowers the temperature and improves heat transmission. In Rahimi et al.[27] they found the impact of different control systems on flow, temperature field, total/local entropy generation, and average/local Nusselt number is discussed. In Mohamadet et al. [28] to overcome the drawbacks of lattice gas cellular automata, McNamara and Zanetti devised the lattice Boltzmann method (LBM) in 1988. For situations involving fluid dynamics, the LBM has since emerged as a feasible option. Navier–Stokes (NS) equations are used to solve mass, energy, and momentum conservation equations on discrete nodes, volumes or elements in conventional CFD approaches. In Zhaoli Guo et al. [29] they found the LBM's foundational theories, basic models, and widespread applications have all advanced rapidly during the previous two decades. The technique has proven effective in modeling and simulating a wide range of complex flows. In Safaei et al.[30] they investigated simulations of nanofluid free convection and heat surface radiation in a two-dimensional shallow cavity using the lattice Boltzmann method. Khan et al.[31] analyzed a Lattice Boltzmann study of natural convection in a MWCNT–Fe3O4/Water hybrid nanofluid. To conduct the experiment, a rectangular enclosure with variable heating is filled with test fluid. Fu et al.[32] studied the Lattice Boltzmann method to investigate the forced convection of nanofluids in a square enclosure with an adiabatic barrier (LBM). They analyzed that Fe–ethylene–glycol nanofluid and three constant temperature thermal sources are housed in this chamber with the latter two accessible through the left wall.

To the author's knowledge, most existing research on the free convention in non-Darcy porous cavities saturated by hybrid nanofluids is restricted to completely filled cavities. This work aims to investigate the impact of nanoparticles on the fluid and thermal properties of such situations, given the significance of cavities partly filled with a porous structure. The present article deals with the incompressible magnetohydrodynamic (MHD) hybrid nanofluid flow through a heated enclosure containing a non-Darcy porous medium. Employing non-Darcy-based model, the non-dimensional governing momentum, mass, and energy equations associated with boundary conditions have been solved by suitable transformations and D2Q9-based Lattice Boltzmann Method via MATLAB. At a fixed value of Pr, the present analysis has been done considering the variation in Hartmann number (Ha), heat generation (Q), Rayleigh number (Ra), thermal radiation (Rd), and Darcy number (Da) to numerically explore the influence of MHD nanofluid flow on considered geometry in terms of temperature contours, streamlines, and Nusselt number distributions.

2 Computational domain

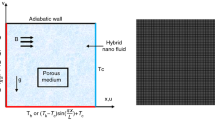
The physical considered geometry (enclosure with non-porous medium) is prescribed in Fig. 1, whereas the bottom and top walls of the square cavity are thermally insulated and the left side hot wall and right-side cold wall are sustained at temperature T_H and T_C, respectively.

Fig. 1

Schematic diagram of computational domain

3 Mathematical formulation

Free convection MHD hybrid nanofluid flow through a two-dimensional square enclosure with non-Darcy medium is governed by following continuity (Eq. 1), $\overline{x}$-momentum (Eq. 2), $\overline{y}$-momentum (Eq. 3) and energy (Eq. 4) equations Miroshnichenko et al. [23].

Continuity: -

$$ \frac{{\partial \overline{u}}}{{\partial \overline{x}}} + \frac{{\partial \overline{v}}}{{\partial \overline{y}}} = 0 $$

(1)

$x$-Momentum: -

$$ \begin{aligned} \left[ {\frac{{\partial \bar{u}}}{{\partial \bar{t}}} + u\frac{{\partial \bar{u}}}{{\partial \bar{x}}} + v\frac{{\partial \bar{u}}}{{\partial \bar{y}}}} \right] &= {\mkern 1mu} - \frac{1}{{\rho _{{hnf}} }}\frac{{\partial \bar{p}}}{{\partial \bar{x}}} + \nu _{{hnf}} \left( {\frac{{\partial ^{2} \bar{u}}}{{\partial \bar{x}^{2} }} + \frac{{\partial ^{2} \bar{u}}}{{\partial \bar{y}^{2} }}} \right) + \frac{{\sigma _{{hnf}} }}{{\rho _{{hnf}} }}B_{0}^{2} \left( {\bar{v}\;sin\phi \;cos\phi - \bar{u}\;sin^{2} \phi } \right) \hfill \\ &\quad - \frac{{1.75}}{{\sqrt {150} }}\frac{\rho }{{k^{{1/2}} }}\bar{u}\sqrt {\bar{u}^{2} + \bar{v}^{2} } - \frac{{\nu _{{hnf}} }}{K}\bar{u} \hfill \\ \end{aligned} $$

(2)

$y$- Momentum: -

$$ \begin{aligned} \left[ {\frac{{\partial \bar{v}}}{{\partial \bar{t}}} + u\frac{{\partial \bar{v}}}{{\partial \bar{x}}} + v\frac{{\partial \bar{v}}}{{\partial \bar{y}}}} \right] &= {\mkern 1mu} - \frac{1}{{\rho _{{hnf}} }}\frac{{\partial \bar{p}}}{{\partial \bar{y}}} + \nu _{{hnf}} \left( {\frac{{\partial ^{2} \bar{v}}}{{\partial \bar{x}^{2} }} + \frac{{\partial ^{2} \bar{v}}}{{\partial \bar{y}^{2} }}} \right) - \frac{{\nu _{{hnf}} }}{K}\bar{v}{\mkern 1mu} - \frac{1}{{k^{{1/2}} }}\bar{v}\sqrt {\bar{u}^{2} + \bar{v}^{2} } \frac{{1.75}}{{\sqrt {150} }} \hfill \\ &\qquad + \frac{{\left( {\rho \beta } \right)_{{hnf}} }}{{\rho _{{hnf}} }}g\left( {\bar{\theta } - \theta _{c} } \right) + \frac{{\sigma _{{hnf}} }}{{\rho _{{hnf}} }}B_{0}^{2} \left( {\bar{v}\;sin\phi \;cos\phi - \bar{u}\;sin^{2} \phi } \right) \hfill \\ \end{aligned} $$

(3)

Energy: -

$$ \frac{{\partial \overline{\theta }}}{{\partial \overline{t}}} + \overline{u}\frac{{\partial \overline{\theta }}}{{\partial \overline{x}}} + \overline{v}\frac{{\partial \overline{\theta }}}{{\partial \overline{y}}} = \left( {\frac{{\partial^{2} \overline{\theta }}}{{\partial \overline{x}^{2} }} + \frac{{\partial^{2} \overline{\theta }}}{{\partial \overline{y}^{2} }}} \right)\alpha_{hnf} + \frac{{_{{Q_{0} }} }}{{\left( {\rho C_{p} } \right)_{hnf} }} $$

(4)

All parameters in Equations (1) - (4) are defined in the notation section.

The non-dimensional parameters are described as below.

$$ x = \frac{{\overline{x} }}{{L_{{{\text{ref}}}} }},\;y = \frac{{\overline{y} }}{{L_{{{\text{ref}}}} }},\;v = \frac{{\overline{v} L_{{{\text{ref}}}} }}{{\alpha_{f} }},\;t = \frac{{\overline{t} \alpha_{f} }}{{L_{{{\text{ref}}}}^{2} }},\;p = \overline{p} \frac{{L_{{{\text{ref}}}}^{2} }}{{\rho \alpha_{f}^{2} }},\;u = \frac{{\overline{u} L_{{{\text{ref}}}} }}{{\alpha_{f} }} $$

$$ \theta = \frac{{\overline{\theta } - \theta_{C} }}{{\theta_{H} - \theta_{C} }},\,Ra = \frac{{gB_{f} q^{\prime\prime}\Delta \theta L_{{{\text{ref}}}}^{4} }}{{v_{f} \alpha_{f} k_{f} }},\;{\text{Pr}} = \frac{{v_{f} }}{{\alpha_{f} }},\;\alpha_{f} = \frac{{k_{f} }}{{\left( {\rho C_{P} } \right)_{{}} }},\;\Delta \theta = \frac{{q^{\prime\prime}L_{{{\text{ref}}}} }}{{k_{f} }} $$

$$ Ha = B_{0} L_{{{\text{ref}}}} \sqrt {\frac{{\sigma_{f} }}{{\mu_{f} }}} ,\;{\text{Da}} = \frac{K}{{L_{{{\text{ref}}}}^{2} }},\,Fc = - \frac{1.75}{{\sqrt {150} }},\;Q = \frac{H}{{q^{^{\prime\prime}} }}Q_{0} ,\;\Delta T = \frac{{q^{^{\prime\prime}} H}}{{k_{f} }} $$

(5)

Here x, y are the dimensionless $\overline{x},\overline{y}$ co-ordinates, u, v are non-dimension velocity components, p is dimensionless pressure, Rayleigh number Ra, $\mu_{hnf}$ is the hybrid nanofluid dynamic velocity, the Darcy number Da, α is thermal diffusivity, t is time, Ha is Hartmann number, θ is dimensionless temperature, $\sigma_{hnf}$ is the hybrid nanofluid electrical conductivity,$Q_{0}$ is the heat generation, Prandtl number Pr and Fc is the Forchheimer (quadratic) drag coefficient.

Heat transferred rates at the boundary condition can be computed with a Nusselt number. On the hot left side wall, the appropriate expression is:

$$ {\text{Nu}} = \frac{{k_{nf} }}{{k_{f} }}\left( {\frac{\partial \theta }{{\partial X}}} \right)_{x = 1} $$

(6)

The related Nusselt number, Nu_ave, can then be calculated as follows:

$$ {\text{Nu}}_{{_{ave} }} = \int_{0}^{L} {\frac{\partial \theta }{{\partial X}}} dy $$

(7)

Using the expression of non-dimensional parameters, the governing equations forms in a below form:

Continuity:

$$ \frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0 $$

(8)

$x$- Momentum:

$$ \begin{aligned} \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} &= {\mkern 1mu} - \frac{{\partial p}}{{\partial x}} + Pr\left( {\frac{{\mu _{{hnf}} }}{{\mu _{f} }}} \right)\left( {\frac{{\rho _{f} }}{{\rho _{{hnf}} }}} \right)\left( {\frac{{\partial ^{2} u}}{{\partial x^{2} }} + \frac{{\partial ^{2} u}}{{\partial y^{2} }}} \right) - \frac{{Pr}}{{Da}}\left( {\frac{{\mu _{{hnf}} }}{{\mu _{f} }}} \right)\left( {\frac{{\rho _{f} }}{{\rho _{{hnf}} }}} \right)u \hfill \\ &\qquad + Ha^{2} Pr{\mkern 1mu} \left( {\frac{{\sigma _{{hnf}} }}{{\sigma _{f} }}} \right)\left( {\frac{{\rho _{f} }}{{\rho _{{hnf}} }}} \right)\left( {v\;sin\phi \;cos\phi - u\;sin^{2} \phi } \right) - \frac{{1.75}}{{\sqrt {150} }}\frac{{u\sqrt {u^{2} + v^{2} } }}{{\sqrt {Da} }} \hfill \\ \end{aligned} $$

(9)

$y$- Momentum:

$$ \begin{aligned} \frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} &= {\mkern 1mu} - \frac{{\partial p}}{{\partial y}} + Pr\left( {\frac{{\mu _{{hnf}} }}{{\mu _{f} }}} \right)\left( {\frac{{\rho _{f} }}{{\rho _{{hnf}} }}} \right)\left( {\frac{{\partial ^{2} v}}{{\partial x^{2} }} + \frac{{\partial ^{2} v}}{{\partial y^{2} }}} \right) - \frac{{Pr}}{{Da}}\left( {\frac{{\mu _{{hnf}} }}{{\mu _{f} }}} \right)\left( {\frac{{\rho _{f} }}{{\rho _{{hnf}} }}} \right)v + \left( {\frac{{\left( {\rho \beta } \right)_{{hnf}} }}{{\rho _{{hnf}} \beta _{f} }}} \right)Ra\;Pr\theta \hfill \\ & \qquad + Ha^{2} Pr{\mkern 1mu} \left( {\frac{{\sigma _{{hnf}} }}{{\sigma _{f} }}} \right)\left( {\frac{{\rho _{f} }}{{\rho _{{hnf}} }}} \right)\left( {v\;sin\phi \;cos\phi - u\;sin^{2} \phi } \right) - \frac{{1.75}}{{\sqrt {150} }}\frac{{v\sqrt {u^{2} + v^{2} } }}{{\sqrt {Da} }} \hfill \\ \end{aligned} $$

(10)

Energy:

$$ \frac{\partial \theta }{{\partial t}} + u\frac{\partial \theta }{{\partial x}} + v\frac{\partial \theta }{{\partial y}} = \frac{{\alpha_{hnf} }}{{\alpha_{f} }}\left( {\frac{{\partial^{2} \theta }}{{\partial x^{2} }} + \frac{{\partial^{2} \theta }}{{\partial y^{2} }}} \right) + Q\frac{{\left( {\rho C_{p} } \right)_{f} }}{{\left( {\rho C_{p} } \right)_{hnf} }} $$

(11)

3.1 Boundary conditions

The following boundary conditions have been used:

$$ u = 0,v = 0,\theta = 0\,{\text{at}}\;t = 0\;{\text{everywhere at}}\;t > 0 $$

$$ u = 0,v = 0,\frac{\partial \theta }{{\partial y}} = 0\;{\text{for}}\;y = 0,L\;{\text{and}}\;0 \le x \le L $$

(12)

$$ \theta = \theta_{h} ,u = 0,v = 0\;{\text{for}}\;x = 0\;{\text{and}}\;0 \le y \le L $$

$$ \theta = \theta_{c} ,u = 0,v = 0\;{\text{for}}\;y = L\;{\text{and}}\;0 \le x \le L $$

3.2 Hybrid nanofluid properties

Mathematical formulation of water/Al₂O₃ nanofluid and hybrid water–Al₂O₃/Cu nanofluid has been described by the following equations:

$$ \rho_{nf} = \left( {1 - \phi } \right)\rho_{bf} + \phi \rho_{p} $$

(13)

$$ \rho_{hnf} = \phi_{{Al_{2} O_{3} }} \rho_{{Al_{2} O_{3} }} + \phi_{Cu} \rho_{Cu} + \left( {1 - \phi } \right)\rho_{bf} $$

(14)

where ϕ is the total bulk concentration which is estimated as; $\phi = \phi_{{{\text{Cu}}}} + \phi_{{{\text{Al}}_{{2}} {\text{O}}_{3} }}$.

The thermal heat capacity of the nanofluid (Eq. 15) and hybrid nanofluid (Eq. 16) has been formalized by the following form of equations Miroshnichenko et al. [23], Rashad et al. [15]:

$$ \left( {\rho C_{p} } \right)_{nf} = \phi \left( {\rho C_{p} } \right)_{p} + \left( {1 - \phi } \right)\left( {\rho C_{p} } \right)_{bf} $$

(15)

$$ \left( {\rho C_{p} } \right)_{hnf} = \phi_{{{\text{Al}}_{{2}} {\text{O}}_{3} }} \left( {\rho C_{p} } \right)_{{{\text{Al}}_{{2}} {\text{O}}_{3} }} + \left( {1 - \phi } \right)\left( {\rho C_{p} } \right)_{bf} + \phi_{{{\text{Cu}}}} \left( {\rho C_{p} } \right)_{{{\text{Cu}}}} $$

(16)

Here, Eq. 15 is taken for calculating nanofluid's coefficient of thermal expansion:

$$ \left( {\rho \beta } \right)_{nf} = \phi \left( {\rho \beta } \right)_{p} + \left( {1 - \phi } \right)\left( {\rho \beta } \right)_{bf} $$

(17)

where $\beta_{p}$ and $\beta_{bf}$ are denoted as the solid fractions and the coefficients of thermal increase in the fluid, respectively.

Therefore, the thermal expansion can be characterized as:

$$ \left( {\rho \beta } \right)_{hnf} = \phi_{{{\text{Al}}_{{2}} {\text{O}}_{{3}} }} \left( {\rho \beta } \right)_{{{\text{Al}}_{{2}} {\text{O}}_{3} }} + \phi_{{{\text{Cu}}}} \left( {\rho \beta } \right)_{{{\text{Cu}}}} + \left( {1 - \phi } \right)\left( {\rho \beta } \right)_{{{\text{bf}}}} $$

(18)

The thermal diffusivity $\left( {\alpha_{nf} } \right)$ of nanofluid is defined as:

$$ \alpha_{nf} = \frac{{k_{nf} }}{{\left( {\rho C_{p} } \right)_{nf} }} $$

(19)

In Eq. (19), $k_{nf}$ is a measure of thermal conductivity of the nanoflow [Maxwell-Garnetts model], which for spherical nanoparticles, as below

$$ \frac{{k_{nf} }}{{k_{bf} }} = \frac{{\left( {k_{p} + 2k_{bf} } \right) - 2\phi \left( {k_{bf} - k_{p} } \right)}}{{\left( {2k_{bf} + k_{p} } \right) - \phi \left( {k_{bf} - k_{p} } \right)}} $$

(20)

Thus, the thermal diffusivity $\alpha_{hnf}$ of the hybrid nanofluid can be defined as:

$$ \alpha_{hnf} = \frac{{k_{hnf} }}{{\left( {\rho C_{p} } \right)_{hnf} }} $$

(21)

If one were to compute the thermal conductivity of the hybrid nano-fluid using the Maxwell model, the results would be as follows and Eq. (13) should be used.

$$ \begin{aligned} \frac{{k_{{hnf}} }}{{k_{{bf}} }}& = \left( {\frac{{\left( {\phi _{{{\text{Al}}_{2} {\text{O}}_{3} }} k_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi _{{{\text{Cu}}}} k_{{{\text{Cu}}}} } \right)}}{\phi } + 2k_{{bf}} + 2\left( {\phi _{{{\text{Al}}_{2} {\text{O}}_{3} }} k_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi _{{{\text{Cu}}}} k_{{{\text{Cu}}}} } \right) - \left( {2\phi k_{{bf}} } \right)} \right) \hfill \\ &\qquad \times \left( {\frac{{\left( {\phi _{{{\text{Al}}_{2} {\text{O}}_{3} }} k_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi _{{{\text{Cu}}}} k_{{{\text{Cu}}}} } \right)}}{\phi } + 2k_{{bf}} - \left( {\phi _{{{\text{Al}}_{2} {\text{O}}_{3} }} k_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi _{{{\text{Cu}}}} k_{{{\text{Cu}}}} } \right) + \left( {\phi k_{{bf}} } \right)} \right) \hfill \\ \end{aligned} $$

(22)

The effectual dynamic thickness of the nanofluid Nath et al. [8] is given by

$$ \mu_{nf} = \frac{{\mu_{bf} }}{{\left( {1 - \phi } \right)^{2.5} }} $$

(23)

$$ \mu_{hnf} = \frac{{\mu_{bf} }}{{\left( {1 - (\phi_{{{\text{Al}}_{{2}} {\text{O}}_{3} }} + \phi_{{{\text{Cu}}}} )} \right)^{2.5} }} $$

(24)

Maxwell introduced the effective conductivity of nanofluid as

$$ \frac{{\sigma_{nf} }}{{\sigma_{bf} }} = 1 + \frac{{3\left( {\frac{{\sigma_{p} }}{{\sigma_{bf} }} - 1} \right)\phi }}{{\left( {\frac{{\sigma_{p} }}{{\sigma_{bf} }} + 2} \right) - \left( {\frac{{\sigma_{p} }}{{\sigma_{bf} }} - 1} \right)\phi }} $$

(25)

Thus, the effectual electric conductivity of the Al₂O₃/Cu hybrid nanofluid is given by (Table 1)

$$ \frac{{\sigma_{hnf} }}{{\sigma_{bf} }} = 1 + \frac{{3\left( {\frac{{\left( {\phi_{{{\text{Cu}}}} \sigma_{{{\text{Cu}}}} + \phi_{{{\text{Al}}_{{2}} {\text{O}}_{3} }} \sigma_{{{\text{Al}}_{{2}} {\text{O}}_{3} }} } \right)}}{{\sigma_{bf} }} - \left( {\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi_{{{\text{Cu}}}} } \right)} \right)\phi }}{{\left( {\frac{{\left( {\sigma_{{{\text{Al}}_{2} {\text{O}}_{3} }} \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi_{{{\text{Cu}}}} \sigma_{{{\text{Cu}}}} } \right)}}{{\phi \sigma_{bf} }} + 2} \right) - \left( {\frac{{\left( {\sigma_{{{\text{Al}}_{2} {\text{O}}_{3} }} \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi_{{{\text{Cu}}}} \sigma_{{{\text{Cu}}}} } \right)}}{{\sigma_{bf} }} - \left( {\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi_{{{\text{Cu}}}} } \right)} \right)\phi }} $$

(26)

Table 1 Water and nanoparticles thermophysical properties: Mehryan et al.[2]; Nath & Murugesan et al. [18]

4 Solving procedures of LBM

The governing Eqs. 8–12 have been solved by LBM approach and approximated using BGK method. Sheikholeslami et al. [3]. In this methodology, f and g are two types of distribution functions that are utilized for velocity and temperature respectively. The LBM can be used to derive f and g. The associated D2Q9 lattice is seen in Fig. 2.

Fig. 2

D2Q9 lattice model

Velocity field:

$$ \tau_{\alpha } f_{i} \left( {x + C_{i} \Delta t,t + \Delta t} \right) = \tau_{\alpha } f_{i} \left( {x,t} \right) - \left( {f_{i} \left( {x,t} \right) - f_{i}^{{{\text{eq}}}} \left( {x,t} \right)} \right) + \tau_{\alpha } \Delta tF_{i} $$

(27)

Temperature field:

$$ g_{i} \left( {x + C_{i} \Delta t,t + \Delta t} \right)\tau_{\alpha } = g_{i} \left( {x,t} \right)\tau_{\alpha } - \left( {g_{i} \left( {x,t} \right) - g_{i}^{{{\text{eq}}}} \left( {x,t} \right)} \right) $$

(28)

In Eqs. (27) and (28), C_i denotes discrete velocity vectors of individual particles defined by the lattice model. Additionally, $f_{i}$ signifies the function of particle dispersion for various lattice directions while t and x denote time and the fluid node spatial location, respectively. The displacement value in various directions is $c_{i} \,\,\,\partial \,t$ and the collision operator is $\Omega$. The impact of particle collisions and changes in external forces (F) on the distribution function is represented on the right side of the velocity field Eq. (27) and can be re-defined in two steps to simplify the numerical algorithm. These steps are termed collision and streaming Girimaji et al. 2013

$$ f_{i}^{eq} = w_{i} \rho \left[ {1 + \frac{{3(C_{i} u)}}{{C_{S}^{2} }} + \frac{{9(C_{i} u)^{2} }}{{2C_{S}^{4} }} - \frac{{3u^{2} }}{{2C_{S}^{2} }}} \right] $$

(29)

$$ g_{i}^{eq} = w_{i}^{^{\prime}} T\left[ {1 + 3\frac{{C_{i} u}}{{C_{S}^{2} }}} \right] $$

(30)

Two populations use the D2Q9-D2Q9 thermal model which are associated with the weighting functions as follows:

$$ C_{i} = \left\{ \begin{gathered} (0,0),\frac{4}{9},i = 0 \hfill \\ ( \pm 1,0),(0, \pm 1),\frac{1}{9},i = 1,2,3,4 \hfill \\ ( \pm 1, \pm 1),\frac{1}{36},i = 5,6,7,8 \hfill \\ \end{gathered} \right. $$

(31)

$$ w_{i} = \left\{ \begin{gathered} \frac{4}{9},i = 0 \hfill \\ \frac{1}{9},i = 1,2,3,4 \hfill \\ \frac{1}{36},i = 5,6,7,8 \hfill \\ \end{gathered} \right. $$

(32)

The thermal diffusivity (α) and kinematic thickness (ν) are linked to the moment of relaxation time by means of a continuous Eq. (32):

$$ \nu = \left[ {\tau_{\nu } - \frac{1}{2}} \right]c_{s}^{2} {\Delta }t,\;\alpha = \left[ {\tau_{\alpha } - \frac{1}{2}} \right]c_{s}^{2} {\Delta }t $$

(33)

where

$$ c_{s} = \frac{c}{\sqrt 3 } $$

(34)

The force term F_i is defined as follows and refers to the external force.

$$ F_{i} = \frac{{w_{i} }}{{C_{S}^{2} }}F.C_{i} $$

(35)

The total external physical force is signified by F:

$$ F = F_{x} + F_{y} $$

(36)

The macroscopical quantities u, $\theta$ and $\rho$ are defined in LBM as follows:

Density of flow:

$$ \rho = \mathop \sum \limits_{i}^{{}} f_{i} $$

(37)

Momentum:

$$ \rho u = \mathop \sum \limits_{i}^{{}} f_{i} C_{{\mathbf{i}}} $$

(38)

Temperature:

$$ \theta = \mathop \sum \limits_{i}^{{}} {\text{g}}_{i} $$

(39)

5 Grid independency test and model validation

Grid independency test has been done by MATLAB-based LBM for less computational cost and to study the effect of mesh size. To select the proper grid size, five different grid sizes have been considered. From Table 2 and Fig. 2, it has been found that the grid size (101 *101) is the proper grid size to carry forward the present work. Because after the specific grid size, the value of mean Nusselt number becomes constant. The present work has been validated with the studies of Khan et al. [31]. The comparative analysis is shown in Table 3, which provides us enough confidence to carry forward the work. Figure 3b demonstrates Nusselt number distribution on the bottom wall of the cavity at Ra = 105, Pr = 0.7 against the numerical simulation of Sathiyamoorthy et al. [33].

Table 2 Grid independence study for the pure fluid when Ra = 10³

Table 3 Comparative analysis of Ra vs. Nu

Fig.3

a Comparison Streamlines and Isotherms Ra = 10⁴, Da = 0.01. b Comparison of the Nusselt number distribution at Ra = 10⁵

The percentage error of the mesh size is less than 1% when the grid size is 101 * 101 during testing. For Nu exactly 1.00 therefore, a grid size of 101 *101 is confidently used to isolate the computational domain.

6 Results and discussions

For different values of Rayleigh number (Ra = 10³, 10⁴, 10⁵, and 10⁶), Hartmann number (Ha = 0, 25, 50, and 100), Darcy number (Da = 0.1, 0.01, 0.001, and 0.0001), and Heat generation (Q = 3, 5, 7 and 9), the current section describes the characteristics of MHD free convective flow (isotherm, streamline, and Nusselt number distribution) of hybrid nanofluid in a differential heated square enclosure. In Table 3 we compare the value of Ra with the previously studied value and the study shows that we have calculated almost the same value.

In the absence of the thermal physical properties of the magnetic field, Rayleigh number, Darcy number, Hartmann number with modifications in the geometry and boundary conditions, the current model is equal to the same of the results proposed by ref [34] Fig. 3a clarifies the comparison outcomes of both the investigations. Figure 3b demonstrates Nusselt number distribution on the bottom wall of the cavity at Ra = 10.⁵, Pr = 0.7 against the numerical simulation of Sathiyamoorthy et al. [33]

6.1 Influence of considered parameters on flow characteristics

Figure 4a-d demonstrates the influence of Ra on the distribution of streamlines. At Ra = 10³ symmetric vortices have been clockwise circulated and for Ra = 10⁴ a symmetric clockwise circulated the same eddy has been found. In addition, at Ra = 10⁵ the length of the vortex expands diagonally from the upper right wall to the bottom left corner and which stretched more in the vertical direction for Ra = 10⁶. Furthermore, they found that the length of vortices to stretch to the center causes the formation of an ellipse toward the top right corner and down-left corner.

Fig. 4

Profile of Streamlines for vs Ra, with Pr = 7, Ha = 10, Q = 1, Da = 0.01. a Ra = 10³, b Ra = 10⁴, c Ra = 10⁵, d Ra = 10⁶

The contours of the isotherms for different values of Ra are presented in Fig. 5a–d. For Ra = 10³ and 10⁴ the isotherm contours are parallel to the side walls and perpendicular to the top and bottom walls. As the largest deformation is observed, at Ra = 10⁵ the isotherms collapse and shrink toward the top right and bottom left corners. The isotherms reveal asymmetric. The left wall heat zone is gradually pushed toward the right wall. For Ra = 10⁶ the profiles of the isotherms almost topper in the top-right and bottom-left corners. With the increase in Ra, the left wall heat is gradually transferred to the cold wall. The cluster isotherms obey the top left and lower right corners.

Fig. 5

Profile of isotherms for vs Rayleigh numbers, a Ra = 10³, b Ra = 10⁴, c Ra = 10⁵, (d) Ra = 10⁶ with Pr = 7, Ha = 10, Q = 1, Da = 0.01

For different values of the magnetic field, the profiles of streamlines are presented in Fig. 6a-d. At magnetic field Ha = 0, a clockwise streamline circulated asymmetric eddy has been found which moved toward the top right corner to the down left corner. It can be seen moving toward the top right corner and the down left corner of the cage when the Hartmann number is very low and equal to 0. A clockwise streamline circulated symmetric eddy is maintained inside creating a small ellipse top to bottom sides at an increased magnetic field of Ha equal to 25. At magnetic field Ha = 50, the distortion progressively becomes much more than substantial, as a result, the flow eddy stretched toward the top wall and the flow becomes symmetric at the downside of the wall. This is because the magnetic field is proportional to the strength relative to the viscous force. When the magnetic field Ha = 0, 25, and 50, the streamline profiles are symmetrical when seen from the center of the vertical wall. When magnetic field Ha = 100, however, the profiles of the eddies become more stretched out when viewed from the center of the vertical wall.

Fig. 6

Profile of Streamlines for a Ha = 0, b Ha = 25, c Ha = 50, d Ha = 100 with Pr = 7, Ha = 10, Q = 1, Da = 0.01

The Contours of isotherms for various values of magnetic field Ha are shown in Fig. 7a–d. The isotherm is clustered on the lower left wall and upper right wall. The isotherm extends along the isotherm at the top of the left wall and at the bottom of the right wall. When magnetic field Ha = 25, the isotherm spreads from the left hot wall to the right cold wall. The isotherm moves along the left lower wall and the right upper wall at uniform intervals. The isotherm expands at the top of the left wall and at the bottom of the right wall. As magnetic field Ha = 50, the isotherm moves parallel to the left hot wall and the right cold wall and perpendicular to the top wall to the bottom wall. At magnetic field Ha = 100, the hybrid nanofluid leads to a symmetrical distribution perpendicular to the left hot wall to the right cold wall.

Fig. 7

Profile of isotherms for a Ha = 0, b Ha = 25, c Ha = 50, d Ha = 100 with Pr = 7, Ha = 10, Q = 1, Da = 0.01

Figure 8a–d presents the streamlined plots for different values of the Darcy effect. At Darcy effect Da = 0.0001, asymmetric two-eddy cells tallied have been observed in the center of the enclosure due to high permeability. As a result, a single hot vertex cell generates on the left side and a single cold vertex cell format on the right side. In addition, Darcy effect Da = 0.001, vortices developed diagonally, meanwhile from the top right corner to the bottom-left corner. The fluid flow is revved and the enclosure always extends in the Darcy effect However, for Da = 0.01, a symmetric eddy cell generates at the center of the enclosure due to the lowest permeability. Furthermore, it has been seen that at Da = 0.1, the Darcian bulk drag decreases, which is characterized by a warping of the single eddy cell which occurs diagonally from the bottom left corner to the top right corner of the enclosure. The flow speeds up and the size of the container also increases.

Fig. 8

Profile of Streamlines for a Da = 0.0001, b Da = 0.001, c Da = 0.01, d Da = 0.1 with Pr = 7, Ha = 10, Q = 1, Da = 0.01

The influence of the Darcy effect has been analyzed by the contour plots of temperature, as seen in Fig. 9a-d. At Darcy effect Da = 0.0001, streamlines are vertical because of the low permeability as a result internal flow slows down. While the streamlines produce symmetric distributions which are parallel to the left and right walls due to relatively high permeability at Darcy effect (Da = 0.001). As a result, in the upper left and downright corners the streamlined begins to loosen up but it expands beyond the hot zone. In addition, at the Darcy effect, Da = 0.01, symmetry flow behavior has been found at the top zone wall. Further increase in Da, asymmetry behavior of flow has been observed between the upright and left corner. The top left and lower right corners have been streamlined. It's possible that the hot zone was first restricted to the upper zone near the upright wall because of its proximity to the left wall.

Fig. 9

Profile of isotherms for a Da = 0.0001, b Da = 0.001, c Da = 0.01, d Da = 0.1 with Pr = 7, Ha = 10, Q = 1, Da = 0.01

6.2 Effect of considered parameters on heat transfer characteristics

Figure 10a–d shows the streamlines plot for various values of Q. explores the streamlines distribution with the hybrid nanofluid in the square enclosure i.e., the heat generation an asymmetric eddy can be seen moving near the up-right corner and the low left corner of the cage when the heat generation number is very low. Due to the subsequent increased heat generation, a symmetric vortex is observed in the enclosure.

Fig. 10

Profile of Streamlines for a Q = 3, b Q = 5, c Q = 7, d Q = 9 with Pr = 7, Ha = 10, Q = 1, Da = 0.01

Fig. 11

Profile of isotherms for a Q = 3, b Q = 5, c Q = 7, d Q = 9 with Pr = 7, Ha = 10, Q = 1, Da = 0.01

In Figure 11a–d when Q = 3 isothermal distribution from the left heat wall to the right cold wall, the isotherms are close to each other in the bottom left corner and the top right corner. The isothermal expansion in the top left corner and down right corner can be seen. When Q = 5, the isothermal distribution from the left heat wall to the right cold the isotherm for the wall moves at a certain distance, the isotherms are slightly spaced at the down left corner and the top right corner. More penetrating Behavior has been observed at Q = 7, as a result the isotherm moves more widely from the left hot wall to the right cold wall. The isotherm is less extended in the top left corner and the lower right corner. As Q = 9, the isotherm moves vertically between the upper and lower walls.

The variations of Nu have been shown for various values of Ra as shown in Fig. 12. It has been demonstrated that the increased value of Ra causes the significant enhancement of the trend of Nu but it’s decaying vertically from the upper of the heat left wall to the base of the enclosure. Generally, this figure describes that thermal convection increases more than thermal conduction and heat transfer to the wall slows down as the flow reaches the top of the cavity and the bottom of the left hot wall.

Fig. 12

Plots of Nu vs. Ra for Ha = 10, Q = 1, Da = 0.01, Pr = 7

From Fig. 13, it has been found that the trend of Nusselt number decreases sharply with the rise of Ha. The heat generated by the increasing Hartmann number boosts the temperatures within the enclosure. This reduces the rate of heat transferred to the heat wall and causes the Nusselt number to fall. i.e., however, a strong increase in Nusselt’s number as we progress from the upper of the left hot wall to the base.

Fig. 13

Plots of Nu vs. Ha for Q = 1, Da = 0.01, Ra = 10⁵, Pr = 7, at the left hot wall

Figure 14 presents the plot of Nu vs. Da. From these figures, it has been seen that the graph trend of local Nu initially increases close to the upper of the left hot wall, while its decreases with the reduces of the values of Da = 0.1, 0.01, and 0.001. At Da = 0.0001, opposite trend has been found. Therefore, the rate of heat transfer becomes high for higher values of Da.

Fig. 14

Plots of Nu vs. Da for Pr = 7, Ha = 10, Q = 1, Ra = 10⁵, at the left hot wall

Figure 15 describes the linear relation between Q vs curve trend of Local Nu. As the value of heat generation increases from low to high in the Nusselt number diagram the upper left-hand side expands from the low value to the high value in the lower right-hand side. Abdelsalam et al. [35] investigated the effect of electroosmotic forces on sperm swimming across the cervical canal. Thumma et al. [36] analysed numerically the impact of a non-linear density temperature and a non-uniform heat source/sink on the flow of a 3D Maxwell nanofluid.

Fig. 15

Plots of Nu vs. Q for Pr = 7, Ha = 10, Da = 0.01, Ra = 10⁵ at the left hot wall

7 Conclusions

Numerically, the present article describes the two-dimensional MHD natural convection hybrid nanofluid flow in a differentially heated enclosure containing a non-Darcy flow with heat generation effects. Major findings have been described as below:

• 1. With the increase in Ra, the single eddy cell skewness is intensified and the streamlined are further consolidated in the down-left and up-right corners. For higher value of Ra, the graph trend of local Nu increases toward the upper hot wall to base.

• 2. Nusselt number is increased from the upper of the hot wall to the base with greater Rayleigh number.

• 3. The profiles of the streamlines created in the square enclosure are symmetrical when viewed from the center of the vertical wall. When the Hartmann number is raised to high the profiles of the eddies become more stretched out when seen from the middle of the vertical wall.

• 4. The Local Nusselt number reduces dramatically as the Hartmann number rises. However, there is a significant elevation in local Nusselt's number as we progress from the upper of the left hot wall to the base.

• 5. As Darcy number is increased, as a consequence the Darcian bulk drag decreases, which is characterized by a warping of the single eddy cell diagonally from the bottom left corner to the top right corner of the single eddy cell. The top left and lower right corners have been streamlined. It's possible that the hot zone was first restricted to the upper zone near the upright wall because of its proximity to the left wall.

• 6. Nusselt number at the left wall is generally a maximum for highest permeability (largest value of Darcy number) after a critical location near the top left corner.

• 7. Elevating Heat generation produces a strong elevation in local Nusselt number which also increases significantly from top of the left hot wall to its base.