Introduction

Large-scale power generation equipment connected to long-range load centers through long-distance transmission lines has many technical challenges [1]. In the process of actual long-distance transmission, a large number of line impedances will be introduced in the power grid. Under the joint action of these line impedances and non-linear loads, the grid impedances can be overlooked, where the power grid is called weak grid [2,3,4], and the power grid generally has many inductive components within a certain frequency range [5, 6]. The grid-connect inverter will reduce the stability of the system when considering the power network impedance. Therefore, the research on the control strategy of a grid connected inverter in the weak gird has gradually become the focus of scholars all over the world.

Weighted average current control, as a damping control strategy, has received extensive attention due to its ring-like order reduction characteristics [7,8,9]. Grid pattern considering the influence of impedance is equals to the form of resistance series inductance, and the influence of impedance on grid-connect system is analyzed [10]. In reference [11], Zhou Lin et al. converted the mathematical model of the three-phase LCL inverter into the Norton equivalent circuit form, discusses the relationship between the grid-connected current and the voltage at the common coupling point, and obtains the closed-loop transfer function of the grid-connected system, and then uses Routh’s decision table and root locus method analyze the stability of its system, which lays a theoretical foundation for the inverter control scheme under weak grid. Xu Jinming and his colleagues [12] through in-depth analysis of the influence of the grid voltage feedforward control on the double closed-loop control of the filter capacitor current and the grid-connected current in a weak grid, an adaptive current control method for grid impedance estimation is proposed, which can dynamically update the regulator parameters. Adapt to the characteristics of weak power grids, but the dynamic measurement of power grid impedance makes the control system design more complicated and difficult to implement. In Reference [13], Yang Dongsheng et al. used virtual series impedance and virtual parallel impedance to adjust the phase angle and modulus of the inverter output impedance. The requirements of robustness and anti-interference performance can be considered at the same time, and the adaptability of the inverter to the weak power grid is improved. In Reference [14, 15] First, the AC is fed forward by adding resonance to the grid voltage, and then the fundamental voltage is extracted for feedforward control. Finally, it is combined with the quasi-PR controller and the resonance controller to better reduce the grid current harmonics. Xu Jinming and his colleagues [16] analyzed The influence of the grid impedance on the control system of the grid-connected inverter is analyzed, and the grid voltage feedforward control is improved to improve the stability of the inverter in a weak grid. Active damping of LCL filter is very important to control LCL grid-connect inverter. Active damping can reduce the resonance peak caused by LCL filter and stabilize the whole system easily [17,18,19]. In their work, a current weighted feed-back on-line inductive reactance detection technology is adopted. After dynamic measurement of inductive reactance, the weighting coefficient is adjusted to improve the performance of current weighted control and improve the robustness of the system [20].

In this article, based on the active damping control of grid voltage feed-forward, the weighted average current method is introduced to design a new weighting coefficient, which can restrain the influence of the inductive component in the grid impedance, reduce the system order and improve the stabilization of the system.

LCL grid cinnected inverter mathematical pattern

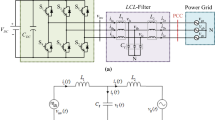
Figure 1 is the mathematical pattern of LCL three-phase grid-connect inverter considering the existence of grid impedance, where e is three-phase grid voltage, vsk (k = a,b,c) is inverter-side voltage, Saq 、 Sap 、 Sbq 、 Sbp 、 Scq 、 Scp are six IGBT, Vdc is DC voltage, Cdc is DC capacitance, L1 is inverter side inductance, L2 is grid-side inductance, i1 is inverter side current, i2 is grid side current, ic is filter capacitor current, Zg is the grid impedance, eg is the Common Coupling Point (PCC) voltage, and eg includes the grid voltage and the voltage on the grid impedance Zg.

Fig. 1
figure 1

Mathematical model of LCL type inverter considering grid impedance

Full size image

According to Fig. 1, the grid impedance and common coupling point voltage are expressed as follows.

$$ {Z}_g={r}_g+ sLg $$
(1)
$$ {e}_g=e+{Z}_g\ast i2 $$
(2)

In eqs. (1) and (2), rg and Lg are the resistive and inductive components of the grid impedance, respectively, and Lg = β(L1 + L2), β is the percentage of the inductive component of the power network impedance in the total inductance of the inverter.

This paper will take a three-phase grid-connect inverter as an example for analysis, and it related parameters are shown in Table 1.

Table 1 Inverter default parameters
Full size table

Analysis of active damping control scheme based on grid voltage feedforward

Figure 2 is the double closed-loop current control block diagram based on grid voltage feed-forward, in which kc is the feedback coefficient and kPWM is the PWM inverter link. In this paper, we uses SVPWM modulation, in which the value of kPWM is 1 and Gf(s) is the feed-forward coefficient.

Fig. 2
figure 2

Active damping control block diagram based on grid voltage feed-forward

Full size image

From Fig. 2, the open-circus transfer function of grid-connect current can be expressed as follows

$$ Gi2\_O=\frac{kPWMGi\left(\mathrm{s}\right)\mathrm{G}1\left(\mathrm{s}\right)\mathrm{G}\mathrm{m}\left(\mathrm{s}\right)\mathrm{G}2\left(\mathrm{s}\right)}{1+G1\left(\mathrm{s}\right)\mathrm{G}2\left(\mathrm{s}\right) kPWMkc\mathrm{G}2\left(\mathrm{s}\right)\mathrm{G}\mathrm{m}\left(\mathrm{s}\right)- Gf\left(\mathrm{s}\right)\mathrm{Zg} kPWM\mathrm{G}1\left(\mathrm{s}\right)\mathrm{G}2\left(\mathrm{s}\right)\mathrm{G}\mathrm{m}\left(\mathrm{s}\right)} $$
(3)

where, Gi(s) is PI controller, G1(s) = 1/sL1, G2(s) = 1/sC, Gm(s) = 1/(sL2 + Zg), Gf(s) = 1/kPWM, kC = 10.7.

It can obtain the relationship by expanding the eq. (3):

$$ Gi2\_O=\frac{Gi(s) kPWM}{s^2L1C\left( sL2+ Zg\right)+ kPWMkcsC\left( sL2+ Zg\right)+s\left(L1+L2\right)+ Zg- ZgGf(s) kPWM} $$
(4)

If Gf(s) =1/ is introduced into eq. (4), then:

$$ Gi2\_O=\frac{Gi(s) kPWM}{s^2L1C\left( sL2+ Zg\right)+ kPWMkcsC\left( sL2+ Zg\right)+s\left(L1+L2\right)} $$
(5)

When the power network impedance is pure resistance, Bode diagram of double current closed-loop control based on grid voltage feedforward can be obtained through the eq. (5), as shown in Fig. 3, with rg = 0.7 and 2 Ω, corresponding to Fig. 3a and b, respectively.

Fig. 3
figure 3

Bode diagram of active damping control based on grid voltage feedforward under pure resistance. a rg = 0.7Ω. b rg = 2Ω

Full size image

Obviously, if the grid impedance is pure resistance, the Bode diagram of the system changes very little, and the marginal changes only a few degrees, if the resistance increases, the phase margin of the system decreases slightly, with little change range, and the phase frequency curve basically coincides. Therefore, when the impedance is pure resistance, it has little effect on the system and it still runs stably, this is the influence of the resistive component in the power network impedance on the system, which can be almost ignored.

When the grid impedance is pure inductance, the frequency of conjugate open-circus poles of the system can be obtained from eq. (5) as follows

$$ {\omega}_{z_g}=\sqrt{\frac{L_1+{L}_2}{L_1\left({L}_2+{L}_g\right)C}} $$
(6)

From eq. (6), we can get the Bode diagram of active damping control based on grid voltage feed-forward under pure inductance, as shown in Fig. 4.

Fig. 4
figure 4

Bode diagram of active damping control based on grid voltage feed-forward under pure inductance. a β=1. b β=4. c β=6

Full size image

It can be seen from Fig. 4 and eq. (6) that the resonance frequency of the system will decrease with the increase of the inductive reactance of the power grid, and the decrease of the resonance frequency has a very obvious attenuation effect on the phase margin. Therefore, as the power grid’s inductive reactance increases, the margin of the system will always decrease until the grid connected system of the inverter loses its stability completely, so the existence of the inductive impedance of the power grid has a large impact on the feed-forward active damping control because of the large noise, it is necessary to suppress the influence of grid impedance.

Control strategy

Through the above analysis, we known that when the grid impedance exists, and because of the truth that the inductive component will have a great impact on the feed-forward control, while the resistive component can be ignored. Therefore, in order to ensure the stable operation of the system in the weak current network environment, here we introduce the weighted average current method to suppress the effect of the power network impedance based on the active damping control of power network voltage feed-forward.

Traditional weighted average current control strategy

The principle of the weighted average current strategy is to sum the part of grid-connect current and the inverter side current by weight, then take it as the feed-back value of the input current, which can not only ensure the tracking accuracy of the system, but also make the system have a higher power factor. The weighted average current traditional control flow chart under the weak current network is shown in Fig. 5, and the i12 in the figure meets the relationship.

$$ i12\_d=\left(1-\alpha \right)\kern1em {i}_1+\alpha i2d $$
(7)
Fig. 5
figure 5

Traditional weighted average current control block diagram under weak grid

Full size image

Where i1 is inverter side current, i2 is grid connection current, i12-d is weighted average current and α stand for weighting factor.

From Fig. 5, we can get the open-circus transfer function Gopen from iref_d to i12_d

$$ {\displaystyle \begin{array}{l}{G}_{open}=\frac{i_{12\_d}}{i_{ref\_d}}=\frac{G_i(s){k}_{\mathrm{PWM}}\left[\left(1-\alpha \right){s}^2C\left({L}_2+{L}_g\right)+1\right]}{s^3{L}_1C\left({L}_2+{L}_g\right)+s\left({L}_2+{L}_1+{L}_g\right)}\\ {}\kern4.25em =\frac{G_i(s){k}_{\mathrm{PWM}}\left[\left(1-\alpha \right){s}^2C\left({L}_2+{L}_g\right)+1\right]}{\left({L}_g+{L}_1+{L}_2\right)\left[1+\frac{L_1}{L_g+{L}_1+{L}_2}\left({L}_2+{L}_g\right){Cs}^2\right]}\end{array}} $$
(8)

Considering the inductive reactance of the power grid, the weighting coefficient of traditional weighted average current is designed as follows

$$ \alpha =1-\frac{L_1}{L_g+{L}_1+{L}_2}=\frac{L_g+{L}_2}{L_g+{L}_1+{L}_2} $$
(9)

The control blocks diagram after introducing the grid voltage feedforward is shown in Fig. 6. It can be seen that after considering the grid voltage feed-forward, the grid side voltage forms an additional positive feedback path through the grid inductive reactance Lg. This path does not exist in the strong power grid, and the additional positive feedback path will have an impact on the weighting coefficient.

Fig. 6
figure 6

shows the control flow chart after grid voltage feed-forward

Full size image

In Fig. 6, the open-circus transfer function from iref _ d to i12 _ d is as follows

$$ {G}_{open\_g}(s)=\frac{i_{12\_d}}{i_{ref\_d}}=\frac{G_i(s){k}_{PWM}\left[\left(1-\alpha \right)\left({L}_2+{L}_g\right){Cs}^2+1\right]}{L_1\left({L}_2+{L}_g\right){Cs}^3+\left({L}_1+{L}_2+{L}_g\right)s-{G}_f(s){k}_{PWM}{L}_gs} $$
(10)

Take the weighting coefficient of eq. (9) into eq. (10) to obtain

$$ {G}_{open\_g}=\frac{i_{12\_d}}{i_{ref\_d}}=\frac{G_i(s){k}_{PWM}\left[\frac{L_1}{L_g+{L}_1+{L}_2}{s}^2C\left({L}_2+{L}_g\right)+1\right]}{s\left({L}_g+{L}_1+{L}_2\right)\left[\frac{L_1}{L_g+{L}_1+{L}_2}\left({L}_2+{L}_g\right){Cs}^2-\frac{G_f(s){k}_{PWM}{L}_g}{L_g+{L}_1+{L}_2}+1\right]} $$
(11)

It can be seen from eq. (11) that there is an additional term GfkPWMLg/(L1 + L2 + Lg) in the transfer function of the system, and this term is related to the inductive reactance of the power grid. In order to reduce the system to the first order, this term must be eliminated. It is necessary to make Gf(s) = 0, that is to say, to eliminate the feed-forward term of the power grid voltage, and inductive reactance of the power grid will have an impact on the feed-forward term in the weak grid. Therefore, improved weighted average current control strategy is proposed.

An improved weighted average current control strategy

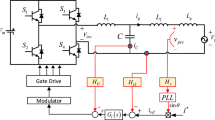
With the weighted average current method based on grid voltage feed-forward-based active damping control introduced, the control flow chart is shown in Fig. 7. As analyzed above, the grid voltage feed-forward link uses the grid impedance to introduce a positive feedback path to the control system block diagram, so the main idea of improving the adaptability of the weighted average current in a weak grid is to adopt a new weighting calculation method, then the system is reduced to the first-order form by the pole-zero cancellation method. Meanwhile, the regenerative feed-back circuit introduced by grid front feed is eliminated.

Fig. 7
figure 7

An improved weighted average current control method in weak current network

Full size image

In Fig. 7, it can be concluded that the transfer function of the system iref _ d to i12 _ d is

$$ {G}_{open\_g}=\frac{i_{12\_g}}{i_{ref\_g}}=\frac{G_i{k}_{PWM}\left[\left(1-\alpha \right)\left( Lg+L2\right){Cs}^2+1\right]}{L_1\left( Lg+L2\right){Cs}^2+\left({L}_1+ Lg+L2\right)s+{kckPWMs}^2C\left( Lg+L2\right)-{G}_f(s){k}_{PWM}{L}_gs} $$
(12)

Substituting Gf(s) = 1/kPWM into (12) can obtain

$$ {G}_{open\_g}(s)=\frac{i_{12}}{i_{ref}}=\frac{\frac{G_i(s){k}_{PWM}}{s\left({L}_1+{L}_2\right)}\left[\left(1-\alpha \right)\left({L}_2+{L}_g\right){Cs}^2+1\right]}{\frac{L_1}{L_1+{L}_2}\left({L}_2+{L}_g\right) sC\left[s+\frac{k_C{k}_{PWM}}{L_1}\right]+1} $$
(13)

It can be seen from eq. (13) that in order to perform pole-zero cancellation, the circuit of kCkPWM(L2 + Lg)s2C needs to be eliminated, so kC = 0, namely, the capacitive current feedback circuit is not needed at this time. Then eq. (13) can be changed as

$$ {G}_{open\_\mathrm{g}}=\frac{\frac{G_i(s){k}_{PWM}}{s\left({L}_1+{L}_2\right)}\left[\left(1-\alpha \right)\left({L}_2+{L}_g\right){Cs}^2+1\right]}{\frac{L_1}{L_1+{L}_2}\left({L}_2+{L}_g\right){s}^2C+1} $$
(14)

Obviously, the new weighting coefficient can be expressed as

$$ \alpha =\frac{L_2}{L_1+{L}_2} $$
(15)

After that the open-circus transfer function of the system is reduced to the first-order form, as follows

$$ {G}_{open\_g}=\frac{G_i(s){K}_{\mathrm{PWM}}}{s\left({L}_1+{L}_2\right)} $$
(16)

Equations (15)–(16) reveal that the current inner loop control is decreased from the third-order to the first-order, and is not affected by the grid impedance, and the weighting coefficient is completely determined by the parameters of the LCL filter.

From eqs. (11) and (16), it is easy to obtain Bode diagram of traditional weighted average current control and improved weighted average current control (see Fig. 8).

Fig. 8
figure 8

Bode diagram of weighted average current before and after improvement

Full size image

As shown in Fig. 8 when the grid impedance Lg = 0.4, 0.6 and 2 mH. Under the traditional weighted average current, the system has resonance spikes, and the phase angle crosses − 180 degree, the system is unstable. However, the phase-frequency curve of the improved method changes with the impedance of the power grid, and the phase angle margin is always stable at about 90 degree, there is almost no change. The first-order characteristic is always maintained and being no longer affected by the power network impedance, the system can still operate stably.

Stability analysis

In the improved weighted average current method, the transfer function from iref _ d to i12 _ d is not affected by the grid impedance. However, the control target of the inverter is the grid current i2, so it is necessary to analyze the grid current stability after improving the weighted average current.

In Fig. 7, it can be concluded that the closed-loop transfer function from i12 _ d to iref _ d is

$$ Gclose=\frac{i2\_d}{iref\_d}=\frac{GikPWM}{L1\left( Lg+L2\right){Cs}^2+\left(L1+ Lg+L2\right)s+{kckPWMs}^2C\left( Lg+L2\right)+ GikPWM- GfkPWMLgs} $$
(17)

Equation (17) shows that the order of the system is relatively high and it is difficult to analyze the stabilization of the grid-connect current. Therefore, the control characteristics from i2 _ d to can be transformed into the control characteristics from i2 _ d to iref _ d, that is

$$ \frac{i_{2\_d}}{i_{ref\_d}}=\frac{i_{2\_d}}{i_{12\_d}}\cdot \frac{i_{12\_d}}{i_{ref\_d}} $$
(18)

From eq. (16), we know that the open-loop transfer function from i12 _ d to iref _ d is a first-order form, and it is not affected by the impedance of the grid. Thus, the current control characteristics from i2 _ d to iref _ d are consistent with the those from i2 _ d to i12 _ d. In Fig. 7, the closed-loop transfer function of i2 _ d to i12_d can be

$$ {{G_{close}}_{\_}}_g(s)=\frac{i_{2\_d}}{i_{12\_d}}=\frac{1}{\left(1-\alpha \right)\left({L}_2+{L}_g\right){Cs}^2+2} $$
(19)

The Routh table of its closed-circus transfer function can be obtained from eq. (19), as shown in Tab. 2. It can be seen from the table that the first column is all positive, so the system is stable, and the current control characteristics from i2 _ d to iref _ d are consistent with the current control characteristics from i2 _ d to i12 _ d, so when the grid impedance occurs, only a small change of phase angle margin and amplitude margin of i2 _ d to iref _ d current control is made. But it is still within the allowable stability margin and the system operates stably.

Table 2 Closed-loop transfer function Rolls decision table
Full size table

In Fig. 7, the open-circus transfer function from i2_d to iref_d is as follows

$$ Gclose=\frac{i2\_d}{iref\_d}=\frac{GikPWM}{L1\left( Lg+L2\right){Cs}^2+\left(L1+ Lg+L2\right)s+{kckPWMs}^2C\left( Lg+L2\right)- GfkPWMLgs} $$
(20)

Through the eq. (20), the grid-connected current open-loop function Bode diagram with different grid impedances can be obtained in MATLAB, as shown in Fig. 9. The diagram tell us that when the grid impedance changes, the amplitude margin and phase margin from i2_d to iref_d will change in a small range, but the system is still in stable operation.

Fig. 9
figure 9

The grid-connected current open-loop Bode diagram when the grid impedance changes

Full size image

Simulation analysis

To prove the correctness of the control method, we propose, building grid connected inverter model in MATLAB. By selecting different grid impedance values for comparison, the simulation parameters are shown in Table 1, and the weighting coefficient is set to be α = L2/(L1 + L2) = 0.545.

Taking A-phase current as the analysis object, when the grid impedance Lg = 0, the grid is in a strong state. The grid current simulation diagram of the two methods is shown in Fig. 10a and b, respectively. It can be find out from the figure that when the effect of grid impedance is ignored, both methods can operate stably with little difference, the waveform is smooth and convergent, and the output current quality of inverter is good.

Fig. 10
figure 10

Grid-connect current waveform at Lg = 0 mH. a Grid-connect current waveform at traditional weighted average current. b Grid-connect current waveform with improved weighted average current

Full size image

When considering the grid impedance, 0.6 mH grid inductive reactance is connected in series at PCC, as shown in Fig. 11a and b. The waveform is obviously distorted after using the traditional weighted average current, the waveform is not smoothly convergent, and the THD is 4.6%. However, with the improved method, the waveform has no obvious distortion, only a few defects, and the waveform is basically smoothly convergent. The system can run stably, and THD is 2.2%. The output current quality of inverter is better.

Fig. 11
figure 11

Grid-connected current waveform at Lg = 0.6 mH. a Grid-connected current waveform when traditional weighted average current. b Improved weighted average current grid-connected current waveform

Full size image

When a 2 mH grid impedance is connected in series with PCC, the current weighted average traditional distortion becomes more serious. As shown in Fig. 12a, there are many waveform defects, the system is no longer stable, and the inverter output current quality is poor, at this time THD = 5.1%. After the improved method is adopted, the waveform has a little distortion and few defects. Generally, it is smooth convergence, and the system can still operate stably with THD = 2.8%. The output current quality of the inverter is good.

Fig. 12
figure 12

Grid-connected current waveform at Lg = 2 mH. a Grid-connected current waveform at traditional weighted average current. b Grid-connected current waveform with improved weighted average current

Full size image

Figure 13 shows the emulation oscillogram of the switching process of traditional weighted average current and improved weighted average current when Lg = 2 mH. The figure includes the voltage waveform of the common parallel node and the grid current waveform. Before 0.2 s, the grid-connect inverter adopts the improved weighted average current method. The output current waveform of the inverter is of good quality, contains less harmonics, and basically runs smoothly at 0.2 s When switching to the traditional weighted average current method, it can be find out that the grid-connect current waveform and voltage waveform have the phenomenon of oscillation and divergence, and the harmonic content is more, the system becomes unstable. At the time of 0.24 s, the improved weighted average current method is put into use again, the system slowly recovers from an unstable state to a stable state, the waveform is smooth and converges, and the harmonic content is reduced.

Fig. 13
figure 13

Simulation waveform diagram of traditional and improved method switching process. a PCC voltage waveform of public grid connection point. b Grid-connected current waveform

Full size image

Conclusion

The active damping control method based on grid voltage feed-forward is analyzed under the power network impedance. With the feed-forward control introduced, a regenerative feed-back circuit with grid impedance has been added from the merging node, which will reduce the stability of grid current control.

For reduce the influence of power network impedance, the weighted average current control method is added to the control method. The current control method deduces that the traditional weighting coefficient is related to the grid impedance. It needs to measure the change of the grid impedance at any time to correct the weighting coefficient, which makes the control system very complex.

In order to solve the shortcomings of the traditional weighting coefficient, an improved weighted average current method is proposed. By redesigning the weighting coefficient, the influence of the grid impedance is suppressed. System decreased from third-order to first-order, the stability of the grid impedance will not decrease, and the parameter calculation of the filter will directly obtain the weighting coefficient.