1 Introduction

Renewable energy resources (RESs) integration is a vital opportunity to develop a sustainable power system to address the high energy demand and climate concerns. The distributed generation system (DGS) facilitates the RESs integration with low voltage distribution network [1]. The grid-connected voltage source inverter (VSI) is a key component in DGS where the filter part is subjected to attenuate high-frequency harmonics [1]. The inverter control structure is overall responsible for the output current quality, injected power and voltage level [2] according to the grid interconnection standards [3]. The two inductors one capacitor LCL-type filter is considered the viable choice over single inductor L-type owing to the better high-frequency harmonics attenuation and smaller inductor volume [2]. However, the inherent resonance challenge of the LCL-filter deteriorates the control performance and may lead to instability that must be damped for stable operation of the inverter system.

The passive damping and active damping are two main approaches [4, 5] to address the resonance challenge subjected to passive components addition with filter hardware or control structure modification, respectively. The active damping is more attractive approach due to lossless damping by compromising the control complexity [5]. The active damping approach can be classified into single-loop [6,7,8] and multi-loop [9,10,11,12,13] methods based on additional damping loop requirement. The multi-loop active damping methods are preferable due to higher control bandwidth and less parameters sensitivity. The multi-loop methods can be further divided into the capacitor voltage [9, 10, 14] and the capacitor current [15,16,17] damping methods based on measured filter capacitor variable for damping loop.

Among the capacitor voltage [9, 10, 18], grid current [19, 20] and robust control [21, 23] based damping methods, capacitor current feedback (CCF) active damping methods [11, 15,16,17] are widely discussed in the literature. The CCF methods are popular due to the high-quality output current. The proportional CCF damping method employed in [17] by the capacitor current feedback through a damping co-efficient with straightforward design and effective damping performance. However, it may suffer ineffectiveness of damping at a certain resonance frequency due to parameters variation in the presence of control loop delays [24]. The indirect delay compensations [16, 25] is one possible solution to minimize the delay impact and extend the stable damping region. A first-order high-pass filter (HPF) [26], band-pass compensator [27], proportional-integral (PI) function [16] and the recursive infinite impulse response compensator [25] are employed in CCF path to achieve effective damping with good robustness against filter parameters variations. In [28], a repetitive block is proposed to widen the damping region. However, the repetitive block results in infinite gain at the Nyquist frequency that may require additional treatment.

The direct delay reduction methods [15, 24, 29] are another way to improve the phase characteristics by modifying the pulse width modulation (PWM) process and therefore enhance the damping loop stability. A capacitor current sampling instant shifting technique is proposed in [24] for high robustness against grid impedance variations. Nevertheless, the reliability issue may arise due to aliasing and switching noise. A two-sampling technique with real-time computation technique [29] can overcome sampling and aliasing issue; however, its application is only limited to single-phase inverter due to modulation scheme limitation. A non-instantaneous loading and pulse-width equivalence scheme are reported in [15] to eliminate the delay without reliability issue and improve control performance. Besides, an observer method is applied in [30] to estimate the damping variable and wave-off additional sensor requirement. However, its performance is influenced by parameters variation, which is resolved by disturbance observer design in [31] that may add the complexity.

An alternative scheme is proposed in this paper to modify the capacitor current damping loop. According to the proposed method, a compensator is added across the filter, and feedback the augmented plant’s output, and termed as parallel feedforward compensation (PFC) method. This method has been explored in [9, 32,33,34] for resonance damping and reported good stability and improved control performance. The capacitor voltage damping based on PFC configuration has been applied in [9, 33] with a band-pass compensator design. The capacitor current damping with suggested configuration is employed in [35] with a damping co-efficient and reported the better potential for delay compensation. This work extended the PFC configuration for three-phase LCL-filtered grid-connected inverter (GCI) system. The capacitor current damping is employed and opted a high-pass filter (HPF) as a compensator. The proposed solution improves the control performance, extend the stable damping region and better resonance suppression without increasing the control complexity.

The paper organization is as follows. Section 2 starts with the modelling of three-phase GCI, followed by the control structure design based on the proposed scheme in section 3. It also includes the high-pass filter (HPF) compensator design used in the proposed configuration. The control performance and robustness studies, and its comparison with the proportional CCF method is presented in section IV. Section V covers the simulation and experimental results, and the conclusion is given in section IV.

2 Modelling of LCL-Filtered GCI System

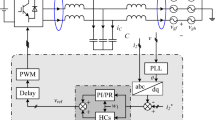
Figure 1a shows the schematic diagram of a three-phase VSI interfaced with the grid through the LCL-filter. It consists of the conversion unit, filter section and the power grid. The input DC-link voltage VDC is assumed constant, which can be supplied by a renewable energy source. The inverter output AC voltage vinv is fed to filter part to minimize the ripple current and obtain sinusoidal grid voltages at the point of common coupling (PCC) according to the grid standards [3]. The LCL-filter is composed of inverter-side inductors L1, grid-side inductor L2 and filter capacitor Cf. The equivalent series resistances of filter components are ignored for worse resonance case, and filter capacitors are connected in a delta configuration. The inverter-side current, grid-side current and filter capacitor current are represented by i1x, i2x and ifx respectively, where x is the respective phase. The grid inductance is combined with the grid-side filter inductance for convenience and assumed the voltage at PCC equal to the grid voltage vector vgx.

Fig. 1
figure 1

A three-phase LCL-filtered GCI diagram a schematic diagram b single-phase equivalent circuit diagram

Full size image

Figure 1b shows the equivalent single-phase representation of the three-phase GCI system. The following equations can be derived for the plant model when the Kirchhoff’s voltage law (KVL) and Kirchhoff’s current law (KCL) are applied as:

$$- v_{{{\text{inv}}}} (t) + L_{1} \frac{{{\text{d}}i_{1} (t)}}{{{\text{d}}t}} + \frac{1}{{C_{{\text{f}}} }}\int {i_{{\text{f}}} (t)dt = 0} .$$
(1)
$$\frac{1}{{C_{{\text{f}}} }}\int {i_{{\text{f}}} (t)dt} + L_{2} \frac{{{\text{d}}i_{2} (t)}}{{{\text{d}}t}} = 0.$$
(2)
$$i_{1} (t) - i_{{\text{f}}} (t) - i_{2} (t) = 0.$$
(3)

By taking the Laplace transform of (1)–(3) and after simplification, the transfer functions between output grid current, filter capacitor current and input voltage can be obtained as

$$G_{{i_{2} }} (s) = \frac{{i_{2} (s)}}{{v_{{{\text{inv}}}} (s)}} = \frac{1}{{L_{1} L_{2} C_{{\text{f}}} s(s^{2} + \omega_{{{\text{res}}}}^{2} )}},$$
(4)
$$G_{{i_{{\text{f}}} }} (s) = \frac{{i_{{\text{f}}} (s)}}{{v_{{{\text{inv}}}} (s)}} = \frac{s}{{L_{1} (s^{2} + \omega_{{{\text{res}}}}^{2} )}},$$
(5)

where fres is the nominal resonance frequency of LCL-filter and represented as

$$\omega_{{{\text{res}}}} = \sqrt {\frac{{L_{1} + L_{2} }}{{L_{1} L_{2} C_{{\text{f}}} }}} {\text{ or }}f_{{{\text{res}}}} = \frac{1}{2\pi }\sqrt {\frac{{L_{1} + L_{2} }}{{L_{1} L_{2} C_{{\text{f}}} }}}$$

The GCI system design parameters are enlisted in Table 1, which are opted by following the ripple current attenuation, reactive power generation and harmonics limit requirement guidelines given in [2]. The frequency response of (4) is plotted in Fig. 2, which shows the high gain peak at fres in magnitude curve. This resonance peak limits the controller performance that must need to damp for improved stable operation and control performance.

Table 1 GCI system design parameters
Full size table
Fig. 2
figure 2

Bode diagram of LCL-filter plant \(G_{{i_{2} }} (s)\)

Full size image

The linearised average model control block diagram of inverter is shown in Fig. 3. It contains the outer current loop and inner damping loop. The current loop is employed by measuring grid-side current owing to better injected current quality. The error current \(\delta i\) is calculated by measured current \(i_{2}\) and the reference current \(i_{2}^{*}\), which is regulated by the proportional resonant (PR) current controller GPR(s) and generates the reference signal for the inner damping loop. The capacitor current is measured for the damping loop to suppress the filter resonance peak and feedback at the controller output. The control loop delay Gd(s) constitutes one-sample computational and half-sample PWM delays which occurred during digital control implementation [36]. The total delay can be represented by the expression \(G_{d} (s) = e^{{ - 1.5T_{s} s}}\) where Ts is the sampling time (i.e. equal to 1/fs) [36]. The reference modulation signal um generated by the damping loop is compared with the high-frequency carrier signal Vtri to generate the gating signals for switching devices of the conversion unit. The conversion unit is represented by a constant Ginv, which is equal to the magnitude ratio \({{V_{{{\text{DC}}}} } \mathord{\left/ {\vphantom {{V_{{{\text{DC}}}} } {V_{{{\text{tri}}}} }}} \right. \kern-\nulldelimiterspace} {V_{{{\text{tri}}}} }}\) between the input voltage and carrier signal magnitude [24].

Fig. 3
figure 3

The linearized averaged model of inverter control system with control structure

Full size image

3 Proposed Method Based Inverter Control Structure Design

The main objectives of the inverter control structure are high quality injected current, minimum steady-state error, faster dynamic response, and robustness under system parameters variation. In this section, the control structure of inverter is designed based on the proposed damping loop method to ensure the required objectives.

3.1 Proposed Configuration for Damping Loop

The stability and control performance dynamics of an inverter depends on the damping loop configuration and compensator selection. In literature [10, 15, 16, 25], the capacitor current is usually feedback via a compensator to suppress the resonance peak. This conventional configuration has been shown in Fig. 4a where the filter plant \(G_{{i_{{\text{f}}} }} (s)\) with the output if feedback at the reference point while passing through the compensator H(s) in the feedback path. A constant damping gain as a compensator in capacitor current feedback path proposed in [17] is one of the simple solutions for damping loop design. This method emulates the equivalent resistance characteristics in series with the filter capacitor and can damp the resonance peak effectively. However, it suffers from limited effective damping region under filter parameters or grid inductance variations conditions as discussed in [24].

Fig. 4
figure 4

Damping loop realization a CCF compensation b the proposed PFC configuration c equivalent diagram of proposed configuration

Full size image

An alternative configuration is proposed to form the damping loop inspired by the concept of parallel feedforward compensation (PFC) initially introduced in [37, 38]. According to the proposed configuration, the damping compensator can be envisaged as a linear compensator in parallel with the plant. Figure 4b shows the proposed configuration where a compensator K(s) is added across the plant, and the feedback loop is employed by the augmented plant’s output. From the stability point of view, Fig. 4c is the equivalent diagram of the proposed configuration expressed in Fig. 4b. The key idea is to enhance the output impedance of the GCI at higher frequencies. Therefore, the resonance suppression capability will improve further. This method effectively damps the resonance peak with extended damping region and enhanced stability characteristics.

3.2 Damping Loop Design Based on Proposed Scheme

The complete schematic diagram of GCI system with the control structure based on the proposed damping loop configuration is shown in Fig. 5a. It can be observed that three-phase vectors of measured variables such as capacitor current if_abc, grid current if_abc, and PCC voltage vg_abc are transformed into stationary reference (\(\alpha \beta\)) frame for control realization using \({\text{abc}} \to \alpha \beta\) module [1]. The phase-locked loop (PLL) system [1] is used to extract the phase angle \(\theta\) of PCC voltages used for grid current synchronization, reference current \(i_{\alpha \beta }^{*}\) generation and phase transformation purposes. The I* is the reference DC quantity calculated by the outer voltage loop, which is ignored here for simplicity [1]. The \(\alpha \beta\) vectors of capacitor current and grid current are used to employ the damping loop and current loop, respectively.

Fig. 5
figure 5

GCI system based on proposed damping loop a schematic diagram b linearized control block diagram

Full size image

From the inner damping loop based on the proposed scheme, it can be noticed that the feedback damping signal is the sum of the capacitor current and the reference modulation signal, which is passed through the compensator K(s). A proportional gain P is introduced in the damping loop forward path to obtain desired control performance. The proposed damping loop is highlighted by the red colour dotted area. The reference modulation signal um is further transformed back to three-phase vectors using \(\alpha \beta \to {\text{abc}}\) module. These three-phase modulating signals are used to generate the gate signals (\({\text{S}}_{1} \sim {\text{S}}_{6}\)) for conversion unit switching by modulation block. The linearised control block diagram of GCI system with the proposed damping loop is shown in Fig. 5b. The block diagram reduction techniques are applied, and after simplification, the transfer function of the closed damping loop is obtained as

$$T_{{{\text{d\_HPF}}}} (s) = \frac{{{\text{P}}G_{d} {(}s{\text{)G}}_{{{\text{inv}}}} }}{{1 + {\text{P}}G_{d} {(}s{)}(K(s) + {\text{G}}_{{{\text{inv}}}} G_{{i_{{\text{f}}} }} (s))}}.$$
(6)

From (6), the characteristics equation of the damping loop shows that the stability and performance dynamics of proposed damping loop depends on the compensator K(s) type and gain P. Different expressions can be used for compensation in proposed configuration. A first-order HPF is considered here owing to adequate oscillation damping capability at higher frequencies with good robustness and dynamic response [26]. The expression for HPF compensator can be represented as

$$K(s) = \frac{{{\text{k}}_{{{\text{rc}}}} s}}{{s + \omega_{{{\text{rc}}}} }}{; (}\omega_{{{\text{rc}}}} = 2\pi f_{{{\text{rc}}}} {),}$$
(7)

From (10), it can observe that the control dynamics of the current loop depends on the inner damping loop parameters and current controller parameters. The reasonable line frequency fluctuation compensation with the good tracking performance and steady-state error minimization, the PR controller parameters have opted as given in Table 2.

3.3 Current Control Loop Design

where krc and ɷrc are the filter gain, and the cut-off frequency, respectively. Intuitively, the HPF position in the proposed damping loop can be envisaged as a parallel resistor and capacitor branch across the filter capacitor. This choice allows the filter capacitor current if multiplied by a gain krc which produce the effect of the resistor in series with the filter capacitor. The frequency ɷrc compensates the lagging phase around the fres. The desired leading phase of the compensator in the lower frequency band-pass region is shown by the frequency response of (7) plotted in Fig. 6a. The frequency response of K(s) under parameters variation are also given to analyze the magnitude and phase characteristics. The higher value of krc at constant frc offers increasing magnitude curve with reduced actual cut-off frequency (represented by \(f_{{{\text{rc}}}}^{^{\prime}}\)) and constant phase curve characteristics as shown in Fig. 6b. On the other hand, for increasing frc shows varying phase curves for a wider frequency range given in Fig. 6c. These characteristics are critical for compensator parameters selection which will be done analytically from stability plots of current loop in the following section.

Fig. 6
figure 6

Frequency response of HPF compensator with a constant krc and frc b varying krc c varying frc

Full size image

The PR controller is employed for current regulation due to better control performance for sinusoidal control variables in αβ form, [1]. The PR controller minimizes the steady-state error owing to the higher gain at the line frequency fL with lower settling and rise time. Its hardware implementation is also easier and requires relatively less signal processing work. The transfer function of an ideal PR controller is expressed as

$$G_{{{\text{PR\_i}}}} (s) = {\text{K}}_{{\text{p}}} + \frac{{2{\text{K}}_{{\text{r}}} s}}{{s^{2} + \omega_{{\text{L}}}^{{2}} }}{, (}\omega_{{\text{L}}} = 2\pi f_{{\text{L}}} {),}$$
(8)

where Kp, Kr and ɷL are the proportional gain, resonant gain, and resonant frequency (which is equal to the angular line frequency with fL = 50 Hz) respectively. The ideal PR controller is difficult to implement practically due to infinite gain at fL. Thus, an improved quasi-PR controller is proposed in [39], which limit the infinite gain and considered here. The transfer function of the quasi-PR controller is given as

$$G_{{{\text{PR}}}} (s) = {\text{K}}_{{\text{p}}} + \frac{{2{\text{K}}_{{\text{r}}} \omega_{{{\text{PR}}}} s}}{{s^{2} + 2\omega_{{{\text{PR}}}} s + \omega_{{\text{L}}}^{2} }}{, }$$
(9)

where ɷPR is the cut-off resonant frequency that forms a damping term in the denominator of (9). This damping term also helps to reduce the controller sensitivity against the line frequency variations. The frequency response of ideal PR and quasi PR controller is given in Fig. 7, which indicate the finite magnitude peak of the controller at fL and comparatively higher gain in the surrounding frequency region for the latter case. These frequency characteristics result in the compensation capability of fL along with good steady-state performance. After simplification of the linearized model in Fig. 5b and combining (4), (6) and (9), the transfer function for open current loop can be derived as

$$T_{{i\_{\text{HPF}}}} (s) = G_{PR} (s) \cdot T_{{{\text{d}}\_{\text{HPF}}}} (s) \cdot G_{{i_{2} }} (s).$$
(10)
Fig. 7
figure 7

Bode-diagram of PR current controllers

Full size image

3.4 The Compensator Parameters Selection and Its Performance Influence

Table 2 Controller and compensator design parameters
Full size table

With suitable compensation parameters selection, the proposed scheme can ensure better stability margin, which leads to improving the control performance dynamics. In this section, the current loop stability plots are analyzed under the compensator parameters variation to opt the suitable values for desired stability and control performance.

Figure 8a shows the bode diagram of (10) under HPF gain krc variation. When a nominal increment in krc value is considered, the magnitude and phase curves move downward that lead to greatly reduced phase margin and the gain crossover frequency. While the harmonics rejection capability in resonance frequency surrounding region and the high-frequency region is increased. This indicates the reasonably smaller value of krc for better dynamic response and phase characteristics with satisfactory harmonics rejection capability. By increasing frc value, the low-frequency phase region characteristics improved, and the medium frequency region phase characteristics reduced. This will result in a better phase margin with lower fres as compared to higher fres and vice versa at lower frc value. The gain crossover frequency increased at nominal inverter design with higher frc, which is unlike trend as compared to krc parameter variation. A slight shift in resonance frequency can also be observed with higher frc while there is no considerable change in high-frequency noise rejection capability. This helps to opt the higher value of frc for better dynamic response and phase characteristics without current quality constraint at nominal design. However, the cut-off frequency must less than half of the sampling frequency such as frc < fs/2 to avoid the possible instability due to poor phase characteristics in a higher frequency range. It is also important to note that the HPF parameters have a negligible influence on tracking performance and steady-state due to insignificant magnitude variations in the low-frequency region shown in Fig. 8a and b.

Fig. 8
figure 8

Bode diagrams of open current loop under a krc variation at fcr = 4 kHz, P = 50 b fcr variation at krc = 0.1, P = 50 c P variation at krc = 0.1, fcr = 4 kHz

Full size image

The proportional gain P introduced in the damping loop forward path strongly influences the open-loop control dynamics, which is analyzed in Fig. 8c. The higher value of P shifts the magnitude curve upward that subsequently enhances the tracking performance, steady-state error minimization and faster dynamic response. The poorer phase curve characteristics in the medium frequency region show the reduced phase margin in a specific range with increasing gain P. Therefore, the reasonable higher proportional gain is understandably more suitable for desired better control performance. Moreover, it is important to note the fact that the higher gain is only possible due to the proposed configuration for damping as compared to feedback compensation techniques [40].

In view of the above discussion, the suitable compensation parameters are optimized for damping loop based on the proposed scheme as given in Table 2 to fulfil the excellent stability and control performance requirements with good current quality.

4 Comparative Study for Robustness and Control Performance Analysis

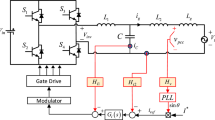
This section presents the comparative analysis study to highlight the significance of control design based on the proposed method. The proportional CCF method is considered for comparison due to its widely acceptance in literature [16, 17, 24, 41] and straightforward implementation. The linear control block diagram of GCI with proportional CCF method is shown in Fig. 9. The damping loop is employed by capacitor current feedback at current controller output while passing through damping gain Kad. From Fig. 9, the damping loop and current loop transfer functions can be derived as

$$T_{{{\text{d\_ad}}}} (s) = \frac{{G_{d} {(}s{\text{)G}}_{{{\text{inv}}}} }}{{1 + G_{d} {(}s{\text{)G}}_{{{\text{inv}}}} G_{{i_{{\text{f}}} }} (s)}}$$
(11)
$$T_{i\_ad} (s) = G_{PR} (s) \cdot T_{{{\text{d\_ad}}}} (s) \cdot G_{{i_{2} }} (s).$$
(12)
Fig. 9
figure 9

The Control block diagram of GCI system with the proportional CCF damping method

Full size image
Fig. 10
figure 10

Bode diagram of open current loop with different methods for control performance comparison

Full size image

In proportional CCF method, the damping gain Kad and PR controller parameters are tuned separately according to [17, 24, 39] to satisfy the good dynamic response, effective resonance suppression with an excellent gain margin for a fair comparison. The detailed control performance and stability comparison are given as follows:

4.1 Control Performance Analysis

Figure 10 represents the bode diagram of undamped filter and damping loops with two methods to analyze the open current loop control performance. It can observe that the resonance peak at fres damped well in both methods with relatively better attenuation with the proposed method. The higher gain in magnitude curve at low-frequency range will bring better tracking performance with the proposed method. The higher gain is also evident in the medium frequency range for the proposed method depicted by higher gain crossover frequency fco2 as compared to fco1 for proportional CCF method. This will lead to higher closed-loop bandwidth and ensure a faster dynamic response. While approximately the similar gain at fL and gain margin (GM) shows the good steady-state performance and excellent stability characteristics for both methods. On the other hand, the significant higher phase margin (PM) shows superior delay compensation capability of the proposed method to overcome the control performance degradation caused by digital control loop delays.

4.2 Robustness Evaluation

The damping loop robustness is tested under different resonance frequencies which can be resulted by weak grid conditions. The variation in resonance frequency is obtained by changing the filter capacitor Cf. The frequency response of (10) and (12) are plotted in Fig. 11 at high resonance frequency 3.04 kHz taken against capacitor value 3.6 µF. An un-damped resonance peak at higher fres shows the ineffective damping loop of proportional CCF method which may lead to instability. On the other hand, the proposed method can suppress the resonance peak well as shown by the red trace and offers excellent stability margins. This demonstrates the wider stable damping region of the proposed method.

Fig. 11
figure 11

Bode diagram of open current loop with higher fres for damping effectiveness comparison

Full size image

The distinctive advantages of the proposed method over proportional CCF method are summarised in Table 3 in terms of steady-state performance, dynamic performance, and stability characteristics.

The robustness is examined further for the proposed method under wide range of resonance frequency variation as shown by pole-zero map given in Fig. 12. When the capacitor is set to the smaller value 2.5 µF to emulate higher resonance frequency (i.e. 3.59 kHz), the resonant poles shift towards left half plane (LHP) and completely stable damped system obtained. The incremental step change is considered in capacitor value up to 12.5 µF to imitate the resonance frequency variation to smaller one 1.61 kHz. The resonant poles shifting tendency towards LHP becomes more noticeable in the zoomed-in view of Fig. 12 that shows the wider stable damping region with the proposed damping loop.

Fig. 12
figure 12

The pole-zero map of open current loop with proposed method under fres variation

Full size image

4.3 Performance Analysis Under Filter Parameters Variation

The control performance and robustness characteristics of the proposed method open current loop Ti_HPF(s) are investigated under LCL-filter parameters variations to count the passive components ageing impact. The ± 50% deterioration in each parameter’s nominal value is assumed in the worst scenario. The variation in inverter side inductor L1 influences the gain crossover frequency considerably without significant change in stability margins, as noticed in the bode diagram in Fig. 13a. The reduced inductor L1 value entails larger gain crossover frequency and slightly better gain margin as compared to increased case. This shows comparatively better dynamic response and tracking performance with lower L1 without much influence on the delay compensation capability. In filter capacitor variation, the steady-state and dynamic performance will be identical under lower and higher capacitor value as evident by a similar magnitude curve in Fig. 13b. However, a slightly better resonance suppression is expected with higher Cf as indicated by green trace. In grid-side inductor variation, the resonance suppression trend is consistent as in Cf variation while slightly better performance at increased L2 value as depicted in Fig. 13c. However, the stability margins are comparable in reduced and increased L2 value. The stability margins of the open current loop at nominal system design and under different filter parameters variations are summarised in Table 4. It can perceive that the proposed method maintains the good stability and performance indices with effective resonance suppression under considered filter parameters variation.

Fig. 13
figure 13

Bode diagram of Ti_HPF(s) under a L1 ± 50% b Cf ± 50% c L2 ± 50%

Full size image
Table 3 Control performance comparison chart of open-current loop with different methods
Full size table
Table 4 Stability margins of proposed method under filter parameters variations
Full size table

5 Simulation and Experiment Results Verification

A three-phase LCL-filtered GCI model is developed in MATLAB/Simulink for non-linear simulation by following the design parameters given in Table 1. The control structure for the proposed method and the proportional CCF is employed. The sinusoidal pulse width modulation (SPWM) technique is considered for gate signal generation to switch insulated gate bipolar transistor (IGBT) devices.

Figure 14, 15 and 16 show the steady-state response of phase A where the grid-injected current i2a is in phase the grid voltage vga. When the damping loop is disabled, the resonant component amplifies in vga and i2a shown by the waveforms in Fig. 14a. The harmonics spectrum of i2a in Fig. 14b shows 24.78% total harmonics distribution (THD) which indicates the highest contribution of the resonant component. The resonance component attenuated by enabling the damping loop with the proportional CCF method as shown by the waveform in Fig. 15a which brings down the THD to 6.39% in the harmonics spectrum given in Fig. 15b. Similarly, the resonance component damped effectively in Fig. 16a when the proposed damping loop is enabled. However, relatively lower THD up to 3.28% in Fig. 16b shows somewhat better resonance component suppression capability. The THD level with the proposed method is less than 5% which fulfill the grid interconnection standards [3].

Fig. 14
figure 14

Undamped simulation results a vga and iga waveforms b harmonics spectrum of iga

Full size image
Fig. 15
figure 15

Steady-state response of the proportional CCF method a vga and iga waveforms b Harmonics spectrum of iga

Full size image
Fig. 16
figure 16

Steady-state response of the proposed PFC method a vga and iga waveforms b harmonics spectrum of iga

Full size image

The simulated transient response of the proportional CCF in Fig. 17a shows the significant oscillations during the transition between full load to half load current rating. These oscillations attenuated in a very short period with the proposed method as revealed by Fig. 17b. This is due to better gain crossover frequency of the proposed damping method, which demonstrates the faster dynamic response under transient or load variation conditions.

Fig. 17
figure 17

Simulation results for transient response a the proportional CCF method b the proposed PFC method

Full size image

The damping effectiveness of both designed loops is tested under higher resonance frequency (i.e. 3.01 kHz) as discussed in previous analysis in section IV. Figure 18a shows that the proportional CCF method is failed to remove the higher resonance frequency component as expected and results in the larger THD value of 14.34%. On the other hand, the PFC method effectively mitigate the resonance and limit the overall THD with 3.12%. This exhibits the wider damping region, which illustrates the enhanced stability of designed control with the suggested configuration.

Fig. 18
figure 18

Simulation results at higher fres a the proportional CCF method (b) the proposed PFC method

Full size image

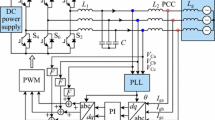
An experimental prototype of 1 kW power is developed to validate the theoretical and simulation results. The hardware setup includes DC supply, three-phase inverter, LCL-filter, sensor board, PWM board and isolation transformer with the grid which are shown in snapshot given in Fig. 19. The isolation transformer is used to integrate the inverter with the power grid. The control algorithms are implemented in a dSPACE DS1006 platform using the system and control design parameters of Tables 1 and 2, respectively. The sensor board measures the DC-link voltages, grid voltage and filter currents. These measured variables are sampled by dSPACE unit and transformed into αβ frame for control part realization in MATLAB environment in the interfaced computer system. The output control signals from the MATLAB model are sent back to the dSPACE unit, which generates PWM signals and supplied to IGBT devices of the inverter through the PWM control board.

Fig. 19
figure 19

The experimental prototype setup of three-phase GCI system

Full size image

Figure 20a shows the experimental waveform of voltage and current during disabled damping loop. The harmonics spectrum of current waveform in Fig. 20b shows the resonance frequency contributes highly in overall THD 16.31%. The resonance frequency harmonics mitigated effectively when the damping loop enabled with the proportional CCF method and the proposed PFC method in Figs. 21a and  22a respectively. However, 2.91% THD in Fig. 21b comparatively lower than 5. 51% THD in Fig. 22b verifies the slightly better resonance suppression capability of the proposed method.

Fig. 20
figure 20

Undamped experimental results a vga and iga waveforms b harmonics spectrum of iga

Full size image
Fig. 21
figure 21

The proportional CCF method experimental results a vga and iga waveforms b harmonics spectrum of iga

Full size image
Fig. 22
figure 22

The proposed PCF method experimental results a vga and iga waveforms b harmonics spectrum of iga

Full size image

Figure 23a shows the transient response of the proportional CCF method, which indicates the poor dynamic response in the presence of significant transient oscillations during the step change in the current reference value. On the other hand, the minor affected current waveform at a transition time validates the faster dynamic response of the proposed methodology in Fig. 23b. A filter capacitor of 3.6 µF is used to imitate the higher resonance frequency and testify the damping loop effectiveness. Figure 24a represents the distorted three-phase current vector with 16.32% THD where the proportional CCF method failed to suppress the resonance due to limited effective damping region. Nevertheless, the proposed PFC method efficiently mitigate the resonance in Fig. 24b with 3.42% THD level. This observation confirms the claim of enhanced stability owing to the wider damping region associated with the suggested method.

Fig. 23
figure 23

Experimental results for transient response a the proportional CCF method b the proposed PFC method

Full size image
Fig. 24
figure 24

Experimental results at higher fres a the proportional CCF method b the proposed PFC method

Full size image

In summary, the experimental results are in good agreement with the simulation and theoretical findings. These results validate the advantages in terms of faster dynamic response, effective resonance suppression and enhanced stability characteristics. Thus, the proposed method is more suitable for distributed generation system in filter parameters variation, weak grid conditions and load current variation scenarios.

6 Conclusion

In this paper, a three-phase voltage source inverter (VSI) is considered for distributed generation applications to facilitate renewable energy resources integration with the grid. An alternative configuration of the inverter control structure is introduced, which modifies the inner damping loop to suppress LCL-filter resonance peak. According to the proposed scheme, the inner damping loop can be employed by adding a compensator in parallel with the LCL-filter and feedback the output of the augmented plant. This is named parallel feedforward compensation method. The filter capacitor current is measured to implement the inner damping loop along with the grid-side current for the outer current loop. A high-pass filter (HPF) compensator is deployed across the filter in proposed damping loop design, and a proportional resonant controller is employed for grid current regulation purpose. The proportional capacitor current feedback (CCF) method has opted for comparison with the proposed method. It has been shown that the proposed method offers a better dynamic response, delay compensation capability, relatively improved resonance suppression, and potential for better tracking performance without compromising injected current quality.

Moreover, the stability investigation under changing resonance frequency demonstrate the enhanced stable damping region of the current loop with the proposed design as compared to its counterpart. Furthermore, the current loop performance analysis under filter parameters variation exhibits that the proposed method maintains excellent stability margins. These advantages prove the suitability of the proposed method for inverter control design under filter parameters variation and weak grid conditions. The simulation and experimental results validate the control performance and stability improvements to confirm the effectiveness of the proposed method.