Adaptive active damping method of grid-connected inverter based on model predictive control in weak grid

Abstract

The LCL-type grid-connected inverter based on finite control set model predictive control (FCS-MPC) is suitable for weak grids because of its good robustness and fast dynamic response. However, in an FCS-MPC-based system, the variable switching frequency causes the spread of the inverter-side current harmonic spectrum. Thus, the grid-side current may be distorted because the harmonics are amplified to the grid side due to the resonance peak of the LCL filter. To solve the above problem, this paper proposes an adaptive active damping (AD) method to eliminate the resonant effects. First, the system based on an MPC controller is regarded as a closed-loop system of the grid-side current, and the resonance peak is suppressed effectively by an AD, which consists of a virtual resistor and a virtual capacitor. Second, to balance the resonance suppression and dynamic performance of the system under weak grid conditions, the grid impedance is measured and the optimal AD values for different grid impedance are calculated online. Compared with the fixed-value AD, the proposed method has better resonance suppression and higher bandwidth. The effectiveness and feasibility of the proposed control strategy are verified by simulations and experiments.

1 Introduction

LCL-type grid-connected inverters are widely employed in renewable energy systems because of their good switching ripple attenuation and small sizes. However, under weak grid conditions, the varied grid impedance challenges the stability of the conventional LCL filter-based current controlled system [1]. Therefore, to improve the adaptability of the grid-connected inverters to weak grids, modern control strategies that provide good robustness such as sliding mode control [2], neural network algorithm [3], or predictive control schemes [4,5,6] can be alternatives to the conventional control approaches.

Recently, finite control set model predictive control (FCS-MPC) has been widely used in inverters with LC filter [7] and L filter [8,9,10,11], while inverters with LCL filter have more advantages in increasing the mitigation of switching harmonics with smaller components [12,13,14,15]. The FCS-MPC strategies, which are applied to the LCL-type grid-connected inverter, can be classified into inverter-side current control, grid-side current control, and multivariable control. In these control methods, the inverter-side current control has the least sensitivity to parameter variations [14]; thus, it is more suitable for weak grid conditions. Even so, the grid-side current may be distorted due to the spread of the inverter-side current harmonic spectrum and the harmonic amplification of the LCL-filter resonance peak. Therefore, an additional active damping (AD) is necessary.

In conventional linear control strategies, capacitor–current feedback AD method [16,17,18], capacitor–voltage feedback AD method [19, 20], and multiple state variables feedback AD method [21] are extensively used in PWM-based systems to eliminate the resonant effects. Generally, the principle of the above methods can be regarded as the different state variables added to the PWM modulation wave. FCS-MPC is nonlinear and does not have a modulator; thus, the conventional AD method cannot be directly applied to the FCS-MPC-based inverter. Nowadays, frequency-weighted predictive control [22, 23] and the virtual resistance (VR) AD method [24, 25] are proposed to eliminate the resonant effects in FCS-MPC-based systems. In frequency-weighted predictive control strategies, a notch filter is added to the cost function to shape the current harmonic spectrum [22]. On this basis, an adaptive notch filter is designed based on the least mean square (LMS) algorithm [23]. However, the LMS algorithm requires multiple iterations to train the appropriate notch filter coefficients, thus reducing the practicability of this method. In VR AD strategies, to attenuate the grid current harmonics, the capacitor voltage is filtered by a digital high-pass filter, and the filtered signal is added to the inverter-side current reference by the virtual resistance [24, 25]. However, these methods are studied under strong grid conditions and without the consideration of the influence of the grid impedance on the system. The optimal selection of AD parameters has not been analyzed either.

In this paper, an adaptive AD method for the grid-connected inverter based on FCS-MPC is proposed. The AD, which consists of a virtual resistor in series with a virtual capacitor (virtual RC), is applied to reduce the grid current harmonics caused by the resonance peak. Moreover, the influence of the varied grid impedance on the AD resonance suppression is analyzed, and an adaptive AD algorithm based on grid impedance identification is studied. The effectiveness of the proposed control strategy is validated by simulations and experiments.

The remainder of this paper is organized as follows. In Sect. 2, a discrete-time model of the LCL-type grid-connected inverter is established, and a current controller based on FCS-MPC is designed. In Sect. 3, an AD method with virtual RC is proposed. In Sect. 4, an adaptive AD algorithm is designed for weak grid conditions. In Sect. 5, an analysis of simulation and experimental results is presented. Finally, in Sect. 6, the conclusion is given.

2 FCS-MPC strategy of the LCL-type grid-connected inverter

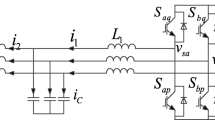
The main circuit of the single-phase LCL-type grid-connected inverter under a weak grid condition is shown in Fig. 1. The LCL filter is composed of the inverter-side inductance L₁, the filter capacitor C, and the grid-side inductance L₂. U_dc is the DC-link voltage. u_pcc, u_g, and L_g are the point of common coupling (PCC) voltage, grid voltage, and grid impedance, respectively.

Fig. 1

Main circuit of single-phase LCL-type grid-connected inverter in a weak grid condition

To build a model for predictive control, the LCL-type grid-connected inverter circuit is simplified and the equivalent circuit is shown in Fig. 2, where u_inv is the output voltage of the inverter. u_c is the capacitor voltage. i₁ and i₂ are the inverter-side current and the gird-side current, respectively.

Fig. 2

Equivalent circuit of LCL-type grid-connected inverter under a weak grid condition

The differential equations of the circuit are given by

$$\left\{ \begin{gathered} C\frac{{{\text{d}}u_{\text{c}} }}{{{\text{d}}t}} = i_{1} - i_{2} \hfill \\ (L_{2} + L_{{\text{g}}} )\frac{{{\text{d}}i_{2} }}{{{\text{d}}t}} = u_{\text{c}} - u_{{\text{g}}} \hfill \\ L_{1} \frac{{{\text{d}}i_{1} }}{{{\text{d}}t}} + u_{\text{c}} = u_{{{\text{inv}}}} \hfill \\ \end{gathered} \right..$$

(1)

The backward difference scheme is used to discretize the first and second equations of (1) with a sampling time T_s. The reference value of the inverter-side current at time k is given by (2), where i_2ref is the reference value of the grid-side current i₂, and its phase is synchronized with u_pcc:

$$\left\{ \begin{gathered} i_{{1{\text{ref}}}} (k) = i_{{2{\text{ref}}}} (k) + C\frac{{u_{{{\text{cref}}}} (k) - u_{{{\text{cref}}}} (k - 1)}}{{T_{{\text{s}}} }} \hfill \\ u_{{{\text{cref}}}} (k) = (L_{2} + L_{{\text{g}}} )\frac{{i_{{2{\text{ref}}}} (k) - i_{{2{\text{ref}}}} (k - 1)}}{{T_{{\text{s}}} }} + u_{{\text{g}}} (k) \hfill \\ \end{gathered} \right..$$

(2)

Through the discretization of the third equation of (1) using the forward difference scheme, the future inverter-side current i₁(k + 1) is given by

$$i_{1} (k + 1) = \frac{{T_{{\text{s}}} }}{{L_{1} }}\left( {u_{{{\text{inv}}}} (k) - u_{{\text{c}}} (k)} \right) + i_{1} (k),$$

(3)

where u_inv(k) is determined by the state of the four switches S₁–S₄. If S_n = 1, then the switch is turned on; if S_n = 0, then the switch is turned off. Considering the different states of S₁–S₄, (1, 0, 0, 1), (0, 1, 1, 0), (1, 0, 1, 0), (0, 1, 0, 1) are obtained. If (S₁, S₂, S₃, S₄) = (1, 0, 0, 1), then u_inv = U_dc; if (S₁, S₂, S₃, S₄) = (0, 1, 1, 0), then u_inv =  − U_dc; if (S₁, S₂, S₃, S₄) = (1, 0, 1, 0) or (0, 1, 1, 0), then u_inv = 0. (1, 0, 1, 0) is used as the switching state for u_inv = 0. Therefore, three available switching states exist in this MPC strategy.

When T_s is sufficiently small, i_1ref(k + 1)≈i_1ref(k) can be assumed; thus, the cost function g_j is defined by

$$g_{j} = \left( {i_{{1{\text{ref}}}} (k) - i_{1} (k + 1)} \right)^{2} ,$$

(4)

where j = 1, 2, 3, and the switching state that corresponds to the minimum value of g_j is applied to the next sampling period.

3 Method of virtual RC damping

Considering that FCS-MPC is a nonlinear control strategy, designing an AD using the analysis method of linear systems is difficult. This paper simplifies the MPC-based system at first; thus, the system based on an FCS-MPC controller can be regarded as a closed-loop system of the grid-side current.

3.1 Simplification of the MPC-based system

As the direct control object of the system is the inverter-side current i₁ and the response speed of the MPC controller is relatively fast, u_inv and L₁ can be considered as a current source i₁ [26]. The simplified circuit is shown in Fig. 3, and the control block diagram of the system is shown in Fig. 4.

Fig. 3

Equivalent output stage of the system without damping

Fig. 4

Control block diagram of the system without damping

From Fig. 3, the relationship between |i_2ref| and |i_1ref| is given by

$$\left| {i_{{2{\text{ref}}}} } \right| = \left| {i_{{1{\text{ref}}}} } \right|\frac{{\left| {Z_{{\text{c}}} } \right|}}{{\left| {Z_{{\text{c}}} } \right| + \left| {Z_{2} } \right|}} - \frac{{\left| {u_{{\text{g}}} } \right|}}{{\left| {Z_{{\text{c}}} } \right| + \left| {Z_{2} } \right|}},$$

(5)

where |i_1ref|, |i_2ref| and |u_g| are the amplitude of i_1ref, i_2ref, and u_g, respectively. |Z_c| and |Z₂| are the impedance modulus of the filter capacitor C and L₂ + L_g.

At the fundamental frequency (50 Hz), when C = 4.7 μF, |Z_c| ≈ 680 Ω; when L₂ + L_g = 0.6–8.6 mH, |Z₂|= 0.2 Ω–2.6 Ω. Therefore, (5) can be simplified to

$$\left| {i_{{2{\text{ref}}}} } \right| = \left| {i_{{1{\text{ref}}}} } \right| - \frac{{\left| {u_{{\text{g}}} } \right|}}{{\left| {Z_{{\text{c}}} } \right|}}.$$

(6)

In this paper, |u_g|= 155 V, |i_2ref|= 20 A. The error between |i_2ref| and |i_1ref| is only 0.23 A, which can be regarded as i_2ref ≈ i_1ref. Therefore, Fig. 4 is approximated as Fig. 5.

Fig. 5

Simplified control block diagram of the system

In an ideal situation, the loop of the MPC controller can be regarded as a proportional component with k = 1. Hence, the path from i₁ to i₂ is equivalent to the closed-loop system of i₂, as shown in Fig. 6, where G_z(s) = 1/sC.

Fig. 6

Closed-loop control system of the grid-side current

In the system without damping, the closed-loop transfer function G_i2cl(s) is given by (7), and the Bode diagram of G_i2cl(s) is shown in Fig. 7, where L₂ + L_g = 0.6 mH, C = 4.7 μF:

$$G_{{i2{\text{cl}}}} (s) = \frac{1}{{s^{2} (L_{2} { + }L_{{\text{g}}} )C + 1}}.$$

(7)

Fig. 7

Bode diagram of the closed-loop system without damping

The resonance frequency f_r is given by

$$f_{{\text{r}}} = \frac{1}{{2\pi \sqrt {(L_{2} { + }L_{{\text{g}}} )C} }}.$$

(8)

From (7), the closed-loop system has a pair of complex conjugate poles on the imaginary axis of the s-plane, which may impair the stability of the system. Moreover, the resonance peak at f_r can greatly amplify the inverter-side current harmonics to the grid side. Hence, additional AD is necessary.

3.2 Virtual RC damping for MPC Controller

To suppress the resonance peak and improve the performance of the system, a virtual RC damping is connected in parallel with the filter capacitor C as an AD. The improved circuit is shown in Fig. 8, and the new G_z(s) is given by (9), where R_d is a virtual resistance, and C_d is a virtual capacitor:

$$G_{z}^{{{\text{AD}}}} (s) = \frac{{sR_{d} C_{d} + 1}}{{s(sCR_{d} C_{d} + C + C_{d} )}}.$$

(9)

Fig. 8

Equivalent circuit of the system with virtual RC damping

The closed-loop transfer function of the system with virtual RC damping is given by

$$G_{{i2{\text{cl}}}}^{{{\text{AD}}}} (s) = \frac{{sR_{d} C_{d} + 1}}{{s^{3} (L_{{2}} + L_{{\text{g}}} )CR_{d} C_{d} + s^{2} (L_{{2}} + L_{g} )(C + C_{d} ) + sR_{d} C_{d} + 1}}.$$

(10)

The Bode diagram of $G_{{i2{\text{cl}}}}^{{{\text{AD}}}} (s)$ is shown in Fig. 9, where R_d = 8 Ω, C_d = 20 μF. The resonance peak is effectively suppressed by the virtual RC damping, and the performance of the system is improved.

Fig. 9

Bode diagram of the closed-loop system with and without the virtual RC damping

To add the virtual RC damping to the cost function, this paper uses the u_c feedback scheme to obtain the current reference $i_{{{\text{1ref}}}}^{{{\text{AD}}}}$. The principle of this method is shown in Fig. 10, where the virtual RC damping current i_RC is

$$i_{{{\text{RC}}}} = C_{d} \frac{{{\text{d}}(u_{{\text{c}}} - i_{{{\text{RC}}}} R_{d} )}}{{{\text{d}}t}}.$$

(11)

Fig. 10

Block diagram of the virtual RC damping for u_c feedback

(11) is discretized by the backward difference scheme to obtain the i_RC(k):

$$i_{{{\text{RC}}}} (k) = \frac{{C_{d} \left( {u_{{\text{c}}} (k) - u_{{\text{c}}} (k - 1)} \right) + R_{d} C_{d} i_{{{\text{RC}}}} (k - 1)}}{{T_{{\text{s}}} + R_{d} C_{d} }},$$

(12)

and the current reference with virtual RC damping at time k is given by

$$i_{{1{\text{ref}}}}^{{{\text{AD}}}} (k) = i_{{1{\text{ref}}}} (k) - i_{{{\text{RC}}}} (k).$$

(13)

With $i_{{{\text{1ref}}}}(k)$ being replaced with $i_{{{\text{1ref}}}}^{{{\text{AD}}}} (k)$ in (4), the cost function with virtual RC damping is obtained:

$$g_{j}^{{{\text{AD}}}} = \left( {i_{{1{\text{ref}}}}^{{{\text{AD}}}} (k) - i_{1} (k + 1)} \right)^{2} .$$

(14)

4 Adaptive AD method for weak grid conditions

4.1 Influence of the varied grid impedance on the system

Under weak grid conditions, the performance of the system changes due to the variation of L_g. The Bode diagram and the performance parameters of the $G_{{i2{\text{cl}}}}^{{{\text{AD}}}} (s)$ for different L_g are shown in Fig. 11 and Table 1, respectively, where the values of R_d and C_d are both fixed (R_d = 8 Ω, C_d = 20 μF).

Fig. 11

Bode diagram of the closed-loop system with fixed-value AD for different L_g

Table 1 Performance parameters of the closed-loop system with fixed-value AD for different L_g

When $G_{{i2{\text{cl}}}}^{{{\text{AD}}}} (s)$ is regarded as the transfer function from i₁ to i₂, the magnitude of resonance peak M_r increases with the increase of L_g and reaches 10.5 dB when L_g = 6 mH. Under this condition, the current harmonics from i₁ are amplified 3.4 times at f_r. This finding shows that the resonance suppression of virtual RC damping is impaired due to the increase of L_g.

Moreover, when $G_{{i2{\text{cl}}}}^{{{\text{AD}}}} (s)$ is regarded as the closed-loop transfer function of i₂, the bandwidth f_bw decreases rapidly with the increase of L_g. Thus, the dynamic performance of the system worsens. To solve the problems above, this paper proposes an adaptive AD algorithm based on impedance identification. Therefore, the optimal virtual RC parameters can be calculated for different grid impedance values.

4.2 Impedance identification of the weak grid

To obtain the grid impedance L_g, this paper uses non-characteristic harmonic injection [27] to measure the grid impedance online, as shown in Fig. 12, where i_{_75} is the current harmonic with a frequency of 75 Hz.

Fig. 12

Control block diagram of 75 Hz harmonic injection

When i_{_75} is added to i_2ref, the grid-side current i₂ contains the harmonic component at 75 Hz, and a response of u_pcc is generated at the same time. The amplitude and the phase of i₂ and u_pcc at 75 Hz are extracted by discrete Fourier transform, and the grid impedance L_g can be obtained by (15):

$$L_{{\text{g}}} = \frac{\sin \angle \varphi }{{2\pi f_{i} }}\frac{{\left| {{\varvec{u}}_{{{\mathbf{pcc}}\user2{\_}{\mathbf{75}}}} } \right|}}{{\left| {{\varvec{i}}_{{{\mathbf{2\_75}}}} } \right|}},$$

(15)

where f_i = 75 Hz, u_{pcc_75} and i_{2_75} are the harmonic components of u_pcc and i₂ at 75 Hz, and φ is the phase difference between u_{pcc_75} and i_{2_75}.

4.3 Calculation of virtual RC parameters

From (10), the characteristic equation D(s) of the closed-loop system is

$$\begin{aligned} D(s) & = s^{3} (L_{{2}} + L_{{\text{g}}} )CR_{d} C_{d} \\ & \quad + s^{2} (L_{{2}} + L_{{\text{g}}} )(C + C_{d} ) + sR_{d} C_{d} + 1. \\ \end{aligned}$$

(16)

An ideal third-order system should have one real pole and two complex conjugate poles on the left half of the s-plane. Thus, the ideal characteristic equation D_r(s) is constructed by

$$D_{{\text{r}}} (s) = \left( {s(L_{2} + L_{{\text{g}}} )CR_{d} C_{d} + K} \right)(s^{2} + 2\zeta \omega_{n} s + \omega_{n}^{2} ),$$

(17)

where ζ is the damping coefficient, and ω_n is the natural frequency. The 3 poles and 1 zero of the closed-loop system are calculated by

$$\left\{ \begin{gathered} z_{1} = - \frac{1}{{R_{d} C_{d} }} \hfill \\ p_{1} = - \frac{1}{{(L_{2} + L_{{\text{g}}} )CR_{d} C_{d} \omega_{n}^{2} }} \hfill \\ p_{2,3} = - \zeta \omega_{n} \pm \omega_{n} \sqrt {\zeta^{2} - 1} \hfill \\ \end{gathered} \right.,$$

(18)

where z₁ is the real zero, p₁ is the real pole, and p_2,3 are the complex conjugate poles. With the ratio of the distance between p₁ and p_2,3 to the imaginary axis set as η, the ratio of the distance between p₁ and z₁ to the imaginary axis is λ:

$$\left\{ \begin{gathered} \eta = \frac{1}{{(L_{2} + L_{{\text{g}}} )CR_{d} C_{d} \zeta \omega_{n}^{3} }} \hfill \\ \lambda = 1 + 2\eta \zeta^{2} \hfill \\ \end{gathered} \right.,$$

(19)

where ω_n is given by

$$\omega_{n} = \frac{1}{{\sqrt {(1 + 2\eta \zeta^{2} )(L_{2} + L_{{\text{g}}} )C} }}.$$

(20)

With the combination of (16), (17), and (20), C_d and R_d are calculated by

$$\left\{ \begin{gathered} C_{d} = C\left( {\frac{2\lambda }{\eta } + \lambda - 1} \right) \hfill \\ R_{d} = \frac{2\zeta }{{\omega_{n} C_{d} \left( {1 - (L_{2} + L_{{\text{g}}} )C\omega_{n}^{2} } \right)}} \hfill \\ \end{gathered} \right.,$$

(21)

where η and λ determine the distribution of closed-loop poles on the s-plane and the performance of the system. η = 1 is set to ensure the damping and the response speed of the system. According to (19), the value of λ is always greater than 1. When λ approaches 1, p₁ and z₁ form a dipole, and the complex conjugate poles p_2,3 become the dominant poles. Thus, the damping ratio ζ and the resonance suppression are greatly reduced. When λ ≥ 3, the complex conjugate pole disappears and the closed-loop poles consist of real poles only. Thus, the dynamic performance of the system is impaired. Consequently, setting λ = 2 balances the resonance suppression and dynamic performance.

From (21), if η = 1, λ = 2, C = 4.7 µF, then C_d = 23.5 µF. When C_d is obtained, the value of R_d is related to L₂ and L_g only. The relationship between L_g and R_d in the case of L₂ = 0.6 mH is shown in Fig. 13. The Bode diagram and the performance parameters of the closed-loop system with adaptive AD algorithm for different L_g are shown in Fig. 14 and Table 2, respectively.

Fig. 13

Relationship between grid impedance L_g and virtual resistance R_d

Fig. 14

Bode diagram of the closed-loop system with adaptive AD algorithm for different L_g

Table 2 Performance parameters of the closed-loop system with adaptive AD algorithm for different L_g

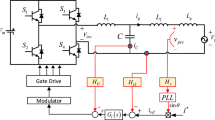
As can be seen in Table 2, after the adaptive AD algorithm is added, the magnitude of the resonance peak M_r is maintained at 3.04 dB when L_g varies. For the case of L_g = 6 mH, compared with the system without adaptive AD algorithm (Fig. 11; Table 1), the M_r of the system with adaptive AD algorithm drops by 71.0%, and the closed-loop bandwidth f_bw increases by 56.3%. This result shows that the system with adaptive AD algorithm can balance the resonance suppression ability and dynamic performance under weak grid conditions. The overall control block diagram of the system is depicted in Fig. 15.

Fig. 15

Control block diagram of the single-phase LCL-type grid-connected inverter with adaptive AD strategy

5 Simulation and experimental results

5.1 Simulation results

The LCL-type grid-connected inverter model was built in MATLAB/Simulink according to Fig. 15, as shown in Fig. 16. The MPC controller and the adaptive AD are implemented in s-function, and the simulation parameters are shown in Table 3.

Fig. 16

Implementation of the system in MATLAB/Simulink

Table 3 Simulation parameters

For the case of L_g = 0 mH, the simulation waveforms and the grid-side current spectrum are shown in Fig. 17a. When the system without AD, the harmonic amplitude of i₂ at f_r is 5.0% of the fundamental current (50 Hz), and the total harmonic distortion (THD) of i₂ is 6.93%. In contrast, for the system with the adaptive AD, the harmonic amplitude of i₂ at f_r is less than 0.1% of the fundamental current, and the THD of i₂ is reduced to 1.55%.

Fig. 17

Simulation waveforms and the spectrum of the grid-side current i₂ for different L_g: a L_g = 0 mH; b L_g = 2 mH; c L_g = 4 mH

Figure 17b and c shows the simulation results for L_g = 2 mH and L_g = 4 mH, respectively. In the system without adaptive AD, the distortion of u_pcc becomes significant under weak grid conditions. The harmonic amplitude of i₂ at f_r is more than 5% of the fundamental current, and the THDs of i₂ are 8.47% (L_g = 2 mH) and 7.63% (L_g = 4 mH). After the adaptive AD is added, the distortion of u_pcc is greatly reduced and the THDs of i₂ drop to 1.65% (L_g = 2 mH) and 1.58% (L_g = 2 mH), respectively.

To verify the dynamic performance of the system, a reference-value step of grid current (|i_2ref| from 20 to 10 A) is applied for L_g = 4 mH, as shown in Fig. 18. The current step process is stable and has no oscillation, and the system has a good dynamic response.

Fig. 18

Dynamic simulation results for L_g = 4 mH

5.2 Experimental results

To validate the practicability of the proposed method, a 2 kW LCL-type grid-connected inverter prototype was constructed, as shown in Fig. 19. The current controller is implemented on a DSP with TMS320F28335 for IGBT (Infineon FF100R12KS4) pulse signal generation, and the weak grid is composed of a voltage source (with a value of u_g) in series with an inductor (with a value of L_g). The experimental parameters are the same as the simulation parameters, as given in Table 3.

Fig. 19

Photograph of the experimental platform

First, the system without AD, the system with conventional VR AD (the virtual resistance with a value of 30 Ω), and the system with proposed adaptive AD are compared under different grid conditions. In the steady-state experiment, the amplitude of the grid current reference value is 20 A. Figure 20 shows the experimental waveforms of the three methods under a strong grid condition (L_g = 0 mH). In the system without AD, the distortion of i₂ is obvious and the THD of i₂ is 7.55%. In contrast, the grid current harmonics are effectively suppressed by adding the VR AD or the adaptive AD. The THDs of i₂ are reduced to 2.42% and 2.39%, respectively.

Fig. 20

Steady experimental results for L_g = 0 mH: a the system without AD; b the system with conventional VR AD; c the system with adaptive AD

Figures 21a and 22a show the experimental waveforms of the system without AD under weak grid conditions. The u_pcc and i₂ are significantly distorted due to the grid impedance. The THDs of i₂ are 8.24% for L_g = 2 mH and 8.18% for L_g = 4 mH. Figures 21b and 22b show the experimental results of the system with conventional VR AD. Compared with the strong grid condition, the harmonic suppression capability of VR AD decreases because of the influence of grid impedance (the THDs of i₂ rise to 4.86% for L_g = 2 mH and to 4.74% for L_g = 4 mH). Figures 21c and 22c show the experimental results of the system with proposed adaptive AD. Compared with the two methods above, the adaptive AD improves the quality of the grid currents and reduces the THDs of i₂ to 2.62% (L_g = 2 mH) and 2.45% (L_g = 4 mH), respectively. The experimental results validate that when the grid impedance varies, adaptive AD can still suppress the grid current harmonics effectively.

Fig. 21

Steady experimental results for L_g = 2 mH: a the system without AD; b the system with conventional VR AD; c the system with adaptive AD

Fig. 22

Steady experimental results for L_g = 4 mH: a the system without AD; b the system with conventional VR AD; c the system with adaptive AD

To evaluate the dynamic performance of the system, a step in grid current reference i_2ref is shown in Fig. 23 for L_g = 4 mH. The peak of i_2ref changes from 20 to 10 A and 10–20 A, as shown in Fig. 23a and b respectively. The grid current can reach the given value rapidly with a small overshoot, and the system shows a fast dynamic response. Finally, on the basis of the experimental results, the advantages and disadvantages of the proposed method and the conventional methods are compared, as shown in Table 4.

Fig. 23

Dynamic experimental results for L_g = 4 mH: a |i_2ref| from 20 to 10 A; b |i_2ref| from 10 to 20 A

Table 4 Comparison of the advantages and disadvantages of different control methods

6 Conclusion

This paper proposed an adaptive AD strategy for the grid-connected inverter based on FCS-MPC. The virtual RC damping method can effectively suppress the resonance peak of the LCL filter and reduce the impact of the variable switching frequency in the FCS-MPC-based system. Under weak grid conditions, the adaptive AD algorithm can obtain the optimal virtual RC value online. Unlike the fixed-value AD, the proposed method can maintain the resonance suppression of the virtual RC damping under different grid impedance values, and the system has higher bandwidth at the same time. The simulations and experimental results show that when the grid impedance varies, the proposed method can ensure the reduction of grid current harmonics, and the system has good dynamic performance.