1 Introduction

Nowadays, multi-axis machine tool plays a more and more important role in the manufacturing industry with the increased tightening requirements of machining products [1]. For multi-axis machine tools, accuracy, processing rate and reliability are the common indicators of application performance. Especially, accuracy is the most important one which is directly related to the final precision of machined workpieces [2]. Considering the accuracy of machine tools, the main influence factors include geometric errors, thermal deformation errors, force-induced errors and control system errors, where the combination proportion of geometric errors and thermal deformation errors is more than 60% [3]. Therefore, accurate modeling and controling of geometric errors is an economical and effective way to improve the application accuracy of machine tools considering the stability, repeatability and measurability of geometric errors.

Many geometric error modeling and compensation methods have been presented over the past decade. The Homogeneous transformation matrix (HTM) [4,5,6] based on rigid multi-body kinematics [7, 8] is the common method for geometric error modeling of machine tools. Based on HTM, multi-body system theory [9] has also been successfully applied in practical uses. In recent years, the stream of variation [10], differential transformation [11, 12], differential motion matrix [2], and screw theory [13] have achieved significant developments in the geometric error modeling for multi-axis machine tools, which provide meaningful guidance to describe the geometric error sources and their propagations in the assembly process. However, these models strongly rely on the determined configuration and relative pose of machine tools under static or quasi-static states. For different moving positions, it is necessary to build an improved geometric error expression model. For multi-axis machine tools, the geometric error is eventually generated by the error propagation of components in the assembly process and it is highly related to the determined pose of the machine tool. Therefore, accurate modeling of the non-uniformly distributed geometric errors relies on a spatial expression in the whole working space of the multi-axis machine tool.

Consequently, it is necessary to establish a spatial expression model of assembly geometric errors in the whole working space of the multi-axis machine tool. To achieve this goal, a description method of manufacturing and assembling tolerances of each part in the assembly body and their propagation relations of multi-axis synthetic errors should be established in previous. Thanks to the previous studies, several methods have been applied to the synthesis analysis of tolerances [14,15,16]. In preliminary explorations of 3D tolerance methods, the networks of zone and datum [17], the kinematic formulation [18], and the spatial dimensional chain [19] are first presented focusing on the tolerance expression. Then, the direct linearization method (DLM) [20], the matrix model [21], and the Jacobian matrix model [22, 23], have developed correspondingly focusing on the tolerance propagation description. For Jacobian-Torsor [24], it combines both the advantages of the torsor model in tolerance expression and the Jacobian model in tolerance propagation expression, which is theoretically suitable for geometric error analysis of complex assemblies. Jacobian-Torsor has successfully applied Jacobian-Torsorfor static tolerance analysis of mechanical mechanisms. Chen et al. [25] introduced the Jacobian-Torsor model to geometric error analysis of the crank-slider mechanism and then applied it to the tolerances analysis of the engine assembly process successfully. Ding et al. [26] proposed an improved Jacobian-Torsor model for the multi-stage rotor assembly process of aero-engine, which greatly improved the accuracy and efficiency of the assembly process for the aero-engine rotor. Du et al. [27] applied the Jacobian-Torsor model to the error modeling of the machine tool to explain how the fundamental errors in mechanical parts influence and accumulate to the final assembly error of the single-axis part. These theoretical studies verified the validity and practicability of the Jacobian-Torsor model in dealing with the description and propagation expression of tolerances in the multi-body mechanism. The application of the Jacobian-Torsor model in geometric modeling for the multi-body mechanism is helpful for the geometric error expression of machine tools efficiently and accurately.

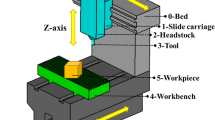
Figure 1 shows the topological motion diagram of a typical multi-axis machine tool which contains one rotation axis and three translation axes. The connection characteristics of this machine tool can be described in two aspects as a plane to plane contact and cylindrical contact. For example, along with the movement of the machine tool axis, the propagation path of contact characteristic is correspondingly changing, and so it is the related geometric error.

Figure 1
figure 1

The topological motion diagram of multi axis machine tool

Full size image

This paper focuses on developing a spatial modeling methodology based on an improved kinematic Jacobian-Torsor model, to deal with the spatial expression of geometric errors in a whole working space for multi-axis machine tool, which can express the continuous changes of geometric error in motion movement. Firstly, a general Jacobian-Torsor expression is given for the description of tolerance and its propagation in the assembly process. Secondly, the concept of improved kinematic Jacobian matrix is introduced to describe the propagation characteristic between two contact parts while considering the relative motion of components for multi-axis machine tools. The definitions of “direct relative motion” and “indirect relative motion” are proposed respectively. The influence of translational motion and rotational motion for the Jacobian-Torsor model is inferred. Thirdly, according to the error linkage effects among axes, the geometric model for the multi-axis machine tool is established. Finally, experiments are carried out to verify the effectiveness of the proposed improved kinematic Jacobian-Torsor model in modeling spatial geometric error.

The rest of the paper is organized as follows: Section 2 gives a simple review of the unified Jacobian-Torsor model for tolerance expression. Section 3 proposes an improved kinematic Jacobian-Torsor model for the spatial expression of geometric error distribution in working space accommodating the relative motion of the multi-axis machine tool. Case studies are taken to study the geometric error expression of the multi-axis machine tool based on the proposed kinematic Jacobian-Torsor model in Section 4. In Section 5, experiments are carried out to validate the proposed method in dealing with the spatial expression of geometric error based on the proposed model. Section 6 gives the conclusions.

2 Expression of Unified Jacobian-Torsor Model for Tolerance Analysis

With the Torsor model [28, 29], a set of vectors moving along the coordinate axis and a set of vectors rotating around the coordinate axis are defined to describe the various features of geometric errors in the tolerance domain. The torsor expression of the variation is

$${\varvec{T}} = \left[ {\begin{array}{*{20}c} \varvec{u} & \varvec{v} & \varvec{w} & \varvec{\alpha} & \varvec{\beta} & \varvec{\gamma} \\ \end{array} } \right]\,^{{\text{T}}} ,$$
(1)

where u, v and w are the three translation vectors along x, y and z axis, respectively. Similarly, the α, β and γ are the three rotation vectors around x, y and z axis, respectively.

The Jacobian matrix is divided into two parts used to describe the translation and rotation motions of features, respectively. For the translation vector, the direct cumulative operation can be done for the translation of the target point and it does not affect the rotation movement. For the rotation vector of the feature, the effect on the translation of the target point is equal to the cross-product between the rotation vector and the translation distance (here, [Win] is defined to represent it) of the target point, which is called leverage effect. And the effect of rotation vector on the rotation of target point can be directly accumulated. [Win] is a skew-symmetric matrix and can be defined as Eq. (2).

$$\left[ {{\varvec{W}}_{i}^{n} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & {\text{d}z_{i}^{n} } & { - \text{d}y_{i}^{n} } \\ { - \text{d}z_{i}^{n} } & 0 & {\text{d}x_{i}^{n} } \\ {\text{d}y_{i}^{n} } & { - \text{d}x_{i}^{n} } & 0 \\ \end{array} } \right]_{3 \times 3} ,$$
(2)

where, dxin= dxn- dxi, dyin= dyn- dyi, dzin= dzn- dzi. n represents the n-th target point, and i represents the i-th feature. A complete Jacobian matrix is obtained by combining these two matrices:

$$\left[ {\varvec{J}} \right]_{FEi} = \left[ {\begin{array}{*{20}c} {\left[ {{\varvec{R}}_{0}^{i} } \right]_{3 \times 3} } & \vdots & {\left[ {{\varvec{W}}_{i}^{n} } \right]_{3 \times 3} \cdot \left[ {{\varvec{R}}_{0}^{i} } \right]_{3 \times 3} } \\ \cdots & \vdots & \cdots \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & \vdots & {\left[ {{\varvec{R}}_{0}^{i} } \right]_{3 \times 3} } \\ \end{array} } \right],$$
(3)

where [R0i]3×3 indicates local orientation of the i-th coordinate system relative to the global system, here the global coordinate system is represented by the 0-th coordinate system.

Here, the Torsor model can be used for tolerance expression and the Jacobian matrix is used to describe the tolerance propagation in assembly. Because the variation range of tolerance is small, the Torsor model can be improved as a small displacement torsor (SDT). Consequently, in the Jacobian-Torsor model, the torsor model is applied for tolerance representation and the Jacobian matrix is used to represent tolerance propagation. The integrated expression can be written as follows:

$$\left[ {\begin{array}{*{20}c} {\left( {\underline{u} ,\overline{u} } \right)} \\ {\left( {\underline{v} ,\overline{v} } \right)} \\ {\left( {\underline{w} ,\overline{w} } \right)} \\ {\left( {\underline{\alpha } ,\overline{\alpha } } \right)} \\ {\left( {\underline{\beta } ,\overline{\beta } } \right)} \\ {\left( {\underline{\gamma } ,\overline{\gamma } } \right)} \\ \end{array} } \right]_{FR} = \left[ {\left[ {\varvec{J}} \right]_{FE1} \cdots \left[ {\varvec{J}} \right]_{FEn} } \right] \times \left[ {\left[ {\begin{array}{*{20}c} {\left( {\underline{u} ,\overline{u} } \right)} \\ {\left( {\underline{v} ,\overline{v} } \right)} \\ {\left( {\underline{w} ,\overline{w} } \right)} \\ {\left( {\underline{\alpha } ,\overline{\alpha } } \right)} \\ {\left( {\underline{\beta } ,\overline{\beta } } \right)} \\ {\left( {\underline{\gamma } ,\overline{\gamma } } \right)} \\ \end{array} } \right]_{FE1} \cdots \left[ {\begin{array}{*{20}c} {\left( {\underline{u} ,\overline{u} } \right)} \\ {\left( {\underline{v} ,\overline{v} } \right)} \\ {\left( {\underline{w} ,\overline{w} } \right)} \\ {\left( {\underline{\alpha } ,\overline{\alpha } } \right)} \\ {\left( {\underline{\beta } ,\overline{\beta } } \right)} \\ {\left( {\underline{\gamma } ,\overline{\gamma } } \right)} \\ \end{array} } \right]_{FEn} } \right]^{{\text{T}}} ,$$
(4)

where \(\left( {\underline{u} ,\overline{u} } \right)\) represents the tolerance interval along x axis. And the representations of torsors of other components are following the identical way as u. The functional requirement (FR) and functional elements (FEs) are the component elements of dimension chain.

3 Expression of Kinematic Jacobian-Torsor Model for Spatial Geometric Error

The Jacobian-Torsor model is generally applied for the description of tolerance propagation of complex assemblies which contain the number of joints for a determined pose. Whereas it is difficult to be applied dealing with movement in assemblies under a kinematic state. Eq. (4) is defined according to the type, tolerance, and position of feature in assembly. Therefore, when the relative position of two features changes, the Jacobian-Torsor is meant to be changed correspondingly.

Here, two definitions are given to deal with the changing of configuration in assemblies. The “direct relative motion”, which means there is kinematic pair between two parts, such as rotating or sliding pair, while there is relative motion between these two parts. The “indirect relative motion”, which means there is no kinematic pair between two parts, but these two parts have indirectly relative motion through another part which is connected to both of them.

3.1 Kinematic Jacobian-Torsor Expression for Translation Motion of CNC Machine Tool

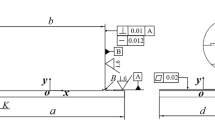
The motions of the multi-axis machine tool can be described as two typical types: translation motion and rotation motion. For translation motion, taking Z-axis as an example, it can be shown as the Z-axis translation motion of the CNC machine tool in Figure 2.

Figure 2
figure 2

The Z-axis translation motion of CNC machine tool

Full size image

The rotary table on the slider moves along the guide from point A to point B. The top surfaces of the guide and the slider respectively are specified by profile tolerances of T1 and T2 with the corresponding datum. The profile of the moving contact part between the guide and the slider is defined as Tz. FR is the contact profile between the upper surface of the slider and the bottom of the guide after assembly. When the slider moves along the guide with a distance of z, there will be a translation joint between these two components.

When the slider is at point A, the complete Jacobian matrix for the guide-slider assembly can be written as:

$${\varvec{J}}_{A} = \left[ {{\varvec{J}}_{FEA1} {\varvec{J}}_{FEA2} } \right] = \left[ \begin{gathered} \left[ {\begin{array}{*{20}c} {\left[ {{\varvec{R}}_{0}^{1} } \right]_{3 \times 3} } & {\left[ {{\varvec{W}}_{1}^{2} } \right]_{3 \times 3} \cdot \left[ {{\varvec{R}}_{0}^{1} } \right]_{3 \times 3} } \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & {\left[ {{\varvec{R}}_{0}^{1} } \right]_{3 \times 3} } \\ \end{array} } \right]_{FEA1} \hfill \\ \left[ {\begin{array}{*{20}c} {\left[ {{\varvec{R}}_{0}^{2} } \right]_{3 \times 3} } & {\left[ {{\varvec{W}}_{2}^{2} } \right]_{3 \times 3} \cdot \left[ {{\varvec{R}}_{0}^{2} } \right]_{3 \times 3} } \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & {\left[ {{\varvec{R}}_{0}^{2} } \right]_{3 \times 3} } \\ \end{array} } \right]_{FEA2} \hfill \\ \end{gathered} \right]^{{\text{T}}} .$$
(5)

Similarly, when the slider is at point B, the complete Jacobian matrix for the guide-slider assembly can be written as:

$${\varvec{J}}_{B} = \left[ {{\varvec{J}}_{FEB1} {\varvec{J}}_{FEB2} } \right] = \left[ \begin{gathered} \left[ {\begin{array}{*{20}c} {\left[ {{\varvec{R}}_{0}^{{1^{^{\prime}} }} } \right]_{3 \times 3} } & {\left[ {{\varvec{W}}_{{1^{^{\prime}} }}^{2} } \right]_{3 \times 3} \cdot \left[ {{\varvec{R}}_{0}^{{1^{^{\prime}} }} } \right]_{3 \times 3} } \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & {\left[ {{\varvec{R}}_{0}^{{1^{^{\prime}} }} } \right]_{3 \times 3} } \\ \end{array} } \right]_{FEB1} \hfill \\ \left[ {\begin{array}{*{20}c} {\left[ {{\varvec{R}}_{0}^{{2^{^{\prime}} }} } \right]_{3 \times 3} } & {\left[ {{\varvec{W}}_{{2^{^{\prime}} }}^{2} } \right]_{3 \times 3} \cdot \left[ {{\varvec{R}}_{0}^{{2^{^{\prime}} }} } \right]_{3 \times 3} } \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & {\left[ {{\varvec{R}}_{0}^{{2^{^{\prime}} }} } \right]_{3 \times 3} } \\ \end{array} } \right]_{FEB2} \hfill \\ \end{gathered} \right]^{{\text{T}}} ,$$
(6)

where \(\left[ {{\varvec{W}}_{1}^{2} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & {(z_{1} - z_{0} )} & { - (y_{1} - y_{0} )} \\ { - (z_{1} - z_{0} )} & 0 & {(x_{1} - x_{0} )} \\ {(y_{1} - y_{0} )} & { - (x_{1} - x_{0} )} & 0 \\ \end{array} } \right]_{3 \times 3}\), \(\left[ {{\varvec{W}}_{2}^{2} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & {(z_{3} - z_{2} )} & { - (y_{3} - y_{2} )} \\ { - (z_{3} - z_{2} )} & 0 & {(x_{3} - x_{2} )} \\ {(y_{3} - y_{2} )} & { - (x_{3} - x_{2} )} & 0 \\ \end{array} } \right]_{3 \times 3}\),

\(\left[ {{\varvec{W}}_{{1^{^{\prime}} }}^{2} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & {(z^{^{\prime}}_{1} - z_{0} )} & { - (y^{^{\prime}}_{1} - y_{0} )} \\ { - (z^{^{\prime}}_{1} - z_{0} )} & 0 & {(x^{^{\prime}}_{1} - x_{0} )} \\ {(y^{^{\prime}}_{1} - y_{0} )} & { - (x^{^{\prime}}_{1} - x_{0} )} & 0 \\ \end{array} } \right]_{3 \times 3}\), \(\left[ {{\varvec{W}}_{{2^{^{\prime}} }}^{2} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & {(z^{^{\prime}}_{3} - z^{^{\prime}}_{2} )} & { - (y^{^{\prime}}_{3} - y^{^{\prime}}_{2} )} \\ { - (z^{^{\prime}}_{3} - z^{^{\prime}}_{2} )} & 0 & {(x^{^{\prime}}_{3} - x^{^{\prime}}_{2} )} \\ {(y^{^{\prime}}_{3} - y^{^{\prime}}_{2} )} & { - (x^{^{\prime}}_{3} - x^{^{\prime}}_{2} )} & 0 \\ \end{array} } \right]_{3 \times 3}\) respectively.

In this case, the coordinate system 1 and 2, 1’ and 2’ are defined as coincident pairs, respectively. Compared with point A, the coordinate system of point B only has a displacement of z in the Z direction to point A. The local orientation of the coordinate systems relative to the global system are all unit matrices.

There, Eq. (6) can be rewritten as:

$${\varvec{J}}_{B} = {\varvec{J}}_{A} + \Delta {\varvec{J}}_{T} ,$$
(7)

where, \(\Delta J_{T} { = }\left[ {\left[ {\begin{array}{*{20}c} {\left[ 0 \right]_{3 \times 3} } & {\left[ {\begin{array}{*{20}c} 0 & z & 0 \\ { - z} & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]_{3 \times 3} } \\ {\left[ 0 \right]_{3 \times 3} } & {\left[ 0 \right]_{3 \times 3} } \\ \end{array} } \right]_{6 \times 6} \left[ 0 \right]_{6 \times 6} } \right]\).

SDT is a special expression of feature variation in the tolerance domain. The SDT expression of tolerance is defined according to both the tolerance type and joint configuration. When the location of the feature changes, the contact joint between two features and the value of the contact error will change correspondingly. Therefore, the SDT expression of tolerance propagation will be changed along with the change of feature location. According to the SDT expression described above, the Torsor expression of the upper surface of the guide that contact with the slider can be written as follows:

$$\left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FEB1} = \left[ {\begin{array}{*{20}c} {\left( { - \frac{{T_{z} }}{2},\frac{{T_{z} }}{2}} \right)} \\ 0 \\ 0 \\ 0 \\ {\left( { - \frac{{T_{z} }}{2c},\frac{{T_{z} }}{2c}} \right)} \\ {\left( { - \frac{{T_{z} }}{2b},\frac{{T_{z} }}{2b}} \right)} \\ \end{array} } \right]_{FEB1} ,$$
(8)

where Tz is the profile error of the guide contacted to the slider, and Tz = Tst+zθ, θ=(T−Tst)/L. L is the total length of the guide. Tst is the profile error of nominal length of guide. It can be seen that the profile error changes with the slider position on the guide. b and c are the width of the guide and the length of slider, respectively.

Considering the relative translation motion inside the assemblies, when the slider is at point A, the Jacobian-Torsor expression for assemblies can be expressed as:

$$\left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FRA} = {\varvec{J}}_{A} \times \left[ {\left[ {\begin{array}{*{20}c} {\left( { - \frac{{T_{0} }}{2},\frac{{T_{0} }}{2}} \right)} \\ 0 \\ 0 \\ 0 \\ {\left( { - \frac{{T_{0} }}{2c},\frac{{T_{0} }}{2c}} \right)} \\ {\left( { - \frac{{T_{0} }}{2b},\frac{{T_{0} }}{2b}} \right)} \\ \end{array} } \right]_{FEA1} \left[ {\begin{array}{*{20}c} {\left( { - \frac{{T_{2} }}{2},\frac{{T_{2} }}{2}} \right)} \\ 0 \\ 0 \\ 0 \\ {\left( { - \frac{{T_{2} }}{2c},\frac{{T_{2} }}{2c}} \right)} \\ {\left( { - \frac{{T_{2} }}{2a},\frac{{T_{2} }}{2a}} \right)} \\ \end{array} } \right]_{FEA2} } \right]^{{\text{T}}} .$$
(9)

Similarly, when the slider is at point B, the Jacobian-Torsor expression for assemblies can be expressed as:

$$\left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FRB} = {\varvec{J}}_{B} \times \left[ {\left[ {\begin{array}{*{20}c} {\left( { - \frac{{T_{0} }}{2},\frac{{T_{0} }}{2}} \right)} \\ 0 \\ 0 \\ 0 \\ {\left( { - \frac{{T_{0} }}{2c},\frac{{T_{0} }}{2c}} \right)} \\ {\left( { - \frac{{T_{0} }}{2b},\frac{{T_{0} }}{2b}} \right)} \\ \end{array} } \right]_{FEB1} \left[ {\begin{array}{*{20}c} {\left( { - \frac{{T_{2} }}{2},\frac{{T_{2} }}{2}} \right)} \\ 0 \\ 0 \\ 0 \\ {\left( { - \frac{{T_{2} }}{2c},\frac{{T_{2} }}{2c}} \right)} \\ {\left( { - \frac{{T_{2} }}{2a},\frac{{T_{2} }}{2a}} \right)} \\ \end{array} } \right]_{FEB2} } \right]^{{\text{T}}} .$$
(10)

In this situation, Eq. (10) can be rewritten as

$$\left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FRB} = \left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FRA} + \left[ {\begin{array}{*{20}c} {\frac{{\left( {T_{2} - T_{st} } \right)z^{2} }}{2cL} + \frac{{zT_{st} }}{2c}} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right].$$
(11)

3.2 Kinematic Jacobian-Torsor Expression for Rotation Motion of CNC Machine Tool

The rotation motion of the CNC machine tool, taking A-axis as an example, can be seen as the A-axis rotation motion of the CNC machine tool shown in Figure 3. The base and rotary parts of the rotary table are assembled concentrically. And the rotary table can rotate around the center of the base. The bottom surface of each cylinder is defined as the base surface of the part, and the top surface contains a contour tolerance to its nominal surface.

Figure 3
figure 3

The assembly of rotary table and base

Full size image

In this case, FR is defined as the profile tolerance of the upper surface of the rotary table relative to the bottom of the base after assembly. The rotary table rotates around the center of the base by the angle of θ, and there is a revolution joint between them. The complete Jacobian matrix for the rotary components before the rotation of the rotary table can be written as:

$${\varvec{J}}_{C} = \left[ {{\varvec{J}}_{FEC1} {\varvec{J}}_{FEC2} } \right] = \left[ \begin{gathered} \left[ {\begin{array}{*{20}c} {\left[ {{\varvec{R}}_{0}^{1} } \right]_{3 \times 3} } & {\left[ {{\varvec{W}}_{1}^{2} } \right]_{3 \times 3} \cdot \left[ {{\varvec{R}}_{0}^{1} } \right]_{3 \times 3} } \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & {\left[ {{\varvec{R}}_{0}^{1} } \right]_{3 \times 3} } \\ \end{array} } \right]_{FEC1} \hfill \\ \left[ {\begin{array}{*{20}c} {\left[ {{\varvec{R}}_{0}^{2} } \right]_{3 \times 3} } & {\left[ {{\varvec{W}}_{2}^{2} } \right]_{3 \times 3} \cdot \left[ {{\varvec{R}}_{0}^{2} } \right]_{3 \times 3} } \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & {\left[ {{\varvec{R}}_{0}^{2} } \right]_{3 \times 3} } \\ \end{array} } \right]_{FEC2} \hfill \\ \end{gathered} \right].$$
(12)

In the same way, the complete Jacobian matrix for the rotary components after the rotation of the rotary table can be written as:

$${\varvec{J}}_{D} = \left[ {{\varvec{J}}_{FED1} {\varvec{J}}_{FED2} } \right] = \left[ \begin{gathered} \left[ {\begin{array}{*{20}c} {\left[ {{\varvec{R}}_{0}^{{1^{^{\prime}} }} } \right]_{3 \times 3} } & {\left[ {{\varvec{W}}_{{1^{^{\prime}} }}^{2} } \right]_{3 \times 3} \cdot \left[ {{\varvec{R}}_{0}^{{1^{^{\prime}} }} } \right]_{3 \times 3} } \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & {\left[ {{\varvec{R}}_{0}^{{1^{^{\prime}} }} } \right]_{3 \times 3} } \\ \end{array} } \right]_{FED1} \hfill \\ \left[ {\begin{array}{*{20}c} {\left[ {{\varvec{R}}_{0}^{{2^{^{\prime}} }} } \right]_{3 \times 3} } & {\left[ {{\varvec{W}}_{{2^{^{\prime}} }}^{2} } \right]_{3 \times 3} \cdot \left[ {{\varvec{R}}_{0}^{{2^{^{\prime}} }} } \right]_{3 \times 3} } \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & {\left[ {{\varvec{R}}_{0}^{{2^{^{\prime}} }} } \right]_{3 \times 3} } \\ \end{array} } \right]_{FED2} \hfill \\ \end{gathered} \right]^{{\text{T}}} ,$$
(13)

where \(\left[ {{\varvec{W}}_{1}^{2} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & {H_{1} } & 0 \\ { - H_{1} } & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]_{3 \times 3}\), \(\left[ {{\varvec{W}}_{2}^{2} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & {H_{2} } & 0 \\ { - H_{2} } & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]_{3 \times 3}\), \(\left[ {{\varvec{W}}_{1^{\prime}}^{2} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & {H_{1} } & 0 \\ { - H_{1} } & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]_{3 \times 3}\), \(\left[ {{\varvec{W}}_{2^{\prime}}^{2} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} 0 & {H_{2} } & 0 \\ { - H_{2} } & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right]_{3 \times 3}\), \(\left[ {{\varvec{R}}_{0}^{{2^{^{\prime}} }} } \right]_{3 \times 3} = \left[ {\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } & 0 \\ {\sin \theta } & {\cos \theta } & 0 \\ 0 & 0 & 1 \\ \end{array} } \right]_{3 \times 3}\), respectively.

In this situation, Eq. (13) can be rewritten as

$${\varvec{J}}_{D} = {\varvec{J}}_{C} + \Delta {\varvec{J}}_{R} ,$$
(14)

where, \(\Delta {\varvec{J}}_{R} { = }\left[ {\left[ {\varvec{0}} \right]_{6 \times 6} \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - 1 + \cos \theta } & { - \sin \theta } & 0 \\ {\sin \theta } & { - 1 + \cos \theta } & 0 \\ 0 & 0 & 0 \\ \end{array} } & {\begin{array}{*{20}c} {H_{2} \sin \theta } & { - H_{2} + H_{2} \cos \theta } & 0 \\ {H_{2} - H_{2} \cos \theta } & {H_{2} \sin \theta } & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ {\left[ {\varvec{0}} \right]_{3 \times 3} } & {\begin{array}{*{20}c} { - 1 + \cos \theta } & { - \sin \theta } & 0 \\ {\sin \theta } & { - 1 + \cos \theta } & 0 \\ 0 & 0 & 0 \\ \end{array} } \\ \end{array} } \right]_{6 \times 6} } \right].\)

With the rotation of the rotary table from the base, the Torsor expression of the matching part of the two cylinders can be written as follows:

$$\left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FED1} = \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\left( { - \frac{{T_{1} }}{2},\frac{{T_{1} }}{2}} \right)} \\ {\left( { - \frac{{T_{1} }}{2R},\frac{{T_{1} }}{2R}} \right)} \\ {\left( { - \frac{{T_{1} }}{2R},\frac{{T_{1} }}{2R}} \right)} \\ 0 \\ \end{array} } \right]_{FED1} ,$$
(15)

where T1 is the profile error of the rotary table. R is radius of the two cylinders. The Torsor expression remains unchanged with the rotation of the rotary table from the base.

The Jacobian-Torsor expression for the rotary components before the rotation of the rotary table can be written as:

$$\left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FRC} = {\varvec{J}}_{C} \times \left[ {\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\left( { - \frac{{T_{1} }}{2},\frac{{T_{1} }}{2}} \right)} \\ {\left( { - \frac{{T_{1} }}{2R},\frac{{T_{1} }}{2R}} \right)} \\ {\left( { - \frac{{T_{1} }}{2R},\frac{{T_{1} }}{2R}} \right)} \\ 0 \\ \end{array} } \right]_{FEC1} \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\left( { - \frac{{T_{2} }}{2},\frac{{T_{2} }}{2}} \right)} \\ {\left( { - \frac{{T_{2} }}{2R},\frac{{T_{2} }}{2R}} \right)} \\ {\left( { - \frac{{T_{2} }}{2R},\frac{{T_{2} }}{2R}} \right)} \\ 0 \\ \end{array} } \right]_{FEC2} } \right]^{{\text{T}}} .$$
(16)

Similarly, the Jacobian-Torsor expression for assemblies after the rotary table rotates around the center of the base can be expressed as:

$$\left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FRD} = {\varvec{J}}_{D} \times \left[ {\left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\left( { - \frac{{T_{1} }}{2},\frac{{T_{1} }}{2}} \right)} \\ {\left( { - \frac{{T_{1} }}{2R},\frac{{T_{1} }}{2R}} \right)} \\ {\left( { - \frac{{T_{1} }}{2R},\frac{{T_{1} }}{2R}} \right)} \\ 0 \\ \end{array} } \right]_{FED1} \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ {\left( { - \frac{{T_{2} }}{2},\frac{{T_{2} }}{2}} \right)} \\ {\left( { - \frac{{T_{2} }}{2R},\frac{{T_{2} }}{2R}} \right)} \\ {\left( { - \frac{{T_{2} }}{2R},\frac{{T_{2} }}{2R}} \right)} \\ 0 \\ \end{array} } \right]_{FED2} } \right]^{{\text{T}}} .$$
(17)

With Eq. (16), Eq. (17) can be rewritten as

$$\left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FRD} = \left[ {\begin{array}{*{20}c} {\left( {\underline{{\varepsilon_{x} }} ,\overline{{\varepsilon_{x} }} } \right)} \\ {\left( {\underline{{\varepsilon_{y} }} ,\overline{{\varepsilon_{y} }} } \right)} \\ {\left( {\underline{{\varepsilon_{z} }} ,\overline{{\varepsilon_{z} }} } \right)} \\ {\left( {\underline{{\rho_{x} }} ,\overline{{\rho_{x} }} } \right)} \\ {\left( {\underline{{\rho_{y} }} ,\overline{{\rho_{y} }} } \right)} \\ {\left( {\underline{{\rho_{z} }} ,\overline{{\rho_{z} }} } \right)} \\ \end{array} } \right]_{FRC} + \left[ {\begin{array}{*{20}c} {\frac{{T_{2} H_{2} }}{2R}\left( {\sin \theta + \cos \theta - 1} \right)} \\ {\frac{{T_{2} H_{2} }}{2R}\left( {1 + \sin \theta - \cos \theta } \right)} \\ 0 \\ {\frac{{T_{2} }}{2R}\left( {\cos \theta - \sin \theta - 1} \right)} \\ {\frac{{T_{2} }}{2R}\left( {\cos \theta + \sin \theta - 1} \right)} \\ 0 \\ \end{array} } \right].$$
(18)

As can be seen, only the Jacobian matrix and Torsor expression of the functional element with direct relative motion will be changed, when there is relative motion between the components in assemblies. And the change of the Jacobian matrix is only reflected by increasing the corresponding increment in the direction of relative motion. Therefore, when the coordinate origin of the assembly is determined, no matter what relative motion occurs inside the assemblies, the functional requirements after the change can be easily expressed through Eqs. (11) and (18).

Therefore, the process of geometric error modeling for machine tool based on the proposed kinematic Jacobian-Torsor model can be shown as Figure 4.

Figure 4
figure 4

The process of modeling machine tool geometric error based on kinematic Jacobian-Torsor model

Full size image

The main advantages of the proposed method compared with other existing methods are shown in Table 1.

Table 1 The main advantages of the proposed method compared with other existing methods
Full size table

4 Modeling of Spatial Geometric Error for Multi-axis Machine Tool

In this paper, a four-axis horizontal machining center is applied to validate the geometric error model. The 3D model and topological structure of the horizontal machining center are shown in Figure 5. The four-axis horizontal machining center has four degrees of freedom which include one rotation motion (A-axis) and three translation motions (X-axis, Y-axis, Z-axis) and their basic parameters are shown in Table 2.

Figure 5
figure 5

The structure and topological structure of a horizontal machining center

Full size image
Table 2 The basic parameters of machine tool
Full size table

The accuracy of the machine tool is described as the error variation of the tool center point in the worktable coordinate system. Therefore, FR represents the position and direction deviation of the tool center point in the workpiece coordinate system. The connection graph of functional pairs is shown in Figure 6.

Figure 6
figure 6

Connection graph of functional pairs

Full size image

The detail parameters of the machine tool are shown in Table 3.

Table 3 The detail parameters of the machine tool
Full size table

The improved Jacobian-Torsor model can be built according to the connection graph of functional pairs and based on the proposed model in Section 3. The propagation route of geometric errors can be shown as IFE1-CFE1-IFE2-CFE2-IFE3-IFE4-IFE5-IFE6. The Jacobian matrices and the corresponding tolerance torsors can be given in Table 4.

Table 4 Jacobian matrixes and deviation torsors
Full size table

According to the kinematic Jacobian-Torsor model of tolerance analysis, as given in Table 1, the expression of the spindle and tool error in Z direction in the table coordinate system can be resulted as:

$${\varepsilon }_{Z}=\left[A,B\right],$$
(19)

where, A=0,

$$B =\, \frac{{z^{2} \left( {T_{Z} - T_{st} } \right)}}{43L} + \frac{{z\left( {T_{st} \cdot L - 300T_{Z} + 300T_{st} } \right)}}{43L} - \frac{{300T_{st} }}{43} + 18.79 + \left| {3.72\sin \alpha } \right| + \left| {0.28\cos \alpha } \right|,$$

where, Z is the stroke of the spindle and tool error in Z direction in the table coordinate system and it lies in the interval of [0, 600], α is the rotation angle of the turntable along X axis and it lies in the interval of [0, 360°], the rotary shaft is called A axis, and the tolerance accumulation must lie in the interval of [−εz, εz].

5 Experimental Verification and Discussion

In order to validate the proposed kinematic Jacobian-Torsor model in geometric error modeling for multi-axis machine tool, experiments were conducted on five four-axis machining centers (type CNC-PT50) with a laser interferometer which was used to measure the linear axis errors. The Renishaw multi-laser interferometer XL-80 is used to measure the geometric errors of the machine tool. The linear measurement accuracy of ± 0.5 \(\mathrm{\upmu m}/\mathrm{m}\) is guaranteed and the linear resolution can reach 1 nm. Two kinds of measurement processes have been carried out for each machining center. One is to make a forward movement along the linear axis and the rotation axis, and the other is to make a backward movement along the linear axis and the rotation axis. The setup of the measurement experiment is shown in Figure 7.

Figure 7
figure 7

The setup of the measurement experiment

Full size image

As shown in Figure 8, the movement variation of geometric errors along Z axis is figured out both for the modeling based on the proposed kinematic Jacobian-Torsor model and for the measured results in validation experiments. In Figure 8, the upper bound is the tolerance range modeled by the proposed geometric error expression model based on the kinematic Jacobian-Torsor model. The y1f and y1b are the measurement results of the machining centers when there are forward movement and backward movement along the linear axis and the rotation axis, respectively. It can be observed that all the curved surfaces of the positioning error in experiments are within the tolerance range gotten by the proposed expression model.

Figure 8
figure 8

Multiple measurement results of the positioning error of the machine tool of PT50

Full size image

Furthermore, the distributions of geometric errors of machine tools at different Z coordinate positions are analyzed. Set Z value as (–300, 0, 100, 300), respectively, the geometric error distribution of the machine tool in four positions is shown in Figure 9. The mean value of the geometric error distribution is shown in Table 5. The μm is the mean value of the geometric error distribution of the machine tool calculated by the model, and μe is the mean value of the geometric error distribution of the machine tool obtained in experiments, respectively. It can be seen that the mean value of the geometric error distribution of the machine tool obtained in experiments is close to those obtained by the kinematic Jacobian-Torsor model. And the fluctuation range and fluctuation degree trend of the error are consistent with the change of Z. It can be seen from Figure 9 that the mean value of the theoretical value and the measured value are consistent, and the standard deviation difference is large. The consistent mean value indicates the accuracy and effectiveness of the model. For the standard deviation, the measured value fluctuates less, and the theoretical value fluctuates more. The reason is that the establishment of the model is based on the premise that the errors of machine tool parts are randomly distributed within the tolerance range. However, the machine tool parts belong to the same batch and the sampling number is limited, the error distribution will be more convergent than those in simulation for the random distribution sampling.

Figure 9
figure 9figure 9

The geometric error distribution of the machine tool in four different Z coordinates

Full size image
Table 5 The mean and standard deviation of geometric error distribution
Full size table

6 Conclusions

  1. (1)

    The non-uniformly distributed geometric errors of the multi-axis machine tool can be spatially expressed in the different moving positions.

  2. (2)

    It can be applied for different types of machine tools with different configurations, thus providing thermotical guidance for the comprehensive tolerance design of machine tools.

  3. (3)

    Furthermore, by introducing variables such as speed and acceleration, the relationship between tolerances and kinematic characteristics of the machine tool can be analyzed.