1 Introduction

As a typical highly nonlinear mechatronics equipment, multi-axis CNC machine tools are often used to process parts with complex surfaces [1, 2], so they are necessary to maintain high machining accuracy. With the extension of working time and the uncertainty of the working environment, machine tool components will be worn and performance will decline. The total errors caused by the manufacturing and assembly of components, the temperature change during processing, and the different chip parameters during processing will always affect the machining accuracy [3, 4]. In the main error sources of machine tools, geometric and thermal error accounts for about 50–70%, especially the former accounts for about 40% [5, 6]. In this paper, the geometric error parameters in the machining cycle of MAMT are measured and statistically analyzed. Based on the digital characteristics of the error parameters, the machining accuracy reliability is evaluated, and the AFS analysis of the machine tool is studied.

Generally speaking, the reliability of MAMT is mostly from the perspective of mechanics (such as stress and strength, etc.), or the machine tool is divided into multiple subsystems (such as tool axis system, workpiece box system, coolant system), and the reliability of machine tool is studied through fault tree, Bayesian estimation, and other analysis methods [7,8,9]. The machining accuracy reliability defined in this paper is the ability of MAMT to maintain a specific machining accuracy after a certain period of cutting under specific working conditions. Up to now, more and more researchers have begun to pay attention to the damage to the accuracy reliability of MAMT due to the change of geometric error parameters, and have done more research [10, 11]. Based on the measured geometric error parameters, combined with the response surface method, Wu et al. analyzed the machining accuracy reliability of machine tools, but the reliability analysis results were not verified [12]. When evaluating the reliability of the press, Xiao et al. established a reliability model of its motion accuracy, and by the Monte Carlo simulation, simulated its bottom dead center position, and proposed a novel method to study the accuracy for the press [13]. After defining the failure mode of linear guide positioning accuracy, Wang et al. proposed a method to evaluate the dynamic reliability of linear guide positioning accuracy and carried out reliability sensitivity analysis [14]. Most of the above analysis uses Monte Carlo simulation, but this method in reliability analysis is limited in actual engineering applications because it needs more sample data and a large amount of calculation.

The establishment of spatial machining accuracy model is the basis of all analysis work, and a large number of researchers have proposed many modeling methods [15]. Among them, the modeling method based on MBS theory has been widely used [16, 17, 31]. Under the assumption that each body of the machine tool is regarded as a rigid body, Zhu et al. established the accuracy model of the five-axis machining center by MBS, completed the modeling of geometric errors, and then launched the research on the identification and compensation of machine tool errors [18]. Fan et al. established the functional relationship between the tolerance and the volume error of a five-axis machine tool by MBS theory and tolerance model [19]. In this paper, based on the theory of MBS with high application maturity, the spatial machining accuracy model of the selected MAMT is established, to obtain the accuracy values in three spatial directions.

The measurement process of geometric error parameters has randomness [20], and its uncertainty and complex correlation exist objectively [21, 22]. A large number of works of literature show that geometric error parameters are multi-dimensional random variables that approximately obey normal distribution [23, 24]. In reliability analysis, it is necessary to analyze the correlation between multi-dimensional random variables [25, 26]. Chen et al. introduced the Spearman rank correlation method to describe the relationship between a single error parameter and the tool attitude error in the whole sampling space. [27]. Cai et al. optimized the accuracy of machine tools based on geometric error correlation analysis [28]. Zhang et al. proposed a pipeline reliability calculation method based on the correlation analysis of random variables and researched the correlation of variables and pipeline corrosion failure [29]. In this paper, from the randomness and uncertainty in the process of geometric error measurement, considering the time series of error data, the cross-correlation analysis method is used to analyze the correlation between error parameters for reliability analysis. Cross-correlation analysis has been maturely applied in signal processing [25], vibration signal power spectrum analysis [30], and other fields.

In the research on the sensitivity of machine tool geometric errors, researchers have proposed many analysis methods. Aiming at the influence of geometric error for a five-axis machine tool on the accuracy, Guo et al. introduced the global quantitative sensitivity method to analyze and performed error compensation on the analysis results [31]. Fu et al. analyzed the structure of the three measurement modes of TFFIA, and researched the identification of the rotation axis error that affects the accuracy of the sensitive direction in each mode [32]. Xia et al. analyzed the relationship between the installation position of the club and the direction of sensitivity and carried out a sensitivity analysis to reduce the influence of the installation error of the ball club [33]. This paper starts from each measurement point in the working space of the machine tool, analyzes the accuracy failure modes in three directions of the machine tool, and proposes a method for analysis of the machining accuracy reliability and accuracy failure sensitivity considering the cross-correlation of random errors. To find some accuracy failure machining points and the most critical geometric error of the MAMT.

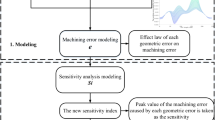
The structure of the rest of this paper is as follows: In the second section, based on the multi-body system kinematics theory, the spatial machining accuracy model of machine tool is established. In the third section, the analysis method of machining accuracy reliability and accuracy failure sensitivity proposed in this paper is mainly elaborated. In the fourth section, a high-precision 3-axis machine tool is taken as an example to verify the effectiveness of the proposed method. Section 5 is to reveal the conclusion of this paper.

2 Constructing the CNC machine tool spatial machining accuracy model

Multi-body system refers to a complex mechanical system formed by connecting multiple rigid or flexible bodies in some form. MBS is currently an optimal model for analyzing and studying complex mechanical systems. For a general CNC machine tool, it is a typical multi-body system, which is composed of bed, column, workbench, motion axis, spindle, cutter, and other parts.

2.1 The main structural parameters of the machine tool

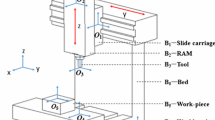
The structure of the high-precision 3-axis machine tool studied in this paper is shown in Figure 1. According to the MBS theory, the moving bodies of the machine tool are numbered. The dimensions of each part of the machine tool are listed in Table 1. According to the design requirements of the machine tool, the maximum accuracy index of the machining error in the X, Y, and Z directions is shown in Table 2. The machine tool error can be divided into static error independent of motion and motion error related to the amount of motion. Each axis has 6 basic errors, respectively, so the machine tool has 18 position-related system geometric errors. Among them, the motion parameter of the rotary unit is angle rather than length. In addition, the machine tool also contains three system geometric errors independent of position. Table 3 shows the symbols of all errors and their physical meanings.

Fig. 1
figure 1

The main structure of the machine tool

Full size image
Table 1 Basic parameters of machine tool
Full size table
Table 2 Maximum allowable machining error in X, Y, and Z directions
Full size table
Table 3 Geometric errors symbol and meaning
Full size table

2.2 Establish the motion characteristic matrix of machine tool

Each part of the machine tool can be simplified into several arbitrary classic bodies. The machine tool can be described as a double-chain topology structure, one is the Bed-Slide Carriage-Headstock-Tool, and the other is the bed-workbench-workpiece. This article can clearly describe the motion transfer relationship between the bodies by establishing the low-order volume array of the machine tool, as shown in Table 4. At the same time, analyze the degrees of freedom between each body, as shown in Table 5, where “0” means no degree of freedom and “1” means a single degree of freedom (that is, translation in a certain direction).

Table 4 Multi-body system low-order volume array
Full size table
Table 5 The freedom of vertical CNC machine tool
Full size table

Based on MBS theory and the set generalized coordinate system, the motion between bodies can be simplified as the motion of the rigid body in space, and the motion of the rigid body is composed of rotation and translation. To represent rotation and translation with the same matrix, it is necessary to introduce a 4 × 4 homogeneous coordinate transformation matrix. Therefore, the characteristic matrices describing the motion between adjacent bodies of high-precision vertical CNC machine tools are as follows, in which the superscript p is static, s is motion, and I4 × 4 means that when the error is relatively small, it can be ignored as the identity matrix.

Ideal stationary and moving homogeneous transformation matrix between adjacent bodies 0–1 are as follows:

$$ {M}_{01}^p={I}_{4\times 4},\kern0.5em {M}_{01}^s=\left[\begin{array}{cccc}1& 0& 0& x\\ {}0& 1& 0& 0\\ {}0& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right], $$
(1)

Homogeneous transformation matrix of static and motion errors between 0 and 1 bodies are as follows:

$$ \boldsymbol{\Delta} {M}_{\mathbf{01}}^{\mathbf{p}}=\left[\begin{array}{cccc}1& -{\varepsilon \gamma}_{xy}& {\varepsilon \beta}_{xz}& x\\ {}{\varepsilon \gamma}_{xy}& 1& 0& 0\\ {}-{\varepsilon \beta}_{xz}& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right],\boldsymbol{\Delta} {M}_{\mathbf{01}}^{\mathbf{s}}=\left[\begin{array}{cccc}1& -\varepsilon \gamma x& \varepsilon \beta x& \delta xx\\ {}\varepsilon \gamma x& 1& -\varepsilon \alpha x& \delta yx\\ {}-\varepsilon \beta x& \varepsilon \alpha x& 1& \delta zx\\ {}0& 0& 0& 1\end{array}\right] $$
(2)

Similarly, the motion characteristic matrices of other bodies can be obtained, as shown in the following Eqs. 3–8.

$$ {M}_{12}^p={I}_{4\times 4},\kern0.5em {M}_{12}^s=\left[\begin{array}{cccc}1& 0& 0& 0\\ {}0& 1& 0& 0\\ {}0& 0& 1& z\\ {}0& 0& 0& 1\end{array}\right], $$
(3)
$$ \boldsymbol{\Delta} {M}_{\mathbf{12}}^{\mathbf{p}}=\left[\begin{array}{cccc}1& 0& 0& 0\\ {}0& 1& -{\varepsilon \alpha}_{yz}& 0\\ {}0& {\varepsilon \alpha}_{yz}& 1& 0\\ {}0& 0& 0& 1\end{array}\right],\boldsymbol{\Delta} {M}_{\mathbf{12}}^{\mathbf{s}}=\left[\begin{array}{cccc}1& -\varepsilon \gamma z& \varepsilon \beta z& \delta xz\\ {}\varepsilon \gamma z& 1& -\varepsilon \alpha z& \delta yz\\ {}-\varepsilon \beta z& \varepsilon \alpha z& 1& \delta zz\\ {}0& 0& 0& 1\end{array}\right] $$
(4)
$$ {M}_{23}^p={I}_{4\times 4},{M}_{23}^s={I}_{4\times 4},\boldsymbol{\Delta} {M}_{23}^{\mathbf{p}}={I}_{4\times 4},\boldsymbol{\Delta} {M}_{23}^{\mathbf{s}}={I}_{4\times 4} $$
(5)
$$ {M}_{04}^p={I}_{4\times 4},\kern0.5em {M}_{04}^s=\left[\begin{array}{cccc}1& 0& 0& 0\\ {}0& 1& 0& y\\ {}0& 0& 1& 0\\ {}0& 0& 0& 1\end{array}\right] $$
(6)
$$ \boldsymbol{\Delta} {M}_{\mathbf{04}}^{\mathbf{p}}={I}_{4\times 4},\boldsymbol{\Delta} {M}_{\mathbf{04}}^{\mathbf{s}}=\left[\begin{array}{cccc}1& -\varepsilon \gamma y& \varepsilon \beta y& \delta xy\\ {}\varepsilon \gamma y& 1& -\varepsilon \alpha y& \delta yy\\ {}-\varepsilon \beta y& \varepsilon \alpha y& 1& \delta zy\\ {}0& 0& 0& 1\end{array}\right] $$
(7)
$$ {M}_{45}^p={I}_{4\times 4},{M}_{45}^s={I}_{4\times 4},\boldsymbol{\Delta} {M}_{45}^{\mathbf{p}}={I}_{4\times 4},\boldsymbol{\Delta} {M}_{45}^{\mathbf{s}}={I}_{4\times 4} $$
(8)

2.3 Establishment of the spatial machining accuracy model

By analyzing the double-chain topology of the machine tool, combined with the established homogeneous motion transformation characteristic matrices among the various moving bodies, the spatial machining accuracy model can be constructed.

Suppose the coordinates of the tool processing point and the workpiece forming point in their respective coordinate systems are Pt and Pw,

$$ {P}_t={\left[{P}_{tx}\kern0.5em {P}_{ty}\kern0.5em {P}_{tz}\kern0.5em 1\right]}^T $$
(9)
$$ {P}_w={\left[{P}_{wx}\kern0.5em {P}_{wy}\kern0.5em {P}_{wz}\kern0.5em 1\right]}^T $$
(10)

When the machine tool works in the ideal state without error, the ideal coordinates of the workpiece forming point in the tool coordinate system are as follows:

$$ {P}_{\mathrm{tideal}}={\left[{M}_{01}^p{M}_{01}^s{M}_{12}^p{M}_{12}^s{M}_{23}^p{M}_{23}^s\right]}^{-1}{M}_{04}^p{M}_{04}^s{P}_w $$
(11)

In the actual situation (i.e., machining under the influence of geometric error), the actual coordinates of the forming point of the workpiece in the tool coordinate system are

$$ {P}_{\mathrm{tactual}}={\left[\Delta {M}_{03}\right]}^{-1}\Delta {M}_{04}{P}_w $$
(12)

Among them:

$$ \Delta {M}_{03}={M}_{01}^p\Delta {M}_{01}^{\mathrm{p}}{M}_{01}^s\Delta {M}_{01}^{\mathrm{s}}{M}_{12}^p\Delta {M}_{12}^{\mathrm{p}}{M}_{12}^s\Delta {M}_{12}^{\mathrm{s}}{M}_{23}^p\Delta {M}_{23}^{\mathrm{p}}{M}_{23}^s\Delta {M}_{23}^{\mathrm{s}} $$
$$ \Delta {M}_{04}={M}_{04}^p\Delta {M}_{04}^p{M}_{04}^s\Delta {M}_{04}^s $$

The total error matrix of machine tool can be represented by the symbol E(G) as:

$$ \mathbf{E}\left(\mathbf{G}\right)={P}_{\mathrm{tideal}}-{P}_{\mathrm{tactual}}=\left[\begin{array}{c}{E}_X(G)\\ {}{E}_Y(G)\\ {}{E}_Z(G)\\ {}0\end{array}\right] $$
(13)

The machining process of this paper is to analyze the accuracy of the machine tool when simulating the machining of a certain size workpiece under the fixed workpiece and fixed tool installation position. Therefore, Pw and x, y, and z in the above matrix are predetermined values.Ex(G), Ey(G), Ez(G), respectively, represent the machining accuracy functions with geometric error as variables in three directions. G = [g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, g15, g16, g17, g18, g19, g20, g21] represents a vector composed of 21 errors. δxx, δyx, δzx, εαx, εβx, εγx, δxy, δyy, δzy, εαy, εβy, εγy, δxz, δyz, δzz, εαz, εβz, εγz, εγxy, εβxz, εαyz = g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, g15, g16, g17, g18, g19, g20, g21.

3 Analysis of machining accuracy reliability and failure sensitivity for machine tool

3.1 Establishment of accuracy failure state function and failure mode analysis

According to the accuracy design requirements in Table 2, the maximum allowable error of the machine tool in three directions of the processing space can be expressed by the matrix emax as follows.

$$ {e}_{\mathrm{max}}={\left[{e}_X\kern0.5em {e}_Y\kern0.5em {e}_Z\kern0.5em 0\right]}^T $$
(14)

The reliability of machining accuracy proposed in this paper emphasizes that after a period of service, the machining errors in X, Y, and Z directions of the machine tool are greater than the machining accuracy requirements in their respective directions, and the machining accuracy of the machine tool is considered to be invalid. Therefore, the accuracy failure state function of machine tool is as follows.

$$ F=\left[\boldsymbol{E}(G)-{e}_{\mathrm{max}}\right]=\left[\begin{array}{c}{E}_X\left(\boldsymbol{G}\right)-{e}_X\\ {}{E}_Y\left(\boldsymbol{G}\right)-{e}_Y\\ {}{E}_Z\left(\boldsymbol{G}\right)-{e}_Z\\ {}0\end{array}\right]=\left[\begin{array}{c}{A}_X\left(\boldsymbol{G}\right)\\ {}{A}_Y\left(\boldsymbol{G}\right)\\ {}{A}_Z\left(\boldsymbol{G}\right)\\ {}0\end{array}\right] $$
(15)

In formula 15, the values of the symbols AX(G), AY(G), AZ(G) have two cases of >0 and <0, respectively. When the accuracy in a certain direction exceeds the maximum accuracy allowed by the machine design, it means that the accuracy in a certain direction is in a state of failure. In this paper, permutation and combination of all possible situations of the machine tool can get all its accuracy failure modes, as shown in the following formula. Figure 2 is the VN diagram that visually shows all accuracy failure modes.

$$ \left\{\begin{array}{l}{Q}_1=\left\{{A}_X\ge 0,\kern0.5em {A}_Y\le 0\right.\ \mathrm{and}\left.{A}_Z\le 0\right\}\\ {}{Q}_2=\left\{\begin{array}{cc}{A}_X\le 0,& {A}_Y\ge 0\end{array}\right.\ \mathrm{and}\left.{A}_Z\le 0\right\}\\ {}{Q}_3=\left\{\begin{array}{cc}{A}_X\le 0,& {A}_Y\le 0\end{array}\right.\ \mathrm{and}\left.{A}_Z\ge 0\right\}\\ {}{Q}_4=\left\{\begin{array}{cc}{A}_X\ge 0,& {A}_Y\ge 0\end{array}\right.\ \mathrm{and}\left.{A}_Z\le 0\right\}\\ {}{Q}_5=\left\{\begin{array}{cc}{A}_X\le 0,& {A}_Y\ge 0\end{array}\right.\ \mathrm{and}\left.{A}_Z\ge 0\right\}\\ {}{Q}_6=\left\{\begin{array}{cc}{A}_X\ge 0,& {A}_Y\le 0\end{array}\right.\ \mathrm{and}\left.{A}_Z\ge 0\right\}\\ {}{Q}_7=\left\{\begin{array}{cc}{A}_X\ge 0,& {A}_Y\ge 0\end{array}\right.\ \mathrm{and}\left.{A}_Z\ge 0\right\}\end{array}\right. $$
(16)
Fig. 2
figure 2

VN diagram of machining accuracy failure mode for the machine tool

Full size image

3.2 Cross-correlation analysis of geometric errors

The original definition of correlation is as follows: if there are two-time functions recording x1(t) and x2(t), then the correlation value between them is

$$ \left\langle {x}_1(t),{x}_2(t)\right\rangle =\frac{1}{N}\sum \limits_{i=1}^N{x}_1\left({t}_i\right),{x}_2\left({t}_i\right) $$
(17)

In the formula, A represents the average value of the product of x1(t) and x2(t). According to this definition, if X1 (T) and X2 (T) are similar or equal, their correlation will be the largest. For two dissimilar records, the product must be positive in part and negative in part, and the average value must be smaller because of the positive and negative offset, so the correlation will also decrease. Cross-correlation analysis belongs to the concept of signal analysis, which represents the correlation degree between the values of two-time series; that is, the cross-correlation function describes the correlation degree between the values of random signal x(t), y(t) at any two different times t1, t2. The cross-correlation function of x(t) and y(t) is

$$ {R}_{xy}\left(\tau \right)=E\left[x(t)y\left(t+\tau \right)\right]=\left\langle x(t),y\left(t+\tau \right)\right\rangle =\underset{T\to \infty }{\lim}\frac{1}{T}{\int}_{\raisebox{1ex}{$-T$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}^{\raisebox{1ex}{$T$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}x(t)y\left(t+\tau \right) dt $$
(18)

The maximum point of the function is τ0, and the maximum value is R(τ0).

For most random processes, we can still expect that when the time interval T is very large, there is no correlation between x(t) and y(t). In this paper, we measure the error parameters at a single measurement point in a short period. A total of 10 repeated measurements can get 10 groups of different 18 geometric error values, so there must be relevant information between each group of data.

3.3 Machining accuracy reliability and failure sensitivity analysis of machine tool

Response surface method is widely used in engineering reliability analysis, such as dam system reliability analysis [34, 35] and bridge structure reliability analysis [36, 37]. However, most of the variables in these studies are based on independent assumptions, and the reliability index β is calculated iteratively. In this paper, based on the objective correlation of geometric errors, an improved response surface reliability index is proposed to analyze the machining accuracy reliability of the high-precision vertical machine tool, as shown in the following formula. The symbol βmachine tool represents the reliability index of machining accuracy; The symbol preliabilityrepresents that the reliability of machine tool measure points can be obtained by integrating the reliability index.

$$ {\beta}_{\mathrm{machine}\ \mathrm{tool}}={R}_{x_i-\mu {x}_i}\sqrt{{\left(\frac{x_1-{\mu}_{x_1}}{\sigma_{x_1}}\right)}^2+{\left(\frac{x_2-{\mu}_{x_2}}{\sigma_{x_2}}\right)}^2+\cdots +{\left(\frac{x_{18}-{\mu}_{x_{18}}}{\sigma_{x_{18}}}\right)}^2} $$
(19)
$$ {p}_{\mathrm{reliability}}=\Phi \left({\beta}_{\mathrm{machine}\ \mathrm{tool}}\right) $$
(20)

In this paper, cross-correlation analysis is used to measure the correlation between the selected error data groups in the reliability index. The data group \( \left({\mu}_{x_1},{\mu}_{x_2},\cdots, {\mu}_{x_i}\right) \) is the mean value of 10 groups of measurement data, and the data group (x1, x2, ⋯, xi) is the mean value of the middle two groups of data. In theory, the time interval between the two groups of data is very small. Therefore, with the help of MATLAB tools, this paper selects and calculates the maximum value of the function as the correlation coefficient between xi and \( {\mu}_{x_i} \), and uses the symbol \( {R}_{x_i-\mu {x}_i} \) to express it.

To identify the geometric errors which have a major impact on the accuracy failure modes that occur, the accuracy failure sensitivity analysis of the multi-axis machine tool is carried out based on the geometric error parameters. Based on fully considering the objectively existing correlation of the error parameter sources, this paper uses the state function when the accuracy failure occurs to calculate the partial derivative of the error parameter mean value and multiply it with the error cross-correlation coefficient to establish the global sensitivity analysis model of machine tool geometric error, as shown in formula 21. The symbol w indicates the number of accuracy failure directions.

$$ {\mathrm{Error}}_{AFS}=\frac{1}{w}{R}_{x_i-\mu {x}_i}\frac{\partial {Q}_i}{\partial \mu {x}_i}=\left\{\begin{array}{c}{R}_{x_i-\mu {x}_i}\frac{\partial {A}_m(G)}{\partial \mu {x}_i}\\ {}\frac{1}{2}{R}_{x_i-\mu {x}_i}\left(\frac{\partial {A}_m(G)}{\partial \mu {x}_i}+\frac{\partial {A}_n(G)}{\partial \mu {x}_i}\right)\\ {}\frac{1}{3}{R}_{x_i-\mu {x}_i}\left(\frac{\partial {A}_X(G)}{\partial \mu {x}_i}+\frac{\partial {A}_Y(G)}{\partial \mu {x}_i}+\frac{\partial {A}_Z(G)}{\partial \mu {x}_i}\right)\end{array}\right.\left\{\begin{array}{c}w=1,2,3\\ {}m,n=X,Y,Z\\ {}m\ne n\end{array}\right. $$
(21)

According to formula 21, when two or more machining directions fail, the paper first uses the accuracy failure function to calculate the partial derivative of the geometric error and then obtains the sensitivity coefficient of the geometric error in this failure mode by the weighted average method. Finally, considering the geometric error terms of all accuracy failure modes, several items with a larger sensitivity coefficient are selected as the key geometric errors of the multi-axis machine tool.

4 Case study

The Monte Carlo simulation method is limited in the actual engineering application due to its disadvantages in the analysis of engineering problems such as a large amount of sample data and a large amount of calculation, and it is often used to verify whether the calculation results of other methods are accurate and reliable. In order to verify the effectiveness of the proposed method, this paper selects a high-precision 3-axis vertical CNC machine tool to carry out the machining accuracy reliability analysis and failure sensitivity and compares the reliability analysis results at each measuring point of the machine tool with the results of Monte Carlo simulation. At the same time, according to the accuracy failure mode and the X-, Y-, and Z-axis of the machine tool, the accuracy reliability of the three axes is calculated by using the weighted average method. To identify the key geometric errors which have a great influence on the accuracy of machine tools under various failure modes, the global sensitivity analysis is carried out. According to the analysis results, combined with the mapping relationship between geometric errors and component parameters, the improvement measures of accuracy reliability for machine tools are proposed.

4.1 Geometric error parameters measurement

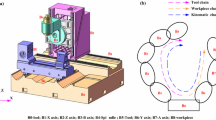
Laser interferometer is widely used in the geometric error detection of CNC machine tools because of its advantages of comprehensive detection items, automatic data acquisition, and diversified influence elimination. The XD laser interferometer used in this paper can achieve the measurement resolution of nanometer level. It takes the wavelength of laser in a vacuum as the length reference, and its installation method is simple. Six basic geometric errors of machine tool moving parts in six degrees of freedom can be measured at one time. To comprehensively analyze the geometric errors of machine tool, the workspace is abstracted as a cuboid region composed of X, Y, and Z machining directions. To make the selected test points representative, this paper selects several measurement points evenly along the four body diagonals of the machine tool workspace, as shown in Figure 3. Taking (0, 400, 500) as an example, the measured data at this point are listed in Tables 6–8. The orientation errors of the machine tool are listed in Table 9.

Fig. 3
figure 3

Geometric error measurement in the whole working space of machine tool

Full size image
Table 6 Measurement values of geometric errors along the X-axis at point (0, 400, 500) (mm)
Full size table
Table 7 Measurement values of geometric errors along the Y-axis at point (0, 400, 500) (mm)
Full size table
Table 8 Measurement values of geometric errors along the Z-axis at point (0, 400, 500) (mm)
Full size table
Table 9 Test values of orientation errors (mm)
Full size table

4.2 Accuracy reliability and AFS analysis of machine tool

According to formula 19–21, the geometric error parameters at each measuring point are brought in. The machining accuracy reliability analysis results and the analysis results based on Monte Carlo simulation are listed in Table 10, where “0” means that the failure mode does not occur, and “1” means that the failure mode occurs. The correlation coefficients between reliability analysis data groups at each point are also shown in Table 10. Fig. 4 shows the distribution of measurement points where accuracy failure occurs in the machine tool workspace. Figures 5–7 shows the cross-correlation function relationship between the geometric error parameter (x1, x2, ⋯, xi) and the data group \( \left({\mu}_{x_1},{\mu}_{x_2},\cdots, {\mu}_{x_i}\right) \) at some measurement points.

Table 10 Machining accuracy reliability analysis results
Full size table
Fig. 4
figure 4

Measuring points of accuracy failure in machine tool workspace

Full size image
Fig. 5
figure 5

Cross-correlation function of errors at measurement points (0, 0, 100)

Full size image
Fig. 6
figure 6

Cross-correlation function of errors at measurement points (0, 400, 500)

Full size image
Fig. 7
figure 7

Cross-correlation function of errors at measurement points (−200, 0, 300)

Full size image

Through analysis and calculation, in the seven failure modes, there are only five kinds of accuracy failure at each measuring point, among which the point (200, −400, 500) in three machining directions is greater than the maximum error allowed by the machine tool, and the accuracy reliability at this point is the lowest. Through comparative analysis, the analysis results and Monte Carlo simulation are very close, which verifies the accurateness and effectiveness of the proposed method. In addition, considering the relationship between accuracy failure mode and machine tool motion axis, the reliability of the three motion axes is calculated, and the results are listed in Table 11.

Table 11 Reliability of three motion axes
Full size table

According to formula 21, the accuracy failure sensitivity analysis of machine tool in service state is carried out, in which orientation errors have nothing to do with machine tool motion, so only 18 geometric errors related to motion are considered. The analysis results are shown in Table 12. When a failure mode occurs repeatedly, the weighted average method is used to obtain the global sensitivity coefficient of the error term in this mode. To display the results visually, make a histogram as shown in Figure 8.

Table 12 Accuracy failure sensitivity analysis results
Full size table
Fig. 8
figure 8

Sensitivity coefficient of geometric errors under five failure modes

Full size image

4.3 Improvement and promotion strategy

According to Sect. 4.2, under the accuracy failure mode Q2, the geometric error terms that have a great influence on the machining accuracy reliability of the machine tool areεαx, εαy. Under the failure mode Q3, the geometric error terms εαy, εαz, εαx have a great influence on the machining accuracy reliability. In the accuracy failure mode Q5, the geometric error terms which have a great influence on the machining accuracy reliability areεαx, εαy, εαz,. In the accuracy failure mode Q6, the geometric error terms εαy, εγy, εβy, εβx have a great influence on the machining accuracy reliability. In the accuracy failure mode Q7, the geometric error terms εαy, εαx, εγy have a great influence on the machining accuracy reliability. Comprehensively considering the analysis results of five failure modes, the key geometric errors that affect the accuracy reliability for the multi-axis CNC machine tool in the whole workspace are identified as εαx, εαy, εγy, εαz.

According to the mapping relationship between geometric error parameters and accuracy parameters of machine tool components [38], and combined with the analysis results of this method, the following strategies are proposed to improve the accuracy reliability: (1) improve the parallelism of the machine tool guide rails and (2) correct the straightness of the vertical plane and horizontal plane of guide rail. For the improved vertical machine tool, the geometric error parameters are repeatedly measured at the lowest reliability measuring point (200, −400, 500), and are brought into formulas 13 and 20 to compare the machining accuracy and reliability values before and after the improvement, as shown in Table 13. It can be seen from the table that the accuracy of Y and Z directions of the machine tool is greatly improved after the improvement, and the accuracy reliability is significantly enhanced, which further verifies the effectiveness of the proposed method.

Table 13 At the point (200, −400, 500), the performance parameters of the machine tool before and after optimization
Full size table

5 Conclusion

By the MBS theory and geometric error parameters, this paper establishes the accuracy failure state function of the machine tool and analyzes seven possible failure modes. Based on the cross-correlation analysis and the digital characteristics of error parameters, a new machining accuracy reliability analysis method for machine tools is proposed. The analysis results are very close to those of Monte Carlo simulation. The analysis shows that the reliability of the X- and Y-axes of the machine tool is similar, and the Z-axis has the highest reliability. The types of geometric errors that cause various accuracy failures are similar, and the identification of key errors is high. At the same time, to guide the staff to carry out targeted repair and maintenance of the machine tool, the AFS analysis model of the machine tool is established, and the key geometric errors affecting the accuracy reliability are identified, to fundamentally ensure the accuracy requirements of the machine tool processing.