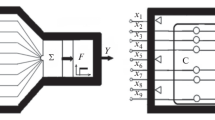
Abstract
In the classical neural networks, information is presented as a set of the stable equilibrium states. This review considers a series of papers devoted to an urgent topic of development of the neural networks models that do not have equilibrium states. Oscillatory conditions in neural networks are interpreted as patterns, i.e. a reflection of some information. Based on the physiological concepts, a model of a neural environment is proposed that is capable of storing information presented in a wave form. Effective analytical methods for the asymptotic analysis of non-linear, non-local oscillations in a system of equations with delay describing a neuronal population are described. Theoretical studies have made it possible to effectively solve important specific problems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
All models of neural networks are based to some extent on the ideas about the principles of information processing by the brain. Sensory information, as shown by Adrian [1], is transmitted as the impulses (short-term signals ‘all or nothing’) in the form of a frequency code. This determines our interest in the models of neurons that generate impulses.
In accordance with the hypothesis put forward by Hebb [2] and developed by Eccles [3], nerve cells react (generate impulses) in response to the sequences of incoming impulses depending on synaptic permeability, i.e. the distribution of synaptic weights that characterize input efficiency. According to synaptic theory, information is reflected in the structure of synaptic weights. The theory underlies all neural network models.
Currently, there is no a single point of view on the ways of presenting and storing information in the brain. Conventionally the viewpoints (and the neural networks models) can be divided into two classes: frequency and phase-frequency. The first one assumes, that a neuron state is characterized by the firing frequency. The neuronal association state reflects the distribution of the elements firing frequencies. The phase relations are not taken into account. A change in the state is possible only as a result of the exposure change. Conventionally, this insight can be called a detecting approach. It originates from the papers [2, 4] and developed in the papers [3, 5,6,7, 9]. Different points of view within this insight are compared in [10,11,12].
Currently, most researches on neural networks are performed by means of the detecting approach. This is the basis of the papers [13,14,15,16] about the network models of operational amplifiers. At the input of each element the output signals of another elements are summed with the weights. Depending on the total input the operational amplifier unambiguously generates the output signal. In the process of learning (remembering) a set of the stable equilibrium states is formed in the corresponding phase space. In the replay mode, under the external signal exposure the network enters the attraction basin of one of them. Describing the network system of equations can have the limit cycles (more complex attractors also), in principle. However, these objects are difficult to interpret and their presence is tried to be avoided. For example, the assumption about the symmetry of the connections allows to prove that all the trajectories in the Hopfield net tend to the equilibrium states. Thus, the modeling the detecting approach networks are static, as the information stored in them. In fact, it seems that the role of the cycles and their planning in classic networks are insufficiently studied and require an additional research.
According to the phase-frequency approach to the information storage in the the brain, it is extremely important to coordinate the operation of neurons not only with respect to the space, but with respect to time also. Neurons have the property of the temporal selectivity. One and the same exposure may or may not lead to the generation of impulse depending on the state. According to Bekhtereva [17, 18] the information coding is not a static but rather a dynamic process associated with the formation of the ensembles of coherently operating neurons. Accounting of the oscillation phases leads to a new quality: the information encoding is performed in the form of the neural activity waves. This approach can be called wave-based.
The networks with nonstationary behavior models a wave approach. They can be divided into two classes. In the first case the network elements do not have their own autorhythmicity, but the whole system can operate under an oscillatory conditions. An example of such a network is the Wiener net [19], which describes the excitation propagation process through the heart muscle. The oscillatory conditions in the Winer net have been studied in [20]. The paper [21] proposes a design called W-neuron network, which can memorize and reproduce a sequence of binary vectors. In the replay mode a part of the sequence is presented to network. The model of the neural system with the stationary behavior is developed in [22, 23], for which, however, it is shown that the periodic exposure on the common input of the associative network as a part of the system is an indispensable condition for information remembering and reproduction.
The second case considers the nonstationary networks, which consist of neural oscillators. The networks arise naturally in the simulation of the human and animal olfactory and visual systems [24,25,26]. The oscillatory neural networks can be also divided into two classes with respect to the element types: close and far removed from harmonic oscillators. In the first case, a population of interconnected close to harmonic oscillators is considered (for example, the Van der Pol oscillator [27,28,29]). The distribution of the phases and amplitudes of oscillations can be can be interpreted as a pattern code [24, 30, 31]. A very detailed review devoted to the networks of close to harmonic oscillators is presented in [32]. Despite the variety of these networks studying methods, it seems to us that all of them fit into the following scheme. The transition to slow variables is carried out: amplitudes — phases. In terms of these variables the assumptions about the structure of interaction (sometimes the nature of the interaction is specified within the original variables) are made. Further, all the amplitudes are often assumed to be the same, and the corresponding equations are omitted. The resulting object is called a system of the phase oscillators [33]. The problem of learning is set: the synaptic weights should be arranged in such a way, that the system of phase oscillators has a stable mode with a predetermined phase distribution (stationary or more complicated) [34, 35]. This problem in a number of cases can be solved analytically [35]. For example, in [36] such rule of the weights selection is specified that a predetermined part of the oscillators operates in phase, and the other part — in the antiphase.
Relating the above to the biological data, we note the following. First, the close to harmonic oscillations are not typical for the nervous system in our opinion. In the normal state its individual elements (neurons) generate short-term impulses called spikes. By means of pulses transmission the communication between the neurons occurs. Averaged with respect to the neural associations oscillations are also far from the harmonic one after removal of the pulse component. It is reflected, for example, in the human alpha rhythm wave dissymmetry. Secondly, the possibility of transition to the phase oscillators assumes ‘homogeneity’ of neural oscillators interaction in time. We note that in the nervous system the individual neurons as well as the neural associations possess the property of absolute and relative refractoriness (insensitivity or weak susceptibility to external exposure at the certain time intervals). In particular, a biological neuron at the time of spike generation and at some interval after is incapable (or almost incapable) to perceive the exposure. Thus, the interaction process is highly heterogeneous in time. Refractoriness is considered in [19, 31, 37] (certainly, not within the harmonic approximation).
The networks of far from harmonic oscillators are insufficiently studied in our opinion. A systematic description of the oscillatory elements types and a review of some results on the organization of oscillations in the corresponding networks are given in [38, 39]. The autowave processes in the autowave environments are reviewed and accompanied by a detailed bibliography in [40].
According to a number of biologists (for example, Crick [41]), oscillatory networks belong to the future. It is more natural to explain the information processing in the brain by their means. At the same time, the development of the oscillatory networks theory provides an opportunity to create the fundamentally new neurocomputers.
The nonstationary network models are based on the idea of the so-called Boltzmann machine (for example, see [42]). The latter is a network each element of which has a certain probability of being in one of two states. According to the Boltzmann law this probability depends on a variable called temperature (hence the name of the model). In turn, the temperature of an element is determined by the synaptic weights of the neurons and their states. The state of the Boltzmann machine is constantly changing. The pattern codes are the spatial distributions of the neuron states averaged in time. For networks with a ring topology an analogue of the Boltzmann machine has been developed in [43].
The model of a neural network in which its state is described by the spatial distribution of the densities of the random binary flows generated by the neurons is proposed and studied in [44]. At the inputs of each neuron the flows are mixed with the random flows according to a certain rule, and act as the synaptic weights. Depending on the total input flow, the output flow of neuron is formed.
The papers [45, 46] are dedicated to the nonstationary network models. The elements of the networks in them are the neurons with a stochastic dynamics. It is shown that these networks differ favorably from the classic ones in terms of the fight with the false patterns (unplanned states).
An equation with delay for an oscillatory neural element, whose oscillations are far removed from harmonic, are proposed in [47, 48]. In a series of publications by the authors of this paper it is shown, that the equation admits the possibility of not only computer, but also analytical research by means of asymptotic methods.
Recently, the prospects for the new approaches development to the problem of the information processing are increasingly associated with the ideas of the nonlinear dynamics [49, 50]. They are based on the idea that the carrier of the information can be not a stationary bit value distribution, but a complex and, generally speaking, not periodic mode of the dynamical system. In this case, the procedures of the recording, storing and reproducing information should be based on the control of the oscillatory processes [51]. The structuring, scheduling and synchronization problems of the oscillatory conditions for the networks from the proposed in [47, 48] oscillators are studied analytically. This paper is devoted to a review of the research results. A substantially more complete presentation of the results is given in the monograph [52].
2 Neuron model based on equation with delay
A nerve cell (neuron) consists of a central part, called the soma, and neurodendrones. The single long nerve-cell process is called the axon, and the shorter ones are called the dendrites. The cell body of a neuron is enclosed by a membrane. The state of the neuron is characterized by the potential difference between the inner and outer membrane surface of the neuron body (membrane potential). The neuron functioning is associated with the generation of the short-term high amplitude impulses called spikes. They, as well as any change in membrane potential, are caused by the ionic currents flowing through the active membrane channels.
One of the important properties of the neural elements is their ability to spontaneous pulsing [53, 54]. The problem of the periodicity of neural activity has long attracted researchers. The generation of spikes by a neuron cannot be explained by external influence only. This fact complicates the problem modeling.
Two aspects can be distinguished in the problem of the periodicity. Firstly, a periodic activity as an expression of the nerve cells function normalcy. Secondly, the role of periodic processes in the mechanisms of information processing and storage in the nervous system. Even A.A. Ukhtomsky had written that ‘a regular rhythm of the bioelectrical activity is an important condition for receiving the sensory information and the development of associative processes’ (a quote from [53], p.9). From this point of view, the periodic processes modeling, both for the individual cell and for the neural system acquires a special importance.
The Hodgkin-Huxley model is the best known and generally accepted to describe the process of spike generation [55]. It is the system of four ordinary differential equations. The first of them is the balance equation for the currents flowing through the membrane. The following are taken into consideration: capacitive, sodium, potassium, and leakage currents. The second and the third equations describe the processes of activation and inactivation of the sodium channels, respectively. The last equation describes the potassium channels. The system of the equations is complex and is not amenable to analytical study. In addition, it is sensitive to the parameters selection. The Hodgkin-Huxley model is substantially simplified with the preservation of the biophysical meaning in [56]. Unfortunately, this option allows the computer study only. The overview of further simplifications of the Hodgkin-Huxley equation system, the FitzHugh model in particular, is given in [38, 39]. The number of phenomenological models are also proposed there. All of them are studied by the computer methods.
A sufficiently simple spike generation model, which agrees well with biological data, is proposed in [47, 48]. It allows an analytical study. This model phenomenology is based on the analysis of the sodium and potassium currents flowing through the active membrane channels. The observed fact of the delay of the potassium current with respect to the sodium current is taken into account [55]. The value of the delay is taken as a unit of time. For the membrane potential \(u(t)>0\) the following differential-difference equation is suggested.
Here, \(f_{Na}(u)\) and \(f_{K}(u)\) are the positive sufficiently smooth functions characterizing the state of the sodium and potassium channels that transport ions through the membrane. We assume, that \(f_{Na}(u)\rightarrow 0\) and \(f_{K}(u)\rightarrow 0\) for \(u\rightarrow \infty\) faster than \(O(u^{-1})\). The parameter \(\lambda >0\) and the condition
holds. It is readily seen that the last inequality ensures an instability of the zero-state equilibrium of the Eq. (1).
The functions \(f_{Na}\) and \(f_{K}\) selection in the Eq. (1) seems to be difficult problem. However, as the analysis shows, under a certain and very natural assumption the specific type of these functions is not essential.
The results of the computer analysis of the Eq. (1) for the specific type of the functions \(f_{Na}=R_1 \exp (-u^{-2})\), \(f_K=R_2\exp (-u^{-2})\) are presented in [47, 48]. On the whole, it has been shown that the shape of the spikes and the membrane potential evolution agree closely with experimental data.
Further research was carried out analytically [57] and was based on the following important assumption. The parameter \(\lambda >0\) in the Eq. (1) is determined by the rate of the electrical processes. According to the meaning of the problem its value is great \((\lambda \gg 1)\). This observation allows to use a special asymptotic method for the Eq. (1) analysis.
To solve the Eq. (1), we introduce the class of initial functions S which contains all the continuous on the interval \(s \in [-1,0]\) functions \(\varphi (s)\), for which \(\varphi (0)=1\) and \(0<\varphi (s) <\exp (\lambda \alpha s/2)\) as \(s \in [-h,0]\). We stand \(u(t,\varphi )\) for the Eq. (1) solution with the initial condition \(u(s)=\varphi (s)\), where \(s\in [-1, 0]\) and \(\varphi \in S\).
We associate the beginning and the end of the spike (pulse) with the moments of time when \(u(t,\varphi )\) crosses the unit value with the positive and negative speed, respectively. Thus, the beginning of the neuron spike is associated with the zero time. Let \(t_1(\varphi )\) and \(t_2(\varphi )\) be the moments of the current spike end and the beginning of the next one, respectively. Let us describe the asymptotic behaviour of \(u(t,\varphi )\) on the time interval \(t\in [0,t_2(\varphi )]\) as \(\lambda \rightarrow \infty\).
Let the equation
has no positive roots. For this, it is sufficient to assume that the functions \(f_{Na}(u)\) and \(f_K(u)\) monotonically decrease by virtue of (2) as \(\lambda \rightarrow \infty\). We introduce the notation
where \(\alpha\) is defined by the formula (2). Let \(\delta >0\) be an arbitrarily fixed small number. We stand o(1) for the summands, which tend to zero uniformly with respect to \(varphi(s)\in S\) and with respect to the specified in each case values of t, as \(\lambda \rightarrow \infty\).
Lemma 1
The asymptotic equalities
hold for \(u(t,\varphi )\) as \(\lambda \rightarrow \infty\). The values \(t_1(\varphi )\) and \(t_2(\varphi )\) satisfy the relations
To prove the Lemma 1 the Eq. (1) is integrated by the method of steps. The obtained formulas are asymptotically simplified as \(\lambda \rightarrow \infty\). The form of the solution is shown in Fig. 1.
The form of the solution (1)
From a biological point of view the meaning of Lemma 1 is very simple. The formula (6) gives an exponential approximation of the spike upward phase AB, the duration of which is approximately equal to one. Respectively, (7) is an approximation of the spike downward phase, the section BC in Fig. 1. The formula (8) describes the behaviour of the membrane potential on the section CD immediately after the spike, and (9) is the exponential approximation of the section DF of the membrane potential slow evolution (drift). It follows from the formula (10), that the duration of the spike is close to the value \(T_1\), defined by the formula (5) as \(\lambda \rightarrow \infty\). The points A and C are the beginning and the end of the spike, respectively.
We especially note an important consequence of Lemma 1. We introduce a sequence operator \(\Pi\) in the set of initial conditions S according to the rule: \(\Pi \varphi (s)=u(t_2+s,\varphi )\; (s\in [-1, 0])\). It follows from the formula (9), that \(\Pi S\subset S\). From here, the solutions with the belonging to \(\Pi S\) initial conditions form an attractor with a wide basin of attraction, which contains the set S. Obviously, the attractor contains the periodic solution of the Eq. (1).
All the solutions (including periodic) belonging to the attractor have a common asymptotic representation on any finite time interval as \(\lambda \rightarrow \infty\). The asymptotic formulas are repeated after the time \(T_2\), approximately. Thus, it is proved that the model neurons are appeared to be the active oscillators.
The case when the Eq. (3) has the positive roots is studied in [57]. The conditions on the functions \(f_{Na}(u)\) and \(f_K(u)\) are indicated, under which the spike is preceded by a sequence of discontinuous changes of the membrane potential \(u(t, \varphi )\)
for the belonging to the attractor solutions. Here, \(v_j\) are the constants. Further, the formulas of Lemma 1 (with the time delay and the substitution \(\alpha _1=f_K(v_m)-1\)) are also valid. The form of the solutions is shown in Fig. 2.
Under certain assumptions [57] about the functions \(f_{Na}(u)\) and \(f_K(u)\) a spike-free evolution of the membrane potential is possible, as shown in Fig. 3. After the discontinuous changes (11) the value of \(u(t, \varphi )\) returns to the zero neighborhood. Then, the process is repeated. Such dynamics of the membrane potential is typical for detecting neurons [58], which are not able to generate the impulses without any external exposure.
3 Synaptic exposure on neuron model equation
The spike born in the body of the nerve cell spreads along the axon (long process of the body) and its branches, which terminate in the close proximity to the surface of the other neurons. The domains of contact are called synapses. Under the incoming impulse exposure, specific chemical agents called mediators are produced in the synapse. They have an excitatory or inhibitory exposure on the receiving neuron. Depending on the type of the mediator released, the synapses are divided into excitatory and inhibitory ones. All the branches of a neuron’s axon end with the synapses of one type, either excitatory or inhibitory. Accordingly, the neurons are divided into excitatory and inhibitory ones.
The number of the released mediators in the synapses as a result of the incoming impulse rapidly arises, relatively stabilizes, and then rather quickly the mediator is destroyed [3, 59]. At the first approximation, we assume that the mediator is present only during the incoming spike, and its number is constant. Let v(t) be a membrane potential of the transmitting neuron. Then, the function \(V(t)=\theta (v(t)-1)\) is an indicator of the mediator presence at the synapses that terminate the branches of its axon. Here, \(\theta (*)\) is the Heavyside function.
The result of the mediator exposure on the neuron depends on the state of the latter. During the spike and for some time after the mediator, even if it is present, has no (or almost no) exposure on the neuron. This time interval is called the refractory period and is of two or three spikes duration.
We accept the hypothesis that on the susceptibility interval the mediator increases or decreases (according to its type) the rate of the change of the membrane potential by a proportional quantity. The coefficient of proportionality characterizes the efficiency (weight) of the synapse.
We note that the true picture of the mediator exposure is much more complicated. A neuron is a distributed entity. The mediator exposure initially causes the membrane potential change on the part of the adjacent to the synapse membrane. The so-called postsynaptic (local) potential appears here. Postsynaptic potentials ‘control’ the dynamics of the membrane potential on the whole. They ‘spread out’ with attenuation along the membrane and are accumulated in the axon hillock, where the spike is actually appears.
We consider a neuron that is under the synaptic exposure of m other neurons. To describe its dynamics, we add the synaptic exposure modeling terms in the Eq. (1). According to the the accepted hypothesis, we obtain the equation [57, 60, 61]
Let us make the remarks. In (12), V(t) is an indicator of the mediator presence: \(V(t)=1\) at \(t\in \left[ 0, T_1\right]\) and \(V(t)=0\) at \(t\notin \left[ 0, T_1\right]\). Here, \(T_1\) is the asymptotic spike duration set by the formula (5). Further, \(t_k\; (k=1,\ldots ,m)\) is the time of the start of the mediator release at the \(k^{th}\) synapse. In its turn, \(\alpha g_k\) [\(\alpha\) is calculated by the formula (2)] are the multipliers, which determine the contribution of the \(k^{th}\) synapse to the membrane potential dynamics. Let us call the numbers \(g_k\) the synaptic weights. If \(g_k>0\), then we are talking about an excitatory synapse, if \(g_k<0\) then we are talking about an inhibitory one. Finally, H(u) is a functional in (12), which ensures the refractory period presence. It can be written out in different ways. We dwell on the most natural (though rather cumbersome) representation:
where \(\theta (*)\) is the Heavyside function, and \(0<\varepsilon <0.5\). The functional H(u) turns to zero during the spike and over a period of time \(2(1-\varepsilon )T_1\) after. The duration of the refractory period including the spike time interval is \(T_R=(3-2\varepsilon )T_1\). We assume, that the refractory period is shorter than own period of neuron, i.e. \(T_R<T_2\), where \(T_2\) is set by the formula (5) and coincide asymptotically with the period of its own activity.
Let us apply the already described above scheme of the asymptotic study of the Eq. (12) dynamic properties. We introduce a class of the initial conditions for the Eq. 12 solutions. Let \(h=2(1-\varepsilon )T_1\), and we consider the set \(S_h\) which is similar to the set S. It consists of the continuous on the interval \(s\in \left[ -h, 0\right]\) functions \(\varphi (s)\) for which \(\varphi (0)=1\) and \(0<\varphi (s)<\exp (\lambda \alpha s / 2)\). Let \(u(t, \varphi )\) be the solution of the Eq. (12) with the initial condition \(u(s, \varphi )= \varphi (s)\in S_h\). The beginning of the neuron spike is associated with the zero time.
We consider the case where a neuron carries a single synapse, i.e. \(m=1\) in (12). Let the mediator is started to release at the time \(T_R<t_1<T_2\), when the refractory period is already passed, but the generation of the next spike has not yet begun. Then, according to the condition \(u(t, \varphi )\ll 1\) (before the mediator eliminates and the next spike starts) we integrate the Eq. (12) asymptotically and obtain \(u(t,\varphi )= u(t_1,\varphi )\exp \ \lambda \alpha (1+g_1+o(1))(t-t_1)\) over the time interval \(t_1<t<t_1+T_1\). A comparison with the formula (9) of Lemma 1 shows, that the presence of the mediator changes the exponent, which approximates \(u(t,\varphi )\). For an excitatory synapse (\(g_1>0\)) the exponent increases and the next spike starts earlier, and for an inhibitory one (\(g_1<0\)) the exponent decreases and the time of the next spike is getting further away.
Let \(g_1>0\), i.e. the synapse is of an excitatory type. Let us say that a neuron directly responds to the exposure if its spike starts at the time \(t^{Sp}\), when the mediator released in the synapse has not yet eliminated, i.e. \(t_1<t^{Sp}<t_1+T_1\). We stand \(Q=t^{Sp}-t_1\) for the delay of the spike start with respect to the moment of the mediator releasing. A direct response means that \(0<Q<T_1\) (the spikes of the transmitting and receiving neurons overlap in time). We note, that the spike form is determined by the asymptotical Eqs. (6) and (7).
Lemma 2
Let the neuron directly responds to the exposure of a single excitatory synapse. Then, the asymptotic formula
holds as \(\lambda \rightarrow \infty\). Herewith, \(u(t^{Sp}+s,\varphi )\in S_h\) for \(s\in \left[ -h, 0\right]\).
The formula obtained can be used to predict the exposure result for \(t_1>t^{Sp}\), if \(t_1\) is replaced by \(t_1-t^{Sp}\). In this connection, we consider the problem of a periodic exposure on a neuron coming through a single excitatory synapse. Let the exposure period T satisfies the inequality: \(T_2-g_1T_1<T<T_2\). By means of Lemma 2 it can be proved [61], that the periodic exposure imposes its frequency to the neuron. The neuron spike is delayed by the value \((T_2-T)/g_1+o(1)\) with respect to the next moment of the mediator release at a single excitatory synapse as \(\lambda \rightarrow \infty\) and \(t\rightarrow \infty\).
4 Dynamics of closed in ring neurons
We consider a ring of the N identical neurons, in which the i th neuron (\(i=1,\ldots , N\)) is coupled with the neighbor \(i-1^{th}\) and \(i+1^{th}\) neurons by the excitatory synapses. The neuron number \(N+1\) is identified with the first one, and the precursor of the first neuron is considered to be the N th neuron. By virtue of the modeling the synaptic exposure Eq. (12), we obtain the system of equations for the neural formation description [60, 62, 63]:
Here, the functional H(u) is determined by the expression (13), \(\theta (u_{i, i-1}-1)\) and \(\theta (u_{i, i+1}-1)\) are the indicators of the mediator release in the corresponding synapses of the \(i^{th}\) neuron as a result of \(i-1^{th}\) and \(i+1^{th}\) neuron spikes. The weights \(g_{i, i-1}\) and \(g_{i, i+1}\) of these synapses we determine as follows. Let us consider two vectors \((\xi _1^0,\ldots ,\xi _N^0)\) and \((\xi _1^{00}, \ldots ,\xi _N^{00})\). Let
According to the biological meaning of all the parameters, it is necessary to consider that
and also
for all \(i=1,\ldots ,N\). Now we determine the synaptic coefficients by the formulas
where the indexes i and \(i\pm N\) are equated.
Let us turn to the initial conditions setting. To apply the asymptotic method, the information about the neurons behavior on the time interval h is necessary. When considering an individual neuron, such information is the moment of the spike onset and the prehistory of the process on the time interval of h duration. In the case of the several neurons system, it is also known how does the membrane potential of each of them behave at a similar interval before the spike onset. Unfortunately, the moments of the spike onset are different. In this regard, a special technique is proposed [62, 63], which allows to construct the asymptotics of the system (15) solutions, whose initial conditions of each of the components are set at the different moments of time.
Let us introduce the vector \(\tau =\left( t_1, \ldots , t_N \right)\) which consists of time moments of the neurons spikes onset, and the vector of the initial functions \(\varphi =\left( \varphi _1(s), \ldots , \varphi _N(s) \right)\), where \(\varphi _i(s)\in S_h \ \left( i=1, \ldots , N\right)\). We are interested in the solution \(u_i(t, \varphi , \tau )\; (i=1, \ldots , N)\) of the system (15) for which \(u_i(t_i+s, \varphi , \tau ) =\varphi _i(s)\in S_h)\), where \(s \in \left[ -h, 0\right]\), ? \(i=1, \ldots , N\). Let us explain its construction algorithm. We assume that
Let also
We arbitrarily redefine the function \(u_N(t, \varphi ,\tau )\) on the interval \(t\in \left[ 0, t_N-h \right]\) observing the condition \(0<u_N(t,\varphi ,\tau )<1\).
We note, that \(H(u)=0\) for \(u>1\), and each of the Eq. (15) may be integrated (independently from the others) in the time interval \(t\in \left[ t_i, t_i^c \right]\), where \(t_i^c\) is the moment of the end of spike. By means of Lemma 1, \(t_i^c-t_i=T_1+o(1)\). Due to (19) and (20) we obtain \(t_2+T_1<T_R\). Since \(H(u_1)=0\) for \(t<T_R\), then the Eq. (15) does not depend on \(u_2\) for \(i=1\). It can be integrated independently of the other equations over the interval \(t\in \left[ 0, t_N \right]\). For \(t>t_N\) the Eq. (15) at \(i=1\) represents a problem about the \(N^{th}\) neuron exposure on a neuron. In this case, we make an a priori assumption that the conditions of Lemma 2 are met (the first neuron directly reacts on the exposure of the N th neuron). It is obvious, that within this assumption the first neuron does not affect on the N th neuron (over the corresponding time interval in the Eq. (15) \(H(u_N)=0\) for \(i=N\)). This reasoning is repeated for the further equation pairs. As a result we obtain the new moments of the spikes onset \(\tau ^\prime =(t_1^\prime ,\ldots , t_N^\prime )\) and the new initial functions
Herewith, the functions \(u_1(t, \varphi , \tau ), \ldots , u_N(t, \varphi , \tau )\) satisfy the system (15) as \(t \in (t_N, t_1^\prime )\). Continuing with the algorithm, it is possible to construct a solution of the system (15) on any finite time interval.
It follows from the algorithm that the most important parameters of the problem are the time intervals between the spikes onsets of the neighboring neurons. The process of the system (15) solution construction on time interval, starting with the spike of the first neuron and ending with the spike of the last neuron, we call the cycle of the algorithm. From Lemmas 1, 2 and from the algorithm it follows
Lemma 3
Let \(\xi _i\) be time intervals between the spikes onsets of the \(i-1{th}\) and i th neurons obtained at some cycle of the algorithm, and \(\xi ^\prime _i\) be the new values ??of these quantities in the subsequent single application of the algorithm. Let each neuron reacts directly to the exposure of the previous neuron (spikes of the neurons overlap in time). Then, the asymptotic formulas
hold as \(\lambda \rightarrow \infty\) to within o(1).
The result is a linear iterative process with a positive definite symmetric matrix. From the last property the convergence of this process follows. As is easy to see, that the introduced above vector \(\xi ^0\) is the limit point. Thus, from the inclusion (21) and from the limitations (16), (17) on the vector components \(\xi ^0\) the next statement follows.
Theorem 1
The system (15) has an attractor, the spikes of the neighboring neurons \(i-1{th}\) and i th (\(i=1,\ldots , N\)) of which start after the time interval \(xi_i^0+o(1)\) as \(\lambda \rightarrow \infty\), and the shape of spikes is given by the asymptotic expressions (6), (7) (with an appropriate time shift).
The solutions, the attractor in the theorem consists of, we call the excitation waves which propagate in the direction of increasing the neurons numbers. The periodic solution with the period \(T_s^0+o(1)\) belongs to this attractor too. The forming the attractor solutions have a common asymptotic behavior on any finite time interval. The attractor has a wide basin of attraction. By the cycle of the wave propagation we call the process of a sequential generation of the spikes, from the first neuron to the last one.
The scheme of the cyclic propagation of the excitation wave over the ring of four neurons is illustrated in Fig. 4. The graphs of the membrane potentials of the neurons from 1 to 4 are shown below one after another. The lines with arrows show the moments when the \(i-1^{th}\) neuron starts affect on the i th neuron. The spike of the first neuron starts the cycle at zero time. After the time \(\xi _2^0\) the second neuron generates an impulse, under whose exposure the spike of the third neuron starts at time \(\xi _2^0+\xi _3^0\). The spike of the fourth neuron is induced by the third one with an additional delay \(\xi _4^0\). Finally, the fourth neuron after the time \(\xi _1^0\), i.e. at the moment of time \(T_s =\xi _2^0 +\xi _3^0 +\xi _4^0 +\xi _1^0\) causes spike of the first neuron. Then the second cycle of the excitation wave propagation begins. According to the inequality (16), the time intervals between the spikes of the neighboring neurons are shorter than the spikes duration. The time interval between the neighbor wave cycles is shorter than the period of the neurons own activity. It is important, that the moment when the fourth neuron begins to affect on the first neuron (as for the other pairs) occurs after the end of the refractory period [see the inequality (17)]. It is pointed on the first graph with the dot \(T_R\).
At the same time, the attractor consisting of the waves, propagating in the direction of the neurons numbers decreasing, exists. For them, the intervals between the spikes onset of the i th and \(i-1{th}\) neurons are asymptotically close to the numbers \(\xi _i^{00}\), and a period of the corresponding periodic solution is not much different from \(T_s^{00}\).
If the number N of the neurons included in the ring structure is large, then the described waves do not exhaust the sets of all the attractors of the system (15). In this case, there are the oscillatory conditions, called the multiple waves [63]. Let us explain the phenomenon in a particular case, when \(g_{i-1, i}=0\; (i=1,\ldots , N)\) and \(g_{i, i-1}=g\; (i=1,\ldots , N)\) in the system (15), i.e. each neuron in the ring affects only the following one, and all the synaptic coefficients are equal.
In such a situation the system of the Eq. (15) has an attractor consisting of the excitation waves, which propagates in the direction of the neurons numbers increasing. The time intervals between the spikes onsets of the neighboring neurons are asymptotically similar and are close to the number
as \(\lambda \rightarrow \infty\). From (16) and (17), the condition for this attractor existence follows:
Under certain correlations between the parameters, the other attractor is present along with the first one. It corresponds to the following situation. Suppose that a spike of the first neuron started at the zero time, which generates an excitation wave propagating in the direction of the neurons numbers increasing. Then, we suppose that at the moment of time, when the first wave has not yet reached the N th neuron, a new spike of the first neuron started (for example, the spontaneous spike due to the self-oscillating properties of neurons). As a result, the secondary wave of excitation propagates along the ring structure after the first one. This mode of the excitation conducting is called a double wave [63]. Obviously, the propagation of the double wave has a certain feature, because each of the waves propagates through an already ‘organized’ environment.
Let the spike of the first neuron starts at zero time. We stand \(\xi _i\; (i=2, \ldots , N)\) for the time intervals between the spike onsets of the neighboring neurons for the first wave in the initial excitation propagating cycle. In turn, let \(\eta _i \; (i=1, \ldots , N)\) be the delay of the secondary spike of the \(i^{th}\) neuron in the same cycle. Then, the quantities
are the spike onsets for the first and second waves in the initial cycle. We introduce the numbers \(\xi ^{\prime }_i\) and \(\eta ^{\prime }_i \; (i=1, \ldots , N)\), which have the same meaning for the next cycle of the excitation wave propagation.
We make a priori assumptions similar to the previous ones. Firstly, we assume that at the moment when any neuron starts spiking, the next numbered neuron has already left the refractory state. Secondly, we assume that the spikes of the neighboring by number neurons overlap in time (neurons directly respond to the exposure). Let \(\xi _{N+i}=\xi ^{\prime }_i,\, \eta _{N+i}=\eta ^{\prime }_i \; (i=1, \ldots , N)\). To meet the conditions, the inequations
and
have to be valid, respectively.
Under the a priori assumptions we obtain the relations
to within o(1). The system of difference Eqs. (29), (30) has the stationary solution
For the asymptotic stability the roots of the characteristic polynomial of the homogeneous problem must be located on the complex plane inside the unit circle. The polynomial \(P(\mu )\) is written out easily:
The polynomial roots \(P(\mu )\) satisfy the inequality \(\vert \mu \vert <1\). So, the stationary solution (31) of the difference equations system (29), (30) is asymptotically stable.
The a priori conditions, under which the asymptotics of the spikes onset moments mismatch in the attractor of the double waves of the system (15) is constructed, mean that the stationary solution \(\xi ^{00}\), \(\eta ^{00}\) of the difference system (29), (30) must satisfy the relations
The first inequality means that the spikes of neighboring neurons overlap in time for each of the waves. The second inequality means that at the moment when the first wave approaches any of the neurons, that neuron has already left the refractory state after the generation of the second spike. It follows from these inequalities that the synaptic coefficients \(g_{i, i-1}=g\) in the system of the Eq. (15) satisfy the inequality
For compatibility, the condition \(2T_R <(N-2)T_1\) must be valid. From this we obtain an evaluation on the number N of the neurons in the ring structure: \(N>2T_R/T_1+2\). Considering the relation (20), we conclude that the ring structure must contain more than six neurons.
So, if the conditions (33) on the synaptic weights g are met, then the system of Eq. (15) has an attractor consisting of two waves, running one after another, for the case under consideration. The intervals between the spikes of the neighboring neurons for each of them are close to \(\xi ^{00}\) as \(\lambda \rightarrow \infty\). Therewith, the second wave delays with respect to the first wave by the asymptotically close to \(\eta ^{00}\) time.
We note, that if the quantity g satisfies the inequality (33), then it satisfies (26) too. Hence, the second attractor coexists along with the first. Thus, one could talk about triple waves of excitation and etc.
5 Organized in double ring neurons dynamics
We consider a ring structure consisting of N similar neurons, each of them affects on two neurons following after it. Therewith, it is considered that the first neuron follows the N th neuron. Such a network is called a double ring [63]. The system of equations for the neural population looks like
where, just as before, the functional H(u) is defined by the expression (13), and \(g_{i,j}\) are the synaptic weights. Let the number of the neurons be odd: \(N= 2m+1\; (N \ge 5)\). The system (34) can have a sufficiently rich array of the attractors. Two of them are worth mentioning.
The first attractor consists of the waves, in which the excitation is transmitted through one neuron, i.e. from the i th to the \(i+2{th}\) neuron. This is possible if during the spike of the i th neuron, the \(i+1{th}\) neuron is in the refractory state. Due to the odd number of the neurons, the wave path is closed. Starting with the spike of the first neuron, it sequentially causes the spikes of odd numbered neurons overlapping in time. After the spike of the N th neuron, the spikes of the even neurons are induced sequentially. Finally, the wave reaches the \(N-2{th}\) neuron, which generates a spike of the first one. This case does not differ from the one analyzed in the previous section. If the expected in the stationary state time intervals between the spikes onsets of the \(i-2{th}\) and i th neurons are the numbers \(\xi _i^0\), then the synaptic weights \(g_{i,i-2}\) are determined according to the formulas (18) (the values of the weights \(g_{i,i-1}\) are not essential). In addition, it is necessary to ensure that during the spike of the i th neuron the \(i+1{th}\) neuron is in a refractory state for the stationary mode. This can be achieved by controlling the refractory period \(T_R\).
The second attractor corresponds to the case when the spikes occur in the natural order of neuron numbers increasing. The wave propagation is specific because there is an anticipatory synaptic connection. Both, the \(i-1{th}\) and \(i-2{th}\) neurons participate in the i th neuron excitation process. Generally speaking, depending on the values of the synaptic weights there can be several such of attractors. Let us consider one of them. For the included in the attractor solutions, the spikes of the neighboring in numbers neurons overlap in time, but the spikes of the neurons following through one number do not have this property. Let \(\xi _i^{00}\) be the expected time intervals between the spikes onsets of the \(i-1{th}\) and i th neurons in the stationary mode. We determine the synaptic weights \(g_{i, i-1}\) by the formulas
.
Then the system of Eq. (34) has an attractor, in which time intervals between the spikes of the \(i-1{th}\) and i th neurons are close to the numbers \(\xi _i^{00}\) as \(\lambda \rightarrow \infty\). This attractor coexists along with the described above. All calculations and strict justification of the corresponding statements are carried out according to the scheme above.
6 Adaptation model of individual neurons
The problem of the synaptic weights selection in the neural systems is called the learning problem. There are two fundamentally different approaches to its solution. According to one of them, the weights are computed outside the neural network, and then imported into synapses (external learning). In the previous sections, the problem of external learning of the ring structure has already been solved.
According to the second approach to the learning problem, the synaptic weights are adjusted in the process of the neural network operation. This approach goes back to the paper by D. Hebb [2], it was developed by F. Rosenblblatt [5]. Some authors [7, 8, 10] consider the presence of the adaptation mechanism as an inherent feature of the neural system.
The adaptation problem as applied to dynamical systems does not appear to be simple. However, it can be solved for the ring neuronal entities [64].
This section discusses the uptake mechanism by the neurons ring of other elements not belonging to it. In the next section, an algorithm of ring structure adaptation is proposed based on this mechanism.
We consider the ring of N neurons which is described by the system of the Eq. (15), where the synaptic weights are set by the formulas (18). We call it a reference ring, as well as the neurons belonging to it.
Along with the reference ring neurons we consider another N neurons, called adaptive. Each i th adaptive neuron is exposed by the i th and \(i-1^{th}\) reference neurons. The synaptic weight of the i th reference neuron exposure on the i th adaptive neuron is equally fixed. In turn, the synaptic weight of the \(i-1{th}\) reference neuron exposure on the i th adaptive neuron is changing in the operation process of the network. The purpose of adaptation is to achieve the operating synchronization of the i th reference neuron and the i th adaptive neuron.
The problem can be interpreted as follows. The spike of an individual reference neuron is a relatively weak signal, which can be masked in the neural noise. The uptake of the adaptive neuron by the reference one leads to the signal amplification. It is obvious, that the i th reference neuron can uptake several (many) adaptive neurons. This leads to the further signals amplification.
We stand \(w_{i}\) for the membrane potentials of the adaptive neurons. The system (15) for the ring of the reference neurons is supplemented by the adaptive neurons equations
where g is a common fixed value of the synaptic weight of the i th reference neuron exposure on the i th adaptive neuron. The synaptic weights \(G_{i}\) of the \(i-1{th}\) reference neuron exposure on the i th adaptive neuron are changing in the operation process of the network.
Along the reference ring the excitation wave is propagated independently of the adaptive neurons, in which the spike of the i th neuron delays with respect to the spike of the \(i-1{th}\) neuron by the value \(\xi ^{0}_{i}+o(1)\).
Each i th adaptive neuron is exposed by the spikes of the \(i-1{th}\) and i th reference neurons. The exposure on each neuron is periodically repeated at the interval of time \(T_v=\sum _{j=1}^N \xi _j^0 +o(1)\). The problem of such exposure is solved by the asymptotic methods in [61]. The following is established. If the synaptic weight g is not small, and the weight \(G_i\) is not much large, then the spike onset of the i th adaptive neuron delays with respect to the spike onset of the i th reference neuron. Herewith, the spike of the i th adaptive neuron occurs before the spike of the \(i-1{th}\) reference neuron completes. Such a reaction is called direct. The synaptic weight \(G_i\) increase leads to a decrease of the spike onset delay of the i th adaptive neuron with respect to the spike onset of the i th reference neuron. The idea of adapting is based on this fact.
The modification of the synaptic weight \(G_{i}\) is performed at the time interval \(T_{Ad}<T_{1}\) after the spike onset of the i th adaptive neuron under the condition of the spike of the i th reference neuron observation (at this time interval the synaptic contact is not used, because the neuron is refractory).
The functional
at time t takes on the unit value only when the following events coincide. The spike of the i th adaptive neuron is already started and no later than the moment of time \(t-T_{Ad}\). At the same time, the spike of the i th reference neuron is observed. Under other conditions, the functional H takes on the zero value. The synaptic weight \(G_{i}\) modification occurs at the time intervals, where the functional \(H_{v}=1\).
Further, we introduce a functional
At the time interval when the spikes of the \(i^{th}\) reference neuron and the \(i^{th}\) adaptive neuron are simultaneously observed, the value of the difference \(H_{Sp}(w_{i})-H_{Sp}(u_{i})\) coincides with the mismatch of the spike onsets of these neurons. We consider, that the rate of synaptic weight \(G_{i}\) change (where this change is possible) is proportional to the indicated difference. We obtain the equation, which describes the modification of the synaptic weight.
where \(q^{*}>0\). The system of Eqs. (15), (35) and (33) describes the adaptation process.
Let at the initial cycle of the excitation wave propagation along the reference ring the numbers \(\eta _{i}\; (0<\eta _{i}<T_{1}-T_{Ad})\) be the mismatches of the spikes onset of the \(i^{th}\) adaptive neuron and the \(i^{th}\) reference neuron, and let \(G_{i}\) be the values of the synaptic weights after initial adaptation. The Eqs. (15), (35) are asymptotically integrated. The new delays of the adaptive neurons spikes onset at the next cycle of the wave propagation \(\eta ^{\prime }_{i}\) and the new values of the synaptic weights \(G^{^\prime }_{i}\) are determined. The formulas look like:
to within o(1). They are derived under the assumption, that the adaptive neurons respond directly to the exposure. The condition is satisfied if the inequality
holds.
The formulas (37), (38) determine an iterative process, which reflects the sequential adaptation cycles. Let
In the domain \(0 \le G_{i} \le g_{i,i-1}\), \(0 \le \eta _{i}<T_{1}-\xi ^{0}_{i}\) the process converges to the point \(\eta _{i}=0\), \(G_{i}=g_{i,i-1}\), where the numbers \(g_{i,i-1}\) are the synaptic weights in the reference ring calculated by the formulas (18).
An important addition needs to be made. The mapping (37), (38) is obtained under the a priori condition \(\eta _i \ge 0\) and the terms of the order o(1) are not taken into account. Since \(\eta _i\) tends to zero during the adaptation process, the a priori condition may be violated. The system (15), (35) asymptotic analysis allows to find the value \(\eta ^{\prime }_{i}\) under the condition \(\eta _{i}<0\). The corresponding expression can be joined with the formula (37). It is proved that the resulting mapping has the stable stationary point \(\eta _{i}=0\), \(G_{i}=g_{i,i-1}\).
7 Ring neural structure adaptation model
We suppose that a sequence of spikes is generated as a result of some processes. Duration of each of them is close to \(T_{1}\). Let \(\xi ^{0}_{i}<T_{1}\) be the time intervals between the spikes onsets of the \(i-1^{th}\) and \(i^{th}\) impulses. The spikes overlap in time: \(\xi _i^0<T_1\). We assume, that the sequence is repeated periodically: \(\xi ^{0}_{i+N}\equiv \xi ^{0}_{i}\), where \(N>4\). The spikes sequence is called reference one.
We consider an oriented ring of N neurons, where the i th element is affected by \(i-1{th}\) neuron and by the spikes of the reference sequence. During the ring structure operation the synaptic weights of the \(i-1{th}\) neuron exposure on the i th neuron is modified. After disconnecting the external signals the ring structure must generate spike sequence identical to the reference sequence. The belonging to this ring neurons are called adaptive.
Let the spikes sequence with the intervals \(\xi ^{0}_{i}\) between them generates a reference ring, which consists of N neurons. In biological systems, there are synaptic contacts of a special kind. Via each of them, a neuron can be affected quite equally by two other neurons. Such a contact is conventionally called a common synapse. We assume, that the i th adaptive neuron is affected via common synapse by the \(i-1{th}\) reference and the \(i-1{th}\) adaptive neurons. Along with this, let the i th adaptive neuron is also affected by the i th reference neuron, the exposure synaptic weight of which we consider to be equal for all pairs of neurons, for simplicity.
We stand \(u_{i}\) and \(w_{i}\) \((i=1,\ldots ,N)\) for the membrane potentials of the reference and adaptive neurons, respectively. The reference ring is determined by the system (15), and the adaptive one is determined by the equations
where \(i=1,\ldots ,N\) (\(i=0\) is identified with \(i=N\)). The function \(\theta (u_{i-1}+w_{i-1}-1)\) indicates the exposure to the i th adaptive neuron via the common synapse of the \(i-1{th}\) reference and the \(i-1{th}\) adaptive neurons. It goes to the unit value only if there is a spike in one of these neurons. The synaptic weight \(G_{i}\) characterizes the exposure of common synapse, and the weight g reflects the exposure strength of the i th reference neuron. The functional \(H(*)\) is given by the formula (13).
In the adaptation process the synaptic weights \(G_i\) change. The idea of modification is based on the following considerations. We imagine that the spikes of each adaptive neuron are delayed with respect to the spikes of the corresponding reference neuron. Then, the i th adaptive neuron is actually affected only by the \(i-1{th}\) and i th reference neurons. It follows from the properties of the common synapse. We start the weights \(G_i\) synaptic modification mechanism considered in the previous section. Over time, the values of \(G_i\) tend to the numbers \(g_{i,i-1}\). After modification the reference ring can be disconnected. The oscillatory mode is kept in the adaptive ring, in which the spike of the i th neuron is delayed with respect to the spike of the \(i-1{th}\) neuron by the value of \(\xi _i^0 +o(1)\). This is due to the fact, that now the i th adaptive neuron is affected via common synapse by the adaptive \(i-1{th}\) neuron equivalently instead of the reference one.
Let the weights \(G_{i}\) satisfy the Eq. (36). We agree that each cycle of the wave propagation through the reference ring opens with the spike of the first neuron, and ends with the pulse of the N th neuron. Let us consider some cycle of the wave propagation. We stand \(\eta _{i}\) \((i=1,\ldots ,N)\) for the difference of the moments of the i th adaptive neuron and the reference i th neuron spikes onset at this cycle. Let \(G_{i}\) be the value of synaptic weights after the modification that occurred on it. We stand \(\eta ^{\prime }_{i}\) and \(G^{\prime }_{i}\) for the similar values for the next cycle of the wave propagation.
The asymptotic analysis of the system of Eqs. (15), (41) for \(\lambda \rightarrow \infty\) allows to get the relations for \(\eta ^{\prime }_{i}\) and \(G^{\prime }_{i}\)
to within o(1). Here, \(i=1,\ldots ,N\), \(\eta ^{\prime }_{0}=\eta _{N}\), \(q=q^{*}T_{Ad}\), where \(q^{*}>0\) is the coefficient from (36).
The given by formulas (43), (42) mapping has a fixed point \(\eta _{i}=0\), \(G_{i}=g_{i,i-1}\). Let the inequalities (39) and (40) hold. Then, the weight \(g>0\) of the \(i^{th}\) reference neuron exposure on the \(i^{th}\) adaptive neuron is not small, and the parameter \(q>0\) is not large. In the domain \(0 \le G_{i}\le g_{i,i-1}\), \(0 \le \eta _{i}<T_{1}-\xi ^{0}_{i}\) the relations (43), (42) turn into the formulas (37), (38). It is shown earlier that the adaptation process converges.
A computer analysis of the mapping (43), (42) convergence on the whole was performed (without assuming about the original signs of the values \(\eta _{i}\) and \(g_{i,i-1}-G_{i}\)). It turns out that the mapping converges in a wide range of the parameters and initial conditions. No examples of divergence are found.
The described adaptation process is essentially supplemented by the insights into the properties of ring neural systems. It turned out, that they can not only store the wave packets, but also remember them by adjusting. Herewith, it does not matter at all the nature of the reference sequence of the spikes. It can be generated by sensory structures. Thus, it is acceptable to consider the adaptation scheme as a model for remembering of information presented in the wave form.
8 Synchronizing oscillations in ring neural structures system model
The problem of the identification of two phase-differentiated similar excitation waves, which propagate over the two ring neural structures, is arisen. A system, which performs the synchronization of the oscillatory conditions, is developed below. The assumption about the existence of such synchronization mechanisms in the human brain is the basis of the hypothesis of the memory wave nature [65, 66]. According to [66], excitation waves can serve as the codes of information in the brain. According to [66], the waves that are not too different in phase represent the same code. If the waves are synchronized over time, it means the identification of the codes.
The theory of the wave coding is developed in [66] just empirically. We set the problem of developing a neural network, which synchronizes identical excitation waves with different phases.
Mathematically, the problem arises of local dynamics study of two coupled active oscillators in neighborhood of a set of attractors, the trajectories of which have rather complex structure, but asymptotically close to the cycles. In the considered problem, the method of normal forms applies effectively, with the help of which it is possible to determine the structure of the attractor at different couplings between the systems.
We consider two similar neural rings, which are described by the system of Eq. (15). We need to construct the connections between the rings so that the spikes of the neurons of the different rings were synchronized. The connections must be addressless, because the true numbering of neurons in the rings is unknown. The interaction model is based on the synapse, which is called a correlation synapse. Its idea is mentioned in [67].
Correlation synapse is the communication channel with two inputs. The first input is activating, it turns the synapse in the state of readiness. If a spike arrives at the second input of the synapse in the active state, then the correlation synapse affects the evolution of the membrane potential of the neuron on which it is located. The time during which the correlation synapse is activated coincides with the spike duration \(T_{1}\). We denote by \(h_s\) the time of its exposure.
For definiteness, let us choose the first neural ring. The connections architecture for the second one is symmetric. A wave of spikes propagates over the ring, caused by the fact that the \(i-1{th}\) neuron affects the i th neuron. It is reasonable to adjust the phases at the exposure interval. To implement the no-address principle, all neurons of the second ring must have equal access to the second input of the correlation synapse. We assume, that they affect additively with the equal weights g. To keep synchronization (if it is observed), the time delay \(h_{0}\) of the activating channel must be introduced and the inequality \(h_s<h_{0}\) must be valid.
We stand \(u_{i}\) and \(v_{i}\; (i=1,\ldots ,N)\) for the membrane potentials of the neurons of the first and second rings, respectively. For simplicity, we assume that the i th neuron can not affect on the \(i-1{th}\) neuron in any ring (in (18) \(g_{i-1, i}=0\)). By virtue of the above, we obtain the system of equations
where \(i=1,\ldots ,N\), \(u_{N+1} = u_{1}\), \(u_{0} = u_{N}\), \(v_{N+1} = v_{1}\), \(v_{0} = v_{N}\). In (44), (45) g is the common value of the synaptic weights of the neurons exposure of one ring on another, the synaptic weights \(g_{i, i-1}\; (i=1,\ldots ,N)\) are set by the formula (18), the functional \(H(*)\) is set by the formula (13). Further, in (44)
are the sum synaptic signals accepted by the first ring from the neurons of the second one. In (45), S(u) has a similar meaning. Each of the single signals is called a sync pulse. Their duration is equal to \(h_{s}\). At the same time \(h_{s}<h_{0}\), where \(h_{0}\) in (44), (45) is the activation delay of the correlation synapse. We consider that \(h_{0}+h_{s} < \min (\xi ^{0}_{i})\). It is appropriate to remind, that for \(g=0\) due to the weights \(g_{i, i-1}\; (i=1,\ldots ,N)\) selection each of the Eqs. (44) and (45) has an attractor which consists of the solutions, where the spike of the i th neuron is delayed with respect to the spike of the \(i-1{th}\) neuron by the close to \(\xi ^{0}_{i}\) value.
For asymptotic integration of the system (44), (45) the described in Sect. 4 method is used. At the initial cycle of the excitation waves propagation the moments of the neuron spikes onsets are set a priori. Let these be the numbers \(t_{i,j}\; (i=1,\ldots ,N;\, j=1,2)\) for the \(i^{th}\) neuron of the \(j^{th}\) ring, respectively. We assume that \(0 \le t_{1,j}< t_{2,j}< \ldots< t_{N,j} < T_{2}\; (j=1,2)\). The initial conditions of the system of equations (44), (45) are set individually: \(u_{i}(t_{i,1}+s) = \varphi _{i,1}(s) \in S_{h}\), \(v_{i}(t_{i,1}+s) = \varphi _{i,2}(s) \in S_{h}\; (i=1,\ldots ,N)\), for which the set of functions \(S_{h}\) is described in Sect. 3. The system (44), (45) is integrated recursively. The formulas are asymptotically simplified, if we consider \(\lambda \rightarrow \infty\). There are the moments \(t_{i,j}^\prime \; (i=1,\ldots ,N;\, j=1,2)\) of the spike onsets of the neurons on the new wave propagation cycle. At the same time \(u_{i}(t_{i,1}^\prime +s) \in S_{h}\), \(v_{i}(t_{i,2}^\prime +s) \in S_{h}\), which allows to continue the algorithm.
We stand \(\xi _{i}\; (i=2,\ldots ,N)\) for the time between the spikes onset of the \(i-1^{th}\) and \(i^{th}\) neurons of the first ring on the initial wave propagation cycle. Let \(\eta _{i} = t_{i,2}- t_{i,1}\; (i=1,\ldots , N)\) be the spikes onset mismatch of the \(i^{th}\) neurons of the first and the second ring on the initial cycle. We stand \(\xi _{1}^\prime\) for the time interval between the spikes onset of the \(N^{th}\) and the first neurons of the first ring (it is calculated). The quantities \(\xi _{i}^\prime \; (i=2,\ldots , N)\), \(\eta _{i}\prime \; (i=1,\ldots ,N)\) have the same meaning, but relate to the next wave propagation cycle.
Theorem 2
There is such a positive value \(\delta _{0}\) that for \(\vert \xi _{i}-\xi ^{0}_{i}\vert < \delta _{0}\; (i=2,\ldots ,N)\), \(\vert \eta _{i}\vert < \delta _{0}\; (i=1,\ldots ,N)\) the asymptotic formulas
hold as \(\lambda \rightarrow \infty\).
By means of Theorem 2 it is possible to study the sequential cycles of excitation wave propagation. Let \(\xi ^{(j)}_{k}\), and let \(\eta ^{(j)}_{k}\; (k=1,\ldots ,N)\) be the values of the described at the \(j^{th}\) cycle variables. It follows from the formulas (46) and (48) that \(\eta ^{(j)}_{k} \rightarrow o(1)\) as \(j \rightarrow \infty\). If we omit the terms which contain \(\eta _{k}^\prime\) and the summands o(1) in the formulas (47), (49) and (50), we obtain the convergent iterative process (22), (23), (24) (see Sect. 4) with the limit point \((\xi ^{0}_{1},\ldots ,\xi ^{}_{N})\).
Theorem 3
There is such a positive value \(\delta _{0}\) that for \(\vert \xi _{i}-\xi ^{0}_{i}\vert < \delta _{0}\; (i=2,\ldots ,N)\), \(\vert \eta _{i}\vert < \delta _{0}\; (i=1,\ldots ,N)\) with the number j of the propagation wave cycle increase, the time intervals \(\xi ^{(j)}_{i}\; (i=1,\ldots ,N)\) between the spikes onset of the \(i-1^{th}\) and \(i^{th}\) neurons of the first ring tend to \(\xi ^{0}_{i}+o(1)\), and the mismatches \(\eta ^{(j)}_{i}\; (i=1,\ldots ,N)\) of the spikes onset of the \(i^{th}\) neurons of the first and second rings tend to o(1) as \(\lambda \rightarrow \infty\).
Thus, the described by the system of Eqs. (44), (45) neural network really implements the synchronization of identical, but phase-differing excitation waves. The problem of synchronization is important in many problems, and it is of particular importance for neural networks. A waves synchronization can be interpreted [65, 66] as matching of patterns whose codes they are.
9 Wave structures in ring systems of homogeneous neural modules
Some time is needed for synapse modification during neurons ring adaptation, and wave packets are the variable formations. Adapting the properties of the neural environment requires at least a few cycles of the wave packet repeating. So, the wave coding hypothesis, in our opinion, assumes the existence of a special memory for the temporary packing of the wave packets. We call it short-term memory, though storage time can be long. In our opinion, there are no synaptic changes in the neural environment that temporarily preserves wave packets. Remembering is performed by adjusting the oscillation phases, i.e. through their self-organization. We note, that short-term and long-term memory do not differ in the models of classical neural networks [5, 13, 14]. On the contrary, biologists and psychologists classify them [68].
The model [52, 69] of a neural population that is capable to store for an infinitely long time quite diverse wave packets is considered below. The model is a ring and oriented structure of neural modules, which contain excitatory and inhibitory elements. It appears that within each module, a part of the excitatory elements synchronizes the generation of spikes, and the rest are inhibited (do not generate impulses). Between groups of neural spikes of neighboring modules temporal mismatches arise that are uniquely determined by the number of uninhibited neurons. The structure and the size of groups of synchronously functioning neurons in the modules depend on the initial conditions.
Thereby, the network is a ‘flexible’ system, which allows to store a variety of periodic sequences. Such the environments can be used, for example, in the systems of identification or partial mapping of periodic sequences. When configuring adaptive systems for classification or forecasting the need for multiple periodic repeating of the learning sample appears.
If we interpret the spatial distribution of spikes in a module as a pattern, the network can store a given sequence of patterns for an infinitely long time. Both the patterns themselves and their temporal distribution can be informative.
We presuppose a number of important constructions to the description of the network. We return to the Eq. (12) of the neuron which is under a synaptic exposure of m other neurons. We consider its solution \(u(t, \varphi )\) with the initial condition \(u(s, \varphi )=\varphi (s)\in S_h\), i.e. the neuron spike onset is associated with the zero time.
Let all the synapses be excitatory and all the synaptic weights are equal: \(g_k =g>0\; (k=1, \ldots , m)\). We consider the situation, when \(T_R<t_1 \le t_2 \le \ldots \le t_m <T_2\) and \(t_m <t_1 +T_1\). This means that a group of spikes (burst) arrived to the neuron which is come out of the refractory state. Herewith, the last spike in the burst began before the first one ended. Such exposure is called bursting. The arrived at the synapses spikes cause the release of a mediator, what approximates the next spike onset \(t^{Sp}\) of the neuron \((t^{Sp}<T_2)\). Let us say that a neuron directly responds to a burst of impulses, if \(t_m<t^{Sp} <t_1 +T_1\), i.e. its spike is started before the first impulse is ended. Let us introduce the quantities \(Q=t^{Sp}-t_m\) and \(\xi _k =t_k -t_{k-1}\), \(k=2,\ldots , m\).
Lemma 4
Let the neuron directly responds to the burst exposure. Then the inclusion \(u(t^{Sp}+s, \varphi )\in S_h\) and the asymptotic equality
hold as \(\lambda \rightarrow \infty\).
The obtained formula can be used to predict the results of exposure for \(t^{Sp}<t_k \; (k=1, \ldots , m)\), if we replace \(t_k\) by \(t_k-t^{Sp}\; (k=1, \ldots , m)\). It can be shown that periodic burst exposure imposes its frequency to the neuron.
A burst of spikes may alternatively affect on the neuron, if it has both excitatory and inhibitory synapses. Let \(m_1\) and \(m_2\), \(m_1 +m_2 =m\), their number and all the synaptic weights are equal modulo \((|g_k|=g)\). Let \(P^\gamma\) be the class of the continuous for \(s\in [-h, 0]\) functions \(\psi (s)\), for which \(0<\psi (s)<exp(-\lambda \gamma )\) as \(\gamma >0\).
Lemma 5
Let \(t_m +T_1 +h<t_* <T_*\), \(\beta =gT_1 (m_2 -m_1 )-T_* >0\) and \(u(t, \varphi )\) be the solution of the Eq. (12) with the initial condition \(u(s, \varphi ) \in P^\gamma\), where \(\gamma >\alpha (T_* +g m_1 T_1 )\). Then, for the sufficiently large \(\lambda\) and \(t\in [0, t_* ]\) the inequality \(0<u(t, \varphi )<1\) and the inclusion \(u(t_* +s,\varphi ) \in P^{\gamma _*} \subset P^\gamma\) hold, where \(\gamma _* =\gamma +\alpha \beta\).
It follows from Lemma 5 that a periodic inhibitory (\(m_2>m_1\)) exposure is able to completely suppress the generation of the impulses (inhibit the neuron).
We consider a system of two neurons that are affected by the same burst of m spikes. In addition, the first neuron affects on the second one. We consider all the synapses to be excitatory and equal in weight. The neural formation is described by the equations
Here, \(u_1\) and \(u_2\) are the membrane potentials of the first and second neurons, the summand \(\theta (u_1(t)-1)\) indicates the presence of the released as a result of the first neuron spike mediator, \(g>0\) are the synaptic weights.
Let the spike of the first neuron is started at the zero time, and the second one is started at the moment \(\xi \in (0, T_1)\), and \(u_1(s, \varphi ), u_2(\xi +s, \varphi ) \in S_h\). We stand \(t_1^{Sp}\), \(t_2^{Sp}\) for the moments of the following neuron spikes onsets, and we set \(\xi ^\prime =t_2^{Sp}-t_1^{Sp}\).
Lemma 6
Let the neurons respond directly to the burst exposure. Then, for sufficiently large \(\lambda\) the inclusions \(u_1(t_1^{Sp}+s) \in S_h\), \(u_2(t_2^{Sp}+s) \in S_h\) and the asymptotic representation:
hold.
We describe the following neural network with modular organization. It consists of N neural associations (modules). Each module contains n neurons with excitatory and q neurons with inhibitory synapses (excitatory and inhibitory neurons). Within a module each excitatory neuron affects on every other neuron, but each inhibitory one affects only on the excitatory elements.
The neural modules form an oriented ring structure. Each excitatory element of the \(i^{th}\) module affects on any excitatory neuron of the \(i+1^{th}\) module, but it has no access to the inhibitory neurons of this module. Associations with the numbers \(i+kN\), \(k=0,\pm 1,\ldots\) are identified. Absolute values of the synaptic weights are considered to be similar.
We number the excitatory and inhibitory elements separately by a pair of indices (i, j), where i is the module number, and j is the neuron number. We stand \(u_{i, j}\) and \(v_{i, m}\) for the membrane potential values of the \((i,j)^{th}\) excitatory and the \((i,m)^{th}\) inhibitory neurons, respectively. These values satisfy the system of equations
where \(i=1,\ldots , N\); \(j=1,\ldots , n\); \(m=1,\ldots , q\), the functional \(H(*)\) is given by the formula (13), and \(g>0\) is common in magnitude the synaptic weights value. We consider that the number of inhibitory neurons in the modules satisfies the condition \(\beta _0 =gT_1 (q-2n)-T_2 >0\), i.e. it is sufficiently large.
The initial moments of time for different equations are selected separately with asymptotic integration of the system (53), (54). Usually, they coincide with the moments of the corresponding neurons spikes onset. Let \(t_{i, j}\) be the moments of spikes onsets of the first \(n_i\) excitatory neurons of the \(i^{th}\) module. We consider, that \(t_{i, j+1} \ge t_{i, j}\), \(t_{i+1, 1}>t_{i, n_i}\), \(t_{i, n_i}- t_{i-1, 1}<T_1\), \(t_{N, n_N}-t_{i, 1} <T_2\). We assume, that \(u_{i, j}(t_{i, j}+s) \in S_h\) for \(j=1,\ldots , n_i\), and \(u_{i, j}(t_{i,1}+s) \in P^{\gamma _0}\), where \(\gamma _0 =\alpha (T_2 +2nT_1)\) for \(j=n_i +1, \ldots , n\). Let \(\tau _{i, j}\) be the moments of spikes onsets of the \((i,j)^{th}\) inhibitory neurons, herewith \(\tau _{i, j} > t_{i, n_i}\), \(\tau _{i, j}-t_{i, 1} <T_1\) and \(v_{i, j}(\tau _{i, j}+s) \in S_h\). The functional \(H(*)\) is such, that each of the equations (53), (54) can be integrated independently of the other ones during the spike of the corresponding neuron and on the time interval of the h duration after it is ended. Because of this and the selection of the moments of the spikes onset, the equation for the first excitatory neuron of the first module is the problem of the \(n_N\) excitatory elements of the \(N^{th}\) module exposure. The starting moment \(t_{1, 1}^\prime\) of a new impulse can be got, herewith \(u_{1, 1}(t_{1, 1}+s) \in S_h\) (Lemma 4). For the second excitatory neuron of the first module we obtain the problem of external exposure, to which the first neuron is also connected (Lemma 6). Similarly, the equations for the (1, j) neurons are considered for \(j=3,\ldots , n_1\). Then the equations for the inhibitory neurons of the first module are analyzed. The last \(n-n_1\) excitatory neurons of the first module do not generate spikes on the interval \(t \in [t_{1, 1}, t_{1,1}^\prime ]\), and \(u_{1,j}(t_{1, 1}^\prime +s) \in P^{\gamma _0+\alpha \beta _0}\) (Lemma 6). Further, the equations for the next modules are considered in the system (53), (54). Applying the algorithm we can construct its solution at any finite time interval.
It follows from the algorithm, that the system (53), (54) has the solutions of the following structure. In the \(i^{th}\) module the burst of spikes of \(n_i\) excitatory neurons induces the spikes of inhibitory ones, which suppress the firing of the remaining excitatory elements of the module. The spikes of excitatory neurons of the \(i^{th}\) module induce the burst of spikes of \(n_{i+1}\) excitatory elements of the \(i+1^{th}\) module. As a result, a wave of spike groups propagates through the ring structure.
The most important parameters of the described solutions are the time intervals between the spikes onsets. Let us select some module with the number i. We stand \(\xi _{k, 1} >0\), \(k=i+1, \ldots , i+N-1\) for the intervals between the onsets of neighboring in time spikes of the \((k-1,n_{k-1})^{th}\) and \((k, 1)^{th}\) excitatory neurons. Let \(\xi _{k, j}>0\), \(j=2,...,n_k\) be the similar intervals for the \((k, j-1)^{th}\) and \((k, j)^{th}\) excitatory neurons, \(\eta _{k, j}>0\) be the spikes onset mismatch of the \((k, n_k)^{th}\) excitatory and the \((k, j)^{th}\) inhibitory neurons. By means of these quantities we can calculate time interval \(\xi _{i, 1}\) between the spikes onset of the excitatory \((i+N-1, n_{i+N-1}) \equiv (i-1, n_{i-1})^{th}\) and \((i, 1)^{th}\) neurons and get a new values of \(\xi _{i,j}^\prime\), \(j=1, \ldots , n_i\), \(\eta _{i, j}^\prime\), \(j=2,\ldots , q\). We obtain the equalities
as \(\lambda \rightarrow \infty\) to within o(1). From (55)– (57) follows, that as \(t\rightarrow \infty\) the mismatches of the impulses onset have the following properties: \(\xi _{i,j}\rightarrow 0\), \(j=2,\ldots , n\), \(\xi _{i,1}\rightarrow \xi _i^0\) and \(\eta _{i,j} \rightarrow \xi _i^0\). Here,
The Lemmas 4– 6 are used to derive the relations (55)– (57). Thus, the inequalities \(\xi _i^0 <T_1\), \(T_R < \sum _{j=1}^N \xi _j^0 -\xi _i^0, i=1,\ldots , N\) are necessary to hold.
Theorem 4
We distinguish \(n_i\) excitatory neurons in each module so that for \(i=1, \ldots , N\) the inequalities
hold. We consider the number q of the inhibitory neurons in each module to be sufficiently large: \(\beta _0 =gT_1 (q-2n)-T_2 >0\). Then, for sufficiently large \(\lambda\) the system (53), (54) has an attractor, consisting of the solutions with the following properties. The time intervals between the spikes onsets of the distinguished excitatory neurons inside each module differ by the amount o(1). The intervals between the spikes onsets of the excitatory neurons of the \(i-1^{th}\) and \(i^{th}\) modules are close to the numbers \(\xi _i^0\), which are given by the formula (58). Within the \(i^{th}\) module the spikes of the inhibitory neurons are delayed with respect to excitatory impulses by the close to \(\xi _{i+1}^0\) value. The remaining excitatory elements do not generate the spikes.
The described spike waves do not exhaust all the attractors of the system (53), (54). For example, several waves can propagate through a ring modular system one after another.
In the statement above a neural system is proposed through which, depending on the initial state (it can be set by the external exposure), the waves of a given structure propagate. Choosing the number of active excitatory neurons in the modules, It is possible to regulate the time intervals between the bursts of spike onsets in neighboring modules. At the same time, the spatial structure of the active excitatory elements inside the modules can be informative. These problems are important and related to the short-term memory modeling [65, 66].
10 Closing remarks
The information is reflected as a set of stable equilibrium states in classic neural networks. The present review considers a series of papers devoted to the actual problem: the development of neural networks models without the equilibrium states. Oscillatory conditions in neural networks are interpreted as patterns, i.e. the reflection of some information. On the basis of physiological insights, a model of capable to store information neural environment is suggested in a wave form. The effective analytical methods of asymptotic analysis of nonlinear nonlocal oscillations in system of the equations with delay, which describe the neural population, are described.
Theoretical research has made it possible to solve the important specific problems effectively. The following statements are of the greatest interest among them.
-
1.
A new model of a generating short-term, high-amplitude impulses neuron, based on the equation with delay, is developed and studied. It is shown that under certain natural assumptions the concrete form of the included in the equation functions \(f_{Na}\) and \(f_{K}\) is not essential. A model of neurons interaction and, thus, of a neural network is proposed.
-
2.
New mathematical methods for studying the systems of equations for a neural population are developed. By their means, it is analytically proved that the ring system of the model neurons is capable to store the predetermined periodic sequences of impulses (the ability to store information).
-
3.
It is proved that the adaptation of the neurons interaction force in the model forms a population which generates a set periodic sequence of impulses (the ability to record information).
-
4.
The model of neural structures synchronization is constructed, which allows to establish the identity of the impulse sequences.
-
5.
It is shown that impulse sequences can be temporarily stored in a ring population of neural modules without weights adjusting (model of short-term wave memory).
Let us discuss the ways of possible development of the model. They are based on a detailed scheme of biological neurons interaction. It is considered [59], that during the neuron spike the mediators on the adjacent synapses are destroyed, and later the mechanism of the mediators release is suppressed for some time. We accept the hypothesis that during the refractory period the mediator is not released in the synapses of the receiving neuron. Let u and v be the membrane potentials of the transmitting and the receiving neurons, respectively. In the model discussed above, the functional \(\theta (v(t)-1)\) serves as an indicator of the mediator presence. It can be modified so, that the new indicator functional M(u, v) satisfies the formulated hypothesis.
This idea is used in [70] in conformity to the networks of neural-like elements, the operation scheme of which simulates impulse neurons. The homogeneous fully connected networks are considered. The following statement is proved. The neurons are numbered arbitrary. It is considered, that the first neuron follows the last one. There are the stable oscillatory conditions of the network operation in which the spikes occur in ascending order of the neuron numbers. Further, the set of neurons can be divided into a system of disjoint subsets, which are randomly numbered (in the cycle the last one is followed by the first subset). There is an attractor in which neural spikes occur in ascending order of subset numbers. Within each subset, the neurons operate synchronously. So, the network [70] is a flexible system for the impulse sequences storage.
The results above can be applied to the networks of impulse neurons.
Another aspect is of interest. Previously, it was believed that the mediator is present during the spike of the transmitting neuron. For biological neurons, the time interval during which the exposure of the mediator is noticeable is long. The mentioned above indicator functional M(u, v) can be modified for this phenomenon account.
Finally, we note that there is another type of contacts between its elements in the nervous system. These are the electrical synapses. The model of a neural network with electrical interaction is considered in [71]. It is of some interest to consider neural networks with combined interaction of the elements (both electrical and chemical synapses are present).
Data availability
Not applicable.
Code availability
Not applicable.
Change history
09 March 2023
A Correction to this paper has been published: https://doi.org/10.1140/epjs/s11734-023-00805-9
References
E.D. Adrian, Electrical activity of the nervous system. Arch. Neurol. Psychiatr. 34, 1125–1136 (1934)
D.O. Hebb, The organization of behaviour: neuropsychological theory (Wiley, 1949), p.335
J. Eccles, The physiology of synapses (Springer, 1964)
W.A. McCulloch, W. Pitts, A logical calculus of ideas immanents in nervous activity. Bull. Math. Biophys. 5, 115–133 (1943)
F. Rosenblatt, Principles of neurodinamics. Perceptrons and the theory of brain mechanisms (Springer, Berlin, Heidelberg, 1962)
M. Minsky, S. Papert, Perceptrons an introduction to computational geometry (The MIT Press Massachusetts Institute of Technology, Massachusetts and London, Cambridge, England, 1969)
I.M. Karandashev, W.L. Dunin-Barkowski, Computational verification of approximate probabilistic estimates of operational efficiency of random neural networks. Opt. Mem. Neural Netw. 24, 8–17 (2015)
T. Kohonen, Associative Memory: A System-Theoretical Approach (Springer-Verlag, Berlin, Heidelberg, 1977)
G.M. Edelman, V.B. Mountcastle, The mindful brain: cortical organization and the group-selective theory of higher brain function (MIT press, 1982)
A.A. Frolov, I.P. Muraviev, D. Husek, Informational capacity and recall quality in sparsely encoded Hopfield-like neural network: analytical approaches and computer simulation. Neural Netw. 10(5), 845–855 (1997)
A.A. Frolov, I.P. Muraviev, D. Husek, P.Y. Polyakov, Boolean factor analysis by attractor neural network. IEEE Trans. Neural Netw. 18(3), 698–707 (2007)
A.A. Frolov, D. Husek, P.Y. Polyakov, Recurrent-neural-network-based Boolean factor analysis and its application to word clustering. IEEE Trans. Neural Netw. 20(7), 1073–1086 (2009)
J.J. Hopfield, Neural networks and physical systems mith emergent collective computational abilities. Proc. Nat. Acad. Sci. USA 79, 2554–2558 (1982)
J.J. Hopfield, Neurons with gradual response have collective computational properties line those of two-state. Neurons 81, 3088–3092 (1984)
L. Chua, L. Yang, Cellular neural networks: theory. IEEE Trans. Circuits Syst. 35, 1257–1272 (1988)
L.O. Chua, L. Yang, Cellular neural networks: Applications. IEEE Trans. Circuits Syst.t 35, 1273 (1988)
N. P. Bekhterova, The Neurophysiological Aspects of Human Mental Activity, Oxford Univ. Pr., 2nd edition, (1977)
N.P. Bekhterova, Bioelectrical correlates of protective mechanisms of the brain. Neurosci. Behav. Physiol. 15(1), 27–32 (1985)
N. Wiener, A. Rosenblueth, The mathematical formulation of the problem of conduction of impulses in a network of connected excitable elements, specifically in cardiac muscle. Arch. Inst. Cardlol. 16, 205–265 (1946)
S.A. Kashchenko, V.V. Maiorov, Wave structures in cellular networks of formal Hutchinson neurons. J. Commun. Technol. Electron. 40(6), 61–71 (1995)
V.V. Maiorov, G.V. Shabarshina, W-neural networks in the problem of associative memory. Comput. Math. Math. Phys. 41(8), 1227–1233 (2001)
G.I. Shulgina, V.N. Ponamaryov, I.R. Rezvova, A.A. Frolov, The Influence of Background Network Activity from Exitating Neural-like Units on Carrying Exitation through it. SJVND 38, 715–724 (1988). ((in Russian))
G.I. Shulgina, Investigation of Rhythmic Activity Role in the Proccesses of Information Recording and Display on Model of Neural-like Elements. DAN SSSR 312(5), 1275–1279 (1990). ((in Russian))
W.J. Freeman, Y. Yao, B. Burke, Central pattern generating and recording in olfactory bulb: a correlation learning rule. Neural Netw. 1, 14 (1988)
W.J. Freeman, The physiology of perception. Sci. Am. 2, 34–41 (1991)
Z. Li, J.J. Hopfield, Modelling the olfactory bulb and its neural oscillatory processing. Biol. Cybern. 61, 379–392 (1989)
M. Ohsusa, Y. Yamaguchi, H. Shimuzi, Entrainment among coupled van der Pol Oscillations by an external oscillation. Biol. Cybern. 51, 325–333 (1989)
S. Omata, Y. Yamaguchi, H. Shimuzi, Entrainment among coupled limit cycle oscillator with frustration. Physica D 31, 397–408 (1988)
Y. Yamaguchi, H. Shimuzi, The theory of self-synchronization in the presence of native frequency distribution and external noises, Phisica D, 212–226, (1984)
V.I. Kryukov, Short-Term Memory as a Metastable State. V. Neurolocator, A Model of Attention, Cybernetics systems’88. (Kluwer Acad. Pub., 1988), pp. 999–1006
C. Malsbyrg, W. Schneider, A neural cocktail-party prosessor. Biol. Cybern. 54, 29–40 (1986)
G. N. Borisyuk, R. M. Borisyuk, Ya. B. Kazanovich, T. B. Luzyanina, T. S. Turova, G. S. Cymbalyuk, Oscillatory neural networks. Mathematics and applications, Matem. Mod., 4:1, 3–43, (1992)
G.B. Ermentrout, N. Kopell, Frequency plateaus in a chain of weakly coupled oscillators I. SLAM J. Math. Anal. 15(2), 215–237 (1984)
B. Baird, Nonlinear dynamics of pattern formation and pattern recognition in the rabbit olfactory bulb. Physica 22D, 150–175 (1986)
B. Baird, A bifurcation theory approach to the programming of periodic attractors in network models of olfactory cortex, In: Advances in Neural Inform. Proc. Syst., 459–467, Morgan Kaufmann Publishers Inc., CA (1989)
Ya. B. Kazanovich, V. I. Kryukov, T. B. Luzianina, Synchronization via phase-locking in oscillatory models of neural networks, In: Neurocomputers and attention. Neurobiology, Synchronization and Chaos, 269–284, Manchester University Press, UK (1991)
G.N. Borisyuk, R.M. Borisyuk, The metastable and unstable states in the brain. Neural Netw. 1, 264 (1988)
H.D. Abarbanel, M.I. Rabinovich, A. Selverston, M.V. Bazhenov, R. Huerta, M.M. Sushchik, L.L. Rubchinskii, Synchronisation in neural networks. Phys. Usp. 39(4), 337–362 (1996)
M.I. Rabinovich, Chaos and neurodynamics. Radiophys. Quantum Electron. 39, 502–510 (1996)
G.R. Ivanitskii, A.B. Medvinskii, M.A. Tsyganov, From the dynamics of population autowaves generated by living cells to neuroinformatics. Phys. Usp. 37(10), 961–989 (1994)
F. Crick, C. Koch, Towards a neurobiological theory of consciousness. Semin. Neurosci. 2, 163–191 (1990)
A.Y. Loskutov, A.S. Mikhaylov, Introduction to Synergetics (Nauka, Moscow, 1990) (in Russian)
S.A. Semenov, I.B. Shuvalova, Associative memory in a circular neural network. Matem. Mod. 5(10), 32–47 (1993)
E.A. Timofeev, Neuron modelling of a neuron conveying information by pulse stream density. Automat. Remote Control 58, 484–491 (1997)
E.M. Izhikevich, G.G. Malinetskii, A Neural Network with Chaotic Behavior. Keldysh Institute preprints. (Keldysh Institute of Applied Mathematics, Moscow, 1993) (in Russian)
E.M. Izhikevich, G.G. Malinetskii, On the possible role of chaos in neural systems. Dokl. Math. 37(10), 492–495 (1992)
V.V. Maiorov, I.Yu. Myshkin, Mathematical modeling of a neuron net on the basis of the equation with delays. Matem. Mod. 2(11), 64–76 (1990) (in Russian)
V.V. Maiorov, IYu. Myshkin, Mathematical modeling of a neuron net on the basis of the equation with delays. Matem. Mod. 2(11), 64–76 (1990)
H. Haken, Information and self-organization: a macroscopic approach to complex systems (Springer Series in Synergetics, 2006)
J.S. Nicolis, Dynamics of Hierarchical Systems: An Evolutionary Approach. Springer Series in Synergetics, vol. 25 (Springer, 1986)
A.S. Dmitriev, Chaos and information processing in nonlinear dynamics systems. Radio Eng. Electron. 38(1), 1–24 (1993) (in Russian)
S.A. Kashchenko, Models of wave memory (Springer International Publishing, Cham, 2015), p.267
N.N. Vasilevsky, V.V. Trubachov, Neuronal mechanisms of the temporary connections. EEG Clin. Neuroph. 27, 447–453 (1969)
G.G. Somjen, Sensory Coding in the Mammalian Nervous System (Appleton-Century-Crofts, New York, 1972)
A.L. Hodgkin, The Conduction of the Nervous Impulse (C.C. Thomas, Springfield, IL, 1964)
G.R. Ivanickiy, V.I. Krinskiy, E.E. Selkov, Mathematical Biophysics of a Cell (Nauka, Moscow, 1978) (in Russian)
S. A. Kashchenko, V. V. Maiorov, Investigation of differential-difference equations that model neuron dynamics. Moscow : IPM. 30 p. (1992) (Prepr. Inst. Prikl. Mat. im. M. V. Keldysha Ross. Akad. Nauk ; 8)
E.N. Sokolv, G.G. Vaotkyavicus, Neural Intellect: from Neuron to Neuron Computers (Nauka, Moscow, 1989) (in Russian)
Von R. Eckert, D. Randall, Animal Physiology. Biologie in Unserer Zeit 8, 193–194 (1978)
S.A. Kashchenko, V.V. Maiorov, I.Y. Myshkin, Oscillations in neuron ring structures. Phys. Dokl. 38(12), 483–485 (1993)
V.V. Mayorov, Self-organization of oscillations in a ring system of homogeneous neuron modules. Part 1. Model of neurons and interaction between them. Appl. Nonlinear Dyn. 3(4), 87–96 (1999) (in Russian)
S.A. Kashchenko, V.V. Maiorov, I.Y. Myshkin, Wave propagation in the simplest ring neural structures. Math. Models Comput. Simul. 7(12), 3–18 (1995)
S.A. Kashchenko, V.V. Maiorov, I.Y. Myshkin, Wave structures in ring neuron systems. Math. Models Comput. Simul. 9(3), 29–39 (1997)
S. A. Kashchenko, V. V. Maiorov, Adaptive education of ring neuronal structures, Proceeding 5th International Spesialist Workshop “Nonlinear Dynamics of Electronic Systems”, Moscow, 503–507
A.N. Lebedev, Human Memory, Its Mechanisms and Boundaries. Research of Memory (Nauka, Moscow, 1990), pp. 104–118 (in Russian)
A.N. Lebedev, Neurophysiological parameters of human memory. Sjurnal Vish. Nervn. Deyat. 43(2), 277–285 (1993). (In Russian)
A.A. Vedenov, A.A. Ezjov, E.B. Levchenko, Architectural Models and Functions of Neural Ensembles, Physical and Mathematical Models of Neural Networks. V.1, Part 1, Spin Glasses and Neural Networks. Results of Science and Technology. VINITI, Moscow, 1990), pp. 45–92 (in Russian)
K.H. Pribram, The languages of the brain (Prentice-Hall, 1971)
S.A. Kashchenko, V.V. Maiorov, Wave structures in ring-shaped systems of homogeneous neuron modules. Dokl. Math. 51(3), 444–447 (1995)
G.V. Shabarshina, Self-organization in a completely connected homogeneous network of neural cellular automata of excitation type. Autom. Remote Control 60(2), 236–242 (1999)
S.A. Kashchenko, V.V. Maiorov, M.L. Myachin, Oscillations in systems of equations with delay and difference diffusion that model local neuron nets. Dokl. Math. 52(2), 289–292 (1995)
Funding
This work was carried out within the framework of a development programme for the Regional Scientific and Educational Mathematical Center of the Yaroslavl State University with financial support from the Ministry of Science and Higher Education of the Russian Federation (Agreement on provision of subsidy from the federal budget No. 075-02-2022-886).
Author information
Authors and Affiliations
Contributions
These authors contributed equally to this work.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Additional information
The original online version of this article was revised: The Funding information section was missing from this article and should have read ‘This work was carried out within the framework of a development programme for the Regional Scientific and Educational Mathematical Center of the Yaroslavl State University with financial support from the Ministry of Science and Higher Education of the Russian Federation (Аgreement on provision of subsidy from the federal budget No. 075-02-2022-886).’.
Brain Physiology Meets Complex Systems. Guest editors: Thomas Penzel, Teemu Myllylä, Oxana V. Semyachkina-Glushkovskaya, Alexey Pavlov, Anatoly Karavaev.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Kashchenko, S., Mayorov, V. & Mayorova, N. Analysis of oscillating processes in spiking neural networks. Eur. Phys. J. Spec. Top. 232, 509–527 (2023). https://doi.org/10.1140/epjs/s11734-023-00783-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1140/epjs/s11734-023-00783-y