Nonlinear Dynamics, Quasi-Periodic Summation, Self-Oscillating Processes, and Information Coding in Selective Spiking Neural Networks

Abstract

Nonlinear dynamics, physical processes, and information processing in selective spiking neurons are investigated. Summation of pulse inputs are considered on the basis of the theory of quasi-periodic functions and nonlinear transformation via relaxation of the self-oscillating system of a neuron. A way of encoding input information is also considered in which the information unit is a pulse sequence, and the intensity of the input signal is encoded by a synchronous change in the frequency of the pulse sequences.

INTRODUCTION

The nonlinear dynamics of electrical processes and information processing in spiking neurons (SNs) and artificial spiking neural networks (SNNs) is closest to real biological processes in biological neuron and biological neural networks. However, the dynamics of the processes in SNs and SNNs, along with ways of processing information, have yet to be adequately studied. The main applications of neural networks are currently recognition, control, and simulation of artificial intelligence. Most of these applications employ neural networks with McCulloch–Pitts neurons that use binary input signals. The most important distinction that radically alters the principle and efficiency of the system is different signaling in artificial neural networks and in the biological network of neurons. The problem is that neurons in artificial neural networks (ANNs) transmit values ​​that are real (i.e., numbers). Information is transmitted in the human brain via pulses with fixed amplitude.

The basic operations performed in binary ANNs are the summation of input signals with certain weights in McCulloch–Pitts neurons, clustering and summation of input signals in selective neurons, processing by a nonlinear element in McCulloch–Pitts neurons, and the generation of self-oscillation in the form of a single pulse or a series of pulses in a spiking neuron or a selective neuron. Input information is dynamically processed simultaneously in all ANNs by means of specific encoding, along with the compression of information with minimal loss.

Nonlinear dynamic systems of spiking neurons and neural networks are best suited to real biological systems and are promising in applications. Two important features of a spiking neuron should be noted: (1) The summation of the input pulse sequences in the SN differs greatly from that of binary sequences in binary neurons. (2) The nonlinear part of an SN is an impulse self-oscillatory system. This system can be potentially self-oscillating and generate one response pulse at its output in response to an input pulse. A periodic sequence of pulses or bursts can be generated [1–3].

The aim of work was to study the physical sense of the dynamics of electrical processes in a neuron as an information system that performs complex dynamic information processing.

SELECTIVE NEURONS AND NEURAL NETWORKS

Artificial McCulloch–Pitts neurons are used in all known neural networks. Learning is achieved in such neural networks by selecting weighting coefficients. However, real neural networks do not contain weighting coefficients. In addition, calculations of weighting coefficients using iterative procedures are fairly complicated and time-consuming. We therefore use the selective neurons and selective neural networks described in [4, 5] and patents [6–9]. Selectivity is achieved in selective neurons and selective neural networks through the selective clustering of communication channels and not by selecting weight coefficients, as in the familiar neural networks based on the use of McCulloch–Pitts neurons. Selectivity is achieved in biological neurons (dendrites) via the information properties of input signals; i.e., clustering is ensured by adjusting the input signals according to the code sequences. Selective properties can be achieved in neural networks that operate on both binary input signals and impulse (spike) input signals. The structure of the selective neuron proposed in [6–9] is shown on the right side of Fig. 1. The structure of a McCulloch–Pitts neuron is shown on the left side of Fig. 1 for comparison.

Fig. 1.

Structure of mathematical models of neurons. A McCulloch–Pitts neuron is on the left; a selective neuron is on the right.

Figure 1 uses notation in which $\vec {x} = ({{x}_{1}},...,{{x}_{n}}),$$\vec {w} = ({{w}_{1}},...,{{w}_{n}})$ are the input signals and weight coefficients of a McCulloch–Pitts neuron; n is the number of input signals; CC is the communication channels (dendrites); $\sum$ is an adder; F is the nonlinear threshold function in a McCulloch–Pitts neuron; $L = F$ is the relaxation self-oscillating system in a selective pulsed neuron; and C is a cluster of communication channels. Some input signals in the selective neuron are blocked during the formation of clusters.

Let us consider a mathematical model of artificial neurons. Output response

$$y = F\left( {\sum\limits_{i = 1}^n {\left( {{{w}_{i}}{{x}_{i}} - \theta } \right)} } \right)$$

is obtained after passing through the threshold device and converting threshold function $F(S)$ in a McCulloch–Pitts neuron. Here, $n$ is the number of neuron inputs and $\theta$ is the excitation threshold. The output response for a selective neuron is

$$y = L\left( {\sum\limits_{i \in K} {({{x}_{i}} - \theta )} } \right),$$

where $i \in K$ are the numbers of the communication channels belonging to selective cluster K; $L = F$ is a nonlinear operator that characterizes the relaxation self-oscillating system of a selective spiking neuron.

Selective neurons are used in the proposed mathematical model of a selective neural network (a single-layer perceptron). The selective neural network is shown on the right side of Fig. 2. The familiar model of a Rosenbluth perceptron in which McCulloch–Pitts neurons are used is shown on the left side of Fig. 2 for comparison.

Fig. 2.

A selective neural network; the familiar model of a Rosenbluth perceptron with McCulloch–Pitts neurons is shown on the left for comparison. The number of recording neurons in the single-layer perceptrons on the left and the right is m.

ROLE OF SYNAPSES IN THE SUMMATION OF PULSED STREAMS

Pulsed streams enter a neuron directly from dendrites due to the connection between their biological membranes; i.e., there is a common biological membrane for dendrites. Another part of the pulsed streams enters the neuron’s soma through synapses connecting the dendrites to the neuron’s soma. Synapses serve as transducers of the electrical potential of the dendrites into a chemical mediator with subsequent summation in the neuron’s soma. They protect the weak electrical potentials of the dendrites from the potential effects that arise in the trigger zone near an axon.

The temporal electrical constant of synapses under the action of neural pulses should be on the order of 1/ms. Only this condition can ensure that the pulsed streams entering the neuron input are in most cases summed in an almost noninertial manner. Some of the pulsed streams enter the neuron’s soma directly from the dendrites; others come through the synapses connecting the dendrite to the neuron’s soma. The electrical potentials of pulsed streams after their chemical transformation by synapses are summed in the neuron’s soma [1–3]. The synapses themselves thus do not actually participate in the summation of pulsed streams; instead, they protect the weak electrical potentials of the dendrites from the action of the strong potential that arises in the trigger zone of the soma near an axon. The main role of synapses is therefore to form one-way pulsed streams in neural networks.

SUMMING OF INPUT PULSE SEQUENCES

A feature of summation is that the time position of the pulses may not coincide for sequences of short pulses with different periods. When this happens, amplitudes do not add up. For example, there is no summation of amplitudes even for two pulse sequences that have identical periods of repetition but differ in phase. The sum of pulse sequences with different periods is generally a uniform quasi-periodic function, and their summation is based on the properties of quasi-periodic functions (QPFs). Below, we give a definition of quasi-period $\varepsilon$ of function f(x).

Definition 1. Function $f(x)$ is continuous over the real axis. According to Bohr, it is quasi-periodic if there is a positive number $l = l(\varepsilon )$ such that any segment $[\alpha ,\alpha + l]$ (where $\alpha$ is any real number) contains at least one number $\tau ,$ for which $\left| {f(x + \tau ) - f(x)} \right|$ < $\varepsilon \,{\text{(}}{\kern 1pt} - {\kern 1pt} \infty < x < \infty )$ when $\varepsilon > 0$.

Number $\tau (\varepsilon )$ is referred to as quasi-period ε of function $f(x).$ The class of quasi-periodic functions was studied in the works of P. Bohl and H. Bohr. These results were presented in [10].

According to the fundamental property of quasi-periodic functions, there is $t$ such that [10]

$$\left| {t - {{T}_{i}}{{n}_{i}}} \right| < \varepsilon ;\,\,\varepsilon \,{\text{ = }}\,\frac{\tau }{{\text{2}}},$$

where $T = ({{T}_{1}},...,{{T}_{N}});\,\,{{n}_{i}} \in N,$${{T}_{i}}$ are the periods of partial periodic functions; in our case, periods of partial impulse sequences ${{u}_{i}}(t)$ with amplitudes ${{A}_{i}}$$(i = 1,...,n).$ We then have quasi-period ε of function $f(t)$ = $\sum\nolimits_{i = 1}^N {{{u}_{i}}} (t),$ such that $\left| {f(t + {{T}_{\varepsilon }}) - f(t)} \right| < \varepsilon .$ There is a maximum value of the amplitudes of impulse functions that is equal to $A = \sum\nolimits_{i = 1}^n {{{A}_{i}}}$ and repeats with interval T_ε of quasi-period ε.

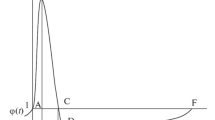
According to Kronecker’s theorem, this function has condensations and discharges of pulses that follow with intervals of so-called quasi-periods ε. Let us consider an illustration of quasi-periods ε. Signals at the inputs and outputs of neurons can be presented as the sums of quasi-periodic functions, as is shown on the left side of Fig. 3. The total pulsed stream is shown above the time axis on the right side of Fig. 3.

Fig. 3.

Schematic representation of the sequence of electrical impulses of a neuron in the form of rectangular pulses. Four pulse sequences have periods ${{T}_{1}} - {{T}_{4}},$ and $\varepsilon$ is a quasi-period approximately equal to ${{T}_{\varepsilon }} = 15{{T}_{1}} = 12{{T}_{2}} = 6{{T}_{3}} = 5{{T}_{4}} = 10.5;$$\varepsilon$ is the quasi-period between two maxima. Condensations and rarefactions for pulsed flows with noncommensurable pulse repetition periods ${{T}_{1}} = 0.7;$${{T}_{2}} = 0.875;$${{T}_{3}} = 1.75;$ and ${\text{ }}{{T}_{4}} = 2.1$ are shown on the right.

There is a maximum amplitude of the sum of the pulses that is reached through quasi-period ε: 4А = 2, where A is a pulse amplitude of 0.5. The pulse amplitude is amplified in range $t \in \left| {t - 7} \right| < \varepsilon$ of every quasi-period ε. We know the sum of pulses arriving from dendrites should exceed the excitation threshold of a neuron. A specific property of quasi-periodic functions is the existence of quasi-periods ε and the maximum sum of pulses that follow with the interval of quasi-periods ε. This allows us to selectively process information encoded in pulsed streams, and to reduce the redundancy of input information.

NONLINEAR BLOCK OF A SPIKING NEURON AS A RELAXATION SELF-OSCILLATING SYSTEM

The nonlinear part of an SN is a self-oscillating system. This system can be potentially self-oscillating and generate one response pulse, a periodic pulse train, or clusters of pulses (bursts) in response to an input pulse. The series of pulses in a cluster then usually have a shrinking period, but they can have approximately the same period of repetition or even chaotic dynamics. The types of responses of a nonlinear dynamic system to input impact pulses are illustrated in Fig. 4.

Fig. 4.

Types of responses of the nonlinear self-oscillating system of a spiking neuron.

Let us consider a familiar mathematical model of a neuron (the conceptual model of Van der Pol–Fitzhugh [11]) to understand the excitation of the self-oscillatory relaxation subsystem of a neuron in a so-called axon hillock. The Van der Pol–Fitzhugh equations have the form

$$\frac{{du}}{{dt}} = u - \frac{{{{u}^{3}}}}{3} - \upsilon + I + U{\text{;}}\,\,\,\frac{{d\upsilon }}{{dt}} = \varepsilon (a - u + b\upsilon ),$$

where $I$ is the displacement current and $a,{\text{ }}b,{\text{ }}\varepsilon$ are parameters ($a = 0.7,$$b = 0.8$). If $I$ = 0.142, a single pulse caused by external excitation is the solution to the equation. The equations describe relaxation oscillations at $I$ = 0.4 [11]. The phase portrait of the Van der Pol–Fitzhugh equation has the form shown in Fig. 5.

Fig. 5.

Phase portraits of point system $\frac{{du}}{{dt}} = F(u,\upsilon ),$$\frac{{d\upsilon }}{{dt}} = \varepsilon G(u,\upsilon ),$ Z, where $\varepsilon \ll 1$ is a small parameter. The corresponding medium has different properties, depending on the location of the points of intersection of O-isoclines: (a) An excitable medium: O is a stable equilibrium state of the system; line OA is an inverting from external influence; the solid line ABCDO is the trajectory of the further evolution of the system. In this case, the segment AB corresponds to the leading edge of the excitation wave, and CD corresponds to the trailing edge of the excitation wave. (b) A self-oscillating medium: O is an unstable equilibrium state of the system; solid line ABCD is the limit cycle described by the system upon self-oscillation. (c) A bistable medium: F and E are the points of the stable equilibrium states.

As follows from an analysis of the isoclines shown in Fig. 5, a nonlinear neuron block (a self-oscillating relaxation system) can generate a single electrical pulse, a periodic sequence of pulses, and clusters of impulses (bursts) whose frequency usually diminishes sequentially until they are terminated.

INFORMATION CODING IN SPIKING NEURAL NETWORKS

There are different ways of encoding information in an SN [12, 13]: (1) the phase (time) approach, which depends on the exact position of the pulses in time, relative to some common reference position; (2) coding according to the time before the appearance of the first pulse, in which information about the signal is given by time of the first pulse appearing at any output; (3) the ordinal approach, which depends on the order of pulses received at the outputs of a network; (4) the interval (delayed) approach, in which information about the signal is provided by the distance between pulses received at the outputs of a network; (5) the resonance approach, in which information about the signal is provided by a dense sequence of pulses leading to resonance when single pulses decay and do not contribute to the transfer of information. The known types of coding are illustrated in Fig. 6.

Fig. 6.

Known types of coding in spiking neural networks.

In addition, there are ways of coding information that are mixed forms of several simple types. It should be noted that there is currently no full agreement on ways of coding information in spiking neural networks, and this problem requires further investigation.

A way of coding information in an SNN that adequately allows for features and properties of coding and describes the processes that arise is proposed in this work. The unit of information is the impulse sequence. For comparison, one pixel of the image on a monitor screen is a unit of information for McCulloch–Pitts binary neurons. The input object is thus determined by a cluster of pulse sequences generated by the input object (e.g., the image on a monitor screen). The input signals are summed by summing the pulse sequences, using the properties of quasi-periodic functions.

The next question is of fundamental importance: Will recognition remain correct when the intensity of the input signal is increased, altering the frequency of the pulse sequences coming from an object? It is natural to assume that all frequencies of pulse sequences change synchronously upon a change in intensity. The change in the frequency of stimuli resulting from their intensity is described by the Fechner equation [14]

$$\frac{f}{{{{f}_{0}}}} = \ln \frac{I}{{{{I}_{0}}}},\,\,\,\frac{T}{{{{T}_{0}}}} = {1 \mathord{\left/ {\vphantom {1 {\ln }}} \right. \kern-0em} {\ln }}\frac{I}{{{{I}_{0}}}},$$

where $I,f$ are the pulse intensity and the corresponding frequency; ${{I}_{0}},{{f}_{0}}$ are their initial values. Using the Kronecker inequality in the QPF theory, we can show that recognition is topologically invariant with respect to the intensity of the input signal. The basic property of the inertial summation of the maximum values ​​of pulse sequences is completely preserved. Recognition remains invariant with respect to the change in the intensity of the input signal.

How does the dynamics of recognition change when the intensity of the input signal changes? The recognition process is not violated, but the pulse repetition rate at the output of the recording neuron or pool of neurons increases in proportion to the change in the intensity of the input signal. This has been confirmed by experimental studies of the neuron activity in certain regions of the brain. The model of a spiking neural network considered in this work requires further research.

CONCLUSIONS

Nonlinear dynamics, physical processes, and information processing in selective spiking neurons were investigated. We considered summation of the pulse inputs, based on the theory of quasi-periodic functions and nonlinear transformation using the self-oscillating relaxation system of a neuron. A way of encoding input information was also considered, in which the unit of information was the pulse sequence and the intensity of the input signal was encoded by a synchronous change in the frequency of the pulse sequences.