1 Introduction

Rhythms are ubiquitous in the nervous system (Buzsaki 2004). Although they are not yet fully understood, the study of their functional role has gained extensive attention in recent years. For instance, brain oscillations have been linked to specific cognitive states (Baldauf and Desimone 2014). On the other hand, mental disorders such as epilepsy (Milton and Jung 2003), schizophrenia (Ford and Mathalon 2008) and Parkinson’s disease (Hammond et al. 2007) are associated to altered brain rhythms. Therefore, it is a crucial task to identify and analyse the mechanisms leading to oscillatory activity in neuronal networks.

However, the underlying mechanisms responsible for the emergence of brain oscillations are not trivial. It is known they are generated by the synchronized activity of groups of neurons (Buzsaki 2004). The question then becomes: How can we identify the key features that influence the occurrence of rhythmic activity and develop a mathematical model that simplifies their representation? There have been a number of earlier efforts to study the emergence of brain oscillations. The generation of synchronized oscillations in neural networks involves a complex interplay of several key mechanisms, including synaptic integration dynamics (Ratas and Pyragas 2019), spike frequency adaptation and synaptic depression mechanisms (Gast et al. 2020), gap junctions (Pietras et al. 2019), synaptic delays (Karbowski and Kopell 2000) or synaptic coupling strengths (Brunel and van Rossum 2007). Although progress has been made, many questions remain unsolved. The complex mechanism leading to oscillatory behaviour is still an open-ended problem, especially when considering a noisy setting.

Given that the noise is inherent in neuronal dynamics (Longtin 2013), a fully stochastic neural network provides a natural setting for investigating the dynamical emergence of oscillations. There are two general ways to implement noise in mathematical neuronal models (Longtin 2013). One approach accounts for variability generated through synaptic transmission of electrical signals, which is generically defined as extrinsic noise. The other approach considers internal cell mechanisms leading to an action potential, referred to as intrinsic noise. Each category corresponds to a specific mathematical formalization involving a partial differential equation for the probability density function of the respective stochastic process. The use of extrinsic noise leads to the well-known Fokker–Planck (FP) equation (Brunel and Hakim 1999; Brunel 2000), while the formalism for intrinsic noise takes the form of another well-known equation introduced by van Foerster (Foerster 1959) commonly referred to as the age-structured (AS) equation. Surprisingly, despite their contrasting nature, the mathematical formalization of internal and external variability are strikingly similar and can be mapped one to the other (Dumont et al. 2016a, b, 2020).

In computational neuroscience, most attempts to produce a tractable description of neural networks have relied on mean-field theory (Deco et al. 2008). In the mean-field limit, both FP and the AS equations generate relevant descriptions of spiking neuronal networks. The FP equation has been extensively studied, starting with analytical properties of the solutions (Carrillo et al. 2013), global behaviour and steady-state existence (Cáceres et al. 2011) and it is an important tool for investigating special dynamics of neural populations. By the use of the FP equation, one can study various phenomena, such as the emergence of global oscillations in inhibitory networks and excitatory/inhibitory neurons (Brunel and Hakim 1999; Brunel 2000), of cascade assemblies (Newhall et al. 2010a, b), or blow-up events (Dumont and Henry 2013; Cáceres et al. 2011). Additionally, this framework has been used to investigate the onset of oscillations generated by correlated noise via linear response theory (Lindner et al. 2005) and the synchronization of neurons induced by gap junctions (Ostojic et al. 2009).

Known in Neuroscience as the refractory density equation (Gerstner and van Hemmen 1992) or the time elapsed model (Pakdaman et al. 2009), the AS formalism was initially used in Gerstner and van Hemmen (1992). It consists of a partial differential equation describing the dynamics of neurons with respect to the time that has elapsed since their last action potential and it can be rigorously derived from a stochastic process (Chevallier et al. 2015). Despite its simplicity, there is a substantial amount of evidence supporting its suitability in describing non-trivial phenomena observed in spiking networks. Up to now, it has proved to be useful for analysing phenomena such as locking mechanism of excitatory networks (Gerstner 2000), low dimensional reduction (Pietras et al. 2020) or activity dynamics of finite-size networks (Schwalger et al. 2017; Deger et al. 2014; Dumont et al. 2017; Meyer and Vreeswijk 2002). From a mathematical perspective, solutions of the model and qualitative properties have been analysed, such as the construction of periodic analytical solutions (Pakdaman et al. 2013), reduction to delay equations (Caceres et al. 2021) and generalization to the case that includes the time elapsed since the penultimate discharge (Torres and Perthame 2022). Although the AS formalization considers only the time structure of neural populations, it has been proved suitable to reflect the case of noisy integrate-and-fire neuron model (Dumont et al. 2016a, b, 2020) and spike response neuron model (Gerstner 2000). Connections with conductance-based models can be found in Chizhov (2014), Chizhov and Graham (2007), and approximation schemes have been proposed when incorporating coloured-noise current (Chizhov and Graham 2008) and adaptation (Deger et al. 2014; Schwalger and Chizhov 2019), see also Schwalger (2021) for a numerical approach. For a comprehensive overview, interested readers can refer to a recent review on the topic (Schwalger and Chizhov 2019).

Unfortunately, the FP formalism remains difficult to use and the AS equation does not directly give access to the key structuring variable such as the neural voltage for instance. Our primary goal is to propose a simpler formulation than the traditional FP equation, yet one that retains enough complexity to entail most of the relevant neural parameters. This formalism will facilitate the study of neural oscillations while preserving connections between microscopic cellular properties, network coupling and the emergence of brain rhythms.

To do so, we consider a network of leaky integrate-and-fire (LIF) neurons, a well-established current-based neural model (Izhikevich 2007; Ermentrout and Terman 2010), consisting in sub-threshold dynamics given by a deterministic law, introduced first by L. Lapique in 1907 (Brunel and van Rossum 2007). To account for neural noise, the spiking mechanism is considered to be stochastic: the firing occurs with a probability that depends on the internal state of the neuron. A refractory period is explicitly taken into consideration and synaptic delay is included to model possible long-range synaptic transmission (Swadlow and Waxman 2012).

Next, we take advantage of the thermodynamic limit and use the mean-field formalism to give rise to a continuity equation (Deco et al. 2008). The resulting continuity equation endows processes taking place at the cellular scale as well as at the network level: a transport term given by the LIF dynamics, a spiking term induced by firing events, a singular source term modelling the reset after an action potential and a nonlinear term expressing the network connectivity. A similar equation was introduced at a formal level in Gerstner (2000), but it has only recently been rigorously derived in the context of Neuroscience (Schmutz et al. 2023). In a simpler scenario, without a refractory period and synaptic delay, the emergence of a Hopf bifurcation has been demonstrated (Cormier et al. 2021).

Interestingly, the continuity equation derived from the above considerations falls within the broader category of physiologically structured population models and shares specific similarities with size-structured populations. With origins going back by decades (Sinko and Streifer 1967), the size-structured models have been subject of interest in more recent years. Mathematically, analytical aspects of the solutions (Kato 2004), numerical schemes (Abia et al. 2004), dynamic optimization methods (Gasca-Leyva et al. 2007), optimal control problems (Tarniceriu and Veliov 2009) are few of the issues investigated. Applications of these models are manifold: forestry (Reed and Clarke 1990) and fishery (Arnason 1992), dynamics of competing populations for the same resource (Ackleh et al. 2004), cell maturation processes (Doumic et al. 2011) or cancer tumour growth models (Liu and Wang 2019).

The aim of the presents manuscript is to shed light on the synaptic mechanisms that enable emergence of global oscillations in a network of excitatory neurons. We specifically focus on the roles played by synaptic conduction delay and synaptic coupling, showcasing their central roles in driving rhythmic dynamics. Our results emphasize the critical importance of the nonlinear term, which describes the interaction between cells, in shaping the network’s dynamics.

The paper is organized as follows. First, we present the network and the neuron model that will be used throughout. Next, we derive the associated mean-field representation, which takes the form of a nonlinear partial differential equation. We then calculate the steady state of the equation, giving access to the average activity in the asynchronous regime. By linearizing around the asynchronous solution, we apply a perturbation analysis method to compute the bifurcation diagram predicting the emergence of oscillations in the nonlinear continuity equation. Throughout this study, we illustrate our theoretical results with numerical simulations. Furthermore, we systematically compare simulations of the continuity equation with those of the finite-size network. Taking parameters below or above the bifurcation line, we show that the simulated spiking activity of the full network confirms the emergence of a transition from an asynchronous to a synchronized activity regime.

2 The Neural Network

One of the simplest single-neuron models, yet exhibiting rich behaviours, is the leaky integrate-and-fire (LIF) model (Izhikevich 2007). It consists of an ordinary differential equation describing the sub-threshold dynamics of the membrane’s voltage of a neuronal cell. Up to a re-scaling, the dynamics of the sub-threshold potential, v(t), are given by

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}v(t)=\mu (t) -v(t), \end{aligned}$$
(1)

where \(\mu (t)\) represents the time-dependent total current the neuron receives. To account for the emission of action potentials, the model must be endowed with a reset mechanism.

However, spike generation is known to be stochastic. Internal noise is thus embedded via a probabilistic firing mechanism: a cell will emit a spike with a probability that depends on the momentary distance between its membrane potential and a fixed threshold value. When the voltage is below the threshold \(v_\textrm{th}\), the firing probability is low. As the voltage approaches the threshold, the probability increases, and once the voltage surpasses the threshold, the probability continues to rise. Denoting

$$\begin{aligned} {\tilde{\rho }}(v(t)-v_\textrm{th}):=\rho (v(t)), \end{aligned}$$
(2)

then, during a time interval \([t,t+\hbox {d}t]\), the probability that a spike occurs is given by \(\rho (v(t)) \hbox {d}t\). From a mathematical perspective, the probability of spiking is conditionally Poisson, with a voltage-dependent Poisson rate given by the momentary distance between the membrane potential and the threshold. The population activity can then be extracted and is obtained by summing all occurring spikes:

$$\begin{aligned} r_N(t)= \dfrac{1}{N} \sum _{k=1}^{N} \sum _{f} \delta \left( t-t_k^f\right) , \end{aligned}$$
(3)

where \(\delta \) is the Dirac mass, N the number of neurons and \(t_k^f\) the instants of firing events of the cell numbered k. The summation in Eq. (3) is made over all \(t_k^f\), and the total input current is then defined as:

$$\begin{aligned} \mu (t) = \mu _\textrm{ext}(t) +Jr_N(t-\tau ). \end{aligned}$$
(4)

Here, \(\mu _\textrm{ext}(t)\) represents the external input, J is a connectivity parameter and \(\tau \) is the synaptic delay. Finally, we assume a refractory period, denoted as T, during which the neuron cannot fire after spiking. We furthermore impose that \(r_N(t)=0\) for all \(t\in [-\max (\tau ,T),0)\).

In Fig. 1, a numerical simulation of the fully connected network is displayed. In the first panel, Fig. 1A, the time course of a given external current \(\mu _\textrm{ext}(t)\) is shown. The corresponding spiking activity of the full network of neurons described by (1) and the firing rate extracted from it (3) can be observed in Fig. 1B.

A standard tool for analysing the dynamics of a large network of neurons described by a stochastic process is to introduce its associated probability density function. This is obtained in the so-called thermodynamic limit.

Fig. 1
figure 1

Comparison of the firing rate activity between the full network and its corresponding mean-field equation. A A time-dependent external current \(\mu _\textrm{ext}\). B Raster plot and the firing rate extracted from Monte–Carlo simulations of the model (3). C Firing rate given by the simulation of the probability density function (7). Parameters: \(v_\textrm{th}=17\), \(v_r=3\), \(\tau =5\), \(J=20\), \(T=5\), \(\rho (u)=\exp (u)\)

Full size image

3 Mean-Field Description: Density Function

In the limit of an infinitely large number of neurons N (the thermodynamic limit), the full network description reduces to a single continuity equation. Denoting p(t, v) the probability that the membrane’s potential is in a certain state v at a given time t, the time evolution of the density function is then described by a nonlinear partial differential equation which takes into account three phenomena: a drift term due to the continuous evolution in the LIF model, a negative source term due to the Poisson spiking process and a singular term due to the reset mechanism.

Denoting by r(t) the firing rate of the network, which is the proportion of firing cells, then the dynamics of the probability density p(t, v) are given by:

$$\begin{aligned} \frac{\partial }{\partial t}p(t,v)+\overbrace{\frac{\partial }{\partial v}[(\mu (t) -v)p(t,v)]}^{\text {LIF}} +\overbrace{ \rho (v) p(t,v)}^{\text {Poisson Spiking}} = \overbrace{\delta (v-v_{r}) r(t-T)}^{\text {Reset}}, \end{aligned}$$
(5)

where once again, \(\mu (t)\) represents the time-dependent total current, \(v_r\) is the reset potential, T is the refractory period and \(\rho (v)\) is the probability rate of firing. Reflecting boundary conditions are imposed to guarantee the probability conservation property

$$\begin{aligned} \lim \limits _{v \rightarrow \pm \infty } [(\mu (t)-v)p(t,v)] =0. \end{aligned}$$
(6)

The firing rate r(t) is now given by

$$\begin{aligned} r(t) = \int _{-\infty }^{+\infty }\rho (v)p(t,v) \,\hbox {d}v. \end{aligned}$$
(7)

The total input current is given by

$$\begin{aligned} \mu (t)= \mu _\textrm{ext}(t) +Jr(t-\tau ), \end{aligned}$$
(8)

where \(\mu _\textrm{ext}(t)\) represents the time-dependent external input, J is a connectivity parameter and \(\tau \) is the synaptic delay. Using the boundary condition together with the expression of r(t), one can easily check the conservation property of Eq. (5) by direct integration, so that if the initial condition satisfies

$$\begin{aligned} \int _{-\infty }^{+\infty } p_0(v)\,\hbox {d}v=1, \end{aligned}$$
(9)

then the solution to (5) necessarily satisfies

$$\begin{aligned} \int _{-\infty }^{\infty }p(t,v)\mathrm{\,d}v+\int _{t-T}^t r(s)\mathrm{\,d}s=1. \end{aligned}$$
(10)

Here we assumed that \(r(s)=0\) for \(s\in [-\max \{\tau ,T\},0)\). Importantly, the firing activity can be seen as:

$$\begin{aligned} r(t) = \lim \limits _{N \rightarrow + \infty } r_N(t), \end{aligned}$$
(11)

see Schmutz et al. (2023) for a rigorous derivation.

In Fig. 1, the time course of the firing rate given by the density approach (7) is presented. The mean-field approximation captures the essential dynamical shape of the firing activity of the full network shown in Fig. 1C. Note, nonetheless, that it completely ignores the finite-size fluctuations, see Schwalger et al. (2017), Dumont et al. (2017), Schwalger (2021) for recent studies on finite-size effects in spiking neural networks.

In Fig. 2, a comparison between the finite network and its associated nonlinear partial differential equation is presented. In the first panel, Fig. 2A, the initial condition is shown. The subsequent panels (Fig. 2B–C) display the density function at different time instants, where one can see the evolution of the density towards the firing threshold (B) and the re-injection process (C). In this case, the density function reaches its stationary state, as depicted in 2D.

Note that this type of continuity equation is known to dissipate over time when the model is linear (Michel et al. 2005), that is, in our situation, when the coupling parameter is set to \(J=0\). Therefore, it is natural to observe the convergence towards a steady state when the synaptic coupling is not too strong. In what follows, we will demonstrate that when the coupling is sufficiently large, oscillations can emerge.

Fig. 2
figure 2

Comparison of the time evolution of the full network of 20,000 neurons and its corresponding mean-field equation at different instants of time: A \(t=0.2\), B \(t=8\), C \(t=18\), D \(t=50\). Parameters: \(v_\textrm{th}=18\), \(v_r=3\), \(\mu _\textrm{ext}=26\), \(\tau =3\), \(T=2\), \(J=3\). The spiking probability: \(\rho (u)=\exp (u)\)

Full size image

4 The Asynchronous State: Time-Independent Solution

The average activity in the asynchronous state \(r_{\infty }\) can be computed using the time-independent solution \(p_{\infty }(v)\) of the nonlinear partial differential Eq. (5). This means that the partial derivative with respect to time is set to zero and we are therefore looking for a solution to the following problem:

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\hbox {d}}{\hbox {d} v}[(\mu _{\infty }-v)p_{\infty }(v)]+\rho (v)p_{\infty }(v)=0,\quad v\in (v_r,\mu _{\infty })\\ (\mu _{\infty }-v_r)p_{\infty }(v_r)=r_{\infty }:=\displaystyle \int _{v_r}^{\mu _{\infty }}\rho (v)p_{\infty }(v)\mathrm{\,d}v,\\ \displaystyle \int _{v_r}^{\mu _{\infty }} p_\infty (v)\mathrm{\,d}v+r_\infty T=1, \end{array}\right. \end{aligned}$$
(12)

where we have used the notation

$$\begin{aligned} \mu _{\infty } = \mu _\textrm{ext} +J r_{\infty }. \end{aligned}$$
(13)

The first equation in (12) can be integrated with the initial condition in \(v_r\), to get:

Fig. 3
figure 3

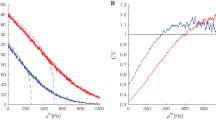
Numerical solution of the stationary problem. A Stationary firing rate found as the intersection of the curves of I(r) and f(r). The stationary rate \(r_{\infty }\) given by (15) is plotted as the red dot. B The stationary firing rate obtained via explicit formula (black line) and as asymptotic solution of the simulation of the full network (red dots) for a range of external current \(\mu _\textrm{ext}\). C: Raster plot of the activity of the full network and the extracted firing rate. In panel D, the black line represents the value of the stationary firing rate. Parameters: \(v_\textrm{th}=17\), \(v_r=3\), \(\tau =5\), \(J=3\), \(T=2\), \(\mu _\textrm{ext}=26\), \(\rho (u)=\exp (u)\) (Color figure online)

Full size image
$$\begin{aligned} p_{\infty }(v)=\frac{r_{\infty }}{\mu _{\infty }-v}\exp \left\{ -\int _{v_r}^v \frac{\rho (s)}{\mu _{\infty }-s}\mathrm{\,d}s\right\} , \quad v\in (v_r,\mu _\infty ). \end{aligned}$$
(14)

Next, the stationary firing rate should satisfy, due to the conservation property, the following integral equation:

$$\begin{aligned} \int _{v_r}^{\mu _{\infty }}\frac{r_{\infty }}{\mu _{\infty }-v}\exp \left\{ -\int _{v_r}^v\frac{\rho (s)}{\mu _{\infty }-s}\mathrm{\,d}s\right\} \mathrm{\,d}v + Tr_{\infty } =1. \end{aligned}$$
(15)

The way of solving the nonlinear equation expressing \(r_{\infty }\) is shown in Fig. 3A. The solution of the stationary firing rate \(r_{\infty }\) is obtained as an intersection of the curves:

$$\begin{aligned} I(r)=\int _{v_r}^{\mu _\textrm{ext}+Jr}\frac{1}{\mu _\textrm{ext}-v+Jr}\exp \left\{ -\int _{v_r}^v\frac{\rho (s)}{\mu _\textrm{ext}-s+Jr}\mathrm{\,d}s\right\} \mathrm{\,d}v, \end{aligned}$$

and

$$\begin{aligned} f(r)=\frac{1}{r}-T. \end{aligned}$$

Let us notice that there exists at least one crossing point between the two curves. Indeed, one can easily show that

$$\begin{aligned} I(r)\le & {} f(r), \quad \text {for} \quad r<<1,\\ I(r)\ge & {} f(r),\quad \text {for} \quad r>>1. \end{aligned}$$

Therefore, the two curves defined by the continuous functions I and f must cross in a point \(r_{\infty }\) belonging to \((0,+\infty )\). Consequently, there exist at least one solution to the stationary problem (12).

In Fig. 3B, a comparison between the stationary firing rate given by (15) and by the simulation of the whole network is shown, along with the extracted firing rate Fig. 3C and its comparison with the stationary value numerically obtained from Eq. (15).

In Fig. 4, we illustrate the stationary firing rate—the red curve—given by Eq. (14) for two sets of parameters. The stationary solution is compared to the long time solution obtained by simulating the system (10)—the black curve—and also with the one obtained by simulating a network of neurons given by (1). Convergence towards the corresponding stationary state can be observed in both cases.

Fig. 4
figure 4

Comparison of the stationary state given by formula (14) (red line) with the density solution obtained by the simulation of the time-dependent problem (5)–(10) in large time (black line), while the blue line is given by simulation of a network of neurons described by (1). The panels have been obtained for two sets of different parameters: A \(J=7\), \(\tau =5\), \(T=2\), \(v_r=3\), \(v_\textrm{th}=20\), \(\mu _\textrm{ext}=32\). B: \(J=2\), \(\tau =5\), \(T=2\), \(v_r=3\), \(v_\textrm{th}=17\), \(\mu _\textrm{ext}=23\). In all simulations, \(\rho (u)=\exp (u)\) (Color figure online)

Full size image

5 Emergence of Oscillations

In what follows, we are interested to find the critical points where the stationary state defined by (12) becomes unstable, giving rise to oscillations. The asynchronous state can lose stability through an oscillatory instability. To identify the conditions under which this oscillatory instability occurs, we linearize Eq. (5) around the steady-state solution given by (12). Namely, let us consider small deviations from the stationary solution given by (12), i.e.

$$\begin{aligned} p(t,v)=p_\infty (v)+\varepsilon {\tilde{p}}(t,v)+O(\varepsilon ^2),\quad r(t)=r_\infty +\varepsilon {\tilde{r}}(t)+O(\varepsilon ^2), \quad \varepsilon<<1. \end{aligned}$$

We will focus on the case of excitatory connections (\(J>0\)) and consider the initial condition in the potential value \(v_r < \mu _\infty \). Substituting this expression of p into (5), we find that \({\tilde{p}}\) must satisfy:

$$\begin{aligned}{} & {} \frac{\partial }{\partial t} {\tilde{p}}(t,v)+\frac{\partial }{\partial v}[(\mu _{\infty }-v){\tilde{p}}(t,v)]+\rho (v){\tilde{p}}(t,v)\nonumber \\ {}{} & {} \quad =\delta (v-v_r){\tilde{r}}(t-T) -J{\tilde{r}}(t-\tau ) p'_\infty (v), \end{aligned}$$
(16)

for all \(t>0\) and \(v\in (v_r,\mu _\infty )\).

Using Eq. (7), it follows that \({\tilde{r}}(t)\) is given by:

$$\begin{aligned} {\tilde{r}}(t)=\int _{v_r}^{\mu _\infty }\rho (v){\tilde{p}}(t,v)\mathrm{\,d}v. \end{aligned}$$
(17)

We now look for a solution to (16) in the separable form

$$\begin{aligned} {\tilde{p}}(t,v)=e^{\lambda t} {\tilde{P}}(v), \quad {\tilde{r}}(t)=e^{\lambda t} {\tilde{r}}, \end{aligned}$$

with \(\lambda \in {\mathbb {C}}\). Then, we obtain that \({\tilde{P}}\) is solution to

$$\begin{aligned} \frac{\partial }{\partial v}[(\mu _{\infty }-v){\tilde{P}}(v)]+[\rho (v)+\lambda ]{\tilde{P}}(v)=\delta (v-v_r){\tilde{r}}e^{-\lambda T} -J{\tilde{r}}e^{-\lambda \tau } p'_\infty (v),\qquad \end{aligned}$$
(18)

with

$$\begin{aligned} {\tilde{r}}=\int _{v_r}^{\mu _\infty }\rho (v){\tilde{P}}(v)\mathrm{\,d}v. \end{aligned}$$
(19)

Due to the positivity of the transport function, we can express the above equation equivalently as:

$$\begin{aligned} {\tilde{P}}'(v)+\frac{\rho (v)-1+\lambda }{\mu _{\infty }-v}{\tilde{P}}(v)=\delta (v-v_r)\frac{{\tilde{r}} e^{-\lambda T}}{\mu _{\infty }-v}-\frac{J{\tilde{r}}e^{-\lambda \tau } p'_\infty (v)}{\mu _{\infty }-v}. \end{aligned}$$

Integrating the above equation from the initial point \(v_r\), we obtain that \({\tilde{P}}\) is given by:

$$\begin{aligned} {\tilde{P}}(v)= & {} \frac{{\tilde{r}} e^{-\lambda T} }{\mu _{\infty }-v_r}\exp \{-\int _{v_r}^{v} \frac{\rho (w)-1+\lambda }{\mu _{\infty }-w} \mathrm{\,d}w\}\nonumber \\{} & {} -J{\tilde{r}}e^{-\lambda \tau }\int _{v_{r}}^{v}\frac{p'_\infty (w)}{\mu _{\infty }-w}\exp \{-\int _{w}^{v} \frac{\rho (s)-1+\lambda }{\mu _{\infty }-s} \mathrm{\,d}s\}\mathrm{\,d}w. \end{aligned}$$
(20)

Since \({\tilde{r}}\) satisfies (19), we obtain:

$$\begin{aligned} 1= & {} \frac{e^{-\lambda T}}{\mu _{\infty }-v_r}\int _{v_r}^{\mu _{\infty }}\rho (v)\exp \{-\int _{v_r}^{v} \frac{\rho (w)-1+\lambda }{\mu _{\infty }-w} \mathrm{\,d}w\} \mathrm{\,d}v \end{aligned}$$
(21)
$$\begin{aligned}{} & {} -Je^{-\lambda \tau }\int _{v_r}^{\mu _{\infty }}\rho (v-v_{th})\int _{v_{r}}^{v}\frac{p'_\infty (w)}{\mu _{\infty }-w}\exp \{-\int _{w}^{v}- \frac{\rho (s)-1+\lambda }{\mu _{\infty }-s} \mathrm{\,d}s\}\mathrm{\,d}w \mathrm{\,d}v\nonumber \\= & {} I_1+I_2. \end{aligned}$$
(22)

It is now useful to plug in \(I_2\) the expression

$$\begin{aligned} p_\infty '(w)=\frac{\delta (w-v_r)r_{\infty }}{\mu _{\infty }-w}-\frac{\rho (w)-1}{\mu _{\infty }-w}p_\infty (w), \end{aligned}$$
(23)

and formula (14). Furthermore, through direct integration, we find that:

$$\begin{aligned} \exp \{-\int _w^v \frac{\lambda }{\mu _{\infty }-s}ds\}=\left( \frac{\mu _{\infty }-v}{\mu _{\infty }-w}\right) ^\lambda . \end{aligned}$$

To simplify the equations, let us denote

$$\begin{aligned} E(v)=\exp \{-\int _{v_r}^v \frac{\rho (s)}{\mu _{\infty }-s}\mathrm{\,d}s\}. \end{aligned}$$

Then, we have

$$\begin{aligned} I_1=\frac{e^{-\lambda T }}{(\mu _{\infty }-v_r)^\lambda }\int _{v_r}^{\mu _{\infty }}\rho (v)E(v)(\mu _{\infty }-v)^{\lambda -1}\mathrm{\,d}v. \end{aligned}$$

Using the expression (23) and subsequently breaking down the second integral as \(I_2=I_{21}+I_{22}\), we get that

$$\begin{aligned} I_{21}=\frac{-Jr_\infty e^{-\lambda \tau }}{(\mu _{\infty }-v_r)^{\lambda +1}}\int _{v_r}^{\mu _{\infty }}\rho (v)E(v)(\mu _{\infty }-v)^{\lambda -1}\mathrm{\,d}v, \end{aligned}$$

and, finally,

$$\begin{aligned} I_{22}=Jr_\infty e^{-\lambda \tau }\int _{v_r}^{\mu _{\infty }}\rho (v)E(v)(\mu _{\infty }-v)^{\lambda -1}\int _{v_r}^v\frac{\rho (w)-1}{(\mu _{\infty }-w)^{\lambda +2} }\mathrm{\,d}w\mathrm{\,d}v. \end{aligned}$$

We therefore obtain a characterization of the eigenvalues of the linearized operator by defining the characteristic equation

$$\begin{aligned} C(\lambda )=0, \end{aligned}$$
(24)

where

$$\begin{aligned} C(\lambda )= & {} -1+\dfrac{e^{-\lambda T}(\mu _{\infty }-v_r)-Jr_{\infty }e^{-\lambda \tau }}{(\mu _{\infty }-v_r)^{\lambda +1}}\displaystyle \int _{v_r}^{\mu _{\infty }}\rho (v)E(v)(\mu _{\infty }-v)^{\lambda -1}\mathrm{\,d}v\\{} & {} +Jr_\infty e^{-\lambda \tau }\displaystyle \int _{v_r}^{\mu _{\infty }}\rho (v)E(v)(\mu _{\infty }-v)^{\lambda -1}\displaystyle \int _{v_r}^v\frac{\rho (w)-1}{(\mu _{\infty }-w)^{\lambda +2} }\mathrm{\,d}w\mathrm{\,d}v. \end{aligned}$$

The eigenvalues are given by the roots of the characteristic equation. The time-independent solution will be stable if all eigenvalues have negative real parts and becomes unstable if at least one eigenvalue has a positive real part. Therefore, by setting \(\lambda :=i\omega \) in (24), the equation giving the critical points should satisfy

$$\begin{aligned} C(i\omega )=0. \end{aligned}$$
(25)

The bifurcation line which separates the oscillatory regime from the asynchronous one can be drawn numerically, as depicted in Fig. 5A. The red line constitutes the boundary between the stability and the instability regions with respect to two parameters of the system: the connectivity parameter J and the delay \(\tau \). The shaded area defines the region in parameter space where self-sustained oscillations are going to emerge. Well below the transition line, in the asynchronous regime, damped oscillations may occur.

As we can see from Fig. 5A, for a sufficiently large synaptic strength J and/or synaptic delay \(\tau \), the asynchronous state undergoes a bifurcation towards oscillations. The simulated spiking activity of the full network in Fig. 5B–E confirms the emergence of a transition from an asynchronous state (panels B, C) to a synchronized activity regime (panels D, E) when parameters are adjusted below or above the bifurcation line. Corresponding firing rates obtained by simulating the entire network (blue line) and the density equation (black line) are displayed in panels H and I. In panels F and G, initial damped oscillations gradually decay in amplitude over time and ultimately converge to a stationary state. Notably, as one approaches the boundary separating the two regimes, a longer time is required for convergence. Upon entering the oscillatory domain (panels H and I), oscillatory behaviour becomes evident. In both cases, whether closer to or farther from the bifurcation line, the simulations suggest convergence towards stable limit cycles, indicative of a supercritical Hopf bifurcation.

The numerical method for obtaining the bifurcation curve relies on solving Eq. (25) by taking one of the parameters fixed while iterating the second parameter until the real part of the roots of \(C(\lambda )\) becomes zero. The computations of the roots is based on Newton method for solving nonlinear equations.

Fig. 5
figure 5

Emergence of oscillations. The figure illustrates the emergence of oscillations in the fully stochastic neural network as a function of the parameters \(\tau \) and J. A Graphic solution to (25) represented by the red curve that separates the oscillatory and non-oscillatory domains. B–E Raster plots obtained by simulating the full network of neurons using the values of parameters depicted in A, B \((\tau ,J)=(2.5,3)\). C \((\tau , J)=(2.6,3.5)\). D \((\tau , J)=(2.7,4)\). E \((\tau , J)=(2.8,4.5)\). In the first two B, C, one can notice the convergence of the system towards the stationary state. In D, the emergence of oscillations is already visible, while in E the convergence towards an oscillatory state becomes obvious. F–I display the time evolution of the firing rates corresponding to raster plots B–E, respectively. It is evident that there is a gradual transition when crossing the bifurcation curve: from convergence towards a stationary state (F, G) to convergence towards stable limit cycles (H, I). Parameters: \(v_\textrm{th}=18\), \(v_r=3\), \(\mu _\textrm{ext}=26\), \(T=2\). The spiking probability: \(\rho (u)=\exp (u)\)

Full size image
Fig. 6
figure 6

Effect of neuron parameters on the bifurcation onset. A The figure shows the bifurcation lines for refractory times \(T=2\), \(T=2.1\), \(T=2.2\). Parameters: \(v_\textrm{th}=18\), \(v_r=3\), \(\mu _\textrm{ext}=26\). B The bifurcation lines corresponding to external current values \(\mu _\textrm{ext}=24\), \(\mu _\textrm{ext}=25\), \(\mu _\textrm{ext}=26\). Parameters: \(v_\textrm{th}=18\), \(v_r=3\), \(T=2\). In both panels, the shaded region indicates the oscillatory regime and the spiking probability is \(\rho (u)=\exp (u)\)

Full size image

To illustrate how other parameters influence the onset of emerging oscillations, we show in Fig. 6 how changes in these parameters shift the bifurcation line. As shown, variations in the parameter T, respectively \(\mu _\textrm{ext}\), result in a shift of the bifurcation line that separates the non-oscillatory region (white region) from the oscillatory one (grey region). Specifically, increasing the external current (Fig. 6B) requires lower values for parameters \(\tau \) and J to generate oscillations. Conversely, higher values of the refractory period (Fig. 6A) tend to desynchronize the network.

6 Conclusion

Brain oscillations are known to play a pivotal role in many aspects of brain function, including attention (Fries 2005), learning and memory (Herweg et al. 2020) and motor control (Brittain and Brown 2014). Oscillatory phenomena are also involved in the pathophysiology of neurological disorders, such as epilepsy (Rich et al. 2020) or Parkinson’s disease (Gong et al. 2021). Moreover, an integral aspect of this endeavour involves exploring the origins of specific brain oscillations, such as gamma oscillations (Whittington et al. 2010), which are closely tied to cognitive processes and have been implicated in numerous neurological conditions. Hence, a comprehensive grasp of the factors contributing to oscillation emergence is imperative, at both the cellular and network levels.

There have been a number of earlier efforts to study the emergence of rhythms in spiking neural networks. Among all the mechanisms that contribute to the synchronized activity of networks of neurons, synaptic delay and the strength of synaptic connections are recognized as crucial factors. The strength of synaptic connections, encompassing both excitatory and inhibitory synapses, plays a pivotal role in modulating the emergence and characteristics of oscillations. For instance, strong excitatory connections can promote synchronized firing (Strogatz 2000). Conversely, synaptic delays, another significant factor influencing the period of oscillations (Brunel and Hakim 1999), impact synchronization properties in networks of excitatory–inhibitory neurons (Ermentrout and Kopell 1998) and influence the quality of correlation-induced oscillations in large networks, especially in the presence of internal noise.

While there have been numerous earlier efforts to investigate the emergence of rhythms in spiking neural networks, the problem of synchronization remains a topic of ongoing research. In this paper, we developed a theoretical framework to study the emergent macroscopic network oscillations in a population model described by Poisson LIF neurons. Our methodology, applied to spiking networks of excitatory cells, offers a path to explore the intricate relationships between microscopic cellular parameters, network coupling and the emergence of brain rhythms. As we have demonstrated, the strength of connectivity, once again, plays a pivotal role in generating oscillations. Moreover, we have illustrated how other parameters, such as external current, and cellular properties, such as the refractory period, contribute to shaping the onset of synchrony in a noisy setting.

While our study has been limited to a single population of neurons, the mathematical framework employed throughout this paper is adaptable to multiple interacting populations. This could be an interesting subject of research for future work. A number of other extensions of the model are also possible, such as considering a nonlinear spiking rate or including a spatial feature.

Another interesting direction would be the analysis of a finite-size network of neurons with Poisson spiking mechanism (Dumont et al. 2017). Among the methods that can be used to analyse the computational role of oscillations, the analysis of the phase resetting curve—see Winfree (2001), for instance—relying on the adjoint method (Brown et al. 2004) stands out. This method has been extended for networks of neurons by applying the adjoint method for the equations describing the dynamics of density functions (Dumont et al. 2022; Kotani et al. 2014). This could be an interesting subject of research for future work.