Spectral quasi-linearization and irreversibility analysis of magnetized cross fluid flow through a microchannel with two different heat sources and Newton boundary conditions

Abstract

Fluid flow in a microchannel with heat transport effects can be seen in various applications such as micro heat collectors, mechanical–electromechanical systems, electronic device cooling, micro-air vehicles, and micro-heat exchanger systems. However, little is known about the consequence of internal heat source modulations on the flow of fluids in a microchannel. Therefore, in this work, the heat transfer of a magnetized cross fluid is carried out in a micro-channel subjected to two different heat source modulations. Entropy production analysis is also performed. The mathematical model consists of a cross fluid model. In addition, the effects of Joule heating, external magnetism, and the boundary conditions of Newton's heating are also examined. Determinant equations are constructed under steady-state conditions and parameterized using dimensionless variables. The numerical spectral quasi-linearization (SQLM) method was developed to interpret the Bejan number, entropy production, temperature, and velocity profiles. It is established that the power-law index of the cross fluid reduces the magnitude of the entropy production, velocity, and thermal field in the entire microchannel region. Furthermore, a larger Weissenberg number is capable of producing greater entropy, velocity, and thermal fields throughout the microchannel region. The variation in temperature distribution is more noticeable for the ESHS aspect than the THS aspect. The values of the pressure gradient parameter and the Eckert number must be kept high for maximum heat transport of the cross fluid. The entropy production of the cross fluid increases significantly with the physical aspects of Joule heating and convection heating in the system.

1 Introduction

Currently, universal (generalized) Newtonian materials have gained enormous attention from various researchers due to their importance in chemical, industrial and technological applications. The viscosity of a universal Newtonian material depends on the shear rate. Therefore, a modified constitutive expression is introduced which takes into account the change in viscosity with fluctuating shear rate [1, 2]. The fluid model of the power-law [3] is one of the general universal Newtonian materials illustrating forms of thinning/thickening by shear. However, this model does not describe the behavior of the material for very high and very low shear rates. The Sisko model is used when the eccentricity of the power-law material model is only significant at very high shear rates [4]. Furthermore, the Ellis model [5] describes the flow of material in the power-law region and a very low shear rate. Cross [6] proposed the generalized Newtonian fluid model to overcome all the drawbacks of the aforementioned models. This cross rheological model is competent to describe the transition in the power-law region as well as in regions with very high and very low shear rates. The polymer solution is one of the examples of the Cross fluid model [7]. Since there is a time constant in the cross model, it is useful in many engineering applications. The experimental study of the cross fluid model, conducted by Escudier et al. [8], found an excellent collaboration.

Khan et al. [9] studied the heat transport and symmetrical flow of the cross fluid and found that the velocity increases with the power-law index. Hayat et al. [10] considered the cross fluid model to study the stagnation point flow of generalized Newtonian material on an elongated surface and established that the magnitude of the velocity decreased as the Weissenberg number increased. Munzur et al. [11] performed a Newton boundary condition analysis of heat transfer through the fluid in a vertical flared sheet with flotation effects. Mustafa et al. [12] examined the cross fluid flow model in which flow is created by a pressure gradient together with flow near the still inelastic plate. Khan et al. [13] found that the structure of the moment boundary layer is amplified by the power-law factor in their study of fluid flow across an elongated surface. Recent work on the cross fluid can be seen in [14,15,16]. However, the cross fluid flow and heat transport studies in a microchannel are very limited.

The main emphasis in the design of thermal devices is the involvement of energy efficiency. This can be achieved by decreasing entropy production in thermal device processes. The development of machines for heat removal and energy optimization requires the minimization of entropy production due to viscous friction work, heat conduction, and electric field. Available energy efficiency may be more desirable by optimizing entropy production. Chamkha et al. [17] examined the entropy production and thermal analysis of magnetized nanoliquids in a porous space. Mehryan et al. [18] performed an irreversibility analysis in a ferromagnetic fluid with the Lorentz force. Shamsabadi et al. [19] examined the thermal and viscous irreversibility of nanofluids. Seyyedi et al. [20] reported the radiative entropy production of the copper water nanoliquid flowing in the half-ring. Madhu et al. [21] performed a second law analysis of Carreau fluid flow in a microchannel with Newton's boundary conditions. They found a higher temperature field due to Newton's heating conditions on the walls. Shehzad et al. [22] also performed the irreversibility analysis of the flow of non-Newtonian material in a microchannel. The heat source/sink that affects heat transfer is another that deserves attention in light of many real-world problems. The distribution of heat throughout the domain can be changed significantly when a heat source or heat sink is introduced. In this view, Shehzad et al. [23] analyzed the impact of two modulations of different heat sources (heat-dependent heat source (THS) and space-based exponential heat source (ESHS)) on the production of nanoliquid entropy in a microchannel. To conclude, the study of entropy production in cross fluid with THS and ESHS is an open question. Furthermore, the importance of this study lies in how to use the generation or absorption of heat in a cross fluid moving within microchannels, which has been a major concern for many researchers due to its necessity in industrial and engineering applications to avoid hazards and also to increase productivity.

However, to the authors’ knowledge, no studies have thus far been communicated concerning the significance of internal temperature-dependent heat source and exponential space-dependent heat source modulations on the dynamics and heat transfer of cross fluid in a microchannel with entropy production. This regime is of immediate importance in the accurate simulation of magnetic liquids in the mechanical–electromechanical systems and materials processing industry. The novelty of the present work is that a comparative analysis between two different forms of internal heat source in the presence of Joule heating, convective heating boundary conditions, and applied magnetic field effects on the dynamics of cross fluid in a microchannel. The following objectives should be addressed:

• Study heat transport and flow of generalized Newtonian cross fluid in a microchannel.

• Perform the second law analysis of cross fluid in a microchannel.

• Examine the influences of two different modulations of the internal heat source (THS and ESHS) on the cross fluid flow in a microchannel.

• To analyze how external magnetism influences the production of entropy during the dynamics of the cross fluid in a microchannel.

• To analyze the consequences of Newton's boundary conditions on entropy production of cross fluid.

• Application of more efficient and robust spectral quasi-linearization technique to tackle the nonlinear boundary value problem.

2 Mathematical formulation

2.1 Flow and heat transfer

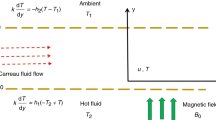
Consider fully developed incompressible non‐Newtonian cross fluid flow through a microchannel separated by a distance $h$. Suppose the two plates are of infinite length (see Fig. 1). The lower and upper plates are located at $y = 0$ and $y = h$, respectively. The fluid is evenly injected into the bottom plate and suction occurs on the top plate. The lower plate of the microchannel exchanges heat through convection with temperature $T_{2}$ while the other plate is with temperature $T_{1}$. The magnetic field and constant pressure gradient $\frac{{\rm d}p}{{{\rm d}x}}$ are also taken into account. Aspects of a space-related exponential heat source (ESHS), Joule heating, a temperature-related internal heat source (THS), and viscous dissipation are considered. From the above assumptions and the Boussinesq approximation of the equations are(see [6, 21, 23]):

$$ \frac{{\rm d}v}{{{\rm d}y}} = 0 $$

(1)

$$ \rho v_{0} \frac{{\rm d}u}{{{\rm d}y}} = - \frac{{\rm d}p}{{{\rm d}x}} + \mu \frac{{\rm d}}{{\rm d}y}\left( {\frac{{\frac{{\rm d}u}{{{\rm d}y}}}}{{1 + \left( {{\Gamma }\frac{{\rm d}u}{{{\rm d}y}}} \right)^{n} }}} \right) - \sigma B_{0}^{2} u $$

(2)

$$ \rho C_{p} v_{0} \frac{{\rm d}T}{{{\rm d}y}} = \frac{{{\rm d}^{2} T}}{{{\rm d}y^{2} }} + \mu \left( {\frac{{\left( {\frac{{\rm d}u}{{{\rm d}y}}} \right)^{2} }}{{1 + \left( {{\Gamma }\frac{{\rm d}u}{{{\rm d}y}}} \right)^{n} }}} \right) + \sigma B_{0}^{2} u^{2} + {\mathbb{Q}}_{T} \left( {T - T_{1} } \right) + {\mathbb{Q}}_{E} \left( {T_{2} - T_{1} } \right)exp\left( { - m\frac{y}{h}} \right) $$

(3)

Fig. 1

Geometry of the Problem

The corresponding boundary conditions are

$$ \begin{gathered} u = 0, k\frac{{\rm d}T}{{{\rm d}y}} = h_{1} \left( { - T_{2} + T} \right),\,\,\,\,\,\,\,{\text{at}}\,\,\, y = 0 \hfill \\ u = 0, k\frac{{\rm d}T}{{{\rm d}y}} = h_{1} \left( {T - T_{1} } \right),\,\,\,\,\,\,\,\,\,{\text{at}}\;\;\; y = h \hfill \\ \end{gathered} $$

(4)

Here, u velocity component along the x-direction,$k$ —thermal conductivity,$\sigma$ —electrical conductivity, $\rho$ —density,$\mu$ —dynamic viscosity, ${\Gamma }$ —material fluid parameter, $B_{0}$ —constant magnetic field strength, ${\mathbb{Q}}_{E}$—coefficient of exponential space heat source, ${\mathbb{Q}}_{T}$—coefficient of thermal dependent heat source, T—temperature, $m$ —positive constant, $h_{1}$ —heat transfer coefficient, $p$ —pressure, $n$ —power-law index, and the subscripts 2 and 1 refer to the upper and lower plates, respectively, index.

Introduce the following dimensionless variables [1]

$$ \eta = \frac{y}{h}, u = \frac{\mu }{\rho h}f\left( \eta \right),\,\theta = \frac{{T - T_{1} }}{{T_{2} - T_{1} }}, $$

(5)

where $\eta$ —dimensionless space variable, $f$ —dimensionless velocity, and $\theta$ —dimensionless temperature. Using Eq. (5) in Eqs. (1)–(3) yields

$$ \left( {1 + \left( {1 - n} \right)\left( {{\rm We}f^{\prime}} \right)^{n} } \right)f^{\prime\prime} + \left( {P - {\rm Re}f^{\prime} - Mf} \right)\left( {1 + \left( {{\rm We}f^{\prime}} \right)^{n} } \right)^{2} = 0 $$

(6)

$$ \theta^{\prime\prime} - {\rm RePr}\theta^{\prime} + {\rm PrEc}\left[ {\frac{{f^{{\prime}{2}} }}{{\left( {1 + \left( {{\rm We}f^{\prime}} \right)^{n} } \right)}} + Mf^{2} } \right] + Q_{t} \theta + Q_{E} {\rm exp}\left( { - m\eta } \right) = 0 $$

(7)

Subject to the boundary conditions

$$ \begin{gathered} f\left( 0 \right) = 0,\quad \theta^{\prime} - \delta_{1} \left( {\theta - 1} \right) = 0,\quad {\text{at}}\quad \eta = 0, \hfill \\ f\left( 0 \right) = 0,\quad \theta^{\prime} + \delta_{2} \theta = 0,\quad {\text{at}}\quad \eta = 1 \hfill \\ \end{gathered} $$

(8)

Here,

$P = \frac{{\rho h^{3} }}{\mu }\left( { - \frac{{\rm d}p}{{{\rm d}x}}} \right)$ pressure gradient parameter,

$We = \frac{{\sqrt 2 {\Gamma }\mu }}{{\rho h^{2} }}$ Weissenberg number,

$Q_{t} = \frac{{h^{2} {\mathbb{Q}}_{T} }}{{k(T_{2} - T_{1} )}}$ thermal-dependent heat source parameter (THS parameter),

$Q_{E} = \frac{{h^{2} {\mathbb{Q}}_{E} }}{k}$ exponential space-dependent heat source parameter (ESHS parameter).

$\Pr = \frac{\upsilon }{\alpha }$ is Pr and Tl number,

$Ec = \frac{{\mu^{2} }}{{h^{2} \rho^{2} c_{p} (T_{2} - T_{1} )}}$ is Eckert number,

$\delta_{i} = \frac{{ - hh_{i} }}{k}$ is Biot Number,

$M = \frac{{\sigma hB_{0}^{2} }}{\mu }$ Magnetic parameter.

${\text{Re}} = \frac{{\rho hv_{0} }}{\mu }$ Reynolds number,

2.2 Entropy production and Bejan number

The velocity $f(\eta )$ and temperature $\theta (\eta )$ profiles are used for the illustration of entropy production $Ns$ within the micro-channel. The representation of entropy production for cross fluid in the presence of Joule heating and viscous dissipation is described as:

$$ E_{g} = \frac{k}{{T_{1}^{2} }}\left( {\frac{{\rm d}T}{{{\rm d}y}}} \right)^{2} + \frac{\mu }{{T_{1} }}\left[ {\frac{{\left( {\frac{{\rm d}u}{{{\rm d}y}}} \right)^{2} }}{{\left( {1 + \left( {{\Gamma }\frac{{\rm d}u}{{{\rm d}y}}} \right)^{n} } \right)}} + \sigma B_{0}^{2} u^{2} } \right] $$

(9)

Using dimensionless variables (5) Eq. (9) can be explained as

$$ N_{s} = \frac{{E_{g} }}{{E_{0} }} = \theta ^{{\prime}{2}} + {\rm Ec}\Pr \left( {\frac{{f^{{\prime}{2}} }}{{\left( {1 + \left( {Wef^{^{\prime}} } \right)^{n} } \right)}} + Mf^{2} } \right) $$

(10)

Here, $E_{0} = \frac{{k(T_{2} - T_{1} )}}{{h^{2} T_{1}^{2} }}$ and $L = \frac{{T_{1} }}{{(T_{2} - T_{1} )}}$ is the temperature ratio.

Equation (10) can be written as

$$ N_{s} = N_{v} + N_{h} $$

Here, $N_{v} =$ the irreversibility owed to the effects of the magnetic field and viscous dissipation,

$$ N_{h} = {\text{irreversibility due to heat transfer}} $$

The Bejan number Be is denoted as the ratio of heat transfer irreversibility to the total entropy generation is given by

$$ Be = \frac{{N_{h} }}{{N_{h} + N_{v} }} $$

3 Solution methodology and validation

3.1 Spectral quasi-linearization method (SQLM)

The nonlinear ODE’s (9)–(11) along with (12) have been cracked numerically using the spectral quasilinearization method (SQLM). This technique is a simplification of the Newton–Raphson method it was proposed by Bellman and Kalaba [24]. The QLM (quasilinearization method) is employed to linearize the (9)-(11), the resultant equations are

$$ X_{1,r} f_{r + 1}^{{\prime\prime}} + X_{2,r} f_{r + 1}^{{\prime}} + X_{3,r} f_{r + 1} = R_{1} $$

(11)

$$ Y_{1,r} f_{r + 1} + Y_{2,r} f_{r + 1}^{{\prime}} + Y_{3,r} \theta_{r + 1}^{{\prime\prime}} + Y_{4,r} \theta_{r + 1}^{{\prime}} + Y_{5,r} \theta_{r + 1} = R_{2} $$

(12)

Boundary conditions are

$$ \begin{gathered} f_{r + 1} = 0,\,\theta_{r + 1}^{{\prime}} = \delta_{1} \left( {\theta_{r + 1} - 1} \right),\,{\text{at}}\,\,\eta = 0 \hfill \\ f_{r + 1} = 0,\,\theta_{r + 1}^{{\prime}} = - \delta_{2} \theta_{r + 1} \,{\text{at}}\,\, \eta = 1 \hfill \\ \end{gathered} $$

(13)

where

$$ \begin{aligned} X_{1,r} & = 1 + \left( {1 - n} \right)\left( {{\rm We}f_{r}^{{\prime}} } \right)^{n} ,\, X_{3,r} = - M\left( {1 + \left( {{\rm We}f_{r}^{{\prime}} } \right)^{n} } \right)^{2} , \\ X_{2,r} & = n\left( {1 - n} \right){\rm We}^{n} f_{r}^{{\prime\prime}} f_{r}^{{\prime}{\left( {n - 1} \right)}} + 2{\rm PnWe}^{n} f_{r}^{{\prime}{\left( {n - 1} \right)}} + 2{\rm PnWe}^{2n} f_{r}^{{\prime}{\left( {2n - 1} \right)}} \\ & \quad - {\rm Re} - 2{\rm MnWe}^{n} f_{r} f_{r}^{{\prime}( {n - 1})} - 2Re\left( {n + 1} \right){\rm We}^{n} f_{r}^{{\prime}n} - {\rm Re}\left( {2n + 1} \right){\rm We}^{2n} f_{r}^{{\prime}2n}\\ & \quad - 2n{\rm MWe}^{2n} f_{r} f_{r}^{{\prime}2n - 1} \\ Y_{1,r} & = 2{\rm PrEcMf}_{r} ,\, Y_{2,r} = {\rm PrEc}\left( {2f_{r}^{{\prime}} + \left( {n + 2} \right){\rm We}^{n} f_{r}^{{\prime}n + 1} + \left( {2n + 2} \right){\rm We}^{2n} f_{r}^{{\prime}2n + 1} } \right) \\ \end{aligned} $$

$Y_{3,r} = 1$, $Y_{4,r} = - {\rm RePr}$, $Y_{5,r} = Q_{t}$, and

$$ R_{1} = X_{1,r} f_{r + 1}^{{\prime\prime}} + X_{2,r} f_{r + 1}^{{\prime}} + X_{3,r} f_{r + 1}^{{}} - {\rm FF }$$

$$ R_{2} = Y_{1,r} f_{r + 1} + Y_{2,r} f_{r + 1}^{{\prime}} + Y_{3,r} \theta_{r + 1}^{{\prime\prime}} + Y_{4,r} \theta_{r + 1}^{{\prime}} + Y_{5,r} \theta_{r + 1} - {\rm TT} $$

Here,

$$ {\rm TT }= \theta_{r}^{{\prime\prime}} - {\rm RePr}\theta_{r}^{{\prime}} + {\rm PrEc}\left( {{\raise0.7ex\hbox{${f_{r}^{{\prime}2} }$} \!\mathord{\left/ {\vphantom {{f_{r}^{{\prime}2} } {\left( {1 + \left( {{\rm We}f_{r}^{{\prime}} } \right)^{n} } \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {1 + \left( {Wef_{r}^{{\prime}} } \right)^{n} } \right)}$}} + Mf_{r}^{2} } \right) + Q_{t} \theta_{r} + Q_{E} {\rm exp}\left( { - m\tau } \right) $$

The above system (13) and (14) establishes a linear system of coupled ODE’s with variable coefficients and which were solved by the Chebyshev spectral collocation method [25]. To apply this method, first transform the computational domain $\left[ {0,1} \right]$ into computational domain $\left[ { - 1,1} \right]$ by using the transformation $\eta = \frac{{\left( {\tau + 1} \right)}}{2},$ where $\tau \in \left[ { - 1,1} \right].$

The Gauss–Lobatto points defined as

$$ \tau_{i} = {\rm cos}\left( {\frac{\pi i}{N}} \right),\, - 1 \le \tau \ge 1,\,i = 0, 1, 2, \ldots ..N $$

(14)

where $N$ is number of grid points. The derivative of $f_{r + 1}$ at the grid points are signified as

$$ \frac{{\partial^{p} f_{r + 1} }}{{\partial \eta^{p} }} = \left( \frac{2}{L} \right)^{p} \mathop \sum \limits_{k = 0}^{N} D_{N,k}^{p} f_{r + 1} \left( {\tau_{k} } \right) = {\mathbf{D}}^{p} {\varvec{F}} $$

(15)

where ${\mathbf{D}} = \frac{2}{L}{\text{D}}$ and ${\text{D}}$ is the Chebyshev spectral differentiation matrix [26],

$$ {\mathbf{F}} = \left[ {f\left( {\tau_{0} } \right), f\left( {\tau_{1} } \right), \ldots ..f\left( {\tau_{N} } \right)} \right]. ^{{\varvec{T}}} $$

the derivative of $\theta$ defined as $\theta^{p} = {\mathbf{D}}^{p} {\Theta }$, where $p$ is derivative order, and ${\mathbf{D}}$ is the matrix of size $(N + 1) \times (N + 1).$ using (16)–(17) into Eqs. (13)–(15), we obtain

$$ \left[ {X_{1,r} {\mathbf{D}}^{3} + X_{2,r} {\mathbf{D}}^{2} + X_{3,r} {\mathbf{D}}} \right]{\mathbf{F}}_{r + 1} = R_{1} $$

(16)

$$ \left[ {Y_{1,r} {\mathbf{I}} + Y_{2,r} {\mathbf{D}}} \right]{\mathbf{F}}_{r + 1} + \left[ {Y_{3,r} {\mathbf{D}}^{2} + Y_{4,r} {\mathbf{D}} + Y_{5,r} {\mathbf{I}}} \right]{\Theta }_{r + 1} = R_{2} $$

(17)

Associated boundary conditions become

$$ \begin{gathered} f_{r + 1} \left( {\tau_{N} } \right)\, = 0,\,\mathop \sum \limits_{k = 0}^{N} D_{N,k} \theta_{r + 1} \left( {\tau_{k} } \right) = \delta_{1} \left( {\theta_{r + 1} \left( {\tau_{N} } \right) - 1} \right) \hfill \\ f_{r + 1} \left( {\tau_{0} } \right)\, = 0\mathop \sum \limits_{k = 0}^{N} D_{N,k} \theta_{r + 1} \left( {\tau_{k} } \right) = - \delta_{2} \theta_{r + 1} \left( {\tau_{0} } \right) \hfill \\ \end{gathered} $$

(18)

The above system (18) and (19) can be written as

$$ \left[ {\begin{array}{*{20}c} {{\Pi }_{11} } & {{\Pi }_{12} } \\ {{\Pi }_{21} } & {{\Pi }_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\text{F}}_{{{\text{r}} + 1}} } \\ {{{\varvec{\Theta}}}_{{{\text{r}} + 1}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{1} } \\ {R_{2} } \\ \end{array} } \right] $$

(19)

here

$$ \begin{gathered} {\Pi }_{11} = {\rm diag}\left[ {X_{1,r} \left] {{\mathbf{D}}^{2} + {\rm diag}\left[ {X_{2,r} } \right]{\varvec{D}} + {\rm diag}[X_{3,r} } \right]} \right]{\mathbf{I}} \hfill \\ {\Pi }_{12} = {\rm diag}\left[ {X_{4,r} } \right]{\varvec{I}} \hfill \\ {\Pi }_{21} = {\rm diag}\left[ {Y_{1,r} } \right]{\mathbf{I}} + {\rm diag}[Y_{2,r} ]{\varvec{D}}, \hfill \\ {\Pi }_{22} = {\rm diag}\left[ {Y_{3,r} } \right]{\mathbf{D}}^{2} + {\rm diag}\left[ {Y_{4,r} \left] {{\mathbf{D}} + {\rm diag}} \right[Y_{5,r} } \right]{\mathbf{I}} \hfill \\ \end{gathered} $$

where $X$, $Y$, and I, are diagonal matrices of size $\left( {N + 1} \right) \times \left( {N + 1} \right)$ and I is the unit matrix. The solutions for ${\mathbf{F}}$, ${{\varvec{\Theta}}}$ are attained by solving the matrix system (19).

3.2 Convergence analysis and validation

The governing differential Eqs. (6–7) along with (8) were solved using SQLM. To check the exactness of the numerical scheme, residual error norms were evaluated. Figures 1, 2 explore the residual error norms of the applied SQLM scheme against the number of iterations for various values of (M). It is clearly shown that the residual error of $f\left( \eta \right)$ after the seventh iteration is of the order $Res_{\infty } f \ll 10^{ - 10}$ and residual error of $\theta$ after sixth iteration is of the order ${\rm Re}s_{\infty } f \ll 10^{ - 9}$. A grid independence test was used to evaluate the precision of the results (Fig. 3). To produce the results for flow properties different step sizes and collocation points were used and fixed to $N = 70.$

Fig. 2

Variations $f\left( \eta \right)$ error via $M$

Fig. 3

Variations $\theta \left( \eta \right)$ error via $M$

Table1 presented a comparison of the SQLM against bvp4c results for $- f^{\prime}\left( 1 \right)$ and results are generated using a tolerance of $10^{ - 5}$ which are in excellent agreement.

Table 1 Comparison of SQLM and bvp4c for $- f^{\prime}\left( 1 \right)$ when $n = 1.5, P = {\rm Re} = 1, We = 0.5$

4 Results and discussion

In this article, we studied the steady laminar flow of the Cross-fluid in the presence of the applied magnetic field and the Joule heating through a convective heated microchannel subjected to two different heat sources. The spectral quasi-linearization (SQLM) method is used to estimate the numerical solutions of the nonlinear two-point boundary value problem. Figures 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 and 31 are drawn to examine the behavior of the velocity $f\left( \eta \right)$, the temperature $\theta \left( \eta \right)$, the local entropy minimization rate ${\rm Ns}$, and the Bejan number ${\rm Be}$ for diverse values of key parameters such as magnetic field parameter ($M$), power-law index ($n$), Weissenberg number (${\rm We}$), Reynolds number (${\rm Re}$), pressure gradient parameter ($P$), THS parameter ($Q_{t}$), ESHS parameter ($Q_{E}$), Biot number ($\delta$), and Eckert number ($Ec$).

Fig. 4

Variations of $f$ via $M$

Fig. 5

Variations of $\theta$ via $M$

The significance of magnetic field on the velocity $f\left( \eta \right)$, temperature $\theta \left( \eta \right)$, rate of local entropy minimization ${\rm Ns}$ and Bejan number ${\rm Be}$ across the dynamics of cross fluid in the microchannel was investigated from Figs. 4, 5, 6 and 7. It is observed that the higher values of $M$ make the velocity and temperature distribution a decreasing property. Physically, an increase in the strength of magnetism implies an increase in the intensity of the resistive force (Lorentz force), and this was highlighted in the study by Shehzad et al. [22]. This is a classic effect of the Lorentzian magnetic drag force. The imposition of the magnetic field, as simulated via the magnetic number (M), necessitates extra work expenditure by the fluid that has to be dragged in the microchannel, against the Lorentzian retarding forces. Figure 6 depicts that the entropy production is lower at both walls of the microchannel and increases in the middle of the channel ($0.3 < \eta < 0.8$). The supplementary work of the magnetic field is dissipated in the form of thermal energy that manifests with an increase in entropy production in the fluid. This trend is exactly the opposite of the influence of $M$ on the Bejan number (${\rm Be}$) compared to the influence of $M$ on the production of entropy ($Ns$).

Fig. 6

Variations of $N_{s}$ via $M$

Fig. 7

Variations of ${\rm Be}$ via $M$

The consequence of the power-law index ($n$) on the velocity $f\left( \eta \right)$, the temperature $\theta \left( \eta \right)$, the rate of local entropy minimization ${\rm Ns}$ and the Bejan number ${\rm Be}$ is shown in Figs. 8, 9, 10 and 11. Here, the velocity $f\left( \eta \right)$, temperature $\theta \left( \eta \right)$, rate of local entropy minimization ${\rm Ns}$ are decreasing functions of $n$. Furthermore, the impact of $n$ is more evident on velocity than on temperature and entropy production, while Bejan number increases significantly with $n$. The impact of the cross fluid parameter (Weissenberg number) on the velocity $f\left( \eta \right)$, temperature $\theta \left( \eta \right)$, rate of local entropy minimization ${\rm Ns}$ and Bejan number ${\rm Be}$ is shown in Figs. 12, 13, 14 and 15. It is seen from these figures that increasing the Weissenberg number boosts the velocity and temperature distribution but causes the Bejan number $Be$ to be a decreasing property. The dimensionless Weissenberg number relates the elastic forces to the viscous forces. The dimensionless Weissenberg number relates elastic forces to viscous forces. The higher numerical values of the Weissenberg number indicate the lower viscous force; therefore, the magnitude of the velocity increases significantly with the Weissenberg number.

Fig. 8

Variations of $f$ via $n$

Fig. 9

Variations of $\theta$ via $n$

Fig. 10

Variations of $N_{s}$ via $n$

Fig. 11

Variations of $Be$ via $n$

Fig. 12

Variations of $f$ via ${\rm We}$

Fig. 13

Variations of $\theta$ via ${\rm We}$

Fig. 14

Variations of $N_{s}$ via ${\rm We}$

Fig. 15

Variations of ${\rm Be}$ via ${\rm We}$

The variation in the velocity ${\text{f}}\left( {\upeta } \right)$, temperature ${\uptheta }\left( {\upeta } \right)$, entropy production ${\text{Ns}},$ and Bejan number ${\text{Be}}$ across the microchannel with ${\rm Re}$ is shown in Figs. 16, 17, 18 and 19. The dual behavior is found for the velocity, entropy production, and Bejan number concerning Reynolds number; however, the temperature field is affected significantly by Reynolds number. The magnitude of the velocity of cross fluid gets reduced in the lower region of the microchannel ($0 \le {\upeta } \le 0.6$), and then it starts to a{\rm d}vance in the rest part of the microchannel. Further, the magnitude of temperature is an increasing property of Reynolds number (${\text{Re}}$). Figures 20, 21, 22 and 23 examined the performance of pressure gradient factor on the velocity ${\text{f}}\left( {\upeta } \right)$, temperature ${\uptheta }\left( {\upeta } \right)$, entropy production ${\text{Ns}},$ and Bejan number ${\text{Be}}$. The dimensionless pressure gradient factor (${\text{P}}$) explains at what rate and in which direction pressure increases in the cross fluid system. By increasing the numeric values of pressure gradient factor (${\text{P}}$), the velocity of cross fluid gets enhanced significantly (see Fig. 20). From Figs. 21 and 22, it is noted that the magnitude of the thermal field and the entropy production escalate when the value of $P$ increases. This trend is quite opposite for the Bejan number as shown in Fig. 23.

Fig. 16

Variations of $f$ via ${\rm Re}$

Fig. 17

Variations of $\theta$ via ${\rm Re}$

Fig. 18

Variations of $N_{s}$ via ${\rm Re}$

Fig. 19

Variations of ${\rm Be}$ via ${\rm Re}$

Fig. 20

Variations of $f$ via $P$

Fig. 21

Variations of $\theta$ via $P$

Fig. 22

Variations of $N_{s}$ via $P$

Fig. 23

Variations of ${\rm Be}$ via $P$

Figures 24, 25, 26 and 27 are plotted to note the aspects of the THS factor ($Q_{t}$) and ESHS parameters ($Q_{E}$) on temperature field of the cross fluid. Here, both THS factor ($Q_{t}$) and ESHS parameter ($Q_{E}$) are augmenting functions of temperature field $\theta \left( \eta \right)$, but the variation of temperature field is more prominent by varying ESHS parameter as compared with THS factor. This is an expected outcome because the heat source mechanisms provide additional heat into the cross fluid system. Further, the entropy production gets enhanced with incrementing values of $Q_{t}$ and $Q_{E}$ except at the middle of the microchannel. The observed results in the study by Shehzad et al. [23] on Forchheimer slip flow of nanoliquids subject to exponential space and thermal‐dependent heat source corroborate with the observations in this study.

Fig. 24

Variations of $\theta$ via $Q_{t}$

Fig. 25

Variations of $Ns$ via $Q_{t}$

Fig. 26

Variations of $\theta$ via $Q_{E}$

Fig. 27

Variations of $N_{s}$ via $Q_{E}$

To portrait the outcomes of Biot number ($\delta$) on the temperature field ($\theta \left( \eta \right)$) and entropy production ($Ns$) Figs. 28 and 29 are elucidated. The temperature field ($\theta \left( \eta \right)$) declined for larger values of $\delta$ (see Fig. 28). Figure 29 illustrates that the entropy production (${\rm Ns}$) gets enhanced in the region $0.3 \le \eta \le 1$ of the microchannel whereas this trend is quite opposite in the rest part of the channel. Figures 30 and 31 are plotted to note the aspect of the Joule heating on the temperature field ($\theta \left( \eta \right)$) and entropy production (${\rm Ns}$). Enhancing the values of ${\rm Ec}$ increase the temperature field $\theta \left( \eta \right)$; the Joule heating is responsible for the enhancement in the thermal field $\theta \left( \eta \right)$. Figure 31 demonstrates that entropy production (${\rm Ns}$) gets enhanced significantly due to the aspect of Joule heating.

Fig. 28

Variations of $\theta$ via $\delta$

Fig. 29

Variations of $N_{s} { }$ via $\delta$

Fig. 30

Variations of $\theta$ via ${\rm Ec}$

Fig. 31

Variations of ${\rm Ns}$ via ${\rm Ec}$

5 Concluding remarks

In this article, we investigated the importance of the temperature-related heat source (THS) and space-related exponential heat source (ESHS) in the transport of cross liquids in a microchannel. An attempt was made to study the variation in entropy production, heat transfer, Bejan number, and velocity field. It is worth concluding.

• The cross liquid velocity profile is parabolic, and the temperature is maximum at the walls of the microchannel.

• The power-law index of the cross fluid reduces the amount of entropy production, velocity, and thermal field throughout the microchannel region, while the Bejan number turned out to be higher with the power-law index.

• A larger Weissenberg number is capable of producing greater entropy, velocity, and thermal field production throughout the microchannel region.

• A larger cross-fluid parameter causes a lower Bejan number in the microchannel.

• The temperature and velocity of the cross fluid are decreasing the property of the applied magnetism due to the Lorentz force associated with the magnetism.

• The amplitude of the thermal field is an increasing property of the Reynolds number.

• The temperature distribution increases significantly with higher THS and ESHS parameters. Furthermore, the change in temperature distribution is more evident in the presence of the ESHS aspect.

• The entity of the temperature distribution of the cross fluid increases as the pressure gradient parameter and the Eckert number increase.

• The entropy production of the cross fluid is improved when the resistance of Joule heating and convective heating is substantially large.