Introduction

Combined convection in enclosures saturated porous media is presented in several transport operations in engineering devices. Indeed, the combined convection is advised for altitude heat-dissipating electronic ingredients, where free convection is notable for providing effective cooling. Significance of the combined convection flow can be located in heat exchangers, solar energy storage, greasing technology, cooling the electronic systems and desiccation technologies [1,2,3,4]. Among these applications, convection in porous media with inner energy provenances is practical in the notion of thermal inflammation and in investigations considering the chemical reactions and these interested for detaching fluids [5, 6]. Also, the new suspension called nanofluid [7] can be applied to develop thermal conduct system in several engineering implementations like transport, micromechanics, instrument and cooling equipment.

A comparatively little issue of studies dealing with mixed convective of nanofluids saturated in porous medium was reported. Ahmed and Pop [8] investigated the combined convective of nanofluid over a vertical plate applying three various nanoparticles followed the common pattern of Tiwari and Das [9], which combines only the nanofluid volume fraction. Cimpean and Pop [10] considered the fully developed mixed convection flow of a nanofluid in a permeable channel. Gorla et al. [11] examined the mixed convective flow of a nanofluid adjacent to a vertical wedge embedded in porous media. Ghalambaz and Noghrehabadi [12] investigated the influences of heat generation/absorption on natural convective of nanofluids along a plate saturated porous media. Matin and Ghanbari [13] studied the Brownian motion and the thermophoresis effects on combined convection of nanofluid in a permeable channel. Recently, Srinivasacharya and Kumar [14] investigated combined convection through a wavy surface saturated with a nanofluid in porous media. MHD mixed convective flow of a nanofluid adjacent to a vertical cylinder embedded in porous media was investigated by Jafarian et al. [15]. Some more pertinent investigations on the presented study can be found in the references [16,17,18,19,20,21,22].

All of the above-mentioned investigations are based on the first-law analysis. Lately, the second-law-based works have acquired concern for analyzing thermal systems. Entropy generation is applied like a gauging to evaluate the rendering of thermal systems. The studying of the energy employment and the entropy generation is one of the fundamental aims in styling a thermal system. Bejan [23,24,25] pointed to the several causes back to entropy generation in applied thermal engineering. Generation of entropy devastates ready mission of a system. Hence, it produces good engineering significance of focus on irreversibility of heat transfer and fluid friction operation. There are just extremely little works that study the second-law analysis in the existence of a nanofluid as an active fluid in porous medium. Many investigators [26,27,28] presented theoretical and numerical contributions on entropy generation due to flow and heat transfer of nanofluids in several geometries and flow regimes. The nanofluids flow along a permeable moving surface was studied by Sheikholeslami et al. [29]. They exhibited that an augment in the volume fraction reduced the momentum boundary-layer thickness and the rate of entropy generation, while the thermal boundary-layer thickness promoted. Ting et al. [30] examined the entropy generation of nanofluids flow in thermic non-equilibrium saturated porous medium in microchannels. The analysis of MHD entropy generation on non-Newtonian nanofluid through a radiate shrinking surface was investigated by Bhatti et al. [31]. Das et al. [32] also investigated the unsteady MHD entropy generation on nanofluid past accelerating stretching sheet. Ismael et al. [33] studied the entropy generation due to free convection in an enclosure domain. They suggested a novel gauge for assessment of the thermal rendering. Armaghani et al. [34] investigated the heat transfer and entropy generation of nanofluid in a partially porous media in an inclined cavity. Entropy and heat transfer analysis in a conduit partially filled with porous media-LTNE condition and exothermicity effects was studied by Torabi et al. [35].

The above studies guide us to be certain that the entropy generation and MHD combined convection in a porous enclosure filled with a nanofluid with heat generation/absorption and partial slip effects have not been studied yet. Hence, this work is the focus of the current article. It is considered that this investigation will contribute in developing the thermal rendering in several engineering devices.

Problem description and mathematical modeling

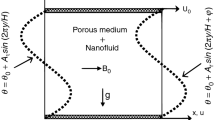
The problem of steady two-dimensional MHD mixed convection of a nanofluid inside a lid-driven square porous enclosure of length H is considered with internal heat generation Q and partial slip effects. The scheme of the current problem is displayed in Fig. 1a. A heat sink and an opposite heat source are located on a segment of the lower and upper walls, respectively, each with a length b. Two parts of the lower and upper walls of the enclosure are kept at T c and T h such that T h > T c while the other parts are kept adiabatic. The left and right walls are isolated and move with a constant velocity V 0. A magnetic field with strength \( B_{0} \) is applied on left side of the enclosure with angle Ф along the positive horizontal direction.

Fig. 1
figure 1

a Scheme of the problem under the consideration. b Control volume for the current investigation

Full size image

The nanofluid used in the analysis is supposed to be incompressible, laminar and exposed to internal heat generation at a uniform rate Q, and the base fluid (water) and the solid spherical nanoparticles (Cu) are in thermal equilibrium and also the solid matrix and nanofluid are in thermal equilibrium. The single-phase approach is used for modeling the nanofluid heat transfer. The thermophysical properties of the base fluid and the nanoparticles are found in Table 1. The Boussinesq approximation is performed for the nanofluid properties to relate density variation to temperature variation and to pair in this way the temperature profiles to the flow profiles. Thus, the governing equations for steady mixed convection can be presented as, see [36, 37]:

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0, $$
(1)
$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = - \frac{1}{{\rho_{\text{nf}} }}\frac{\partial p}{\partial x} + \upsilon_{\text{nf}} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - \frac{{\nu_{\text{nf}} }}{K}u + \frac{{\sigma_{\text{n}} B_{0}^{2} }}{{\rho_{\text{nf}} }}\left( {v{ \sin }\Phi { \cos }\Phi - u{ \sin }^{2} \Phi } \right), $$
(2)
$$ \begin{aligned} u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} &= - \frac{1}{{\rho_{\text{nf}} }}\frac{\partial p}{\partial y} + \upsilon_{\text{nf}} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - \frac{{\nu_{\text{nf}} }}{K}v + \frac{{\sigma_{\text{nf}} B_{0}^{2} }}{{\rho_{\text{nf}} }}(u\sin \varPhi \cos \varPhi - v\cos^{2} \varPhi ) \\ & \quad + \frac{{(\rho \beta )_{\text{nf}} }}{{\rho_{\text{nf}} }}g(T - T_{0} ), \\ \end{aligned} $$
(3)
$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{\text{nf}} \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \frac{{Q_{0} }}{{(\rho C_{\text{p}} )_{\text{nf}} }}(T - T_{0} ), $$
(4)

where \( u \) and \( v \) are the velocity components along the \( x \)- and \( y \)- axes, respectively, \( T \) is the fluid temperature, \( p \) is the fluid pressure, \( g \) is the gravity acceleration, Q 0 is the heat generation (Q 0 > 0) or absorption (Q 0 < 0) coefficient, \( \rho_{\text{nf}} \) is the density, \( \mu_{\text{nf}} \) is the dynamic viscosity, \( \nu_{\text{nf}} \) is the kinematic viscosity.

Table 1 Thermophysical properties of water and nanoparticle materials [42]
Full size table

The boundary conditions are:

$$ \begin{aligned} & {\text{On}}\;{\text{the}}\;{\text{lower}}\,{\text{wall}}{:}\begin{array}{*{20}l} {y = 0,} \hfill & {u = v = 0,} \hfill \\ {T = T_{\text{h}} ,} \hfill & {(d - 0.5b) \le x \le (d + 0.5b),} \hfill \\ {\frac{\partial T}{\partial y} = 0} \hfill & {\text{otherwise}} \hfill \\ \end{array} \\ & {\text{On}}\;{\text{the top wall:}}\begin{array}{*{20}l} {y = H,} \hfill & {u = v = 0,} \hfill \\ {T = T_{\text{c}} ,} \hfill & {(d - 0.5b) \le x \le (d + 0.5b),} \hfill \\ {\frac{\partial T}{\partial y} = 0} \hfill & {\text{otherwise}} \hfill \\ \end{array} \\ & {\text{On the right wall}}{:}\begin{array}{*{20}l} {x = H,\quad u = \frac{\partial T}{\partial x} = 0,} \hfill \\ {v = \lambda_{\text{r}} V_{0} + N\mu_{\text{nf}} \frac{\partial v}{\partial x}} \hfill \\ \end{array} \\ & {\text{On the left wall}}{:}\begin{array}{*{20}l} {x = 0,\quad u = \frac{\partial T}{\partial x} = 0,} \hfill \\ {v = \lambda_{\text{l}} V_{0} + N\mu_{\text{nf}} \frac{\partial v}{\partial x}.} \hfill \\ \end{array} \\ \end{aligned} $$
(5)

Thermophysical properties of nanofluid

The effective density and heat capacitance of the nanofluid are determined by [38]:

$$ \rho_{\text{nf}} = (1 - \phi )\rho_{\text{f}} + \phi \rho_{\text{p}} , $$
(6)
$$ (\rho c_{\text{p}} )_{\text{nf}} = (1 - \phi )(\rho c_{\text{p}} )_{\text{f}} + \phi (\rho c_{\text{p}} )_{\text{p}} . $$
(7)

The thermal expansion coefficient of the nanofluid can be given as Khanafer et al. [38]:

$$ (\rho \beta )_{\text{nf}} = (1 - \phi )(\rho \beta )_{\text{f}} + \phi (\rho \beta )_{\text{p}} . $$
(8)

Thermal diffusivity, \( \alpha_{\text{nf}} \), of the nanofluid was introduced by Abu-Nada and Chamkha [39] as:

$$ \alpha_{\text{nf}} = \frac{{k_{\text{nf}} }}{{(\rho c_{\text{p}} )_{\text{nf}} }}. $$
(9)

In Eq. (9), \( k_{\text{nf}} \) is the thermal conductivity of the nanofluid which for spherical nanoparticles, based on the Maxwell–Garnetts model [40], is:

$$ \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \frac{{(k_{\text{p}} + 2k_{\text{f}} ) - 2\phi (k_{\text{f}} - k_{\text{p}} )}}{{(k_{\text{p}} + 2k_{\text{f}} ) + \phi (k_{\text{f}} - k_{\text{p}} )}}. $$
(10)

The effective dynamic viscosity of the nanofluid based on the Brinkman model [41] is given by:

$$ \mu_{\text{nf}} = \frac{{\mu_{\text{f}} }}{{(1 - \phi )^{2.5} }}. $$
(11)

The effective electrical conductivity of the nanofluid was presented by Maxwell [40] as

$$ \frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }} = 1 + \frac{3(\gamma - 1)\phi }{(\gamma + 2) - (\gamma - 1)\phi }, $$
(12)

where \( \gamma = \frac{{\sigma_{\text{p}} }}{{\sigma_{\text{f}} }}. \)

Dimensionless forms of equations

The following non-dimensional parameters

$$ \begin{aligned} & X = \frac{x}{H},Y = \frac{y}{H},U = \frac{u}{{V_{0} }},V = \frac{v}{{V_{0} }},P = \frac{p}{{\rho_{\text{nf}} U^{2} }},\theta = \frac{{(T - T_{0} )}}{\Delta T},Ri = \frac{Gr}{{Re^{2} }},S_{\text{l}} = S_{\text{r}} = \frac{{N\mu_{\text{f}} }}{H}, \\ & \Delta T = (T_{\text{h}} - T_{\text{c}} ),T_{0} = \frac{{T_{\text{c}} + T_{\text{h}} }}{2},Q = \frac{{Q_{0} H^{2} }}{{(\rho c_{\text{p}} )_{\text{f}} \cdot \alpha_{\text{f}} }},B = \frac{b}{H},D = \frac{d}{H}, \\ \end{aligned} $$
(13)

are introduced into Eqs. (1)–(5) to yield the following dimensionless equations:

$$ \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0, $$
(14)
$$ \begin{aligned} & U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + \frac{1}{Re}\left( {\frac{{\upsilon_{\text{nf}} }}{{\upsilon_{\text{f}} }}} \right)\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }} - \frac{U}{Da}} \right) \\ & \quad + \left( {\frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}} \right)\left( {\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }}} \right)\frac{{Ha^{2} }}{Re}(V\sin \varPhi \cos \varPhi - U\sin^{2} \varPhi ), \\ \end{aligned} $$
(15)
$$ \begin{aligned} & U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial P}{\partial Y} + \frac{1}{Re}\left( {\frac{{\upsilon_{\text{nf}} }}{{\upsilon_{\text{f}} }}} \right)\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }} - \frac{V}{Da}} \right) + Ri\frac{{(\rho \beta )_{\text{nf}} }}{{\rho_{\text{nf}} \cdot \beta_{\text{f}} }}\theta \\ & \quad + \left( {\frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}} \right)\left( {\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }}} \right)\frac{{Ha^{2} }}{Re}(U\sin \varPhi \cos \varPhi - V\cos^{2} \varPhi ), \\ \end{aligned} $$
(16)
$$ U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} = \frac{1}{Pr\;Re}\frac{{\alpha_{\text{nf}} }}{{\alpha_{\text{f}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right) + \frac{1}{Re\;Pr}\frac{{(\rho c_{\text{p}} )_{\text{f}} }}{{(\rho c_{\text{p}} )_{\text{nf}} }}Q\theta , $$
(17)

where

$$ Pr = \frac{{\nu_{\text{f}} }}{{\alpha_{\text{f}} }},Re = \frac{{V_{0} H}}{{\upsilon_{\text{f}} }},Gr = \frac{{g\beta_{\text{f}} H^{3} \Delta T}}{{\upsilon^{2}_{\text{f}} }},Ha = B_{0} H\sqrt {\sigma_{\text{f}} /\mu_{\text{f}} } ,Da = K/H^{2} , $$

are the Prandtl number, Reynolds number, Grashof number, Hartmann number and Darcy number, respectively.

The dimensionless boundary conditions for Eqs. (14)–(17) are written as:

$$ \begin{aligned} & {\text{On the bottom wall:}}\begin{array}{*{20}l} {Y = 0,} \hfill & {U = V = 0,} \hfill \\ {\theta = 0.5,} \hfill & {(D - 0.5B)\, \le X \le (D + 0.5B),} \hfill \\ {\frac{\partial \theta }{\partial Y} = 0} \hfill & {\text{otherwise}} \hfill \\ \end{array} \\ & {\text{On the top wall}}{:}\begin{array}{*{20}l} {Y = 1,} \hfill & {U = V = 0,} \hfill \\ {\theta = - 0.5,} \hfill & {(D - 0.5B) \le X \le (D + 0.5B),} \hfill \\ {\frac{\partial \theta }{\partial Y} = 0} \hfill & {\text{otherwise}} \hfill \\ \end{array} \\ & {\text{On the right wall:}}\begin{array}{*{20}l} {X = 1\quad U = \frac{\partial \theta }{\partial X} = 0,} \hfill \\ {V = \lambda_{\text{r}} + \frac{{S_{r} }}{{(1 - \phi )^{2.5} }}\frac{\partial V}{\partial X}} \hfill \\ \end{array} \\ & {\text{On the left wall:}}\begin{array}{*{20}l} {X = 1,\quad U = \frac{\partial \theta }{\partial X} = 0,} \hfill \\ {V = \lambda_{\text{l}} + \frac{{S_{\text{l}} }}{{(1 - \phi )^{2.5} }}\frac{\partial V}{\partial X}.} \hfill \\ \end{array} \\ \end{aligned} $$
(18)

The local Nusselt number is defined as:

$$ Nu_{\text{s}} = - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\left( {\frac{\partial \theta }{\partial Y}} \right)_{{{\text{Y}} = 0,1}} , $$
(19)

and the average Nusselt number is defined as:

$$ Nu_{{{\text{m}}0}} = \left( {\frac{1}{B}\int\limits_{D - 0.5B}^{D + 0.5B} {Nu_{\text{s}} {\text{d}}X} } \right)_{{{\text{Y}} = 0}} ,\quad Nu_{{{\text{m}}1}} = \left( {\frac{1}{B}\int\limits_{D - 0.5B}^{D + 0.5B} {Nu_{\text{s}} {\text{d}}X} } \right)_{{{\text{Y}} = 1}} , $$
(20)
$$ Nu_{\text{m}} = \frac{{Nu_{{{\text{m}}0}} + Nu_{{{\text{m}}1}} }}{2}. $$
(21)

Governing equation for entropy generation

The entropy generation in the flow profiles is caused by the non-equilibrium flow imposed by boundary conditions. According to [42, 44], the dimensional local entropy generation can be expressed by:

$$ \begin{aligned} s &= \left( {\frac{{k_{\text{nf}} }}{{T_{0}^{2} }}} \right)\left[ {\left( {\frac{\partial T}{\partial x}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] + \left( {\frac{{\mu_{\text{nf}} }}{{T_{0} }}} \right)\left\{ {\frac{1}{K}(u^{2} + v^{2} ) + 2\left[ {\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial v}{\partial y}} \right)^{2} } \right] + \left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} } \right\} \\ & \quad + \left( {\frac{{\sigma_{\text{nf}} }}{{T_{0} }}} \right)B_{0}^{2} (u\sin \varPhi - v\cos \varPhi )^{2} . \\ \end{aligned} $$
(22)

Employing the dimensionless parameters given in Eq. (14), the formulation of the dimensionless entropy generation (S) can be written as:

$$ \begin{aligned} S & = s \cdot \frac{{H^{2} \cdot T_{0}^{2} }}{{k_{\text{f}} (\Delta T)^{2} }} = \left( {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }}} \right)\left[ {\left( {\frac{\partial \theta }{\partial X}} \right)^{2} + \left( {\frac{\partial \theta }{\partial Y}} \right)^{2} } \right] \\ & \quad + \varTheta \cdot \left( {\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }}} \right) \cdot Re^{2} \cdot Pr^{2} \left\{ {\frac{1}{Da}(U^{2} + V^{2} ) + 2\left[ {\left( {\frac{\partial U}{\partial X}} \right)^{2} + \left( {\frac{\partial V}{\partial Y}} \right)^{2} } \right] + \left( {\frac{\partial V}{\partial X} + \frac{\partial U}{\partial Y}} \right)^{2} } \right\} \\ & \quad + \varTheta \cdot \left( {\frac{{\sigma_{nf} }}{{\sigma_{f} }}} \right) \cdot Ha^{2} \cdot Re^{2} \cdot Pr^{2} \cdot (U\sin \varPhi - V\cos \varPhi )^{2} \\ & \quad = Sh + Sv + Sj. \\ \end{aligned} $$
(23)

here Sh, Sv and Sj are, respectively, the dimensionless local entropy generation rate due to heat transfer, fluid fraction and Joule heating. In Eq. (23), Θ is the irreversibility factor, which defines the proportion of the viscous entropy generation to the thermal entropy generation. It is expressed as:

$$ \varTheta = \frac{{\mu_{\text{f}} \cdot T_{0} }}{{k_{\text{f}} }}\left( {\frac{{\alpha_{\text{f}} }}{\Delta TH}} \right)^{2} . $$
(24)

The Bejan number, Be, defined as the proportion between the entropy generation due to heat transfer by the total entropy generation, is given as:

$$ Be = \frac{Sh}{S}. $$
(25)

With a view to current the influence of nanoparticles, the magnetic field and the difference of temperature on the average Nusselt number, total entropy generation and Bejan number, the Nusselt number ratio, total entropy generation ratio and Bejan number ratio are given as follows:

$$ Nu^{ + } = \frac{{Nu_{\text{m}} }}{{(Nu_{\text{m}} )_{\phi = 0} }}\;{\text{and}}\;Nu^{ + + } = \frac{{Nu_{\text{m}} }}{{(Nu_{\text{m}} )_{{{\text{Ha}} = 0}} }}, $$
(26)
$$ S^{ + } = \frac{S}{{(S)_{\phi = 0} }}\;{\text{and}}\;S^{ + + } = \frac{S}{{(S)_{{{\text{Ha}} = 0}} }}. $$
(27)

The thermal performance criterion can be presented as [31]:

$$ \varepsilon = \frac{S}{Nu} . $$
(28)

In this paper, we introduce the ratio of the thermal performance as:

$$ \varepsilon^{ + } = \frac{{S^{ + } }}{{Nu^{ + } }}.$$
(29)

Numerical solution and validation

Because of the nonlinear interactions among Eqs. (14)–(17) in the current investigation, the solution for these equations with the boundary conditions (18) and 20) can be calculated computationally by using the collocated finite volume method. In order to demonstrate this solution, let us take Eq. (15) as an example. This equation can be written as:

$$ \begin{aligned} & \frac{{\partial U^{2} }}{\partial X} + \frac{\partial UV}{\partial Y} = - \frac{\partial P}{\partial X} + \frac{1}{Re}\left( {\frac{{\upsilon_{\text{nf}} }}{{\upsilon_{\text{f}} }}} \right)\left( {\frac{\partial }{\partial X}\left( {\frac{\partial U}{\partial X}} \right) + \frac{\partial }{\partial Y}\left( {\frac{\partial U}{\partial Y}} \right) - \frac{U}{Da}} \right) \\ & \quad + \left( {\frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}} \right)\left( {\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }}} \right)\frac{{Ha^{2} }}{Re}(V\sin \varPhi \cos \varPhi - U\sin^{2} \varPhi ). \\ \end{aligned} $$
(30)

Integrating this equation over the control volume presented in Fig. 1b

$$ \begin{aligned} \iint_{\varOmega } {\left[ {\frac{{\partial U^{2} }}{\partial X} + \frac{\partial UV}{\partial Y}} \right]}{\text{d}}X{\text{d}}Y & = - \iint_{\varOmega } {\frac{\partial P}{\partial X}}{\text{d}}X{\text{d}}Y \\ & \quad + \frac{1}{Re}\left( {\frac{{\upsilon_{\text{nf}} }}{{\upsilon_{\text{f}} }}} \right)\iint_{\varOmega } {\left[ {\left( {\frac{\partial }{\partial X}\left( {\frac{\partial U}{\partial X}} \right) + \frac{\partial }{\partial Y}\left( {\frac{\partial U}{\partial Y}} \right) - \frac{U}{Da}} \right)} \right]}{\text{d}}X{\text{d}}Y \\ & \quad + \left( {\frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}} \right)\left( {\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }}} \right)\frac{{Ha^{2} }}{Re}\iint_{\varOmega } {\left[ {V\sin \varPhi \cos \varPhi - U\sin^{2} \varPhi } \right]}{\text{d}}X{\text{d}}Y. \\ \end{aligned} $$
(31)

The upwind differencing scheme and the central difference scheme are taken for the convective terms and the diffusion terms, respectively. Evaluating these integrals and re-arranging, the following algebraic equation is obtained:

$$ a_{\text{P}}^{U} U_{\text{P}} = \sum\limits_{i} {a_{\text{i}}^{U} U_{\text{i}} } + S^{U} , $$
(32)

where i = E, W, N, S. Similar treatments are utilized for Eqs. (16) and (17). The resulting algebraic equations have been solved iteratively, through the alternate direction implicit procedure (ADI), by utilizing the SIMPLE algorithm [45]. The velocity correction has been done utilizing the Rhie and Chow interpolation. For convergence, the under-relaxation technique has been employed. The iteration is performed until the normalized residuals of the mass, momentum, temperature and entropy generation equations become less than 10−6. The non-uniform grid contains of 101 × 101 grid nodes in the X and Y directions, respectively. The obtained data are separated of the number of the grids. The grid independency data are found at \( Ha = 10,Da = 10^{ - 3} ,Gr = Re = 10^{4} , D = 0.5, B = 0.5, Q = 1.0, \varPhi = 45, \phi = 0.05,S_{\text{l}} = S_{\text{r}} = 1.0,\lambda_{\text{l}} = - \lambda_{\text{r}} = 1.0 \) and displayed in Table 2. The CPU time is also appeared in Table 3 for different Richardson numbers.

Table 2 Grid-independency study for Cu–water nanofluid
Full size table
Table 3 CPU time for obtaining the results at different Richardson numbers and fixed values of the other parameters
Full size table

Figure 2 displays a comparison between the temperature contour reported in this investigation with those of Khanafar and Chamkha [36] and Iwatsu et al. [37]. The data show an excellent endorsement between this investigation and the previously published investigations.

Fig. 2
figure 2

Comparison of the present study with Re = 1000, pr = 0.71, \( \phi = K = 0 \)

Full size image

Results and discussion

Eclectic data results performed by streamlines, isotherms, local and global entropy generation, local and global Bejan number, and local and average Nusselt number are illustrated in this section. The thermal rendering criterion is also presented. The effects on each of the mentioned parameters are studied for various nanofluid volume fractions (ϕ = 0–0.2), heat generation/absorption parameters (Q = −2–2) and Hartmann numbers (Ha = 0–100). The outcomes are gained for the following fixed parametric values: Da = 10−3, Θ = 10−2, Ф = 45°, \( B = 0.5,D = 0.5,S_{\text{l}} = S_{\text{r}} = 1 \).

Influence of Hartmann number (Ha)

Figure 3 indicates the effect of the Hartmann number on the streamlines, isotherms, local entropy generation and the Bejan number for \( Ri = 1,\phi = 0.05,\lambda_{\text{l}} = - \lambda_{\text{r}} = 1,Q = 1 \). Generally, the effects of the buoyancy together with the enjoined boundary condition make the fluid rotates clockwise with a single-cell circulation near the left wall and counterclockwise in the middle and within the right wall. The streamlines and the core shape of the cell are more symmetric when Ha = 0. For Ha = 100, the counterclockwise rotation is stronger and more expanded than the clockwise rotation. The cells are moved to the upper of the enclosure because of the buoyancy influence and the inclined magnetic field. By enhancing the Hartmann number, the streamlines tend to be diagonal for Ha = 100. The isothermal lines show a similar trend for both Ha = 0 and Ha = 100. The temperature gradient near the sink and the source is greater than at other places of the cavity, and therefore, the beginning and end of the heat source and heat sink experience more heat transfer and therefore a greater Nusselt number. The entropy generation is also significant near the left and the right walls because of the temperature gradient and the boundary layers and vanishes in the middle of the enclosure. The local Bejan number shows a more concentration at the lower and upper surfaces for Ha = 0 and Ha = 100, respectively.

Fig. 3
figure 3

Streamlines, isotherms, total entropy generation and local Bejan number, \( Ri = 1,\phi = 0.05,B = 0.5,D = 0.5,\lambda_{\text{l}} = 1,\lambda_{\text{r}} = - 1,Sr = S_{\text{l}} = 1,Q = 1 \) . a Ha = 0, b Ha = 100

Full size image

As observed in Fig. 4, the local Nusselt number is decreased through raising the Hartmann number. When the Hartmann number is decreased, an augmentation in the temperature gradient leads to enhance the Nusselt number. This reason is also being acceptable for variation in the Nusselt number with the Hartmann number within the heat source at the lower wall.

Fig. 4
figure 4

Profiles for local Nusselt number for CuO–water nanofluid at \( Ri = 1,\phi = 0.05,D = 0.5,B = 0.5,Sr = S_{\text{l}} = 1,Q = 1,\lambda_{\text{l}} = - \lambda_{\text{r}} = 1. \)

Full size image

Figure 5 shows the same purpose and parameters of Fig. 3 but for λ l = λ r = 1. Contrariwise with λ l = − λ r = 1, the fluid rotates clockwise shaping a single-cell circulation. The core form of this cell is transformed from mostly vertically extended to mostly horizontally extended with two cells when Ha increases from 0 to 100. The isotherms in the center of the enclosure tend to be horizontal via increasing the Hartman number from 0 to 100. The local entropy generation is also significant within the left and right walls because the velocity and temperature gradient are sensible. The local Bejan number is significant in the center of the enclosure for Ha = 0, and because of the heat transfer irreversibility near the heat sink/source, the Bejan number is sizable at the upper and lower walls.

Fig. 5
figure 5

Streamlines, isotherms, total entropy generation and local Bejan number \( Ri = 1,\phi = 0.05,B = 0.5,D = 0.5,\lambda_{\text{l}} = 1,\lambda_{\text{r}} = 1,Sr = S_{\text{l}} = 1,Q = 1 \). a Ha = 0, b Ha = 100

Full size image

Figure 6 illustrates Nu s for \( \lambda_{\text{l}} = \lambda_{\text{r}} = 1 \) at Y = 0, 1. As Fig. 5 indicates, for Ha = 100, the isothermal lines are more crowded than those corresponding to Ha = 0 at the beginning of the heat source, and thus, the temperature gradient has a higher value, and hence, the maximum Nusselt number happens at the beginning of the heat source for Ha = 100, but at the end of heat source, the temperature gradient at Ha = 0 is more than that for Ha = 100, and therefore, the Nusselt number is greater in value at Ha = 0 at the end of heat sink. A comparable conduct is found for the Nusselt number at Y = 1 in Fig. 6, but for Ha = 0 and Ha = 100, the maximum Nusselt number happens at the end and the beginning of the heat sink, respectively. Generally, at Ha = 100, the symmetric profiles of the isothermal lines near the heat sink and source lead to an equal value for the Nusselt number at the end and the beginning of the heat source and sink.

Fig. 6
figure 6

Profiles of the local Nusselt number for Cu–water at \( Ri = 1,\phi = 0.05,D = 0.5,B = 0.5,Sr = S_{\text{l}} = 1,Q = 1,\lambda_{\text{l}} = \lambda_{\text{r}} = 1. \)

Full size image

Influence of Richardson number (Ri)

The ratio of natural to forced convection modes is measured by the Richardson number. Its influence is examined by keeping the other dependent parameters at \( Ha = 10, = 0.05,Q = 1 \).

Figure 7 shows the influences of the Richardson number on the streamlines, isotherms, local entropy generation and the Bejan number at \( \lambda_{\text{l}} = - \lambda_{\text{r}} = 1 \). For Ri = 0.001, the predominance of forced convection can be described by the predominant shear action where two counter-rotated vortices everyone is guided by a moving wall. Moving up the core and a third vortex within the lower wall due to enhanced buoyancy effect can be observed in the streamlines for Ri = 10. The corresponding isotherms trend to be nearly plumed from the heat source toward the heat sink with isothermal zones localized close the moving walls and dense isotherms near the heat sink for Ri = 0.001. For Ri = 10, the isotherms tend to be horizontal in the middle of the enclosure and with approximately equal isotherms distribution on both portions of the heat sink/heat source. The formation and growth of the boundary layer and the fluid friction irreversibility lead to more generation of entropy at the top wall for Ri = 10 than for Ri = 0. The Bejan number is significant within the upper and lower walls for both of the Richardson numbers, and for Ri = 10 it is sensible in the middle of the cavity because of the heat transfer irreversibility.

Fig. 7
figure 7

Streamlines, isotherms, total entropy generation and local Bejan number \( Ha = 25,\phi = 0.05,B = 0.5,D = 0.5,\lambda_{\text{l}} = 1,\lambda_{\text{r}} = - 1,Sr = S_{\text{l}} = 1,Q = 1 \). a Ri = 0.001, b Ri = 10

Full size image

Figure 8 indicates the influences of the Richardson number on the streamlines, isotherms, local entropy generation and the Bejan number at \( \lambda_{\text{l}} = \lambda_{\text{r}} = 1 \). When the Richardson number is raised from 0.001 to 10 and due to the dominance of natural convection, the streamlines are strengthened and dominated by a single main clockwise circulation, while the particularly vertical isotherms disclose the ascendancy of the convection mode. By enhancing the boundary-layer thickness for Ri = 10 and the fluid irreversibility as well as the heat transfer irreversibility near the walls, the entropy generation is more sensible than that for Ri = 0.001.

Fig. 8
figure 8

Streamlines, isotherms, total entropy generation and local Bejan number \( Ha = 25,\phi = 0.05,B = 0.5,D = 0.5,\lambda_{\text{l}} = 1,\lambda_{\text{r}} = 1,Sr = S_{\text{l}} = 1,Q = 1 \). a Ri = 0.001, b Ri = 10

Full size image

Figure 9 displays the local Nusselt number at Y = 0, 1 for \( \lambda_{\text{l}} = - \lambda_{\text{r}} = 1\& \lambda_{\text{l}} = \lambda_{\text{r}} = 1 \). As displayed in the isotherms figures, for little Richardson number, the temperature gradient is very high within the heat sink/source, and therefore, the maximum Nusselt number happens for Ri = 0.001. In other words, the predominance of forced convection over natural convection for low Richardson number produces an increment in heat transfer. At the beginning and the limit of the heat sink/source, the isothermal lines are very crowded, and therefore, these areas experience maximum Nusselt numbers for Ri = 0.001 and \( \lambda_{\text{l}} = - \lambda_{\text{r}} = 1 \). As displayed in Fig. 8a, the temperature gradient at the limit of the heat sink and the beginning of the heat source is very significant, and thus, the maximum Nusselt number happens at the limit of the heat source and beginning of the heat sink for Ri = 0.001 and \( \lambda_{l} = \lambda_{r} = 1 \).

Fig. 9
figure 9

Profiles of the local Nusselt number for Cu–water at \( Ha = 25,\phi = 0.05,B = 0.5,D = 0.5,Sr = S_{\text{l}} = 1,Q = 1 \)

Full size image

Figure 10 displays the variation of \( Nu^{ + } \) with the Richardson number. Generally, by raising the nanofluid volume fraction, the average Nusselt number is decreased for all range of values of the Richardson number. Supplementing highly conductive solid nanoparticles will cause a nanofluid with an elevation in the viscosity, density and thermal conductivity. The first two properties enhance the viscous and inertia forces, respectively, while the increased thermal conductivity enhances the heat transfer. Thus, the tendency of the Nusselt number ratio is exhibited in Fig. 10. This figure elucidates that the increased viscous and inertia forces govern over the increased thermal conductivity and both the buoyancy and the shear influences as well. This is a sensible cause for the reduction in the Nusselt number with the addition of nanoparticles. For \( \varphi \le 0.05 \), the rate of reduction of \( Nu^{ + } \) for high Richardson numbers is more than that of low Ri values. But for \( \varphi \ge 0.05 \), enhancing the volume fraction shows a more reduction for \( Nu^{ + } \) at little Richardson numbers. The impact of enhancing the volume fraction is observed by the reduction of the entropy generation ratio (\( S^{ + } \)) at Ri = 1–1000 as presented in Fig. 11. This figure indicates that \( S^{ + } \) is enhanced by raising the volume fraction at Ri = 0.001 and 0.01.

Fig. 10
figure 10

Variation of the average Nusselt number ratio with Richardson number

Full size image
Fig. 11
figure 11

Variation of the total entropy generation ratio via Richardson number

Full size image

Figure 12 presents that the supplement of nanoparticles causes increment in \( \varepsilon^{ + } \) at low Richardson numbers (Ri = 0.001–1). As presented in Fig. 11a, b, \( \varepsilon^{ + } \) is reduced by enhancing the nanofluid volume fraction for Ri = 100 and 1000, and therefore, the nanoparticles addition may be useful for high Richardson numbers.

Fig. 12
figure 12

Variation of \( \varepsilon^{ + } = \frac{{S^{ + } }}{{Nu_{\text{m}}^{ + } }} \) with Richardson number. a \( \lambda_{\text{l}} = 1,\lambda_{\text{r}} = 1 \), b \( \lambda_{\text{l}} = - \lambda_{\text{r}} = 1 \)

Full size image

Influence of heat generation (Q)

Figures 13–16 display the influence of the heat generation parameter on the mentioned items for the constant parametric values of: \( Ri = 1,Ha = 10,\lambda_{\text{l}} = - \lambda_{\text{r}} = 1 \;{\text{and}}\;\lambda _{\text{l}} = \lambda_{\text{r}} = 1 \). Figures 13 and 14 display the influences of the heat generation parameter on the streamlines, isotherms, entropy generation and Bejan number at \( \lambda_{\text{l}} = - \lambda_{\text{r}} = 1 \) and \( \lambda_{\text{l}} = \lambda_{\text{r}} = 1 \), respectively. The stream lines keep their general pattern with rising values of Q, but their strength and intensity are rarely decreased for both of the vertical partial slips. The isotherms in Fig. 13 exhibit that the temperature gradient is reduced within the heat source when the heat generation parameter is increased. Also, as exhibited in Fig. 14, when Q is increased, the isotherms have a tendency to be vertical in the middle of the enclosure. As displayed in Fig. 13, by raising the heat generation parameter, the local entropy generation has no significant change and the local Bejan number is vanished near the heat sink. Figure 14 also shows that the Bejan number is increased when the heat generation is enhanced.

Fig. 13
figure 13

Streamlines, isotherms, total entropy generation, local Bejan number at \( \lambda_{\text{l}} = - \lambda_{\text{r}} = 1 \). a \( Q = - 2 \), b \( Q = 2 \)

Full size image
Fig. 14
figure 14

Streamlines, isotherms, total entropy generation, local Bejan number at \( \lambda_{\text{l}} = 1,\lambda_{\text{r}} = 1 \). a \( Q = - 2 \), b \( Q = 2 \)

Full size image

Figure 15 shows the variation of \( S^{ + } \) with rising values of the volume fraction for both of \( \lambda_{\text{l}} = - \lambda_{\text{r}} = 1 \) and \( \lambda_{\text{l}} = \lambda_{\text{r}} = 1 \). It is noticed that S+ decreases as a result of increasing \( \varphi \) for low nanofluid volume fractions (\( \phi = 0 \cong 0.05\;{\text{for}}\,\lambda_{\text{l}} = - \lambda_{\text{r}} = 1\,\& \,\varphi = 0 \cong 0.07\;{\text{for}}\,\lambda_{\text{l}} = \lambda_{\text{r}} = 1 \)) and then increases with increasing \( \varphi \)(\( \phi = 0 \ge 0.05\;{\text{for}}\;\lambda_{\text{l}} = - \lambda_{\text{r}} = 1\,\& \,\varphi = 0 \ge 0.07\;{\text{for}}\;\lambda_{\text{l}} = \lambda_{\text{r}} = 1 \)) for all covered ranges of Q. It should be seen that S + for all ranges of values of Q and \( \phi \) is less than unity, and therefore, adding nanoparticles to the pure fluid produces the reduction of the entropy generation. Figure 16 shows the change in \( \varepsilon^{ + } \) with the increment in the volume fraction. As displayed in Fig. 16, when the volume fraction is enhanced, the thermal rendering criterion is enhanced as well. The figure depicts that a little volume fraction nanofluid can be useful for this subject.

Fig. 15
figure 15

Variation of the total entropy generation via heat generation

Full size image
Fig. 16
figure 16

Variation of \( \varepsilon^{ + } \) with heat generation

Full size image

Conclusions

The influences of nanofluid volume fraction, Hartmann number, Richardson number and heat generation/absorption on the entropy generation of mixed convection in a lid-driven square porous enclosure saturated by a Cu–water nanofluid with partial slip are numerically studied. The outcomes have produced the following concluding remarks:

  1. 1.

    A raise in the volume fraction of the nanoparticles decreases the entropy generation inside the porous cavity for all values of the heat generation parameter Q.

  2. 2.

    A raise in the nanofluid volume fraction reduces the average Nusselt number for all values of the Richardson number Ri.

  3. 3.

    A nanofluid with small volume fraction shows a suitable effect on the thermal rendering.

  4. 4.

    The local Nusselt number is enhanced via raising the Hartman number.

  5. 5.

    The best thermal performance is seen at Ri = 0.001 for both \( \lambda_{\text{l}} = - \lambda_{\text{r}} = 1 \) and \( \lambda_{\text{l}} = \lambda_{\text{r}} = 1. \)

  6. 6.

    The Nusselt number at all ranges of the Richardson number for \( \lambda_{\text{l}} = \lambda_{\text{r}} = 1 \) is greater than that corresponding to \( \lambda_{\text{l}} = - \lambda_{\text{r}} = 1. \)