Introduction

It is well-known fact that the distinct liquids used in our daily routine and industry differ from the rheology of Newtonian materials. Such distinct liquids are termed as “Newtonian fluids.” Examples of such materials are juices, shampoos, blood, toothpaste, ketchup, sugar solutions, polymer solutions, drilling muds, lubricants oils, slurries, soaps and many others. There is not a single mathematical formula which addresses the complete nature of these materials. The non-Newtonian fluids have abundant implications in science and engineering fields such as blade and wire coating, dying of textiles and papers, plastic manufacturing, motion of biological liquids and food processing. The nature of such fluids has attained the focal involvement of the researchers to discuss the dynamics and rheology. The researchers had established distinct mathematical relationships for different rheological behavior fluids. Among multiple non-Newtonian models, we involved the Carreau fluid for recent research demonstration. This model is very complex and nonlinear and very popular among the present researchers [1,2,3,4,5,6,7,8,9,10].

The main objective in the designing of thermal devices is the efficient energy implication. This can be made through the entropy generation minimization (EGM) in the processes of thermal devices. The development of heat removal machines and energy optimization require the minimization of entropy destruction and production because of work by viscous friction, heat transport and conduction of electric field. The available energy efficacy can be more desirable via the optimization of entropy production. Chamkha et al. [11] studied the thermal analysis and MHD copper (Cu)–water (H2O) nanoliquid flow in a porous enclosure. Mehryan et al. [12] executed the analysis of EG in ferromagnetic fluid through square enclosure under horizontal Lorentz force. Shamsabadi et al. [13] inspect the thermal and viscous irreversibilities of nanofluid inside a duct geared up with porous baffles. Seyyedi et al. [14] reported the radiative EG of Cu–water nanoparticles flow in semi-annulus cavity. Abbasi et al. [15] developed the EG model of peristaltic flows through long-wavelength theory. They also reported the temperature-dependent characteristics of viscosity and Hall phenomenon. Shafee et al. [16] addressed the EG analysis for magnetized ferrofluid induced by semi-porous annulus. They reported that the system disorder is enhanced due to Darcy constraint. The EG under viscous heating flow of peristaltic fluid in channel has been numerically described by Abbasi et al. [17]. Sheikholeslami [18] described the EG and exergy analysis in nanofluid through Lorentz force in porous space. Bahrami et al. [19] discussed the spectral analysis of EG in non-gray planer medium. Hayat et al. [20] demonstrated the statistical analysis of EG in nanomaterial flow induced by the rotation of two disks. They also computed the statistical and probable error in this study. Recently, the same theory has been interestingly used by many researchers with different perspectives [21,22,23,24,25,26].

In present, many practical and theoretical studies are conducted on the microfluidic systems. The applications microfluidic is in micro pumps, micro device, micro mixer, polymers, biomedical micro cell and MCHS. Venkateswarlu et al. [27] studied the effect of slip velocity boundary condition with the temperature jump under influence of magnetic field. The impact of heat generation and thermal radiation by considering slip velocity boundary condition and temperature jump on the channel walls was investigated by Venkateswarlu [28]. Monaledi and Makinde [29] numerically studied Cu–water nanofluid flow inside a microchannel in the presence of nanoparticles shape effect. Madhu et al. [30] numerically studied steady, laminar and nanofluid flow inside a horizontal microchannel by implementing finite element method. The fluid flow in microchannel has been investigated in recent studies [31, 32].

This research focusses on the thermal and entropy minimization features in laminar non-Newtonian magneto-Carreau fluid. The fluid flows through convectively heated microchannel. The combined consideration of entropy and magnetic field on Carreau fluid in microchannel has not been addressed in the literature. Further, the involvement of convective heating process strengthened this research. The simplified expressions are converted to dimensionless model with the help of appropriate variables. These expressions are executed with the implication of finite element scheme. The outcomes of these expressions are labeled for distinct values of arising constraints to address the behavior of Bejan number, temperature and velocity local rate of entropy generation.

Mathematical development and solution

Flow and heat transport

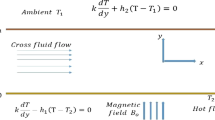
A fully developed dissipative, incompressible, electrically conducting non-Newtonian Carreau fluid flow between two fixed permeable infinite plates of microchannel of width h is considered. The below plate is at transversal coordinate \(y = 0\) and upper plate is at \(y = h\) (see Fig. 1).

Fig. 1
figure 1

Geometry of the flow

Full size image

An unvarying magnetic potency with strength \(B_{0}\) is imposed transversely to the plates. Suction takes place at upper plate, while the liquid is injected at lower plate. The right plate of microchannel has connection with ambient temperature \(T_{1}\), while the below plate interchanges heat through convection with hotter fluid of temperature \(T_{2}\). Based on the above suppositions, the governing balances for non-Newtonian Carreau fluid are given as follows:

$$\frac{{{\text{d}}v}}{{{\text{d}}y}} = 0,$$
(1)
$$\rho v_{0} \frac{{{\text{d}}u}}{{{\text{d}}y}} = - \frac{{{\text{d}}p}}{{{\text{d}}x}} + \mu \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }}\left( {1 + \varGamma^{2} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right)^{{\left( {\frac{\rm{n} - 1}{2}} \right)}} + \mu (n - 1)\varGamma^{2} \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }}\left( {1 + \varGamma^{2} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right)^{{\left( {\frac{\rm{n} - 3}{2}} \right)}} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} - \sigma B_{0}^{2} u,$$
(2)
$$\rho C_{\text{p}} v_{0} \frac{{{\text{d}}T}}{{{\text{d}}y}} = k\frac{{{\text{d}}^{2} T}}{{{\text{d}}y^{2} }} + \mu \left( {1 + \varGamma^{2} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right)^{{\left( {\frac{\rm{n} - 1}{2}} \right)}} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} + \mu (n - 1)\varGamma^{2} \left( {1 + \varGamma^{2} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right)^{{\left( {\frac{\rm{n} - 3}{2}} \right)}} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{4} + \sigma B_{0}^{2} u^{2},$$
(3)

and the corresponding conditions have the forms:

$$\begin{aligned} u & = 0,\;\;k\frac{{{\text{d}}T}}{{{\text{d}}y}} = h_{1} ( - T_{2} + T),\;\;{\text{at}}\;\;y = 0, \\ u & = 0,\;\;k\frac{{{\text{d}}T}}{{{\text{d}}y}} = - h_{2} (T - T_{1} ),\;\;{\text{at}}\;\;y = h. \\ \end{aligned}$$
(4)

Here, \(u\) is the component of velocity in x-direction, \(\mu\) viscosity coefficient, \(k\) thermal conductivity, \(\rho\) fluid density, \(p\) pressure, \(\sigma\) electrical conductivity, \(n\) positive constant, \(\varGamma\) is the material fluid parameter, \(B_{0}\) constant magnetic field strength, \(T_{2}\) hot fluid temperature, \(T_{1}\) ambient temperature, \(T\) temperature and \(h_{1} ,h_{2}\) coefficients of convective heat transport.

Dimensionless form of Eqs. (2)–(4) is given as follows:

$$\left( {1 + \left( {f^{\prime}} \right)^{2} nW_{\text{e}}^{2} } \right)\left( {1 + \left( {f^{\prime}} \right)^{2} W_{\text{e}}^{2} } \right)^{{\left( {\frac{\rm{n} - 3}{2}} \right)}} f^{\prime\prime} - \text{Re} f^{\prime} - M^{2} f + P = 0,$$
(5)
$$\theta^{\prime\prime} - \text{Re} \,\Pr \theta^{\prime} + {\text{Ec}}\,\Pr \left[ {\left( {1 + \left( {f^{\prime}} \right)^{2} nW_{\text{e}}^{2} } \right)\left( {1 + \left( {f^{\prime}} \right)^{2} W_{\text{e}}^{2} } \right)^{{\left( {\frac{\rm{n} - 3}{2}} \right)}} \left( {f^{\prime}} \right)^{2} + M^{2} f^{2} } \right] = 0,$$
(6)

with

$$\begin{aligned} f = 0,\;\;\theta^{\prime} - Bi_{1} (\theta - 1\,) = 0\;\;{\text{at}}\;\;\eta = 0 , \hfill \\ f = 0,\;\;\theta^{\prime} + Bi_{2} (\theta \,) = 0\;\;{\text{at}}\;\;\eta = 1. \hfill \\ \end{aligned}$$
(7)

The above-said equations are obtained upon using following dimensionless variables:

$$u = \frac{\mu }{\rho h}f(\eta ),\;\;\eta = \frac{y}{h},\;\;\theta = \frac{{T - T_{1} }}{{T_{2} - T_{1} }}.$$
(8)

In Eqs. (5–7), \(P = \frac{{\rho h^{3} }}{{\mu^{2} }}\left( { - \frac{{{\text{d}}p}}{{{\text{d}}x}}} \right)\) is the pressure gradient parameter, \({\text{We}} = \frac{\mu \varGamma }{{\rho h^{2} }}\) the Weissenberg number, \(\text{Re} = \frac{{\rho \nu_{0} h}}{\mu }\) Reynolds number, \(M = \sqrt {\frac{{\sigma B_{0}^{2} h^{2} }}{\mu }}\) magnetic parameter, \(\Pr = \frac{{\mu C_{\text{p}} }}{k}\) Prandtl number, \({\text{Ec}} = \frac{{\mu^{2} }}{{h^{2} \rho^{2} }}\frac{1}{{C_{\text{p}} (T_{2} - T_{1} )}}\) Eckert number and \({\text{Bi}}_{\text{i}} = \frac{{ - hh_{\text{i}} }}{k}\;\;{\text{for}}\;\;i = 1,2\) Biot number.

The dimensionless skin friction coefficient and Nusselt number are given by:

$${\text{Cf}} = \frac{{\rho h^{2} \tau_{\text{w}} }}{{\mu^{2} }} = \left\{ {1 + {\text{We}}\left[ {f^{\prime}\left( 1 \right)} \right]^{2} } \right\}^{{\frac{\rm{n} - 1}{2} }} f^{\prime}\left( 1 \right) \;{\text{and}}\;{\text{Nu}} = \frac{{hq_{\text{m}} }}{{k_{\text{f}} \left( {T_{2} - T_{1} } \right)}} = - \theta^{\prime}\left( 1 \right),$$
(9)

where \(\tau_{\text{w}} = \left\{ {\mu \left[ {1 + \varGamma^{2} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right]^{{\frac{n - 1}{2}}} \frac{{{\text{d}}u}}{{{\text{d}}y}}} \right\}_{y = 1}\) and \(q_{\text{m}} = - k\left( {\frac{{{\text{d}}T}}{{{\text{d}}y}}} \right)_{y = 1}\).

Entropy analysis

The temperature and velocity fields are utilized for the computation of the rate of entropy production within the microchannel. In the transport of non-Newtonian Carreau fluid due to microchannel, the entropy production must include irreversibility created by viscous heating, Joule heating and heat transport.

$$E_{\text{g}} = \frac{k}{{T_{1}^{2} }}\left( {\frac{{{\text{d}}T}}{{{\text{d}}y}}} \right)^{2} + \frac{1}{{T_{1} }}\left[ {\mu \left( {1 + \varGamma^{2} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right)^{{\left( {\frac{\rm{n} - 1}{2}} \right)}} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} + \mu (n - 1)\varGamma^{2} \left( {1 + \varGamma^{2} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} } \right)^{{\left( {\frac{\rm{n} - 3}{2}} \right)}} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{4} + \sigma B_{0}^{2} u^{2} } \right].$$
(10)

The local entropy production rate is described as:

$$N_{\text{s}} = \frac{{E_{\text{g}} }}{{E_{0} }} = \left( {\theta^{\prime}} \right)^{2} + {\text{Ec}}\,\Pr L\left[ {\left( {1 + nW_{\text{e}}^{2} \left( {f^{\prime}} \right)^{2} } \right)\left( {1 + W_{\text{e}}^{2} \left( {f^{\prime}} \right)^{2} } \right)^{{\left( {\frac{\rm{n} - 3}{2}} \right)}} \left( {f^{\prime}} \right)^{2} + M^{2} f^{2} } \right],$$
(11)

where \(E_{0} = \frac{{k\left( {T_{2} - T_{1} } \right)}}{{h^{2} T_{1}^{2} }}^{2}\) classifies the characteristics entropy generation rate and \(L = \frac{{T_{1} }}{{T_{2} - T_{1} }}\) is the characteristic temperature ratio.

Equation (11) can be expressed as:

$$N_{\text{s}} = N_{\text{v}} + N_{\text{h}} .$$
(12)

The first term denotes the entropy generation by the heat transport irreversibility, and the second term denotes the entropy generation by viscous dissipation. To examine the irreversibility distribution, the constraint Be (Bejan number) is used. This number is the ratio of entropy production by heat transport to overall entropy generation and can be described as

$${\text{Be}} = \frac{{N_{\text{h}} }}{{N_{\text{h}} + N_{\text{v}} }}.$$
(13)

Finite element analysis

The nonlinear coupled differential expressions (5) and (5) having conditions (6) are executed through finite element procedure. The whole flow domain is divided into 1000 linear elements having equal size. The complete domain has 1001 nodes because every element is two nodded. We developed a system of expressions which has 2002 equations. The developed system is nonlinear, due to which an iterative technique is implemented in the solution. The system of expressions is reduced to 1998 expressions after the implementation of conditions. Subsequent system is treated under accuracy of 10−5 by using the Gauss elimination scheme.

Results and discussion

Finite element scheme is introduced to evaluate the solutions of constructed mathematical expressions. These solutions are executed by plotting graphs of distinct constraints values on important quantities from physical point of view. Plots are labeled for distinct constraints to examine the nature of velocity \(f,\) temperature \(\theta ,\) rate of local entropy minimization Ns and Bejan number Be. Default values of various parameters are fixed as

$${\text{We}} = 2,\;M = 1.5,\;n = 1.5,\;\text{Re} = 0.5,\;{\text{Ec}} = 0.2,\;P = 1,\;{\text{Bi}} = 0.5.$$

Figures 2–5 demonstrate the behavior of curves of velocity \(f,\) temperature \(\theta ,\) rate of local entropy minimization Ns and Bejan number Be against the distinct values of magnetic field constraint M. Figure 2 clearly executes that the velocity \(f\) of liquid reduces by improving the values of magnetic constraint. The curves of velocity \(f\) achieve the peak at \(\eta = 0.5.\) Temperature \(\theta\) is decayed by enhancing magnetic constraint \(M\) (Fig. 3). A comparative examination of these two figures reports that the change in velocity is more prominent as we found in temperature. This behavior of velocity and temperature is due to existence of Lorentz force factor in magnetic constraint. This factor has dominant nature with the increasing trend of magnetic constraint that produces reduction in the profiles. Figure 4 shows that the local rate of entropy generation Ns has sinusoidal behavior against the incrementing values of magnetic constraint M. The local entropy minimization rate has both increasing and decreasing nature in various parts of microchannel. The impact of magnetic constraint on Bejan number is contrary as we observed for Ns (Figs. 4 and 5). The behavior of Reynolds number \(\text{Re}\) on velocity \(f,\) temperature \(\theta ,\) rate of local entropy minimization Ns and Bejan number Be is visualized in Figs. 6–9. The velocity of liquid becomes the weaker at first half of microchannel, but it starts to improve in the second part at velocity \(f,\) temperature \(\theta ,\) rate of local entropy minimization Ns and Bejan number \(\eta = 0.61\) against the incrementing values of \(\text{Re}\) (Fig. 6). Figure 7 explains that the larger temperature curve is visualized against the higher Reynolds number. Temperature at channel wall is also enhanced for incrementing Reynolds number values. Figure 8 reflects that the curves have both increasing and decreasing nature for improving Reynolds number. The decreasing nature is noticed in profiles of Ns up to \(\eta = 0.7\), and after that, it starts to boost. The curves of Be demonstrate the similar trend as of Ns for incrementing Reynolds number (Figs. 8 and 9).

Fig. 2
figure 2

Effect of M on velocity

Full size image
Fig. 3
figure 3

Effect of M on temperature

Full size image
Fig. 4
figure 4

Effect of M on Ns

Full size image
Fig. 5
figure 5

Effect of M on Be

Full size image
Fig. 6
figure 6

Effect of Re on velocity

Full size image
Fig. 7
figure 7

Effect of Re on temperature

Full size image
Fig. 8
figure 8

Effect of Re on Ns

Full size image
Fig. 9
figure 9

Effect of Re on Be

Full size image

The role of Weissenberg number We on velocity \(f,\) temperature \(\theta ,\) rate of local entropy minimization Ns and Bejan number Be is characterized in Figs. 10–13. Figures 10 and 11 reflect that the curves of velocity \(f\) and temperature \(\theta\) have decreasing behavior for larger Weissenberg number. The curve of velocity is at maximum peak at \(\eta = 0.6\). This trend is due to stronger material factor \(\varGamma .\) This factor is directly connected with Weissenberg number, and larger Weissenberg number corresponds to stronger material factor. This stronger material factor is responsible for decrement in the velocity and temperature of liquid. The behavior of Weissenberg number on Ns and Be profiles is quite reverse. The increasing trend of Weissenberg number reduces the profile of Ns while boosting the curves of Be (Figs. 12 and 13). The behaviors of temperature \(\theta ,\) rate of local entropy minimization Ns and Bejan number Be for distinct Eckert number Ec are addressed in Figs. 14–16. Temperature \(\theta\) is boosted for larger Eckert number. The internal energy factor is higher for larger \(Ec\) due to which heat of liquid is augmented that improves the temperature profiles in Fig. 14. Figures 15 and 16 declare that the larger Eckert number \(Ec\) leads to higher Ns and lower Be profiles. From these figures, we recognized that the local entropy generation rate and Bejan number behavior is stable for certain portion of the channel.

Fig. 10
figure 10

Effect of We on velocity

Full size image
Fig. 11
figure 11

Effect of We on temperature

Full size image
Fig. 12
figure 12

Effect of We on Ns

Full size image
Fig. 13
figure 13

Effect of We on Be

Full size image
Fig. 14
figure 14

Effect of Ec on temperature

Full size image
Fig. 15
figure 15

Effect of Ec on Ns

Full size image
Fig. 16
figure 16

Effect of Ec on Be

Full size image

Figures 17–19 are displayed to characterize the trend of Biot number Bi on temperature \(\theta ,\) rate of local entropy minimization Ns and Bejan number Be. Figure 17 reveals that the temperature is improved in the first part and decayed in the second part of channel for the increasing Biot number values. The behavior of temperature is changed from higher to lower at \(\eta = 0.4.\) The local entropy generation Ns and Bejan number Be are higher corresponding to incremented values of Biot number (Figs. 18 and 19). Both the quantities are also boosted at the channel wall for larger Biot number values. The effects of pressure gradient constraint \(P\) on velocity \(f,\) temperature \(\theta ,\) rate of local entropy minimization Ns and Bejan number Be are reported in Figs. 20, 21, 22, 23. These figures address that the velocity \(f,\) temperature \(\theta\) and rate of local entropy minimization Ns are boosted by enhancing the pressure gradient constraint, but the profiles of Bejan number are decaying for rising pressure gradient constraint. The significance of n on velocity, temperature, rate of local entropy minimization and Bejan number are reported in the Figs. 24, 25, 26, 27 correspondingly. These figures reveal that the velocity, temperature and rate of local entropy minimization are enhanced via stronger values of n whereas the Bejan number declined for increasing values of n. Impact of M on skin friction coefficient and Nusselt number is unpacked in Figs. 28, 29 respectively. Here both skin friction coefficient and Nusselt number are decreasing functions of M. Fig. 30 shows that the Nusselt number increases with Ec.

Fig. 17
figure 17

Effect of Bi on temperature

Full size image
Fig. 18
figure 18

Effect of Bi on Ns

Full size image
Fig. 19
figure 19

Effect of Bi on Be

Full size image
Fig. 20
figure 20

Effect of P on velocity

Full size image
Fig. 21
figure 21

Effect of P on temperature

Full size image
Fig. 22
figure 22

Effect of P on Ns

Full size image
Fig. 23
figure 23

Effect of P on Be

Full size image
Fig. 24
figure 24

Effect of n on velocity

Full size image
Fig. 25
figure 25

Effect of n on temperature

Full size image
Fig. 26
figure 26

Effect of n on Ns

Full size image
Fig. 27
figure 27

Effect of n on Be

Full size image
Fig. 28
figure 28

Effect of We and M on skin friction coefficient

Full size image
Fig. 29
figure 29

Effect of We and M on Nusselt number

Full size image
Fig. 30
figure 30

Effect of Re and Ec on Nusselt number

Full size image

Concluding remarks

The thermal and entropy generation nature in magneto-Carreau non-Newtonian material induced by convectively heated microchannel has been addressed. Finite element-based numerical scheme is adopted for the solutions of physical model. The results of various quantities are addressed by plotting graphs. It is noted that the Bejan number Be and rate of local entropy generation Ns have sinusoidal nature for increasing values of magnetic field constraint M. The velocity \(f\) of liquid is reduced first, but it starts to boost up after \(\eta = 0.6\) for increasing trend of Reynolds number \(\text{Re} .\) The behaviors of Ns and Be for increasing \(\text{Re}\) are similar in a qualitative way. Both quantities decreased firstly and then boost up when the values of \(\eta\) increased from 0.7. Temperature \(\theta\) is retarded for larger values of We. The increasing trend of Weissenberg number leads to lower curves of local entropy generation Ns. The Biot number improves the profile of local entropy generation Ns and Bejan number Be. An increase in pressure gradient constraint enhances the velocity profile dramatically in the microchannel.