Yukawa–Casimir wormholes in the framework of f(R) gravity

Abstract

In this article, we explore the Yukawa modification of the Casimir wormhole within the framework of f(R) gravity. To accomplish this, we adopt an approach proposed by Garattini (Eur Phys J C 81:824, 2021), wherein the original Casimir source is modified by a Yukawa term in three distinct scenarios. We utilize these Yukawa Casimir energy densities to assess the feasibility of traversable wormholes. The resulting shape function satisfies the criteria for traversability under the specified parameter values. Furthermore, we scrutinize the energy conditions and the violation of the null energy conditions suggests the presence of exotic matter within the Yukawa Casimir wormholes. Additionally, we analyze the embedding procedures for the wormhole geometry.

1 Introduction

A prominent structure known as a wormhole serves to connect two distinct spacetime regions within the same universe or even different universes. This structure consists of a narrow passage called the wormhole throat, functioning similarly to a bridge or tunnel that joins these distinct regions of the cosmos. The concept of inter-universe connections has its origins in the groundbreaking research of Flamm in 1916 [1], which emerged shortly after the introduction of General Relativity (GR). In 1935, Einstein and Rosen [2] further developed this concept by proposing a bridge model based on Flamm’s theories. Later, Morris and Thorne [3] formulated the concept of traversable wormholes and delineated its geometric structure via the Morris–Thorne metric. This study clarifies that the exotic fluid within the wormhole possesses negative energy, thus violating the null energy conditions (NEC). This exotic matter presents a problematic issue, and numerous initiatives have been undertaken to address it [4,5,6,7,8,9,10,11,12]. In semiclassical gravity, quantum effects lead to the emergence of specific wormhole solutions such as Casimir effects and Hawking evaporation [13], resulting in violations of energy conditions. Other forms of exotic matter encompass the generalized Chaplygin gas [14], phantom energy [15,16,17], tachyon matter [18], and certain non-minimal kinetic couplings, etc.

In the realm of theoretical physics, one of the notable modifications to GR is f(R) gravity, proposed by Buchdahl in 1977 [19]. In this framework, the usual term representing the curvature scalar or Ricci scalar R in the Einstein-Hilbert action is replaced by f(R), indicating an arbitrary function of the Ricci scalar. This adjustment results in a more generalized version of the Einstein field equations within this theoretical framework. Indeed, these generalized equations have exhibited portrayals of cosmic phenomena. Lobo and Oliveira [20] delved into the geometries of traversable wormholes, discussing various solutions incorporating shape functions and specific equations of state. In 2015, Pavlovica and Sossich examined Lorentzian wormhole solutions that satisfy the Weak Energy Condition (WEC) [21]. Additionally, a class of thin-shell wormhole solutions within the framework of f(R) gravity was developed [22]. Recent studies indicate that f(R) gravity might offer a feasible explanation for various cosmological and astrophysical phenomena [23,24,25,26,27,28].

Furthermore, the Casimir effect represents one manifestation of vacuum energy within the framework of quantum mechanics. Initially predicted by H. Casimir [29], and then experimentally validated by various researchers [30,31,32,33,34]. The Casimir effect is characterized by the emergence of an attractive force between two closely situated, neutral, and parallel conducting plates within a vacuum. This force arises from the disturbance of the electromagnetic field in the vacuum and is associated with the zero-point energy of a quantum electrodynamics (QED) vacuum modified by the presence of the plates. Moreover, the Casimir effect is a macroscopic quantum phenomenon that manifests as the attraction of plates through negative energy. In reference [35], the author examined the potential of utilizing Casimir energy exclusively for the construction of Morris–Thorne wormholes in three spatial dimensions and one temporal dimension. Furthermore, they explored the implications of the Quantum Weak Energy Condition (QWEC) on the traversability of these wormholes.

Recently, Garattini [36] conducted a study on the theoretical characteristics of traversable wormholes within the framework of GR, delving into the requirement of exotic energy densities for their viability. They examined the consequences of Yukawa-like energy distributions in achieving these configurations. The Yukawa–Casimir wormhole is formulated by modifying the original Casimir source with Yukawa terms. In [37], the author rigorously investigated Yukawa modifications on Casimir wormholes, aiming to attain zero tidal forces using an equation of state. They explored two methodologies: one fixing the shape function of modified Casimir wormholes, while the other adjusted the original Casimir source with a Yukawa term. Inspired by this research, our objective is to investigate solutions for traversable wormholes while considering the implications of modified Casimir energy density. The concept of the Yukawa Casimir wormhole was thoroughly examined and analyzed in references [38, 39].

The manuscript is organized in the following manner: Sect. 2 presents the criteria for determining the traversability of wormholes. In Sect. 3, we establish the mathematical framework for f(R) gravity. The energy conditions are examined in Sect. 4. Section 5 provides a brief review of Yukawa–Casimir energy density. Section 6 presents a detailed analysis of Yukawa–Casimir wormholes, including three different scenarios. In Sect. 7, we consider the specific form of energy density to explore the wormhole solution in f(R) gravity. Additionally, embedding procedures with diagrams are examined in Sect. 8. Finally, our conclusions are presented in Sect. 9.

2 Traversability criteria for wormhole

The Morris–Thorne metric for the traversable wormhole is given by

$$\begin{aligned} ds^2=-e^{2\Phi (r)}dt^2+\left( 1-\dfrac{b(r)}{r} \right) ^{-1}dr^2 + r^2 d\Omega ^2, \end{aligned}$$

(1)

where, $d\Omega =d\theta ^2+\sin ^2\theta d\phi ^2$. The redshift function $\Phi (r)$ and the shape function b(r) both depend on the radial coordinate r. These functions demonstrate significant characteristics that illustrate a feasible wormhole solution, as outlined below:

• The redshift function must be finite throughout the domain and must also satisfy the absence of horizon restriction. In this current study, we consider it to be constant.

• The shape function b(r) satisfies the throat condition, flaring-out condition and asymptotic flatness conditions, namely $1-\frac{b(r)}{r}>0$ for $r>r_0$, $b'(r_0)<1$ and $b(r)/r \rightarrow 0$ as $r\rightarrow \infty$ respectively.

• Another important criterion for traversable wormhole is proper radial distance function l(r),

  $$\begin{aligned} l (r)=\pm \int _{r_0}^r \dfrac{dr}{\sqrt{\dfrac{r-b(r)}{r}}}. \end{aligned}$$

  (2)

  Here, the expression ± combines the upper and lower parts of the wormhole. This connection decreases from the upper universe to the throat, and then it increases to the lower universe.

3 Mathematical formulation of f(R) gravity

In the framework of Einstein’s general theory of relativity, the Lagrangian for geometry is typically expressed as $L_G = R$, where R represents the Ricci scalar. However, a more generalized approach involves using $L_G = f(R)$. This newly formulated gravitational theory is commonly referred to as the f(R) theory of gravity. Further, the Einstein–Hilbert action for f(R) gravity can be written as

$$\begin{aligned} S=\int \left[ \frac{1}{16\pi }f(R)+L_m\right] \sqrt{-g}d^4x, \end{aligned}$$

(3)

where $L_m$ is the matter lagrangian and g is the determinant of the metric $g_{\mu \nu }$. Now, applying the metric approach and varying the action with respect to $g_{\mu \nu }$ yields the following field equations

$$\begin{aligned} F R_{\mu \nu }-\frac{1}{2}f g_{\mu \nu }-\nabla _{\mu } \nabla _{\nu } F + g_{\mu \nu } \square F =T_{\mu \nu }, \end{aligned}$$

(4)

where $F=\frac{df(R)}{dR}$ and $\square F=\frac{1}{\sqrt{-g}}\partial _\mu (\sqrt{-g}g^{\mu \nu }\partial _\nu F)$.

Upon contracting Eq. (3), we get

$$\begin{aligned} (3\square +R)F-2f=T, \end{aligned}$$

(5)

which demonstrates that the Ricci scalar is entirely a dynamic degree of freedom and T is the trace of the energy-momentum tensor.

From Eqs. (4) and (5), the effective field equation is obtained as

$$\begin{aligned} G_{\mu \nu }=R_{\mu \nu }-\dfrac{1}{2}R g_{\mu \nu }=T^{ef}_{\mu \nu }, \end{aligned}$$

(6)

where, $T^{ef}_{\mu \nu }$ is the combination of curvature stress-energy tensor $T^{(c)}_{\mu \nu }=\frac{1}{F}\left[ \nabla _\mu \nabla _\nu F- \frac{1}{4}g_{\mu \nu } (RF+\square F+T)\right]$ and matter stress-energy tensor $\hat{T}^{(m)}_{\mu \nu }=\frac{T^{(m)}_{\mu \nu }}{F}$ [20]. In this article, we assume that the distribution of matter is characterized by an anisotropic stress-energy tensor, expressed as:

$$\begin{aligned} T_{\mu \nu }=(\rho +p_t) \eta _\mu \eta _\nu +(p_r-p_t)\zeta _\mu \zeta _\nu +p_t g_{\mu \nu }, \end{aligned}$$

(7)

with $\zeta ^\mu \zeta _\mu =-\eta ^\mu \eta _\mu =1$. Here, $\rho , p_t$ and $p_r$ represent the energy density, tangential pressure, and radial pressure, respectively.

Furthermore, the gravitational field equation for the f(R) theory can be expressed as follows:

$$\begin{aligned} \rho&=F \dfrac{ b'(r)}{r^2}, \end{aligned}$$

(8)

$$\begin{aligned} p_r&=F'' \dfrac{b(r)-r}{r}+F' \dfrac{r\,b'(r) -b(r)}{2r^2}-F\dfrac{b(r)}{r^3}, \end{aligned}$$

(9)

$$\begin{aligned} p_t&=F'\dfrac{b(r)-r}{r^2}+F\dfrac{b(r)-r\,b'(r)}{2r^3}. \end{aligned}$$

(10)

4 Energy bounds

The energy bounds play a crucial role in assessing the physical viability of specific cosmological structures, particularly for analyzing the geometric properties of wormholes. In this section, we discuss the energy bounds, including the Null Energy Conditions (NEC), Weak Energy Conditions (WEC), Strong Energy Conditions (SEC), and Dominant Energy Conditions (DEC), which are expressed as follows:

• NEC: $\rho +p_t\ge 0$ and $\rho +p_r\ge 0$.

• WEC: $\rho \ge 0\implies$ $\rho +p_t\ge 0$ and $\rho +p_r\ge 0$.

• SEC: $\rho +p_r\ge 0$, $\rho +p_t\ge 0$ and $\rho +p_r+2 p_t\ge 0$.

• DEC: $\rho \ge 0\implies$ $\rho -|p_r|\ge 0$ and $\rho -|p_t|\ge 0$.

5 Yukawa–Casimir energy density

In 1935, Yukawa [40] introduced a proposition to elucidate nonrelativistic strong interactions among nucleons, employing a potential. The profile of potential is defined as

$$\begin{aligned} V(r)=-\dfrac{\chi }{r}e^{-\beta r}, \end{aligned}$$

(11)

where $\chi$ defines the strength of nucleon interactions and its range is determined by $\frac{1}{\alpha }$. Numerous researchers adopted this short-range interaction to comprehend deviations from the Newtonian potential. If similar deviations were to occur, the gravitational Newtonian potential would consequently undergo a Yukawa correction, formally resembling Eq. (11) as follows:

$$\begin{aligned} V(r)=-\dfrac{\mathscr {G}m_1 m_2}{r}(1+\chi e^{-\alpha r}). \end{aligned}$$

(12)

Here, $m_1$ and $m_2$ represent two points separated by a distance r. Notably, potentials in the form of Eq. (12) have undergone extensive study from an astrophysical perspective, with a specific focus on the graviton mass [41,42,43]. These Yukawa-type forces are also anticipated within the context of modified gravity theories [44,45,46]. Moreover, in different frameworks, the potential for obtaining traversable wormholes always exists [38, 47].

In this article, we concentrate on the Casimir source of energy density modified by the Yukawa term, commonly referred to as Yukawa–Casimir energy density. This modification results in three distinct Yukawa energy densities, as outlined below [37]:

• 1. $\rho _{y}=r_0\, \rho _c \dfrac{e^{\lambda (r_0-r)}}{r}$,

• 2. $\rho _{y}=\dfrac{\rho _c }{2r}\left( \mu \, r+\nu \,r_0\,e^{\lambda (r_0-r)}\right)$ and

• 3. $\rho _{y}=\dfrac{\rho _c\, r_0 }{r}\left( \mu \, e^{\lambda (r_0-r)}-(1-\nu ) \,e^{\lambda (r_0-r)}\right)$.

6 Yukawa–Casimir wormhole solutions in f(R) gravity

In this manuscript, we study the wormhole solution with the function f(R) given by $f(R)=\dfrac{\alpha }{m+1}R^{m+1}$ with $F=\alpha \,R^m$ [48]. Here, the Ricci scalar R is articulated as

$$\begin{aligned} R=\dfrac{2b'(r)}{r^2}. \end{aligned}$$

(13)

Further, we delve into the previously mentioned modified Casimir energy density and analyze both the properties of shape function and energy conditions.

Fig. 1

Asymptotic behavior of b(r), b’(r) and b(r)/r with $m=2,r_0=0.5$, and $\lambda =1.45$

6.1 Case -1

Now, we consider the Yukawa energy density written as

$$\begin{aligned} \rho _{y}=r_0\, \rho _c \dfrac{e^{\lambda (r_0-r)}}{r}, \end{aligned}$$

(14)

with $\lambda >0$. If $r_0=r$, then the above equation reduces to Casimir energy density $\rho _c$. We match the Yukawa energy density (14) with Eq. (8), we get the following differential equation

$$\begin{aligned} 2^m \alpha \left( \frac{b'(r)}{r^2}\right) ^{m+1}=-\dfrac{\pi ^2\, r_0 \,e^{\lambda (r_0-r)}}{720 r^5}. \end{aligned}$$

(15)

Upon solving the aforementioned equation, the resulting shape function is expressed as follows:

$$\begin{aligned} & b(r) = \mathscr {C}-r\,45^{-\frac{1}{m+1}} \pi ^{\frac{2}{m+1}} e^{\frac{\lambda r}{m+1}} \left( \frac{\lambda r}{m+1}\right) ^{\frac{2-3 m}{m+1}} \nonumber \\ & \, \times \Gamma \left( \frac{3 m\!-\!2}{m\!+\!1},\frac{r \lambda }{m\!+\!1}\right) \left( -\!\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m\!+\!1}},\nonumber \\ \end{aligned}$$

(16)

where $\mathscr {C}$ is an integration constant. To determine the value of $\mathscr {C}$ by imposing an initial condition $b(r_0) = r_0$, we obtain

$$\begin{aligned} \mathscr {C} \!= & \!45^{-\frac{1}{m\!+\!1}} r_0 \left( \frac{\lambda r_0}{m+1}\right) ^{-\frac{3 m}{m\!+\!1}}\! \left[ \pi ^{\frac{2}{m+1}} \left( \!-\frac{2^{-m-4} r_0^{2 m-2}}{\alpha }\right) ^{\frac{1}{m+1}} \right. \nonumber \\ & \times e^{\frac{\lambda r_0}{m+1}} \left( \frac{\lambda r_0}{m+1}\right) ^{\frac{2}{m+1}} \Gamma \left( \frac{3 m-2}{m+1},\frac{r_0 \lambda }{m+1}\right) \nonumber \\ & \left. +45^{\frac{1}{m+1}} \left( \frac{\lambda r_0}{m+1}\right) ^{\frac{3 m}{m+1}}\right] . \end{aligned}$$

(17)

Fig. 2

The graphical representation of the shape function for Yukawa–Casimir wormhole against radial coordinate with $m=2,r_0=0.5$, and $\lambda =1.45$

To investigate the asymptotic behavior of the shape function (16), we examine its expansions for large r. The second-order expansions are given by

$$\begin{aligned} b(r) \underset{r \rightarrow \infty }{\simeq }&-\frac{45^{-\frac{1}{m+1}} (m+1) \pi ^{\frac{2}{m+1}} \left( 2 m^2+m (2 \lambda r-11)+\lambda r (\lambda r-3)+12\right) \left( -\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m+1}}}{\lambda ^3 r^2},\\ b'(r) \underset{r \rightarrow \infty }{\simeq }&\frac{45^{-\frac{1}{m+1}} \pi ^{\frac{2}{m+1}} \left( \lambda ^3 r^3-2 (m-4) (m+1) (2 m-3)\right) \left( -\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m+1}}}{\lambda ^3 r^3},\\ \frac{b(r)}{r} \underset{r \rightarrow \infty }{\simeq }&-\frac{45^{-\frac{1}{m+1}} (m+1) \pi ^{\frac{2}{m+1}} (2 m+\lambda r-3) \left( -\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m+1}}}{\lambda ^2 r^2}. \end{aligned}$$

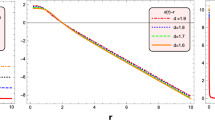
Upon examining these expressions, it becomes clear that as r approaches infinity, the term $e^{\frac{(r0-r)\lambda }{m+1}}$ tends to zero. This indicates that the shape function is convergent for large values of r. Furthermore, for large r, the shape function is independent of the choice of m, whereas it depends on the choice of m for finite values. The asymptotic behavior of the shape function is depicted in Fig. 1. As observed, our obtained shape function converges as r approaches infinity.

Fig. 3

Pictures of the Yukawa energy density and energy conditions with respect to r, where the model parameter values are $m=2$, $r_0=0.5$, and $\lambda =1.45$

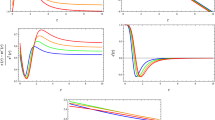
Further, the derived shape function exhibits a monotonically increasing function with $b(r)<r$ for $\alpha \in (-\infty , 0)$. The $\alpha$ range is restricted to $(-\infty ,0)$, meeting all the criteria necessary for a wormhole. However, it leads to the emergence of imaginary terms within the range $(0,\infty )$. This suggests that the solution is valid exclusively for negative $\alpha$ values. Mathematically, the presence of imaginary terms indicates that the solution becomes complex for positive $\alpha$ values, potentially signifying a breakdown in its physical interpretation beyond a certain threshold. Consequently, the geometry depicted by the solution may lack physical significance or stability in the positive $\alpha$ region. Figure 2 illustrates the fulfillment of criteria for a traversable wormhole, including the throat condition, flaring-out condition, and asymptotic flatness condition. Additionally, our investigation extends to the features of energy density and energy conditions, as depicted in Fig. 3. The traits of stress-enery components are shown in Fig. 3a. The NEC and DEC are violated, while the SEC is upheld. The infringement of NEC suggests the existence of a hypothetical fluid.

Fig. 4

The characteristics of the shape function b(r) for Yukawa–Casimir wormhole with $m=2,r_0=0.5$, and $\lambda =1.45$

By substituting Eqs. (16) and (17) into Eqs. (9) and (10), we obtain the pressure elements as:

$$\begin{aligned} & p_r=-\dfrac{2^{m-1} \,45^{-\frac{1}{m+1}} \,\alpha }{(m+1)^2 r^3}\nonumber \\ & \quad \times \left( \frac{45^{-\frac{1}{m+1}} \pi ^{\frac{2}{m+1}} \left( -\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m+1}}}{r^2}\right) ^m \nonumber \\ & \quad \times \left[ 45^{\frac{1}{m+1}} \Bigg (m^2(r(2\lambda ^2 r^2-2r\lambda ^2r_0+20r\lambda -21r_0\lambda \right. \nonumber \\ & \quad +60\lambda )-63r_0)-mr\lambda r_0-10mr+11mr_0+2r_0\Bigg )\nonumber \\ & \quad +m (m+1) \pi ^{\frac{2}{m+1}} r (\lambda r+5) \left( -\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \quad + \pi ^{\frac{2}{m+1}} (-2 + 11m + m r \lambda + m^2 (2r^2 \lambda ^2+21 r \lambda +63))\nonumber \\ & \quad \times \Bigg (r e^{\frac{\lambda r}{m+1}} E_{\frac{5}{m+1}-2}\left( \frac{r \lambda }{m+1}\right) \left( -\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m+1}} \nonumber \\ & \left. \quad -r_0 \left( -\frac{2^{-m-4} r_0^{2 m-2}}{\alpha }\right) ^{\frac{1}{m+1}} e^{\frac{\lambda r_0}{m+1}} E_{\frac{5}{m+1}-2}\left( \frac{r_0 \lambda }{m+1}\right) \Bigg ) \right] , \end{aligned}$$

(18)

$$\begin{aligned} & p_t=\frac{\alpha 2^{m-1} 45^{-\frac{1}{m+1}}}{(m+1) r^3}\nonumber \\ & \quad \times \left( \frac{45^{-\frac{1}{m+1}} \pi ^{\frac{2}{m+1}} \left( -\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m+1}}}{r^2}\right) ^m \nonumber \\ & \quad \times \Bigg [45^{\frac{1}{m+1}} (2 m r (\lambda r-\lambda r_0+5)-9 m r_0+r_0) -(m+1) \pi ^{\frac{2}{m+1}} r\nonumber \\ & \quad \times \left( -\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m+1}}+\pi ^{\frac{2}{m+1}} (m (2 \lambda r+9)-1) \nonumber \\ & \quad \times \Bigg (r e^{\frac{\lambda r}{m+1}} E_{\frac{5}{m+1}-2}\left( \frac{r \lambda }{m+1}\right) \left( -\frac{2^{-m-4} r_0 r^{2 m-3} e^{\lambda (r_0-r)}}{\alpha }\right) ^{\frac{1}{m+1}} \nonumber \\ & \quad -r_0 e^{\frac{\lambda r_0}{m+1}} E_{\frac{5}{m+1}-2}\left( \frac{r_0 \lambda }{m+1}\right) \left( -\frac{2^{-m-4} r_0^{2 m-2}}{\alpha }\right) ^{\frac{1}{m+1}} \Bigg ) \Biggl ]. \end{aligned}$$

(19)

Fig. 5

The behavior of energy density and various energy conditions for Yukawa–Casimir wormhole with $m=2$, $r_0=0.5$, and $\lambda =1.45$

6.2 Case -2

In this scenario, our analysis explores the modified Casimir energy density provided by:

$$\begin{aligned} \rho _{y}=\dfrac{\rho _c }{2r}\left( \mu \, r+\nu \,r_0\,e^{\lambda (r_0-r)}\right) , \end{aligned}$$

(20)

where $\lambda >0$ and $\mu =\nu =1$. At $r = r_0$, the Yukawa energy density (20) reduces to the Casimir energy density. Now, by comparing Eqs. (20) and (8), one can get

$$\begin{aligned} 2^m \alpha \left( \frac{b'(r)}{r^2}\right) ^{m+1}=-\frac{\pi ^2 \left( r_0\,e^{\lambda (r_0-r)} +r\right) }{1440 r^3}. \end{aligned}$$

(21)

The aforementioned non-linear differential equations are generally more difficult to solve analytically than linear ones due to their inherent complexity and the lack of a universal solving method. While most non-linear equations require numerical or approximate methods due to their intricate and often unpredictable nature. Consequently, we utilize numerical methods to solve it, taking into account the initial condition $b(0.5)=0.5$. Additionally, specific values will be substituted for other unknown parameters, such as $m = 2, r_0=0.5,$ and $\lambda =1.25$. Figure 4 illustrates the behavior of the shape function b(r) with different values of $\alpha$. In this depiction, the shape function maintains a non-negative and increasing nature across the entire domain of r. Notably, it adheres to the asymptotic flatness condition, as the ratio of $b(r)/r \rightarrow 0$ as $r\rightarrow \infty$. Additionally, the derivative of the shape function at the throat remains less than one. Consequently, it can be observed that the shape function satisfies all the essential criteria for traversable wormholes.

In Fig. 5, we present the graphical trends of the Yukawa energy density, pressure elements and energy conditions. It can be observed that the Yukawa energy density is consistently negative across the entire domain of r. Furthermore, both the NEC and DEC are violated, while the SEC remains satisfied.

6.3 Case -3

In this scenario, we examine another form of Yukawa energy density, denoted as

$$\begin{aligned} \rho _{y}=\dfrac{\rho _c\, r_0 }{r}\left( \mu \, e^{\lambda (r_0-r)}-(1-\nu ) \,e^{\lambda (r_0-r)}\right) , \end{aligned}$$

(22)

with $\lambda >0$. In this instance, Eq. (22) is simplified to the Casimir energy density when $\mu =1, \nu =0$ and $r_0=r$. From Eqs. (22) and (8), we obtain the differential equation

$$\begin{aligned} & 2^m \alpha \left( \frac{b'(r)}{r^2}\right) ^{m+1}\nonumber \\ & \quad =-\frac{\pi ^2 r_0 \left( \mu e^{\lambda _1 (r_0-r)}+(\nu -1) e^{\lambda _2 (r_0-r)}\right) }{720 r^5}. \end{aligned}$$

(23)

Fig. 6

The profile of $b(r), b'(r),b(r)-r$ and b(r)/r versus r with $m=2, r_0=0.5,$ and $\lambda =1.45$

Fig. 7

The profile of energy density and energy conditions with $m=2, r_0=0.5$ and $\lambda =1.45$

Since Eq. (23) is a non-linear differential equation, it proves challenging to find analytical solutions. Hence, we will employ a numerical approach to explore the behavior of the shape function with the initial condition $b(0.5)=0.5$. The visual representation of $b(r), b'(r), b(r)/r, b(r)-r$ are shown in Fig. 6. In this case, we choose some particular values of parameters to satisfy all the properties of the shape function associated with $m=2, r_0=0.5,$ and $\lambda =1.45$. Clearly, the shape function is a monotonically increasing function. The derivative of the shape function is less than one, thereby fulfilling the flaring-out condition. Additionally, the ratio b(r)/r approaches 0 as the radial coordinate increases, indicating the asymptotic flatness of the metric. The throat of the wormhole occurs where $b(r)-r$ intersects the r-axis.

Both the NEC and DEC are found to be violated. The breach of the NEC suggests the existence of hypothetical matter at the throat of the wormhole. On the other hand, the SEC is upheld. These features are visually depicted in Fig. 7.

7 Power-law form of specific energy density

In this portion, we shall consider the specific power-law form of energy density denoted as [49,50,51]

$$\begin{aligned} \rho =\rho _0\left( \dfrac{r_0}{r}\right) ^n, \end{aligned}$$

(24)

where $n,\rho _0>0$ are some constants. By comparing the specific energy density (SED) (24) and Eq. (8), we derive the shape function in the following form:

$$\begin{aligned} b(r)=\frac{(m+1) r \left( \dfrac{ 2^{-m} r_0^n r^{2 m-n+2}\rho _0}{\alpha }\right) ^{\frac{1}{m+1}}}{3 m-n+3}+\mathscr {C}. \end{aligned}$$

(25)

Through the imposition of an initial condition $b(r_0)=r_0$, we find out the value of $\mathscr {C}$ as given below:

$$\begin{aligned} \mathscr {C}\!=\! -\!\dfrac{r_0 \left( \!m \left( \dfrac{ 2^{-m} r_0^{2 m\!+\!2}\rho _0}{\alpha }\right) ^{\frac{1}{m\!+\!1}}\!\!+\!\!\left( \dfrac{ 2^{-m} r_0^{2 m\!+\!2}\rho _0}{\alpha }\right) ^{\frac{1}{m\!+\!1}}\!\!-3 m\!+\!n\!-\!3\right) }{3 m-n+3}.\nonumber \\ \end{aligned}$$

(26)

Fig. 8

The profile shows the behavior of shape function with $m=2, n=5, r_0=0.5,$ and $\lambda =1.45$

For our investigation, we know that $0< b(r) < r$ for $r \ge r0$ will satisfy if $-1< m < n-1$. Using the aforementioned expression of the shape function, we plot $b(r), b'(r), b(r)-r, b(r)/r$ in Fig. 8. It is evident that the shape function is a positively increasing function throughout the region. It also satisfies the throat condition, flaring-out condition, and asymptotic flatness condition. This characteristic ensures that the derived shape function fulfills the traversability conditions for a wormhole.

Figure 9 illustrates the features of stress- energy tensor components and energy conditions. It is important to note that the energy density remains positive throughout the entire spacetime. By examining the inequalities $\rho +p_r<0$ and $\rho +p_t>0$, we observe a violation of the NEC for various $\alpha$ values. Furthermore, the conditions $\rho -|p_r|,\rho -|p_t|$ and $\rho +p_r+2p_t$ are violated.

Fig. 9

The profile represents the characteristics of energy density and energy conditions with $m=2, n=5, r_0=0.5,$ and $\lambda =1.45$

Now, by substituting Eqs. (25) and (26) into (9) and (10), the pressure elements can be rewritten as

$$\begin{aligned} & p_r =\! \frac{\alpha 2^{m-1} }{(m\!+\!1)^2 r^3 (3 m\!-\!n\!+\!3)}\!\times \left( \frac{\left( \frac{\rho _0 2^{-m} r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}}}{r^2}\right) ^m\nonumber \\ & \quad \times \left[ -\Bigg ((3 + 3 m - n) (2 m n (1 + m + m n) r\right. \nonumber \\ & \quad - (2 + m (2 + n)) (-1 + m (-1 + 2 n)) r_0)\Bigg )\nonumber \\ & \quad \times 2 m^3 n^2 r \left( \frac{\rho _0 2^{-m}r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \quad -2 m^3 r \left( \frac{\rho _0 2^{-m} r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \quad +3 m^2 n^2 r \left( \frac{\rho _0 2^{-m} r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}} \nonumber \\ & \quad -6 m^2 r \left( \frac{\rho _0 2^{-m} r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \quad +m n^2 r \left( \frac{\rho _0 2^{-m} r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \quad -6 m r \left( \frac{\rho _0 2^{-m} r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}} \nonumber \\ & \quad -2 r \left( \frac{\rho _0 2^{-m} r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \quad -(m+1) r_0 (m (n+2)+2) (m (2 n-1)-1) \nonumber \\ & \left. \quad \times \left( \frac{\rho _0 2^{-m} r_0^{2 m+2}}{\alpha }\right) ^{\frac{1}{m+1}} \right] , \end{aligned}$$

(27)

$$\begin{aligned} & p_t = \frac{\alpha 2^{m-1}}{(m+1) r^3 (3 m-n+3)}\nonumber \\ & \quad \times \left( \frac{\left( \frac{\rho _0 2^{-m} r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}}}{r^2}\right) ^m\nonumber \\ & \quad \left[ 2 m^2 n r_0 \left( \frac{\rho _0 2^{-m} r_0^{2 m+2}}{\alpha }\right) ^{\frac{1}{m+1}}\right. \nonumber \\ & \quad +2 m n r_0 \left( \frac{\rho _0 2^{-m} r_0^{2 m+2}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \quad -2 m r_0 \left( \frac{\rho _0 2^{-m} r_0^{2 m+2}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \quad -r_0 \left( \frac{\rho _0 2^{-m} r_0^{2 m+2}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \quad -m^2 r_0 \left( \frac{\rho _0 2^{-m} r_0^{2 m+2}}{\alpha }\right) ^{\frac{1}{m+1}} \nonumber \\ & \quad -(m+1) r (2 m (n+1)-n+2)\nonumber \\ & \quad \times \left( \frac{\rho _0 2^{-m} r_0^n r^{2 m-n+2}}{\alpha }\right) ^{\frac{1}{m+1}}\nonumber \\ & \left. \quad +(3 + 3 m - n) (r_0 + m (2 n (r - r_0) + r_0))\right] \end{aligned}$$

(28)

8 Embedding procedures for wormhole geometry

In this section, we have employed an embedding diagram to visually elucidate the characteristics of wormhole geometry. The effectiveness of this visualization depends on the selection of the shape function b(r). In the framework of spherically symmetric spacetime, we specifically focus on the equatorial slice defined by $\theta =\frac{\pi }{2}$ for a fixed time i.e., $t=$ constant. Under these conditions, the metric (1) reduces to

$$\begin{aligned} ds^2=\left( 1-\frac{b(r)}{r}\right) ^{-1} dr^2 + r^2 d\phi ^2. \end{aligned}$$

(29)

Now, the aforementioned slice can be embedded into its hypersurface with cylindrical coordinates $(r,\phi ,z)$ as

$$\begin{aligned} ds^2=dz^2+dr^2+r^2 d\phi ^2. \end{aligned}$$

(30)

By comparing Eqs. (29) and (30), we can find the embedding surface, which is expressed as follows:

$$\begin{aligned} \frac{dz}{dr}= \pm \left[ \dfrac{b(r)}{r-b(r)}\right] ^{1/2}. \end{aligned}$$

(31)

Fig. 10

The two-dimensional embedding diagram of Yukawa–Casimir Wormhole solutions

The two-dimensional embedding diagrams for three distinct scenarios are depicted in Fig. 10.

9 Conclusion

Our research is centered on investigating the existence of Yukawa–Casimir wormholes within the framework of f(R) gravity. To achieve this, we have scrutinized the influence of anisotropic fluid in a spherically symmetric spacetime. Casimir energy serves as a source of exotic energy with a negative nature, and it has the capacity to facilitate the traversable nature of wormhole geometries. By introducing the Yukawa term into the initial Casimir wormhole, we have constructed the Yukawa–Casimir wormhole. Presently, the concept of Yukawa–Casimir wormholes signifies pioneering research within the scientific community. Throughout this investigation, we incorporated modified Casimir energy density to explore the feasibility of traversable wormholes under three distinct scenarios. In [37], Garattini introduced the concept of modified Casimir energy density. Our aim in examining the implications of this modified Casimir energy density was to elucidate the fundamental principles dictating the behavior of traversable wormholes. Furthermore, our investigation extended to examine the wormhole solution utilizing a specific energy density and to elucidate the embedding procedures for wormhole geometry. The summary of results obtained from our analysis are as follows:

• In this document, we considered the power-law form of wormhole model expressed as $f(R)=\dfrac{\alpha }{m+1}R^{m+1}$ with $F=\alpha \,R^m$ [48], where F is derivative of the model. We assumed a constant redshift function in our analysis to derive asymptotically flat wormhole solutions using Yukawa–Casimir energy density.

• In the first case, we examined the original Casimir energy density modified by a Yukawa term, given by $\rho _{y}=r_0\, \rho _c \dfrac{e^{\lambda (r_0-r)}}{r}$, where $\lambda >0$ and $\rho _c$ is Casimir energy density. We observed that when $r_0=r$, one can readily obtain the pure Casimir energy density. Here, we derived the shape function and conducted a comprehensive examination of the energy conditions. Notably, the shape function is found to meet the necessary conditions for traversable wormholes as shown in Fig. 2. Moreover, the features of stress-energy tensor components and energy conditions are depicted in Fig. 3, revealing a violation of the NEC.

• Secondly, we considered the modified Casimir energy density $\rho _{y}=\dfrac{\rho _c }{2r}\left( \mu \, r+\nu \,r_0\,e^{\lambda (r_0-r)}\right)$, where parameters $\mu =\nu =1$ and $\lambda >0$. In this scenario, the obtained differential equation proves challenging to solve analytically. Therefore, we employed a numerical method with initial condition $b(0.5)=0.5$ to solve it. The visual representation of shape function and energy conditions are presented in Figs. 4 and 5. Clearly, one can observe that the violation of the NEC indicates the presence of a hypothetical fluid at the throat of the wormhole.

• In the third case, we explored the implication of Yukawa–Casimir energy density, which is in the form of $\rho _{y}=\dfrac{\rho _c\, r_0 }{r}\left( \mu \, e^{\lambda (r_0-r)}-(1-\nu ) \,e^{\lambda (r_0-r)}\right)$ with $\lambda ,\mu ,\nu$ are some parameters. Similarly, we employed the initial condition $b(0.5)=0.5$ to solve the obtained differential equation numerically. Remarkably, we also found that the wormhole throat contains exotic fluid, evidenced by the violation of the NEC at the throat (Fig. 7).

• Subsequently, we assumed the power law form of specific energy density to investigate wormhole solutions within f(R) gravity. The resulting shape function demonstrated satisfactory behavior, meeting all necessary criteria within the specified parameter range, where $n,\rho _0>0, m=2$ and $\alpha \in (0,\infty )$ (Fig. 8). In this instance, the conditions $\rho +p_r<0$ and $\rho +p_t>0$ indicate a violation of the NEC (Fig. 9).

• The asymptotic expansion was discussed in the first case, but in the remaining two cases, we solved the differential equation numerically, so we did not obtain an analytic expansion. Furthermore, the asymptotic series expansion also provided the same expression of the shape function, so here we check the range of m in the specific energy density case.

• Finally, we have provided detailed explanations and diagrams illustrating the embedding of wormhole configurations in both two and three-dimensional Euclidean space.

Overall, this research elucidates the physically plausible behavior of Yukawa–Casimir wormholes within the framework of f(R) gravity.