1 Introduction

Our universe raises marvelous questions for the scientific community due to its mysterious nature. The existence of hypothetical structures are considered the most controversial issues that create the wormhole (WH) structures. It is defined as a speculative tunnel through which observers may be able to travel freely from one part of spacetime to another. An intra-universe WH is a bridge that connects distant parts of the same spacetime, while an inter-universe WH joins distant regions of the separate spacetime. In 1916, Flamm [1] established WH geometry through the Schwarzschild solution. Later, Einstein and Rosen [2] demonstrated that a curved-space structure can connect two separate parts of the universe through a tunnel named as Einstein-Rosen bridge. In 1950, Wheeler [3] found that Schwarzschild WH is non-traversable because two-way traveling is not possible in it, and anything attempting to pass through would be destroyed by the tremendous tidal forces present at the WH throat. Moreover, the WH throat rapidly expands from zero to finite circumference and then compresses to zero with time, thus prevents the access to anything. However, Wheeler and Fuller [4] investigated that WHs would collapse instantly after the formation.

The existence of a viable WH geometry is questioned due to a large amount of exotic matter (which violates energy conditions). Hence, the exotic matter in the bridge must be minimum for a viable WH structure. The first traversable WH was proposed by Morris and Thorne [5]. One may confine the exotic matter at the WH throat with the help of matching conditions [6]. Vacaru et al. [7] studied the anisotropic WH solutions through a holonomic approach. Wormholes can be classified into static and dynamic WHs [8,9,10]. In contrast to non-static WHs configuration, static WHs have a fixed radius on the throat. Dzhunushaliev et al. [11] investigated the stability of WH configurations in the presence and absence of an electromagnetic field. The static spherically symmetric Lorentzian WH solutions have been explored in [12]. The study of WH shape function with its properties is one of the interesting subject in traversable WH geometry. Recently, some people [13,14,15] proposed different shape functions to explain the WH geometry.

Several methods have been used to analyze the WH geometry such as particular form of the equation of state, the solution of metric potentials and constraint on matter variables. In this regard, the embedding class-I technique has been established that provides a relation between radial and time coordinates which helps to study the cosmic objects. According to this strategy, an n-dimensional manifold can be embedded into \((n+m)\)-dimensional manifold. The embedding class-I condition is developed to examine static spherically symmetric solution [16]. A necessary condition for a static spherically symmetric line element which belongs to class-I was developed by Karmarkar [17]. Recently, spherically symmetric objects with various matter configurations through the Karmarkar condition have been discussed [18,19,20,21,22]. Fayyaz and Shamir [23] used Karmarkar condition to examine the viable as well as stable WH structures.

In the literature, several hypotheses have been proposed to analyze dark energy such as quintessence fields, positive cosmological constant and Chaplygin gas. To explain the accelerated expansion of the universe, one may only need to include the cosmological constant or any other exotic resource. In this perspective, modified gravitational theories are considered the most effective techniques to describe the cosmic mysteries. Accordingly, one of the simplest modified theory is f(R) gravity which describes dark energy and accelerated expansion of the universe. Harko et al. [24] generalized f(R) theory by introducing the concept of curvature-matter coupling and named as f(R, T) theory of gravity. This modified theory is non-conserved that ensures the presence of an extra force and consequently, non-geodesic motion of particles. Houndjo [25] numerically established holographic dark energy model to discuss the cosmic expansion and found that this theory reproduces a similar extension history as produced by general relativity (GR). In the f(R, T) framework, many cosmic topics have been studied such as anisotropic solutions, energy constraints, thermodynamics, viscosity solution, phase space and stability analysis [26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42].

The physical viable features of WHs yield interesting results in the context of alternative theories of gravity. Lobo and Oliveira [43] studied traversable WH geometry through different shape functions and equations of state in f(R) gravity. Bertolami and Ferreira [44] examined that curvature-matter coupled theory yields viable WH solutions. The viable traversable WH geometry with a specific equation of state in f(R, T) gravity has been examined in [45]. Sharif and Fatima [46] considered viable f(G) model to investigate static spherically symmetric WH solutions (G is the Gauss-Bonnet invariant). Sharif and Shahid [47] explored viable static WH solutions through Noether symmetry technique in the framework of f(G, T) gravity. Shamir et al. [48] considered static spherical geometry with anisotropic fluid source to discuss WH solutions in f(R) theory. Mustafa et al. [49] obtained physically realistic traversable WH solutions through the Karmarkar condition in f(Q) gravity (Q is the non-metricity scalar).

Shamir and Fayyaz [50] constructed a shape function through Karmarkar condition in f(R) gravity and found that WH structure can be obtained with a negligible amount of exotic matter. Sharif and Gul [51] examined static WH solutions through Noether symmetry approach in the context of \(f(R,T^2)\) theory, where \(T^2\) is the self-contraction of energy-momentum tensor. Naz et al. [52] investigated the geometry of compact stars by using Karmarkar condition in the background of f(R) gravity. Mustafa et al. [53] examined the Gaussian and Lorentzian distributed spherically symmetric WH solutions in \(f(\tau ,T)\) gravity, where \(\tau\) is torsion. Godani [54] explored the traversable WHs in the context of f(R, T) theory of gravity with \(f(R,T)=R+2\lambda T\), where \(\lambda\) is an arbitrary constant. Malik et al. [55] examined traversable WH models in f(R) theory by applying the Karmarkar condition.

In this paper, we investigate traversable WH solutions in f(R, T) gravity by using the Karmarkar condition. For this purpose, we evaluate the behavior of the shape function and null energy condition (NEC). The paper is planned as follows. In Sect. 2, we employ the Karmarkar condition to formulate a WH shape function. The field equations are constructed in Sect. 3 to give a brief overview of f(R, T) theory. We take three different viable models of this theory to examine the behavior of NEC graphically. In Sect. 4, we study the stability of a viable WH through the speed of sound and adiabatic index. We summarize our results in Sect. 5.

2 Wormhole and Karmarkar condition

In this section, we formulate the WH shape function through Karmarkar condition which determines the structure of WH. For this purpose, we consider a static spherically symmetric spacetime as

$$ds^{2} = - e^{{\mu (r)}} dt^{2} + e^{{\nu (r)}} dr^{2} + r^{2} \left( {d\theta ^{2} + \sin ^{2} \theta d\phi ^{2} } \right).{\text{ }}$$
(1)

The corresponding non-zero Riemann curvature components are

$$\begin{aligned} R_{1212}= & {} \frac{e^{\mu }\left(2\mu ''+\mu ^{\prime 2}-\mu '\nu '\right)}{4}, \quad R_{3434}=\frac{r^{2}\sin ^{2}\theta (e^{\nu }-1)}{e^{\nu }}, \\ R_{1414}= & {} \frac{r\sin ^{2}\theta \mu 'e^{\mu -\nu }}{2}, \quad R_{2323}=\frac{r\nu '}{2}, \quad R_{1334}=R_{1224}\sin ^{2}\theta=0 . \end{aligned}$$

The well-known Karmarkar constraint is fulfilled by the above Riemann elements as

$$\begin{aligned} R_{1414}= & {} \frac{R_{1212}R_{3434}+R_{1224}R_{1334}}{R_{2323}},\quad R_{2323}\ne 0. \end{aligned}$$
(2)

The spacetime which satisfies the Karmarkar constraint is named as embedding class-I. Substituting the values of Riemann components in Eq.(2), we obtain

$$\begin{aligned} \frac{\mu '\nu '}{1-e^{\nu }}=\mu '\nu '-2\mu ''-\mu ^{\prime 2}, \end{aligned}$$

where \(e^{\nu }\ne 1\). The corresponding solution is

$$\begin{aligned} e^{\nu }=1+A e^{\mu }\mu ^{\prime 2}, \end{aligned}$$
(3)

where A is an integration constant.

We assume the Morris-Thorne metric to describe the shape function as

$$\begin{aligned} ds^{2}=-e^{\mu (r)}dt^{2}+\frac{1}{1-\frac{\epsilon (r)}{r}}dr^{2} +r^{2}d\theta ^{2}+r^{2}\sin \theta d\phi ^{2}, \end{aligned}$$
(4)

here \(\mu (r)=\frac{-2\xi }{r}\) (\(\xi\) is an arbitrary constant) is considered the redshift function as \(\mu (r)\rightarrow 0\), when \(r\rightarrow \infty\) [56]. By comparing Eqs.(1) and (4), we have

$$\begin{aligned} \nu (r)=\ln \bigg [\frac{r}{r-\epsilon (r)}\bigg ]. \end{aligned}$$
(5)

We evaluate the WH shape function from Eqs.(3) and (5) as

$$\begin{aligned} \epsilon (r)=r-\frac{r^{5}}{r^{4}+4\xi ^{2}Ae^{\frac{-2\xi }{r}}}. \end{aligned}$$
(6)

According to Morris and Thorne [5], the shape function must fulfill the following conditions to obtain a traversable WH solution.

  1. 1.

    \(\epsilon (r)<r\),

  2. 2.

    \(\epsilon (r)-r=0\) at \(r=a\),

  3. 3.

    \(\frac{\epsilon (r)-r\epsilon '(r)}{\epsilon ^{2}(r)}>0\) at \(r=a\),

  4. 4.

    The condition \(\epsilon '(r)<1\) should be satisfied,

  5. 5.

    \(\frac{\epsilon (r)}{r}\rightarrow 0\) must satisfy as \(r\rightarrow \infty\),

where a is the WH throat radius. Equation (6) has a trivial solution at WH throat, i.e., \(\epsilon (a)-a=0\). To obtain a non-trivial solution, we modify Eq.(6) with the inclusion of free parameter c as

$$\begin{aligned} \epsilon (r)=r-\frac{r^{5}}{r^{4}+4\xi ^{2}Ae^{\frac{-2\xi }{r}}}+c. \end{aligned}$$
(7)

The value of c should be confined in the range \(0<c<a\). For other values of c, the conditions of wormhole shape function are not satisfied that are necessary for a physically viable WH structures. Using the condition \(\epsilon (r)-r=0\) at \(r=a\) in the above equation, we obtain \(A=\frac{a^{4}(a-c)}{4\xi ^{2}e^{\frac{-2\xi ^{2}}{a}}}\). Substituting the value of A in the above equation, the shape function becomes

$$\begin{aligned} \epsilon (r)=r-\frac{r^{5}}{r^{4}+a^{4}(a-c)}+c. \end{aligned}$$
(8)

This can easily be seen that this shape function satisfies the condition (5) as follows

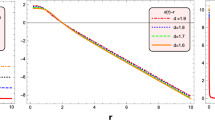
$$\begin{aligned} \lim_{r\rightarrow \infty }\frac{\epsilon (r)}{r}=0. \end{aligned}$$
(9)

Thus, asymptotically flat traversable WHs are obtained through this WH shape function. For our convenience, we consider \(a=2\) and \(\xi =-1\) in all the graphs. The graphical behavior of the WH shape function is given in Fig. 1 which shows that the WH shape function satisfies all the necessary conditions.

Fig. 1
figure 1

Behavior of shape function corresponding to radial coordinate for \(c=1.9\) (blue line), \(c=1.8\) (green line), \(c=1.7\) (orange line) and \(c=1.6\) (red line)

Full size image

3 Basic formalism of f(R, T) gravity

The action of this modified theory is defined as

$$\begin{aligned} I=\int dx^{4}\sqrt{-g}[f(R,T)+L_{m}], \end{aligned}$$
(10)

where g represents determinant of the line element and \(L_{m}\) is the matter-Lagrangian density. The corresponding field equations are

$$\begin{aligned} R_{\alpha \beta }f_{R}-\frac{1}{2}g_{\alpha \beta }f +(g_{\alpha \beta }\Box -\nabla _{\alpha} \nabla_{\beta} )f_{_{R}}+f_{T}\Theta _{\alpha \beta }+f_{T}T_{\alpha \beta }=T_{\alpha \beta }. \end{aligned}$$
(11)

Here, \(f\equiv f(R,T)\) and \(f_{R}\) represents derivative with respect to the Ricci scalar and \(f_{T}\) denotes derivative with respect to trace of the energy-momentum tensor. The expression of \(\Theta _{\alpha \beta }\) is given by

$$\begin{aligned} \Theta _{\alpha \beta }=-2T_{\alpha \beta }+g_{\alpha \beta }L_{m}-2g^{\upsilon \tau } \frac{\partial ^{2}L_{m}}{\partial g^{\alpha \beta }\partial g^{\upsilon \tau }}. \end{aligned}$$
(12)

The f(R, T) gravity provides non-conserved stress-energy tensor implying the presence of an extra force which acts as a non-geodesic motion of particles given by

$$\begin{aligned} \nabla ^{\alpha }T_{\alpha \beta }=\frac{f_{T}}{1-f_{T}}\bigg [(T_{\alpha \beta } +\Theta _{\alpha \beta })\nabla ^{\alpha }\ln f_{T}+\nabla ^{\alpha }\Theta _{\alpha \beta }-\frac{1}{2}g_{\alpha \beta }T\bigg ]. \end{aligned}$$

This shows that the covariant derivative of the stress-energy tensor in f(R, T) theory does not vanish.

We consider anisotropic fluid configuration as

$$\begin{aligned} T_{\alpha \beta }=(P_{r}-P_{t})\chi _{\alpha }\chi _{\beta }-P_{t}g_{\alpha \beta }+({\rho} +P_{t})V_{\alpha }V_{\beta }, \end{aligned}$$
(13)

where \({\rho}\), \(P_{r}\) and \(P_{t}\) represent the energy density, radial and tangential pressures, respectively. Using Eqs.(1) and (11), the resulting field equations become

$$\begin{aligned} {\rho}= & {} \frac{1}{e^{\nu }}\bigg [-\frac{f}{2}e^{\nu }+\bigg (\frac{\mu '}{r} -\frac{\mu '\nu '}{4}+\frac{\mu ''}{2}+\frac{\mu ^{\prime 2}}{4}\bigg )f_{R} +\bigg (\frac{\nu '}{2}-\frac{2}{r}\bigg )f'_{R}-f''_{R}\bigg ], \end{aligned}$$
(14)
$$\begin{aligned} P_{r}= & {} \frac{1}{{e^{\nu }(1+f_{T})}}\bigg [\frac{f}{2}e^{\nu }+\bigg (\frac{\mu ''}{2}-\frac{\nu '}{r}-\frac{\mu '\nu '}{4}+\frac{\mu ^{\prime 2}}{4}\bigg )f_{R}+\bigg (\frac{\mu '}{2}+\frac{2}{r}\bigg )f'_{R} -{\rho} f_{T}e^{\nu }\bigg ], \end{aligned}$$
(15)
$$\begin{aligned} P_{t}= & {} \frac{1}{{e^{\nu }(1+f_{T})}}\bigg [\frac{f}{2}e^{\nu }+\bigg (\frac{(\nu '-\mu ')r}{2}+e^{\nu }-1\bigg )\frac{f_{R}}{r^{2}}+\bigg (\frac{\mu '-\nu '}{2}+\frac{1}{r}\bigg ) f'_{R} +f''_{R}-{\rho} f_{T}e^{\nu }\bigg ]. \end{aligned}$$
(16)

The field equations (14)-(16) appear to be more complex due to the existence of multivariate functions and their derivatives. We assume a particular f(R, T) model to solve these equations as [24]

$$\begin{aligned} f(R,T)=f_{1}(R)+f_{2}(T). \end{aligned}$$
(17)

Different viable models of f(R, T) theory can be discussed by considering various forms of \(f_{1}(R)\) and \(f_{2}(T)\). However, for the sake of simplicity, we take \(f_{2}(T)=\lambda T\) [24] to solve the field equations. There can be other choices of f(T) such that one can take non-minimal model. The field equations corresponding to the model (17) are given in Eqs.(A1)-(A3) of Appendix A.

Now, we study various f(R, T) models corresponding to \(f_{1}(R)\) in the following subsections.

3.1 Model 1: Exponential gravity model

Cognola et al. [57] investigated the exponential gravity model as

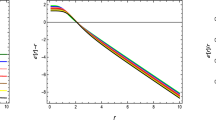
$$\begin{aligned} f(R)=R-KB\bigg [1-e^{\frac{-R}{B}}\bigg ], \end{aligned}$$
(18)

which explains the current cosmic expansion as well as inflation of the early time. Here K and B are arbitrary constants. The resulting equations of motion are given in Eqs.(A4)-(A6) of Appendix A. Energy constraints play a significant role to determine the physical existence of cosmic structures. These energy bounds must be violated for the existence of realistic WH geometry. In modified theories, the violation of NEC \(({\rho} +P_{t}\), \({\rho} +P_{r})\) ensures the existence of a viable traversable WH geometry. The graphical behavior of NEC for different values of K and B is given in Fig. 2. This shows that matter variables violate the null energy bound for positive values of B and negative values of K which ensures the presence of viable traversable WH. However, positive values of model parameters satisfy the NEC and hence show the absence of exotic matter at WH throat.

Fig. 2
figure 2

NEC versus radial coordinate for \(K=-7\), \(B=9\) (blue line), \(K=-5\), \(B=8\) (green line), \(K=-3\), \(B=6\) (orange line), \(K=5\), \(B=14\) (red line), \(K=6\), \(B=12\) (black line), \(K=7\), \(B=10\) (purple line)

Full size image

3.2 Model 2: Starobinsky gravity model

Here, we use the Starobinsky model [58] as

$$\begin{aligned} f(R)=R-\gamma B\bigg [1-\bigg (1+\frac{R^{2}}{B^{2}}\bigg )^{-n}\bigg ], \end{aligned}$$
(19)

which satisfies the solar system tests, complies all the cosmic as well as localized gravity restrictions and has attributes of dark energy models, \(\gamma\) and n are constants. The field equations corresponding to this model are given in Eqs.(A7)-(A9) of Appendix A. The graphical behavior of NEC for positive as well as negative values of n is given in Fig. 3. For \(n<0\), the NEC violates corresponding to negative values of B and positive values of \(\gamma\) which gives the presence of traversable spherically symmetric WH geometry. For \(n>0\), when \(B<0\) and \(\gamma <0\), a small amount of exotic matter is present at the WH throat so a viable WH can be obtained.

Fig. 3
figure 3

NEC versus radial coordinate for \(\gamma =1\), \(B=-23\), \(n=-1\) (blue line), \(\gamma =1.5\), \(B=-25\), \(n=-0.9\) (green line), \(\gamma =1.8\), \(B=-27\), \(n=-0.85\) (orange line), \(\gamma =-0.6\), \(B=-5.4\), \(n=2\) (red line), \(\gamma =-0.8\), \(B=-5.2\), \(n=1.5\) (black line), \(\gamma =-1\), \(B=-5\), \(n=1\) (purple line)

Full size image

3.3 Model 3: Tsujikawa gravity model

Finally, we consider another well-known model [59], defined as

$$\begin{aligned} f(R)=R-\omega B\tanh \bigg (\frac{R}{B}\bigg ), \end{aligned}$$
(20)

where \(\omega\) is an arbitrary constant and the corresponding field equations are given in Eqs.(A10)-(A12) of Appendix A. Figure 4 shows the graphical behavior of NEC for different values of \(\omega\) and B. This indicates the existence of viable traversable WH for negative values of B and \(\omega\). However, positive values of \(\omega\) and negative values of B satisfy the NEC.

Fig. 4
figure 4

NEC versus r for \(\omega =-10\), \(B=-6\), (blue line), \(\omega =-9.5\), \(B=-5.5\), (green line), \(\omega =-9\), \(B=-5\), (orange line), \(\omega =8\), \(B=-5.2\), (red line), \(\omega =9\), \(B=-6\), (black line), \(\omega =10\), \(B=-7\), (purple line)

Full size image

4 Stability analysis

Stability is significant to analyze the valid and consistent cosmic structures. It is more interesting to examine cosmic objects that display stable behavior under the external perturbations. Here, we examine the stability of viable and traversable WH solutions through sound speed and adiabatic index.

4.1 Speed of sound

We investigate the stability of WH solution through causality condition and Herrera’s cracking method. The causality criteria states that the speed of sound components \((v^{2}_{r}=\frac{dP_{r}}{d{\rho}},~v_{t}^{2} =\frac{dP_{t}}{d{\rho}})\) should be confined in the range [0,1] for stable structures. Figure 5 shows that traversable WH satisfy the required causality condition in the presence of modified terms. According to Herrera cracking technique, the difference in sound speed components should be \(0\le \mid v_{t}^{2}-v^{2}_{r}\mid \le 1\). Figure 6 demonstrates that WH solutions are in the stable state as they satisfy the required condition corresponding to all considered f(R, T) models. Hence, we obtain physically stable traversable WH in this modified theory.

Fig. 5
figure 5

Behavior of causality condition versus r

Full size image
Fig. 6
figure 6

Behavior of Herrera cracking versus r

Full size image

4.2 Adiabatic index

Fig. 7
figure 7

Behavior of adiabatic index versus r

Full size image

The adiabatic index is another factor used to explore the stability of celestial objects. The radial and transverse components of adiabatic index for anisotropic fluid are defined as

$$\begin{aligned} \Gamma _{r}=\frac{{\rho} +P_{r}}{P_{r}}\frac{dP_{r}}{d{\rho}},\quad \Gamma _{t}=\frac{{\rho} +P_{t}}{P_{t}}\frac{dP_{t}}{d{\rho}}. \end{aligned}$$

According to Heintzmann and Hillebrandt [60], a system is stable if \(\Gamma >4/3\), otherwise it is unstable. Figure 7 shows that traversable WH solutions have adiabatic index greater than 4/3, indicating that our system is stable even when higher-order matter source terms are present.

5 Final remarks

There have been different methods to obtain viable WH solutions in the literature. One of them is to evaluate the shape function by making certain hypotheses for the matter ingredients and the other is to investigate how the energy conditions behave by considering the shape function. In this paper, we have examined whether WH solutions exist or not by building the shape function using Karmakar condition in f(R, T) theory. We have explored exact solutions of static spherically symmetric traversable WHs corresponding to three viable f(R, T) models, i.e., the exponential gravity model, Starobinsky gravity model and Tsujikawa gravity model. We have checked the graphical behavior of NEC to examine the traversable WH geometry. The stability is examined through the causality condition, Herrera cracking approach and the adiabatic index. The summary of the obtained results is given as follows.

  • The considered shape function yields a viable WH structure by satisfying all the required conditions as shown in Fig. 1.

  • The exponential gravity model shows that NEC violates for \(K<0\) and \(B>0\), which ensures the presence of exotic matter at WH throat. Hence, viable traversable WH is obtained for specific values of the model parameters.

  • For the Starobinsky gravity model, WH solutions exist for a wide range of parameters, i.e., for \(B<0\), \(n<0\) and \(\gamma >0\) which shows the existence of exotic matter at WH throat (Fig. 3). When \(n>0\) and \(\gamma <0\), NEC is again violated with negligible amount of exotic matter. Thus we have found viable traversable WH with suitable values of the model parameters.

  • The presence of exotic matter at the throat is confirmed for the Tsujikawa gravity model when \(\omega <0\) and \(B<0\).

  • The stability requirements are verified in the presence of modified terms (Figs. 5, 6 and 7).

In the framework of GR, Fayyaz and Shamir [23] found viable and stable traversable WH structure in the presence of exotic matter. The same authors [50] concluded that there exist WH solution with a negligible amount of exotic matter in f(R) theory for the specific shape function. It is worth mentioning here that we have obtained WH solutions in f(R, T) gravity as NEC is violated which ensures the presence of exotic matter at WH throat. Thus we can conclude that viable and stable traversable WH solutions exist for anisotropic matter configuration through Karmarkar condition in this modified theory.