Exact Invariants of Chemical Reactions with Participation of Two Reagents

Abstract

Autonomous (temporal) invariants of nonlinear chemical reactions between two reagents are determined. For dynamic models of such reactions, analytical solutions exist that allow exact invariants to be found. Such invariants are ratios that connect non-equilibrium values of reagent concentrations, measured in two experiments with different initial conditions (dual experiments). These ratios remain strictly constant throughout the reaction. The relations obtained in this paper were applied to the study of the nonstationary properties of one-, two-, and three-stage nonlinear reactions proceeding in a closed system with the kinetic law of mass action. The invariant curves found for these reactions are compared with the curves of change in the concentrations of reagents over the entire transition process. It is shown that the dependences of the invariants on time remain strictly constant (have zero order), while the reagent concentrations undergo exponential changes during the transition process. The results obtained expand the understanding of the characteristics of nonlinear chemical reactions and can be used to solve inverse problems of unsteady chemical kinetics and modeling chemical reactors of ideal mixing under isothermal conditions.

INTRODUCTION

The determination of the exact autonomous (time-independent) kinetic invariants of chemical reactions is one an urgent problem in nonstationary chemical kinetics. Currently, this problem has been solved only for a few linear reactions. The dual method, introduced by G.S. Yablonsky et al. [1–8], was used for this problem. This method is based on the analysis of two non-equilibrium experiments with inverse initial boundary (thermodynamic) conditions; it is used as the theoretical basis [3] for the experimental methods of the non-equilibrium kinetics and chemical reactors construction, such as the technology of temporal analysis of products (TAP) [9].

The new results achieved in this field of the study of non-equilibrium chemical kinetics are presented in studies [10–16], where the multimethod that generalizes and expands the possibilities of the dual method for the application to the nonlinear dynamic systems and chemical reactions was introduced. This multimethod allows estimating the approximate autonomous invariants (quasi-invariants) of the nonlinear systems according to the results of two (or more) non-equilibrium initial conditions (not necessarily the boundary ones). Quasi-invariants are the combinations of the non-linear concentrations of the reagents (temperatures) that remain almost constant over the whole course of the reaction.

The search for new non-equilibrium characteristics of the nonlinear reactions attracts interest. Let us complete such a study and find analytical solutions for the exact autonomous invariants of the nonlinear chemical reactions between two reagents.

THEORETICAL CHAPTER

Let us examine the general formula of a chemical reaction between two reagents (A and B) that passes according to stages that can be described as

$${{a}_{i}}{\text{A}} + {{b}_{i}}{\text{B}} = {{a}_{{ - i}}}{\text{A}} + {{b}_{{ - i}}}{\text{B}},\,\,\,\,i = 1, \ldots ,s;$$

(1)

where a_±i ≥ 0, b_±i ≥ 0 (a_±ib_±i ≠ 0) are the stoichiometric coefficients of the reagents A and B, participating in the ith step. The dynamics of this reaction in a closed gradient-free isothermal reactor are described by the ordinary differential Eqs. (ODE) in terms of the law of mass action:

$$A{\kern 1pt} ' = \sum {({{a}_{{ - i}}} - {{a}_{i}})({{r}_{i}} - {{r}_{{ - i}}}) \equiv f({{k}_{i}},{{k}_{{ - i}}},A,B)} ,$$

(2)

$$B{\kern 1pt} ' = \sum {({{b}_{{ - i}}} - {{b}_{i}})({{r}_{i}} - {{r}_{{ - i}}}) \equiv g({{k}_{i}},{{k}_{{ - i}}},A,B)} ,$$

(3)

where A and B are the concentrations of the reagents A and B (molar fractions), respectively; r_i = k_iA^aiB^bi and r_−i = k_−iA^a−iB^b−i are the rates of the reaction steps in the forward and inverse directions (1/s); and k_i, k_−i are rate constants for the corresponding steps (1/s). Let us set initial conditions (IC) using the expressions

$$A\left( 0 \right) = {{A}_{0}},\,\,\,\,B\left( 0 \right) = {{B}_{0}}.$$

(4)

The coordinates of the equilibria A_∞, B_∞ for reaction (1) are determined using the conditions

$$f = g = 0.$$

(5)

A single stable solution [17–25] exists in the closed systems of the equilibrium Eq. (5); nonstationary conservation law (trivial exact autonomous invariant) is fulfilled:

$$A(t) + B(t) = {{A}_{\infty }} + {{B}_{\infty }} = {{A}_{0}} + {{B}_{0}} = 1.$$

(6)

According to Eq. (6), Eq. (7) sets the correlation between the stoichiometric coefficients:

$$\sum {({{a}_{{ - i}}} - {{a}_{i}}) = \sum {({{b}_{i}} - {{b}_{{ - i}}})} } .$$

(7)

Equations (6) and (7) mean that the Eqs. (2) and (3) depend on each other; the system (2), (3) is equivalent to the heterogeneous autonomous ODE:

$$A{\kern 1pt} ' = f\left( {{\mathbf{a}},A} \right),$$

(8)

where a=a(k_i, k_−i, A₀, B₀) is the vector of parameters.

In case of monomolecular steps, Eq. (8) is expressed as

$$A{\kern 1pt} ' = aA + b,$$

(9)

where a ≠ 0, b are the parameters. The general solution for this linear ODE is

$$A\left( t \right) = {{A}_{\infty }} + ({{A}_{0}} - {{A}_{\infty }})\exp ( - at),$$

(10)

where A_∞ = −b/a according to (5). Let us use the generalized method for the calculation of nonlinear quasi-invariants [16] to Eq. (10). Let us set the IC of A₀₁ ≠ A₀₂, introduce convenient designations, and determine the invariant

$$K\left( t \right) \equiv {{\left[ {{{A}_{1}}({{A}_{{02}}} - {{A}_{\infty }}) - {{A}_{2}}({{A}_{{01}}} - {{A}_{\infty }})} \right]} \mathord{\left/ {\vphantom {{\left[ {{{A}_{1}}({{A}_{{02}}} - {{A}_{\infty }}) - {{A}_{2}}({{A}_{{01}}} - {{A}_{\infty }})} \right]} {\left[ {{{A}_{\infty }}({{A}_{{02}}} - {{A}_{{01}}})} \right]}}} \right. \kern-0em} {\left[ {{{A}_{\infty }}({{A}_{{02}}} - {{A}_{{01}}})} \right]}} = 1.$$

(11)

It is clear that K(t) does not depend on time, although it does depend on the nonequilibrium concentrations of reagents, rate constants of the reaction steps and IC; this means that Eq. (11) is an exact autonomous invariant. Let us call the IC pairs A₀₁ = 1, B₀₁ = 0 and A₀₁ = 0, B₀₁ = 1 thermodynamic, meaning that they correspond to the inverse reactions. The Eqs. (9)–(11) can simulate only one inverse reaction: A = B.

In case of bimolecular steps the Eq. (8) is transformed into:

$$A{\kern 1pt} ' = c{{A}^{2}} + aA + b,$$

(12)

where a, b, c ≠ 0 are the parameters. The general solution of this ODE can be expressed as:

$$\begin{gathered} A\left( t \right) = \left[ { - a + D{\text{tan}}\left( {\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}} \right)} \right.} \right. \\ {{\left. {\left. { + \,{\text{arctan}}\left( {{{\left( {a + 2{{A}_{0}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{0}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} \mathord{\left/ {\vphantom {{\left. {\left. { + \,{\text{arctan}}\left( {{{\left( {a + 2{{A}_{0}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{0}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} {2c,}}} \right. \kern-0em} {2c,}} \\ \end{gathered} $$

(13)

where D = (4bc − a²)^1/2. According to (5), the equilibria are determined by the equation A_∞ = [–a ± (a² – 4bc)^1/2]/2с. These equilibria are real at a² > 4bc, i.e. when D = i|D| is the imaginary number (i is the imaginary unit, i² = −1; |D| is the modulus of a number) and tan((Dt/2) + arctan((a + 2A₀c)/D)) is the complex number. The eigenvalue λ = ∂A'/∂A = 2сA + a is equal to λ_{1, 2} = ±(a² − 4bc)^1/2 in two equilibria, i.e., only the smaller (−) equilibrium is stable [26]. This equilibrium is physical (0 < A_∞ < 1) at

$$c + a + b < 0,\,\,\,\,{{a}^{2}} > 4bc,\,\,\,\,a < 0,\,\,\,\,b > 0.$$

(14)

The equilibria are joint at a² = 4bc; their stability can not be determined under a linear approximation (λ_{1, 2} = 0). The equilibria become complex (nonphysical) at a² < 4bc.

Let us use again the generalized dual method [16]. Let us solve the Cauchy problem twice and put the solution (13) and (14) for the IC of A₀₁ ≠ A₀₂:

$$\begin{gathered} {{A}_{1}}\left( t \right) = \left[ { - a + D{\text{tan}}\left( {\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}} \right)} \right.} \right. \\ {{\left. {\left. { + \,\,{\text{arctan}}\left( {{{\left( {a + {\text{ }}2{{A}_{{01}}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + {\text{ }}2{{A}_{{01}}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} \mathord{\left/ {\vphantom {{\left. {\left. { + \,\,{\text{arctan}}\left( {{{\left( {a + {\text{ }}2{{A}_{{01}}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + {\text{ }}2{{A}_{{01}}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} {2c,}}} \right. \kern-0em} {2c,}} \\ \end{gathered} $$

(15)

$$\begin{gathered} {{A}_{2}}\left( t \right) = \left[ { - a + D{\text{tan}}} \right.\left( {\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}} \right)} \right. \\ {{\left. { + \left. {{\text{arctan}}\left( {{{\left( {a + 2{{A}_{{02}}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{{02}}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} \mathord{\left/ {\vphantom {{\left. { + \left. {{\text{arctan}}\left( {{{\left( {a + 2{{A}_{{02}}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{{02}}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} {2c.}}} \right. \kern-0em} {2c.}} \\ \end{gathered} $$

(16)

Let us solve each of these equations with respect to time:

$$\begin{gathered} {\text{arctan}}\left( {{{\left( {a + 2c{{A}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{1}}} \right)} D}} \right. \kern-0em} D}} \right) \\ - \,\,{\text{arctan}}\left( {{{\left( {a + 2c{{A}_{{01}}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{01}}}} \right)} D}} \right. \kern-0em} D}} \right) = {{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}, \\ \end{gathered} $$

$$\begin{gathered} {\text{arctan}}\left( {{{\left( {a + 2c{{A}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{2}}} \right)} D}} \right. \kern-0em} D}} \right) \\ - \,\,{\text{arctan}}\left( {{{\left( {a + 2c{{A}_{{02}}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{02}}}c} \right)} D}} \right. \kern-0em} D}} \right) = {{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}. \\ \end{gathered} $$

Let us subtract the second equation of this system from the first one, divide the obtained expression by its right part, introduce the designations, and put down the result as

$$K\left( t \right) \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$$

(17)

where

$$\begin{gathered} {{z}_{1}} \equiv {\text{arctan}}\left( {{{\left( {a + 2c{{A}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{1}}} \right)} D}} \right. \kern-0em} D}} \right) = - i{\text{arth}}\left( {{{\left( {a + 2c{{A}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{1}}} \right)} {\left| D \right|}}} \right. \kern-0em} {\left| D \right|}}} \right), \\ {{z}_{2}} \equiv {\text{arctan}}\left( {{{\left( {a + 2c{{A}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{2}}} \right)} D}} \right. \kern-0em} D}} \right) = - i{\text{arth}}\left( {{{\left( {a + 2c{{A}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{2}}} \right)} {\left| D \right|}}} \right. \kern-0em} {\left| D \right|}}} \right), \\ {{z}_{{01}}} \equiv {\text{arctan}}\left. {\left( {{{\left( {a + 2c{{A}_{{01}}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{01}}}} \right)} D}} \right. \kern-0em} D}} \right)} \right) \\ = - i{\text{arth}}\left( {{{\left( {a + 2c{{A}_{{01}}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{01}}}} \right)} {\left| D \right|}}} \right. \kern-0em} {\left| D \right|}}} \right), \\ {{z}_{{02}}} \equiv {\text{arctan}}\left. {\left( {{{\left( {a + 2c{{A}_{{02}}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{02}}}} \right)} D}} \right. \kern-0em} D}} \right)} \right) \\ = - i{\text{arth}}\left( {{{\left( {a + 2c{{A}_{{02}}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{02}}}} \right)} {\left| D \right|}}} \right. \kern-0em} {\left| D \right|}}} \right), \\ \end{gathered} $$

(18)

According to (17) and (18), K(t) depends on the non-equilibrium concentration of reagents, rate constants of reaction steps and IC but does not depend on time, i.e., ratio (17) is an exact nonlinear autonomous invariant. This invariant is expressed using the product of two imaginary numbers: imaginary unit (i) and arc-hyperbolic tangent (arth), so its value is always real. The ratios (12)–(18) can simulate six single- and two-stage bimolecular reactions, including the A = B, 2A = 2, and A + B = 2B steps.

The system (2), (3) is transformed into the following equation for the presence of termolecular reaction steps 3A = 3B, A + 2B = 3B, 2A + B = 3A, and A + 2B = B + 2A:

$$A{\kern 1pt} ' = d{{A}^{3}} + c{{A}^{2}} + aA + b.$$

(19)

The general solution for (19) is absent. Exact invariants of such reactions can be determined only for the particular (see Eqs. (1.7) and (1.8) below). The ratios (9)–(19) simulate 24 mechanisms of single-, two- and three-step mono-, bi-, and termolecular reactions. Numerous exact invariants corresponding to the different dual experiments exist for each of them. These invariants are the additional non-equilibrium characteristic of the mechanism of the studied reaction that can be used for its reconstruction. Let us examine the examples.

RESULTS AND DISCUSSION

Example 1. Let us determine the exact invariants of the reaction:

$$n{\text{A}} = n{\text{B}}.$$

(1.1)

The reaction of butylene isomerization t-C₄H₈ = c‑C₄H₈ is an example; it passes linearly if n = 1 [5] or nonlinearly if n > 1. If n = 1, then this reaction is described by the equation of the (9) type:

$$A{\kern 1pt} ' = - ({{k}_{{ - 1}}} + {{k}_{1}})A + {{k}_{{ - 1}}},$$

(1.2)

where a = −(k₋₁ + k₁) < 0, b = k₋₁ > 0. If k₁= 4, k₋₁ = 1, then a = −5, b = 1, A_∞ = 1/5. Let us select, for example, thermodynamic IC of A₀₁ = 1, A₀₂ = 0, then the Eq. (11) can be put down as:

$$K(t) \equiv {{A}_{1}}(t) + 4{{A}_{2}}(t) = 1.$$

(1.3)

The ratio (1.3) corresponds to the horizontal line on the plot of K(t) dependence; it is a linear autonomous invariant.

If n = 2, then reaction (1.1) is described by the Eq. (12):

$$A{\kern 1pt} ' = - {{k}_{1}}{{A}^{2}} + {{k}_{{ - 1}}}{{(1 - A)}^{2}},$$

(1.4)

where c = k₋₁ − k₁ ≠ 0 at k₁ ≠ k₋₁, a = −2k₋₁ < 0, b =$k_{{ - 1}}^{2}$ > 0. The conditions required for equilibrium (14) being physical are fulfilled at, for example, k₁= 4, k₋₁ = 1. Then a = −2, b = 1, c = −3, a² − 4bc = 16, A_∞ = 1/3, D = (−16)^1/2. Let us select thermodynamic IC of A₀₁ = 1, A₀₂ = 0, and the exact invariant (17) and (18) is expressed as:

$$K\left( t \right) \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$$

(1.5)

where

$$\begin{gathered} ~{{z}_{1}} = - {\text{arth}}\left( {{{\left( {2 + 6{{A}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {2 + 6{{A}_{1}}} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{2}} = - {\text{arth}}\left( {{{\left( {2 + 6{{A}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {2 + 6{{A}_{2}}} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{{01}}} = - {\text{arth}}\left( {{{\left( {2 + 6{{A}_{{01}}}} \right)} \mathord{\left/ {\vphantom {{\left( {2 + 6{{A}_{{01}}}} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{{02}}} = - {\text{arth}}\left( {{{\left( {2 + 6{{A}_{{02}}}} \right)} \mathord{\left/ {\vphantom {{\left( {2 + 6{{A}_{{02}}}} \right)} D}} \right. \kern-0em} D}} \right). \\ \end{gathered} $$

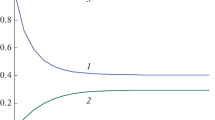
The invariant (1.5) is given in Fig. 1.

Fig. 1.

Solutions of two Cauchy problems and exact invariant for reaction (1.1) at n = 2, k₁= 4, k₋₁ = 1, A₀₁ = 1, A₀₂ = 0: (1) A₁(t); (2) A₂(t); (3) K(t).

Figure 1 shows that K(t) dependence is a horizontal line, i. e. it does not depend on time, therefore, the Eq. (1.5) is an exact autonomous invariant.

If n = 3 then reaction (1.1) is described by the equation:

$$A{\kern 1pt} ' = - {{k}_{1}}{{A}^{3}} + {{k}_{{ - 1}}}{{(1 - A)}^{3}}.$$

(1.6)

The general solution of (1.6) can be obtained only for the irreversible case of k₋₁ = 0:

$${{A}_{1}}(t){\text{ }} = {{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} {{{{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{0}^{2}}}} \right. \kern-0em} {A_{0}^{2}}} - 2{{k}_{1}}t} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{0}^{2}}}} \right. \kern-0em} {A_{0}^{2}}} - 2{{k}_{1}}t} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$$

(1.7)

According to [14–16], the sought invariant for this solution is expressed as:

$$K(t) \equiv {{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{1}^{2}}}} \right. \kern-0em} {A_{1}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{2}^{2}}}} \right. \kern-0em} {A_{2}^{2}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{1}^{2}}}} \right. \kern-0em} {A_{1}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{2}^{2}}}} \right. \kern-0em} {A_{2}^{2}}}} \right)} {\left( {{1 \mathord{\left/ {\vphantom {1 {A_{{01}}^{2}}}} \right. \kern-0em} {A_{{01}}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{{02}}^{2}}}} \right. \kern-0em} {A_{{02}}^{2}}}} \right)}}} \right. \kern-0em} {\left( {{1 \mathord{\left/ {\vphantom {1 {A_{{01}}^{2}}}} \right. \kern-0em} {A_{{01}}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{{02}}^{2}}}} \right. \kern-0em} {A_{{02}}^{2}}}} \right)}} = 1.$$

(1.8)

Here, k(t) also does not depend on time; it is an exact autonomous nonlinear invariant (as it was for (1.3) and (1.5)).

Example 2. In [4] the method of boundary dual experiment (using “thermodynamic” IC) was used to examine the two-step reaction:

$${\text{A}} = {\text{B}},\,\,\,\,2{\text{B}} = 2{\text{A}}.$$

(2.1)

Only approximate invariant was found for this reaction under the detailed balance supposition. The scheme (2.1) for butylene isomerization is going to be put down as: t-C₄H₈ = c-C₄H₈ and 2с-C₄H₈ = 2t-C₄H₈. Let us demonstrate that the given above ratios allow estimating an exact autonomous invariant for this reaction without using the detailed balance hypothesis.

Reaction (2.1) is described by the nonlinear Eq. (12):

$$A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}(1 - A) + 2{{k}_{2}}{{(1 - A)}^{2}} - 2{{k}_{{ - 2}}}{{A}^{2}},$$

(2.2)

where c = 2(k₂ − k₋₂) ≠ 0 at k₂ ≠ k₋₂, a = −(k₁ + k₋₁ + 4k₂) < 0, b = k₋₁+ 2k₂ > 0. The conditions required for the equilibrium (14) being physical are fulfilled at, e. g. k₁= 4, k₋₁ = 1, k₂ = 1, k₋₂ = 0.5. Then a = −9, b = 3, c = 1, a² − 4bc = 69, A_∞ ≈ 0.35, D = (−69)^1/2. The exact invariant (17) and (18) for reaction (2.1) is expressed as:

$$K(t) \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$$

(2.3)

where

$$\begin{gathered} {{z}_{1}} = {\text{arth}}\left( {{{\left( {2{{A}_{1}} - 9} \right)} \mathord{\left/ {\vphantom {{\left( {2{{A}_{1}} - 9} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{2}} = {\text{arth}}\left( {{{\left( {2{{A}_{2}}--9} \right)} \mathord{\left/ {\vphantom {{\left( {2{{A}_{2}}--9} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{{01}}} = {\text{arth}}\left( {{{\left( {2{{A}_{{01}}} - 9} \right)} \mathord{\left/ {\vphantom {{\left( {2{{A}_{{01}}} - 9} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{{02}}} = {\text{arth}}\left( {{{\left( {2{{A}_{{02}}}--{\text{ }}9} \right)} \mathord{\left/ {\vphantom {{\left( {2{{A}_{{02}}}--{\text{ }}9} \right)} D}} \right. \kern-0em} D}} \right). \\ \end{gathered} $$

Invariant (2.3) is shown in Fig. 2.

Fig. 2.

Solutions of two Cauchy problems and exact invariant for reaction (2.1) at k₁= 4, k₋₁ = 1, k₂ = 1, k₋₂ = 0.5, A₀₁ = 0.2, A₀₂ = 0.8: (1) A₁(t); (2) A₂(t); (3) K(t).

Example 3. Let us examine a three-step autocatalytic reaction

$${\text{A}} = {\text{B}},\,\,\,\,2{\text{B}} = 2{\text{A}},\,\,\,\,{\text{A}} + {\text{B}} = 2{\text{B}}.$$

(3.1)

In case of butylene isomerization it is expressed as: t‑C₄H₈ = c-C₄H₈, 2с-C₄H₈ = 2t-C₄H₈, t-C₄H₈ + c‑C₄H₈ = 2c-C₄H₈. Reaction (3.1) is also described by the nonlinear ODE of (12) type:

$$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}(1 - A) + 2{{k}_{2}}{{(1 - A)}^{2}} - \\ - \,\,2{{k}_{{ - 2}}}{{A}^{2}} - {{k}_{3}}A(1 - A) + {{k}_{{ - 3}}}{{(1 - A)}^{2}}, \\ \end{gathered} $$

(3.2)

where

$$\begin{gathered} c = 2({{k}_{2}} - {{k}_{{ - 2}}}) + {{k}_{3}} + {{k}_{{ - 3}}} \ne 0, \\ a = - ({{k}_{1}} + {{k}_{{ - 1}}} + 4{{k}_{2}} + {{k}_{3}} + 2{{k}_{{ - 3}}}) < 0, \\ b = {{k}_{{ - 1}}} + 2{{k}_{2}} + {{k}_{{ - 3}}} > 0. \\ \end{gathered} $$

The conditions for the equilibrium (14) being physical are fulfilled at, e.g. k₁= 4, k₋₁ = 1, k₂ = 1, k₋₂ = 1/2, k₃ = 1, k₋₃ = 1. Then a = −12, b = 4, c = 3, a² − 4bc = 96, A_∞ ≈ 0.37, D = (−96)^1/2. The exact invariant (17) for reaction (3.1) is expressed as:

$$K\left( t \right) \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$$

(3.3)

where

$$\begin{gathered} {{z}_{1}} = {\text{arth}}\left( {{{\left( {6{{A}_{1}}--12} \right)} \mathord{\left/ {\vphantom {{\left( {6{{A}_{1}}--12} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{2}} = {\text{arth}}\left( {{{\left( {6{{A}_{2}}--12} \right)} \mathord{\left/ {\vphantom {{\left( {6{{A}_{2}}--12} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{{01}}} = {\text{arth}}\left( {{{\left( {6{{A}_{{01}}}--12} \right)} \mathord{\left/ {\vphantom {{\left( {6{{A}_{{01}}}--12} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{{02}}} = {\text{arth}}\left( {{{\left( {6{{A}_{{02}}}--12} \right)} \mathord{\left/ {\vphantom {{\left( {6{{A}_{{02}}}--12} \right)} D}} \right. \kern-0em} D}} \right). \\ \end{gathered} $$

The invariant (3.3) is shown in Fig. 3.

Fig. 3.

Solutions of two Cauchy problems and exact invariant for reaction (3.1) at k₁= 4, k₋₁ = 1, k₂ = 1, k₋₂ = 1/2, k₃ = 1, k₋₃ = 1, A₀₁ = 0.3, A₀₂ = 0: (1) A₁(t); (2) A₂(t); (3) K(t).

Example 4. Let us discuss, how invariants can be used to solve the inverse problems of chemical kinetics. Let us suppose that two experimental curves of the dependences A_1exp(t) and A_2exp(t) were obtained by the examination of reaction (1.1) using the dual method at the IC of A₀₁ = 1 and A₀₂ = 0.5 (see Table 1). Let us determine the invariants for these IC, calculate their values at different values of n, and compare them to the theoretical values of the invariants (1.3), (1.5), and (1.8), i.e., to the unit. If n = 1, then the invariant (1.3) is expressed as:

$${{K}_{1}} \equiv 8{{A}_{2}} - 3{{A}_{1}} = 1.$$

(4.1)

Table 1.   Invariants of the reaction nA = nB

If n = 2, then the invariant (1.5) is expressed as:

$${{K}_{2}} \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$$

(4.2)

where

$$\begin{gathered} ~{{z}_{1}} = - {\text{arth}}\left( {{{\left( {a{\text{ }} + 2c{{A}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {a{\text{ }} + 2c{{A}_{1}}} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{2}} = - {\text{arth}}\left( {{{\left( {a{\text{ }} + 2c{{A}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {a{\text{ }} + 2c{{A}_{2}}} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{{01}}} = - {\text{arth}}\left( {{{\left( {a{\text{ }} + 2c} \right)} \mathord{\left/ {\vphantom {{\left( {a{\text{ }} + 2c} \right)} D}} \right. \kern-0em} D}} \right), \\ {{z}_{{02}}} = - {\text{arth}}\left( {{{\left( {a{\text{ }} + {\text{ }}c} \right)} \mathord{\left/ {\vphantom {{\left( {a{\text{ }} + {\text{ }}c} \right)} D}} \right. \kern-0em} D}} \right), \\ D = {{( - 16)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,c \ne 0. \\ \end{gathered} $$

If n = 3, then the invariant (1.8) is expressed as:

$${{K}_{3}} \equiv {{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{2}^{2}}}} \right. \kern-0em} {A_{2}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{1}^{2}}}} \right. \kern-0em} {A_{1}^{2}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{2}^{2}}}} \right. \kern-0em} {A_{2}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{1}^{2}}}} \right. \kern-0em} {A_{1}^{2}}}} \right)} 3}} \right. \kern-0em} 3} = 1.$$

(4.3)

The results of the calculations using the formulas (4.1)–(4.3) are given in Table 1.

The analysis showed that the data given in Table 1 accord equally with two mechanisms of reaction (1.1): bimolecular and termolecular. However, the average value of the invariants K_av is closer to the theoretical value (unit) in case of a bimolecular mechanism, therefore one can consider it the most probable.

CONCLUSIONS

In this study, the analytical formulas for the determination of the exact autonomous invariants of the chemical reactions passing in the closed isothermal systems between two reagents in terms of the law of mass action were derived. The found ratios estimate the correlation between the non-equilibrium values of reagents concentrations measured in two experiments with different initial conditions (not necessarily the boundary ones) and remain strictly constant over the whole reaction. These ratios were applied for the study of the non-equilibrium properties of 24 types of mechanisms of mono-, bi-, and termolecular single, two-, and three-step reactions. The invariant curves determined for these reactions were compared to the curve of concentration change during the whole transition process. The obtained results expand the concept of non-equilibrium characteristics of the nonlinear chemical reactions; they can be used for the solution of the inverse problems of chemical kinetics and modeling of chemical reactions of ideal mixing under closed isothermal conditions.