The search for unknown relaxation tendencies of chemical reactions is a challenge in chemical kinetics [1–5]. One of the recently discovered new regularities are time-independent kinetic invariants that retain their values ​​throughout the transition process of the reaction. Exact invariants of linear reversible reactions involving any number of reagents were also found for some nonlinear reactions [6–16]. Recently, the invariants of a nonlinear reaction were confirmed experimentally [14]. They were found by the dual-experiments method (DEM) proposed by the American-Brussels research group (G. Yablonsky, D. Constales, G. Marin et al. [6–16]) and based on two experiments with reciprocal (“thermodynamic”) boundary initial conditions. One of the dual experiments starts when only the starting material is available, and the other when only the reaction product is present. This approach was further developed in [17–20], where the multi-experiments method (MEM) was described. In this method, the results of two or more nonequilibrium experiments with any physical initial conditions (not necessarily “thermodynamic”) are used to determine approximate autonomous invariants (quasi-invariants) of nonlinear reactions. The quasi-invariants differ from the exact invariants in the fact that they remain only approximately (not strictly) constant during the reaction. The accuracy of the quasi-invariants depends on the kinetic parameters of the reaction and initial conditions. At some values of parameters, MEM can lose stability, leading to increased calculation error, which should be taken into account in its practical applications. Therefore, it is of interest to search for new approaches to the development of methods for determining the exact invariants of various classes of reactions. A new method for calculating the exact kinetic invariants of linear reactions proceeding through any number of elementary stages and involving an arbitrary number of starting materials and reaction products is described below [6–16].

THEORETICAL

Let us consider a linear chemical reaction involving n reagents Аj and proceeding via s elementary stages of the form

$$\Sigma {{a}_{{ij}}}{{{\mathbf{A}}}_{j}} = \Sigma {{a}_{{ - ij}}}{{{\mathbf{A}}}_{j}},\,\,\,\,i = 1, \ldots ,s,\,\,\,\,~j = 1, \ldots ,n,$$
((1))

where a±ij ≥ 0, Σa±ij = 1 are the stoichiometric coefficients of the substances Аj at the ith stage. In closed systems, each stage of the linear reaction should be linear; i.e., the stepwise conservation law (CL) should be valid:

$$\Sigma {{a}_{{ij}}} = \Sigma {{a}_{{ - ij}}} = 1,\,\,\,\,i = {\text{ }}1, \ldots ,s.$$
((2))

In open systems, the linear reactions can include nonlinear stages involving other reagents, whose changes can be neglected (Bodenstein–Semenov quasi-steady state hypothesis [1, 2]). The dynamics of reactions (1), (2) in a gradientless isothermal reactor is described in terms of the mass-action law by a set of ordinary linear differential equations (ODEs)

$${A}_{j}^{'} = \Sigma ({{a}_{{ - ij}}} - {{a}_{{ij}}})({{r}_{i}} - {{r}_{{ - i}}}) + {{q}_{0}}{{A}_{{0j}}} - q{{A}_{j}},\,j = 1, \ldots ,n,$$
((3))

where Аj are the concentrations of reagents Аj (in mole fractions); \({{r}_{i}} = {{k}_{i}}\Pi A_{j}^{{aij}}\) and \({{r}_{{ - i}}} = {{k}_{{ - i}}}\Pi A_{j}^{{a - ij}}\) are the rates of direct and reverse stages linear in Аj (in 1/s), respectively; k−i are the rate constants of stages (in 1/s); and q0 and q are the initial and current flow rates, respectively (in 1/s). The initial conditions are

$${{A}_{j}}\left( 0 \right) = {{A}_{{0j}}}.$$
((4))

The linear reactions have only one stable equilibrium Aj∞ [21], which is determined from the set of linear algebraic equations

$$\begin{gathered} \Sigma ({{a}_{{ - ij}}} - {{a}_{{ij}}})({{r}_{{i~}}} - {{r}_{{ - i}}}){\text{ }} + {{q}_{0}}{{A}_{{0j}}} - q{{A}_{j}} = {\text{ }}0, \\ j = {\text{ }}1, \ldots ,n, \\ \end{gathered} $$
((5))

and can be recorded in explicit form as

$${{A}_{{j\infty }}} = {{{{\Delta }_{{j~}}}} \mathord{\left/ {\vphantom {{{{\Delta }_{{j~}}}} \Delta }} \right. \kern-0em} \Delta },~\,\,\,j = 1, \ldots ,n,$$
((6))

where Δ ≠ 0 and Δj are the main and auxiliary determiners, respectively [22] of system (5). In closed systems, the CLs of substances are always valid:

$$\Sigma {{A}_{j}} = \Sigma {{A}_{{0j}}} = \Sigma {{A}_{{j\infty }}} = {\text{ }}1.$$
((7))

In open systems, the CLs can be recorded in differential form:

$$\Sigma {A}_{j}^{'} = {{q}_{0}}\Sigma {{A}_{{0j}}} - q\Sigma {{A}_{j}}.$$
((8))

These CLs allow the order of system (3) be reduced by unity and should be taken into account when choosing ICs for experiments. The general solution of system (3) is determined by the eigenvalues λ1, λ2, …, λ1n—the roots of the characteristic equation

$${{\varphi }_{0}}{{\lambda }^{n}} + {{\varphi }_{1}}{{\lambda }^{{n - 1}}} + \ldots + {{\varphi }_{{n - 1}}}\lambda + {{\varphi }_{n}} = {\text{ }}0,$$
((9))

where φ = φ(ki, k−i, A0j) are the kinetic parameters (constants). If all eigenvalues are real and different, the general solution of (8) is recorded as [22]

$$\begin{gathered} {{A}_{j}}(t) = \Sigma {{C}_{{jk}}}\exp ({{\lambda }_{k}}t) + {{C}_{j}},\,\,\,\,j = 1, \ldots ,n, \\ k = 1, \ldots ,n, \\ \end{gathered} $$
((10))

where Cjk = Сjk(ki, k−i, A0j) are the constants that depend on the kinetic parameters and ICs, and Сj = Сj(ki, k−i) are the constants that depend only on the kinetic parameters. If there are complex-conjugate pairs λ = m ± in, i2 = −1 among the eigenvalues, the corresponding pairs of the terms in (10) will also be complex-conjugate Cjkexp(m + in)t + Cjkexp(m − in)t (with the same coefficients) and can be replaced by the real equations [22]

$$\begin{gathered} \exp \left( {mt} \right)\left( {P\cos nt + Q\sin nt} \right) \\ = \exp \left( {mt} \right)R\sin (nt + a), \\ \end{gathered} $$
((11))

where P, Q, or R, α are the new real integration constants. The particular case of multiple eigenvalues is not considered here.

Let us use a method similar to the one described in [17–20] for solutions (10) and (11), slightly modifying it. In its original version, this method permits the use of any two different physical ICs. Modification consists in a “stricter” choice of ICs, which should satisfy the following sufficient conditions (criterion) of applicability of the method:

$${{C}_{{jk}}} = 0,\,\,\,\,k \ne {{k}_{0}}\,\,\,\,{\text{and}}\,\,\,\,{{C}_{{jk0}}} \ne 0,\,\,\,\,0 \leqslant {{A}_{{0j}}} \leqslant 1.$$
((12))

These conditions express the requirement that all coefficients at exponentials in (10) and (11) be zero, except one coefficient with the index k0, for at least one reagent with the index j0 at the physical values of ICs. They are represented by a system of (n − 1) linear equations with n unknowns, which has an infinite number of solutions. If there is at least one physical solution among these solutions, then criterion (12) is valid, and solutions (10) and (11) for two different ICs can be represented as

$$\begin{gathered} {{A}_{j}}_{1} = {{C}_{{jk,1}}}\exp ({{\lambda }_{k}}_{0}t) + {{C}_{j}}, \\ ~{{A}_{j}}_{2} = \Sigma {{C}_{{jk,2}}}\exp ({{\lambda }_{k}}_{0}t) + {{C}_{j}}. \\ \end{gathered} $$
((13))

If there are complex-conjugate eigenvalues, the corresponding pairs of terms in (13) have the form (11). Let us find the only t-dependent exponential from the first equation (13) and calculate, taking into account (9), the remaining t-dependent exponentials:

$$\begin{gathered} \exp ({{\lambda }_{k}}_{0}t) = {{({{A}_{j}}_{1} - {{C}_{j}})} \mathord{\left/ {\vphantom {{({{A}_{j}}_{1} - {{C}_{j}})} {{{C}_{{jk,1}}}}}} \right. \kern-0em} {{{C}_{{jk,1}}}}}, \\ \exp ({{\lambda }_{j}}t) = {{[\exp ({{\lambda }_{k}}_{0}t)]}^{{{{\lambda j} \mathord{\left/ {\vphantom {{\lambda j} {\lambda k0}}} \right. \kern-0em} {\lambda k0}}}}} \\ = {{[{{({{A}_{j}}_{1} - {{C}_{j}})} \mathord{\left/ {\vphantom {{({{A}_{j}}_{1} - {{C}_{j}})} {{{C}_{{jk,1}}}}}} \right. \kern-0em} {{{C}_{{jk,1}}}}}]}^{{{{\lambda j} \mathord{\left/ {\vphantom {{\lambda j} {\lambda k0}}} \right. \kern-0em} {\lambda k0}}}}}, \\ \end{gathered} $$

where Aj1 > Сj. Substituting (14) in the second equation (13), we obtain

$${{I}_{j}}(t) \equiv {{A}_{{j2}}} - \Sigma {{C}_{{jk,2}}}[{{({{A}_{j}}_{1} - {{{{C}_{j}})} \mathord{\left/ {\vphantom {{{{C}_{j}})} {{{C}_{{jk,1}}}}}} \right. \kern-0em} {{{C}_{{jk,1}}}}}]}^{{{{\lambda j} \mathord{\left/ {\vphantom {{\lambda j} {\lambda k0}}} \right. \kern-0em} {\lambda k0}}}}} = {{C}_{j}},$$
((15))

or, in normalized form,

$$\begin{gathered} {{K}_{j}}(t) \equiv \{ {{A}_{j}}_{2} - \\ - \,\,{{\Sigma {{C}_{{jk,2}}}[{{{({{A}_{j}}_{1} - {{{{C}_{j}})} \mathord{\left/ {\vphantom {{{{C}_{j}})} {{{C}_{{jk,1}}}}}} \right. \kern-0em} {{{C}_{{jk,1}}}}}]}}^{{{{\lambda j} \mathord{\left/ {\vphantom {{\lambda j} {\lambda k0}}} \right. \kern-0em} {\lambda k0}}}}}\} } \mathord{\left/ {\vphantom {{\Sigma {{C}_{{jk,2}}}[{{{({{A}_{j}}_{1} - {{{{C}_{j}})} \mathord{\left/ {\vphantom {{{{C}_{j}})} {{{C}_{{jk,1}}}}}} \right. \kern-0em} {{{C}_{{jk,1}}}}}]}}^{{{{\lambda j} \mathord{\left/ {\vphantom {{\lambda j} {\lambda k0}}} \right. \kern-0em} {\lambda k0}}}}}\} } {{{C}_{j}}}}} \right. \kern-0em} {{{C}_{j}}}} = 1. \\ \end{gathered} $$
((16))

The left parts of (15) and (16) are independent of time; they depend only on the concentrations of one of the reagents, kinetic parameters, and ICs of reactions; i.e., these are exact autonomous invariants, which are basically nonlinear with respect to the concentrations of any of the reagents measured in two nonequilibrium experiments. If the conditions Aj1 > Сj are satisfied, they take real values, are physical, and are observed in the form of horizontal lines on the plots.

Thus, in closed and open systems, analytical expressions for the invariants of linear chemical reactions (15) and (16) occurring in a gradientless isothermal reactor can be represented, within the framework of the mass-action law, as the sum of reagent concentrations (to the powers of the rate constants of stages) found from two nonequilibrium concentrations with any given pair of initial conditions that satisfy the applicability criterion (12) of the method. The maximum number of these invariants for the chosen pair of initial conditions equals the number of reagents. If another pair of initial conditions is chosen, we can construct the same number of invariants, etc. For their experimental verification, the data of the corresponding two experiments should be substituted into the left part of any invariant expression (15) and (16) and compared with the constants in the right parts of these relations. The mechanism of the chemical reaction is acceptable if these equalities are satisfied, or inacceptable otherwise, which may be useful in solving the inverse problems.

RESULTS AND DISCUSSION

Example 1. Suppose the reaction A = C occurs by the sequential scheme

$$1)\,\,{\mathbf{A}} = {\mathbf{B}},\,\,\,\,2)\,\,{\mathbf{B}} = {\mathbf{C}}.$$
((1.1))

The dynamics of these reactions in the closed system is described by ODEs (3):

$$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B,\,\,\,\,B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B - {{k}_{2}}B + {{k}_{{ - 2}}}C, \\ C{\kern 1pt} ' = {{k}_{2}}B - {{k}_{{ - 2}}}C. \\ \end{gathered} $$
((1.2))

The equilibrium coordinates (5) and (6) for this system are A∞ = k−1k−2/Δ, B∞ = k1k−2/Δ, C∞ = k1k2/Δ, Δ = k1k2 + k1k−2 + k−1k−2, and CL (7) is recorded as

$$A + B + C = {{A}_{0}} + {{B}_{0}} + {{C}_{0}} = {{A}_{\infty }} + {{B}_{\infty }} + {{C}_{\infty }} = {\text{ }}1.$$
((1.3))

Let us have B expressed as B = 1 − A − C. Substituting it into (1.2), we obtain two ODEs in A and C; i.e., the order of system (3) is reduced by unity:

$$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}(1 - A - C), \\ C{\kern 1pt} ' = {{k}_{2}}(1 - A - C) - {{k}_{{ - 2}}}C. \\ \end{gathered} $$
((1.4))

The general solution (1.4) is determined by the roots of CE (9) recorded as

$${{\lambda }^{2}} + {{\varphi }_{1}}\lambda + {{\varphi }_{2}} = 0,$$
((1.5))

where φ1 = k1 + k−1 + k2 + k−2, φ2 = k1k2 + k1k−2 + k−1k−2. An analysis showed that Eq. (1.5) has only real roots. Suppose k1 = 1, k−1 = 1, k2 = 1, k−1 = 1; then φ1 = 4, φ2 = 3 and λ1 = −1, λ2 = −3, and solutions (10) of system (1.4) are recorded as

$$\begin{gathered} A = ({{A}_{0}} - {{C}_{0}}){\text{exp}}{{( - t){\text{ }}} \mathord{\left/ {\vphantom {{( - t){\text{ }}} 2}} \right. \kern-0em} 2} \\ + \,\,({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}){\text{exp}}( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ \end{gathered} $$
((1.6))
$$\begin{gathered} C = {\text{ }}({{C}_{0}} - {{A}_{0}})\exp {{( - t)} \mathord{\left/ {\vphantom {{( - t)} 2}} \right. \kern-0em} 2} + \\ + \,\,({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3})\exp ( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}. \\ \end{gathered} $$
((1.7))

According to (1.6), criterion (12) of applicability of the method to any reagent A (j0 = 1) or С (j0 = 2) is recorded as A0 = C0 for the first (k = 1) exponential and as A0 + C0 = 2/3 for the second (k = 2) one. Suppose, e.g., the second condition is satisfied taking into account CL (1.3). This is one linear equation with two unknowns, which has an infinite number of solutions. One of the physical solutions with allowance for CL (1.3) is A01 = 0, B01 = 1/3, C01 = 2/3. The second IC is chosen arbitrary: A02 = 2/3, B02 = 0, C02 = 1/3, but also taking into account the CL. For these ICs, Eqs. (13) take the form

$$\begin{gathered} {{A}_{1}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}\exp ( - t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ {{A}_{2}} = {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}\exp ( - t) + {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}\exp ( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ \end{gathered} $$
((1.8))
$$\begin{gathered} {{C}_{1}} = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}\exp ( - t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ {{C}_{2}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 6}} \right. \kern-0em} 6}\exp ( - t) + {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}\exp ( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}. \\ \end{gathered} $$
((1.9))

According to (1.8) and (1.9), for reagents A and СEqs. (14) are recorded as

$$\begin{gathered} \exp ( - t){\text{ }} = {\text{ }}1 - 3{{A}_{1}}, \\ \exp ( - 3t) = {{\exp }^{3}}( - t) = {{(1 - 3{{A}_{1}})}^{3}}, \\ \end{gathered} $$
((1.10))
$$\begin{gathered} \exp ( - t) = 3{{C}_{1}} - 1, \\ \exp ( - 3t) = {{\exp }^{3}}( - t) = {{(3{{C}_{1}} - 1)}^{3}}. \\ \end{gathered} $$
((1.11))

Substituting (1.10) into the second equation (1.8), we find the exact А invariant:

$${{I}_{A}}(t) \equiv 6{{A}_{2}} - (1 - 3{{A}_{1}}) - {{(1 - 3{{A}_{1}})}^{3}} = {\text{ }}2,$$
((1.12))

or, in normalized form,

$${{K}_{A}}(t) \equiv 3{{A}_{2}} - (1 - {{3{{A}_{1}})} \mathord{\left/ {\vphantom {{3{{A}_{1}})} 2}} \right. \kern-0em} 2} - (1 - {{3{{A}_{1}}{{)}^{3}}} \mathord{\left/ {\vphantom {{3{{A}_{1}}{{)}^{3}}} 2}} \right. \kern-0em} 2} = {\text{ }}1.$$
((1.13))

Substituting (1.11) into the second equation (1.9), we find the exact C invariant:

$${{I}_{C}}(t) \equiv 6{{C}_{2}} + (3{{C}_{1}} - 1) - {{(3{{C}_{1}} - 1)}^{3}} = 2,$$
((1.14))

or, in normalized form,

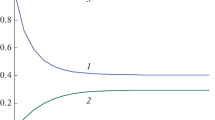
$${{K}_{C}}(t) \equiv 3{{C}_{2}} + (3{{C}_{1}} - {{1)} \mathord{\left/ {\vphantom {{1)} 2}} \right. \kern-0em} 2} - (3{{C}_{1}} - {{1{{)}^{3}}} \mathord{\left/ {\vphantom {{1{{)}^{3}}} 2}} \right. \kern-0em} 2} = 1.$$
((1.15))

Invariants (1.13) and (1.15) and solutions of two Cauchy problems are shown in Figs. 1а and 1b.

Fig. 1.
figure 1

(а) Solutions of two Cauchy problems and exact A invariant for reaction (1.1) at k1= 1, k−1 = 1, k2= 1, k−1 = 1, A01 = 0, B01 = 1/3, C01 = 2/3, A02 = 2/3, B02 = 0, C02 = 1/3: (1) A1(t), (2) A2(t), and (3) KA(t). (b) Solutions of two Cauchy problems and C invariant for reaction (1.1) at k1= 1, k−1 = 1, k2= 1, k−1 = 1, A01 = 0, B01 = 1/3, C01 = 2/3, A02 = 2/3, B02 = 0, C02 = 1/3: (1) C1(t), (2) C2(t), and (3) KC(t).

Full size image

According to Figs. 1а and 1b, the dependences KA(t) and KC(t) are strictly horizontal lines; i.e., these are time-independent exact invariants.

If the same reaction A = С occurs by the parallel scheme

$$1)\,\,{\mathbf{A}} = {\mathbf{B}},\,\,\,\,2)\,\,{\mathbf{A}} = {\mathbf{C}},$$
((1.16))

its dynamics is described, taking into account CL (1.3), by the ODE

$$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}(1 - A - C) - {{k}_{2}}A{\text{ }} + {\text{ }}{{k}_{{ - 2}}}C, \\ C{\kern 1pt} ' = {{k}_{2}}(1 - A - C) - {{k}_{{ - 2}}}C. \\ \end{gathered} $$
((1.17))

The coefficients of CE (9) take the form φ1 = k1 + k−1 + 2k2 + k−2, φ2 = k1k2 + k1k−2 + 2k2k−2 + k−1k−2 + k22, from which we obtain, at the same values of constants, φ1 = 5, φ2 = 6; that is, λ1 = −2, λ2 = −3; Eqs. (13) for reagent A are recorded as

$$\begin{gathered} {{A}_{1}} = {\text{ }}({{A}_{{01}}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3})\exp ( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}, \\ {{A}_{2}} = ({{A}_{{02}}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3})\exp ( - 3t) + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}. \\ \end{gathered} $$
((1.18))

Taking into account (15) and (16) for the same pair of ICs A01 = 0, B01 = 1/3, C01 = 2/3 and A02 = 2/3, B02 = 0, C02 = 1/3, we obtain the non-normalized and normalized invariants from (1.18):

$${{I}_{A}}\left( t \right) \equiv 3{{A}_{1}} + {\text{ }}3{{A}_{2}} = {\text{ }}2,$$
((1.19))
$${{K}_{A}}\left( t \right) \equiv {{3{{A}_{1}}} \mathord{\left/ {\vphantom {{3{{A}_{1}}} 2}} \right. \kern-0em} 2} + 3{{{{A}_{2}}} \mathord{\left/ {\vphantom {{{{A}_{2}}} 2}} \right. \kern-0em} 2} = 1.$$
((1.20))

It is easy to verify that the plots of these dependences are also strictly horizontal lines, i.e., are exact invariants.

Example 2. Let us consider the linear three-stage scheme of reaction A = D

$$1)\,\,{\mathbf{A}} = {\mathbf{B}},\,\,\,\,2)\,\,{\mathbf{B}} = {\mathbf{C}},\,\,\,\,3)\,\,{\mathbf{C}} = {\mathbf{D}}.$$
((2.1))

The dynamics of reaction (2.1) is described by the ODE

$$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B,\,\,\,\,B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B - {{k}_{2}}B + {{k}_{{ - 2}}}C, \\ C{\kern 1pt} ' = {{k}_{2}}B - {{k}_{{ - 2}}}C - {{k}_{3}}C + {{k}_{{ - 3}}}D,\,\,\,\,D{\kern 1pt} ' = {{k}_{3}}C - {{k}_{{ - 3}}}D. \\ \end{gathered} $$
((2.2))

The coordinates of equilibrium (5) and (6) are A∞ = k−1k−2k−3/Δ, B∞ = k1k−2k−3/Δ, C∞ = k1k2k−3/Δ, D∞ = k1k2k3/Δ, where Δ = k1k2k3 + k1k−2k−3 + k1k2k−3 + k−1k−2k−3, and CL (7) takes the form

$$\begin{gathered} A + B + C + D = {{A}_{0}} + {{B}_{0}} + {{C}_{0}} + {{D}_{0}} = \\ = {{A}_{\infty }} + {{B}_{\infty }} + {{C}_{\infty }} + {{D}_{\infty }} = 1. \\ \end{gathered} $$
((2.3))

Recording B from this and substituting it into (2.2), we obtain a system of third-order ODEs

$$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B,\,\,\,\,C{\kern 1pt} ' = {{k}_{2}}B - {{k}_{{ - 2}}}C - {{k}_{3}}C + {{k}_{{ - 3}}}D, \\ D{\kern 1pt} ' = {{k}_{3}}C - {{k}_{{ - 3}}}D, \\ \end{gathered} $$
((2.4))

where B = 1 − A − C − D. The characteristic equation (9) for this system takes the form

$${{\lambda }^{3}} + {{\varphi }_{1}}{{\lambda }^{2}} + {{\varphi }_{2}}\lambda + {{\varphi }_{3}} = {\text{ }}0,$$
((2.5))

where φ1 = k1 + k−1 + k2 + k−2 + k3 + k−3, φ2 = (k1 + k−1)(k2 + k−2 + k3 + k−3) − k2k−1 − k3(k−3−k2) + k−3(k2 + k−2 + k3), φ3 = −k1k−3k2− k1k −2k−3− k1k2k3− k−1k−2k−3. Suppose k1 = 1, k−1 = 1, k2 = 1, k−1 = 1, k3 = 1, k−3 = 1; then λ1 = −2, λ2,3 = −2 ± 21/2 = (−0.5858, −3.4142), and the A solutions of system (2.2) for any ICs are recorded as

$$\begin{gathered} A = ({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4})\exp ({{\lambda }_{1}}t) \\ + \,\,{{C}_{{120}}}\exp ({{\lambda }_{2}}t) + {{C}_{{130}}}\exp ({{\lambda }_{3}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}, \\ \end{gathered} $$
((2.6))

where С120 = α12A0 + β12B0 + γ12C0 + θ12, С130 = α13A0 + β13B0 + γ13C0 + θ13, α12 = −3 730 904 090 310 553, β12 = 5 276 295 164 430 438, γ12 = 9 007 199 254 740 991, θ12 = −2 638 147 582 215 219, α13 = 5 436 325 649 948 134, β13 = 7 688 125 463 633 382, γ13 = 2 251 799 813 685 248, θ13 = −3 844 062 731 816 691 (exact values are given). The applicability criterion of method (12) for reagent А for the second and third exponentials gives a system of two linear equations with three unknown ICs:

$$\begin{gathered} {{\alpha }_{{12}}}{{A}_{0}} + {{b}_{{12}}}{{B}_{0}} + {{\gamma }_{{12}}}{{C}_{0}} + {{\theta }_{{12}}} = {\text{ }}0, \\ {{\alpha }_{{13}}}{{A}_{0}} + {{b}_{{13}}}{{B}_{0}} + {{\gamma }_{{13}}}{{C}_{0}} + {{\theta }_{{13}}} = {\text{ }}0. \\ \end{gathered} $$
((2.7))

This system has infinitely many solutions. Let us choose one physical solution from them, for example, А01 = 0, B01 = 1/2, C01 = 0. The second IC is taken any: A02 = 1, B02 = 0, C02 = 0. Solutions (2.6) for these two ICs take the form

$${{A}_{1}} = - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}\exp ({{\lambda }_{1}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4},$$
((2.8))
$$\begin{gathered} {{A}_{2}} = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}\exp ({{\lambda }_{1}}t) + {{C}_{{120,2}}}\exp ({{\lambda }_{2}}t) \\ + \,\,{{C}_{{130,2}}}\exp ({{\lambda }_{3}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}, \\ \end{gathered} $$
((2.9))

where С120,2 = (21/2 + 1)1592262918131443/9007199254740992, С130,2 = (21/2 − 1)1592262918131443/9007199254740992. From (2.8) it follows that

$$\begin{gathered} \exp ({{\lambda }_{1}}t) = 1 - 4{{A}_{1}},\,\,\,\,\exp ({{\lambda }_{2}}t) = {{(1 - 4{{A}_{1}})}^{{{{\lambda 2} \mathord{\left/ {\vphantom {{\lambda 2} {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}}, \\ \exp ({{\lambda }_{3}}t) = {{(1 - 4{{A}_{1}})}^{{{{\lambda 3} \mathord{\left/ {\vphantom {{\lambda 3} {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}}. \\ \end{gathered} $$
((2.10))

Substituting (2.10) into (2.9), we find the exact А invariant of system (2.2):

$$\begin{gathered} {{I}_{A}}(t) \equiv {{A}_{2}} - (1 - {{4{{A}_{1}})} \mathord{\left/ {\vphantom {{4{{A}_{1}})} 4}} \right. \kern-\nulldelimiterspace} 4} - {{C}_{{120,2}}}{{(1 - 4{{A}_{1}})}^{{{{\lambda 2} \mathord{\left/ {\vphantom {{\lambda 2} {\lambda 1}}} \right. \kern-\nulldelimiterspace} {\lambda 1}}}}} \\ - \,\,{{C}_{{130,2}}}{{(1 - 4{{A}_{1}})}^{{\lambda {3 \mathord{\left/ {\vphantom {3 {\lambda 1}}} \right. \kern-\nulldelimiterspace} {\lambda 1}}}}} = {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-\nulldelimiterspace} 4}, \\ \end{gathered} $$
((2.11))

or, in normalized from,

$$\begin{gathered} {{K}_{A}}(t) \equiv 4{{A}_{2}} + 4{{A}_{1}} - 1 - 4{{C}_{{120,2}}}{{(1 - 4{{A}_{1}})}^{{{{\lambda 2} \mathord{\left/ {\vphantom {{\lambda 2} {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}} \\ - \,\,4{{C}_{{130,2}}}{{(1 - 4{{A}_{1}})}^{{{{\lambda 3} \mathord{\left/ {\vphantom {{\lambda 3} {\lambda 1}}} \right. \kern-0em} {\lambda 1}}}}} = 1. \\ \end{gathered} $$
((2.12))
Fig. 2.
figure 2

Solutions of Cauchy problems and A invariant for reaction (2.1) at k1 = 1, k−1 = 1, k2 = 1, k−1 = 1, k3 = 1, k−3 = 1, A01 = 0, B01 = 1/2, C01 = 0, D01 = 1/2, A02 = 1, B02 = 0, C02 = 0, D02 = 0: (1) A1(t), (2) A2(t), and (3) KA(t).

Full size image

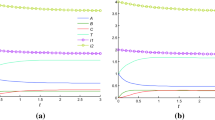
Invariant (2.12) and the solutions of two Cauchy problems are shown in Fig. 2. The solutions of system (2.2) for other reagents are recorded similarly to (2.6):

$$\begin{gathered} C = ({1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4} - {{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} - {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2})\exp ({{\lambda }_{1}}t) \\ + \,\,{{C}_{{220}}}\exp ({{\lambda }_{2}}t) + {{C}_{{230}}}\exp ({{\lambda }_{3}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}, \\ \end{gathered} $$
((2.13))
$$\begin{gathered} D = ({{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} 2}} \right. \kern-0em} 2} + {{{{C}_{0}}} \mathord{\left/ {\vphantom {{{{C}_{0}}} 2}} \right. \kern-0em} 2} - {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}){\text{exp}}({{\lambda }_{1}}t) \\ + \,\,{{C}_{{320}}}{\text{exp}}({{\lambda }_{2}}t) + {{C}_{{330}}}{\text{exp}}({{\lambda }_{3}}t) + {1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}, \\ \end{gathered} $$
((2.14))

where С220 = α22A0 + β22B0 + γ22C0 + θ22, С230 = α23A0 + β23B0 + γ23C0 + θ23, С320 = α32A0 + β32B0 + γ32C0 + θ32, С330 = α33A0 + β33B0 + γ33C0 + θ33, etc. Using these solutions, we find the B and C invariants for reagents B and C, respectively.

Example 3. Let us consider the reaction occurring by the linear cyclic scheme

$$1)\,\,{\mathbf{A}} = {\mathbf{B}},\,\,\,\,2)\,\,{\mathbf{B}} = {\mathbf{C}},\,\,\,\,3)\,\,{\mathbf{C}} = {\mathbf{D}},\,\,\,\,4)\,\,{\mathbf{D}} = {\mathbf{A}}.$$
((3.1))

This reaction is described by the ODEs

$$x{\kern 1pt} ' = {{r}_{1}} - {{r}_{2}},\,\,\,\,y{\kern 1pt} ' = {{r}_{2}} - {{r}_{3}},\,\,\,\,q{\kern 1pt} ' = {{r}_{3}} - {{r}_{4}},\,\,\,\,z{\kern 1pt} ' = {{r}_{4}} - {{r}_{1}},$$
((3.2))

where x ≡ [B], y ≡ [C], q ≡ [D], and z ≡ [A] are the reagent concentrations; r1= k1z− k−1x, r2= k2x − k−2y, r3= k3y − k−3q, r4= k4q − k−4z, and CL takes the form

$$x + y + q + z = 1.$$
((3.3))

Suppose k1= 1, k2 = 2, k3 = 3, k4 = 4, k−1 = 0.5, k−2 = 0.3, k−3 = 0.3, k−4 = 1. Then λ1 = −6.2002 (real), and λ2,3 = −2.9499 ± 1.4520i (complex-conjugate); the x solutions are recorded, taking into account (11), as

$$\begin{gathered} x = {{C}_{{110}}}\exp ({{\lambda }_{1}}t) + ({{C}_{{120}}}\cos nt \\ + \,\,{{C}_{{130}}}\sin nt)\exp \left( {mt} \right) + {{2676} \mathord{\left/ {\vphantom {{2676} {13\,405}}} \right. \kern-0em} {13\,405}}, \\ \end{gathered} $$
((3.4))

where С110 ≈ 0.1587x0 − 0.1081y0 + 0.2123q0 − 0.0598, С120 ≈ 0.8413x0 + 0.1081y0 − 0.2123q0 − 0.1398, С130 ≈ 0.0237x0 + 0.7241y0 + 0.2135q0 − 0.1492. The applicability criterion (12) for x (С120 = С130 = 0) is satisfied, e.g., at x01 = 0.1403, y01 = 0.2015, q01 = 0, z01 = 1 − x0 − y0 − q0. The second IC is chosen arbitrary: x02 = 0, y02 = 0, q02 = 0, z02 = 1, but taking into account CL (3.3). Solutions (3.4) for these two ICs are recorded as

$${{x}_{1}} = {{C}_{{110\_1}}}\exp ({{\lambda }_{1}}t) + {{C}_{1}},$$
((3.5))
$$\begin{gathered} {{x}_{2}} = {{C}_{{110\_2}}}\exp ({{\lambda }_{1}}t) + ({{C}_{{120\_2}}}\cos nt \\ + \,\,{{C}_{{130\_2}}}\sin nt)\exp (mt) + {{C}_{1}}, \\ \end{gathered} $$
((3.6))

where λ1 = −6.2002, m = Re(λ2,3) = −2.9499, n = Im(λ2,3) = 1.452, С110,1 ≈ −0.0593, С110,2 ≈ −0.0598, С120,2 ≈ −0.1492, С130,2 ≈ −0.1398, С1 = 2676/13405 ≈ 0.1996.

From (3.5) we obtain

$$\begin{gathered} {{E}_{1}} \equiv \exp ({{\lambda }_{1}}t) = ({{x}_{1}} - {{{{C}_{1}})} \mathord{\left/ {\vphantom {{{{C}_{1}})} {{{C}_{{110\_1}}}}}} \right. \kern-0em} {{{C}_{{110\_1}}}}}, \\ {{E}_{2}} \equiv \exp (mt) = {{E}_{1}}{{^{m}}^{{/\lambda 1}}}, \\ t = \ln {{[({{x}_{1}} - {{{{C}_{1}})} \mathord{\left/ {\vphantom {{{{C}_{1}})} {{{C}_{{110\_1}}}]}}} \right. \kern-0em} {{{C}_{{110\_1}}}]}}} \mathord{\left/ {\vphantom {{[({{x}_{1}} - {{{{C}_{1}})} \mathord{\left/ {\vphantom {{{{C}_{1}})} {{{C}_{{110\_1}}}]}}} \right. \kern-0em} {{{C}_{{110\_1}}}]}}} {{{\lambda }_{1}}}}} \right. \kern-0em} {{{\lambda }_{1}}}}. \\ \end{gathered} $$
((3.7))

Substituting (3.7) into (3.6), we find the exact x invariant of system (3.2), (3.3):

$$\begin{gathered} {{I}_{x}} \equiv {{x}_{2}} - {{C}_{{110\_2}}}{{E}_{1}} - ({{C}_{{120\_2}}}\cos nt \\ + \,\,{{C}_{{130\_2}}}\sin nt){{E}_{2}} = {{C}_{1}}, \\ \end{gathered} $$
((3.8))

or, in normalized form,

$$\begin{gathered} {{K}_{x}} \equiv {{x}_{2}} - {{C}_{{110\_2}}}{{{{E}_{{1~}}}} \mathord{\left/ {\vphantom {{{{E}_{{1~}}}} {{{C}_{1}}}}} \right. \kern-0em} {{{C}_{1}}}} \\ - \,\,({{C}_{{120\_2}}}\cos nt + {{C}_{{130\_2}}}\sin nt){{{{E}_{2}}} \mathord{\left/ {\vphantom {{{{E}_{2}}} {{{C}_{1}}}}} \right. \kern-0em} {{{C}_{1}}}} = 1. \\ \end{gathered} $$
((3.9))

Invariant (3.9) and solutions of two Cauchy problems are shown in Fig. 3.

Fig. 3.
figure 3

Solutions of Cauchy problems and x invariant for reaction (2.1) at k1 = 1, k2 = 2, k3 = 3, k4 = 4, k−1 = 0.5, k−2 = 0.3, k−3 = 0.3, k−4 = 1, x01 = 0.1403, y01 = 0.2015, q01 = 0, z01 = 1 − x0 − y0 − q0, x02 = 0, y02 = 0, q02 = 0, z02 = 1: (1) x1(t), (2) x2(t), and (3) Kх(t).

Full size image

Solutions (3.4) for other reagents are recorded similarly and give exact y, q, and z invariants for the corresponding reagents.

Example 4. Let us consider one of the possible applications of invariants for solving the inverse problems. Let us compare two alternative linear schemes (1.1) and (1.16) for the reaction А = С. Suppose two sets of data A1exp(t) and A2exp(t) with two different ICs were obtained as a result of experiments. Invariant expressions K1(t) and K2(t) for them are calculated using expressions (1.13) and (1.20) corresponding to these schemes (Table 1). An analysis showed that these experimental data including the experimental errors agree equally well with both possible reaction schemes, namely, with the sequential and parallel schemes. However, the average calculated value of the invariants Kav is closer to the theoretical values Ktheor for the sequential scheme, due to which it is considered more probable.

Table 1.   Concentrations of reagent А in the reaction A = С according to the data of two experiments with ICs*
Full size table

CONCLUSIONS

The method for determining the autonomous kinetic invariants of multistage linear chemical reactions proposed in this study allows us to find exact analytical expressions that relate the nonequilibrium values ​​of reagent concentrations measured in two experiments with different initial conditions (not necessarily “thermodynamic”), but remain strictly constant throughout the entire transition process in a gradientless isothermal reactor. This method is an alternative approach to the search for and detection of analytical expressions for nonequilibrium time invariants of chemical reactions, first proposed by the American-Brussels school of kinetics [6–16]. In these studies, each reaction mechanism is characterized by one invariant in the form of the concentration ratios of all reagents found in two experiments with reciprocal (“thermodynamic”) initial conditions.

The distinctions of our method are as follows:

1. Each reaction mechanism is characterized by a set of invariants (their number equals the number of reagents for each pair of initial conditions).

2. The invariants are represented as the sum of the concentrations of only one (any) reagent measured in two experiments with any nonequilibrium (not necessarily “thermodynamic”) initial conditions.

3. The invariants are applicable to both closed and open systems.

These invariants can be used as new means for identification of the mechanisms of chemical reactions carried out using relaxation experiments. The method can also be used for nonlinear reactions under quasi-steady state conditions, and also for some nonlinear reactions with three or more reagents that allow exact analytical solutions.