Stability of Charged Thin-Shell Wormholes with Weyl Corrections

Abstract

This paper is devoted to examining the effects of charge and Weyl coupling parameter on the stable configuration of thin-shell wormholes. We use a cut and paste approach to develop thin-shell wormholes from the matching of two equivalent geometries of a charged black hole with Weyl corrections. The characteristics of matter surface around wormhole throat are calculated through Lanczos equations. We examine that matter distribution located at the wormhole throat violates the null and week energy conditions. The expansion and collapse of thin-shell are observed through the graphical behavior of surface pressure. We explore the stable behavior of wormhole throat through radial perturbation preserving its symmetries about the static solution. It is found that charge and Weyl coupling parameter enhances the stable regions of thin-shell wormholes but stable regions decrease for highly charged thin-shell wormholes.

1 INTRODUCTION

A non-singular solution of the field equations that connects two different regions of the same universe or faraway universes through a geometrical passage is referred to as a wormhole (WH). This passage can be further partitioned into two types, i.e., inter-universe and intra-universe. A WH that does not allow the observer movement from one universe to another is called non-traversable, otherwise, it is known as traversable. Traversable WHs have remarkable importance to study the far-away as well as multi-universes due to the absence of event horizon and singularity [1]. The presence of exotic matter at WH throat produces enough pressure to counter-balance the effect of gravitational collapse that supports the observer motion across the geometrical passage. Such matter distribution can be realized through the violation of energy conditions.

Visser [2] examined that the distribution of exotic matter can be minimized and found that such a violation can be reduced for some suitable geometrical structures. He analyzed that an observer can travel across the WH tunnel without passing the passage of exotic matter. The same author [3] constructed thin-shell WHs from the junction of interior and exterior spacetimes of the Schwarzschild black hole (BH) through cut and paste technique. The corresponding components of energy-momentum tensor are evaluated through Israel formalism [4]. This technique has been applied to develop thin-shell WHs from different BHs [5–25].

A major concern in cosmological and astrophysical research is the analysis of linearized stability of the geometrical structure of thin-shell WHs through radial perturbation about the static solution as well as the equation of state (EoS). Eiroa and Romero [26] studied the stable characteristics of thin-shell WHs constructed from Reissner–Nordström (RN) BHs and found stable behavior for highly charged distribution. Eiroa and Simeone [27, 28] introduced a new approach to analyzing the stable structure of spherical and cylindrical thin-shell WHs through radial perturbation preserving the symmetries. They investigated the linearized stability of spherical WHs in the presence of Chaplygin gas.

Eiroa [29] examined the stable structure of dilation and RN WHs by using radial perturbation preserving the symmetry. He also linearized the EoS parameter about the equilibrium throat radius. Eiroa and Simeone [30] analyzed the stable characteristics of spherical charged WHs in Einstein–Born–Infeld and Einstein–Maxwell theories through radial perturbation. Sharif and Azam [31] developed thin-shell WHs from the charged black string in the presence of Chaplygin gas and also explored their linear stability through radial perturbation about the static solution.

The generalized Einstein–Maxwell theories are very useful to explore the characteristics and effects of the electromagnetic field. These theories provide information about the electromagnetic field and higher derivative interactions. Such theories can be partitioned into two different classes, i.e., the minimal and non-minimal coupling between the Maxwell and curvature parts [32–34]. In the Einstein and Maxwell equations, the coefficients of second-order derivatives are modified through the appearance of non-minimal couplings in the Lagrangian. This new feature has many interesting applications in different models and systems such as the interaction of the electromagnetic field with gravitational waves, cosmological scenarios, and charged BHs. Black hole solutions in the presence of a non-minimal connection between gravitation and electromagnetic field have also been considered in the modified Maxwell field [35]. The resulting coupled terms produced significant changes in the electromagnetic and gravity structure of charged BHs.

Balakin and his collaborators [36–38] investigated exact solutions of three-parameter non-minimal Einstein–Yang–Mills and Einstein–Maxwell models that represent a new type of WH and the non-minimal magnetic monopoles of the Dirac type, respectively. They also investigated exact solutions supported with non-minimal coupling for the electromagnetic and gravitational fields that express static spherically symmetric objects with and without center. These non-minimal couplings of electromagnetic and gravitational fields modify the geometrical structure of charged BHs. The coupling between the Maxwell field and Weyl tensor is another simple generalization of electromagnetic theories with Weyl corrections [39]. Moreover, the current investigation explains that such non-minimal coupling must occur near the astrophysical compact objects with strong gravitational field and large mass density, i.e., the existence of supermassive BHs at the center of galaxies. Chen and Jing [40] presented dynamical equations of the electromagnetic perturbation coupled with Weyl tensor in the background of Schwarzschild BHs. They also studied the effects of Weyl correction on the stable configuration of BHs. The geometrical structure of charged BHs greatly depends on the electrodynamics of the Maxwell field and hence the Weyl corrections in the Einstein–Maxwell theory modify their structure as well as physical properties.

Chen and Jing [41] introduced rotating and non-rotating charged spherically symmetric BHs with small Weyl corrections. They examined that positive and negative values of the Weyl parameter (α) increase and decrease the region of the event horizon, respectively. For charged rotating BHs with Weyl corrections, the ergosphere in the equatorial plane becomes thick, if α > 0 while it becomes thin if α < 0. Mahapatra [42] investigated the charged BH in d-dimensional anti-de Sitter spacetime with four derivative Weyl correction. He determined the quasinormal frequencies of the massless scalar field perturbation and also analyzed thermodynamics as well as a phase transition. Mureika and Varieschi [43] studied the shadow of rotating BHs neutral with fourth-order conformal Weyl gravity.

In this paper, we are interested to investigate the effects of the coupling parameter on the stability of thin-shell WHs developed from charged BHs with Weyl corrections. The paper has the following format. Section 2 develops the general formalism of thin-shell WHs developed from two equivalent copies of charged BH with Weyl corrections. Section 3 explains the stability procedure of thin-shell through radial perturbation preserving its symmetry. We also observe the corresponding stable regions of thin-shell WHs. In the last section, we summarize our final results.

2 CONSTRUCTION OF THIN-SHELL WORMHOLES

Here, we briefly discuss the geometrical construction of thin-shell WHs from the interior and exterior copies of charged BH with Weyl corrections. The action that represents the coupling of Weyl tensor and electromagnetic field can be proposed as [41]

$$S = \int {{{d}^{4}}x\sqrt { - g} } \left[ {R - \frac{1}{4}{{F}_{{\mu \nu }}}{{F}^{{\mu \nu }}} + \alpha {{C}^{{\mu \nu \rho \sigma }}}{{F}_{{\mu \nu }}}{{F}_{{\rho \sigma }}}} \right],$$

(1)

where ${{F}_{{\mu \nu }}} = {{\partial }_{\mu }}{{A}_{\nu }} - {{\partial }_{\nu }}{{A}_{\mu }}$ is the Maxwell tensor, ${{C}^{{\mu \nu \rho \sigma }}}$ represents the Weyl tensor, ${{A}_{\mu }}$ = (ϕ(r), 0, 0, 0) denotes the vector potential and ϕ(r) is the electric potential. By varying the action (1) with respect to the metric coefficients, we obtain the modified form of the field equations given as

$$\begin{gathered} {{R}_{{\mu \nu }}} - \frac{1}{2}{{g}_{{\mu \nu }}}R = \frac{{{{E}_{{\mu \nu }}}}}{2}(1 - \alpha C_{{\alpha \beta }}^{{\alpha \beta }}) \\ - \;\alpha ({{R}_{{\mu \nu }}} + {{g}_{{\mu \nu }}}{{\nabla }^{2}} - {{\nabla }_{\mu }}{{\nabla }_{\nu }}){{F}_{{\alpha \beta }}}{{F}^{{\alpha \beta }}}, \\ \end{gathered} $$

(2)

where

$${{E}_{{\mu \nu }}} = \frac{1}{{4\pi }}\left( {F_{\mu }^{\alpha }{{F}_{{\nu \alpha }}} - \frac{1}{4}{{g}_{{\mu \nu }}}F_{{}}^{{\alpha \beta }}{{F}_{{\alpha \beta }}}} \right).$$

(3)

These equations are very useful to explore the effects of Weyl coupling parameter over the geometrical configuration of the compact objects.

The line element of static spherically symmetric spacetime is given as

$$d{{s}^{2}} = - \Psi (r)d{{t}^{2}} + \frac{{d{{r}^{2}}}}{{\Psi (r)}} + h(r)(d{{\theta }^{2}} + {{\sin }^{2}}\theta d{{\phi }^{2}}),$$

(4)

where the metric coefficients Ψ(r) and h(r) are the functions of polar coordinate r. By using Eqs. (2) and (3), the respective three coupled equations of motion are obtained as [41]

$$\begin{gathered} 4\alpha \frac{d}{{dr}}\{ \Phi {\kern 1pt} '(r)h(r)(2h(r)\Phi {\kern 1pt} ''(r) + h{\kern 1pt} '(r)\Phi {\kern 1pt} '(r))\} \\ + \;3(h{\kern 1pt} '{{(r)}^{2}} - 2h(r)h{\kern 1pt} ''(r)) = 0, \\ \end{gathered} $$

$$\begin{gathered} 3[\Psi (r)(h{\kern 1pt} '{{(r)}^{2}} - 2h(r)h{\kern 1pt} ''(r)) + \Phi {\kern 1pt} '{{(r)}^{2}}h{{(r)}^{2}} \\ - \;2h(r)(h(r)\Psi {\kern 1pt} ''(r) + h{\kern 1pt} '(r)\Psi {\kern 1pt} '(r))] \\ - \;8\alpha h(r)\Phi {\kern 1pt} ''{{(r)}^{2}}(\Phi {\kern 1pt} '(r)\Psi (r)){\kern 1pt} ' \\ \end{gathered} $$

$$\begin{gathered} - \;8\alpha h(r)h{\kern 1pt} '(r)(\Psi (r)\Phi {\kern 1pt} '{{(r)}^{2}}){\kern 1pt} ' \\ + \;4\alpha \Phi {\kern 1pt} '{{(r)}^{2}}(h{\kern 1pt} '{{(r)}^{2}}\Psi (r) + 2\Psi {\kern 1pt} ''(r)h{{(r)}^{2}}) \\ - \;8\alpha \Psi (r)h(r)\Phi {\kern 1pt} '(r)(h(r)\Phi {\kern 1pt} '''(r) + h{\kern 1pt} ''(r)\Phi {\kern 1pt} '(r)) = 0, \\ \end{gathered} $$

$$\begin{gathered} \frac{d}{{dr}}\left\{ {\Phi {\kern 1pt} '(r)h(r) + \frac{{4\Phi {\kern 1pt} '(r)\alpha }}{{3h(r)}}} \right.(\Psi (r)(h{\kern 1pt} '{{(r)}^{2}} - h(r)h{\kern 1pt} ''(r)) \\ \left. {\mathop + \limits_{}^{} \;h(r)(h{\kern 1pt} '(r)\Psi {\kern 1pt} ''(r) - \Psi {\kern 1pt} '(r)h{\kern 1pt} '(r)) - 2h(r))} \right\} = 0. \\ \end{gathered} $$

The solution of BH with Wely correction is obtained by solving these coupled equations [41]. For α = 0, their solution represents the RN BH.

The line elements of two equivalent copies (±) of charged BH with Weyl corrections can be written in the following form [41]

$$\begin{gathered} ds_{ \pm }^{2} = - \Psi ({{r}_{ \pm }})dt_{ \pm }^{2} + \frac{{dr_{ \pm }^{2}}}{{\Psi ({{r}_{ \pm }})}} \\ + \;\left( {r_{ \pm }^{2} + \frac{{4\alpha Q_{ \pm }^{2}}}{{9r_{ \pm }^{2}}}} \right)(d\theta _{ \pm }^{2} + {{\sin }^{2}}{{\theta }_{ \pm }}d\phi _{ \pm }^{2}), \\ \end{gathered} $$

(5)

where

$$\Psi ({{r}_{ \pm }}) = 1 - \frac{{2{{m}_{ \pm }}}}{{{{r}_{ \pm }}}} + \frac{{Q_{ \pm }^{2}}}{{r_{ \pm }^{2}}} - \frac{{4\alpha Q_{ \pm }^{2}}}{{3r_{ \pm }^{4}}}\left( {1 - \frac{{10{{m}_{ \pm }}}}{{3{{r}_{ \pm }}}} + \frac{{26Q_{ \pm }^{2}}}{{15r_{ \pm }^{2}}}} \right),$$

α, ${{Q}_{ \pm }}$, and ${{m}_{ \pm }}$ denote the coupling parameter, electric charged, and mass of the interior (–) and exterior (+) copies of BHs respectively. For simplicity, we assume that both spacetimes have the same mass and charge distributions, i.e., ${{Q}_{ - }} = Q = {{Q}_{ + }}$ and ${{m}_{ - }} = m = {{m}_{ + }}$. In this case, the electric potential and metric function depend on the charged distribution of BH and coupling parameter while in RN spacetime, it depends only on the charge. This indicates the coupling between electromagnetic and gravitational fields implying that the coupling parameter greatly affects the characteristics of charged BH. Notice that

• if α = 0 and Q ≠ 0, then it represents the RN BH;

• if α = 0 = Q, then it corresponds to Schwarz-schild BH.

To avoid the singularity and event horizon in the geometrical structure of thin-shell WHs, the shell’s radius must be greater than the radius of the event horizon (r_h). It is observed that the region of event horizon increases for negative values of α and decreases for positive values. We consider only positive values of α to avoid the event horizon in the WH geometry. We construct thin-shell WHs from the matching of interior and exterior copies (±) of BHs through Visser’s approach. For this purpose, we take a subset (${{\Upsilon }^{ \pm }}$) of these manifolds (${{\Pi }^{ \pm }}$) through cut and paste technique that does not contain any type of event horizon as well as singularity, i.e., ${{\Upsilon }^{ \pm }} \subset {{\Pi }^{ \pm }}$. Here, ${{\Upsilon }^{ \pm }}$ = $\{ {{x}^{\nu }}\,|\,{{r}_{ \pm }} \geqslant w(\tau ) > {{r}_{h}}\}$, where ${{x}^{\nu }}$, τ and w(τ) represent coordinates of the manifold, proper time on the shell and shell radius, respectively. These subsets are glued at their common timelike hypersurface $\partial \Upsilon$, i.e., $\partial \Upsilon \subset {{\Upsilon }^{ \pm }}$. The matching between ${{\Upsilon }^{ + }}$ and ${{\Upsilon }^{ - }}$ at throat radius provides a connection between interior and exterior spacetimes ($\partial \Upsilon \equiv {{\Upsilon }^{ + }} \cup {{\Upsilon }^{ - }}$) that follows the radial flare-out condition. This manifold ($\partial \Upsilon$) represents a WH throat that connects both manifolds. The corresponding induced metric for hypersurface can be defined as

$$d{{s}^{2}} = - d{{\tau }^{2}} + \left( {{{w}^{2}} + \frac{{4\alpha {{Q}^{2}}}}{{9{{w}^{2}}}}} \right)(d{{\theta }^{2}} + {{\sin }^{2}}\theta d{{\phi }^{2}}).$$

(6)

The components of unit normals to ${{\Pi }^{ \pm }}$ can be expressed as

$${{n}_{\alpha }} = \left( { - {{{\dot {w}}}^{2}},\;\frac{{\sqrt {{{{\dot {w}}}^{2}} + \Psi (w)} }}{{\Psi (w)}},\;0,\;0} \right)$$

and

$$\dot {t} = \frac{{dt}}{{d\tau }} = \frac{{\sqrt {{{{\dot {w}}}^{2}} + \Psi (w)} }}{{\Psi (w)}}.$$

The corresponding extrinsic curvature components are defined as

$$\begin{gathered} K_{{\tau \tau }}^{ \pm } = \frac{{ - 2\ddot {w}\Psi {{{(w)}}^{2}}\, + \,(2{{{\dot {w}}}^{4}} + 2{{{\dot {w}}}^{2}}\Psi (w)\, - \,\Psi {{{(w)}}^{2}})\Psi {\kern 1pt} '(w)}}{{2\Psi {{{(w)}}^{2}}\sqrt {{{{\dot {w}}}^{2}} = \Psi (w)} }}{\kern 1pt} , \\ K_{{\theta \theta }}^{ \pm } = \left( {w - \frac{{4\alpha {{Q}^{2}}}}{{9{{w}^{3}}}}} \right)\sqrt {{{{\dot {w}}}^{2}} + \Psi (w)} , \\ K_{{\phi \phi }}^{ \pm } = {{\sin }^{2}}\theta K_{{\theta \theta }}^{ \pm }, \\ \end{gathered} $$

(7)

where prime denotes the derivative with respect to w.

The presence of matter surface produces extrinsic curvature discontinuity at the hypersurface and its existence can be evaluated by using Israel formalism. Mathematically, such a matter surface can be observed if $K_{{ij}}^{ + } - K_{{ij}}^{ - } \ne 0$. The characteristics of matter surface located at thin-shell are determined by the field equations for the hypersurface known as Lanczos equations

$${{S}_{{ij}}} = - \frac{1}{{8\pi }}\{ [{{K}_{{ij}}}] - {{\eta }_{{ij}}}K\} ,$$

(8)

where ${{S}_{{ij}}}$ and ${{\eta }_{{ij}}}$ represent the stress-energy tensor and induced metric tensor of $\partial \Upsilon$. Here, $[{{K}_{{ij}}}]$ = $K_{{ij}}^{ + }$ – $K_{{ij}}^{ - }$ and K = tr[K_ij] = [$K_{i}^{i}$]. For perfect fluid distribution, the stress-energy tensor yields

$${{S}_{{ij}}} = (\sigma + p){{U}_{i}}{{U}_{j}} + p{{\eta }_{{ij}}},$$

(9)

where U_i, p, and σ represent the velocity of shell, surface pressure and energy density of matter surface located at thin-shell. The corresponding σ and p of thin-shell WHs can be evaluated through the Lanczos equations as

$$\begin{gathered} \sigma = - \frac{{{{{\left( {{{w}^{2}} + \frac{{4\alpha {{Q}^{2}}}}{{9{{w}^{2}}}}} \right)}}^{{ - 1}}}}}{{4\pi }}[{{K}_{{\theta \theta }}}], \\ p = \frac{1}{{8\pi }}\left\{ {[{{K}_{{\tau \tau }}}] - {{{\left( {{{w}^{2}} + \frac{{4\alpha {{Q}^{2}}}}{{9{{w}^{2}}}}} \right)}}^{{ - 1}}}[{{K}_{{\theta \theta }}}]} \right\}, \\ \end{gathered} $$

(10)

which yield

$$\sigma = \frac{{(4\alpha {{Q}^{2}} - 9{{r}^{4}})\sqrt {{{{\dot {w}}}^{2}} + \Psi (w)} }}{{2\pi w(4\alpha {{Q}^{2}} + 9{{w}^{4}})}},$$

(11)

$$p = - \frac{{\frac{{2{{{\dot {w}}}^{4}}\Psi {\kern 1pt} '(w)}}{{\Psi {{{(w)}}^{2}}}} + \frac{{2{{{\dot {w}}}^{2}}\Psi {\kern 1pt} '(w)}}{{\Psi (w)}} - \frac{{2({{{\dot {w}}}^{2}} + \Psi (w))(9{{w}^{4}} - 4\alpha {{Q}^{2}})}}{{4\alpha {{Q}^{2}}w + 9{{w}^{5}}}} - 2\ddot {w} - \Psi {\kern 1pt} '(w)}}{{16\pi \sqrt {{{{\dot {w}}}^{2}} + \Psi (w)} }}.$$

(12)

We assume that the shell does not move in the radial direction. Therefore, the first and second derivatives of the shell radius with respect to τ vanish at equilibrium throat radius (w = w₀), i.e., ${{\dot {w}}_{0}}$ = 0 = ${{\ddot {w}}_{0}}$. The above equations at w = w₀, become

$$\begin{gathered} {{\sigma }_{0}} = \frac{{\sqrt {\Psi ({{w}_{0}})} (4\alpha {{Q}^{2}} - 9w_{0}^{4})}}{{2\pi {{w}_{0}}(4\alpha {{Q}^{2}} + 9w_{0}^{4})}}, \\ {{p}_{0}} = - \frac{{\frac{{2\Psi ({{w}_{0}})(4\alpha {{Q}^{2}} - 9w_{0}^{4})}}{{4\alpha {{Q}^{2}}{{w}_{0}} + 9w_{0}^{5}}} - \Psi {\kern 1pt} '({{w}_{0}})}}{{16\pi \sqrt {\Psi ({{w}_{0}})} }}, \\ \end{gathered} $$

(13)

where σ₀ and p₀ denote the surface energy density and pressure at w = w₀.

To discuss the physical viability of a model, we impose some geometrical constraints, known as energy conditions. There are four well-known energy conditions null (σ₀ + p₀ ≥ 0), weak (${{\sigma }_{0}} \geqslant 0$, ${{\sigma }_{0}} + {{p}_{0}} \geqslant 0$), strong (${{\sigma }_{0}} + 3{{p}_{0}} \geqslant 0$), and dominant (${{\sigma }_{0}} \pm {{p}_{0}} \geqslant 0$, ${{\sigma }_{0}} \geqslant 0$). These constraints must be satisfied with normal matter distribution. A viable WH geometry requires the presence of exotic matter at the WHs throat that repel the gravitational force and prevent it from contraction. Figures 1a and 1b indicate that ${{\sigma }_{0}} < 0$ and ${{\sigma }_{0}} + {{p}_{0}} < 0$ which leads to the physically viable structure of WH. It is also observed that the strong energy condition is satisfied for small values of shell radius (w₀), otherwise, it is violated. The surface pressure of matter distribution explains the expanding and collapsing characteristics of WH throat. The positive values of p₀ prevent WH throat from collapsing while negative values hold its expanding behavior. The corresponding expansion and collapse of thin-shell WHs are shown in Fig. 2. Figure 2a explains that thin-shell shows expanding behavior for small values of shell radius (p₀ < 0) and then represents the collapse (p₀ > 0) for Q = 0.5. It is also observed that thin-shell shows collapse for higher values of charge Q = 0.8 (Fig. 2b).

Fig. 1.

Plots of energy conditions for Q = 0 = α (a) and Q = 0.5, α = 0.1 (b) with m = 0.5. These plots indicate physical viability of the developed WH geometry.

Fig. 2.

Plots of surface pressure for Q = (a) 0.5 and (b) 0.8 with m = 0.5 = α. These plots show the expanding and collapsing behavior of thin-shell WHs.

3 STABILITY ANALYSIS

In this section, we explore stable and unstable characteristics of charged thin-shell WHs with Weyl corrections under radial perturbation preserving the spherical symmetry. We linearize the EoS satisfied by matter surface around the WH throat at equilibrium shell radius [27–29]

$$p - {{p}_{0}} = \eta _{0}^{2}(\sigma - {{\sigma }_{0}}),$$

(14)

where $\eta _{0}^{2} = {{\left. {(\partial p{\text{/}}\partial \sigma )} \right|}_{{w = {{w}_{0}}}}}$ represents the EoS parameter. This parameter is also referred to as speed of sound for normal matter distribution while for exotic matter it is not clear that $\eta _{0}^{2}$ shows the speed of sound. Also, $\eta _{0}^{2} \in (0,1]$ for normal matter and for exotic matter, its range is not defined. Using Eqs. (11)–(13) in (14), we have

$$\begin{gathered} - 8\eta _{0}^{2}\left( {\frac{{\sqrt {\Psi (w) + {{{\dot {w}}}^{2}}} (4\alpha {{Q}^{2}} - 9{{w}^{4}})}}{{9{{w}^{5}} + 4\alpha w{{Q}^{2}}}} + \frac{{\sqrt {\Psi ({{w}_{0}})} (9w_{0}^{4} - 4\alpha {{Q}^{2}})}}{{4\alpha {{w}_{0}}{{Q}^{2}} + 9w_{0}^{5}}}} \right) \\ + \;\frac{{\frac{{2(\Psi (w) + {{{\dot {w}}}^{2}})(9{{w}^{4}} - 4\alpha {{Q}^{2}})}}{{9{{w}^{5}} + 4\alpha w{{Q}^{2}}}} - \frac{{2{{{\dot {w}}}^{4}}\Psi {\kern 1pt} '(w)}}{{\Psi {{{(w)}}^{2}}}} - \frac{{2{{{\dot {w}}}^{2}}\Psi {\kern 1pt} '(w)}}{{\Psi (w)}} + \Psi {\kern 1pt} '(w) + 2\ddot {w}}}{{\sqrt {\Psi (w) + {{{\dot {w}}}^{2}}} }} + \frac{{\frac{{2\Psi ({{w}_{0}})(4\alpha {{Q}^{2}} - 9w_{0}^{4})}}{{4\alpha {{w}_{0}}{{Q}^{2}} + 9w_{0}^{5}}} - \Psi {\kern 1pt} '({{w}_{0}})}}{{\sqrt {\Psi ({{w}_{0}})} }} = 0. \\ \end{gathered} $$

(15)

We consider small radial perturbation ($\epsilon$) about equilibrium throat radius w₀ to explore the effect of shell radius on the stable/unstable behavior of WH throat. Hence, the shell radius can be expressed in the following form

$$w(\tau ) = {{w}_{0}}(1 + \epsilon (\tau )),\quad \left| \epsilon \right| \ll 1.$$

(16)

Using Eq. (16) in (15), we obtain a system of first order differential equations

$$\dot {\epsilon } = \nu ,\quad \dot {\nu } = a(\epsilon ,\nu ),$$

(17)

where

$$\begin{gathered} a(\epsilon ,\nu ) = \frac{{\sqrt {\Psi ({{w}_{0}}\epsilon + {{w}_{0}}) + {{{v}}^{2}}w_{0}^{2}} }}{{2{{w}_{0}}}} \\ \times \;\left( {\mathop {({\kern 1pt} (}\limits_{}^{} {\kern 1pt} 2(4\eta _{0}^{2} + 1){{{v}}^{2}}{{w}_{0}}( - 9_{0}^{4}{{{(\epsilon + 1)}}^{4}} + 4\alpha {{Q}^{2}}){{w}_{0}}\Psi ({{w}_{0}}\epsilon } \right. \\ + \;{{w}_{0}}{{)}^{2}} - (\epsilon + 1)\Psi {\kern 1pt} '({{w}_{0}}\epsilon + {{w}_{0}})(9w_{0}^{4}{{(\epsilon + 1)}^{4}}) + 4\alpha {{Q}^{2}}) \\ \end{gathered} $$

$$\begin{gathered} + \;2{{{v}}^{4}}w_{0}^{5}(\epsilon + 1)\Psi {\kern 1pt} '({{w}_{0}}\epsilon + {{w}_{0}})(4\alpha {{Q}^{2}} + 9w_{0}^{4}{{(\epsilon + 1)}^{4}}) \\ - \;2(4\eta _{0}^{2} + 1)\Psi {{({{w}_{0}}\epsilon + {{w}_{0}})}^{3}}(9w_{0}^{4}{{(\epsilon + 1)}^{4}} - 4\alpha {{Q}^{2}}) \\ + \;2{{{v}}^{2}}w_{0}^{3}(\epsilon + 1)\Psi ({{w}_{0}}\epsilon + {{w}_{0}})\Psi {\kern 1pt} '({{w}_{0}}\epsilon + {{w}_{0}})(4\alpha {{Q}^{2}} \\ \end{gathered} $$

(18)

$$\begin{gathered} + \;9w_{0}^{4}{{(\epsilon + 1)}^{4}}))(\Psi {{({{w}_{0}}\epsilon + {{w}_{0}})}^{2}}\sqrt {\Psi ({{w}_{0}}\epsilon + {{w}_{0}}) + {{{v}}^{2}}w_{0}^{2}} ) \\ \times \;(4\alpha {{Q}^{2}}{{w}_{0}}(\epsilon + 1) + 9w_{0}^{5}{{(\epsilon + 1)}^{5}}){{)}^{{ - 1}}} \\ + \;\frac{{2(4\eta _{0}^{2} + 1)\sqrt {\Psi ({{w}_{0}})} (9w_{0}^{4} - 4\alpha {{Q}^{2}})}}{{4\alpha {{Q}^{2}}{{w}_{0}} + 9w_{0}^{5}}} + \left. {\frac{{\Psi {\kern 1pt} '({{w}_{0}})}}{{\sqrt {\Psi ({{w}_{0}})} }}} \right). \\ \end{gathered} $$

It is assumed that $\left| {\epsilon (\tau )} \right| \ll 1$, so the square and higher powers of $\epsilon (\tau )$ and ν are negligibly small. Therefore, we consider Taylor series expansion up to second order terms in ν and $\epsilon$. The corresponding functions can be expanded as follows

$$\Psi ({{w}_{0}}(1 + \epsilon )) = \Psi ({{w}_{0}}) + {{w}_{0}}\epsilon \Psi {\kern 1pt} '({{w}_{0}}) + {\rm O}{{[{{w}_{0}}\epsilon ]}^{2}},$$

$$\Psi {\kern 1pt} '({{w}_{0}}(1 + \epsilon )) = \Psi {\kern 1pt} '({{w}_{0}}) + {{w}_{0}}\epsilon \Psi {\kern 1pt} ''({{w}_{0}}) + {\rm O}{{[{{w}_{0}}\epsilon ]}^{2}},$$

$$\sqrt {\Psi ({{w}_{0}}(1 + \epsilon ))} = \sqrt {\Psi ({{w}_{0}})} + \frac{{{{w}_{0}}\epsilon \Psi {\kern 1pt} '({{w}_{0}})}}{{2\sqrt {\Psi ({{w}_{0}})} }} + {\rm O}{{[{{w}_{0}}\epsilon ]}^{2}}.$$

By considering these truncated functions in Eq. (18), we get a system of differential equations

$$\dot {\varrho } = \Omega \varrho ,$$

(19)

where

$$\varrho = \left( \begin{gathered} \epsilon \hfill \\ \nu \hfill \\ \end{gathered} \right),\quad \Omega = \left[ {\begin{array}{*{20}{c}} 0&1 \\ \Delta &0 \end{array}} \right],$$

(20)

and

$$\begin{gathered} \Delta = - (2{{w}_{0}}\Psi ({{w}_{0}})((4\eta _{0}^{2} + 1)\Psi {\kern 1pt} '({{w}_{0}})(81w_{0}^{8} - 16{{\alpha }^{2}}{{Q}^{2}}) \\ + \;\Psi {\kern 1pt} ''({{w}_{0}}){{(4\alpha {{Q}^{2}} + 9w_{0}^{4})}^{2}}{{w}_{0}}) - 4(4\eta _{0}^{2} + 1)\Psi {{({{w}_{0}})}^{2}} \\ \times \;( - 16{{\alpha }^{2}}{{Q}^{4}} - 288\alpha {{Q}^{2}}w_{0}^{4} + 81w_{0}^{8}) - w_{0}^{2}\Psi {\kern 1pt} '{{({{w}_{0}})}^{2}} \\ \times \;{{(4\alpha {{Q}^{2}} + 9w_{0}^{4})}^{2}}){{(4\Psi ({{w}_{0}}){{(4\alpha {{Q}^{2}}{{w}_{0}} + 9w_{0}^{5})}^{2}})}^{{ - 1}}}. \\ \end{gathered} $$

It is noted that the above equation is reduced to the RN thin-shell WHs for α = 0 given as

$$\begin{gathered} \Delta = \frac{1}{{\omega _{0}^{4}}}\left[ {\frac{{{{w}_{0}}({{{({{w}_{0}} - m)}}^{3}} + m({{m}^{2}} - {{Q}^{2}}))}}{{({{w}_{0}}({{w}_{0}} - 2m) + {{Q}^{2}})}}} \right. \\ \left. {\mathop + \limits_{}^{} \;4h_{0}^{2}({{w}_{0}}({{w}_{0}} - 3m) + 2{{Q}^{2}})} \right]. \\ \end{gathered} $$

This expression is exactly the same as in reference [29, Eq. (37)].

The system of first-order differential Eqs. (16) can be expressed as

$$\ddot {\epsilon } = \Delta \epsilon ,$$

(21)

which is a second-order differential equation. The eigenvalues of matrix Ω explain the stable/unstable behavior of WH throat [27–29]. There are two eigenvalues of Ω, i.e., ${{\lambda }_{1}} = - \sqrt \Delta$ < 0 and ${{\lambda }_{2}} = - \sqrt \Delta$ > 0. These eigenvalues are used to characterize the geometrical behavior of thin-shell WHs.

• For Δ > 0, we have real eigenvalues. The negative eigenvalue (${{\lambda }_{2}} = - \sqrt \Delta$) does not provide any physical significance while the positive eigenvalue (${{\lambda }_{1}} = \sqrt \Delta$) explains the unstable structure of WH throat.

• For Δ = 0, the corresponding eigenvalues become λ₁ = 0 = λ₂. This case provides solution of the system of differential Eq. (17) as $\nu = {{\nu }_{0}}$ and $\epsilon = {{\epsilon }_{0}} + {{\nu }_{0}}(\tau - {{\tau }_{0}})$, which represent the unstable static solution.

• For Δ < 0, we obtain imaginary eigenvalues, i.e., ${{\lambda }_{1}} = - i\sqrt {\left| \Delta \right|}$ and ${{\lambda }_{2}} = i\sqrt {\left| \Delta \right|}$. This case is used to investigate the stability of WH configuration and the detailed discussion is given in [27, 28].

The stable condition of thin-shell can be written in the following form

$$\Delta < 0 \Rightarrow A({{w}_{0}}) - \chi ({{w}_{0}})\eta _{0}^{2} < 0.$$

(22)

Here, χ(w₀) = χ₀ is the coefficient of the EoS parameter ($\eta _{0}^{2}$) and A(w₀) = A₀ is the remaining term of Eq. (22) in which $\eta _{0}^{2}$ does not involve. We discuss the geometrical behavior of WHs through the stability regions. The stable regions can be characterized as follows

(i) if χ₀ < 0, then $\eta _{0}^{2}$ < A₀/χ₀;

(ii) if χ₀ > 0, then $\eta _{0}^{2}$ > A₀/χ₀,

where

$$\begin{gathered} {{A}_{0}} = 164\,025w_{0}^{{17}}(3{{m}^{2}}{{w}_{0}} - m({{Q}^{2}} + 3w_{0}^{2}) + w_{0}^{3}) \\ + \;(10w_{0}^{2}(66{{m}^{2}} - 48m{{w}_{0}} + 5w_{0}^{2}) + {{Q}^{2}}{{w}_{0}}(366{{w}_{0}} \\ - \;857m) + 252{{Q}^{4}})\,14\,580\alpha {{Q}^{2}}w_{0}^{{12}} \\ \end{gathered} $$

$$\begin{gathered} + \;1296{{\alpha }^{2}}{{Q}^{4}}w_{0}^{8}(50w_{0}^{2}(163{{m}^{2}} - 201m{{w}_{0}} + 40w_{0}^{2}) \\ + \;5{{Q}^{2}}{{w}_{0}}(1052{{w}_{0}} - 1333m) + 1252{{Q}^{4}}) \\ - \;256{{\alpha }^{4}}{{Q}^{8}}(25w_{0}^{2}(1225{{m}^{2}} - 645m{{w}_{0}} + 81w_{0}^{2}) \\ \end{gathered} $$

$$\begin{gathered} - \;390{{Q}^{2}}{{w}_{0}}(95m - 26{{w}_{0}}) + 10\,816{{Q}^{4}}) \\ - \;576{{\alpha }^{3}}{{Q}^{6}}w_{0}^{4}(50w_{0}^{2}(1090{{m}^{2}} - 552m{{w}_{0}} + 69w_{0}^{2}) \\ + \;5{{Q}^{2}}{{w}_{0}}(3326{{w}_{0}} - 1288m) - 18\,512{{Q}^{4}}), \\ \end{gathered} $$

$$\begin{gathered} {{\chi }_{0}} = 4(4\alpha {{Q}^{2}}(5{{w}_{0}}(3{{w}_{0}} - 10m) + 26{{Q}^{2}}) - 45w_{0}^{4} \\ \times \;({{w}_{0}}({{w}_{0}} - 2m) + {{Q}^{2}}))(3645w_{0}^{{12}}({{w}_{0}}({{w}_{0}} - 3m) \\ + \;2{{Q}^{2}}) - 324\alpha {{Q}^{2}}w_{0}^{8}(85{{w}_{0}}({{w}_{0}} - 3m) + 144{{Q}^{2}}) \\ \end{gathered} $$

$$\begin{gathered} + \;64{{\alpha }^{3}}{{Q}^{6}}(5{{w}_{0}}(9{{w}_{0}} - 35m) + 104{{Q}^{2}}) \\ + \;(198{{Q}^{2}} + 5{{w}_{0}}(23{{w}_{0}} - 77m))\,144{{\alpha }^{2}}{{Q}^{4}}w_{0}^{4}). \\ \end{gathered} $$

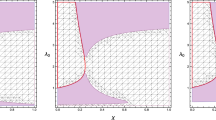
We plot χ₀ and A₀/χ₀ to explore the stable configuration of charged thin-shell WHs with Weyl corrections. It is observed that for each value of charge, positive values of the Weyl coupling parameter with m = 0.5, χ₀ < 0, which shows that stable regions exist for $\eta _{0}^{2}$ < A₀/χ₀. Figure 3 indicates the effect of the coupling parameter on the stable regions of thin-shell WHs. It is found that the presence of charge and coupling parameter enhances the stable regions of thin-shell WHs. It is noted that stable regions increase by increasing α. Figure 4 indicates that initially stable regions increase if 0 < Q ≤ 0.7 and decrease for higher values of charge. These plots explain that thin-shell WHs constructed from charged BHs with Weyl corrections are more stable than Schwarzschild and RN spacetimes.

Fig. 3.

Plots of χ₀ and A₀/χ₀ for different values of coupling parameter with Q = 0.5. The shaded regions indicate the stable regions. It is found that stable regions are increased in the presence of charge and coupling parameter. It is also examined that charged thin-shell WHs with Weyl corrections are more stable than Schwarzschild and RN thin-shell WH.

Fig. 4.

Plots of A₀/χ₀ for different values of charge with α = 0.1. These plots explain that the stability regions are enhanced by increasing charge (0 < Q ≤ 0.7) and stable regions decrease for highly charged thin-shell WHs (Q > 0.7).

4 FINAL REMARKS

In this paper, we have explored the stability of thin-shell WHs in the presence of charge and the Weyl coupling parameter. We have developed WH geometry through the smooth matching of interior and exterior manifolds of charged BHs with Weyl corrections. The stable configuration of WHs is observed by considering radial perturbation about equilibrium throat radius preserving their symmetries. The matter distribution located at the WH throat violates the null and weak energy conditions indicating that the developed model is physically viable. It is noticed that the strong energy condition is verified for small values of shell radius otherwise shows a violation (Fig. 1). We have also investigated the expansion as well as the collapsing nature of thin-shell WHs through different values of charge (Fig. 2). It is found that shell indicates collapsing behavior for highly charged geometry.

The study of stable regions of the developed structure is carried out through the graphical behavior of $h_{0}^{2} = d{{p}_{0}}{\text{/}}d{{\sigma }_{0}}$ in terms of equilibrium shell radius with different values of charge and coupling parameter. We have found that the stability regions are greatly affected by the presence of charge as well as the Weyl coupling parameter. It is observed that stable regions are increased by increasing α (Fig. 3). The stable configuration of WH throat becomes more stable for small values of charge (0 < Q ≤ 0.7) while decreases for its higher values (Fig. 4). It is worthwhile to mention here that the presence of both charge and coupling parameter increase the stable configuration of WHs geometry as compared to Schwarzschild and RN BHs. It is found that all our results follow the geometrical behavior of RN thin-shell WH for α = 0 [29].