1 Introduction

General relativity is the most successful gravitational theory that describes various aspects of evolutionary stages of celestial bodies. In addition to collapsing phenomenon, this theory also describes wormhole dynamics. A wormhole is a solution of the field equations which acts as a shortcut associating distant regions of spacetime. A wormhole connecting distant regions of the same universe is called an intra-universe wormhole, while that connects different universes is an inter-universe wormhole. The word “wormhole”, also known as an Einstein-Rosen bridge, was first suggested by Einstein and Rosen (1935). Due to the presence of event horizons, an observer could not traverse freely across the universes through this wormhole. Morris and Thorne (1988) were the first to propose traversable wormholes which allow freely traversable motion in both universes through its throat due to the absence of event horizons.

Traversable wormholes have two asymptotically flat regions connected by a throat. The flare-out condition is to be fulfilled at the wormhole throat which requires the presence of exotic matter violating the null energy conditions. Visser (1989, 1996) analyzed that the amount of exotic matter can be minimized by choosing suitable geometry of the wormhole. It was suggested that the violation of energy conditions can be made infinitesimally small by applying the cut and paste approach to construct spherically symmetric thin-shell wormholes in which exotic matter is restricted at the wormhole throat (Visser et al. 2003). The Darmois-Israel formalism (Darmois 1927; Israel 1966; Musgrave and Lake 1996) was applied to find the surface stresses at the throat.

The stability/instability of celestial objects has always been a debatable issue (Herrera et al., 1989; Chan et al., 1993; Sharif and Yousaf 2013a, 2013b; Sharif and Bhatti 2013a, 2013b) in gravitational physics. It is well-known that traversable wormholes are of remarkable importance if they are stable under perturbations of linear order preserving the symmetry. The stability analysis has been extensively discussed for different wormholes through linear perturbations around a static solution or by using equation of state (EoS). In this scenario, Poisson and Visser (1995) performed stability analysis under perturbations of thin-shell wormhole formed by connecting two different manifolds of the Schwarzschild spacetime. Eiroa and Romero (2004) studied linearized stability analysis for charged thin-shell wormholes in Reissner-Nordström geometry and found stable solutions with increasing value of charge. Lobo and Crawford (2004) examined stability of spherically symmetric thin-shell wormholes with cosmological constant (Λ) and found that its positive value increases the stability regions but this region decreases with negative Λ.

The thin-shell wormholes preserving cylindrical symmetry have also been constructed in literature (Clement 1995; Aros and Zamorano 1997; Kuhfittig 2005; Bronnikov and Lemos 2009). The instability issues for cylindrical thin-shell wormholes under global and local cosmic strings are widely discussed (Eiroa and Simeone, 2004, 2010; Bejarano et al., 2007; Richarte and Simeone, 2009). It was found that only unstable wormhole configurations exist under radial perturbations in velocity. Some researchers constructed thin-shell wormholes in modified theories of gravity and also analyzed their stability. Thibeault et al. (2006) examined stable five dimensional wormhole solutions with Gauss-Bonnet term, while Amirabi et al. (2013) studied effects of Gauss-Bonnet term on the stability of thin-shell wormholes in higher dimensions. Sharif and Rani (2013) constructed static spherically symmetric thin-shell wormholes with noncommutative geometry in f(T) gravity. Recently, Sharif and Yousaf (2013c) have analyzed stability of cylindrical thin-shell wormholes in f(R) gravity.

The choice of model supporting exotic matter at the wormhole throat is a fascinating issue for stability analysis in general relativity. Various candidates like phantom energy (Lobo, 2005), tachyon matter (Das and Kar, 2005) and Chaplygin gas (Lobo, 2006) have been proposed to explore exotic matter at the wormhole throat. Eiroa and Simeone (2007) constructed spherical thin-shell wormholes with Chaplygin gas and examined their stability. Eiroa (2009) extended the same work for generalized Chaplygin gas and found both stable and unstable wormhole solutions. Bandyopadhyay et al. (2009) discussed stability of spherically symmetric thin-shell wormholes for modified Chaplygin gas. Sharif and Azam (2013) have investigated stable cylindrical wormhole solutions supported by modified generalized Chaplygin gas. Banerjee (2013) examined the stability of charged spherical thin-shell wormholes by considering phantom-energy and generalized Chaplygin gas at the throat. Recently, Sharif and Mumtaz (2013) explored both static stable and unstable charged black string (CBS) wormhole solutions supported by generalized cosmic Chaplygin gas.

The purpose of this paper is to analyze the stability of CBS thin-shell wormholes in the context of Van der Waals (VDW) quintessence fluid. The paper is organized as follows. In Sect. 2, we construct cylindrical thin-shell wormholes from CBS by employing cut and paste technique. The surface stresses are formulated by using Darmois-Israel junction conditions. Section 3 is devoted to develop a general linearized stability formalism. This approach is applied to the constructed CBS thin-shell wormholes. We conclude our results in the last section.

2 Thin-shell wormhole formalism

The static cylindrically symmetric metric, i.e., CBS is given by (Sharif and Azam 2013)

$$ ds^2=-\psi(r)dt^2+\psi^{-1}(r)dr^2+{f}(r) \bigl(d\phi^2+\alpha^2dz^2\bigr), $$
(1)

where \(\psi(r)=\alpha^{2}r^{2}-\frac{4M}{\alpha r}+\frac{4Q^{2}}{\alpha^{2}r^{2}}\) is a positive function for radial coordinate r>0 and f(r)=r2. The parameter Q corresponds to the Arnowitt-Deser-Misner (ADM) charge density, while M is the ADM mass and \(\alpha^{2}=-\frac{\varLambda}{3}>0\). The inner and outer event horizons of CBS for \(Q^{2}\leq\frac{3}{4}M^{\frac{4}{3}}\) are given by

$$ r^{\pm}=\frac{(4M)^{\frac{1}{3}}}{2\alpha} \biggl[\sqrt{p}\pm\sqrt{2 \sqrt{p^2-Q^2 \biggl(\frac{2}{M} \biggr)^{\frac{4}{3}}}-p} \biggr], $$
(2)

where

$$\begin{aligned} p =& \biggl(0.5+0.5\sqrt{1-2.37\frac{Q^6}{M^4}} \biggr)^{\frac{1}{3}} \\ &{}+ \biggl(0.5-0.5\sqrt{1-2.37\frac{Q^6}{M^4}} \biggr)^{\frac{1}{3}}. \end{aligned}$$
(3)

The given spacetime forms naked singularity for \(Q^{2}>\frac{3}{4}M^{\frac{4}{3}}\), while \(Q^{2}=\frac{3}{4}M^{\frac{4}{3}}\) gives extremal black string. We apply the standard Darmois-Israel formalism (Darmois 1927; Israel 1966; Musgrave and Lake 1996) to discuss the dynamics of thin-shell wormhole. The cut and paste technique is a useful way for thin-shell wormhole construction. We cut the interior region of the given CBS with r<a, yielding two 4D copies \(\mathcal{V}^{\pm}\) with r≥a. A new manifold \(\mathcal{V}=\mathcal{V}^{+}\cup\mathcal{V}^{-}\) is obtained by pasting these geometries at

$$\varSigma^\pm=\varSigma=\{r=a\}. $$

The radial flare-out condition, i.e., the minimal size at throat, must be fulfilled at the wormhole throat in order to maintain the wormhole structure. We can define the coordinates ξi=(τ,ϕ,z) at Σ with τ the proper time on the shell. The induced 3D metric at Σ with throat radius a=a(τ) is

$$ ds^2=-d\tau^2+a^2(\tau) \bigl(d \phi^2+\alpha^2dz^2\bigr). $$
(4)

The matter thin layer on Σ yields the extrinsic curvature discontinuity. The extrinsic curvatures joining the two sides of the shell are defined as

$$ K^{\pm}_{ij}=-n^{\pm}_{\beta} \biggl(\frac{\partial^2x^{\kappa}_{\pm}}{\partial\xi^i \partial \xi^j}+\varGamma^\beta_{\mu\nu} \frac{\partial x^{\mu}_{\pm}\partial x^{\nu}_{\pm}}{\partial\xi^i \partial\xi^i } \biggr) \quad(i,j=0,2,3). $$
(5)

The unit four-vector normals \(n^{\pm}_{\beta}\) to \(\mathcal{V}^{\pm}\) are given by

$$ n^\pm_{\beta}=\pm\biggl\vert g^{\mu\nu} \frac{\partial\eta}{\partial x^\mu}\frac{\partial\eta}{\partial x^\nu}\biggr\vert ^{-\frac{1}{2}} \frac{\partial\eta}{\partial x^\beta}= \biggl(-\dot{a},\frac{\sqrt{\psi(r)+\dot{a}^2}}{\psi (r)},0,0 \biggr), $$
(6)

satisfying the relation nβnβ=1. Using Eqs. (1) and (5), we have

$$\begin{aligned} \begin{aligned} &K^\pm_{\tau\tau}=\mp\frac{\psi'(a)+2\ddot{a}}{ 2\sqrt{\psi(a)+\dot{a}^2}},\qquad K^\pm_{\phi\phi}=\pm\frac{1}{a}\sqrt{\psi(a)+ \dot{a}^2},\\ &K^\pm_{zz}=\alpha^2K^\pm_{\phi\phi}, \end{aligned} \end{aligned}$$
(7)

where dot and prime represent \(\frac{d}{d\tau}\) and \(\frac{d}{dr}\), respectively. The dynamical evolution of wormhole is determined by the Lanczos equations

$$ S_{ij}=\frac{1}{8\pi}\bigl\{ g_{ij}K-[K_{ij}] \bigr\} , $$
(8)

where \([K_{ij}]=K_{ij}^{+}-K_{ij}^{-}\) and \(K=\operatorname {tr}[K_{ij}]=[K_{~i}^{i}]\). The surface stress-energy tensor \(S_{ij}=\operatorname {diag}(\sigma,p_{\phi},p_{z})\) provides the surface stresses at Σ. Using Eqs. (7) and (8), the surface stresses σ and p=pϕ=pz at Σ become

$$\begin{aligned} &{ \sigma=-\frac{1}{2\pi a}\sqrt{\psi(a)+\dot{a}^2},} \end{aligned}$$
(9)
$$\begin{aligned} &{ p=p_{\phi}=p_{z}=\frac{1}{8\pi} \frac{2\dot{a}^2+2a\ddot{a}+2\psi(a)+ a{\psi'(a)}}{a\sqrt{\psi(a)+\dot{a}^2}}.} \end{aligned}$$
(10)

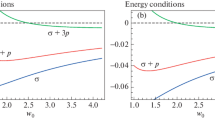
We observe that σ<0 violating the null energy conditions indicates exotic matter at r=a.

In order to discuss the dynamical characterization of the shell, we assume VDW quintessence fluid (Capozziello et al., 2002, 2005) on the shell Σ. The EoS for VDW quintessence is defined as

$$ p=\frac{\gamma\sigma}{1-B\sigma}-A\sigma^2, $$
(11)

where A, B and γ are EoS parameters. The VDW quintessence EoS is a remarkable scenario in which the specific values of the parameters A, B and γ describe the accelerated and decelerated periods. In the limit A,B→0, this EoS gives dust for γ=0 and corresponds to radiation for γ=1/3. Using Eqs. (9) and (10) in (11), we formulate the dynamical equation as follows

$$\begin{aligned} &{\biggl\{ \bigl[2\ddot{a}+{\psi'(a)}\bigr]a^2+ \bigl[\psi(a)+\dot{a}^2\bigr]2a+\frac{2A}{ \pi}\bigl[\psi(a)+ \dot{a}^2\bigr]^{\frac{3}{2}} \biggr\} }\\ &{\quad \times \bigl\{ 2\pi^2a+B\pi\sqrt{\psi(a)+ \dot{a}^2} \bigr\} }\\ &{\quad{} +2\gamma(2\pi a)^2\bigl[\psi(a)+ \dot{a}^2\bigr]=0.} \end{aligned}$$
(12)

3 Stability analysis

In this section, we discuss the wormhole stability through linear perturbations. The surface stresses for the static wormhole solution through Eqs. (9) and (10) become

$$ \sigma_{0}=-\frac{\sqrt{\psi(a_{0})}}{2\pi a_{0}}, \qquad p_{0}= \frac{1}{8\pi}\frac{2\psi(a_{0})+ a_{0}{\psi'(a_{0})}}{a_{0}\sqrt{\psi(a_{0})}}. $$
(13)

Consequently, the dynamical Eq. (12) takes the form

$$\begin{aligned} &{\biggl\{ a_{0}^2{\psi'(a_{0})}+2a_{0} \psi(a_{0})+\frac{2A}{ \pi}\bigl[\psi(a_{0}) \bigr]^{\frac{3}{2}} \biggr\} }\\ &{\quad{}\times \bigl\{ 2\pi^2a_{0}+B\pi \sqrt{\psi(a_{0})} \bigr\} }\\ &{\quad{} +2\gamma(2\pi a_{0})^2 \psi(a_{0})=0.} \end{aligned}$$
(14)

The thin-shell equation of motion describing the dynamics of throat can be obtained by rearranging Eq. (9) as \(\dot{a}^{2}+\varDelta (a)=0\), where the potential function Δ(a) is given by

$$ \varDelta (a)=\psi(a)-\bigl[2\pi a\sigma(a)\bigr]^2. $$
(15)

We observe that σ and p satisfy the conservation equation

$$ \frac{d}{d\tau}(\sigma\mathcal{A})+p\frac{d\mathcal{A}}{d\tau}=0, $$
(16)

where \(\mathcal{A}=4\pi a^{2}\) is the wormhole throat area. This shows that the rate of change of throat internal energy plus work done by the internal forces within the throat vanishes. Using the wormhole throat area definition, this equation takes the form

$$ a\sigma'=-2(\sigma+p), $$
(17)

where we have used \(\sigma'=\frac{\dot{\sigma}}{\dot{a}}\). The EoS leads to

$$\begin{aligned} \sigma'(a)+2p'(a) =&\sigma'(a) \biggl\{ 1+\frac{2}{1-B\sigma(a)} \bigl[\gamma-2A\sigma(a) \\ &{} +B\bigl\{ p(a)+3A \sigma^2(a)\bigr\} \bigr] \biggr\} . \end{aligned}$$
(18)

For the stability analysis, we expand Δ(a) by Taylor series upto second order around a=a0, yielding

$$\begin{aligned} \varDelta (a) =&\varDelta (a_{0})+{\varDelta '(a_{0})}(a-a_{0}) \\ &{}+ \frac{1}{2}\varDelta ''(a_{0}) (a-a_{0})^2+O\bigl[(a-a_{0})^3 \bigr]. \end{aligned}$$

Differentiating Eq. (15) with respect to a and using Eq. (17), it follows that

$$ \varDelta '(a)=\psi'(a)+8\pi^2 a \sigma(a)\bigl[\sigma(a)+2p(a)\bigr]. $$
(19)

The conditions for the stability of wormhole static solution are Δ″(a0)≷0 and Δ′(a0)=0=Δ(a0). By using Eqs. (18) and (19), the second derivative of potential function is written as

$$\begin{aligned} \varDelta ''(a) =&\psi''(a)-8 \pi^2\biggl\{ \bigl[\sigma(a)+2p(a)\bigr]^2 \\ &{}+2\sigma(a) \bigl[\sigma(a)+p(a)\bigr] \\ &{}\times\biggl[1+\frac{2}{ 1-B\sigma}\bigl\{ \gamma-2A\sigma(a) \\ &{}+B \bigl[p(a)+3A\sigma^2(a)\bigr]\bigr\} \biggr]\biggr\} . \end{aligned}$$
(20)

Substituting the values of σ(a0) and p(a0), Δ(a) and Δ′(a) vanish at a=a0, while Eq. (20) becomes

$$\begin{aligned} \varDelta ''(a_{0}) =& \psi''(a_{0})+\frac{[\psi'(a_{0})]^2}{2\psi(a_{0})} \biggl[ \frac{B\sqrt{\psi(a_{0})}}{2\pi a_{0}+\sqrt{\psi(a_{0})}}-1 \biggr] \\ &{} +\frac{\psi'(a_{0})}{a_{0}} \biggl[1 +\frac{1}{2\pi a_{0}+\sqrt{\psi(a_{0})}} \\ &{}\times \biggl\{ 4\pi a_{0}\gamma+4A \sqrt{\psi(a_{0})} \\ &{}+B \biggl(2\sqrt{\psi(a_{0})} +\frac{3AB\sqrt{\psi(a_{0})}}{\pi a_{0}} \biggr) \biggr\} \biggr] \\ &{}- \frac{2\psi(a_{0})}{a_{0}^2}(1+\gamma) \biggl[1+\frac{1}{2\pi a_{0}+\sqrt{\psi(a_{0})}} \\ &{}\times \biggl\{ 4\pi a_{0}\gamma+4A\sqrt{ \psi(a_{0})} \\ &{}+B \biggl(2\sqrt{\psi(a_{0})}+\frac {3AB\sqrt{\psi(a_{0})}}{\pi a_{0}} \biggr) \biggr\} \biggr]. \end{aligned}$$
(21)

We are interested to formulate static CBS thin-shell wormhole solutions and analyze their stability by taking linear perturbations. In this context, the surface energy density and surface tension for static configuration yield

$$\begin{aligned} \begin{aligned} &\sigma_{0}=-\frac{\sqrt{\alpha^4a_{0}^4-4M\alpha a_{0}+4Q^2}}{2\pi\alpha a_{0}^2},\\ & p_{0}= \frac{\alpha^3a_{0}^3-M}{2\pi a_{0}\sqrt{\alpha^4a_{0}^4-4M\alpha a_{0}+4Q^2}}. \end{aligned} \end{aligned}$$
(22)

The corresponding dynamical equation through Eq. (12) turns out to be

$$\begin{aligned} &{\biggl[2\alpha a_{0}^2\bigl( \alpha^4a_{0}^4-M\alpha a_{0}\bigr)+ \frac{A}{\pi}\bigl(\alpha^4a_{0}^4-4M \alpha a_{0}+4Q^2\bigr)^{\frac{3}{2}} \biggr] }\\ &{\quad \times \Bigl[2 \pi^2\alpha a_{0}^2+B\pi \sqrt{\alpha^4a_{0}^4-4M \alpha a_{0}+4Q^2} \Bigr] }\\ &{\quad{} +\gamma\bigl(2\pi\alpha a_{0}^2\bigr)^2\bigl[\alpha^4a_{0}^4-4M \alpha a_{0}+4Q^2\bigr]=0, } \end{aligned}$$
(23)

where its solutions represent static CBS thin-shell wormholes. Using ψ(a) in Eq. (21), Δ″(a0) becomes

$$\begin{aligned} &{\varDelta ''(a_{0}) }\\ &{\quad = \frac{2}{\alpha^4a_{0}^4(\alpha^4a_{0}^4-4M\alpha a_{0}+4Q^2)} }\\ &{\qquad{}\times \biggl[4M\alpha a_{0}\bigl(4Q^2-M\alpha a_{0}\bigr) }\\ &{\qquad{}+\bigl(\alpha^4a_{0}^4+2M \alpha a_{0}-4Q^2\bigr) }\\ &{\qquad{}\times \bigl(\alpha^4a_{0}^4-4M \alpha+4Q^2\bigr) } \\ &{\qquad{}-\alpha^4a_0^4\bigl( \alpha^4a_{0}^4+4M\alpha a_{0}-8Q^2 \bigr) }\\ &{\qquad{}-16Q^4+8\pi X }\\ &{\qquad{}\times\frac{\alpha a_{0}^2(3M\alpha a_{0}-4Q^2)(\alpha^4a_{0}^4-4M\alpha a_{0}+4Q^2)}{2\pi\alpha a_{0}^2+B\sqrt{\alpha^4a_{0}^4-4M\alpha a_{0}+4Q^2}} \biggr], } \end{aligned}$$
(24)

where

$$\begin{aligned} X =&\gamma+\frac{A\sqrt{\alpha^4a_{0}^4-4M\alpha a_{0}+4Q^2}}{\pi\alpha a_{0}^2} \\ &{}+B \biggl[\frac{\alpha^3 a_{0}^3-4M}{2\pi a_{0}\sqrt{\alpha^4a_{0}^4-4M\alpha a_{0}+4Q^2}} \\ &{}+\frac{3A(\alpha^4a_{0}^4-4M\alpha a_{0}+4Q^2)}{4\pi^2\alpha^2a_{0}^4} \biggr]. \end{aligned}$$

Now we investigate the wormhole stability around static configurations. We solve Eq. (23) numerically and insert the value of a0 in Eq. (24) to check the behavior of solutions whether they are stable or unstable. It is important to mention here that we take the specific value of charge Qc=0.866025 to construct a horizon free manifold and discuss the behavior of static solutions for this specific value of charge. For the existence of static solutions, we have the following possibilities.

  • Stable static solution exists if throat radius is greater than horizon radius, i.e., a0>rh and Δ″>0.

  • Unstable static solution is obtained for a0>rh and Δ″<0.

  • For a0≤rh, no static solution exists which corresponds to the non-physical region (grey zone).

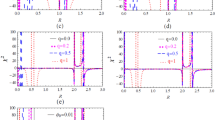
We examine the stability of cylindrical thin-shell wormholes corresponding to A=2 and γ=−0.1, −0.5, 0.4, 1 in Figs. 1–4. We also check the behavior of solutions corresponding to different values of charge and analyze the role of increasing charge on the stability of CBS wormhole configurations. The unstable and stable solutions are represented by dotted and solid curves, respectively. For γ∈(−∞,−0.3], we find that there does not appear stability regions corresponding to \(\frac{|Q|}{Q_{c}}=0,0.7\), i.e., |Q|<Qc. We plot the graphs for γ=−0.5 in Fig. 1. In this case, both stable and unstable wormhole configurations do exist with the increase in charge. We investigate three solutions corresponding to γ∈[−0.2,0] and |Q|<Qc, the larger and the smaller ones are unstable and the middle one is stable.

Fig. 1
figure 1

Plots of CBS thin-shell wormholes corresponding to α=0.6, γ=−0.5, M=1 and A=2

Full size image

In Fig. 2, we plot these solutions for γ=−0.1. Both stable and unstable configurations do exist for \(\frac{|Q|}{Q_{c}}=0.999,1.1\), i.e., |Q|≈Qc and |Q|>Qc. For γ∈[0.1,0.9], we find one stable and one unstable solutions corresponding to \(\frac{|Q|}{Q_{c}}=0,0.7\). In Fig. 3, we evaluate these results for γ=0.4 and find only stable solution for \(\frac{|Q|}{Q_{c}}=0.999\) and both stable and unstable solutions for |Q|>Qc. Finally, we analyze the stability of CBS thin-shell wormholes for γ∈[1,∞) and examine only stable solutions for \(\frac{|Q|}{Q_{c}}=0,0.7,0.999\). The corresponding graphs for γ=1 are shown in Fig. 4. There exist stable and unstable static solutions for charge |Q|>Qc. It is worth mentioning here that stability of solutions increases for increasing value of γ.

Fig. 2
figure 2

Plots with the parameters α=0.6, γ=−0.1, M=1 and A=2 for different values of charge

Full size image
Fig. 3
figure 3

Plots for α=0.6, γ=0.4, M=1 and A=2

Full size image
Fig. 4
figure 4

Plots corresponding to α=0.6, γ=1, M=1 and A=2

Full size image

4 Conclusions

The objective of this paper is to analyze the stability of thin-shell wormholes against linear perturbations preserving the cylindrical symmetry by incorporating the effects of charge. We have constructed CBS thin-shell wormholes by applying the cut and paste scheme. The surface density and pressure have been formulated by Darmois-Israel junction conditions. The standard potential approach has been adopted for stability analysis by taking VDW quintessence EoS at the wormhole throat. We have used numerical technique to find the value of a0 by solving Eq. (23) for γ=−0.1, −0.5, 0.4, 1. We have studied different stability/instability regions for different ranges of the parameter γ and the charge \(\frac{|Q|}{Q_{c}}\).

The results in Figs. 1–4 can be summarized as follows.

  • When \(\frac{|Q|}{Q_{c}}=0,0.7\), only unstable solutions exist for γ=−0.5. We have three solutions for γ=−0.1, two of them are unstable and one is stable. For γ=0.4, only one stable and one unstable solutions are found. It is found that stable region increases by increasing values of the parameter γ and we have all stable solutions for γ=1. The throat radius tends to increase for large values of Bα−(1+γ) but does not touch the horizon radius.

  • When \(\frac{|Q|}{Q_{c}}=0.999\), i.e., |Q|≈Qc, one stable and unstable solutions appear for negative values of γ, i.e., γ=−0.1, −0.5. The throat radius increases with the increase of Bα−(1+γ) in each case. The possibility of stable solutions increases for γ>0 and we have found only stable configurations for γ=0.4. We have examined one unstable as well as stable solution for γ=1. Moreover, the horizon radius continues to step down by increasing the charge \(\frac{|Q|}{Q_{c}}\).

  • For \(\frac{|Q|}{Q_{c}}=1.1\), i.e., |Q|>Qc, both unstable and stable solutions do exist for γ=−0.5. For γ=−0.1, there exist three solutions, the larger one is stable, while the smaller ones are unstable. Four static solutions (one stable and three unstable) appear for γ=0.4, while we have an unstable and stable configurations corresponding to γ=1. The horizon radius decreases gradually and vanishes for |Q|>Qc.

We conclude that the increase in the values of charge and the parameter γ lead to more stable wormhole configurations. It is important to mention here that the wormhole throat radius is an increasing function of Bα−(1+γ) and does not touch the horizon radius in all these cases. Moreover, the horizon radius of the given manifold tends to step down with the increase in charge and eventually vanishes for |Q|>Qc. It is worthwhile to mention that there exist unstable cylindrical thin-shell wormholes in literature (Eiroa and Simeone, 2004, 2010; Bejarano et al., 2007; Richarte and Simeone, 2009). We have found stable thin-shell wormholes with cylindrical background for an appropriate EoS at the wormhole throat which is well consistent with Sharif and Azam (2013).