Capillary Waves and Dipole Electromagnetic Radiation Generated by Nonlinear Oscillations of an Uncharged Droplet in an External Uniform Electrostatic Field

Abstract

Analytical derivations of the second order of smallness with respect to dimensionless amplitude $\varepsilon$ of oscillations of an uncharged electroconducting droplet in an external electric field have yielded an analytical expression for the intensity of its dipole electromagnetic radiation related to the oscillations, with this expression enabling one to study the radiation intensity as depending on the physical parameters of the problem. This problem is of interest in connection with radio-locating probing meteorological objects, such as clouds, fogs, and tornados. The time evolution of the electromagnetic radiation intensity and its components, i.e., the magnitude of the induced charge and dipole moment, of the droplet has been studied. The dipole radiation intensity has been determined in the second order of smallness with respect to the squared ratio between the characteristic linear size of the droplet and the wavelength of the emitted radiation. The intensity has appeared to be higher by a value of $\sim {\kern 1pt} \varepsilon$ than the intensity obtained by the calculations linear with respect to $\varepsilon$. However, a correction (quadratic with respect to $\varepsilon$) to the radiation of the droplet is realized in another frequency range, thereby affecting the spectrum of the electromagnetic radiation.

INTRODUCTION

In the below-presented consideration performed within analytical asymptotic calculations of the second order of smallness with respect to the dimensionless oscillation amplitude, we calculate the intensity of the dipole electromagnetic radiation of an uncharged electroconducting droplet, which is subjected to nonlinear oscillations with a finite amplitude in an external electrostatic field.

It is well known that field-induced charges arise on the surface of an uncharged electroconducting droplet subjected to an external electrostatic field. The charges have opposite signs, i.e., negative ones on the droplet side facing the field and positive signs on the opposite side [1]. Capillary waves always take place in a liquid droplet. Such waves are associated with the thermal motion of molecules [2] and perturb the equilibrium droplet shape in an electrostatic field, with this shape being nearly spheroidal [3, 4]. Capillary waves differ from ordinary gravitational ones only in the fact that they have markedly shorter lengths and are realized under the action of surface tension forces (capillary forces) rather than the gravity force. The amplitude of thermal capillary waves (which are realized in a droplet) is rather small: $\sim {\kern 1pt} \sqrt {{{\kappa T} \mathord{\left/ {\vphantom {{\kappa T} \sigma }} \right. \kern-0em} \sigma }}$, where $\kappa$ is the Boltzmann constant, $T$ is the absolute temperature, and $\sigma$ is the surface tension coefficient [2]. For all liquids, including liquid metals, their amplitude is no larger than 0.1 nm. However, it is of importance for the below-presented consideration that, moving with acceleration together with the surface of an oscillating droplet, the charges induced in the droplet by an external electrostatic field will radiate electromagnetic waves [1, 5–7].

The theory of electromagnetic waves emitted upon the accelerated motion of electric charges has been well developed [8, 9]. According to the multipole ideas [8, 9], the total electromagnetic radiation of a system of charges moving with acceleration, as measured at large distances from the radiating system, may be represented as the sum of the dipole, quadrupole, and magnetodipole components. These components have greatly different intensities. For example, in the case of a water droplet oscillating in an external uniform electrostatic field, the intensity of the dipole radiation from the droplet is nearly ${{10}^{{14}}}$ times higher than the intensity of the quadrupole and magnetodipole radiations [10].

In the theory of electromagnetic radiation, small parameter $\delta$ is introduced, i.e., the squared ratio between the characteristic linear size of the system and the length of the emitted wave [8, 9]. It is this parameter that is used to classify the entire radiation into the multipole components.

For an oscillating conducting liquid droplet, which carries induced charges, one more small parameter $\varepsilon$ should be used, i.e., the ratio between the oscillation amplitude and the droplet radius.

The problem concerning the fact of the existence of electromagnetic radiation emitted by an oscillating droplet in thunderstorm clouds was for the first time formulated previously [5] in connection with the study of electromagnetic interference, which is caused by convective clouds, and the distant electromagnetic probing of such clouds [11–13]. In [5], a method was proposed for the determination of radiation intensity using a model of an oscillating and radiating charged droplet of an ideal liquid, with this method being based on the solution of the electrohydrodynamic problem concerning the oscillations of a charged droplet and the energy conservation law.

In [14], we considered the problem of calculating the intensity of the dipole component of the total radiation of an oscillating charged droplet in an electrostatic field, while, in [15], we solved the problem concerning the intensity of the quadrupole component of the total radiation. In this work, the intensity of the dipole component of the total radiation emitted by an uncharged droplet oscillating in an electrostatic field of a thunderstorm cloud will be qualitatively estimated within the framework of the asymptotic analytical approach using a model droplet of an ideal incompressible electroconducting liquid within the second order of smallness.

MAIN SECTION

1. Problem formulation. Assume that we have an uncharged oscillating droplet of an ideal incompressible liquid, which has ideal conductivity and density $\rho$ and is subjected to a uniform electrostatic field with strength ${{\vec {E}}_{0}}$. Suppose that a medium surrounding the droplet may be simulated by vacuum, and its volume is equisized with the volume of a sphere having radius $R$. In the linear approximation with respect to the amplitude of stationary deformation, the equilibrium shape of the droplet in an electrostatic field may be considered to be spheroidal [16]. Such a spheroidal droplet will be used to simulate a droplet in a thunderstorm cloud.

The numerical values of the droplet sizes and the intracloud electric field strengths, which are necessary for qualitative assessments, will be taken in accordance with [17, 18].

All calculations within the problem will be carried out in a spherical coordinate system $\left( {r,\;\theta ,\;\varphi } \right)$, the origin of which is placed into the mass center of the droplet, and in dimensionless variables, in which $R = \rho = \sigma = {{\left[ {4{{\pi }}{{{{\varepsilon }}}_{0}}} \right]}^{{ - 1}}} = 1$ (ε₀ is the electric constant). The other parameters of the problem will be expressed in the fractions of their characteristic values: $\left[ {{{E}_{0}}} \right] = {{\left[ {4{{\pi }}{{{{\varepsilon }}}_{0}}} \right]}^{{ - 1/2}}}{{R}^{{ - 1/2}}}{{\sigma }^{{1/2}}}$, $\left[ t \right] = {{R}^{{3/2}}}{{\rho }^{{1/2}}}{{\sigma }^{{ - 1/2}}}$, $\left[ V \right] = {{R}^{{ - 1/2}}}{{\rho }^{{ - 1/2}}}{{\sigma }^{{1/2}}}$, $\left[ r \right] = R$, and $\left[ P \right] = {{R}^{{ - 1}}}\sigma$.

The equilibrium droplet eccentricity (the ratio of the interfocal distance of a spheroidal droplet to the length of its major axis) is determined in the aforementioned dimensionless variables as ${{e}^{2}} \approx \frac{{9E_{0}^{2}}}{{16\pi }}$, i.e., ${{e}^{2}} \sim E_{0}^{2}$ [16]. The equation for the generating line of the spheroidal droplet surface is written as

$$r\left( \theta \right) \approx 1 + \frac{1}{3}{{e}^{2}}{{P}_{2}}\left( \mu \right) + O({{e}^{4}}),\,\,\,\,\mu \equiv \cos \theta ,$$

(1)

$O$ is the order symbol [19] and ${{P}_{2}}{\kern 1pt} \left( {\cos {\kern 1pt} \theta } \right) \equiv \frac{1}{2}{\kern 1pt} \left( {3{\kern 1pt} {{{\cos }}^{2}}{\kern 1pt} \theta - 1} \right){\kern 1pt}$ is the second Legendre polynomial [8, 16]. The equilibrium spheroidal shape of the droplet will be used in the subsequent qualitative calculations.

Strictly speaking, in the quadratic approximation with respect to $\varepsilon$, a deviation of the equilibrium shape from the spheroidal one takes place, with this deviation being proportional to the third Legendre polynomial ${{P}_{3}}\left( {\cos {\kern 1pt} \theta } \right) \equiv \frac{1}{2}\left( {5{{{\cos }}^{3}}{\kern 1pt} \theta - 3{\kern 1pt} \cos {\kern 1pt} \theta } \right)$ [16]. However, first, the amplitude of this deviation is rather small (an order of magnitude smaller than the correction that is proportional to the second Legendre polynomial), and, second, there is an obvious advantage of using a spheroidal shape in analytical calculations: in the case of this shape, analytical solutions are available for the electric potential distribution in the vicinity of a droplet in diverse situations [20–22].

It should be noted that the correction to the asymptotically exact solution of the first order with respect to $\varepsilon$ takes place in another frequency range, as compared with the first-order solution, provided that the correction is quadratic with respect to $\varepsilon$. Although this correction is not quite adequate (according to all of the mentioned in the previous paragraph), it should be taken into account if for no other reason that, in the total radiation intensity, it is 10¹³ times higher that the intensities of the quadrupole and magnetodipole radiations [10].

Let the equilibrium spheroidal shape of a droplet with eccentricity e is, at initial time moment $t = 0$, subjected to virtual axially symmetric perturbation $\xi \left( \theta \right)$ of a fixed amplitude. The $\varepsilon \equiv \left( {\frac{{\max \left| {\xi \left( \theta \right)} \right|}}{R}} \right)$ ratio between $\max \left| {\xi \left( \theta \right)} \right|$ and radius $R$ (in the dimensional form) will be used as a small parameter.

Since the initial perturbation of the equilibrium droplet surface is axially symmetric, it is obvious that this symmetry will also remain preserved at $t > 0$, while the equation for its generating line in the spherical coordinate system, with its origin being placed into the mass center of the droplet, will, in the dimensionless variables, have the following form:

$$\begin{gathered} r\left( {\theta ,t} \right) = r\left( \theta \right) + \xi \left( {\theta ,t} \right) = 1 + {{e}^{2}}h\left( \theta \right) + \xi \left( {\theta ,t} \right), \\ h\left( \theta \right) \equiv \frac{1}{3}{{P}_{2}}\left( \mu \right),\,\,\,\,\left| \xi \right| \ll 1. \\ \end{gathered} $$

(2)

The motion of the liquid in the droplet is supposed to be potential, while field $\vec {V}\left( {\vec {r},t} \right) = \nabla \psi \left( {\vec {r},t} \right)$ of the liquid motion velocities in the droplet is assumed to be completely determined by velocity potential $\psi \left( {\vec {r},t} \right)$ [23]. Since the liquid flow in the droplet is generated by the surface perturbation, the value of the flow velocity field for the liquid in the droplet has the same order of smallness as the amplitude of the capillary waves in it. In other words, all three aforementioned values have the same order of smallness: $\left| {\vec {V}\left( {\vec {r},t} \right)} \right| \sim \psi \left( {\vec {r},t} \right)\sim \varepsilon$.

The mathematical formulation for the problem of the electromagnetic radiation emitted by an uncharged droplet in an external electrostatic field is as follows:

$$\Delta \psi (\vec {r},t) = 0,\,\,\,\,\Delta \Phi {\kern 1pt} (\vec {r},t) = 0,$$

(3)

$$r \to 0{\kern 1pt} :\,\,\,\,\psi \left( {\vec {r},t} \right) \to 0,$$

(4)

$$r \to \infty {\kern 1pt} :\,\,\,\,\vec {E}\left( {\vec {r},t} \right) \to {{\vec {E}}_{0}} \equiv {{E}_{0}}{{\vec {e}}_{z}},\,\,\,\,\vec {E} = - \nabla \Phi ,$$

(5)

$$\begin{gathered} r = r\left( \theta \right) + \xi \left( {\theta ,t} \right){\kern 1pt} {\kern 1pt} :\,\,\,\,\frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial t}} = \frac{{\partial \psi \left( {\vec {r},t} \right)}}{{\partial r}} \\ - \,\,\frac{1}{{{{r}^{2}}}}\frac{{\partial \psi \left( {\vec {r},t} \right)}}{{\partial \theta }}\left( {\frac{{\partial r\left( \theta \right)}}{{\partial \theta }} + \frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial \theta }}} \right), \\ \end{gathered} $$

(6)

$$\Delta P - \frac{{\partial \psi }}{{\partial t}} - \frac{1}{2}{{(\nabla \psi )}^{2}} + {{P}_{E}} = {{P}_{\sigma }},$$

(7)

$$\Phi (\vec {r},t) = {{\Phi }_{S}}(t),$$

(8)

where $\Phi \left( {\vec {r},t} \right)$ is the electric potential [9]; ${{\Phi }_{s}}\left( t \right)$ is the electric potential, which is constant along the droplet surface; and ${{\vec {e}}_{z}}$ is the unit vector of the z coordinate.

The above-written set of equations is closed by introducing the following integral conditions: the constancy of the total volume (the consequence of liquid incompressibility), the immobility of the mass center, and the uncharged state of the droplet.

$$\mathop \smallint \limits_V {{r}^{2}}dr\sin \theta d\theta d\varphi = \frac{4}{3}\pi ,\,\,\,\,\mathop \smallint \limits_V \vec {r}{{r}^{2}}dr\sin \theta d\theta d\varphi = 0,$$

(9)

$$\begin{gathered} V = \left[ {0 \leqslant r \leqslant r\left( \theta \right) + \xi \left( {\theta ,t} \right),\,\,0 \leqslant \theta \leqslant \pi ,\,\,0 \leqslant \varphi \leqslant 2\pi } \right], \\ \frac{1}{{4\pi }}\oint\limits_S {\left( {\vec {n},\vec {E}} \right)dS = 0} , \\ S = \left[ {r = r\left( \theta \right) + \xi \left( {\theta ,t} \right),\,\,0 \leqslant \theta \leqslant \pi ,\,\,0 \leqslant \varphi \leqslant 2\pi } \right], \\ \end{gathered} $$

(10)

where $\vec {n}$ is the unit vector of the external normal to the droplet surface; $V$ and $S$ are the droplet volume and surface area, which result from the rotation of the generating line determined by Eq. (2) around the droplet symmetry axis; and the regularities of variations in angles $\theta$ and $\varphi$ are determined by Eqs. (9) and (10).

In the general case, the initial conditions are specified by an initial deformation of the spheroidal droplet shape and the zero initial velocity of the surface motion as follows:

$$\begin{gathered} t = 0{\kern 1pt} {\kern 1pt} :\,\,\,\,\xi \left( \theta \right) = {{\xi }_{0}}{{P}_{0}}\left( \mu \right) + {{\xi }_{1}}{{P}_{1}}\left( \mu \right) \\ + \,\,\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}{{P}_{j}}\left( \mu \right),\,\,\,\,\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}} = 1,\,\,\,\,\frac{{\partial \xi \left( \theta \right)}}{{\partial t}} = 0, \\ \end{gathered} $$

(11)

where $\Xi$ is the set of the values of numbers of initially excited oscillation modes, ${{P}_{j}}\left( \mu \right)$ is the j-order Legendre polynomial, $j$ is an integral number, and $\mu \equiv \cos {\kern 1pt} \theta$.

The following denotations have been introduced in expressions (6)–(11): $\Delta P$ denotes the drops of the constant pressures inside and outside of the droplet at equilibrium; $\vec {E}$ is the electric field strength vector; ${{P}_{E}} = \frac{{{{{\vec {E}}}^{2}}}}{{8\pi }}$ is the electric field pressure; ${{P}_{\sigma }} = {\text{div}}\vec {n}$ is the capillary pressure (note that, according to [23, p. 334], ${{P}_{\sigma }}$ is the Laplace pressure defined as the product of the surface tension coefficient and the doubled average curvature of a liquid surface at a given point determined as the divergence of $\vec {n}$ [24, p. 179]); $\vec {n}$ is the unit vector of the external normal to the liquid surface described by expression (2); ${{h}_{j}}$ refers to the coefficients that determine the partial contributions of jth oscillation modes to the total initial perturbation; ${{\xi }_{0}}$ and ${{\xi }_{1}}$ are constants (amplitudes of the zero and first oscillation modes, respectively), which are equal to zero in the first-order calculations and, in the calculations of the second-order of smallness with respect to $\varepsilon$, are determined from the conditions of the constant volume and quiescent mass center at the initial time moment and, with an accuracy of terms $\sim {\kern 1pt} \varepsilon {{e}^{2}}$ and $\sim {\kern 1pt} {{\varepsilon }^{2}}$, are equal to

$$\begin{gathered} {{\xi }_{0}} \approx - \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {{{\varepsilon }^{2}}\frac{{h_{j}^{2}}}{{\left( {2j + 1} \right)}} + \varepsilon {{e}^{2}}\frac{2}{{15}}{{h}_{j}}{{\delta }_{{j,2}}}} \right] + O({{\varepsilon }^{3}}), \\ {{\xi }_{1}} \approx - \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {{{\varepsilon }^{2}}\frac{{9j{{h}_{{j{\kern 1pt} - {\kern 1pt} 1}}}{{h}_{j}}}}{{\left( {2j - 1} \right)\left( {2j + 1} \right)}} + \varepsilon {{e}^{2}}\frac{9}{{35}}{{h}_{j}}{{\delta }_{{j,3}}}} \right] + O({{\varepsilon }^{3}}), \\ \end{gathered} $$

(12)

where ${{\delta }_{{j,n}}}$ is the Kronecker symbol.

Note that there are two small parameters in the formulated problem: squared droplet eccentricity ${{e}^{2}}$ and dimensionless amplitude $\varepsilon \equiv \left( {\frac{{\max \left| {\xi \left( \theta \right)} \right|}}{R}} \right)$. According to [25, 26], freely falling oscillating rain droplets are subjected to spheroidal oscillations with an amplitude as large 60% of their radii. In other words, it is reasonable to consider a situation, in which small parameters ${{e}^{2}}$ and $\varepsilon$ have the same order of magnitude ${{e}^{2}}\sim \varepsilon$. This will somewhat simplify the cumbersome calculations, but will make narrower the range of applicability of the results obtained, with this circumstance being insubstantial for the qualitative assessment being performed. Confining the consideration of the formulated problem to the quadratic approximation, the subsequent calculations will be carried out retaining terms $\sim {\kern 1pt} {{\varepsilon }^{2}}$ and $\sim {\kern 1pt} {{e}^{2}}\varepsilon$. To be more specific, we take ${{e}^{2}}\sim \varepsilon$, thus reducing the problem to single small parameter $\varepsilon$.

The assumption made in the previous paragraph is accepted because the intracloud electrostatic field strength is, as a rule, low [18, p. 440] (Table 1). However, the electrostatic field strength determines the eccentricity values of droplets, which are, in turn, small. Thus, the value of squared eccentricity ${{e}^{2}}$ may be comparable with dimensionless amplitudes $\varepsilon$ of oscillation modes of a cloud droplet blown around with an ascending air flow.

Taking into account that the deviation of the equilibrium spheroidal shape of a droplet from the spherical one is due to the presence of an electric field, we take ${{E}_{0}}\sim e$. Thus, terms having the order of $\sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$ must be taken into account in the subsequent calculations of the electric potential in the vicinity of a perturbed charged spheroid, which is subjected to an external field, and the value of the charge induced on the perturbed droplet surface. These terms are related to the nonlinear interaction of excited oscillation modes with both stationary droplet deformation $\sim {{E}_{0}}{{e}^{2}}\varepsilon \sim {{e}^{{3/2}}}\varepsilon \sim {{\varepsilon }^{{5/2}}}$ and with each other, as well as with stationary droplet deformation $\sim {{E}_{0}}{{\varepsilon }^{2}}\sim {{e}^{{1/2}}}{{\varepsilon }^{2}}\sim {{\varepsilon }^{{5/2}}}$.

Let us introduce formal parameters ${{\beta }_{E}}$ and ${{\beta }_{e}}$ in accordance with expressions ${{E}_{0}} \equiv {{\beta }_{E}}{{\varepsilon }^{{1/2}}}$ and ${{e}^{2}} \equiv {{\beta }_{e}}\varepsilon$, to have opportunity to distinguish between contributions from ${{E}_{0}}$ and ${{e}^{2}}$ in the final expressions. To get rid of formal denotations in the final result, we take ${{\beta }_{E}} = {{\beta }_{e}} = 1$.

2. Asymptotic expansions of the desired values. We shall solve the problem with an accuracy of ${{\varepsilon }^{2}}$ by the method of many time scales [19]. Let us present desired functions $\xi \left( {\theta ,t} \right)$, $\psi \left( {\vec {r},t} \right)$, and $\Phi \left( {\vec {r},t} \right)$ as power expansions in terms of $\varepsilon$ and consider them to be not dependent just on time $t$, but rather on its different scales determined as ${{T}_{m}} \equiv {{\varepsilon }^{m}}t$, where $m$ is an integral number: $m = 0;\,\,1;\,\,2$:

$$\begin{gathered} \xi \left( {\theta ,t} \right) = \mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} 1}^\infty {{\varepsilon }^{m}}{{\xi }^{{\left( m \right)}}}\left( {\theta ,{{T}_{0}},{{T}_{1}}} \right), \\ \psi \left( {\vec {r},t} \right) = \mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} 1}^\infty {{\varepsilon }^{m}}{{\psi }^{{\left( m \right)}}}\left( {r,\theta ,{{T}_{0}},{{T}_{1}}} \right), \\ \Phi \left( {\vec {r},t} \right) = {{\Phi }^{{\left( {{\text{eq}}} \right)}}}\left( {r,\theta } \right) + {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}\left( {r,\theta ,{{T}_{0}}} \right) \\ + \,\,{{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}{{\Phi }^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}}\left( {r,\theta ,{{T}_{0}}} \right) + O({{\varepsilon }^{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}}). \\ \end{gathered} $$

(13)

Here, the electric field potential is expanded in terms of the half-integral powers of parameter $\varepsilon$, because ${{E}_{0}}\sim {{\varepsilon }^{{1/2}}}$. As a result, the expansion for electric potential ${{\Phi }^{{\left( {{\text{eq}}} \right)}}}\left( {r,\theta } \right)$ in the vicinity of an equilibrium uncharged spheroid in an external field is also carried out in terms of the half-integral powers of parameter $\varepsilon$ and is written as

$$\begin{gathered} {{\Phi }^{{\left( {{\text{eq}}} \right)}}}\left( {r,\theta } \right) = {{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{\beta }_{E}}r\left[ {\frac{1}{{{{r}^{3}}}} - 1} \right]{{P}_{1}}\left( \mu \right) \\ + \,\,{{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{\beta }_{E}}{{\beta }_{e}}\frac{2}{5}\frac{1}{{{{r}^{2}}}}\left[ {{{P}_{1}}\left( \mu \right) + \frac{3}{2}\frac{1}{{{{r}^{2}}}}{{P}_{3}}\left( \mu \right)} \right]. \\ \end{gathered} $$

(14)

The time derivatives will be calculated taking into account the entire set of different time scales according to the following rule [19]:

$$\frac{\partial }{{\partial t}} = {{\varepsilon }^{0}}\frac{\partial }{{\partial {{T}_{0}}}} + {{\varepsilon }^{1}}\frac{\partial }{{\partial {{T}_{1}}}} + {{\varepsilon }^{2}}\frac{\partial }{{\partial {{T}_{2}}}} + {\rm O}\left( {{{\varepsilon }^{3}}} \right).$$

Substituting expansions (13) into relations (3)–(10) and equating the terms of the same order of smallness in each equation, we isolate the problems of the consecutive determination of unknown functions ${{\xi }^{{\left( m \right)}}}\left( {\theta ,t} \right)$, ${{\psi }^{{\left( m \right)}}}\left( {\vec {r},t} \right)$, and ${{\Phi }^{{\left( k \right)}}}\left( {\vec {r},t} \right)$. In these expressions, parenthetic superscripts $m$ and $k$ denote the expansion orders of smallness and are integral and half-integral numbers, respectively.

Solutions of Laplace equations (3) for the corrections to hydrodynamic ${{\psi }^{{\left( m \right)}}}\left( {\vec {r},t} \right)$ and electric ${{\Phi }^{{\left( k \right)}}}\left( {\vec {r},t} \right)$ potentials satisfying conditions (4) and (5), as well as corrections to equilibrium droplet surface shape ${{\xi }^{{\left( m \right)}}}\left( {\theta ,t} \right)$ are written as series in terms of Legendre polynomials:

$$\begin{gathered} {{\psi }^{{\left( m \right)}}}\left( {r,\theta ,{{T}_{0}},{{T}_{1}}} \right) = \mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty D_{n}^{{\left( m \right)}}\left( {r,\theta ,{{T}_{0}},{{T}_{1}}} \right){{r}^{n}}{{P}_{n}}\left( \mu \right), \\ \left( {m = 1;\,\,2} \right), \\ \end{gathered} $$

(15)

$$\begin{gathered} {{\Phi }^{{\left( k \right)}}}\left( {r,\theta ,{{T}_{0}}} \right) = \mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty F_{n}^{{\left( k \right)}}\left( {r,\theta ,{{T}_{0}}} \right){{r}^{{ - \left( {n{\kern 1pt} + {\kern 1pt} 1} \right)}}}{{P}_{n}}\left( \mu \right), \\ \left( {k = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2};\,\,{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right), \\ \end{gathered} $$

(16)

$$\begin{gathered} {{\xi }^{{\left( m \right)}}}\left( {\theta ,{{T}_{0}},{{T}_{1}}} \right) = \mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty M_{n}^{{\left( m \right)}}\left( {\theta ,{{T}_{0}},{{T}_{1}}} \right){{P}_{n}}\left( \mu \right), \\ \left( {m = 1;2} \right). \\ \end{gathered} $$

(17)

3. Problem of the first order of smallness with respect to ε. For determining amplitude coefficients $D_{n}^{{\left( m \right)}}$ and $M_{n}^{{\left( m \right)}}$ in the first order of smallness with respect to ε in solutions (15) and (17) (at $m = 1$), Eqs. (6), (7), and (9) yield the following set of equations:

$$\begin{gathered} r = 1{\kern 1pt} :\,\,\,\,\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial {{T}_{0}}}} = \frac{{\partial {{\psi }^{{\left( 1 \right)}}}}}{{\partial r}}, \\ \frac{{\partial {{\psi }^{{\left( 1 \right)}}}}}{{\partial {{T}_{0}}}} = \left( {2 + {{{\hat {L}}}_{\theta }}} \right){{\xi }^{{\left( 1 \right)}}},\,\,\,\,{{{\hat {L}}}_{\theta }} \equiv \frac{1}{{\sin \theta }}\frac{\partial }{{\partial \theta }}\left( {\sin \theta \frac{\partial }{{\partial \theta }}} \right), \\ \mathop \smallint \limits_0^\pi {{\xi }^{{\left( 1 \right)}}}\sin \theta d\theta = 0,\,\,\,\,\mathop \smallint \limits_0^\pi {{\xi }^{{\left( 1 \right)}}}\cos \theta \sin \theta d\theta = 0. \\ \end{gathered} $$

(18)

Expressions for the first-order corrections to the coefficients of expansions (15) and (17) are easily found from set (18) as

$$\begin{gathered} M_{0}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = 0,\,\,\,\,M_{1}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = 0,\,\,\,\,D_{0}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = 0, \\ D_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = \frac{1}{n}\frac{{\partial M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)}}{{\partial {{T}_{0}}}},\,\,\,\,\left( {n \geqslant 1} \right). \\ \end{gathered} $$

(19)

To find coefficients $M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)$ at $n \geqslant 2$, it is necessary to solve the following second-order homogeneous differential equation:

$$\begin{gathered} \frac{{{{\partial }^{2}}}}{{\partial T_{0}^{2}}}M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) + \omega _{{n,s}}^{2}M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) = 0, \\ \omega _{{n,s}}^{2} = n\left( {n - 1} \right)\left( {n + 2} \right), \\ \end{gathered} $$

(20)

where ${{\omega }_{{n,s}}}$ is the frequency of intrinsic oscillations of an uncharged sphere surface.

The solution of Eq. (20) is represented by harmonic functions of time ${{T}_{0}}$ with coefficients, which depend on time ${{T}_{1}}$:

$$\begin{gathered} M_{n}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) \\ = A_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n,s}}}{{T}_{0}}} \right) + {\text{c}}{\text{.c}}.,\,\,\,\,\left( {n \geqslant 2} \right), \\ A_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right) \equiv a_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left[ {ib_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)} \right]. \\ \end{gathered} $$

(21)

Abbreviation “c.c.” denotes terms that are complex conjugates of the written ones. The dependences of $a_{n}^{{\left( 1 \right)}}$ and $b_{n}^{{\left( 1 \right)}}$ on parameter ${{T}_{1}}$ is determined in the subsequent orders of smallness.

4. The problem of the 3/2 order with respect to ε. The set of equations for determining coefficients $F_{n}^{{\left( {3/2} \right)}}$ in solution (16) is derived from conditions (8) and (10) by grouping terms ~ε^3/2 :

$$\begin{gathered} r = 1{\kern 1pt} :\,\,\,\,{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}} - 3{{\beta }_{E}}{{\xi }^{{\left( 1 \right)}}}{{P}_{1}}\left( \mu \right) = \Phi _{s}^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}, \\ \mathop \smallint \limits_0^\pi \frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}}\sin \theta d\theta = 0. \\ \end{gathered} $$

(22)

Here, $\Phi _{s}^{{\left( {3/2} \right)}}$ is the 3/2-order correction to the value of the droplet potential. Substituting expansion (16) at $k = 3{\text{/}}2$ and first-order solution (17) into set of equations (22), we determine coefficients $F_{n}^{{\left( {5/2} \right)}}\left( {{{T}_{0}}} \right)$ in the form of

$$\begin{gathered} F_{0}^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}\left( {{{T}_{0}}} \right) = 0,\,\,\,\,\Phi _{s}^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}} = 0, \\ F_{n}^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}\left( {{{T}_{0}}} \right) = 3{\kern 1pt} {{\beta }_{E}} \times \\ \times \,\,\left( {\mu _{{n{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{n{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right) + \mu _{{n{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{n{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( {{{T}_{0}},{{T}_{1}}} \right)} \right),\,\,\,\,\left( {n \geqslant 1} \right), \\ \mu _{n}^{ + } = \frac{{n + 1}}{{2n + 1}},\,\,\,\,\mu _{n}^{ - } = \frac{n}{{2n + 1}}. \\ \end{gathered} $$

(23)

The expressions obtained for desired values $\xi \left( {\theta ,t} \right)$, $\psi \left( {\vec {r},t} \right)$, and $\Phi \left( {\vec {r},t} \right)$ may be used to find the analytical expression for the dipole radiation intensity of an uncharged droplet oscillating in an external electrostatic field in the first order of smallness, as was done in, e.g., [10]. However, since the goal of the work is to determine the nonlinear correction revealed in the approximation quadratic with respect to the small parameter, we shall below solve the electrohydrodynamic problem of the second order of smallness with respect to ε.

5. The problem of the second order of smallness with respect to ε. To determine the corrections of the second order of smallness to the found solution (i.e., to find the ${{\xi }^{{\left( 2 \right)}}}\left( {\theta ,t} \right)$ and ${{\psi }^{{\left( 2 \right)}}}\left( {\vec {r},t} \right)$) functions, we present the set of equations that is derived from Eqs. (6)–(10) by equating the terms at ε²:

$$\begin{gathered} r = 1{\kern 1pt} :\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ \frac{{\partial {{\xi }^{{\left( 2 \right)}}}}}{{\partial {{T}_{0}}}} + \frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial {{T}_{1}}}} = \frac{{\partial {{\psi }^{{\left( 2 \right)}}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{\psi }^{{\left( 1 \right)}}}}}{{\partial {{r}^{2}}}} \\ \times \,\,\left[ {{{\xi }^{{\left( 1 \right)}}} + {{\beta }_{e}}h\left( \theta \right)} \right] - \left[ {\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial \theta }} + {{\beta }_{e}}\frac{{\partial h\left( \theta \right)}}{{\partial \theta }}} \right]\frac{{\partial {{\psi }^{{\left( 1 \right)}}}}}{{\partial \theta }}, \\ - \frac{{\partial {{\psi }^{{\left( 2 \right)}}}}}{{\partial {{T}_{0}}}} - \frac{{\partial {{\psi }^{{\left( 1 \right)}}}}}{{\partial {{T}_{1}}}} - \frac{{{{\partial }^{2}}{{\psi }^{{\left( 1 \right)}}}}}{{\partial r\partial {{T}_{0}}}}\left[ {{{\xi }^{{\left( 1 \right)}}} + {{\beta }_{e}}h\left( \theta \right)} \right] + P_{E}^{{\left( 2 \right)}} \\ = - \left( {2 + {{{\hat {L}}}_{\theta }}} \right){{\xi }^{{\left( 2 \right)}}} + 2{{\xi }^{{\left( 1 \right)}}}\left( {1 + {{{\hat {L}}}_{\theta }}} \right){{\xi }^{{\left( 1 \right)}}} \\ + \,\,2{{\beta }_{e}}h\left( \theta \right)\left( {{{{\hat {L}}}_{\theta }} - 4} \right){{\xi }^{{\left( 1 \right)}}}, \\ \mathop \smallint \limits_0^\pi \left[ {3{{\xi }^{{\left( 2 \right)}}} + 3{{{({{\xi }^{{\left( 1 \right)}}})}}^{2}} + 2{{\beta }_{e}}{{\xi }^{{\left( 1 \right)}}}{{P}_{2}}\left( \mu \right)} \right]\sin \theta d\theta = 0, \\ \mathop \smallint \limits_0^\pi \left[ {2{{\xi }^{{\left( 2 \right)}}} + 3{{{({{\xi }^{{\left( 1 \right)}}})}}^{2}} + 2{{\beta }_{e}}{{\xi }^{{\left( 1 \right)}}}{{P}_{2}}\left( \mu \right)} \right]\cos {\kern 1pt} \theta \sin {\kern 1pt} \theta d\theta = 0, \\ P_{E}^{{\left( 2 \right)}} = - \frac{3}{{4\pi }}\left[ {{{\beta }_{E}}{{P}_{1}}\left( \mu \right)\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} + 6\beta _{E}^{2}{{{\left( {{{P}_{1}}\left( \mu \right)} \right)}}^{2}}{{\xi }^{{\left( 1 \right)}}}} \right]. \\ \end{gathered} $$

(24)

Substituting expansions (15) at m = 1; 2 and the 3/2-order solution from Eq. (23) into set of equations (24), we derive expressions for coefficients $M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right)$ and $D_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right)$ as

$$\begin{matrix} M_{0}^{\left( 2 \right)}\left( {{T}_{0}} \right)=-\underset{k{\kern 1pt} ={\kern 1pt} {\kern 1pt} 0}{\overset{\infty }{\mathop \sum }}\,\frac{1}{\left( 2k+1 \right)}{{\left( M_{k}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right) \right)}^{2}} \\ -\,\,\frac{2}{15}{{\beta }_{e}}M_{2}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right), \\ M_{1}^{\left( 2 \right)}\left( {{T}_{0}} \right)=-\underset{k{\kern 1pt} ={\kern 1pt} 0}{\overset{\infty }{\mathop \sum }}\,\frac{9k}{\left( 2k+1 \right)\left( 2k-1 \right)} \\ \times \,\,M_{k{\kern 1pt} -{\kern 1pt} 1}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right)M_{k}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right)-\frac{9}{35}{{\beta }_{e}}M_{3}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right), \\ D_{0}^{\left( 2 \right)}\left( {{T}_{0}} \right)=0,\,\,\,\,D_{n}^{\left( 2 \right)}\left( {{T}_{0}} \right) \\ =\frac{1}{n}\left\{ \frac{\partial M_{n}^{\left( 2 \right)}\left( {{T}_{0}} \right)}{\partial {{T}_{0}}}+\frac{\partial M_{n}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right)}{\partial {{T}_{1}}}+ \right.\frac{1}{3}{{\beta }_{e}}{{N}_{0}} \\ -\,\,\underset{m{\kern 1pt} ={\kern 1pt} {\kern 1pt} 0}{\overset{\infty }{\mathop \sum }}\,\underset{k{\kern 1pt} ={\kern 1pt} {\kern 1pt} 0}{\overset{\infty }{\mathop \sum }}\,\left[ m\left( m-1 \right){{K}_{m,k,n}}-{{\alpha }_{m,k,n}} \right] \\ \left. \times \,\,\frac{1}{m}\frac{\partial M_{m}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right)}{\partial {{T}_{0}}}M_{k}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right) \right\},\,\,\,\,\left( n\ge 1 \right), \\ {{N}_{0}}=\frac{\partial M_{n{\kern 1pt} +{\kern 1pt} 2}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right)}{\partial {{T}_{0}}}\left[ \frac{{{\alpha }_{2,n{\kern 1pt} +{\kern 1pt} 2,n}}}{\left( n+2 \right)}-{{K}_{2,n{\kern 1pt} +{\kern 1pt} 2,n}}\left( n+1 \right) \right] \\ +\,\,\frac{\partial M_{n}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right)}{\partial {{T}_{0}}}\left[ \frac{{{\alpha }_{2,n,n}}}{n}-{{K}_{2,n,n}}\left( n-1 \right) \right] \\ +\,\,\frac{\partial M_{n{\kern 1pt} -{\kern 1pt} 2}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right)}{\partial {{T}_{0}}}\left[ \frac{{{\alpha }_{2,n{\kern 1pt} -{\kern 1pt} 2,n}}}{\left( n-2 \right)}-{{K}_{2,n{\kern 1pt} -{\kern 1pt} 2,n}}\left( n-3 \right) \right], \\ {{K}_{m,k,n}}={{\left[ C_{k0,m0}^{n0} \right]}^{2}}, \\ {{\alpha }_{m,k,n}}=-\sqrt{m\left( m+1 \right)k\left( k+1 \right)}C_{m0,k0}^{n0}C_{m{\kern 1pt} -{\kern 1pt} 1,k1}^{n0}, \\ \end{matrix}$$

(25)

where $C_{{mk,lp}}^{{nq}}$ denotes the Clebsch–Gordan coefficients [27], which are nonzero, only provided that the indices satisfy relations $\left| {m - l} \right| \leqslant n \leqslant m + l$, $m + l + n$ is even, and $k + p = q$.

Using first-order solution (21), let us write the inhomogeneous differential equation for determining amplitude coefficients $M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right)$ at $n \geqslant 2$ in the following form:

$$\begin{gathered} \frac{{{{\partial }^{2}}}}{{\partial T_{0}^{2}}}M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) + \omega _{n}^{2}M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) \\ = {{G}_{n}}\exp \left( {i{{\omega }_{n}}{{T}_{0}}} \right) + {{L}_{{n,1}}}A_{{n{\kern 1pt} - {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n - 2}}}{{T}_{0}}} \right) \\ + \,\,{{L}_{{n,2}}}A_{{n{\kern 1pt} + {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n{\kern 1pt} + {\kern 1pt} 2}}}{{T}_{0}}} \right) \\ + \,\,\mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \mathop \sum \limits_{k{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \left\{ {\lambda _{{m,k,n}}^{{\left( + \right)}}A_{m}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)A_{k}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left[ {i\left( {{{\omega }_{m}} + {{\omega }_{k}}} \right){{T}_{0}}} \right]\mathop {}\limits^{} } \right. \\ \left. {\mathop + \limits^{} \,\,\lambda _{{m,k,n}}^{{\left( - \right)}}A_{m}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\bar {A}_{k}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left[ {i\left( {{{\omega }_{m}} - {{\omega }_{k}}} \right){{T}_{0}}} \right]} \right\} + {\text{c}}{\text{.c}}{\text{.}} \\ \end{gathered} $$

(26)

$$\begin{gathered} {{G}_{n}} \equiv - 2i{{\omega }_{n}}\frac{{\partial A_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)}}{{\partial {{T}_{1}}}} + {{L}_{{n,0}}}A_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right), \\ {{L}_{{n,0}}} = \frac{9}{{4\pi }}\beta _{E}^{2}n\left[ {\left( {n - 2} \right)\mu _{n}^{ - }\mu _{{n{\kern 1pt} - {\kern 1pt} 1}}^{ + } + n\mu _{{n{\kern 1pt} + {\kern 1pt} 1}}^{ - }\mu _{n}^{ + }} \right] \\ + \,\,{{\beta }_{e}}\left[ {\omega _{n}^{2}\frac{{\left( {n + 1} \right)}}{{\left( {n - 1} \right)\left( {2n + 3} \right)}} + {{n}^{3}}{{K}_{{2,n,n}}}} \right], \\ {{L}_{{n,1}}} \equiv \frac{9}{{4\pi }}\beta _{E}^{2}n\left( {n - 2} \right)\mu _{{n{\kern 1pt} - {\kern 1pt} 1}}^{ + }\mu _{{n{\kern 1pt} - {\kern 1pt} 2}}^{ + } \\ \end{gathered} $$

$$\begin{gathered} + \,\,\frac{1}{3}{{\beta }_{e}}n\left[ {9\omega _{{n{\kern 1pt} - {\kern 1pt} 2}}^{2}\frac{{\left( {n - 1} \right)}}{{\left( {n - 3} \right)\left( {n - 2} \right)\left( {2n - 3} \right)\left( {2n - 1} \right)}}} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} + \,\,{{K}_{{2,n{\kern 1pt} - {\kern 1pt} 2,n}}}\left( {3{{n}^{2}} - 11n + 12} \right)} \right], \\ {{L}_{{n,2}}} \equiv \frac{9}{{4\pi }}\beta _{E}^{2}{{n}^{2}}\mu _{{n + 1}}^{ - }\mu _{{n + 2}}^{ - } \\ + \,\,\frac{1}{3}{{\beta }_{e}}\left[ {6\omega _{{n + 2}}^{2}\frac{{\left( {3n + 1} \right)}}{{\left( {2n + 3} \right)\left( {2n + 5} \right)}}} \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} + \,\,{{K}_{{2,n{\kern 1pt} + {\kern 1pt} 2,n}}}n\left( {3{{n}^{2}} + 7n - 8} \right)} \right], \\ \lambda _{{m,k,n}}^{{\left( \pm \right)}} \equiv \frac{1}{2}\left[ {\left( {{{\gamma }_{{m,k,n}}} + {{\gamma }_{{k,m,n}}}} \right) \pm {{\omega }_{m}}{{\omega }_{k}}\left( {{{\eta }_{{m,k,n}}} + {{\eta }_{{k,m,n}}}} \right)} \right], \\ {{\gamma }_{{m,k,n}}} \equiv {{K}_{{m,k,n}}} \\ \times \,\,\left[ {\omega _{m}^{2}\left( {n - m + 1} \right) + 2n\left( {m\left( {m + 1} \right) - 1} \right)} \right] + \frac{{{{\alpha }_{{m,k,n}}}}}{m}\omega _{m}^{2}, \\ {{\eta }_{{m,k,n}}} \equiv {{K}_{{m,k,n}}}\left( {\frac{n}{2} - m + 1} \right) + {{\alpha }_{{m,k,n}}}\frac{1}{m}\left( {1 + \frac{n}{{2k}}} \right). \\ \end{gathered} $$

The horizontal line above ${{A}_{n}}$ in (26) denotes the complex conjugation.

The requirement to exclude the secular terms from the solutions of Eq. (25) indicates that $a_{n}^{{\left( 1 \right)}}$ is independent of ${{T}_{1}}$, while $b_{n}^{{\left( 1 \right)}}$ linearly depends on ${{T}_{1}}$:

$b_{n}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right) = - \frac{{{{L}_{{n,0}}}}}{{2{{\omega }_{n}}}}{{T}_{1}} + b_{n}^{{\left( 0 \right)}}$, where $b_{n}^{{\left( 0 \right)}}$ is a constant, which is determined from the initial conditions.

Hence, the general solution of Eq. (26) at $n \geqslant 2$ will be as follows:

$$\begin{gathered} M_{n}^{{\left( 2 \right)}}\left( {{{T}_{0}}} \right) = A_{n}^{{\left( 2 \right)}}\exp \left( {i{{\omega }_{n}}{{T}_{0}}} \right) \\ + \,\,N_{n}^{{\left( - \right)}}A_{{n{\kern 1pt} - {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n{\kern 1pt} - {\kern 1pt} 2}}}{{T}_{0}}} \right) \\ + \,\,N_{n}^{{\left( + \right)}}A_{{n{\kern 1pt} + {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\exp \left( {i{{\omega }_{{n{\kern 1pt} + {\kern 1pt} 2}}}{{T}_{0}}} \right) \\ + \,\,\mathop \sum \limits_{m{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \mathop \sum \limits_{k{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \left\{ {N_{{m,k,n}}^{{\left( + \right)}}A_{m}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)A_{k}^{{\left( 1 \right)}}{\kern 1pt} {{{\left( {{{T}_{1}}} \right)}}^{{^{{^{{^{{}}}}}}}}}{\kern 1pt} } \right. \\ \times \,\,\exp \left[ {i\left( {{{\omega }_{m}} + {{\omega }_{k}}} \right){{T}_{0}}} \right]\mathop {}\limits^{} \\ \left. {\mathop + \limits^{} \,\,N_{{m,k,n}}^{{\left( - \right)}}A_{m}^{{\left( 1 \right)}}\left( {{{T}_{1}}} \right)\bar {A}_{k}^{{\left( 1 \right)}}{\kern 1pt} \left( {{{T}_{1}}} \right)\exp \left[ {i\left( {{{\omega }_{m}} - {{\omega }_{k}}} \right){{T}_{0}}} \right]} \right\} + {\text{c}}{\text{.c}}., \\ N_{n}^{{\left( - \right)}} \equiv \frac{{{{L}_{{n,1}}}}}{{\omega _{n}^{2} - \omega _{{n{\kern 1pt} - {\kern 1pt} 2}}^{2}}},\,\,\,\,N_{n}^{{\left( + \right)}} \equiv \frac{{{{L}_{{n,2}}}}}{{\omega _{n}^{2} - \omega _{{n{\kern 1pt} + {\kern 1pt} 2}}^{2}}}, \\ N_{{m,k,n}}^{{\left( \pm \right)}} \equiv \frac{{\lambda _{{m,k,n}}^{{\left( \pm \right)}}}}{{\omega _{n}^{2} - {{{\left( {{{\omega }_{m}} \pm {{\omega }_{k}}} \right)}}^{2}}}}. \\ \end{gathered} $$

(27)

After expansions (13) are substituted into initial conditions (11), the latter are transformed into a set of equations for functions of the first and second orders of smallness:

$$\begin{gathered} t = 0{\kern 1pt} :\,\,\,\,{{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right) = \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}{{P}_{j}}\left( \mu \right),\,\,\,\,\frac{{\partial {{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)}}{{\partial {{T}_{0}}}} = 0, \\ {{\xi }^{{\left( 2 \right)}}}\left( {\theta ,t} \right) = {{\xi }_{0}}{{P}_{0}}\left( \mu \right) + {{\xi }_{1}}{{P}_{1}}\left( \mu \right), \\ \frac{{\partial {{\xi }^{{\left( 2 \right)}}}\left( {\theta ,t} \right)}}{{\partial {{T}_{0}}}} = - \frac{{\partial {{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)}}{{\partial {{T}_{1}}}}, \\ \end{gathered} $$

with this set making it possible to determine real constants $a_{n}^{{\left( 1 \right)}}$, $b_{n}^{{\left( 1 \right)}}$, $a_{n}^{{\left( 2 \right)}}$, and $b_{n}^{{\left( 2 \right)}}$ in solutions (21) and (27).

Satisfying the initial conditions, we, under the first approximation with respect to ε, obtain

$$a_{n}^{{\left( 1 \right)}} = \frac{1}{2}\mathop \sum \limits_{j \in \Xi } {{h}_{j}}{{\delta }_{{n,j}}};\,\,\,\,b_{n}^{{\left( 1 \right)}} = 0;\,\,\,\,(j \in \Xi ,\,\,n = 0,1,2, \ldots );$$

(28)

in the second approximation with respect to ε we derive

$$\begin{gathered} a_{n}^{{\left( 2 \right)}} = - \frac{1}{2}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}\left( {N_{n}^{{\left( - \right)}}{{\delta }_{{n{\kern 1pt} - {\kern 1pt} 2,j}}} + N_{n}^{{\left( + \right)}}{{\delta }_{{n{\kern 1pt} + {\kern 1pt} 2,j}}}} \right) \\ - \,\,\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\kern 1pt} {\kern 1pt} \mathop \sum \limits_{q{\kern 1pt} \in {\kern 1pt} \Xi } \frac{{{{h}_{j}}{{h}_{q}}}}{4}\left( {N_{{j,q,n}}^{{\left( + \right)}} + N_{{j,q,n}}^{{\left( - \right)}}} \right),\,\,\,\,b_{n}^{{\left( 2 \right)}} = 0. \\ \end{gathered} $$

(29)

As a result, using expressions (28) and (29), we write the amplitudes of the first and second orders of smallness in solution (17) for the perturbed droplet surface as follows:

$$\begin{gathered} M_{0}^{{\left( 1 \right)}}\left( t \right) = M_{1}^{{\left( 1 \right)}}\left( t \right) = 0, \\ M_{j}^{{\left( 1 \right)}}\left( t \right) = \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}\cos \left( {\omega _{j}^{ + }t} \right), \\ \omega _{j}^{ + } = {{\omega }_{j}} - \varepsilon \frac{{{{L}_{{j,0}}}}}{{2{{\omega }_{j}}}}, \\ M_{0}^{{\left( 2 \right)}}\left( t \right) = - \mathop \sum \limits_{j \in \Xi } \left[ {\frac{{h_{j}^{2}}}{{\left( {2j + 1} \right)}}{{{\left( {\cos \left( {{{\omega }_{j}}t} \right)} \right)}}^{2}}} \right. \\ \left. {^{{^{{^{{^{{^{{}}}}}}}}}} + \,\,\frac{2}{{15}}{{\beta }_{e}}{{h}_{j}}{{\delta }_{{j,2}}}\cos \left( {{{\omega }_{j}}t} \right)} \right], \\ M_{1}^{{\left( 2 \right)}}\left( t \right) = - \mathop \sum \limits_{j \in \Xi } \left[ {\frac{{9j{{h}_{{j - 1}}}{{h}_{j}}}}{{\left( {2j - 1} \right)\left( {2j + 1} \right)}}} \right. \\ \left. { \times \,\,\cos \left( {{{\omega }_{{j - 1}}}t} \right)\cos \left( {{{\omega }_{j}}t} \right) + \frac{9}{{35}}{{\beta }_{e}}{{h}_{j}}{{\delta }_{{j,3}}}\cos \left( {{{\omega }_{j}}t} \right)} \right], \\ M_{n}^{{\left( 2 \right)}}\left( t \right) = \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}\left[ {N_{n}^{{\left( - \right)}}{{\delta }_{{n{\kern 1pt} - {\kern 1pt} 2,j}}}\cos \left( {{{\omega }_{{n - 2}}}t} \right)} \right. \\ + \,\,N_{n}^{{\left( + \right)}}{{\delta }_{{n{\kern 1pt} + {\kern 1pt} 2,j}}}\cos \left( {{{\omega }_{{n{\kern 1pt} + {\kern 1pt} 2}}}t} \right) \\ \left. { - \,\,\left( {N_{n}^{{\left( - \right)}}{{\delta }_{{n{\kern 1pt} - {\kern 1pt} 2,j}}} + N_{n}^{{\left( + \right)}}{{\delta }_{{n{\kern 1pt} + {\kern 1pt} 2,j}}}} \right)\cos \left( {{{\omega }_{n}}t} \right)} \right] + \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{q{\kern 1pt} \in {\kern 1pt} \Xi } \frac{{{{h}_{j}}{{h}_{q}}}}{2} \\ \times \,\,\left[ {N_{{j,q,n}}^{{\left( + \right)}}\left( {\cos \left( {\left( {{{\omega }_{j}} + {{\omega }_{q}}} \right)t} \right) - \cos \left( {{{\omega }_{n}}t} \right)} \right)} \right. \\ \left. { + \,\,N_{{j,q,n}}^{{\left( - \right)}}\left( {\cos \left( {\left( {{{\omega }_{j}} - {{\omega }_{q}}} \right)t} \right) - \cos \left( {{{\omega }_{n}}t} \right)} \right)} \right],\,\,\,\,\left( {n \geqslant 2} \right). \\ \end{gathered} $$

(30)

Thus using relations (2), (13), and (17), we derive an analytical expression that describes the shape of the perturbed surface of an uncharged droplet oscillating in an external electrostatic field with an accuracy of the terms of the second order of smallness in the form of

$$\begin{gathered} r\left( {\theta ,t} \right) = 1 + \frac{1}{3}{{e}^{2}}{{P}_{2}}\left( \mu \right) \\ + \,\,\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } M_{j}^{{\left( 1 \right)}}\left( t \right){{P}_{j}}\left( \mu \right) + {{\varepsilon }^{2}}\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty M_{n}^{{\left( 2 \right)}}\left( t \right){{P}_{n}}\left( \mu \right), \\ \end{gathered} $$

(31)

where amplitude coefficients $M_{n}^{{\left( m \right)}}\left( t \right)$ are determined by Eqs. (30).

6. The problem of the 5/2 order with respect to ε. To find coefficients $F_{n}^{{\left( {5/2} \right)}}$ in solution (16), let us present the set of equations obtained from conditions (8) and (10) by grouping tems $\sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$:

$$\begin{gathered} r = 1{\kern 1pt} :\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ {{\Phi }^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}} + \left[ {{{\xi }^{{\left( 1 \right)}}} + \frac{1}{3}{{\beta }_{e}}{{P}_{2}}\left( \mu \right)} \right]\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} \\ + \,\,3{{\beta }_{E}}\left\{ {\left[ {{{{({{\xi }^{{\left( 1 \right)}}})}}^{2}} - {{\xi }^{{\left( 2 \right)}}}} \right] + {{\beta }_{e}}\left[ {\frac{3}{5} - {{{\left( {{{P}_{1}}\left( \mu \right)} \right)}}^{2}}} \right]{{\xi }^{{\left( 1 \right)}}}} \right\} \\ \times \,\,{{P}_{1}}\left( \mu \right) = \Phi _{s}^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}, \\ \mathop \smallint \limits_0^\pi \left\{ {\frac{{\partial {{\Phi }^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} - \frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial \theta }}\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial \theta }}} \right. \\ + \,\,\left( {2\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial {{r}^{2}}}}} \right){{\xi }^{{\left( 1 \right)}}} \\ + \,\,\frac{1}{3}{{\beta }_{e}}\left[ {\left( {2\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} + \frac{{{{\partial }^{2}}{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial {{r}^{2}}}}} \right){{P}_{2}}\left( \mu \right)} \right. \\ - \,\,\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial \theta }}\frac{{\partial {{P}_{2}}\left( \mu \right)}}{{\partial \theta }} \\ + \,\,3{{\beta }_{E}}\left( {\left( {\frac{6}{5}\left( {4{{P}_{3}}\left( \mu \right) + {{P}_{1}}\left( \mu \right)} \right) - {{P}_{1}}\left( \mu \right){{\xi }^{{\left( 1 \right)}}}} \right){{\xi }^{{\left( 1 \right)}}}} \right. \\ \left. {\left. {\left. { - \,\,2{{P}_{2}}\left( \mu \right)\frac{{\partial {{P}_{1}}\left( \mu \right)}}{{\partial \theta }}\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial \theta }}} \right)} \right]} \right\}\sin \theta d\theta = 0. \\ \end{gathered} $$

(32)

Here, $\Phi _{s}^{{\left( {5/2} \right)}}$ is the correction of the 5/2 order of smallness to the value of the droplet surface potential.

Substituting expansions (17) at m = 1; 2 and solution (16) at k = 3/2; 5/2 into relation (32), we obtain expressions for $F_{n}^{{\left( {5/2} \right)}}\left( {{{T}_{0}}} \right)$ as

$$\begin{matrix} F_{0}^{\left( {5}/{2}\; \right)}\left( {{T}_{0}} \right)=0, \\ \Phi _{s}^{\left( {5}/{2}\; \right)}=-6{\kern 1pt} {{\beta }_{E}}\left[ \underset{n{\kern 1pt} ={\kern 1pt} 0}{\overset{\infty }{\mathop \sum }}\,\frac{n\left( n-2 \right)}{\left( 2n-1 \right)\left( 2n+1 \right)}M_{n}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right) \right. \\ \times \,\,\left. M_{n{\kern 1pt} -{\kern 1pt} 1}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right)+\frac{1}{35}{{\beta }_{e}}M_{3}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right) \right], \\ F_{n}^{\left( {5}/{2}\; \right)}\left( {{T}_{0}} \right)={{\beta }_{E}} \\ \times \left\{ 3\left[ \mu _{n{\kern 1pt} -{\kern 1pt} 1}^{+}M_{n{\kern 1pt} -{\kern 1pt} 1}^{\left( 2 \right)}\left( {{T}_{0}},{{T}_{1}} \right)+\mu _{n{\kern 1pt} +{\kern 1pt} 1}^{-}M_{n{\kern 1pt} +{\kern 1pt} 1}^{\left( 2 \right)}\left( {{T}_{0}},{{T}_{1}} \right) \right]\overset{{}}{\mathop{{}}}\, \right. \\ +\,\,{{\beta }_{e}}\left[ M_{n{\kern 1pt} -{\kern 1pt} 3}^{\left( 1 \right)}\left( t \right){{l}_{1}}\left( n \right)+M_{n{\kern 1pt} -{\kern 1pt} 1}^{\left( 1 \right)}\left( t \right){{l}_{2}}\left( n \right) \right. \\ \left. +\,\,M_{n{\kern 1pt} +{\kern 1pt} 1}^{\left( 1 \right)}\left( t \right){{l}_{3}}\left( n \right)+M_{n{\kern 1pt} +{\kern 1pt} 3}^{\left( 1 \right)}\left( t \right){{l}_{4}}\left( n \right) \right] \\ +\,\,3\underset{m{\kern 1pt} ={\kern 1pt} 1}{\overset{\infty }{\mathop \sum }}\,{\kern 1pt} {\kern 1pt} \underset{k{\kern 1pt} ={\kern 1pt} 2}{\overset{\infty }{\mathop \sum }}\,{{K}_{m,k,n}}M_{k}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right) \\ \left. \times \,\,\left[ \mu _{m{\kern 1pt} -{\kern 1pt} 1}^{+}M_{m{\kern 1pt} -{\kern 1pt} 1}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right)+\mu _{m{\kern 1pt} +{\kern 1pt} 1}^{-}M_{m{\kern 1pt} +{\kern 1pt} 1}^{\left( 1 \right)}\left( {{T}_{0}},{{T}_{1}} \right) \right] \right\},\,\,\,\,\left( n\ge 1 \right), \\ \end{matrix}$$

(33)

with numerical coefficients ${{l}_{1}}\left( n \right)$–${{l}_{4}}\left( n \right)$, which depend only on $n$, being presented in the Appendix.

7. Surface charge density. Let us determine surface density $\nu \left( {\vec {r},t} \right)$ of charges, which are induced by an external electrostatic field and distributed over a perturbed surface of a nonlinearly oscillating conducting droplet, by the following known equation:

$$\begin{gathered} \nu \left( {\vec {r},t} \right) = {{\left. {\frac{{{{E}_{n}}\left( {\vec {r},t} \right)}}{{4\pi }}} \right|}_{{r{\kern 1pt} = {\kern 1pt} r\left( {\theta ,t} \right)}}} \\ = {{\left. { - \frac{1}{{4\pi }}\left( {\vec {n}\left( {\vec {r},t} \right),\nabla \Phi \left( {\vec {r},t} \right)} \right)} \right|}_{{r{\kern 1pt} = {\kern 1pt} r\left( {\theta ,t} \right)}}}, \\ \end{gathered} $$

(34)

where $r\left( {\theta ,t} \right)$ is determined by relation (30).

Substituting expansion (13) with account of relations (2) and (14) and the vector of the normal to the perturbed droplet surface in the form of the power expansion in terms of small parameter ε with an accuracy of terms $\sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$:

$$\begin{gathered} \vec {n}\left( {\vec {r},t} \right) = \left[ {1 - \frac{1}{2}{{\varepsilon }^{2}}{{{\left( {{{\beta }_{e}}\frac{{\partial h\left( \theta \right)}}{{\partial \theta }} + \frac{{\partial {{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)}}{{\partial \theta }}} \right)}}^{2}}} \right]{{{\vec {e}}}_{r}} \\ + \,\,\left\{ { - \varepsilon \left( {{{\beta }_{e}}\frac{{\partial h\left( \theta \right)}}{{\partial \theta }} + \frac{{\partial {{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)}}{{\partial \theta }}} \right)} \right. \\ + \,\,{{\varepsilon }^{2}}\left[ {\left( {{{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right) + {{\beta }_{e}}h\left( \theta \right)} \right)} \right. \\ \left. {\left. { \times \,\,\left( {{{\beta }_{e}}\frac{{\partial h\left( \theta \right)}}{{\partial \theta }} + \frac{{\partial {{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)}}{{\partial \theta }}} \right) - \frac{{\partial {{\xi }^{{\left( 2 \right)}}}\left( {\theta ,t} \right)}}{{\partial \theta }}} \right]} \right\}{{{\vec {e}}}_{\theta }}, \\ \end{gathered} $$

(35)

into Eq. (34), we derive the surface density of the induced charge with an accuracy of terms $\sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$:

$$\begin{gathered} \nu \left( {\vec {r},t} \right) = \frac{1}{{4\pi }}\left\{ {3{{\beta }_{E}}{{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{{P}_{1}}\left( \mu \right) + {{\varepsilon }^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}} \right. \\ \times \,\,\left[ {6{\kern 1pt} {{\beta }_{E}}\left( {\frac{1}{5}{{\beta }_{e}}{{P}_{3}}\left( \mu \right) - {{\xi }^{{\left( 1 \right)}}}{{P}_{1}}\left( \mu \right)} \right) - \frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}}} \right] \\ + \,\,{{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}\left[ { - \frac{{\partial {{\Phi }^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial r}} - } \right.6{{\beta }_{E}}{{\xi }^{{\left( 2 \right)}}}{{P}_{1}}\left( \mu \right) \\ + \,\,{{\beta }_{E}}{{\beta }_{e}}\left( { - \frac{{{{2}^{{}}}}}{5}\left( {{{P}_{1}}\left( \mu \right) + 15{{P}_{3}}\left( \mu \right)} \right){{\xi }^{{\left( 1 \right)}}}} \right. \\ \left. { + \,\,\frac{1}{3}\left( {\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial \theta }}\frac{{\partial {{P}_{2}}\left( \mu \right)}}{{\partial \theta }} - \frac{{{{\partial }^{2}}{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial {{r}^{2}}}}{{P}_{2}}\left( \mu \right)} \right)} \right) \\ + \,\,3{{\beta }_{E}}{{P}_{1}}\left( \mu \right)\left( {4{{{({{\xi }^{{\left( 1 \right)}}})}}^{2}} - \frac{1}{2}{{{\left( {\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial \theta }}} \right)}}^{2}}} \right) \\ {{\left. {\left. {\left. { + \,\,\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial \theta }}\frac{{\partial {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial \theta }} - {{\xi }^{{\left( 1 \right)}}}\left( {3{\kern 1pt} {{\beta }_{E}}\frac{{\partial {{P}_{1}}\left( \mu \right)}}{{\partial \theta }}\frac{{\partial {{\xi }^{{\left( 1 \right)}}}}}{{\partial \theta }} + \frac{{{{\partial }^{2}}{{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}}}{{\partial {{r}^{2}}}}} \right)} \right]} \right\}} \right|}_{{r{\kern 1pt} = {\kern 1pt} 1}}}. \\ \end{gathered} $$

In Eq. (35), ${{\vec {e}}_{r}}$ and ${{\vec {e}}_{\theta }}$ are the unit vectors of the spherical coordinate system.

Taking into account the pattern of the ${{\xi }^{{\left( 1 \right)}}}\left( {\theta ,t} \right)$ and ${{\xi }^{{\left( 2 \right)}}}\left( {\theta ,t} \right)$ functions from relation (31) and the solution for the corrections of the 3/2 and 5/2 orders to the electric potential:

$$\begin{gathered} {{\Phi }^{{\left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)}}}\left( {\vec {r},t} \right) = 3{\kern 1pt} {{\beta }_{E}}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {\mu _{{j{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right) + \mu _{{j{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right)} \right] \\ \times \,\,{{r}^{{ - \left( {j{\kern 1pt} + {\kern 1pt} 1} \right)}}}{{P}_{j}}\left( \mu \right), \\ {{\Phi }^{{\left( {{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}} \right)}}}\left( {\vec {r},t} \right) = {{\beta }_{E}}\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty \left[ {3\left( {\mu _{{n{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{n{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( t \right) + \mu _{{n{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{n{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( t \right)} \right)\mathop {}\limits^{} } \right. \\ + \,\,3\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\kern 1pt} {\kern 1pt} \mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } {{K}_{{j,i,n}}}M_{i}^{{\left( 1 \right)}}\left( t \right) \\ \left. { \times \,\,\left( {\mu _{{j{\kern 1pt} - {\kern 1pt} 1}}^{ + }M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right) + \mu _{{j{\kern 1pt} + {\kern 1pt} 1}}^{ - }M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right)} \right)} \right] \\ \times \,\,{{r}^{{ - \left( {n{\kern 1pt} + {\kern 1pt} 1} \right)}}}{{P}_{n}}\left( \mu \right) + {{\beta }_{e}}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {M_{{j{\kern 1pt} - {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{l}_{1}}\left( j \right) + M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{l}_{2}}\left( j \right)} \right. \\ \left. { + \,\,M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{l}_{3}}\left( j \right) + M_{{j{\kern 1pt} + {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{l}_{4}}\left( j \right)} \right]{{r}^{{ - \left( {j{\kern 1pt} + {\kern 1pt} 1} \right)}}}{{P}_{j}}\left( \mu \right) \\ \end{gathered} $$

(36)

we write the surface charge density as the expansion in terms of the Legendre polynomials:

$$\begin{gathered} \nu \left( {\vec {r},t} \right) = \frac{3}{{4\pi }}{{\beta }_{E}}{{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \\ \times \,\,\left\{ {{{P}_{1}}\left( \mu \right) + \varepsilon \left[ {\frac{2}{5}{{\beta }_{e}}{{P}_{3}}\left( \mu \right)} \right.} \right. \\ + \,\,\left. {\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \left( {M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{1}}\left( j \right) + M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{2}}\left( j \right)} \right){{P}_{j}}\left( \mu \right)} \right] \\ + \,\,{{\varepsilon }^{2}}\left[ {{{\beta }_{e}}\sum\limits_{j{\kern 1pt} \in {\kern 1pt} {{\Xi }}} {\left[ {M_{{j{\kern 1pt} - {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{k}_{3}}\left( j \right) + M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{4}}\left( j \right)} \right.} } \right. \\ \left. {^{{^{{^{{^{{}}}}}}}} + \,\,M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{5}}\left( j \right) + M_{{j{\kern 1pt} - {\kern 1pt} 3}}^{{\left( 1 \right)}}\left( t \right){{k}_{6}}\left( j \right)} \right]{{P}_{j}}\left( \mu \right) \\ + \,\,\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \left( {\left[ {M_{{n{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( t \right){{k}_{1}}\left( n \right) + M_{{n{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 2 \right)}}\left( t \right){{k}_{2}}\left( n \right)} \right]} \right. \\ + \,\,\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\kern 1pt} {\kern 1pt} \mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } {{K}_{{j,i,n}}}M_{i}^{{\left( 1 \right)}}\left( t \right) \\ \left. {\left. {^{{^{{^{{}}}}}} \times \,\,\left. {\left[ {M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{7}}\left( {j,n} \right) + M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{k}_{8}}\left( {j,n} \right)} \right]} \right){{P}_{n}}\left( \mu \right)} \right]} \right\}. \\ \end{gathered} $$

(37)

Numerical coefficients ${{k}_{1}}\left( j \right)$–${{k}_{6}}\left( j \right)$, which depend only on $j$, and ${{k}_{7}}\left( {j,n} \right)$ and ${{k}_{8}}\left( {j,n} \right)$, which depend on $j$ and $n$, are presented in the Appendix to avoid overloading the text with trivial expressions.

It follows from the pattern of relation (37) that, in the absence of perturbation, the surface density of an induced charge is determined by the two first terms in the curly brackets.

8. The values of induced charges. The values of the opposite induced charges on different halves of a perturbed droplet surface $r\left( {\theta ,t} \right)$ are determined by the following equations:

$$\begin{gathered} {{q}_{ \pm }}\left( {\vec {r},t} \right) = \mathop \smallint \limits_{{{S}_{{1,2}}}} d{{q}_{ \pm }}\left( {\vec {r},t} \right) = \mathop \smallint \limits_{{{S}_{{1,2}}}} \nu \left( {\vec {r},t} \right)d{{S}_{{1,2}}} \\ = \mathop \smallint \limits_{{{S}_{{1,2}}}} {{\left. {\frac{{\nu \left( {\vec {r},t} \right)}}{{\left( {\vec {n}\left( {\vec {r},t} \right),{{{\vec {e}}}_{r}}} \right)}}{{r}^{2}}} \right|}_{{r{\kern 1pt} = {\kern 1pt} r\left( {\theta ,t} \right)}}}\sin \theta d\theta d\varphi , \\ {{S}_{1}} \equiv \left[ {r = r\left( {\theta ,t} \right);\,\,0 \leqslant \theta \leqslant \frac{\pi }{2};\,\,0 \leqslant \varphi \leqslant 2\pi } \right], \\ {{S}_{2}} \equiv \left[ {r = r\left( {\theta ,t} \right);\,\,\frac{\pi }{2} \leqslant \theta \leqslant \pi ;\,\,0 \leqslant \varphi \leqslant 2\pi } \right]. \\ \end{gathered} $$

(38)

Here, ${{q}_{ + }}$ and ${{q}_{ - }}$ are the positive and negative induced charges, respectively, while $r\left( {\theta ,t} \right)$ is specified by expression (30).

The induced charge is expanded in terms of the half-integral powers of parameter ε, because ${{E}_{0}}\sim {{\varepsilon }^{{1/2}}}$. In this way, we determine relation (38) with an accuracy of the terms of the $\sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$ order.

Since the induced charge distribution is symmetric with respect to the equatorial plane, let us consider positively charged half S₁ of the perturbed spheroidal droplet.

Substituting surface charge density (37), normal vector (35), and perturbed droplet surface shape (31) into expression (38) and integrating the obtained expression over surface ${{S}_{1}}$, we find the value of the positive induced charge as the power expansion in terms of small parameter ε with an accuracy of terms $\sim {\kern 1pt} {{\varepsilon }^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$:

$$\begin{gathered} {{q}_{ + }}\left( t \right) = \frac{3}{4}{{\beta }_{E}}{{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \\ \times \,\,\left\{ {1 + \varepsilon \left( {\frac{1}{{15}}{{\beta }_{e}} + 2\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } M_{j}^{{\left( 1 \right)}}\left( t \right){{G}_{1}}\left( j \right)} \right)} \right. \\ + \,\,2{{\varepsilon }^{2}}\left[ {{{\beta }_{e}}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } M_{j}^{{\left( 1 \right)}}\left( t \right){{G}_{2}}\left( j \right)} \right. \\ + \,\,\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} {\kern 1pt} 0}^\infty \left( {\sum\limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\sum\limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } {M_{i}^{{\left( 1 \right)}}\left( t \right){\kern 1pt} } \left( {M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{L}_{1}}{{{\left( {j,i,n} \right)}}^{{^{{^{{^{{^{{}}}}}}}}}}}} \right.{\kern 1pt} } } \right. \\ \left. {\left. {\left. {\left. {^{{^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}}} + \,\,M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{L}_{2}}\left( {j,i,n} \right)} \right) + M_{n}^{{\left( 2 \right)}}\left( t \right){{G}_{1}}\left( n \right)} \right)} \right]} \right\}, \\ \end{gathered} $$

(39)

where numerical coefficients ${{G}_{1}}\left( j \right)$ and ${{G}_{2}}\left( j \right)$, which depend only on $j$, and ${{L}_{1}}\left( {j,i,n} \right)$ and ${{L}_{2}}\left( {j,i,n} \right)$, which depend on $j$, $i$, and $n$, are presented in the Appendix, because their expressions are cumbersome.

As a result, taking into account expressions for amplitude coefficients $M_{j}^{{\left( 1 \right)}}\left( t \right)$ and $M_{n}^{{\left( 2 \right)}}\left( t \right)$ from relation (30) and passing from formal parameters ${{\beta }_{e}}$ and ${{\beta }_{E}}$ to physical denotations, we derive the following analytical equation for the opposite induced charges in the dimensional form:

$$\begin{gathered} {{q}_{ \pm }}\left( t \right) = \pm \frac{3}{2}\sqrt {\pi {{\varepsilon }_{0}}} {{E}_{0}}{{R}^{2}}\left\{ {1 + \frac{1}{{15}}{{e}^{2}} + 2\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}} \right. \\ \times \,\,\left[ {{{G}_{1}}\left( j \right)\cos \left( {\omega _{j}^{ + }t} \right) + {{e}^{2}}} \right.\left\{ {G_{1}^{ + }\left( j \right)\cos \left( {{{\omega }_{j}}t} \right)} \right. \\ \left. {\left. { + \,\,G_{2}^{ + }\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}t} \right) + G_{3}^{ + }\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}t} \right)} \right\}} \right] \\ + \,\,{{\varepsilon }^{2}}\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {\sum\limits_{j{\kern 1pt} \in {\kern 1pt} {{\Xi }}} {\sum\limits_{i{\kern 1pt} \in {\kern 1pt} {{\Xi }}} {\left[ {{{S}_{1}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right]} \right.} \right.} } } \\ \left. { + \,\,\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right]} \right\} + {{S}_{2}}\left( {j,i,n} \right) \\ \times \,\,\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right] + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right]} \right\} \\ + \,\,{{S}_{3}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\} \\ \left. {^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}\left. { + \,\,{{S}_{4}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\}} \right]} \right\}, \\ \end{gathered} $$

(40)

where ${{q}_{ - }}$ is written with sign minus. The time dependences for the values of the charge induced in the droplet are presented in Fig. 1 in the dimensional form. Note that all subsequent plots will also be presented in the dimensional form.

Fig. 1.

Time dependences ${{q}_{ + }}\left( t \right)$ of the positive charge induced in a droplet in an electrostatic field at an initial excitation of the equilibrium droplet surface shape having the form of $\varepsilon \left[ {{{P}_{2}}\left( \mu \right) + {{P}_{3}}\left( \mu \right)} \right]{\text{/}}2$, $\sigma = 73 \times {{10}^{{ - 3}}}\;{\text{N/m}}$, $\rho = {{10}^{3}}$ kg/m³, and ${{E}_{0}} = 50$ V/cm (${{\sim 4}} \times {{10}^{{ - 4}}}{{E}_{{{\text{0cr}}}}}$). Curves 1 and 2 correspond to linear and nonlinear droplet oscillations, respectively: R = (a) 10 and (b) 30 µm.

The dependences in Figs. 1a and 1b have been calculated for different droplet radii, because a change in the radius causes noticeable quantitative changes in the plots along both the ordinate and abscissa axes. This fact deserves attention, because it affects both the width and intensity of radiation emitted by a real cloud.

Numerical (depending only on $j$) coefficients $G_{1}^{ + }\left( j \right)$–$G_{3}^{ + }\left( j \right)$ and coefficients ${{S}_{1}}\left( {j,i,n} \right)$–${{S}_{4}}\left( {j,i,n} \right)$, which depend on not only $j$, $i$, and $n$, but also initial amplitudes ${{h}_{i}}$, ${{h}_{j}}$, and ${{h}_{{j \pm 1}}}$, are presented in the Appendix.

Figure 2 illustrates the dependences of deviation $\Delta {{q}_{ + }}\left( t \right)$ in the value of the induced positive charge of the droplet from its stationary value $q_{ + }^{{\left( {{\text{eq}}} \right)}} = \frac{3}{2}\sqrt {\pi {{\varepsilon }_{0}}} {{E}_{0}}{{R}^{2}}\left( {1 + \frac{1}{{15}}{{e}^{2}}} \right)$ on time $t$. It is seen that the asymptotic calculations of the second order of smallness with respect to ε lead to an insubstantial nonlinear correction to the value of ${{q}_{ + }}\left( t \right)$.

Fig. 2.

Time dependences $\Delta {{q}_{ + }}\left( t \right)$ of deviations of the positive charge induced in a droplet from its equilibrium value in an electrostatic field. The dependences have been calculated at the values of the physical parameters the same as in Fig 1: R = (a) 10 and (b) 30 µm.

9. The model of an oscillating dipole. Let us replace equal opposite induced charges ${{q}_{ + }}$ and ${{q}_{ - }}$ by equal point charges (the values of which depend on time) spaced from each other at some distance, which is smaller than the droplet diameter. These charges are located in the symmetry axis of a spheroid at the positions of the “effective” centers of the positive and negative charges, with these positions being determined by the following relations:

$${{\vec {R}}_{{{{q}_{ \pm }}}}}\left( t \right) = \frac{1}{{{{q}_{ \pm }}}}\mathop \smallint \limits_{{{S}_{{1,2}}}} \vec {r}d{{q}_{ \pm }} = \frac{1}{{{{q}_{ \pm }}}}\mathop \smallint \limits_{{{S}_{{1,2}}}} r{{\vec {e}}_{r}}d{{q}_{ \pm }}.$$

The capillary oscillations of the spheroid surface will be accompanied by the oscillations of the values of the “effective” induced charges and the distance between the centers of thereof. As a result, we obtain “effective” dipole

$$\vec {d}\left( t \right) = {{q}_{ + }}\left( t \right)\left( {{{{\vec {R}}}_{{{{q}_{ + }}}}}\left( t \right) - {{{\vec {R}}}_{{{{q}_{ - }}}}}\left( t \right)} \right);$$

(41)

which will oscillate and radiate electromagnetic waves in accordance with the following known expression [8, 9]:

$$I = \frac{2}{{3{{c}^{3}}}}{{\left( {\frac{{{{d}^{2}}\vec {d}\left( t \right)}}{{d{{t}^{2}}}}} \right)}^{2}}.$$

(42)

According to Eq. (42), it is easy to write an analytical expression for the electromagnetic radiation intensity of a single droplet taking into account Eq. (41). To do this, we only need analytical expressions of radius vectors ${{\vec {R}}_{{{{q}_{ \pm }}}}}\left( t \right)$ for the displacements of the “effective” centers of the charges induced in the spheroidal droplet.

Note that the expansions for the displacements of the centers of the opposite induced charges are performed in terms of the integral powers of small parameter ε; therefore, subsequent calculations of ${{\vec {R}}_{{{{q}_{ \pm }}}}}\left( t \right)$ will be carried out with an accuracy of terms on the order of ~ ε².

To determine the position of the “effective” center of the induced charge on a half of a droplet, we take into account that radial unit vector ${{\vec {e}}_{r}}$ in the spherical coordinate system is related to unit vectors ${{\vec {e}}_{x}}$, ${{\vec {e}}_{y}}$, ${{\vec {e}}_{z}}$ of the Cartesian coordinate system as follows:

$${{\vec {e}}_{r}} = {{\vec {e}}_{x}}\sin {\kern 1pt} \theta \cos {\kern 1pt} \varphi + {{\vec {e}}_{y}}\sin {\kern 1pt} \theta \sin {\kern 1pt} \varphi + {{\vec {e}}_{z}}\cos {\kern 1pt} \theta .$$

(43)

Since the electric field strength vector is directed along the $z$ axis, the centers of the opposite induced charges of the droplet are not displaced in the $x,y$ plane:

$${{R}_{{qx}}} = {{R}_{{qy}}} = 0.$$

Taking into account relation (43), we determine the projection of the displacement vector for the center of the positive induced charge along the $z$ axis as

$${{R}_{{qz}}}\left( {\vec {r},t} \right) = \frac{1}{{{{q}_{ + }}}}\mathop \smallint \limits_{{{S}_{1}}} {{\left. {\frac{{\nu \left( {\vec {r},t} \right)}}{{\left( {\vec {n}\left( {\vec {r},t} \right),{{{\vec {e}}}_{r}}} \right)}}{{r}^{3}}} \right|}_{{r = r\left( {\theta ,t} \right)}}}\cos {\kern 1pt} \theta \sin {\kern 1pt} \theta d\theta d\varphi .$$

Calculating the integral over the half of the spheroid surface area ${{S}_{1}}$ with regard to expressions (31), (35), and (37) and substituting the value of the positive induced charge from Eq. (39) into the obtained relation, we determine ${{R}_{{qz}}}$ as a power expansion in terms of small parameter ε with an accuracy of terms on the order of $\sim {\kern 1pt} {{\varepsilon }^{2}}$:

$$\begin{gathered} {{R}_{{qz}}}\left( t \right) = \frac{2}{3}\left\{ {1 + \varepsilon \left( {\frac{1}{3}{{\beta }_{e}} + \varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } M_{j}^{{\left( 1 \right)}}\left( t \right){{J}_{1}}\left( j \right)} \right)} \right. \\ + \,\,{{\varepsilon }^{2}}\left[ {{{\beta }_{e}}\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } M_{j}^{{\left( 1 \right)}}\left( t \right){{{\tilde {J}}}_{2}}\left( j \right)} \right. \\ + \,\,\mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } M_{i}^{{\left( 1 \right)}}M_{j}^{{\left( 1 \right)}}{{{\tilde {J}}}_{3}}\left( {j,i} \right) \\ + \,\,\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty \left( {M_{n}^{{\left( 2 \right)}}{\kern 1pt} \left( t \right){\kern 1pt} {{J}_{1}}\left( n \right) + \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } M_{i}^{{\left( 1 \right)}}{\kern 1pt} \left[ {M_{{j - 2}}^{{\left( 1 \right)}}\left( t \right){{L}_{3}}\left( {j,i,n} \right){\kern 1pt} {{{\kern 1pt} }^{{^{{^{{^{{}}}}}}}}}} \right.} \right. \\ + \,\,M_{j}^{{\left( 1 \right)}}\left( t \right){{L}_{4}}\left( {j,i,n} \right) + M_{{j{\kern 1pt} + {\kern 1pt} 2}}^{{\left( 1 \right)}}\left( t \right){{L}_{5}}\left( {j,i,n} \right) \\ \left. {\left. {\left. {^{{^{{^{{^{{^{{}}}}}}}}}} + \,\,M_{{j{\kern 1pt} - {\kern 1pt} 1}}^{{\left( 1 \right)}}\left( t \right){{{\tilde {J}}}_{4}}{\kern 1pt} \left( {j,i,n} \right) + \left. {M_{{j{\kern 1pt} + {\kern 1pt} 1}}^{{{{{\left( 1 \right)}}^{{^{{^{{}}}}}}}}}{\kern 1pt} \left( t \right){{{\tilde {J}}}_{5}}{\kern 1pt} \left( {j,i,n} \right)} \right]} \right)} \right]} \right\}, \\ \end{gathered} $$

with numerical coefficients ${{J}_{1}}\left( j \right)$, ${{\tilde {J}}_{2}}\left( j \right)$, and ${{\tilde {J}}_{3}}\left( j \right)$, which depend on $j$, and ${{L}_{3}}\left( {j,i,n} \right)$–${{L}_{5}}\left( {j,i,n} \right)$, ${{\tilde {J}}_{4}}\left( {j,i,n} \right)$, and ${{\tilde {J}}_{5}}\left( {j,i,n} \right)$, which depend on $j$, $i$, and $n$, being presented in the Appendix.

Finally, using the expressions for amplitudes $M_{j}^{{\left( 1 \right)}}\left( t \right)$ and $M_{n}^{{\left( 2 \right)}}\left( t \right)$ from relation (30) and passing from formal parameters ${{\beta }_{e}}$ and ${{\beta }_{E}}$ to physical denotations, we determine the position of the “effective” center of the positive induced charge of the droplet in the dimensional form as

$$\begin{gathered} {{R}_{{qz}}}\left( t \right) = \frac{2}{3}R\left\{ {1 + \frac{1}{3}{{e}^{2}} + \varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}\left\{ {{{J}_{1}}\left( j \right)\cos \left( {\omega _{j}^{ + }t} \right)} \right.} \right. \\ + \,\,{{e}^{2}}\left[ {{{J}_{2}}\left( j \right)\cos \left( {{{\omega }_{j}}t} \right)} \right. \\ \left. {\left. { + \,\,{{J}_{3}}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}t} \right) + {{J}_{4}}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}t} \right)} \right]} \right\} \\ + \,\,{{\varepsilon }^{2}}\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {\sum\limits_{j\, \in \,{{\Xi }}} {\sum\limits_{i\, \in \,{{\Xi }}} {\left[ {{{J}_{5}}\left( {j,i,n} \right)\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right]} \right.} \right.} } } \\ \left. { + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right]} \right) + {{J}_{6}}\left( {j,i,n} \right) \\ \times \,\,\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right. \\ \left. { + \,\,\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right) + {{J}_{7}}\left( {j,i,n} \right) \\ \times \,\,\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)t} \right] + } \right.\left. {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)t} \right]} \right) \\ + \,\,{{J}_{8}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right] + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right]} \right) \\ + \,\,{{J}_{9}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right] + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right]} \right) \\ + \,\,{{J}_{{10}}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\} \\ \left. {^{{^{{^{{^{{^{{^{{^{{}}}}}}}}}}}}}}\left. { + \,\,{{J}_{{11}}}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\}} \right]} \right\}. \\ \end{gathered} $$

(44)

Numerical coefficients ${{J}_{1}}\left( j \right)$–${{J}_{4}}\left( j \right)$, which depend only on $j$, and coefficients ${{J}_{5}}\left( {j,i,n} \right)$–${{J}_{{11}}}\left( {j,i,n} \right)$, which depend not only on $j$, $i$, and $n$, but also on initial amplitudes ${{h}_{i}}$, ${{h}_{j}}$, ${{h}_{{j \pm 1}}}$, and ${{h}_{{j \pm 2}}}$, are presented in the Appendix, because the expressions for them are very cumbersome.

Figure 3 illustrates displacements $\Delta {{R}_{{qz}}}\left( t \right)$ of the center of the positive charge induced in the droplet from its stationary equilibrium position $R_{{qz}}^{{\left( {{\text{eq}}} \right)}} = \frac{2}{3}R\left( {1 + \frac{1}{3}{{e}^{2}}} \right)$ as functions of time $t$. It is clearly seen that the nonlinear correction to the ${{R}_{{qz}}}\left( t \right)$ value determined by the calculations of the first order of smallness makes no substantial contribution to this value.

Fig. 3.

Time dependences $\Delta {{R}_{{qz}}}\left( t \right)$ of displacements of the center of the positive charge induced in a droplet from its equilibrium position. The dependences have been calculated at the values of the physical parameters the same as in Fig. 1. Curves 1 and 2 correspond to $\Delta {{R}_{{qz}}}\left( t \right)$ functions at linear and nonlinear droplet oscillations, respectively: R = (a) 10 and (b) 30 µm.

The analytical expression for the position of the “effective” center of the negative induced charge is found in the dimensional form for the other half of the spheroidal droplet in a similar way:

$$\begin{gathered} R_{{qz}}^{ - }\left( t \right) = - \frac{2}{3}R\left\{ {1 + \frac{1}{3}{{e}^{2}} + \varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}} \right.\left\{ {J_{1}^{*}\left( j \right)\cos \left( {\omega _{j}^{ + }t} \right)} \right. \\ + \,\,{{e}^{2}}\left[ {J_{2}^{*}\left( j \right)\cos \left( {{{\omega }_{j}}t} \right)} \right. \\ \left. {\left. { + \,\,J_{3}^{*}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}t} \right) + J_{4}^{*}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}t} \right)} \right]} \right\} \\ + \,\,{{\varepsilon }^{2}}\sum\limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty {\sum\limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {\sum\limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } {\left[ {J_{5}^{*}\left( {j,i,n} \right)} \right.} } } \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right]} \right. \\ \left. { + \,\,\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right]} \right) + J_{6}^{*}\left( {j,i,n} \right){\kern 1pt} \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right.{\kern 1pt} {\kern 1pt} \\ \left. { + \,\,\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right) + J_{7}^{*}\left( {j,i,n} \right) \\ \times \,\,\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)t} \right] + \cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)t} \right]} \right) \\ + \,\,J_{8}^{*}\left( {j,i,n} \right)\left( {\cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right] + \cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right){\kern 1pt} t} \right]} \right) \\ + \,\,J_{9}^{*}\left( {j,i,n} \right)\left( {\cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right] + \cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right){\kern 1pt} t} \right]} \right) \\ + \,\,J_{{10}}^{*}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\} \\ \left. {\left. { + \,\,J_{{11}}^{*}\left( {j,i,n} \right)\left\{ {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right\}} \right]} \right\}, \\ \end{gathered} $$

(45)

where the sign of function $J_{m}^{*}$ in Eq. (44) differs from that of ${{J}_{m}}$ only for the odd values of initially excited oscillation modes $j$.

Substituting expressions (40), (44), and (45) into relation (41), we find the projection of the dipole moment onto the $z$ axis as follows:

$$\begin{gathered} {{d}_{z}}\left( t \right) = \sqrt {\pi {{\varepsilon }_{0}}} {{E}_{0}}{{R}^{3}}\left\{ {2\left( {1 + \frac{1}{3}{{e}^{2}}} \right)\left( {1 + \frac{1}{{15}}{{e}^{2}}} \right)} \right. \\ + \,\,\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}\left\{ {{{f}_{1}}\left( j \right)\cos \left( {\omega _{j}^{ + }t} \right)} \right. \\ + \,\,{{e}^{2}}\left[ {{{f}_{2}}\left( j \right)\cos \left( {{{\omega }_{j}}t} \right) + {{f}_{3}}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}t} \right)} \right. \\ \left. {\left. { + \,\,{{f}_{4}}\left( j \right)\cos \left( {{{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}t} \right)} \right]} \right\} \\ + \,\,{{\varepsilon }^{2}}\left\{ {\mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}{{h}_{i}}{{f}_{5}}\left( {j,i} \right)\cos \left( {{{\omega }_{i}}t} \right)\cos \left( {{{\omega }_{j}}t} \right)} \right. \\ + \,\,\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {{{f}_{6}}\left( {j,i,n} \right)(\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right]} \right. \\ \end{gathered} $$

$$\begin{gathered} \left. { + \,\,\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right]} \right) \\ + \,\,{{f}_{7}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right. + \left. {\cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)t} \right]} \right) \\ + \,\,{{f}_{8}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)t} \right] + \cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right){\kern 1pt} t} \right]} \right) \\ + \,\,{{f}_{9}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right){\kern 1pt} t} \right] + \cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)t} \right]} \right) \\ + \,\,{{f}_{{10}}}\left( {j,i,n} \right){\kern 1pt} \left( {\cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right){\kern 1pt} t} \right] + \cos {\kern 1pt} \left[ {\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)t} \right]} \right) \\ + \,\,{{f}_{{11}}}\left( {j,i,n} \right)\left( {\cos \left[ {\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right) \\ \left. {\left. {\left. {^{{^{{^{{}}}}}} + \,\,{{f}_{{12}}}\left( {j,i,n} \right)\left( {\cos \left[ {\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)t} \right] - \cos \left( {{{\omega }_{n}}t} \right)} \right)} \right]} \right\}} \right\}, \\ {{f}_{1}}\left( j \right) = {{J}_{1}}\left( j \right) + J_{1}^{*}\left( j \right) + 4{{G}_{1}}\left( j \right), \\ {{f}_{2}}\left( j \right) = \frac{1}{{15}}\left( {{{J}_{1}}\left( j \right) + J_{1}^{*}\left( j \right)} \right) \\ + \,\,{{J}_{2}}\left( j \right) + J_{2}^{*}\left( j \right) + 4G_{1}^{ + }\left( j \right) + \frac{4}{3}{{G}_{1}}\left( j \right), \\ \end{gathered} $$

(46)

$$\begin{gathered} {{f}_{3}}\left( j \right) = {{J}_{4}}\left( j \right) + J_{4}^{*}\left( j \right) + 4G_{2}^{ + }\left( j \right), \\ {{f}_{4}}\left( j \right) = {{J}_{3}}\left( j \right) + J_{3}^{*}\left( j \right) + 4G_{3}^{ + }\left( j \right), \\ {{f}_{5}}\left( {j,i} \right) = 2{{G}_{1}}\left( i \right)({{J}_{1}}\left( j \right) + J_{1}^{*}\left( j \right)), \\ {{f}_{6}}\left( {j,i} \right) = {{J}_{5}}\left( {j,i,n} \right) + J_{5}^{*}\left( {j,i,n} \right), \\ {{f}_{7}}\left( {j,i,n} \right) = {{J}_{6}}\left( {j,i,n} \right) + J_{6}^{*}\left( {j,i,n} \right), \\ {{f}_{8}}\left( {j,i,n} \right) = {{J}_{7}}\left( {j,i,n} \right) + J_{7}^{*}\left( {j,i,n} \right), \\ {{f}_{9}}\left( {j,i,n} \right) = {{J}_{8}}\left( {j,i,n} \right) + J_{8}^{*}\left( {j,i,n} \right) + 2{{S}_{1}}, \\ {{f}_{{10}}}\left( {j,i,n} \right) = {{J}_{9}}\left( {j,i,n} \right) + J_{9}^{*}\left( {j,i,n} \right) + 2{{S}_{2}}, \\ {{f}_{{11}}}\left( {j,i,n} \right) = {{J}_{{10}}}\left( {j,i,n} \right) + J_{{10}}^{*}\left( {j,i,n} \right) + 2{{S}_{3}}, \\ {{f}_{{12}}}\left( {j,i,n} \right) = {{J}_{{11}}}\left( {j,i,n} \right) + J_{{11}}^{*}\left( {j,i,n} \right) + 2{{S}_{4}}. \\ \end{gathered} $$

Figure 4 shows projections ${{d}_{z}}\left( t \right)$ of the dipole moment onto the z axis as functions of time t. It is seen that nonlinear oscillations of the droplet give a small correction to the ${{d}_{z}}\left( t \right)$ value, which is related to the linear droplet oscillations.

Fig. 4.

Time dependences ${{d}_{z}}\left( t \right)$ of dipole moment projection onto the z axis. The dependences have been calculated at the values of the physical parameters the same as in Fig. 1. Curves 1 and 2 correspond to ${{d}_{z}}\left( t \right)$ functions at linear and nonlinear droplet oscillations, respectively: R = (a) 10 and (b) 30 µm.

In particular, it is distinctly seen in Fig. 5 that  the correction of the second order of smallness with   respect to ε to stationary value $d_{z}^{{\left( {{\text{eq}}} \right)}} = \sqrt {4\pi {{\varepsilon }_{0}}} {{E}_{0}}{{R}^{3}}\left( {1 + \frac{1}{3}{{e}^{2}}} \right)\left( {1 + \frac{1}{{15}}{{e}^{2}}} \right)$ in Eq. (46) is determined by higher frequencies than the correction of the first order of smallness.

Fig. 5.

Time dependences $\Delta {{d}_{z}}\left( t \right)$ of the correction to the stationary projection of the dipole moment onto the z axis. The dependences have been calculated at the values of the physical parameters the same as in Fig. 1. Curves 1 and 2 correspond to corrections $\Delta {{d}_{z}}\left( t \right)$ of the first and second orders of smallness with respect to ε, respectively: R = (a) 10 and (b) 30 µm.

Figures 6 and 7 show the dependences of the droplet oscillation frequencies on the droplet radius for the linear and nonlinear corrections to the $d_{z}^{{\left( {{\text{eq}}} \right)}}$ value. It is seen that, as the droplet size increases, its oscillation frequencies decrease according to a nearly hyperbolic law.

Fig. 6.

Droplet oscillation frequency $\omega _{2}^{ + }$ as depending on the droplet radius for the correction to $d_{z}^{{\left( {{\text{eq}}} \right)}}$ having the first order of smallness with respect to ε. The dependence has been calculated at the values of the physical parameters the same as in Fig. 1.

Fig. 7.

Droplet oscillation frequencies ${{\omega }_{n}}$ as depending on the droplet radius for the correction to the stationary value of $d_{z}^{{\left( {{\text{eq}}} \right)}}$ having the second order of smallness with respect to ε. The dependences have been calculated at the values of the physical parameters the same as in Fig. 1. Droplet oscillation frequencies are (1) ${{\omega }_{3}} - {{\omega }_{2}}$, (2) ${{\omega }_{2}}$, (3) ${{\omega }_{3}}$, (4) $2{{\omega }_{2}}$, (5) ${{\omega }_{4}}$, (6) ${{\omega }_{2}} + {{\omega }_{3}}$, (7) $2{{\omega }_{3}}$, and (8) ${{\omega }_{5}}$.

Proceeding from relation (42), taking into account Eq. (46), and replacing the cosines and sines in the functions by their maximum values for the qualitative analysis being performed, we obtain the following dimensional analytical expression for the intensity of the dipole radiation of an uncharged droplet nonlinearly oscillating in an external electrostatic field:

$$\begin{gathered} I = \frac{{2\pi {{\varepsilon }_{0}}}}{{3{{c}^{3}}}}E_{0}^{2}{{R}^{6}}\left\{ {\varepsilon \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}} \right.\left[ {{{f}_{1}}\left( j \right)\omega {{{_{j}^{ + }}}^{2}}} \right. \\ \left. { + \,\,{{e}^{2}}\left\{ {{{f}_{2}}\left( j \right)\omega _{j}^{2} + {{f}_{3}}\left( j \right)\omega _{{j{\kern 1pt} + {\kern 1pt} 2}}^{2} + {{f}_{4}}\left( j \right)\omega _{{j{\kern 1pt} - {\kern 1pt} 2}}^{2}} \right\}} \right] \\ + \,\,{{\varepsilon }^{2}}\left\{ {2\mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } {{h}_{j}}{{h}_{i}}{{f}_{5}}\left( {j,i} \right){{\omega }_{i}}{{\omega }_{j}}} \right. \\ + \,\,\mathop \sum \limits_{n{\kern 1pt} = {\kern 1pt} 0}^\infty \mathop \sum \limits_{j{\kern 1pt} \in {\kern 1pt} \Xi } \mathop \sum \limits_{i{\kern 1pt} \in {\kern 1pt} \Xi } \left[ {{{f}_{6}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)}}^{2}}} \right\}} \right. \\ + \,\,{{f}_{7}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 2}}}} \right)}}^{2}}} \right\} \\ + \,\,{{f}_{8}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 2}}}} \right)}}^{2}}} \right\} \\ + \,\,{{f}_{9}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} - {\kern 1pt} 1}}}} \right)}}^{2}}} \right\} \\ + \,\,{{f}_{{10}}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)}}^{2}} + {{{\left( {{{\omega }_{i}} - {{\omega }_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right)}}^{2}}} \right\} \\ + \,\,{{f}_{{11}}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} + {{\omega }_{j}}} \right)}}^{2}} + \omega _{n}^{2}} \right\} \\ {{\left. {\left. {\left. { + \,\,{{f}_{{12}}}\left( {j,i,n} \right)\left\{ {{{{\left( {{{\omega }_{i}} - {{\omega }_{j}}} \right)}}^{2}} - \omega _{n}^{2}} \right\}} \right]} \right\}} \right\}}^{2}}. \\ \end{gathered} $$

(47)

Equation (47) enables one to estimate the intensity of the background noise electromagnetic radiation of various artificial and natural liquid-droplet systems, such as convective clouds.

Large-amplitude oscillations of cloud droplets can be caused by different reasons, such as coagulation, disintegration into smaller droplets due to collisions or realization of electrostatic instability, hydrodynamic and electric interactions between closely flying droplets, and aerodynamic interactions with a developed small-scale turbulence inherent in thunderstorm clouds. According to the data of natural observations [25, 26], oscillation amplitudes of cloud droplets may reach several tens of percents of a droplet radius. In the subsequent estimations, dimensionless oscillation amplitude ε will be taken equal to 0.1. The value of Taylor parameter $w = 4\pi {{\varepsilon }_{0}}E_{0}^{2}R{\text{/}}\sigma$ in the electrostatic fields of thunderstorm clouds [18] is much lower than the critical value of parameter w_cr [4]; i.e., the majority of the cloud droplets are rather far from the limit of instability with respect to the induced charge.

Figure 8 shows the dependence of radiation intensity $I$ on external electric field strength ${{E}_{0}}$, with this dependence being calculated by Eq. (47). It is seen that the radiation intensity rapidly increases with ${{E}_{0}}$.

Fig. 8.

Dipole electromagnetic radiation intensity $I$ as depending on external electrostatic field strength for an uncharged droplet nonlinearly oscillating in a uniform electrostatic field. The dependence has been calculated at the values of the physical parameters the same as in Fig. 1.

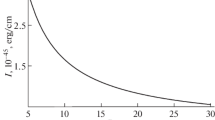
Figure 9 illustrates the dependence of $I$ on droplet radius $R$. This dependence is seen to be rather weak.

Fig. 9.

Dipole electromagnetic radiation intensity $I$ as depending on the droplet radius for an uncharged droplet nonlinearly oscillating in a uniform electrostatic field. The dependence has been calculated at the values of the physical parameters the same as in Fig. 1.

Figure 10 shows the dependences of radiation intensity $I$ on time $t$, with these dependences being calculated at fixed values of $R$ and ${{E}_{0}}$ by exact expression (42) taking into account Eqs. (40) and (46) (without replacing the cosines and sines by their maximum values).

Fig. 10.

Dipole electromagnetic radiation intensities as depending on time t for an uncharged droplet nonlinearly oscillating in a uniform electrostatic field. The dependences have been calculated by Eq. (42) taking into account relations (4) and (46) and the values of the physical parameters the same as in Fig. 1: R = (a) 10 and (b) 30 µm.

In Fig. 10, the scale of variations in time is rather large, and the shapes of individual peaks are difficult to guess. Therefore, the shapes of individual peaks presented in Fig. 11 have been taken from the initial part of Fig. 10 (the very left-hand part of it).

Fig. 11.

Dipole electromagnetic radiation intensities $I$ as depending on time t for an uncharged droplet nonlinearly oscillating in a uniform electrostatic field. The dependences have been calculated at the values of the physical parameters the same as in Fig. 1 for the first three peaks in Fig. 10.

CONCLUSIONS

Dipole electromagnetic radiation emitted by an uncharged droplet in an external electromagnetic field is caused by nonuniform time variations in the value of its oscillating dipole moment, which is induced by the field. Quadratic calculations of dipole radiation intensity performed within the method of many time scales have shown that the results obtained exhibit qualitative similarity to the previously studied dipole radiation of an oscillating charged droplet and some quantitative difference from the latter [14]. It has appeared that the frequency of the quadratic corrections to the frequencies for a droplet in an electric field is several times higher than the frequency of the linear oscillations, as well as it is for a charged droplet. However, the dependence of the electromagnetic radiation intensity on the radius of a droplet oscillating in an electrostatic field is manyfold weaker than that for an oscillating charged droplet. The study of the time evolution of the intensity of the electromagnetic radiation emitted by an individual droplet has shown that the radiation has the character of “beats;” i.e., the pattern of packets composed of elementary (carrier) waves.

APPENDIX

Expressions for coefficients ${{l}_{1}}\left( n \right)$–${{l}_{4}}\left( n \right)$ in Eq. (33):

$$\begin{gathered} {{l}_{1}}\left( n \right) = \frac{{3n\left( {n - 2} \right)\left( {n - 1} \right)\left( {n + 1} \right)}}{{2\left( {2n - 5} \right)\left( {2n - 3} \right)\left( {2n - 1} \right)}}, \\ {{l}_{2}}\left( n \right) = \frac{{n\left( {50{{n}^{4}} + {{n}^{3}} - 103{{n}^{2}} + 39n - 27} \right)}}{{10(4{{n}^{2}} - 9){{{\left( {2n - 1} \right)}}^{2}}}}, \\ {{l}_{3}}\left( n \right) = \frac{{n\left( {n + 1} \right)\left( {50{{n}^{4}} + 321{{n}^{3}} + 621{{n}^{2}} + 278n - 180} \right)}}{{10(4{{n}^{2}} + 8n - 5){{{\left( {2n + 3} \right)}}^{2}}}}, \\ {{l}_{4}}\left( n \right) = \frac{{3\left( {n + 5} \right)\left( {n + 3} \right)\left( {n + 2} \right)\left( {n + 1} \right)}}{{2\left( {2n + 7} \right)\left( {2n + 5} \right)\left( {2n + 3} \right)}}. \\ \end{gathered} $$

Expressions for coefficients ${{k}_{1}}\left( j \right)$–${{k}_{6}}\left( j \right)$, ${{k}_{7}}\left( {j,n} \right)$, and ${{k}_{8}}\left( {j,n} \right)$ in Eq. (37):

$$\begin{gathered} {{k}_{1}}\left( j \right) = \frac{{j\left( {j - 1} \right)}}{{\left( {2j - 1} \right)}},\,\,\,\,{{k}_{2}}\left( j \right) = \frac{{\left( {j + 1} \right)\left( {j - 1} \right)}}{{\left( {2j + 3} \right)}},\,\,\,\,{{k}_{3}}\left( j \right) = - \frac{{j\left( {j - 1} \right)\left( {j - 2} \right)\left( {2{{j}^{2}} + 3j + 7} \right)}}{{2\left( {2j - 1} \right)\left( {2j - 3} \right)\left( {2j - 5} \right)}}, \\ {{k}_{4}}\left( j \right) = - \frac{{j\left( {100{{j}^{5}} + 116{{j}^{4}} - 165{{j}^{3}} - 205{{j}^{2}} + 75j - 81} \right)}}{{30{{{\left( {2j - 1} \right)}}^{2}}\left( {2j - 3} \right)\left( {2j + 3} \right)}}, \\ {{k}_{5}}\left( j \right) = - \frac{{\left( {j + 1} \right)\left( {100{{j}^{5}} + 756{{j}^{4}} + 2159{{j}^{3}} + 2591{{j}^{2}} + 704j - 600} \right)}}{{30\left( {2j - 1} \right){{{\left( {2j + 3} \right)}}^{2}}\left( {2j + 5} \right)}}, \\ {{k}_{6}}\left( j \right) = - \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {j + 3} \right)\left( {2{{j}^{2}} + 11j + 21} \right)}}{{2\left( {2j + 3} \right)\left( {2j + 5} \right)\left( {2j + 7} \right)}}, \\ {{k}_{7}}\left( {j,n} \right) = - \frac{{j\left( {{{j}^{2}} + j - jn - 1} \right)}}{{\left( {2j - 1} \right)}},\,\,\,\,{{k}_{8}}\left( {j,n} \right) = - \frac{{j\left( {j + 1} \right)\left( {j - n + 3} \right)}}{{\left( {2j + 3} \right)}}. \\ \end{gathered} $$

Expressions for coefficients ${{G}_{1}}\left( j \right)$, ${{G}_{2}}\left( j \right)$, ${{L}_{1}}\left( {j,i,n} \right)$ and ${{L}_{2}}\left( {j,i,n} \right)$ in Eq. (39):

$$\begin{gathered} {{G}_{1}}\left( j \right) = {{p}_{1}}{{F}_{{j{\kern 1pt} - {\kern 1pt} 1}}} + {{p}_{2}}{{F}_{{j{\kern 1pt} + {\kern 1pt} 1}}}, \\ {{p}_{1}} = \frac{{{{j}^{2}}}}{{\left( {2j + 1} \right)}},\,\,\,\,{{p}_{2}} = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)}}{{\left( {2j + 1} \right)}}, \\ {{G}_{2}}\left( j \right) = {{q}_{1}}{{F}_{{j{\kern 1pt} - {\kern 1pt} 3}}} + {{q}_{2}}{{F}_{{j{\kern 1pt} - {\kern 1pt} 1}}} + {{q}_{3}}{{F}_{{j{\kern 1pt} + {\kern 1pt} 1}}} + {{q}_{4}}{{F}_{{j{\kern 1pt} + {\kern 1pt} 3}}}, \\ {{q}_{1}} = \frac{{5j\left( {j - 1} \right){{{\left( {j - 2} \right)}}^{2}}}}{{2\left( {2j + 1} \right)\left( {2j - 3} \right)\left( {2j - 1} \right)}}, \\ {{q}_{2}} = \frac{{{{j}^{2}}\left( {146{{j}^{3}} + 73{{j}^{2}} - 246j - 153} \right)}}{{30\left( {2j - 3} \right){{{\left( {2j + 1} \right)}}^{2}}\left( {2j + 3} \right)}}, \\ {{q}_{3}} = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {26{{j}^{3}} + 65{{j}^{2}} + 46j - 20} \right)}}{{30\left( {2j - 1} \right){{{\left( {2j + 1} \right)}}^{2}}\left( {2j + 5} \right)}}, \\ {{q}_{4}} = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {j + 3} \right)\left( {j + 4} \right)}}{{2\left( {2j + 1} \right)\left( {2j + 3} \right)\left( {2j + 5} \right)}}, \\ {{L}_{1}}\left( {j,i,n} \right) = \frac{j}{{\left( {2j - 1} \right)}}\left( {j\left( {n + 1 - j} \right){{K}_{{j,i,n}}} + {{\alpha }_{{j,i,n}}}} \right){{F}_{n}}, \\ {{L}_{2}}\left( {j,i,n} \right) = \frac{{\left( {j + 1} \right)}}{{\left( {2j + 3} \right)}} \\ \times \,\,\left( {\left( { - {{{\left( {j + 1} \right)}}^{2}} + j\left( {n + 1} \right)} \right){{K}_{{j,i,n}}} + {{\alpha }_{{j,i,n}}}} \right){{F}_{n}}, \\ {{F}_{j}} = \int\limits_0^{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} {{{P}_{j}}} \left( \mu \right)\sin \theta d\theta \\ = \left\{ {\begin{array}{*{20}{c}} 1&{\left( {j = 0} \right)} \\ {\frac{{{{{\left( { - 1} \right)}}^{{\frac{{j - 1}}{2}}}}\left( {j - 1} \right)!}}{{{{2}^{{j - 1}}}\left( {j + 1} \right){{{\left( {\left( {\frac{{j - 1}}{2}} \right)!} \right)}}^{2}}}}}&{\left( {j = 2k + 1} \right)} \\ 0&{\left( {j = 2k} \right)} \end{array}} \right.. \\ \end{gathered} $$

Expressions for coefficients $G_{1}^{ + }\left( j \right)$–$G_{3}^{ + }\left( j \right)$, and ${{S}_{1}}\left( {j,i,n} \right)$–${{S}_{4}}\left( {j,i,n} \right)$ in Eq. (40):

$$\begin{gathered} G_{1}^{ + }\left( j \right) = p_{1}^{ + }{{F}_{{j{\kern 1pt} - {\kern 1pt} 3}}} + p_{2}^{ + }{{F}_{{j{\kern 1pt} - {\kern 1pt} 1}}} + p_{3}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 1}}} + p_{4}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 3}}}, \\ p_{1}^{ + } = - \frac{{3\left( {j - 1} \right){{{\left( {j - 2} \right)}}^{2}}({{j}^{3}} - 7{{j}^{2}} + 4j + 4)}}{{4\left( {2j - 3} \right)\left( {2j - 1} \right)\left( {2j + 1} \right)\left( {3j - 4} \right)}}, \\ p_{2}^{ + } = - \frac{{j\left( {180{{j}^{7}} - 1212{{j}^{6}} + 251{{j}^{5}} + 2985{{j}^{4}} + 25{{j}^{3}} - 3453{{j}^{2}} + 324j + 540} \right)}}{{60\left( {2j - 3} \right)\left( {2j - 1} \right){{{\left( {2j + 1} \right)}}^{2}}\left( {2j + 3} \right)\left( {3j - 4} \right)}}, \\ p_{3}^{ + } = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {180{{j}^{6}} + 1572{{j}^{5}} + 4771{{j}^{4}} + 6319{{j}^{3}} + 2816{{j}^{2}} - 988j - 720} \right)}}{{60\left( {2j - 1} \right){{{\left( {2j + 1} \right)}}^{2}}\left( {2j + 3} \right)\left( {2j + 5} \right)\left( {3j + 2} \right)}}, \\ p_{4}^{ + } = \frac{{3{{{\left( {j + 1} \right)}}^{2}}\left( {j + 2} \right)\left( {j + 3} \right){{{\left( {j + 4} \right)}}^{2}}}}{{4\left( {2j + 1} \right)\left( {2j + 3} \right)\left( {2j + 5} \right)\left( {3j + 2} \right)}}, \\ \end{gathered} $$

$$\begin{gathered} G_{2}^{ + }\left( j \right) = q_{1}^{ + }{{F}_{{j{\kern 1pt} - {\kern 1pt} 1}}} + q_{2}^{ + }{{F}_{{j{\kern 1pt} - {\kern 1pt} 3}}}, \\ q_{1}^{ + } = \frac{{j{{{\left( {j - 1} \right)}}^{2}}\left( {3{{j}^{3}} + 9{{j}^{2}} - 28j + 12} \right)}}{{4\left( {2j - 1} \right)\left( {2j + 1} \right)\left( {3j - 4} \right)\left( {2j - 3} \right)}}, \\ q_{2}^{ + } = \frac{{\left( {j - 1} \right){{{\left( {j - 2} \right)}}^{2}}\left( {3{{j}^{3}} + 9{{j}^{2}} - 28j + 12} \right)}}{{4\left( {2j - 1} \right)\left( {2j + 1} \right)\left( {3j - 4} \right)\left( {2j - 3} \right)}}, \\ G_{3}^{ + }\left( j \right) = - \left( {m_{1}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 3}}} + m_{2}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 1}}}} \right), \\ \end{gathered} $$

$$\begin{gathered} m_{1}^{ + } = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {j + 4} \right)\left( {j + 3} \right)(3{{j}^{2}} + 9j + 8)}}{{4\left( {2j + 1} \right)\left( {2j + 3} \right)\left( {3j + 2} \right)\left( {2j + 5} \right)}}, \\ m_{2}^{ + } = \frac{{\left( {j + 1} \right){{{\left( {j + 2} \right)}}^{3}}(3{{j}^{2}} + 9j + 8)}}{{4\left( {2j + 1} \right)\left( {2j + 3} \right)\left( {3j + 2} \right)\left( {2j + 5} \right)}}, \\ {{S}_{1}}\left( {j,i,n} \right) = {{h}_{i}}{{h}_{{j{\kern 1pt} - {\kern 1pt} 1}}}{{L}_{1}}\left( {j,i,n} \right),\,\,\,\,{{S}_{2}}\left( {j,i,n} \right) = {{h}_{i}}{{h}_{{j{\kern 1pt} + {\kern 1pt} 1}}}{{L}_{2}}\left( {j,i,n} \right), \\ {{S}_{3}}\left( {j,i,n} \right) = {{h}_{i}}{{h}_{j}}N_{{j,q,n}}^{{\left( + \right)}}{{G}_{1}}\left( n \right),\,\,\,\,{{S}_{4}}\left( {j,i,n} \right) = {{h}_{i}}{{h}_{j}}N_{{j,q,n}}^{{\left( - \right)}}{{G}_{1}}\left( n \right). \\ \end{gathered} $$

Expressions for coefficients ${{J}_{1}}\left( j \right)$, ${{\tilde {J}}_{2}}\left( j \right)$, ${{\tilde {J}}_{3}}\left( j \right)$, ${{L}_{3}}\left( {j,i,n} \right)$–${{L}_{5}}\left( {j,i,n} \right)$, ${{\tilde {J}}_{4}}\left( {j,i,n} \right)$, and ${{\tilde {J}}_{5}}\left( {j,i,n} \right)$ in Eq. (44):

$$\begin{gathered} {{J}_{1}}\left( j \right) = 3{{G}_{3}}\left( j \right) - 2{{G}_{1}}\left( j \right), \\ {{{\tilde {J}}}_{2}}\left( j \right) = - \left( {\frac{8}{{15}}{{G}_{1}}\left( j \right) + 2{{G}_{2}}\left( j \right) + \frac{1}{5}{{G}_{3}}\left( j \right) - 3{{G}_{4}}\left( j \right)} \right),\,\,\,\,{{{\tilde {J}}}_{3}}\left( {j,i} \right) = - 2{{G}_{1}}\left( i \right){{J}_{1}}\left( j \right), \\ {{G}_{3}}\left( j \right) = {{m}_{1}}{{F}_{{j{\kern 1pt} - {\kern 1pt} 2}}} + {{m}_{2}}{{F}_{j}} + {{m}_{3}}{{F}_{{j{\kern 1pt} + {\kern 1pt} 2}}}, \\ {{m}_{1}} = \frac{{j\left( {j - 1} \right)\left( {j + 1} \right)}}{{\left( {2j - 1} \right)\left( {2j + 1} \right)}},\,\,\,\,{{m}_{2}} = \frac{{\left( {j + 1} \right)\left( {4{{j}^{3}} + 10{{j}^{2}} + 2j - 3} \right)}}{{\left( {2j + 1} \right)\left( {2j - 1} \right)\left( {2j + 3} \right)}}, \\ {{m}_{3}} = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {j + 3} \right)}}{{\left( {2j + 1} \right)\left( {2j + 3} \right)}}, \\ {{G}_{4}}\left( j \right) = k_{1}^{ + }{{F}_{{j{\kern 1pt} - {\kern 1pt} 4}}} + k_{2}^{ + }{{F}_{{j{\kern 1pt} - {\kern 1pt} 2}}} + k_{3}^{ + }{{F}_{j}} + k_{4}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 2}}} + k_{5}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 4}}}. \\ \end{gathered} $$

$$\begin{gathered} k_{1}^{ + } = \frac{{3j{{{\left( {j - 1} \right)}}^{2}}\left( {j - 2} \right)\left( {j - 3} \right)}}{{2\left( {2j - 5} \right)\left( {2j - 3} \right)\left( {2j - 1} \right)\left( {2j + 1} \right)}}, \\ k_{2}^{ + } = \frac{{j\left( {j - 1} \right)\left( {376{{j}^{5}} - 736{{j}^{4}} - 1198{{j}^{3}} + 154{{j}^{2}} + 777j - 45} \right)}}{{15{{{\left( {2j + 1} \right)}}^{2}}\left( {2j - 5} \right)\left( {2j - 3} \right)\left( {2j - 1} \right)\left( {2j + 3} \right)}}, \\ k_{3}^{ + } = \frac{{2\left( {j + 1} \right)\left( {136{{j}^{6}} + 484{{j}^{5}} + 106{{j}^{4}} - 925{{j}^{3}} - 809{{j}^{2}} - 66j + 90} \right)}}{{15{{{\left( {2j + 1} \right)}}^{2}}\left( {2j - 5} \right)\left( {2j - 3} \right)\left( {2j - 1} \right)\left( {2j + 3} \right)}}, \\ k_{4}^{ + } = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {j + 3} \right)\left( {136{{j}^{4}} + 936{{j}^{3}} + 1606{{j}^{2}} + 36j - 365} \right)}}{{15{{{\left( {2j + 1} \right)}}^{2}}\left( {2j + 7} \right)\left( {2j + 5} \right)\left( {2j + 3} \right)\left( {2j - 1} \right)}}, \\ k_{5}^{ + } = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {j + 3} \right)\left( {j + 4} \right)\left( {j + 5} \right)}}{{\left( {2j + 7} \right)\left( {2j + 5} \right)\left( {2j + 3} \right)\left( {2j + 1} \right)}}, \\ {{L}_{3}}\left( {j,i,n} \right) = \frac{{3\left( {j - 1} \right)}}{{\left( {2j - 1} \right)\left( {2j - 3} \right)}}\left( { - j\left( {{{j}^{2}} - 3j + 1} \right){{K}_{{j,i,n}}} + \left( {j - 1} \right){{\alpha }_{{j,i,n}}}} \right){{F}_{n}}, \\ \end{gathered} $$

$$\begin{gathered} {{L}_{4}}\left( {j,i,n} \right) = \frac{1}{{\left( {2j - 1} \right)\left( {2j + 3} \right)}}\left( {\left. { - \frac{{3\left( {4{{j}^{5}} + 6{{j}^{4}} - 2{{j}^{3}} - 4{{j}^{2}} - j + 1} \right)}}{{\left( {2j + 1} \right)}}{{K}_{{j,i,n}}} + j\left( {4{{j}^{2}} - 7} \right){{\alpha }_{{j,i,n}}}} \right){{F}_{n}},} \right. \\ {{L}_{5}}\left( {j,i,n} \right) = - \frac{{\left( {j + 2} \right)}}{{\left( {2j + 3} \right)\left( {2j + 5} \right)}}\left( {\left( {3{{j}^{2}} + 10j + 9} \right){{K}_{{j,i,n}}} + \left( {j + 3} \right){{\alpha }_{{j,i,n}}}} \right){{F}_{n}}, \\ {{{\tilde {J}}}_{4}}\left( {j,i,n} \right) = 3{{L}_{6}}\left( {j,i,n} \right) - 2{{L}_{1}}\left( {j,i,n} \right), \\ {{L}_{6}}\left( {j,i,n} \right) = \frac{{{{j}^{2}}}}{{\left( {2j - 1} \right)}}\left( {\frac{{{{j}^{2}}}}{{\left( {2j - 1} \right)}}{{K}_{{j,i,n{\kern 1pt} - {\kern 1pt} 1}}} + \frac{{\left( {j + 1} \right)\left( {j + 2} \right)}}{{\left( {2j + 3} \right)}}{{K}_{{j,i,n{\kern 1pt} + {\kern 1pt} 1}}}} \right){{F}_{n}}, \\ {{{\tilde {J}}}_{5}}\left( {j,i,n} \right) = 3{{L}_{7}}\left( {j,i,n} \right) - 2{{L}_{2}}\left( {j,i,n} \right), \\ {{L}_{7}}\left( {j,i,n} \right) = \frac{{j\left( {j + 1} \right)}}{{\left( {2j + 3} \right)}}\left( {\frac{{{{j}^{2}}}}{{\left( {2j - 1} \right)}}{{K}_{{j,i,n{\kern 1pt} - {\kern 1pt} 1}}} + \frac{{\left( {j + 1} \right)\left( {j + 2} \right)}}{{\left( {2j + 3} \right)}}{{K}_{{j,i,n{\kern 1pt} + {\kern 1pt} 1}}}} \right){{F}_{n}}. \\ \end{gathered} $$

Expressions for coefficients ${{J}_{1}}\left( j \right)$–${{J}_{4}}\left( j \right)$ and ${{J}_{5}}\left( {j,i,n} \right)$–${{J}_{{11}}}\left( {j,i,n} \right)$ in Eq. (44):

$$\begin{gathered} {{J}_{2}}\left( j \right) = - \frac{8}{{15}}{{G}_{1}}\left( j \right) - \frac{1}{5}{{G}_{3}}\left( j \right) - 2G_{1}^{ + }\left( j \right) + 3G_{1}^{ - }\left( j \right), \\ {{J}_{3}}\left( j \right) = - \left( {2G_{3}^{ + }\left( j \right) + 3G_{3}^{ - }\left( j \right)} \right),\,\,\,\,{{J}_{4}}\left( j \right) = 3G_{2}^{ - }\left( j \right) - 2G_{2}^{ + }\left( j \right), \\ G_{1}^{ - }\left( j \right) = p_{1}^{ - }{{F}_{{j{\kern 1pt} - {\kern 1pt} 4}}} + p_{2}^{ - }{{F}_{{j{\kern 1pt} - {\kern 1pt} 2}}} + p_{3}^{ - }{{F}_{j}} + p_{4}^{ - }{{F}_{{j + 2}}} + p_{5}^{ - }{{F}_{{j{\kern 1pt} + {\kern 1pt} 4}}}, \\ p_{1}^{ - } = - \frac{{3{{{\left( {j - 1} \right)}}^{2}}\left( {j - 2} \right)\left( {j - 3} \right)\left( {3{{j}^{3}} - 27{{j}^{2}} + 20j + 12} \right)}}{{4\left( {2j - 5} \right)\left( {2j - 3} \right)\left( {2j - 1} \right)\left( {2j + 1} \right)\left( {3j - 4} \right)}}, \\ p_{2}^{ - } = - \frac{{\left( {j - 1} \right)}}{{60\left( {2j - 5} \right)\left( {2j - 3} \right){{{\left( {2j - 1} \right)}}^{2}}{{{\left( {2j + 1} \right)}}^{2}}\left( {2j + 3} \right)\left( {3j - 4} \right)}} \\ \times \,\,(720{{j}^{9}} - 8664{{j}^{8}} + 20468{{j}^{7}} + 9762{{j}^{6}} - 56530{{j}^{5}} \\ \left. { + \,\,17109{{j}^{4}} + 25712{{j}^{3}} - 837{{j}^{2}} - 4320j - 540} \right), \\ p_{3}^{ - } = \frac{{\left( {j + 1} \right)}}{{30\left( {2j - 3} \right){{{\left( {2j - 1} \right)}}^{2}}{{{\left( {2j + 1} \right)}}^{2}}{{{\left( {2j + 3} \right)}}^{2}}\left( {3j - 4} \right)\left( {3j + 2} \right)}} \\ \times \,\,\left( {19{\kern 1pt} 584{{j}^{{10}}} + 84{\kern 1pt} 144{{j}^{9}} + 17{\kern 1pt} 104{{j}^{8}} - 327{\kern 1pt} 136{{j}^{7}} - 329{\kern 1pt} 116{{j}^{6}} + 317{\kern 1pt} 277{{j}^{5}}} \right. \\ \left. { + \,\,517{\kern 1pt} 866{{j}^{4}} + 9421{{j}^{3}} - 176{\kern 1pt} 508{{j}^{2}} - 19{\kern 1pt} 116j + 17{\kern 1pt} 280} \right), \\ p_{4}^{ - } = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {j + 3} \right)}}{{60\left( {2j - 1} \right){{{\left( {2j + 1} \right)}}^{2}}{{{\left( {2j + 3} \right)}}^{2}}\left( {2j + 5} \right)\left( {2j + 7} \right)\left( {3j + 2} \right)}} \\ \times \,\,\left( {720{{j}^{7}} + 11{\kern 1pt} 544{{j}^{6}} + 65{\kern 1pt} {\kern 1pt} 836{{j}^{5}} + 166{\kern 1pt} 470{{j}^{4}}} \right. \\ \left. { + \,\,180{\kern 1pt} 340{{j}^{3}} + 47{\kern 1pt} 181{{j}^{2}} - 38{\kern 1pt} 771j - 17{\kern 1pt} 520} \right), \\ p_{5}^{ - } = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {j + 3} \right)\left( {j + 4} \right)\left( {j + 5} \right)\left( {3{{j}^{2}} + 21j + 16} \right)}}{{4\left( {2j + 1} \right)\left( {2j + 3} \right)\left( {2j + 5} \right)\left( {2j + 7} \right)\left( {3j + 2} \right)}}, \\ G_{2}^{ - }\left( j \right) = q_{1}^{ - }{{F}_{j}} + q_{2}^{ - }{{F}_{{j{\kern 1pt} - {\kern 1pt} 2}}} + q_{3}^{ - }{{F}_{{j{\kern 1pt} - {\kern 1pt} 4}}}, \\ q_{1}^{ - } = \frac{{j{{{\left( {j - 1} \right)}}^{2}}\left( {j + 1} \right)\left( {3{{j}^{3}} + 9{{j}^{2}} - 28j + 12} \right)}}{{4{{{\left( {2j - 1} \right)}}^{2}}\left( {2j + 1} \right)\left( {3j - 4} \right)\left( {2j - 3} \right)}}, \\ \end{gathered} $$

$$\begin{gathered} q_{2}^{ - } = \frac{{{{{\left( {j - 1} \right)}}^{2}}\left( {3{{j}^{3}} + 9{{j}^{2}} - 28j + 12} \right)\left( {4{{j}^{3}} - 14{{j}^{2}} + 10j + 1} \right)}}{{4{{{\left( {2j - 1} \right)}}^{2}}\left( {2j + 1} \right)\left( {3j - 4} \right)\left( {2j - 3} \right)\left( {2j - 5} \right)}}, \\ q_{3}^{ - } = \frac{{{{{\left( {j - 1} \right)}}^{2}}\left( {j - 2} \right)\left( {j - 3} \right)\left( {3{{j}^{3}} + 9{{j}^{2}} - 28j + 12} \right)}}{{4\left( {2j - 1} \right)\left( {2j + 1} \right)\left( {3j - 4} \right)\left( {2j - 3} \right)\left( {2j - 5} \right)}}, \\ \end{gathered} $$

$$\begin{gathered} G_{3}^{ - }\left( j \right) = m_{1}^{ - }{{F}_{{j{\kern 1pt} + {\kern 1pt} 4}}} + m_{2}^{ - }{{F}_{{j{\kern 1pt} + {\kern 1pt} 2}}} + m_{3}^{ - }{{F}_{j}}, \\ m_{1}^{ - } = \frac{{\left( {j + 1} \right)\left( {j + 2} \right)\left( {j + 3} \right)\left( {j + 4} \right)\left( {j + 5} \right)\left( {3{{j}^{2}} + 9j + 8} \right)}}{{4\left( {2j + 1} \right)\left( {2j + 3} \right)\left( {3j + 2} \right)\left( {2j + 5} \right)\left( {2j + 7} \right)}}, \\ m_{2}^{ - } = \frac{{\left( {j + 3} \right)\left( {j + 1} \right)\left( {j + 2} \right)\left( {4{{j}^{3}} + 34{{j}^{2}} + 90j + 73} \right)\left( {3{{j}^{2}} + 9j + 8} \right)}}{{4\left( {2j + 1} \right)\left( {2j + 3} \right)\left( {3j + 2} \right)\left( {2j + 5} \right)\left( {2j + 7} \right)}}, \\ m_{3}^{ - } = \frac{{{{{\left( {j + 1} \right)}}^{2}}{{{\left( {j + 2} \right)}}^{2}}\left( {j + 3} \right)\left( {3{{j}^{2}} + 9j + 8} \right)}}{{4\left( {2j + 1} \right){{{\left( {2j + 3} \right)}}^{2}}\left( {3j + 2} \right)\left( {2j + 5} \right)}}, \\ - {{K}_{1}}\left( i \right)J_{1}^{*}\left( j \right), \\ {{J}_{5}}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{j}}\left( { - {{G}_{1}}\left( i \right){{J}_{1}}\left( j \right) + \frac{1}{2}{{L}_{4}}\left( {j,i,n} \right)} \right), \\ {{J}_{6}}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{{j - 2}}}{{L}_{3}}\left( {j,i,n} \right),\,\,\,\,{{J}_{7}}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{{j + 2}}}{{L}_{5}}\left( {j,i,n} \right), \\ {{J}_{8}}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{{j - 1}}}\left( {3{{L}_{6}}\left( {j,i,n} \right) - 2{{L}_{1}}\left( {j,i,n} \right)} \right), \\ {{J}_{9}}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{{j + 1}}}\left( {3{{L}_{7}}\left( {j,i,n} \right) - 2{{L}_{2}}\left( {j,i,n} \right)} \right), \\ {{J}_{{10}}}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{j}}N_{{j,q,n}}^{{\left( + \right)}}{{J}_{1}}\left( n \right),\,\,\,\,{{J}_{{11}}}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{j}}N_{{j,q,n}}^{{\left( - \right)}}{{J}_{1}}\left( n \right). \\ \end{gathered} $$

Expressions for coefficients $J_{1}^{*}\left( j \right)$–$J_{4}^{*}\left( j \right)$ and $J_{5}^{*}\left( {j,i,n} \right)$–$J_{{11}}^{*}\left( {j,i,n} \right)$ in Eq. (45):

$$\begin{gathered} J_{1}^{*}\left( j \right) = 2{{K}_{1}}\left( j \right) + 3{{K}_{3}}\left( j \right), \\ {{K}_{1}}\left( j \right) = {{\left( { - 1} \right)}^{{j{\kern 1pt} - {\kern 1pt} 1}}}{{p}_{1}}{{F}_{{j - 1}}} + {{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 1}}}{{p}_{2}}{{F}_{{j{\kern 1pt} + {\kern 1pt} 1}}}, \\ {{K}_{3}}\left( j \right) = {{\left( { - 1} \right)}^{{j{\kern 1pt} - {\kern 1pt} 2}}}{{m}_{1}}{{F}_{{j{\kern 1pt} - {\kern 1pt} 2}}} + {{\left( { - 1} \right)}^{j}}{{m}_{2}}{{F}_{j}} + {{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 2}}}{{m}_{3}}{{F}_{{j{\kern 1pt} + {\kern 1pt} 2}}}, \\ J_{2}^{*}\left( j \right) = \frac{8}{{15}}{{K}_{1}}\left( j \right) - \frac{1}{5}{{K}_{3}}\left( j \right) + 2K_{1}^{ + }\left( j \right) + 3K_{1}^{ - }\left( j \right), \\ K_{1}^{ + }\left( j \right) = {{\left( { - 1} \right)}^{{j{\kern 1pt} - {\kern 1pt} 3}}}p_{1}^{ + }{{F}_{{j - 3}}} + {{\left( { - 1} \right)}^{{j{\kern 1pt} - {\kern 1pt} 1}}}p_{2}^{ + }{{F}_{{j{\kern 1pt} - {\kern 1pt} 1}}} + \,\,{{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 1}}}p_{3}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 1}}} + {{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 3}}}p_{4}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 3}}}, \\ K_{1}^{ - }\left( j \right) = {{\left( { - 1} \right)}^{{j{\kern 1pt} - {\kern 1pt} 4}}}p_{1}^{ - }{{F}_{{j{\kern 1pt} - {\kern 1pt} 4}}} + \,\,{{\left( { - 1} \right)}^{{j{\kern 1pt} - {\kern 1pt} 2}}}p_{2}^{ - }{{F}_{{j{\kern 1pt} - {\kern 1pt} 2}}} + {{\left( { - 1} \right)}^{j}}p_{3}^{ - }{{F}_{j}} + \,\,{{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 2}}}p_{4}^{ - }{{F}_{{j{\kern 1pt} + {\kern 1pt} 2}}} + {{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 4}}}p_{5}^{ - }{{F}_{{j{\kern 1pt} + {\kern 1pt} 4}}}, \\ \end{gathered} $$

$$\begin{gathered} J_{3}^{*}\left( j \right) = - \left( {2K_{3}^{ + }\left( j \right) + 3K_{3}^{ - }\left( j \right)} \right), \\ K_{3}^{ + }\left( j \right) = {{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 3}}}m_{1}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 3}}} + {{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 1}}}m_{2}^{ + }{{F}_{{j{\kern 1pt} + {\kern 1pt} 1}}}, \\ K_{3}^{ - }\left( j \right) = {{\left( { - 1} \right)}^{{j + 4}}}m_{1}^{ - }{{F}_{{j{\kern 1pt} + {\kern 1pt} 4}}} + \,\,{{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 2}}}m_{2}^{ - }{{F}_{{j{\kern 1pt} + {\kern 1pt} 2}}} + {{\left( { - 1} \right)}^{j}}m_{3}^{ - }{{F}_{j}}, \\ J_{4}^{*}\left( j \right) = 2K_{2}^{ + }\left( j \right) + 3K_{2}^{ - }\left( j \right), \\ K_{2}^{ + }\left( j \right) = {{\left( { - 1} \right)}^{{j - 1}}}q_{1}^{ + }{{F}_{{j{\kern 1pt} - {\kern 1pt} 1}}} + {{\left( { - 1} \right)}^{{j{\kern 1pt} + {\kern 1pt} 1}}}q_{2}^{ + }{{F}_{{j{\kern 1pt} - {\kern 1pt} 3}}}, \\ K_{2}^{ - }\left( j \right) = {{\left( { - 1} \right)}^{j}}q_{1}^{ - }{{F}_{j}} + \,{{\left( { - 1} \right)}^{{j - 2}}}q_{2}^{ - }{{F}_{{j{\kern 1pt} - {\kern 1pt} 2}}} + {{\left( { - 1} \right)}^{{j - 4}}}q_{3}^{ - }{{F}_{{j{\kern 1pt} - {\kern 1pt} 4}}}, \\ J_{5}^{*}\left( {j,i,n} \right) = {{h}_{i}}{{h}_{j}}\left( { - {{K}_{1}}\left( i \right)J_{1}^{*}\left( j \right) + \frac{1}{2}{{L}_{4}}\left( {j,i,n} \right){{{\left( { - 1} \right)}}^{n}}{{F}_{n}}} \right), \\ \end{gathered} $$

$$\begin{gathered} J_{6}^{*}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{{j{\kern 1pt} - {\kern 1pt} 2}}}{{L}_{3}}\left( {j,i,n} \right){{\left( { - 1} \right)}^{n}}{{F}_{n}}, \\ J_{7}^{*}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{{j{\kern 1pt} + {\kern 1pt} 2}}}{{L}_{5}}\left( {j,i,n} \right){{\left( { - 1} \right)}^{n}}{{F}_{n}}, \\ {{J}_{8}}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{{j{\kern 1pt} - {\kern 1pt} 1}}}\left( {3{{L}_{6}}\left( {j,i,n} \right) - 2{{L}_{1}}\left( {j,i,n} \right)} \right){{\left( { - 1} \right)}^{n}}{{F}_{n}}, \\ {{J}_{9}}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{{j{\kern 1pt} + {\kern 1pt} 1}}}\left( {3{{L}_{7}}\left( {j,i,n} \right) - 2{{L}_{2}}\left( {j,i,n} \right)} \right){{\left( { - 1} \right)}^{n}}{{F}_{n}}, \\ J_{{10}}^{*}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{j}}N_{{j,q,n}}^{{\left( + \right)}}J_{1}^{*}\left( n \right), \\ J_{{11}}^{*}\left( {j,i,n} \right) = \frac{1}{2}{{h}_{i}}{{h}_{j}}N_{{j,q,n}}^{{\left( - \right)}}J_{1}^{*}\left( n \right). \\ \end{gathered} $$