INTRODUCTION

Emission of electromagnetic waves has been demonstrated for an oscillating charged droplet of a perfectly conducting uncompressible perfect liquid [1]. Indeed, intrinsic charge of such a droplet is distributed over the surface, charge particles exhibit accelerated motion in the course of oscillations, and, hence, electromagnetic radiation is generated in accordance with the classical physical principles (see, for example, [2]). The calculation method of [1] is reduced to derivation of a dispersion relation for an oscillating droplet of perfect liquid for the wave zone of the electric field of the droplet that has complex solutions. The imaginary part of the frequency corresponds to damping that is impossible for perfect liquid. Therefore, the emission of accelerated charges serves as the source of the energy loss.

In accordance with the electromagnetic theory [3], the radiation of a system of accelerated charges consists of s sum of dipole, quadrupole, and magnetic dipole contributions. Electromagnetic radiation is divided into multipole components using small parameter δ, which represents squared ratio of a linear size of the droplet to the radiation wavelength. The radiation intensities decrease in a row: dipole, quadrupole, and magnetic dipole components. The calculations of an oscillating charged droplet in the first order of smallness with respect to parameter ε [1] (ε is the ratio of the oscillation amplitude to a linear size of the droplet) yield only quadrupole component. The dipole radiation of an oscillating charged droplet is obtained in the calculations of the second order of smallness with respect to parameter ε. However, the intensity of the dipole radiation appears to be greater than the intensity of the quadrupole radiation by 14–15 orders of magnitude.

Different results are obtained for an uncharged droplet of perfectly conducting uncompressible nonviscous liquid in the presence of uniform electrostatic field: dipole radiation is observed in the first order of smallness with respect to parameters δ and ε [5], and quadrupole radiation is observed in the second order of smallness with respect to parameter δ and the first order with respect to parameter ε.

In this work, we calculate the intensity of quadrupole radiation of an uncharged droplet of perfect uncompressible conducting liquid that oscillates in the presence of uniform electrostatic field.

PHYSICAL FORMULATION OF THE PROBLEM

We consider quadrupole electromagnetic radiation generated by an uncharged droplet of perfect uncompressible liquid that oscillates in the presence of uniform electrostatic field E0. The mass density of the liquid is ρ, and the coefficient of surface tension is σ. The droplet is located in vacuum, and its volume is the volume of a sphere with radius R. Capillary wave motion is always excited on the surface of the droplet due to thermal motion of water molecules. The amplitude of such motion is relatively small (about ∝\(\sqrt {kT{\text{/}}\sigma } \), where k is the Boltzmann constant and T is the absolute temperature [6]). At temperatures of about room temperature such an amplitude is less than one angstrom for all liquids.

On the surface of a freely falling droplet that is affected by external forces (e.g., a force related to the air flow), the amplitudes of single modes of the oscillating droplet may amount to several tens of percents of the radius [7, 8]. In this case, the capillary oscillations of the surface of the droplet that is charged by induced charge lead to emission of electromagnetic waves.

In accordance with the general theory of electromagnetic waves, the intensity of the quadrupole radiation of a system of accelerated charges is calculated as [3]

$$I = \frac{1}{{180{{c}^{5}}}}\sum\limits_{\alpha ,\beta = 1}^3 {{{{\left( {\frac{{{{\partial }^{3}}}}{{\partial {{t}^{3}}}}{{D}_{{\alpha \beta }}}} \right)}}^{2}},} $$
((1))

where tensor of quadrupole moment Dαβ is given by

$${{D}_{{\alpha \beta }}}(t) = \iiint\limits_V {\gamma ({\mathbf{r}},t)(3{{x}_{\alpha }}(t){{x}_{\beta }}(t) - {{\delta }_{{\alpha \beta }}}{{r}^{2}}(t))dV.}$$
((2))

Here, γ(r, t) is the volume charge density, δαβ is the Kronecker delta, xα(t) and xβ(t) are the coordinates of radius vector r(t) in Cartesian coordinates (x, y, z) for a point that is located in droplet volume V.

External electrostatic field leads to perturbation of the equilibrium spherical shape of the droplet. In the linear approximation with respect to stationary deformation, we assume spheroid shape [9–13] with squared eccentricity e2

$${{e}^{2}} = \frac{{9E_{0}^{2}R}}{{16\pi \sigma }}.$$

The calculations are performed in spherical coordinates (r, θ, φ) with the origin at the center of mass of the droplet using dimensionless variables: R = ρ = σ = 1. The remaining parameters are represented in fractions of characteristic values:

[E0] = R–1/2σ1/2, [t] = R3/2ρ1/2σ–1/2, [V] = R–1/2ρ–1/2σ1/2, [r] = R, and [P] = R–1σ.

We mathematically formulate the problem of the quadrupole radiation of a spheroid uncharged droplet of nonviscous uncompressible conducting liquid that oscillates in the presence of external electrostatic field.

MATHEMATICAL FORMULATION OF THE PROBLEM

We assume that, at initial moment t = 0, equilibrium spheroid droplet r(θ) is perturbed and virtual axisymmetric perturbation ξ(θ, t) with fixed amplitude ε is significantly less that the radius of the droplet. Based on the smallness and axisymmetric character of the initial perturbation, we assume that the droplet shape is axisymmetric at any time moment. We also assume that the equation that describes the surface of the droplet in the spherical coordinates with the origin at the center of mass is written in terms of dimensionless variables as

$$r(\theta ,t) = r(\theta ) + \xi (\theta ,t),\quad {\text{|}}\xi {\text{|}} \ll 1.$$

We consider potential motion of the liquid and assume that the field of velocities for the liquid in the droplet V(r, t) = ∇ψ(r, t) is fully determined by velocity potential ψ(r, t) [14]. The amplitude of the velocity field for the liquid has the order of smallness that is identical to the order smallness of the oscillation amplitudes on the surface of the droplet: ψ(r, t) ~ ξ(θ, t) ~ ε. In the vicinity of the droplet, the electric field is described using electric potential Φ(r, t).

The mathematical problem of the motion of liquid in the uncharged droplet that oscillates in the presence of external electrostatic field is written as [1, 15]

$$\begin{gathered} \Delta \psi ({\mathbf{r}},t) = 0,\quad \Delta \Phi ({\mathbf{r}},t) = 0, \\ r \to 0{\text{:}}\,\psi ({\mathbf{r}},t) \to 0,\quad r \to \infty {\text{:}}\,\Phi ({\mathbf{r}},t) \to - {{E}_{0}}r\cos \theta , \\ \end{gathered} $$
$$\begin{gathered} r = r(\theta ) + \xi (\theta ,t){\text{:}} \\ \frac{{\partial \xi (\theta ,t)}}{{\partial t}} = \frac{{\partial \psi ({\mathbf{r}},t)}}{{\partial r}} - \frac{1}{{{{r}^{2}}}}\frac{{\partial \psi ({\mathbf{r}},t)}}{{\partial \theta }}\left( {\frac{{\partial r(\theta )}}{{\partial \theta }} + \frac{{\partial \xi (\theta ,t)}}{{\partial \theta }}} \right), \\ \Phi ({\mathbf{r}},t) = {{\Phi }_{s}}(t), \\ \end{gathered} $$
((3))
$$\begin{gathered} t = 0{\text{:}}\,\xi (\theta ) = \varepsilon \sum\limits_{j \in \Xi }^{} {{{h}_{j}}{{P}_{j}}(\mu ),\quad \sum\limits_{j \in \Xi }^{} {{{h}_{j}} = 1,} } \\ \varepsilon \ll 1,\quad \frac{{\partial \xi (\theta )}}{{\partial t}} = 0, \\ \end{gathered} $$

where hj are the coefficients that determine the partial contribution of the jth oscillation mode to the total initial perturbation, Ξ is the set of numbers of the initially excited oscillation modes, Pj(μ) is the Legendre polynomial of the jth order, j is the integer, and μ ≡ cosθ.

For closing of the above system of equations, we use general physical principles and formulate additional natural conditions for constancy of the volume, immobility of the center of mass, and zero charge of the droplet:

$$\int\limits_V^{} {{{r}^{2}}} dr\sin \theta d\theta d\varphi = \frac{4}{3}\pi ,\quad \int\limits_V^{} {{\mathbf{r}}{{r}^{2}}dr\sin \theta d\theta d\varphi = 0,} $$
$$\begin{gathered} V = [0 \leqslant r \leqslant r(\theta ) + \xi (\theta ,t),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ], \\ \frac{1}{{4\pi }}\oint\limits_S {({\mathbf{n}}({\mathbf{r}},t),\nabla \Phi )dS = 0,} \\ \end{gathered} $$
((4))
$$S = [r = r(\theta ) + \xi (\theta ,t),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ].$$

Here, we use the following notation: ∞S(t), electrostatic potential that is constant over the surface; P = P0 – \(\frac{{\partial \psi }}{{\partial t}}\), hydrodynamic pressure; P0, constant internal pressure in the equilibrium state; PE = (∇Φ)2/8π, electric field pressure; Pσ = divn(r, t), capillary pressure; n(r, t), unit vector that is orthogonal to the perturbed surface [16] given by

$${\mathbf{n}}({\mathbf{r}},t) = {{\left. {\frac{{\nabla (r - r(\theta ,t))}}{{{\text{|}}\nabla (r - r(\theta ,t)){\text{|}}}}} \right|}_{{r = r(\theta ,t)}}}.$$
((5))

The desired quantities are expanded in terms of the smallness of dimensionless oscillation amplitude ε [17]:

$$\begin{gathered} \xi (\theta ,t) = {{\xi }^{{(1)}}}(\theta ,t) + {\text{O}}({{\varepsilon }^{2}}),\quad {{\psi }_{j}}({\mathbf{r}},t) = \psi _{j}^{{(1)}}({\mathbf{r}},t) + {\text{O}}({{\varepsilon }^{2}}), \\ P({\mathbf{r}},t) = {{P}^{{(0)}}}({\mathbf{r}}) + {{P}^{{(1)}}}({\mathbf{r}},t) + {\text{O}}({{\varepsilon }^{2}}), \\ \end{gathered} $$
$${{P}_{\sigma }}({\mathbf{r}},t) = P_{\sigma }^{{(0)}}({\mathbf{r}}) + P_{\sigma }^{{(1)}}({\mathbf{r}},t) + {\text{O}}({{\varepsilon }^{2}}),$$
((6))
$$\begin{gathered} {{P}_{E}}({\mathbf{r}},t) = P_{E}^{{(0)}}({\mathbf{r}}) + P_{E}^{{(1)}}({\mathbf{r}},t) + {\text{O}}({{\varepsilon }^{2}}), \\ \Phi ({\mathbf{r}},t) = {{\Phi }^{{(0)}}}({\mathbf{r}}) + {{\Phi }^{{(1)}}}({\mathbf{r}},t) + {\text{O}}({{\varepsilon }^{2}}), \\ \end{gathered} $$

where Φ(0)(r, θ) is the electric potential in the vicinity of the equilibrium position of the uncharged spheroid in the presence of external electric field and Φ(1)(r, θ, t) is the term of the first order of smallness added to the electric potential due to perturbation of the surface. The superscript shows the order of smallness with respect to parameter ε.

Substituting expansions (6) in expressions (3) and (4), we select problems of the zero and first order with respect to parameter ε.

Potential Φ(0)(r, θ) in the linear approximation with respect to e2 can be obtained using a transition from the known expression of [18] for the electric potential of a prolate conducting ellipsoid in the presence of a uniform external field in the spheroidal coordinates to the spherical coordinates or with the aid of a direct solution of the electrostatic problem of the zero order of smallness with respect to parameter ε in the spherical coordinates using the perturbation method:

$$\begin{gathered} {{\Phi }^{{(0)}}}(r,\theta ) = {{E}_{0}}r{{P}_{1}}(\mu )\left( {\frac{1}{{{{r}^{3}}}} - 1} \right) + \frac{2}{5}\frac{1}{{{{r}^{2}}}}{{e}^{2}} \\ \, \times {{E}_{0}}\left( {{{P}_{1}}(\mu ) + \frac{3}{2}\frac{1}{{{{r}^{2}}}}{{P}_{3}}(\mu )} \right). \\ \end{gathered} $$

Accurate to the terms of the first order with respect to small parameters ε and e2, the shape of the perturbed surface r(θ, t) is described using the equation

$$r(\theta ,t) = 1 + {{e}^{2}}h(\theta ) + \varepsilon \sum\limits_{j \in \Xi }^{} {{{M}_{j}}(t){{P}_{j}}(\mu ),} $$
((7))

where amplitude coefficients Mj(t) are represented as

$$\begin{gathered} {{M}_{j}}(t) = {{h}_{j}}{\text{cos}}({{\omega }_{j}}t) + {{e}^{2}}\left( {{{h}_{{j - 2}}}\frac{{j(j - 1)(3{{j}^{2}} - 3j + 2)}}{{4(2j - 1)(2j - 3)(3j - 4)}}} \right. \\ \, \times (\cos ({{\omega }_{{j - 2}}}t) - \cos ({{\omega }_{j}}t)) \\ \, - {{h}_{{j + 2}}}\frac{{(j + 1)(3{{j}^{3}} + 27{{j}^{2}} + 44j + 16)}}{{4(2j + 3)(2j + 5)(3j + 2)}} \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}\, \times (\cos ({{\omega }_{{j + 2}}}t) - \cos ({{\omega }_{j}}t))} \right)\quad (j \in \Xi ). \\ \end{gathered} $$

In the absence of the external electric field, the second term of about e2 vanishes and perturbation amplitude Mj(t) is determined by the term with frequency ωj: Mj(t) = hjcos(ωjt).

The term added to the electric potential in the vicinity of the perturbed spheroid is written as

$$\begin{gathered} {{\Phi }^{{(1)}}}({\mathbf{r}},t) = {{E}_{0}}\varepsilon \left( {\frac{6}{{35}}\frac{{{{e}^{2}}{{M}_{3}}(t)}}{r} + \left( {\sum\limits_{j \in \Xi }^{} {[3(\mu _{{j - 1}}^{ + }{{M}_{{j - 1}}}(t)} } \right.} \right. \\ \, + \mu _{{j + 1}}^{ - }{{M}_{{j + 1}}}(t)) + {{e}^{2}}({{M}_{{j - 3}}}(t){{l}_{1}}(j) + {{M}_{{j - 1}}}(t){{l}_{2}}(j) \\ \left. {\left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}\, + {{M}_{{j + 1}}}(t){{l}_{3}}(j) + {{M}_{{j + 3}}}(t){{l}_{4}}(j))]{{r}^{{ - (n + 1)}}}} \right)} \right){{P}_{j}}(\mu ). \\ \end{gathered} $$

SURFACE CHARGE DENSITY

Surface charge density v(r, t) that is distributed over the perturbed surface of the axisymmetric surface of a perfectly conducting droplet is determined using the known formula

$$\begin{gathered} {\mathbf{v}}({\mathbf{r}},t) = - \frac{1}{{4\pi }}({\mathbf{n}}({\mathbf{r}},t),\nabla \Phi ({\mathbf{r}},t)){{{\text{|}}}_{{r = r(\theta ,t)}}} \\ = - \frac{1}{{4\pi }}({\mathbf{n}}({\mathbf{r}},t),\nabla {{\Phi }^{{(0)}}}({\mathbf{r}}) + \nabla {{\Phi }^{{(1)}}}({\mathbf{r}},t)){{{\text{|}}}_{{r = r(\theta ,t)}}}, \\ \end{gathered} $$
((8))

where r(θ, t) is given by expression (7).

We use expression (8) for the components of the electric potential and the expression for the normal vector orthogonal to the perturbed surface of the spheroid in the presence of the external field

$$\begin{gathered} {\mathbf{n}}({\mathbf{r}},t) = \left( {1 - \frac{1}{3}{{e}^{2}}\frac{{\partial {{P}_{2}}(\mu )}}{{\partial \theta }}\frac{{\partial \xi (\theta ,t)}}{{\partial \theta }}} \right){{{\mathbf{e}}}_{r}} - \left( {\frac{{\partial \xi (\theta ,t)}}{{\partial \theta }}} \right. \\ \left. { + \frac{1}{3}{{e}^{2}}\left( {(1 - \xi (\theta ,t))\frac{{\partial {{P}_{2}}(\mu )}}{{\partial \theta }} - {{P}_{2}}(\mu )\frac{{\partial \xi (\theta ,t)}}{{\partial \theta }}} \right)} \right){{{\mathbf{e}}}_{\theta }} \\ \end{gathered} $$
((9))

to obtain the surface charge density on the perturbed droplet r(θ, t) accurate to the terms on the order of ~E0e2ε and ~\(E_{0}^{3}\)ε:

$$\begin{gathered} {\mathbf{v}}({\mathbf{r}},t) = \frac{1}{{4\pi }}\left( {3{{E}_{0}}{{{\left( {{{P}_{1}}(\mu ) + \frac{2}{5}{{e}^{2}}{{P}_{3}}(\mu )} \right)}}_{{_{{_{{}}}}}}}} \right. \\ - \left( {\frac{{\partial {{\Phi }^{{(1)}}}}}{{\partial r}} + {{E}_{0}}\xi (\theta ,t)\left( {6{{P}_{1}}(\mu ) + \frac{2}{5}{{e}^{2}}({{P}_{1}}(\mu ) + 15{{P}_{3}}(\mu ))} \right)} \right. \\ {{\left. {\left. {\left. { + \frac{1}{3}{{e}^{2}}\left( {\frac{{{{\partial }^{2}}{{\Phi }^{{(1)}}}}}{{\partial {{r}^{2}}}}{{P}_{2}}(\mu ) - \frac{{\partial {{\Phi }^{{(1)}}}}}{{\partial \theta }}\frac{{\partial {{P}_{2}}(\mu )}}{{\partial \theta }}} \right)} \right)} \right)} \right|}_{{r = 1}}}. \\ \end{gathered} $$

Here, functions ξ(θ, t) and Φ(1)(r, t) are the functions of the first order of smallness with respect to parameter ε. In expression (9), er and eθ are the unit vectors of the spherical coordinate system.

Taking into account function ξ(θ, t) from expression (7) and the solution for additional electric potential Φ(1)(r, t), we represent the surface charge density as an expansion in terms of the Legendre polynomials:

$$\begin{gathered} {\mathbf{v}}({\mathbf{r}},t) = \frac{3}{{4\pi }}{{E}_{0}}\left( {{{P}_{1}}(\mu ) + \frac{2}{5}{{e}^{2}}{{P}_{3}}(\mu )} \right. + \varepsilon \sum\limits_{j \in \Xi }^{} {\left( {{{M}_{{j - 1}}}(t){{k}_{1}}} \right.} \\ \, + \,{{M}_{{j + 1}}}(t){{k}_{2}}\, - \,{{e}^{2}}\left( {\frac{2}{{35}}{{M}_{3}}(t){{\delta }_{{j,0}}}\, + \,{{M}_{{j - 3}}}(t){{k}_{3}}\, + \,{{M}_{{j - 1}}}(t){{k}_{4}}} \right. \\ \left. {\left. {_{{_{{_{{_{{_{{_{{}}}}}}}}}}}} + {{M}_{{j + 1}}}(t){{k}_{5}} + {{M}_{{j + 3}}}(t){{k}_{6}}} \right)} \right){{P}_{j}}(\mu )\quad (j \in \Xi ). \\ \end{gathered} $$
((10))

Numerical factors k1–k6 that depend on only subscript j are presented in the Appendix.

CALCULATION OF THE QUADRUPOLE MOMENTS

To obtain the intensity of the quadrupole electromagnetic radiation of the conducting droplet, we calculate tensor of quadrupole moment Dαβ(t) that enters expression (1). Substituting squared radius vector r2 = x2 + y2 + z2 in formula (2), we obtain a general expression for the tensor of quadrupole moment in the Cartesian coordinates [3, 18]:

$$\begin{gathered} {{D}_{{\alpha \beta }}}(t) = \int\limits_V^{} {{\mathbf{v}}({\mathbf{r}},t)\delta (r - r({\mathbf{r}},t))(3{{x}_{\alpha }}{{x}_{\beta }} - {{r}^{2}}{{\delta }_{{\alpha \beta }}})dV,} \\ V = [ - r \leqslant x \leqslant r; - \sqrt {{{r}^{2}} - {{x}^{2}}} \leqslant y \leqslant \sqrt {{{r}^{2}} - {{x}^{2}}} ; \\ - \,\sqrt {{{r}^{2}} - {{x}^{2}} - {{y}^{2}}} \leqslant z \leqslant \sqrt {{{r}^{2}} - {{x}^{2}} - {{y}^{2}}} ]. \\ \end{gathered} $$

Here, r = r(r, t) is the equation for the surface of the droplet, v(r, t) is the surface charge density, r is the radius vector of a point on the surface of the droplet, δ(r – r(θ, t)) is the Dirac delta function [19], and δαβ is the Kronecker delta.

For further calculation of the quadrupole moments, we use the approach of [20].The expression for components of quadrupole moments is represented in the spherical coordinates (r, θ, φ) with the origin at the center of the droplet. The presence of delta function in the expressions for the components of the tensor of quadrupole moment makes it possible to transform integration over the volume into integration over the surface of the droplet that is perturbed due to capillary wave motion. Thus, we obtain

$$\begin{gathered} {{D}_{{11}}}(t) = \int\limits_S^{} {\frac{{{v}(\theta ,t)}}{{({\mathbf{n}}({\mathbf{r}},t),{{{\mathbf{e}}}_{r}})}}} {{r}^{4}}(\theta ,t)((2 - 3{{\sin }^{2}}\varphi ){{\sin }^{2}}\theta \\ - \,\,{{\cos }^{2}}\theta )\sin \theta d\theta d\varphi , \\ \end{gathered} $$
$$\begin{gathered} {{D}_{{22}}}(t) = \int\limits_S^{} {\frac{{{v}(\theta ,t)}}{{({\mathbf{n}}({\mathbf{r}},t),{{{\mathbf{e}}}_{r}})}}} {{r}^{4}}(\theta ,t)((3{{\sin }^{2}}\varphi - 1){{\sin }^{2}}\theta \\ - \,\,{{\cos }^{2}}\theta )\sin \theta d\theta d\varphi , \\ \end{gathered} $$
$$\begin{gathered} {{D}_{{33}}}(t) = \int\limits_S^{} {\frac{{{v}(\theta ,t)}}{{({\mathbf{n}}({\mathbf{r}},t),{{{\mathbf{e}}}_{r}})}}{{r}^{4}}(\theta ,t)(3{{{\cos }}^{2}}\theta - 1)\sin \theta d\theta d\varphi ,} \\ {{D}_{{12}}}(t) = {{D}_{{21}}}(t) = 3\int\limits_S^{} {\frac{{{v}(\theta ,t)}}{{({\mathbf{n}}({\mathbf{r}},t),{{{\mathbf{e}}}_{r}})}}{{r}^{4}}(\theta ,t)} \\ \times \cos \varphi \sin \varphi {{\sin }^{3}}\theta d\theta d\varphi , \\ \end{gathered} $$
((11))
$$\begin{gathered} {{D}_{{13}}}(t) = {{D}_{{31}}}(t) = 3\int\limits_S^{} {\frac{{{v}(\theta ,t)}}{{({\mathbf{n}}({\mathbf{r}},t),{{{\mathbf{e}}}_{r}})}}} {{r}^{4}}(\theta ,t) \\ \times \cos \varphi \cos \theta {{\sin }^{2}}\theta d\theta d\varphi , \\ \end{gathered} $$
$$\begin{gathered} {{D}_{{23}}}(t) = {{D}_{{32}}}(t) = 3\int\limits_S^{} {\frac{{{v}(\theta ,t)}}{{({\mathbf{n}}({\mathbf{r}},t),{{{\mathbf{e}}}_{r}})}}} {{r}^{4}}(\theta ,t) \\ \times \sin \varphi \cos \theta {{\sin }^{2}}\theta d\theta d\varphi , \\ S = [r = r(\theta ,t);0 \leqslant \theta \leqslant \pi ;0 \leqslant \varphi \leqslant 2\pi ]. \\ \end{gathered} $$

Here, quantities r(θ, t), \({v}\)(θ, t), and n(r, t) are given by expressions (7), (10), and (9), respectively.

The droplet is axisymmetric, so that equation of the perturbed surface r(θ, t) is independent on the φ coordinate. After integration of expressions (11) with respect to angle φ, we obtain

$$\begin{gathered} {{D}_{{11}}}(t) = {{D}_{{22}}}(t) = - \frac{1}{2}{{D}_{{33}}}(t) = \pi \int\limits_0^\pi {\frac{{{v}(\theta ,t)}}{{({\mathbf{n}}({\mathbf{r}},t),{{{\mathbf{e}}}_{r}})}}{{r}^{4}}(\theta ,t)} \\ \, \times (1 - 3{{\cos }^{2}}\theta )\sin \theta d\theta = - 2\pi \int\limits_0^\pi {\frac{{{v}(\theta ,t)}}{{({\mathbf{n}}({\mathbf{r}},t),{{{\mathbf{e}}}_{r}})}}} \\ \, \times {{r}^{4}}(\theta ,t){{P}^{2}}(\mu )\sin \theta d\theta , \\ \end{gathered} $$
((12))
$${{D}_{{12}}} = {{D}_{{21}}} = {{D}_{{13}}} = {{D}_{{31}}} = {{D}_{{23}}} = {{D}_{{32}}} = 0.$$

We substitute surface charge density (10) and normal vector (9) on perturbed surface of the droplet r(θ, t) in nonzero tensor components to obtain the corresponding analytical expressions in terms of amplitude coefficients Mj(t):

$$\begin{gathered} {{D}_{{11}}}(t) = {{D}_{{22}}}(t) = - \frac{1}{2}{{D}_{{33}}}(t) = - \frac{3}{2}{{E}_{0}} \\ \, \times \int\limits_0^\pi {\left( {\cos \theta \left( {1 + {{e}^{2}}\left( {3\cos \theta - \frac{{19}}{{15}}} \right)} \right)} \right.} \\ \, + \varepsilon \sum\limits_{j \in \Xi }^{} {\left( {{{M}_{{j - 1}}}(t){{p}_{1}} + {{M}_{{j + 1}}}(t){{p}_{2}}} \right.} \\ \, + {{e}^{2}}\left( {\frac{2}{{35}}{{M}_{3}}(t){{\delta }_{{j,0}}} + {{M}_{{j - 3}}}(t){{p}_{3}} + {{M}_{{j - 1}}}(t){{p}_{4}}} \right. \\ \left. {\left. {\left. {_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}\, + {{M}_{{j + 1}}}(t){{p}_{5}} + {{M}_{{j + 3}}}(t){{p}_{6}}} \right)} \right){{P}_{j}}(\cos \theta )} \right){{P}_{2}}(\mu )\sin \theta d\theta . \\ \end{gathered} $$
((13))

Numerical coefficients p1–p6, which depend only on subscript j, can be found in the Appendix.

We take into account orthogonality of the Legendre polynomials, substitute explicit expression for Mj(t), and make a transition to dimensional variables:

$$\begin{gathered} {{D}_{{11}}}(t) = {{D}_{{22}}}(t) = - \frac{1}{2}{{D}_{{33}}}(t) \\ = - {{E}_{0}}{{R}^{4}}\varepsilon \left( {\frac{9}{7}{{h}_{3}}\cos ({{\omega }_{3}}t) + {{e}^{2}}} \right.\left( {\frac{{52}}{{245}}{{h}_{3}}\cos ({{\omega }_{3}}t)} \right. \\ \left. {\left. { + \frac{2}{{847}}{{h}_{5}}(236\cos ({{\omega }_{3}}t) + 149\cos ({{\omega }_{5}}t))} \right)} \right), \\ \end{gathered} $$
$$\begin{gathered} {{\omega }_{j}} = \left( {\frac{\sigma }{{\rho {{R}^{3}}}}j\left( {(j - 1){{{(j + 2)}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}} \right.} \right. \\ {{\left. {\left. {\, - {{e}^{2}}\frac{{(2{{j}^{5}} + 23{{j}^{4}} + 21{{j}^{3}} - 17{{j}^{2}} - 7{{j}^{2}} - 2)}}{{(2j - 1)(2j + 1)(2j + 3)}}} \right)} \right)}^{{1/2}}}. \\ \end{gathered} $$

Note that the quadrupole moment of the uncharged droplet in the presence of the external field differs from zero only for the perturbed surface of the droplet (the quadrupole moment of an equilibrium uncharged spheroid in the presence of external electrostatic field is zero) and is determined by the third and fifth oscillation modes in the calculations accurate to the squared eccentricity.

We determine the maximum sum of squares of the third derivative with respect to time of the tensor components of the quadrupole moment:

$$\begin{gathered} \sum\limits_{\alpha ,\beta = 1}^3 {\left( {\frac{{{{\partial }^{3}}}}{{\partial {{t}^{3}}}}{{D}_{{\alpha \beta }}}(t)} \right)} _{{\max }}^{2} = 6E_{0}^{2}{{R}^{8}}{{\varepsilon }^{2}}\left( {\frac{9}{7}{{h}_{3}}\omega _{3}^{3}} \right. \\ {{\left. {\, + {{e}^{2}}\left( {\frac{{52}}{{245}}{{h}_{3}}\omega _{3}^{3} + \frac{2}{{847}}{{h}_{5}}(236\omega _{3}^{3} + 149\omega _{5}^{3})} \right)} \right)}^{2}}. \\ \end{gathered} $$
((14))

Substituting expression (14) in formula (1), we find the intensity of the quadrupole electromagnetic radiation of the uncharged droplet that oscillates in the presence of electrostatic field:

$$\begin{gathered} I = \frac{1}{{30{{c}^{5}}}}E_{0}^{2}{{R}^{8}}{{\omega }^{2}}\left( {\frac{9}{7}{{h}_{3}}\omega _{3}^{3} + {{e}^{2}}\left( {\frac{{52}}{{245}}} \right.} \right.{{h}_{3}}\omega _{3}^{3} \\ {{\left. {\left. { + \frac{2}{{847}}{{h}_{5}}(236\omega _{3}^{3} + 149\omega _{5}^{3})} \right)} \right)}^{2}}. \\ \end{gathered} $$
((15))

Based on expression (15), we numerically estimate the quadrupole moment of the quadrupole noise radio radiation of convective clouds.

First, note that a possible source of electromagnetic radiation is related to the oscillations of low modes of small droplets the concentration of which in the cloud is about 103 cm–3 [21]. Characteristic sizes of such droplets range from to 3 to 30 μm. Maximum concentration in the cloud corresponds to size interval of 3–7 μm. The surface oscillations of the droplets are primarily determined by microphysical intracloud processes: coagulation with smaller particles, changes of the aggregate state, splitting into smaller droplets due to collisions or electrostatic instability, and electric and hydrodynamic interaction with the neighboring droplets. Experiments under natural conditions show that the oscillation amplitude of cloud droplets may amount to several tens of percents of the droplet size [7, 8]. Thus, we estimate the radiation intensity on the assumption that the ratio of the oscillation amplitude to the droplet radius ξ(θ, t)/R = ε is 0.1.

We use expression (15) to calculate the quadrupole radiation of a single uncharged droplet that oscillates in the presence of the uniform electrostatic field. For the numerical estimations we use h3 = h5 = 0.5, ε = 0.1, σ = 73 dyn/cm, ρ = 1 g/cm3, R = 30 μm, and E0 = 50 V/cm [22] (about 2 × 10–4E0cr and ~7 × 10–4E0cr at R = 3 and 30 μm, respectively, where E0cr is the critical field). Then, expression (14) yields I ~ 6 × 10–46 erg/cm. For a droplet with a radius of R = 8 μm, we obtain an intensity of I ~ 2 × 10–45 erg/ cm. For a radius of R = 3 μm, the intensity is I ~ 6 × 10–45 erg/cm (Fig. 1).

Fig. 1.
figure 1

Plot of the intensity of the quadrupole electromagnetic radiation of a single uncharged droplet that oscillates in the presence of electrostatic field vs. radius of an equal-size spherical droplet for ε = 0.1, σ = 73 dyn/cm, ρ = 1 g/cm3, and E0 = 50 V/cm (about 2 × 104E0cr and 7 × 10–4E0cr at R = 3 and 30 μm, respectively).

Full size image

The estimated results and Fig. 1 show that an increase in the droplet radius by an order of magnitude (from 3 to 30 μm) leads to a decrease in the intensity by an order of magnitude.

Figure 2 shows the characteristics of radiation versus the external electric field. It is seen that an increase in the electric field causes a rapid increase in the radiation intensity: an increase in the field by a factor of 3 leads to an increase in the radiation intensity by an order of magnitude in accordance with expression (15).

Fig. 2.
figure 2

Plot of the intensity of electromagnetic radiation of a single uncharged droplet that oscillates in the presence of electrostatic field vs. external electric field that is calculated for the parameters of Fig. 1 at R = 30 μm.

Full size image

In comparison with the intensity of the dipole electromagnetic radiation of the uncharged droplet that oscillates in the presence of electrostatic field [5], the intensity of the quadrupole electromagnetic radiation is less by 14–15 orders of magnitude.

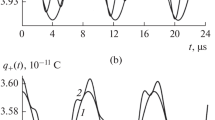
Figure 3 presents the dependences of the dimensionless axisymmetric component D33(t) of the quadrupole moment calculated with the aid of expression (13) for h3 = h5 = 0.5 (curve 1) and dimensionless projection along the symmetry axis of the dipole moment d3(t) (curve 2) on dimensionless time. The dipole moment is calculated with the aid of the expression

$${\mathbf{d}}(t) = \frac{1}{2}{{{\mathbf{e}}}_{z}}{{E}_{0}}\left[ {2\left( {1 + \frac{1}{3}{{e}^{2}}} \right)\left( {1 + \frac{1}{{15}}{{e}^{2}}} \right) + H(t)} \right],$$
$$\begin{gathered} H(t) = 4\varepsilon \sum\limits_{j \in \Xi }^{} {{{h}_{j}}\left( {1 + \frac{1}{3}{{e}^{2}}} \right)({{G}_{1}}\cos ({{\omega }_{j}}t) + {{e}^{2}}({{G}_{2}}\cos ({{\omega }_{j}}t)} \\ \, + {{G}_{3}}\cos ({{\omega }_{{j - 2}}}t) - {{G}_{4}}\cos ({{\omega }_{{j + 2}}}t))) + \varepsilon \sum\limits_{j \in \Xi }^{} {{{h}_{j}}\left( {1 + \frac{1}{{15}}{{e}^{2}}} \right)} \\ \end{gathered} $$
$$\begin{gathered} \, \times ({{G}_{5}}\cos ({{\omega }_{j}}t) + {{e}^{2}}({{G}_{6}}\cos ({{\omega }_{j}}t) + {{G}_{7}}\cos ({{\omega }_{{j + 2}}}t) \\ \, + {{G}_{8}}\cos ({{\omega }_{{j - 2}}}t))) + \varepsilon \sum\limits_{j \in \Xi }^{} {{{h}_{j}}\left( {1 + \frac{1}{{15}}{{e}^{2}}} \right)({{G}_{9}}\cos ({{\omega }_{j}}t)} \\ \, + {{e}^{2}}({{G}_{{10}}}\cos ({{\omega }_{j}}t) + {{G}_{{11}}}\cos ({{\omega }_{{j + 2}}}t) + {{G}_{{12}}}\cos ({{\omega }_{{j - 2}}}t))) \\ \end{gathered} $$

by analogy with [5] for j = 2 and h2 = 1 for the spheroid water droplet in the presence of the uniform electrostatic field E0 = 50 V/cm using numerical coefficients Gi that depend only on the mode number (cumbersome expressions for the coefficients are not presented).

Fig. 3.
figure 3

Plots of the projections of the dimensionless electric dipole and quadrupole moments of an uncharged droplet that oscillates in the presence of the uniform electrostatic field vs. dimensionless time that are calculated for ε = 0.1 and E0 = 50 V/cm: (1) quadrupole moment D33(t) calculated at h3 = h5 = 0.5 and (2) dipole moment d3(t) calculated at j = 2 and h2 = 1.

Full size image

We plot dimensionless quantities, since quadrupole D33(t) and dipole d3(t) moments have different dimensions but it is expedient to represent both quantities on a single plot for clearness.

It is seen that the frequency of variations in the quadrupole moment with time is approximately four times greater than the frequency of variations in the dipole moment. This circumstance can be used for experimental identification of the multipole components of electromagnetic radiation of a water droplet in the presence of external uniform electrostatic field.

CONCLUSIONS

We have estimated the intensity of the quadrupole electromagnetic radiation of an uncharged droplet that oscillates in the presence of electrostatic field in the first order of smallness with respect to the ratio of the oscillation amplitude to the linear size of the droplet and in the second order of smallness with respect to the ratio of the linear size of the droplet to the radiation wavelength. It has been shown that the intensity of the quadrupole radiation is less than the intensity of the dipole radiation of the same droplet by 14–15 orders of magnitude and the frequency of the quadrupole radiation is several times higher than the frequency of the dipole radiation.