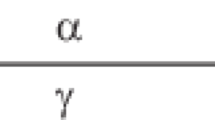INTRODUCTION

The thermodynamics of thin films is remarkable primarily for the fact that it is beyond the framework of the Gibbs capillary theory, which underlies the contemporary thermodynamics of surface phenomena. This new field of thermodynamics was formulated in the mid-20th century and was crowned by the discovery of disjoining pressure. The discovery of the latter and its subsequent studies performed by Derjaguin’s school have been described in detail in monograph [1], while the thermodynamic interpretation of the disjoining pressure has been presented in review [2]. Derjaguin defined disjoining pressure Π as follows [3] (the Derjaguin equation):

$$\Pi \equiv {{p}^{\alpha }} - {{p}^{\beta }},$$

where \({{p}^{\alpha }}\) is the external pressure applied to a film and \({{p}^{\beta }}\) is the pressure in equilibrium mother bulk phase β of the thin film. When brought in contact with an end face of a thin film, phase β may be at equilibrium with the latter; however, the real presence of phase β is not necessary (\({{p}^{\beta }}\) may be equal to a pressure value calculated for phase β at temperature and chemical potentthe Derjaguin equation, which concerns only phase pressures, disjoining pressure was easily introduced into the thermodynamics of phase equilibria [4–9].

The traditional capillarity theory comprises a similar and equally famous pressure difference, i.e., the Laplace capillary pressure:

$${{p}^{\alpha }} - {{p}^{\beta }} = \frac{{2\sigma }}{R},$$

where σ is the surface tension and R is the radius of an interfacial dividing surface. In some cases, pressure differences in the Derjaguin and Laplace equations even coincide with one another (e.g., for a sessile bubble on a planar surface); however, their fates in thermodynamics are different. When solving the problems of the capillarity theory, the capillary pressure is seldom considered as a separate parameter and introduced into thermodynamic equations with a special denotation. Phase pressures are commonly considered as separate variables, and it is correct to do so, because they may vary independently. It is obvious that the same state of affairs holds for pressure difference (1); however, in this case, the disjoining pressure is, on the contrary, considered to be the main variable and, actually, “reigns” in all equations of the theory. In this communication, we would like to focus the attention on the fact that the disjoining pressure is a complex composite value, and its variations owing to \({{p}^{\alpha }}\) or \({{p}^{\beta }}\) alone are different things.

In the historical aspect, Frumkin should be considered to be a pioneer in the thermodynamics of thin films. His interest in thermodynamics is additionally evident from the fact that he (together with Rehbinder) translated Planck’s work Thermodynamics into Russian as early as in 1919 and that, already in 1938, he used the concept of the chemical potential (referring to it as the “thermodynamic potential” or just “potential”) [10, 11]—the main parameter of the entire Gibbs thermodynamics. At that time, the term “disjoining pressure” had not yet been used, and Frumkin (inspired by Derjaguin and Kusakov’s experiments [12] studying equilibrium film thickness h as a function of external pressure P) intended to determine the relation between P and surface tension σ of a “layer under a bubble.” Let us cite Frumkin’s considerations [10] word-for-word. “Since \({v}dP = - d\mu \) (I—А.Р.), where μ is the potential of a layer, v is the molecular volume of the layer substance (with no regard to its dependence on P), and \(sd\sigma = - d\mu \) (II), then \({v}dP = sd\sigma \) (III) and

$$dP = \frac{1}{h}d\sigma ,...\,\,\left( {{\text{IV}}} \right)^{"}.$$

Frumkin equation (IV) is presented in his article [10] under number (1). We assign this number to modification (IV),

$$\frac{{d\sigma }}{{d\Pi }} = h,$$
((1))

because, in Derjaguin’s experiments, the disjoining pressure was varied by altering the values of P.

Now, let us examine the cited text mote intently. A reader acquainted with thermodynamics can see that, among these four equations, only Eq. (II), which looks like the Gibbs equation of adsorption under the condition that only one component is adsorbed, is true. A fundamental mistake is present in Eq. (I). In theory, this is the Gibbs–Duhem equation, but, in such a case, it must have a “plus” rather than “minus.” Moreover, the Gibbs–Duhem equation describes a bulk phase and is inapplicable to a thin film. The more, the merrier. If, in the course of the derivation, we eliminate the erroneous sign, a “minus” arises in Eq. (1). However, this destroys the entire concept of work [10]; i.e., it contradicts Derjaguin’s experiments rather than explain them. Therewith, Eq. (1), which arose as a result of some absurd error, such as a slip of the pen, began to be conveyed through the literature as the “Frumkin equation” after Derjaguin [13] cited work [11] (albeit in another respect). Against this background, it is most surprising that it, nevertheless, appears to be correct under certain conditions. I have derived the Frumkin equation several times [2, 8, 9, 14], and, each time, I complementarily referred to [10], violating my own strict rule of referring only to original works. A reader might say, “what a gem he is! He cited Frumkin’s works all of his life and only now has decided to look into them.” However, as they say, better late than never. Let us now see what approaches to the derivation of relationships similar to the Frumkin equation are available.

FINITE-THICKNESS SURFACE LAYER METHOD

Since any thin film has a finite thickness, it seemed to be most reasonable to consider such a film within the framework of the finite-thickness surface layer method, i.e., as a component of a real surface layer [4–9]. At the same time, the thicknesses of the surface layer and the thin film are completely different things (the former is ambiguous, while the latter is quite concrete). The ambiguity of the surface layer thickness is associated with the formulation of the method itself. In the rigorous interpretation [16–19], the surface layer thickness is specified by introducing two dividing surfaces, while excesses are taken only at the external sides, and only the real content is present in the space between the dividing surfaces. As the dividing surfaces are separated by moving each of them deeper into an adjacent bulk phase, the external excesses become smaller. The position in which the excesses may be ignored is a matter of practical convention (e.g., the excesses must be equal to the measurement error). Therefore, the surface layer thickness is determined individually for each procedure. Statistical mechanics determines the laws for the asymptotic description of surface layers (when the distances tend to infinity); however, finite distances and sizes (e.g., the volumes of macroscopic phases) are used in practice. Therefore, the thermodynamic equations for a finite-thickness surface layer often have the same form do as the equations for a two-phase system as a whole (including the surface layer).

In [4–9], a thin interfacial film was considered in the scale of the entire interfacial nonuniform region including the surface layers of the phases adjacent to the film. The latter phases can be represented by solid bodies, and they were used to study the disjoining pressure of the film. The thermodynamics of solid surfaces had not yet been developed, and the fundamental equations of liquid phases were used for solid bodies. Another circumstance was of importance. Each liquid body was impermeable and insoluble with respect to the film. Therewith, it was rigorously shown that relations similar to the Frumkin equation had to concern only the thickness of the liquid interlayer itself, with the exception of the thicknesses of the surface zones of all adjacent phases. Let us present the equation from [8, p. 295] with its own number as an example:

$${{\left( {\frac{{d\gamma }}{{d\Pi }}} \right)}_{{T,P}}} = \tau {\kern 1pt} ',$$
((XIII.109))

where γ is the film tension (including the contribution from the entire interfacial nonuniformity, i.e., the interfacial tension of the surface including the film), \(\tau {\kern 1pt} '\) is the thickness of the liquid interlayer itself (i.e., the thin film), T is the temperature, and P is the pressure in the mother phase of the film. Thus, Eq. (XIII.109) is distinguished by the fact that the contributions from the surface layers of the bodies adjacent to the film are taken into account in its left-hand side (the value of γ), while they are, on the contrary, excluded from right-hand side.

Of course, the finite-thickness layer method also comprises the elements of the Gibbs approach when the surface tension is under consideration. This value has to be used; however, it requires information on the true (geometric) surface rather than the layer. On the other hand, the study of multicomponent surface layers requires using the concept of “composition,” which is a common notion in chemistry. A set of Gibbs adsorptions can hardly be suitable in this case. Here, we need a set of real molar fractions of surface layer components, and the finite-thickness layer method copes with these problems. These problems can also be solved for thin films, because any of them is a finite-thickness layer as well. However, as thermodynamics of thin films was developed, the Gibbs method occupied increasingly large place in it. It may be stated that, while the finite-thickness layer method promoted the development of the practical applications of the theory, the Gibbs method more often brought up fundamental problems. The Frumkin equation may serve as an efficient indicator for these problems. Below, we shall consider different versions of the Gibbs method, which entail the use of different numbers of dividing surfaces.

GIBBS METHOD WITH ONE DIVIDING SURFACE

This is the simplest approach: a thin film is considered only as a component of an interfacial transition zone, while all conclusions are inferred from the thermodynamics of surface phenomena. Therewith, it does not matter for thermodynamics whether the film is a wetting or an adsorption one, and, in all cases, the Gibbs adsorption equation may be used as a basis. In this work, we shall suppose that one phase is solid (let it be phase γ brought in contact with phase α; superscript β will be saved for the mother phase of the film). In this case, the generalized Gibbs equation [15] is valid (still more general equations for solid surfaces may be found in [14]):

$$d{{\sigma }^{{\alpha \gamma }}} = - \bar {s}dT + (\hat {\gamma } - {{\sigma }^{{\alpha \gamma }}}\hat {1}):d{{\hat {e}}^{\sigma }} - \sum\limits_i {{{\Gamma }_{i}}d{{\mu }_{i}}} ,$$
((2))

where \({{\sigma }^{{\alpha \gamma }}}\) is the thermodynamic surface tension of the αγ interface, \(\bar {s}\) is the excess entropy per unit surface area, T is the temperature, \(\hat {\gamma }\) is the mechanical surface tension tensor, \(\hat {1}\) is the unit tensor (Kronecker symbol), \({{\hat {e}}^{\sigma }}\) is the surface deformation tensor (the colon denotes the biscalar product of tensors), and \({{\Gamma }_{i}}\) and μi are the adsorption and chemical potential of an ith component, respectively. It should especially be noted that the chemical potential of the solid body (a tensor quantity) is absent in the right-hand side of Eq. (2) (it was used when deriving the second term).

For liquids, the mechanical and thermodynamic determinations of the surface tension yield the same result, the parenthetic tensors coincide with each other, and the second term in the right-hand side of Eq. (2) disappears. On the other hand, the second term is eliminated for a perfectly rigid body, because it cannot be deformed, \(d{{\hat {e}}^{\sigma }}\) = 0. Thus, the traditional form of the Gibbs adsorption equation is restored for not only a liquid, but also a solid body, provided that it is undeformable. Taking phase γ to be undeformable and insoluble (to have a distinct boundary surface), Eq. (2) is written as

$$d{{\sigma }^{{\alpha \gamma }}} = - \bar {s}dT - \sum\limits_i {{{\Gamma }_{i}}d{{\mu }_{i}}} .$$
((3))

According to Gibbs, Eq. (3) should be considered in combination with the Gibbs–Duhem equations for bulk phases. In our case of a thin film, we have two such equations: for phase α adjacent to a solid surface covered with the film,

$$d{{p}^{\alpha }} = s_{{v}}^{\alpha }dT + \sum\limits_i {c_{i}^{\alpha }d{{\mu }_{i}}} ,$$
((4))

and for mother phase β of the film,

$$d{{p}^{\beta }} = s_{{v}}^{\beta }dT + \sum\limits_i {c_{i}^{\beta }d{{\mu }_{i}}} ,$$
((5))

where p is the pressure, \({{s}_{{v}}}\) is the bulk density of entropy, and \({{c}_{i}}\) is the concentration of an ith component.

When a film and its mother phase consist of a single substance (let it be component 1) and it is absent in phase α, we, from Eq. (5), obtain

$${{(d{{\mu }_{1}})}_{T}} = {v}_{1}^{\beta }d{{p}^{\beta }}.$$
((6))

Substitution of Eq. (6) into relation (3) yields

$${{(d{{\sigma }^{{\alpha \gamma }}})}_{T}} = - {{\Gamma }_{1}}{{{v}}^{\beta }}d{{p}^{\beta }} - \sum\limits_{i > 1} {{{\Gamma }_{i}}d{{\mu }_{i}}} .$$
((7))

Although adsorption may have any sign, it is, of course, positive for a bulky wetting film, and, supposing that the film density is equal to the density of its mother phase, we may take

$${{\Gamma }_{1}}{{{v}}^{\beta }} \approx {{h}_{{{\kern 1pt} 1}}},$$
((8))

where \({{h}_{{{\kern 1pt} 1}}}\) is the thickness of the film of the first component. Then, Eq. (7) gives

$${{\left( {\frac{{d{{\sigma }^{{\alpha \gamma }}}}}{{d{{p}^{\beta }}}}} \right)}_{{T,{{\mu }_{{i > 1}}}}}} \approx - {{h}_{{{\kern 1pt} 1}}}.$$
((9))

It follows from Eq. (4) that, at constant temperature and chemical potentials, pressure \({{p}^{\alpha }}\) is also constant. Then, according to definition (1), \(d\Pi = - d{{p}^{\beta }},\) and Eq. (9) may be rewritten as follows:

$${{\left( {\frac{{d{{\sigma }^{{\alpha \gamma }}}}}{{d\Pi }}} \right)}_{{T,{{{\mu }}_{{i > 1}}}}}} \approx {{h}_{{{\kern 1pt} 1}}}.$$
((10))

Now, assume that component 1 is also present in phase α. Then, Eq. (9) remains valid; however, the fixation of temperature and other chemical potentials (e.g., by means of a contact with an environment free of component 1) does not lead, in this case, to the constancy of pressure \({{p}^{\alpha }}.\)Equations (4) and (5) acquire the form

$$d{{p}^{\alpha }} = c_{1}^{\alpha }d{{\mu }_{1}},$$
((11))
$$d{{p}^{\beta }} = c_{1}^{\beta }d{{\mu }_{1}},$$
((12))

from which it follows that both pressures vary simultaneously under the condition

$$\frac{{d{{p}^{\alpha }}}}{{d{{p}^{\beta }}}} = \frac{{c_{1}^{\alpha }}}{{c_{1}^{\beta }}}.$$
((13))

If, e.g., phase α is a gas, while phase β is a liquid occurring far from the critical point, the change in \({{p}^{\alpha }}\) will be small compared with a change in \({{p}^{\beta }}.\) Then, not only Eq. (9), but also Eq. (10), will remain valid. However, in the general case, pressures \({{p}^{\alpha }}\) and \({{p}^{\beta }}\) act separately, and the dependence between them may be rather complex. Recent work [20], where phase α was located inside of a sessile bubble under conditions of variable pressure \({{p}^{\beta }},\) may serve as a good example.

Above, we supposed the film to be one-component. Now, let us consider the case of several components. Having attributed subscript k to them and isolated them into a separate sum, let us write Eq. (3) as

$$d{{\sigma }^{{\alpha \gamma }}} = - \bar {s}dT - \sum\limits_k {{{\Gamma }_{k}}d{{\mu }_{k}}} - \sum\limits_i {{{\Gamma }_{i}}d{{\mu }_{i}}} .$$
((14))

In multicomponent phase β, the differential of the chemical potential of component k is given by the following expression:

$$d\mu _{k}^{\beta } = - s_{k}^{\beta }dT + {v}_{k}^{\beta }d{{p}^{\beta }} + {{\sum\limits_k {\left( {\frac{{\partial {{\mu }_{k}}}}{{\partial {{x}_{k}}}}} \right)} }^{\beta }}dx_{k}^{\beta },$$
((15))

where \({{s}_{k}}\) and \({{{v}}_{k}}\) are the partial (as calculated per molecule or mole) entropy and volume of component k, respectively, while the set of molar fractions \({{x}_{k}}\) characterizes the composition of phase β. At fixed temperature and composition of phase β, only the second term remains in the right-hand side of Eq. (15). Under these conditions, the substitution of Eq. (15) into Eq. (14) yields

$${{(d{{\sigma }^{{\alpha \gamma }}})}_{T}} = - d{{p}^{\beta }}\sum\limits_k {{{\Gamma }_{k}}{v}_{k}^{\beta }} - \sum\limits_{i > 1} {{{\Gamma }_{i}}d{{\mu }_{i}}} .$$
((16))

Now, it seems that, applying a relation similar to Eq. (8) to each component, we may compose the total film thickness from the thicknesses of the individual components as the sum over k. However, the situation is complicated by the fact that the Gibbs method deals with excess masses rather than the real ones. The adsorption of several components simultaneously is a competitive process, and, while some substances are adsorbed positively, others are adsorbed negatively. Here, the passage to the thicknesses of the interlayers of real film components is problematic.

GIBBS METHOD WITH TWO DIVIDING SURFACES

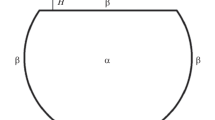
The method of two dividing surfaces [7–9] is to be used to introduce the disjoining pressure into the thermodynamics of phase equilibria. On the external sides, the excesses are specified as usual, while, in the gap between the surfaces, where the film is located, the excesses are preset relative to its mother phase. Moreover, since the film is thin, the excesses (e.g., of the adsorption at different sides the film) are not independent and must be considered jointly. Thus, the space is, now, divided into three rather than two phases, while the film thickness is determined as the distance between two dividing surfaces with different surface tensions \({{\sigma }^{\alpha }}\) (between phases α and β) and \({{\sigma }^{\gamma }}\) (at the interface between a solid body and phase β) (see Fig. 1).

Fig. 1.
figure 1

Arrangement of phases in the method of two dividing surfaces.

Full size image

After all excesses have been specified and the passage from the absolute to the relative adsorptions has been performed by substituting the Gibbs–Duhem equations for the bulk phases, the Gibbs adsorption equation takes the following form [2]:

$$d({{\sigma }^{\beta }} + {{\sigma }^{\gamma }}) = - {{\bar {S}}_{{(j)}}}dT - \Pi d{{H}_{{(j)}}} - \sum\limits_{i \ne j} {{{\Gamma }_{{i(j)}}}d{{\mu }_{i}}} .$$
((17))

Fundamental equation (17) has been formulated in terms of the method of two dividing surfaces alone. Here \({{\Gamma }_{{i(j)}}}\) is the total adsorption of component i relative to component j (the component chosen for the film) for both dividing surfaces, with the adsorption being numerically equal to the adsorption value that corresponds to the zero adsorption of component j, and term \({{\bar {S}}_{{(j)}}}\) is interpreted analogously. The value of \({{H}_{{(j)}}}\) should be especially discussed. The passage to relative adsorption and distance \({{H}_{{(j)}}}\) between the dividing surfaces also means the thermodynamic definition of the thin film thickness. Equation (17) leads to the following important relation [8, 9]:

$${{\left[ {\frac{{\partial ({{\sigma }^{\beta }} + {{\sigma }^{\gamma }})}}{{\partial {{H}_{{(j)}}}}}} \right]}_{{T,{{{\mu }}_{{i \ne j}}}}}} = - \Pi ,$$
((18))

which enables us to calculate the surface tensions of the thin film from the disjoining pressure isotherm.

Now, the comparison between the Gibbs methods with one and two dividing surfaces shows that, for the surface tension of a single dividing surface, which was considered in the previous section, we obtain the relation [8, 9]

$${{\sigma }^{{\alpha \gamma }}} = {{\sigma }^{\alpha }} + {{\sigma }^{\gamma }} + \Pi {{H}_{{(j)}}}.$$
((19))

The substitution of Eq. (19) into Eq. (17) yields

$$d{{\sigma }^{{\alpha \gamma }}} = - {{\bar {S}}_{{(j)}}}dT + {{H}_{{(j)}}}d\Pi - \sum\limits_{i \ne j} {{{\Gamma }_{{i(j)}}}d{{\mu }_{i}}} .$$
((20))

Equation (20) gives the expression

$${{\left( {\frac{{d{{\sigma }^{{\alpha \gamma }}}}}{{d\Pi }}} \right)}_{{T,{{{\mu }}_{{i \ne j}}}}}} = {{H}_{{(j)}}},$$
((21))

which obviously has something in common with Eq. (10). However, in contrast to Eq. (10), expression (21) is exact for undeformable solids and incompressible liquids.

Note that Eqs. (20) and (21) already include three dividing surfaces: one for the surface tension and two for film boundaries. The larger the number of dividing surfaces we used, the clearer and smarter the formulation of the thermodynamics of thin films became. It is interesting that thermodynamics itself presents the determination of the film thickness. According to Gibbs, this is associated with the passage to the relative adsorption values; however, this is the general procedure for the combined solution of the Gibbs adsorption equation and the Gibbs–Duhem equations for bulk phases. The matter is that these equations comprise the general chemical potentials, two of which may be excluded to determine the thin film thickness, which, similarly to the relative adsorption values, is invariant and does not depend on the positions of the dividing surfaces.

Looking at Eq. (21), the following useful remark may be made. Here, j is the number of namely the component that is excluded; hence, it cannot be fixed. It follows from the Gibbs–Duhem equation that, if the temperature and chemical potentials of a phase are fixed, the pressure of this phase is also unchangeable. If at least one chemical potential cannot be fixed, the pressure of a phase can be varied (provided that the component, the chemical potential of which is in question, is present in this phase). Now, it may be stated that, when component j is a substance present in a thin film, the disjoining pressure is attained in Eq. (21) via pressure \({{p}^{\beta }}\) in the mother phase of the film. If component j is, on the contrary, absent in the film and is present only in phase α, the disjoining pressure in Eq. (21) is attained via external pressure \({{p}^{\alpha }}.\)

GRAVITATIONAL-FIELD METHOD

To my surprise, I found that there also exists this method for deriving the Frumkin equation, albeit for the simplest case of a free film. It has been implemented in the section “Equilibrium of Films in the Gravitational Field” of monograph [1, p. 42–44]. To begin with, discouraging thermodynamic mistake should be noted. Let us cite the text: “… chemical potentials \({{\mu }_{i}}\) of all components satisfy the condition

$${{\mu }_{i}} + {{m}_{i}}gH = \operatorname{const} = {{C}_{i}},$$
((II.21))

where \({{m}_{i}}\) is the mass of an ith component, g is the gravitational acceleration, and \({{C}_{i}}\) is some constant. However, the Gibbs equation

$$d{{\sigma }_{{13}}} = - \sum {{{\Gamma }_{i}}d{{\mu }_{i}}} = gdH\sum {{{\Gamma }_{i}}{{m}_{i}}} ,$$
((II.22))

which is applicable to a film whose middle layers possess the properties of a bulk phase, shows that the difference between surface tensions \(d{{\sigma }_{{13}}}\) can compensate only for the weight of the film region that is contained in adsorbed surface layers.”

Let us elucidate this statement. There are chemical potentials and, in the presence of external fields, total chemical potentials. The terms in the left-hand side of Eq. (II.21) represent the total chemical potential in the presence of the gravitational field. Although the total chemical potential is commonly divided into parts, as is shown in Eq. (II.21) by the combination of the chemical and gravitational parts, only the total chemical potential as a whole has a physical meaning. Therefore, when passing to the case of fields, all chemical potentials in thermodynamic relations are replaced by the total chemical potentials. For example, in a system comprising electric fields, the chemical potentials are replaced by electrochemical potentials. It is incorrect to use only the chemical potential of charged particles. Analogously, the use of only the chemical potential of a substance occurring in the gravitational field is inadequate. It is obvious that, in the presence of the gravitational field, the Gibbs adsorption equation includes the total chemical potentials. The entire left-hand side of expression (II.21) should be substituted into it rather than only \({{\mu }_{i}},\) as has been done in (II.22). Relation (II.22) is erroneous, as is everything that follows from it (we have presented only a partial citation).

This blunder does not concern the derivation of the Frumkin equation, with this derivation being very simple in this case. Gibbs himself determined the effect of gravitation on the surface tension. His equation (614) has the following form [21, p. 280]

$$\frac{{d\sigma }}{{dz}} = g\Gamma ,$$

where z is the height (replaced by H in [1]). For a film, we should only replace σ by film tension \({{\sigma }_{0}}\) and Γ by the difference between the densities of the film ρ and the medium \({{\rho }_{1}}\) additionally multiplied by “effective” film thickness h:

$$\frac{{d{{\sigma }_{0}}}}{{dH}} \approx gh(\rho - {{\rho }_{1}}).$$
((II.27))

Concerning the disjoining pressure, the situation is still simpler. According to Eq. (1), it is determined as the pressure difference, while barometric equations are available for each pressure. This immediately yields the following:

$$\frac{{d\Pi (h)}}{{dH}} = (\rho - {{\rho }_{1}})g.$$
((II.33))

Relations (II.27) and (II.33) lead to the “known relation [8, 10, 22]” (the numbers of the cited works have been altered according to our list of references)

$$d\sigma (h) = hd\Pi (h),$$
((II.34))

which coincides with Frumkin equation (1). The following phrase was added to it as the sole comment: “Relation (II.34) is unconditionally correct for a one-component film [12]” (the reference number has been altered). Since the Frumkin equation itself is absent in [12] (it contains only reference [11]), and Frumkin tried to derive an equation namely for a one-component film, it may be concluded that, the unconditional character of the result obtained by Frumkin has been confirmed in [1]. It should be added to the aforementioned references that I failed to find the Frumkin equation in Shcherbakov’s work [22].

In completing the work, I say that I suffer from the fact that I had to criticize the remarkable scientists whose memory we cherish. I console myself with the fact that, for the famous and, moreover, great masters (leaders of world electrochemical and colloid science), accidental mistakes are of no significance. Nobody, even great experts, is immune to real mistakes as well. It may be said that the mistakes made by Lomonosov and Mendeleev have induced an discussion that will never end. Gibbs was considered to be error-free longer than anyone; however, communication [23] has put an end to this (now, it is the very time for the author to confess his own mistakes, which did indeed take place!). So, what shall we do? Let us take it to heart that correction of errors is the normal way in which sciences are. Neither do we correct others, nor others us, but rather the truth forces its way, because it is the truth.