INTRODUCTION

Of the two components of thermodynamics, i.e., heat and work, the latter is incomparably more complex and multifaceted for description; therefore, it may be said that a type of thermodynamics is primarily determined by the manner in which the work is calculated. Gibbs’ thermodynamics differs from previous methods in the fact that the work is calculated with the use of thermodynamic potentials, i.e., special thermodynamic functions having the dimensionality of energy, with the work being determined by variations in these functions under preset external conditions. In addition to the heat and work, Gibbs’ development of the chemical potential, which symbolizes the chemical component of thermodynamics, was a still larger step in this field. Thus, the chemical thermodynamics, within the framework of which we operate, was developed.

Initially, the thermodynamic potentials were formulated for homogeneous (one-phase) systems. They were, e.g., energy

$$U = TS - pV + \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} ,$$
((1))

free energy

$$F \equiv U - TS = - pV + \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} ,$$
((2))

grand thermodynamic potential

$$\Omega \equiv F - \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} = - pV,$$
((3))

and Gibbs free energy

$$G \equiv F + pV = \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} ,$$
((4))

where T is the temperature, S is the entropy, p is the external pressure, V is the volume, and \({{\mu }_{i}}\) and \({{N}_{i}}\) are the chemical potential and the number of molecules (or moles) of an ith component. Thermodynamic potentials (1)–(4) are most widely used in the thermodynamics of solutions.

We should also note hybrid thermodynamic potential

$$\tilde {\Omega } \equiv F - \sum\limits_i {{{\mu }_{i}}{{N}_{i}}} = - pV + \sum\limits_j {{{\mu }_{j}}{{N}_{j}}} ,$$
((5))

in which the summation over i is not extended to all components of a system.

Such a potential was, for the first time, introduced in the solid-state thermodynamics [1], where i and j denoted mobile and immobile components of a solid. However, the components may, in the general case, be divided into the i and j groups arbitrarily, and it is this manner in which hybrid potential (5) should be interpreted. Then, it may be stated that potential \(\tilde {\Omega }\) plays the role of the grand thermodynamic potential for the i-group components and the free energy for the j-group ones.

We have noted that, when passing to the grand thermodynamic potential, the sum comprising the chemical potentials is subtracted from the free energy, while, when passing to the Gibbs free energy, the term –pV is subtracted. What will be obtained if we subtract both of them? For an ordinary (nonhybrid) potential, we shall obtain zero and the sense will be lost. However, this concerns only a homogeneous system. Colloid science deals with complex heterogeneous systems comprising a number of phases, interfaces, and lines; therefore, the introduction of a new thermodynamic potential may appear to be useful. The author has realized this idea in [2, 3]. This new thermodynamic potential has not name yet; however, it has been denoted by character J (this is natural taking into account that energy E, enthalpy H, and thermodynamic potentials are, mainly, denoted by initial letters of the Roman alphabet). It may be referred to as the “J pоtential” for short.

Taking into account that a system may contain solid phases, the J potential under an arbitrary external load may be determined in the most general form as follows [2, 3]:

$$J \equiv \Omega - \oint\limits_{(A)} {({\mathbf{P}} \cdot {\mathbf{u}})dA} ,$$
((6))

where P is an external force (stress) applied to unit surface area of a system as a function of the position on the surface (A), u the local vector of surface displacement, and A is the surface area. The integration is performed throughout the system surface. If the system is surrounded by a fluid medium, and external pressure p is the only mechanical action, the determination of the J potential may be simplified to [3]

$$J \equiv \Omega + pV,$$
((7))

where V is the total volume of the system (proponents of rigor should be reminded that any thermodynamic potential is determined with an accuracy of a constant). According to Eq. (3), for a homogeneous system, definition (7) yields zero; however, we shall deal with complex systems. The J potential was somewhat approved in [3], where the derivations of the classical Neumann equation (for the mechanical surface tension) and Young equation (for the thermodynamic surface tension) were rather strikingly simplified.

In this communication, we would like to introduce the J potential into the thermodynamics of thin films. However, let us initially generalize the definition of the J potential (7) to the following form:

$$J \equiv \Omega + p{\kern 1pt} 'V,$$
((8))

where \(p{\kern 1pt} '\) is some chosen pressure. This may be a pressure external with respect to a heterogeneous system as a whole, a pressure in a phase of a heterogeneous system, or any other pressure. In version (8), the term “J potential” already means a number of potentials of certain types. Similarly to the passage to the Gibbs energy, in the classical approach, \(p{\kern 1pt} '\) is taken to be an external pressure \((p{\kern 1pt} ' = p).\) For short, we shall refer to this type of the J potential as “classical” (denoted as \({{J}_{\operatorname{c} }}),\) while all other types originating from Eq. (8) will be called “special” J potentials (denoted as \({{J}_{\operatorname{s} }}).\) Now, we may state that definition (7) introduced in [3] refers only to the classical J potential, while definition (8) refers to the special J potentials.

The thermodynamics of thin films is a relatively new scope of chemical thermodynamics. This scope goes beyond the limits of the Gibbs thermodynamics and was formulated in the mid-20th century [4–9] (see [10, 11] for a modern review). A thin film is distinguished by the existence of disjoining pressure [12]:

$$\Pi \equiv {{p}^{\alpha }} - {{p}^{\beta }},$$
((9))

where \({{p}^{\alpha }}\) is the external pressure applied to the film and \({{p}^{\beta }}\) is the pressure in equilibrium mother bulk phase β of the thin film. Being in contact with the film edge, phase β may be at equilibrium with the film; however, the real presence of this phase is not necessary (\({{p}^{\beta }}\) may be a pressure calculated for phase β at values of temperature and chemical potentials equal to those in the film). The discovery of the disjoining pressure and its subsequent study by Derjaguin’s school have been described in detail in monograph [13].

GENERAL RELATIONS FOR THE J POTENTIAL

Although solid substrates often appear in film theory, this is of no importance for thermodynamics. For simplicity, we shall deal with the thermodynamic formalism of liquid phases and use definition (8). Let us initially write an equation for the grand thermodynamic potential as applied to an arbitrary multiphase multicomponent system:

$$\Omega = - \sum\limits_k {{{p}^{k}}} {{V}^{k}} + \sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} ,$$
((10))

where k is the number of a phase with pressure \({{p}^{k}}\) and volume \({{V}^{k}},\)s is the number of a surface with surface tension \({{\sigma }^{s}}\) and area \({{A}^{s}}\), and t is the number of a line with line tension \({{\kappa }^{t}}\) and length \({{L}^{t}}.\) Now, let us write a differential fundamental equation for the grand thermodynamic potential. In the simplest case of a homogeneous system, the following is written for grand potential (3):

$$d\Omega = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - pdV.$$
((11))

However, we consider a complex heterogeneous system. In an equilibrium state, the temperatures and chemical potentials in all regions of a system are equal irrespective of its complexity. Therefore, the first two terms in the right-hand side of Eq. (11) always remain preserved. At the same time, the pressures may be different in different regions of the system; however, when a system is in an equilibrium state, a change in any thermodynamic potential due to work is possible only when the work of external forces is concerned. In this case, the third term in the right-hand side of Eq. (11) remains preserved, provided that parameter p denotes the external pressure. In addition, external forces may cause changes in the surface areas and line lengths (of course, those that reach system boundaries; surfaces and lines limited inside of the system may be beyond their number), so that corresponding terms are trivially added to the right-hand side of Eq. (11). As a result, differential fundamental equation (10) for the grand potential acquires the following form:

$$\begin{gathered} d\Omega = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - pdV \\ + \,\,\sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $$
((12))

To make the picture complete, let us, meantime, present the following fundamental equation for hybrid potential \(\tilde {\Omega }{\text{:}}\)

$$\begin{gathered} d\tilde {\Omega } = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + \sum\limits_j {{{\mu }_{j}}d} {{N}_{j}} \\ - \,\,pdV + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $$
((13))

Now, let us find the fundamental equations for the J potential. Using definition (8) and taking into account the obvious condition

$$V = \sum\limits_k {{{V}^{k}}} ,$$
((14))

we, from Eqs. (10) and (12), obtain

$$J = - \sum\limits_k {({{p}^{k}} - p{\kern 1pt} '){{V}^{k}}} + \sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} ,$$
((15))
$$\begin{gathered} dJ = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - (p - p{\kern 1pt} ')dV + Vdp{\kern 1pt} '\,\, \\ + \,\,\sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $$
((16))

Remember that the value of р in Eq. (16) is the external pressure. If \(p{\kern 1pt} '\) is also the external pressure (the case of the classical J potential), Eqs. (15) and (16) are transformed as follows:

$${{J}_{\operatorname{c} }} = - \sum\limits_k {({{p}^{k}} - p){{V}^{k}}} + \sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} ,$$
((17))
$$\begin{gathered} d{{J}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + Vdp \\ + \,\,\sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $$
((18))

Equation (18) may be simplified. For this purpose, using again Eq. (14), we add to and subtract from the right-hand side of Eq. (18) expression \(\sum\nolimits_k {{{V}^{k}}d{{p}^{k}}} \), while keeping in mind that, for each bulk phase, the Gibbs–Duhem equation,

$$ - {{S}^{k}}dT - \sum\limits_i {N_{i}^{k}d{{\mu }_{i}}} + {{V}^{k}}d{{p}^{k}} = 0,$$
((19))

is valid. This equation eliminates the components of the first two terms in the right-hand side of Eq. (18), with these components being relevant to the bulk phases. Then, Eq. (18) takes the following form:

$$\begin{gathered} d{{J}_{\operatorname{c} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} + \sum\limits_k {{{V}^{k}}d(p - {{p}^{k}})} \\ + \,\,\sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} , \\ \end{gathered} $$
((20))

where the bars denote excess values relevant to the surfaces and lines. It may be stated that Eq. (20) for the classical J potential “suggests itself” to be used in surface thermodynamics.

By analogy with Eq. (8), we may obtain the hybrid J potential via hybrid grand thermodynamic potential \(\tilde {\Omega }\) as

$$\tilde {J} \equiv \tilde {\Omega } + p{\kern 1pt} 'V$$
((21))

and write the following fundamental equations:

$$\begin{gathered} \tilde {J} = \sum\limits_j {{{\mu }_{j}}} {{N}_{j}} - \sum\limits_k {({{p}^{k}} - p{\kern 1pt} '){{V}^{k}}} \\ + \,\,\sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} , \\ \end{gathered} $$
((22))
$$\begin{gathered} d\tilde {J} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + \sum\limits_j {{{\mu }_{j}}d} {{N}_{j}} \\ - \,\,(p - p{\kern 1pt} ')dV + Vdp{\kern 1pt} '\, + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $$
((23))

Here, we may also distinguish between the classical hybrid J potential (at \(p{\kern 1pt} ' = p\)) and special hybrid J potentials. For the classical hybrid J potential, fundamental equations (22) and (23) are simplified to the following form:

$$\begin{gathered} {{{\tilde {J}}}_{\operatorname{c} }} = \sum\limits_j {{{\mu }_{j}}} {{N}_{j}} - \sum\limits_k {({{p}^{k}} - p){{V}^{k}}} \\ + \,\,\sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} , \\ \end{gathered} $$
((24))
$$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + \sum\limits_j {{{\mu }_{j}}d{{N}_{j}}} \\ + \,\,Vdp + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $$
((25))

For each special hybrid J potential, Eqs. (22) and (23) are transformed in accordance with the selection of pressure \(p{\kern 1pt} '.\)

CLASSICAL J POTENTIAL OF A SYSTEM COMPRISING A THIN FILM

Assume that the thin film is located between phases α and γ (denotation β will be saved for the mother phase of the film). Both the αγ interface and the thin film at it are assumed to be planar. Let us see how the classical J potential looks for such an object in different approaches.

Standard Gibbs’ Approach

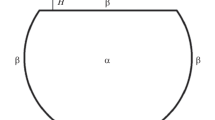
In Gibbs’ thermodynamics, a thin film is not distinguished as a separate object and is considered as any other part of an interface. For an α–γ two-phase system containing a thin film (Fig. 1), the J potential is formulated according to Eq. (17) as follows. Superscript k acquires the meanings of α and γ. Therewith, \({{p}^{\alpha }} = {{p}^{\gamma }},\) because the only surface present in the system is planar. It is obvious that, in this case, \({{p}^{\alpha }}\) plays the role of an external pressure and, hence, is equal to р; then, the first term in the right-hand side of Eq. (17) vanishes. Lines are absent in our system and a single surface is present; hence, according to Eq. (17), we may write

$${{J}_{\operatorname{c} }} = {{\sigma }^{{\alpha \gamma }}}{{A}^{{\alpha \gamma }}},$$
((26))

or (since the areas of the parallel dividing surfaced are equal, the index of the area may be omitted)

$${{j}_{\operatorname{c} }} \equiv {{{{J}_{\operatorname{c} }}} \mathord{\left/ {\vphantom {{{{J}_{\operatorname{c} }}} A}} \right. \kern-0em} A} = {{\sigma }^{{\alpha \gamma }}},$$
((27))

where \({{j}_{\operatorname{c} }}\) is the surface density of the classical J potential.

Fig. 1.
figure 1

Phases, dividing surface, and surface tension in the Gibbs method.

Full size image

On the other hand, according to Eq. (20),

$$d{{J}_{\operatorname{c} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} + {{\sigma }^{{\alpha \gamma }}}dA.$$
((28))

Equations (26) and (28) immediately yield the Gibbs adsorption equation

$$Ad{{\sigma }^{{\alpha \gamma }}} = - {{\bar {S}}^{{\alpha \gamma }}}dT - \sum\limits_i {\bar {N}_{i}^{{\alpha \gamma }}d{{\mu }_{i}}} $$
((29))

or

$$d{{\sigma }^{{\alpha \gamma }}} = - {{\bar {s}}^{{\alpha \gamma }}}dT - \sum\limits_i {\Gamma _{i}^{{\alpha \gamma }}d{{\mu }_{i}}} ,$$
((30))

where \(\bar {s} \equiv {{\bar {S}} \mathord{\left/ {\vphantom {{\bar {S}} A}} \right. \kern-0em} A}\) is the excess entropy per unit surface area and \({{\Gamma }_{i}} \equiv {{{{{\bar {N}}}_{i}}} \mathord{\left/ {\vphantom {{{{{\bar {N}}}_{i}}} A}} \right. \kern-0em} A}\) is the absolute adsorption of component i. Since excess values depend on the chosen position of a dividing surface, Eq. (29) is considered in combination with Gibbs–Duhem equation (19) for the phases adjacent to the surface. By excluding one of chemical potentials \({{\mu }_{j}}\), coefficients at dT and \(d{{\mu }_{i}}\) are transformed into combinations of values that are invariant with respect to displacements of the dividing surface and are denoted as \({{s}_{{(j)}}}\) and \({{\Gamma }_{{i(j)}}}\), respectively. Parameter \({{\Gamma }_{{i(j)}}}\) is referred to as the “relative adsorption” of component i (relative to component j) and does not depend on the position of the dividing surface. Numerically, \({{\Gamma }_{{i(j)}}}\) is equal to \({{\Gamma }_{i}}\) for a position of the dividing surface in which the condition \({{\Gamma }_{j}} = 0\) is fulfilled. The passage from the absolute to relative adsorption values is a very simple operation in Gibbs’ thermodynamics of surfaces. This is a way to transform Gibbs adsorption equation (30) into the real physical relation

$$d{{\sigma }^{{\alpha \gamma }}} = - \bar {s}_{{(j)}}^{{\alpha \gamma }}dT - \sum\limits_i {\Gamma _{{i(j)}}^{{\alpha \gamma }}d{{\mu }_{i}}} ,$$
((31))

which is also called “Gibbs’ adsorption equation.” No relation with a thin film is seen in Eqs. (26) and (28), but it is hidden in the value of \({{\sigma }^{{\alpha \gamma }}}.\) For example, some terms of the Gibbs adsorption equation for \({{\sigma }^{{\alpha \gamma }}}\) may be relevant to the components of the thin film.

Gibbs Method with Two Dividing Surfaces

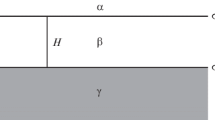
To transform a thin film into an explicit object of an interface, it is necessary to introduce two dividing surfaces [8–10]. This approach follows from the idea of the existence of a third bulk phase (mother phase β of the film), the thinning of which has resulted in the formation of the thin film. A real or imaginary phase β must be at equilibrium with the thin film (i.e., it must have the same values of temperature and chemical potentials). Hence, it is clear that definition (9) of disjoining pressure has a thermodynamic character, although it comprises mechanical parameters. Now the Gibbs excesses are determined as follows. The space between two parallel interfaces is mentally filled with phase β, thereby passing to a three-phase system with interfaces αβ and βγ (Fig. 2). For the αβ interface, the excesses are taken from the sides of phases α and β, while they are taken from the sides of phases β and γ for the βγ interface. It is essential that, in the case of a thin film, excesses (of, e.g., adsorption) on both sides of phase β are not independent and must be considered jointly. This also concerns, in particular, surface tensions \({{\sigma }^{\alpha }}\) (between phases α and β) and \({{\sigma }^{\gamma }}\) (between phases γ and β) presented in Fig. 2.

Fig. 2.
figure 2

Arrangement of phases and the surface tensions in the method of two dividing surfaces located at distance H from one another.

Full size image

Now, let us formulate an expression for the J potential in accordance with Eq. (17). Obviously, it is of no significance which phase (α or γ) is considered to be external, because they both have the same pressure \({{p}^{\alpha }},\) which is external pressure p. In this case, the awkward terms for phases α and γ in Eq. (17) disappear and only one term relevant to phase β remains preserved. On the contrary, two surface-related terms remain, because we now have two dividing surfaces. As a result, we, from Eq. (17), obtain

$${{J}_{\operatorname{c} }} = - ({{p}^{\beta }} - {{p}^{\alpha }}){{V}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A$$
((32))

or, after disjoining pressure (9) is introduced,

$${{J}_{\operatorname{c} }} = \Pi {{V}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A.$$
((33))

Equation (33) yields the following expression for the surface density of the J potential:

$${{j}_{\operatorname{c} }} = \Pi H + {{\sigma }^{\alpha }} + {{\sigma }^{\gamma }},$$
((34))

where \(H \equiv {{{{V}^{\beta }}} \mathord{\left/ {\vphantom {{{{V}^{\beta }}} A}} \right. \kern-0em} A}\) is the distance between the dividing surfaces, which, after corresponding refinements, may be taken to be the thin film thickness.

The comparison between Eqs. (26) and (34) leads to relation

$${{\sigma }^{{\alpha \gamma }}} = {{\sigma }^{\alpha }} + {{\sigma }^{\gamma }} + \Pi H,$$
((35))

which has been known in the thermodynamics of thin films since the publication of [4–8] and was obtained there in another way. At \(H \to \infty \), the disjoining pressure more rapidly tends to zero, thereby leading product \(\Pi H\) to zero. Thus, the right-hand sides of Eqs. (34) and (35) are transformed into the sum of now independent surface tensions \({{\sigma }^{{\alpha \beta }}}\) and \({{\sigma }^{{\beta \gamma }}},\) while the thin film is transformed into a thick one. Let us express this important result as follows:

$${{\left. {{{j}_{\operatorname{c} }}} \right|}_{{H \to \infty }}} = {{\left. {{{\sigma }^{{\alpha \gamma }}}} \right|}_{{H \to \infty }}} = {{\sigma }^{{\alpha \beta }}} + {{\sigma }^{{\beta \gamma }}}.$$
((36))

Now, let us consider the differential fundamental equation for the classical J potential. Once more, assuming that \(p \equiv {{p}^{\alpha }}\) and taking into account the existence of two surfaces and the absence of lines, we, from Eq. (20), find

$$\begin{gathered} d{{J}_{\operatorname{c} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} \\ + \,\,{{V}^{\beta }}d({{p}^{\alpha }} - {{p}^{\beta }}) + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA \\ \end{gathered} $$
((37))

or, with allowance for definition of disjoining pressure (9),

$$d{{J}_{\operatorname{c} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} + {{V}^{\beta }}d\Pi + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA.$$
((38))

Now, comparing Eqs. (33) and (38), we derive the Gibbs adsorption equation in the following form:

$$Ad({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }}) = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} - \Pi d{{V}^{\beta }},$$
((39))

where \(\bar {S} \equiv {{\bar {S}}^{\alpha }} + {{\bar {S}}^{\gamma }}\) and \({{\bar {N}}_{i}} \equiv \bar {N}_{i}^{\alpha } + \bar {N}_{i}^{\gamma }.\) After dividing by А, Eq. (39) is transformed as follows [10]:

$$d({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }}) = - \bar {s}dT - \sum\limits_i {{{\Gamma }_{i}}d{{\mu }_{i}}} - \Pi dH,$$
((40))

or, using Eq. (35) [11], we obtain

$$d{{\sigma }^{{\alpha \gamma }}} = - \bar {s}dT - \sum\limits_i {{{\Gamma }_{i}}d{{\mu }_{i}}} + Hd\Pi .$$
((41))

After the standard passage from the absolute to relative adsorption values, Eqs. (40) and (41) acquire the following form [10, 11]:

$$d({{\sigma }^{\beta }} + {{\sigma }^{\gamma }}) = - {{\bar {s}}_{{(j)}}}dT - \Pi d{{H}_{{(j)}}} - \sum\limits_{i \ne j} {{{\Gamma }_{{i(j)}}}d{{\mu }_{i}}} ,$$
((42))
$$d{{\sigma }^{{\alpha \gamma }}} = - {{\bar {s}}_{{(j)}}}dT - \sum\limits_i {{{\Gamma }_{{i(j)}}}d{{\mu }_{i}}} + {{H}_{{(j)}}}d\Pi .$$
((43))

The meaning of the values entering into Eqs. (42) and (43) was discussed in detail in [10], including \({{H}_{{(j)}}}\) as the thermodynamic definition of the thickness of a thin film, with this definition being related to the passage to relative adsorption and the pattern of the surface with zero adsorption.

HYBRID CLASSICAL J POTENTIAL

Now, let us consider the use of the classical J potential in the hybrid form. The general notation that we used above does not exclude the possibility of penetration of all system components into all phases, and this is the most complex case for the identification of a thin film. However, as a matter of fact, there is no film in this case, but there is a surface layer, i.e., a transition interfacial zone. The term “film” implies a certain segregation of a substance. The simplest case is represented by phases α and γ that are insoluble in everything and dissolve nothing; i.e., they are absolutely indifferent with respect to other substances in the system. Such substrates are incapable of penetration and have distinct boundary surfaces, the distance between which specifies the thickness of the thin film. These substrates may be formally considered to be one-component. Let the components of phases α and γ have numbers m and n, respectively. As in the previous section, let us determine the pattern of the fundamental equations for the hybrid classical potential in the cases of one and two dividing surfaces.

One Dividing Surface

In this case, we, from Eqs. (24) and (25), have

$${{\tilde {J}}_{{\text{c}}}} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma } + {{\sigma }^{{\alpha \gamma }}}A,$$
((44))
$$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } \\ + \,\,{{\mu }_{n}}dN_{n}^{\gamma } + Vd{{p}^{\alpha }} + {{\sigma }^{{\alpha \gamma }}}dA, \\ \end{gathered} $$
((45))

where the only residual term with the summation symbol obviously refers to the components of the thin film. The differentiation of Eq. (44) and comparison with Eq. (45) yields the relation

$$\begin{gathered} Ad{{\sigma }^{{\alpha \gamma }}} = - SdT + Vd{{p}^{\alpha }} - N_{m}^{\alpha }d{{\mu }_{m}} \\ - \,\,N_{n}^{\gamma }d{{\mu }_{n}} - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} , \\ \end{gathered} $$
((46))

which is an analog of the Gibbs adsorption equation for a surface layer with a finite thickness [8] (it must be \({{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }};\) however, since \({{p}^{\alpha }} = {{p}^{\gamma }}\) and, at one dividing surface, \(V = {{V}^{\alpha }} + {{V}^{\gamma }},\) this is \(Vd{{p}^{\alpha }}\)).

Phases α and γ obey the Gibbs–Duhem equations

$$\begin{gathered} {{V}^{\alpha }}d{{p}^{\alpha }} = {{S}^{\alpha }}dT + N_{m}^{\alpha }d{{\mu }_{m}}, \\ {{V}^{\gamma }}d{{p}^{\gamma }} = {{S}^{\gamma }}dT + N_{n}^{\gamma }d{{\mu }_{n}}, \\ \end{gathered} $$
((47))

allowance for which leads to the mutual cancellation of all terms for both bulk phases in (46). This transforms Eq. (46) into the Gibbs adsorption equation

$$Ad{{\sigma }^{{\alpha \gamma }}} = - \bar {S}dT - \bar {N}_{m}^{\alpha }d{{\mu }_{m}} - \bar {N}_{n}^{\gamma }d{{\mu }_{n}} - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} ,$$
((48))

where the bar denotes an excess generated at a given dividing surface relative to phases α and γ. The last term has remained unchanged; however, this does not mean that we have not passed to excesses. The issue at hand is that thin film components denoted by subscript i are absent in both phases α and γ; therefore, their real amounts \({{N}_{i}}\) simultaneously represent the excesses with respect to these phases.

Two Dividing Surfaces

For this case (see Fig. 2), the same Eqs. (24) and (25) yield

$${{\tilde {J}}_{\operatorname{c} }} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma } + \Pi {{V}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A,$$
((49))
$$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } \\ + \,\,{{\mu }_{n}}dN_{n}^{\gamma } + Vd{{p}^{\alpha }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $$
((50))

Using definition (9), condition (14), and equality \({{p}^{\alpha }} = {{p}^{\gamma }},\) we obtain

$$Vd{{p}^{\alpha }} = {{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }} + {{V}^{\beta }}d{{p}^{\beta }} + {{V}^{\beta }}d\Pi ,$$
((51))

and, then, Eq. (50) acquires the form

$$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{c} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } + {{\mu }_{n}}dN_{n}^{\gamma } \\ + \,\,{{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }} + {{V}^{\beta }}d{{p}^{\beta }} \\ + \,\,{{V}^{\beta }}d\Pi + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $$
((52))

Now, the differentiation of Eq. (49) and comparison with (52) lead to the equation

$$\begin{gathered} Ad({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }}) = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} \\ - \,\,N_{m}^{\alpha }d{{\mu }_{m}} - N_{n}^{\gamma }d{{\mu }_{n}} - \Pi d{{V}^{\beta }}, \\ \end{gathered} $$
((53))

which represents an analog of the Gibbs adsorption equation for a finite-thickness surface layer when two dividing surfaces are used. When simplifying Eq. (53) with the use of the Gibbs–Duhem equations, it should be kept in mind that Eqs. (48) are supplemented with their analogs for phase β:

$${{V}^{\beta }}d{{p}^{\beta }} = {{S}^{\beta }}dT + \sum\limits_i {N_{i}^{\beta }d{{\mu }_{i}}} .$$
((54))

Taking into account Eqs. (48) and (54), Eq. (53) is transformed as follows:

$$\begin{gathered} Ad({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }}) = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} \\ - \,\,\bar {N}_{m}^{\alpha }d{{\mu }_{m}} - \bar {N}_{n}^{\gamma }d{{\mu }_{n}} - \Pi d{{V}^{\beta }}. \\ \end{gathered} $$
((55))

Remember that, in the method of two dividing surfaces, the excesses are taken not only from the sides of phases α and γ, as in the previous example, but also from the side of phase β. As a consequence, instead of \({{N}_{i}}\), excess values \({{\bar {N}}_{i}}\) have appeared in Eq. (55). Equation (55) itself in fact coincides with Eq. (39), where subscript i refers to all phases. Therefore, everything that applied to Eq. (39) is applicable to Eq. (55). Equation (48) occurs in an analogous situation, and, to avoid repetition, the discussion of Eqs. (48) and (55) in this context may be ended.

SPECIAL J POTENTIAL OF A THIN FILM

Let us return to fundamental equations (15) and (16) and take \(p{\kern 1pt} ' = {{p}^{\beta }}.\) Since \({{p}^{\beta }}\) is the pressure in the mother phase of a thin film, this choice is distinguished by the fact it may refer only to the case in which a thin film exists. When addressing to Figs. 1 and 2, we shall, as before, consider \({{p}^{\alpha }}\) to be an external pressure \((p = {{p}^{\alpha }} = {{p}^{\gamma }}).\) Accordingly, we rewrite Eqs. (15) and (16) as follows:

$${{J}_{\operatorname{s} }} = - \sum\limits_k {({{p}^{k}} - {{p}^{\beta }}){{V}^{k}}} + \sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} ,$$
((56))
$$\begin{gathered} d{{J}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - ({{p}^{\alpha }} - {{p}^{\beta }})dV \\ + \,\,Vd{{p}^{\beta }} + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $$
((57))

Let us determine the pattern of Eqs. (56) and (57) in approaches with different dividing surfaces.

One Dividing Surface

It is seen in Fig. 1 that there are only two phases (α and γ) in this case, and the use of the pressure in a third phase may seem to be strange. However, as we have mentioned above, phase β may be imaginary. Let us, nevertheless, see what we shall have as a result. Taking into account definition (9) and the absence of lines, Eqs. (56) and (57) acquire the form

$${{J}_{\operatorname{s} }} = - \Pi V + {{\sigma }^{{\alpha \gamma }}}A,$$
((58))
$$d{{J}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - \Pi dV + Vd{{p}^{\beta }} + {{\sigma }^{{\alpha \gamma }}}dA$$
((59))

(remember that, in this approach, \(V = {{V}^{\alpha }} + {{V}^{\gamma }}\)). Having added and subtracted \(Vd{{p}^{\alpha }}\) in the right-hand side of Eq. (59) and using Gibbs–Duhem equation (47), Eq. (59) is simplified to

$$d{{J}_{\operatorname{s} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} - d(\Pi V) + {{\sigma }^{{\alpha \gamma }}}dA.$$
((60))

Now, differentiating Eq. (58) and comparing with Eq. (60), we, as might be expected, arrive at Gibbs adsorption equation (29). This indicates that the formulation of this approach is physically valid.

Two Dividing Surfaces

Now, we have two surfaces and three bulk phases (Fig. 2). Therefore, Eqs. (56) and (57) are written in the following form:

$${{J}_{\operatorname{s} }} = - \Pi ({{V}^{\alpha }} + {{V}^{\gamma }}) + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A,$$
((61))
$$\begin{gathered} d{{J}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - \Pi dV \\ + \,\,Vd{{p}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA, \\ \end{gathered} $$
((62))

where \(V = {{V}^{\alpha }} + {{V}^{\gamma }} + {{V}^{\beta }}.\) Taking into account this relation and definition (9), Eq. (62) may be represented as

$$\begin{gathered} d{{J}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} - \Pi d{{V}^{\beta }} \\ - \,\,d[\Pi ({{V}^{\alpha }} + {{V}^{\gamma }})] + {{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }} \\ + \,\,{{V}^{\beta }}d{{p}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $$
((63))

Now, using Gibbs–Duhem equations (47) and (54), we reduce Eq. (63) to

$$\begin{gathered} d{{J}_{\operatorname{s} }} = - \bar {S}dT - \sum\limits_i {{{{\bar {N}}}_{i}}d{{\mu }_{i}}} - \Pi d{{V}^{\beta }} \\ - \,\,d[\Pi ({{V}^{\alpha }} + {{V}^{\gamma }})] + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $$
((64))

Finally, differentiating Eq. (61) and comparing it with Eq. (64), we obtain the above-considered variant of Gibbs adsorption equation (39), which enables us to interrupt the discussion of this approach.

HYBRID SPECIAL J POTENTIAL OF A THIN FILM

Let us return to general fundamental equations (22) and (23) for the hybrid J potential and apply them to the hybrid special J potential at \(p = {{p}^{\alpha }} = {{p}^{\gamma }}\) and \(p{\kern 1pt} ' = {{p}^{\beta }}{\text{:}}\)

$$\begin{gathered} {{{\tilde {J}}}_{\operatorname{s} }} = \sum\limits_j {{{\mu }_{j}}} {{N}_{j}} - \sum\limits_k {({{p}^{k}} - {{p}^{\beta }}){{V}^{k}}} \\ + \,\,\sum\limits_s {{{\sigma }^{s}}{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}{{L}^{t}}} , \\ \end{gathered} $$
((65))
$$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + \sum\limits_j {{{\mu }_{j}}d} {{N}_{j}} \\ - \,\,\Pi dV + Vd{{p}^{\beta }} + \sum\limits_s {{{\sigma }^{s}}d{{A}^{s}}} + \sum\limits_t {{{\kappa }^{t}}d{{L}^{t}}} . \\ \end{gathered} $$
((66))

As in the case of the hybrid classical J potential, we use as an illustrative example

$$\sum\limits_j {{{\mu }_{j}}{{N}_{j}}} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma },$$
((67))

when phases α and γ are insoluble, impermeable, and formally one-component. Now, let us monitor the transformations of Eqs. (65) and (66) that occur in the approaches with one and two dividing surfaces.

One Dividing Surface

Taking into account definition (9), condition (67), and the existence of only two phases (\(V = {{V}^{\alpha }} + {{V}^{\gamma }}),\) we have

$${{\tilde {J}}_{\operatorname{s} }} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma } - \Pi V + {{\sigma }^{{\alpha \gamma }}}A,$$
((68))
$$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } + {{\mu }_{n}}dN_{n}^{\gamma } \\ - \,\,\Pi dV + Vd{{p}^{\beta }} + {{\sigma }^{{\alpha \gamma }}}dA. \\ \end{gathered} $$
((69))

It is convenient to transform Eq. (69) by adding and subtracting \(Vd{{p}^{\alpha }}\) in the right-hand side and using definition of disjoining pressure (9):

$$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } + {{\mu }_{n}}dN_{n}^{\gamma } \\ - \,\,d(\Pi V) + Vd{{p}^{\alpha }} + {{\sigma }^{{\alpha \gamma }}}dA. \\ \end{gathered} $$
((70))

Now, differentiating Eq. (68) and comparing it with (70), we arrive at an analog of the Gibbs adsorption equation for a finite-thickness surface layer [8] written above as Eq. (46). Subsequent manipulations involving the Gibbs–Duhem equations transform Eq. (46) into the traditional Gibbs adsorption equation.

Two Dividing Surfaces

In this case (\(V = {{V}^{\alpha }} + {{V}^{\gamma }} + {{V}^{\beta }}\)), Eqs. (65) and (66) acquire the form

$${{\tilde {J}}_{\operatorname{s} }} = {{\mu }_{m}}N_{m}^{\alpha } + {{\mu }_{n}}N_{n}^{\gamma } - \Pi ({{V}^{\alpha }} + {{V}^{\gamma }}) + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})A,$$
((71))
$$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } + {{\mu }_{n}}dN_{n}^{\gamma } \\ - \,\,\Pi dV + Vd{{p}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $$
((72))

Similarly to the passage from (62) to (63), Eq. (72) may be written as follows:

$$\begin{gathered} d{{{\tilde {J}}}_{\operatorname{s} }} = - SdT - \sum\limits_i {{{N}_{i}}d{{\mu }_{i}}} + {{\mu }_{m}}dN_{m}^{\alpha } + {{\mu }_{n}}dN_{n}^{\gamma } \\ - \,\,\Pi d{{V}^{\beta }} - d[\Pi ({{V}^{\alpha }} + {{V}^{\gamma }})] + {{V}^{\alpha }}d{{p}^{\alpha }} + {{V}^{\gamma }}d{{p}^{\gamma }} \\ + \,\,{{V}^{\beta }}d{{p}^{\beta }} + ({{\sigma }^{\alpha }} + {{\sigma }^{\gamma }})dA. \\ \end{gathered} $$
((73))

Now, differentiating Eqs. (71) and comparing them with (73), we again arrive at Eq. (53) as an analog of the Gibbs adsorption equation for the interfacial region containing a thin film. All subsequent operations are the same as those performed for Eq. (53), and they are omitted here.

CONCLUSIONS

This work has acquainted readers with the contemporary apparatus of chemical thermodynamics, including the J potential, which symbolizes a number of thermodynamic potentials. It is known that the physical result must not depend on the choice of a thermodynamic potential. In this work, we have repeatedly illustrated this fact by the example of the Gibbs adsorption equation. In our case, this was of additional importance from the point of view of verifying the adequacy of the formulation of the new thermodynamic potential. The usefulness of the latter is determined by the convenience of its use and the external conditions under which it manifests itself. The J potential is convenient for use in colloid science, because, being not an excess value itself, it comprises the Gibbs excesses of the thermodynamic parameters with respect to surfaces and lines.

Of course, the represented set of the J potentials is not exhaustive. We have focused our attention on heterogeneous systems comprising thin films, but confined ourselves to the case of planar films. However, within this framework, the question arises as to the reason for which the J potential was not formulated implying the value of \({{p}^{\beta }}\) to be the external pressure. In reality, there are systems in which the external phase is represented by a mother phase of a thin film (e.g., that surrounding a wall-adherent bubble with a wetting film [14]). The answer is as follows. Since we have begun to search for the J potential from the grand thermodynamic potential, the spatial region (which determines the volume) of a system may be outlined on the basis of considerations of convenience. For example, the system boundaries may be chosen in a manner such that the external phase would be represented by phase α (or γ), as is shown in Figs. 1 and 2. Then, \({{p}^{\alpha }}\) will always be the external pressure.