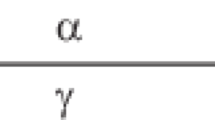Thin Films of Quantum Fluids: History, Phase Transitions, and Wetting

Abstract

Thin films of quantum fluids, i.e., ⁴He, ³He, and H₂, have played an important role in understanding the phenomenology of quantum fluids and the role of spatial dimension on the development of long-range order in condensed matter. Standard experimental probes used to study these systems include heat capacity measurements, torsional oscillators, third sound, quartz crystal microbalances, and x-ray and neutron scattering. We describe the historical development of important models and experiments in quantum films which underpin our understanding of superfluid onset in helium, phases, and phase transitions in adsorbed films, and wetting and growth of bulk phases.

1 Early Work and Background

The first quantum fluid that was seriously investigated was ⁴He. Researchers in the 1920s and 1930s measured the thermodynamic properties of bulk ⁴He such as the heat capacity and latent heat and determined that the liquid behaved quite differently above and below $T_{\lambda }=2.17$ K. The high temperature state of the liquid was called He I, and the low temperature state was called He II. The first transport measurements were carried out in the late 1930s by Kapitza [1] and by Allen and Meisner [2]. Kapitza showed that the viscosity below $T_{\lambda }$ was remarkably low, and coined the word “superfluid” and suggested an analogy to superconductors, which had been discovered many years earlier. Allen and Meisner were the first to demonstrate that the hydrodynamics was not classical so the viscosity could not be defined. The history of this era is described in [3, 4]. Even in the early days, the behavior of thin films of helium was of great interest [5, 6]. An experiment first carried out in 1939 [6] and repeated many times since then involves a beaker partially filled with liquid helium suspended over a bath. When the helium is in the normal state, the level of fluid in the beaker remains constant for hours. Below $T_{\lambda }$, the liquid in the beaker drains into the bath via a superfluid film of microscopic thickness and provides a particularly simple and dramatic illustration of superfluidity in thin films. Explaining this phenomenon requires understanding the reason the film (either superfluid or normal) forms on the walls of the container and the difference between the super fluid and normal fluid dynamics.

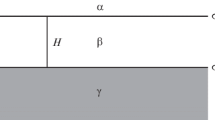
Thin adsorbed films form when a vapor is in diffusive contact with a (typically solid) substrate. All molecules have a long-range attractive force due to an induced dipole–dipole interaction whose strength is related to the product of the polarizability of the molecules. A low polarizability atom like helium can reduce its potential energy by being in close proximity to a dense polarizable material typical of most solid substrates. This attractive interaction is the zeroth-order reason that a film of helium coats the walls of the beaker in Fig. 1. A more detailed analysis requires minimizing the free energy of the system. Because the bulk liquid, vapor, and the adsorbed film are all in diffusive contact, the fundamental rule that determines the equilibrium thickness d of the film is the requirement that the chemical potential of the vapor $\mu _{{\rm v}} (P,T)$ is equal to the chemical potential of the film of thickness d, $\mu _{{\rm f}} (P,T,d)$. Calculating the chemical potential of the vapor, particularly in the ideal gas limit, is an elementary result of statistical mechanics; for ⁴He, the result is

$$ \mu _4= k\, T\, \log \left( \frac{{(2 \pi )}^{3/2} \hbar ^3 P}{ m^{3/2} {(k\,T)}^{5/2}}\right) $$

(1)

Fig. 1

Beaker of superfluid suspended over a bath of superfluid. A film forms on the walls of the beaker and flows up and over the lip and eventually empties the beaker. From [6]

Calculating the chemical potential of the film for arbitrary d is a subtle and complex problem, but in the limit $d\rightarrow \infty$, the film becomes indistinguishable from the bulk phase, in which case we have $\mu _{{\rm v}}(P_{{\rm sat}}(T),T)=\mu _{{\rm bulk}}(P_{{\rm sat}}(T),T)$ which defines the saturated vapor pressure of the bulk phase as a function of T. For pressures below $P_{{\rm sat}}(T)$, the bulk liquid phase cannot stably exist, but a film of finite thickness can be stabilized in the attractive potential V(z) generated by the substrate, where z is the distance normal to the substrate. Calculating V(z) in general is also a very complicated problem [7, 8], but for simple atoms and molecules and in a restricted range of 1 nm < z < 50 nm, V(z) is dominated by van der Waals-type forces with $V(z)=-\frac{C_3}{z^3}$, where $C_3$ measures the strength of the long-range attractive potential. This form of the potential is the first term of an asymptotic series which contains higher inverse powers of d. The form of the potential has been experimentally verified in detail for helium [9].

A naive, simple, but nevertheless useful thermodynamic description of the film is to assume that the film has the same properties as the bulk condensed phase with a correction for the surface potential:

$$ \mu _{{\rm v}}(P,T) = \mu _{{\rm bulk}}(P_{{\rm sat}},T)-\frac{C_3}{d^3} $$

(2)

Because the chemical potential is logarithmic in P, the film thickness is given by

$$ d=\left( \frac{-C_3}{\ln (P/P_{{\rm sat}})}\right) ^{1/3} $$

(3)

This relationship between d and P is sometimes called the Frenkel–Halsey–Hill isotherm. In a container on Earth, the pressure in a fluid is not uniform, but rather varies as $\rho g h$, where h is the height above some reference level. Due to this hydrostatic head effect, the pressure near the top of the beaker in Fig. 1 is slightly lower than the saturated vapor pressure. Inserting this pressure variation into Eq. 3 implies that the film thickness will also vary with height. In practice, the film is a few microns thick near the bulk liquid level in the beaker and a few nanometers thick near the top of the beaker. The expression for d in Eq. 3 makes no reference to the superfluid or normal nature of the film, so superfluidity does not affect the equilibrium film thickness. The dramatic difference in the behavior of superfluid films is due to the kinetics and transport properties of the superfluid, not the equilibrium properties. The beaker shown in Fig. 1 is not strictly in equilibrium because the gravitational potential of the system would be reduced if the contents flowed into the bath.

The standard phenomenological description of superfluids is known as the two-fluid model [10]. This theoretical description of superfluids was developed within a few years of the experimental discovery of superfluidity and arose from a creative competition between Tiza and Landau [11]. In this model, the mass density of the fluid $\rho$ is divided into a normal part with density $\rho _{{\rm n}}$ and a superfluid part with density $\rho _{{\rm s}}$, where $\rho =\rho _{{\rm s}}+\rho _{{\rm n}}$. The superfluid fraction $\rho _{{\rm s}}/\rho _{{\rm n}}$ is zero above $T_\lambda$ but increases continuously but rapidly below $T_\lambda$ and reaches approximately 0.9 at T = 1.4 K. This continuous increase in the order parameter is the hallmark of a second-order phase transition. The two fluids are regarded as interpenetrating, each described by an independent velocity $v_{{\rm s}}$ and $v_{{\rm n}}$. The normal component obeys a Navier–Stokes equation with an effective viscosity and no-slip boundary conditions at a solid wall; in most situations, thin films of normal fluid can be regarded as viscously clamped to the substrate. The superfluid component obeys an inviscid Euler equation with perfect slip boundary conditions. A superfluid will respond to a chemical potential gradient by accelerating up to a velocity known as the critical velocity, where the flow becomes unstable to formation of vortices (see Sect. 4); typical critical velocities are of the order 10 cm/s. Because of the no-slip boundary condition, it can maintain this velocity even a fraction of a nanometer away from the substrate. Although the chemical potential gradient due to the hydrostatic pressure head in the beaker experiment is very small, it will drive superflow in the adsorbed film at the critical velocity  [12]. The superflow removes mass from the beaker, but not entropy, so then entropy per unit mass increases which generates a temperature gradient. It is this complex nonequilibrium flow that accounts for the phenomena illustrated in Fig. 1.

Once a film becomes very thin, one might reasonably expect it to behave as a two-dimensional material. A paradox which influenced early work is that elementary arguments suggest that phases, and therefore phase transitions, cannot exist in 2D. For example, a standard homework problem in statistical mechanics requires one to show that although Bose condensation of an ideal gas in 3D occurs at a temperature remarkably (and somewhat serendipitously) close to $T_{\lambda }$, Bose condensation does not occur at any finite temperature in 2D. Since Bose condensation is related to superfluidity, the observation of superfluidity in films only a few atoms thick was puzzling. More generally, the Mermin–Wagner theorem asserts that long-range order (e.g., a crystal lattice) can exist in 3D but not in 2D. Trying to understand the role of dimensionality on phase transitions was an important goal of early work on quantum films [13].

2 Third Sound, Critical Velocities, and Persistent Currents

Although the beaker emptying experiment shown in Fig. 1 provides a simple and dramatic illustration of superfluidity in thin films, it is not well suited for careful quantitative measurements. Among the first probes of superfluidity in thin films was a phenomenon called third sound. Conventional sound is a wave with peaks and troughs of pressure and density, and within the two-fluid model is known as first sound. First sound can be excited with, e.g., a piezo transducer, and its properties in bulk fluid are similar above and below $T_{\lambda }$; in the superfluid, the superfluid and normal densities oscillate in phase. Second sound is a propagating wave peculiar to superfluids in which the total density is constant, but the oscillations of the superfluid density and the normal density are out of phase. Because the superfluid fraction carries no entropy, the second sound wave can be regarded as an entropy wave or, equivalently, as a temperature wave, and the standard means of generating second sound is to periodically pulse a heater immersed in the fluid. In a normal fluid, heat transport is diffusive and a spatial modulation of temperature is rapidly smoothed out. In a superfluid, the thermal second sound wave has a well-defined velocity which depends on temperature but has a typical value of 20 m/s, and the thermal wave can propagate many centimeters with very little attenuation.

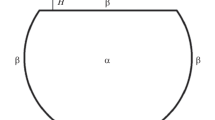
Third sound is a sound mode in a thin film in which the normal component is clamped by viscosity and the superfluid density oscillates. This results in modulation of the surface height and the temperature, as shown in Fig. 2. Third sound is typically generated with a thin film heater on a substrate. The height oscillations in the waves were first detected using ellipsometry [14], but most subsequent measurements [15] used a thin film bolometer to detect the temperature oscillations. The velocity [15,16,17] of third sound $c_3$ measures a combination of the superfluid fraction $\rho _{{\rm s}} /\rho$ and the chemical potential offset from coexistence $-C_3 /d^3$ and is given approximately by:

$$ c_3=\frac{\rho _{{\rm s}}}{\rho } \frac{C_3}{d^3} $$

(4)

Fig. 2

Schematic diagram of a third sound wave showing peaks and troughs due to motion of the superfluid component; the normal component is localized by viscous interaction with the substrate. At the peaks, the superfluid fraction is high and the effective temperature is low, so condensation from the vapor takes place there. The opposite is true at the troughs. From [16]

The superfluid fraction of the bulk is a smooth function of temperature, and both $C_3$ and d can be reliably estimated. Equation 4 predicts many aspects of the experimental data [18] except for the fact that the third sound signal abruptly becomes undetectable for sufficiently thin films. This seems to imply that $\rho _{{\rm s}}/\rho$ is a discontinuous function of d, which in turn suggests some kind of first-order transition. The critical d required for superfluidity of a ⁴He film is shown in Fig. 3.

Fig. 3

Total ⁴He thickness (including the dead layer) required to observe superfluid onset. Even at T = 0, slightly less than 1nm of total thickness is required to observe superfluidity. From [25]

If nonuniform forces are applied to an ideal dissipationless Euler fluid, it will accelerate indefinitely. In contrast, when a superfluid is subject to a thermodynamic stress such as a gradient of temperature or pressure, it will flow at a steady finite velocity, even though there is no intrinsic dissipation mechanism such as viscosity. This behavior is apparent in flows through small capillaries and porous media [19,20,21,22]. The work done on the fluid by the thermodynamic gradient is removed by the flow of vorticity [23]. It is also possible to prepare a superfluid system in a state with no thermodynamic gradients, but a finite velocity. These so-called persistent currents have a lifetime that is determined by the rate at which vortices are nucleated. Since this a thermally activated process, lifetimes of persistent currents depend exponentially on temperature and can be effectively infinite at low temperature. Similar phenomena are observed in film flow: for a finite driving force, a thin superfluid film will flow at constant velocity [12] that is independent of the driving force, and the lifetime of persistent currents depends in a systematic way on temperature and film thickness [24]. In both of these experiments, third sound is used as a probe of the film flow velocity. Equation 4 gives the speed of third sound in a static film, but in a flowing film, the speed is increased if the wave travels with the flow and is decreased if it travels against it. This Doppler shift of the wavefronts provides a means of detecting the velocity of the background flow.

3 Mechanical Oscillators

Another important probe of thin film growth in general and superfluidity in particular is transverse mechanical oscillators; the two types in widespread use are torsional oscillators and quartz crystal microbalances (QCM). Both cases can be modeled as a damped driven harmonic oscillator with an effective mass M, a spring constant K, and a quality factor Q. A generic equation of motion for the driven oscillator is:

$$ M \ddot{x}=-K x-M\frac{ \sqrt{K/M}}{\pi Q} \dot{x}+ f \cos (\omega \ t) $$

(5)

The resonant frequency $f_0=2\pi \omega _0=2 \pi \sqrt{ (\frac{K}{M} )}$ is typically 1 KHz for torsional oscillators and 5–20 MHz for QCMs. Q is a dimensionless number which measures the number of cycles required for the oscillator to lose 1/e of its kinetic energy; Q is in the range 10⁴–10⁶ for both types of oscillators. The spring constant K is determined by the properties of the materials used to construct the oscillator and can usually be considered to be constant (see, however, [26]). The behavior of the oscillator is thus determined by M and Q, and the oscillator can be used to measure these properties. If the drive frequency $\omega$ is varied, there will be a sharp maximum in the amplitude response at the resonance frequency $\omega _0$. The width of the resonance is of order $\omega _0/Q$, so the resonant frequency can be determined with a precision of about 1 part in 10⁹, which provides a very sensitive way of detecting changes in M. Q can be determined by measuring the width of the resonance or, equivalently, by measuring the out-of-phase response.

A QCM is a piezoelectric quartz disk about a centimeter in diameter and 0.3 mm thick with gold electrodes on each flat face. Applying a voltage causes a shear motion so that the flat faces move in opposite directions with a typical amplitude of a fraction of a nanometer. The restoring force is the elastic stiffness of the quartz plate, and the effective mass is the mass of the disk plus the mass of the fluid that is set into motion by the oscillating disk. Since the QCM is about 1 million atoms thick, the adsorption of an additional layer on the surface makes an easily detectable change in frequency. A torsional oscillator consists of a cylindrical cell of centimeter dimensions on the end of a torsion rod which can be metal or other materials and provides the restoring torque. A driving torque can be applied using capacitive electrodes. The effective moment of inertia is determined by the mass and geometry of the contents of the cell and whatever fluid is dragged along with it. Because torsional oscillators are bulkier and have a lower surface-to-volume ratio, it is usually impossible to detect a single monolayer on the surface. To increase the surface-to-volume ratio, many torsional oscillator experiments use a cell filled with a high surface area material such as Vycor glass  [27, 28] or graphite [29]. A solid oscillating with frequency $\omega$ parallel to itself in a fluid which obeys no-slip boundary conditions will generate a highly damped transverse wave into the fluid. The characteristic length scale of the fluid motion depends on the frequency and is called the viscous penetration depth $\delta = \sqrt{\frac{2 \eta }{\omega \, \rho }}$ where $\eta$ is the viscosity. The viscous stresses produce a retarding force on the oscillator and reduce the Q. For a superfluid, one would naively expect perfect slip boundary conditions, $\delta =0$, and no decrease in Q. Further details on the experimental implementation of QCMs are given in refs  [25, 30, 31] and for torsional oscillators in refs  [29, 32].

4 Vortices and the KT Transition

Vortices play an important role in understanding the properties of 3D superfluids. In a singly connected volume, the superfluid velocity is curl-free, but the fluid can change its topology by forming a line-like singularity called a vortex [33]. The superfluid can flow around the singularity with a velocity that drops off like 1/r from the vortex core, and because the flow is dissipationless, this flow can last indefinitely. The strength of the vortex, or its circulation, is not arbitrary; it is $\hbar$/2 m, which is required by angular momentum quantization. In 3D, vortex lines must close on themselves to form a smoke ring-like structure, or the ends of the vortex can terminate on the walls of the container. Vortices are dynamic structures and respond to externally imposed flows and the flows generated by other vortices [33]. The mathematical description of superfluid flow and electromagnetic fields is similar ($\nabla \cdot B=0, \nabla \cdot v=0,\nabla \times B=0,\nabla \times v=0$), so electromagnetic analogies between the magnetic field B and the superfluid velocity v are helpful to understand superfluid flows. In this analogy, a current carrying wire is like a vortex, and the magnetic field circling around the wire is like the superfluid flow around the vortex. Both the forces on the wire from external magnetic fields and the force on the vortex from external flows are given by a Biot–Savart type formula.

Vortices in 2D are point-like singularities with a quantized circulation which can be clockwise or counterclockwise. Because of the no-slip boundary condition, there is no dissipation due to viscous coupling to the substrate, except perhaps with the vortex core, which has radius $a_0$ of atomic dimensions. If there are no external forces on a vortex, it will drift with the local velocity of the superfluid and the flow will remain dissipationless. Dissipative forces, due, for example, to core interactions with the substrate or inelastic collisions with phonons or rotons, can generate a drag force which will cause the vortex velocity to differ from the local superfluid velocity. The superfluid will respond to this velocity difference by generating a Magnus force transverse to the external superflow, and the vortex will drift across the flow lines, so a drag force, the Magnus force, and motion across the flow lines are all related. The energy required to move the vortex comes from the background superfluid, so if mobile vortices are present, a finite pressure or temperature gradient is required to maintain a steady flow, similar to the flow of an ordinary viscous fluid.

To understand the behavior of thin films of superfluid, we need to know about the density of vortices, but where do vortices come from and what determines their density? The detailed answer is complicated, but a simple argument illustrates the basic physics. A vortex is a quantized excitation of the superfluid which can either increase or decrease the free energy of the superfluid. The kinetic energy of a vortex, which involves an integral of the 1/r velocity field, is $E_{{\rm v}}=\frac{\pi \hbar ^2 \sigma }{m^2} \ln(L/a_0)$, where $\sigma$ is the mass density per unit area and is linearly proportional to the film thickness. The integral requires a short distance cutoff of $a_0$ and a large distance cutoff of L, which is the characteristic system size. The entropy associated with the vortex is proportional to the logarithm of the number of ways of placing a vortex core of area $a_0^2$ in a region of size $L^2$, so $S_{{\rm v}}=2 k ln(L/a_0)$, where k is Boltzmann’s constant. The free energy is thus $F_{{\rm v}}=E_{{\rm v}}-T S_{{\rm v}}$. Since both the energy and the entropy are proportional to $\ln (L/a_0)$, there is a temperature at which the free energy changes sign:

$$ T_{{\rm KT}}=\frac{\pi \hbar ^2\sigma }{2 m^2 k} $$

(6)

Above this temperature, the system lowers its free energy by adding vortices, and they will proliferate and destroy the superfluid state. Below $T_{{\rm KT}}$, which is called the Kosterlitz–Thouless transition temperature, free vortices will be exponentially suppressed. For an approximately 2D quantum film, Eq. 6 predicts an abrupt first-order-like transition between a superfluid and normal state at a temperature which depends linearly on the film thickness. Furthermore, the transition temperature is independent of the interactions of helium with itself or with the underlying substrate. All of these predictions are supported by a variety of experiments.

The model which leads to Eq. 6 is extremely simple and naive, so it is somewhat remarkable that a much more realistic and technically complicated calculation [34, 35] leads to the same conclusions (see also the article by M. Kosterlitz in this Special Issue). To be physically realistic, it is important to include many vortices. Vortices of opposite circulation have an attractive interaction, and a pair of such vortices has a lower energetic cost than a single vortex. Many vortices of both circulations interact in a way that is precisely analogous to a plasma of 2D positive and negative charges, and most of the theoretical literature is written in terms of this analogy. Bound vortex pairs can have any size, and it is possible for large pairs to have smaller pairs between them, which can affect the interaction. Solving the complete many-body problem of interacting vortices was an early and important application of renormalization group techniques which were cited in the 2016 Nobel Prize in Physics which was shared by Kosterlitz [36], Thouless and Haldane.

Recall that in 3D, the superfluid fraction increases smoothly from zero to one as the temperature is reduced below the transition temperature. In contrast, the KT theory predicts an abrupt jump in the superfluid density at the transition, and the size of the jump depends linearly on the temperature. This qualitative behavior was seen in early third sound [37] and QCM experiments [38], but it was difficult to rule out other explanations which invoked the heterogeneity of realistic substrates or 2D liquid–vapor transitions [39, 40]. On a heterogeneous substrate, it seems likely that “puddles” of thicker liquid might be nucleated and pinned by cracks and crevices and that even if the puddles were superfluid, a macroscopic probe would not detect superfluidity until the puddles percolated into a cluster that spanned the experimental region. Even on a perfectly smooth surface, islands of 2D liquid would coexist with a 2D vapor, and a similar percolation transition would be necessary to observe macroscopic superfluidity. In both of these scenarios, the “superfluid fraction” would appear to abruptly jump from zero to some finite value. The comparison of theory and experiment was further complicated by the fact that although experiments indicated a rapid variation in the superfluid fraction around the transition, the variation always had a finite slope and was not convincingly first order.

A decisive test to distinguish between the vortex unbinding and the percolation models came from a detailed theory of the dynamics (in contrast to the thermodynamics) of superfluid films [41] which was developed at roughly the same time as the first measurements of the dissipation in torsional oscillator experiments  [42]. These experiments showed that there was a distinct enhancement of the dissipation which was coincident with the superfluid transition as detected by mass decoupling (see Fig. 4). The dissipation peak is a uniquely 2D phenomenon and does not occur in bulk superfluid [30] or in percolation models. The theory for the mechanical response of a substrate covered with a superfluid film exploits the analogy between a 2D superfluid and a 2D plasma, and the response is characterized by a frequency-dependent dielectric constant $\epsilon (\omega )$. In the fluid language, $\epsilon (\omega )$ is the ratio of the normal fluid velocity to the velocity difference between the normal and superfluid components, so $\epsilon (\omega ) \rightarrow 1$ means the superfluid is not moving, while $\epsilon (\omega ) \rightarrow \infty$ means the super and normal components move together. The motion of the two components is not generally in phase, which means that $\epsilon (\omega )$ is complex. The out-of-phase component, measured by $\hbox{Im}(\epsilon (\omega ))$, determines the dissipation or, equivalently, the Q of the oscillator.

Fig. 4

Data from a torsional oscillator with a (2D) Mylar substrate coiled into a roll with ⁴He dose of about three layers. The filled circles show the period shift as a function of temperature which shows the superfluid mass that decouples from the oscillator. The thinness of the film depresses the superfluid transition to about 1.216 K. The open circles show 1/Q due to the film as a function of temperature. Increased dissipation near the transition leads to a peak in 1/Q. From [42]

The detailed calculation [41] leads to the prediction of a dissipation peak at the transition. Although the calculations are rather technical and opaque, a few physical insights help to make the result plausible. The primary objects in the model are bound pairs of vortices with opposite sense of rotation separated by a distance d. The energy of such a pair is proportional to log(d), so near thermal equilibrium, there are more small, tightly bound vortices than big ones, but the concentration of all sizes increases with temperature. In an otherwise static fluid, vortex pairs with separation d move together in a straight line with velocity proportional to 1/d. In an externally imposed flow, the vortex pairs will readjust their size d and therefore their energy, with the energy going up if the pair is moving with the external flow and going down if it is moving against it. In a periodic oscillatory flow, if the relaxation of the vortex separation was in phase with the oscillatory flow, there would be no net dissipation. In addition to deterministic mechanical forces, the vortices are also subject to random Brownian motion characterized by a diffusion coefficient D whose magnitude on dimensional grounds should be of order $\hbar$/m. The out-of-phase response and therefore the dissipation is maximized when the distance the vortex diffuses in one cycle $\sqrt{D/ \omega }$ is of order d. For a given oscillator frequency, the Arrhenius temperature dependence of the vortex size distribution together with the phase matching requirement leads to a sharp increase in the dissipation as a function of temperature from the low temperature side. On the high temperature side where the film is effectively normal (due to a proliferation of unbound vortices), the film is viscously locked so there is no relative motion of the film and the substrate and therefore no dissipation. Measurements of the thermal conductance of thin films are another way to probe vortex dynamics. The theory predicts an abrupt change at the transition with characteristic power law and exponential behavior above and below the transition; these behaviors were observed in experiments [43,44,45,46].

5 Solid and Liquid Phases in 2D

The KT theory is the answer to the question of how the superfluid transition works in 2D and how the 2D and 3D transition differs. This is one example of a broader set of questions [47]: What is the relationship between phase transitions in 3D matter and matter in quasi 2D films? What is the effect of an inert substrate on these phase transitions? How do phase transitions evolve from 2D to 3D as the film thickness is increased? These issues overlap with surface physics, crystal growth, and materials science, and experiments on quantum films have played an important role.

The simplest phase transitions in 3D condensed matter are between the familiar solid, liquid, and gas phases. Recall that the Mermin–Wagner type of theorems prohibits long-range order in 2D, so one of the early questions was to experimentally establish whether solid monolayers exist in nature. The main experimental challenge is that in any conventional cell or substrate, the number of atoms in a 2D adlayer is small compared to the number of atoms in the substrate or cell walls, so probes of 2D transitions have to be extremely surface sensitive, or some strategy must be devised to enhance the surface contribution and suppress the substrate and cell contribution to the experimental signal. A characteristic feature of a first-order bulk phase transition is a peak in the heat capacity/latent heat at the transition. Quantum films on high specific area substrates are convenient experimental systems for calorimetric measurements because the Debye temperature of the cell and substrate materials is quite high, so the heat capacity at a few Kelvin is deep into the $T^3$ regime and is quite low, while the heat capacity of the quantum film is still near its classical high temperature value. Early experiments used various powders and porous solids as substrates [48] and provided preliminary evidence for 2D solid an 2D gas phases in both ³He and ⁴He, but it was soon realized that the atomic-scale cracks and steps in a disordered substrate presented such a heterogeneous adsorption potential that interpretation of the calorimetric data was unreliable (Fig. 5).

Fig. 5

⁴He vapor pressure isotherm on HOPG graphite. The steps are indicative of layer-by-layer growth. The inset shows the first two layers. The smooth curves are derived from the FHH isotherm equation 3 From [50]

An experimental breakthrough came with the commercial availability of grafoil, an exfoliated high specific area (approximately 25 m²/g) version of graphite which has crystallites with a characteristic size of 200 $\AA$. A broad overview of calorimetric measurements for the monolayer regime of ⁴He on Grafoil substrates is shown in Fig. 6. Although graphite binds helium strongly ($E_{{\rm binding}}=143$ K), for most of the regions with T > 3 K, the monolayer behaves like a classical gas with a heat capacity of 1 k/atom. The strongest effect of the substrate is the feature near T=3K and a coverage of 6 atoms/nm², which is due to a second-order Ising-like transition to a commensurate solid phase with one helium atom for every three carbon hexagons in the substrate. The ridge near 8 atoms/nm² is a transition to an incommensurate 2D solid. ³He has a similar phase diagram in this regime [49].

Fig. 6

Contour plot of the heat capacity of ⁴He adsorbed on Grafoil in the coverage–temperature plane in the monolayer regime (1 layer $\approx$ 12 atom/nm²). From [51]

Calorimetric measurements [52,53,54,55,56, 56] were complimented by theoretical modeling [57,58,59,60,61,62] and neutron scattering measurements [63, 64]. The picture that emerges is that as the coverage is increased from zero, there is a 2D gas, a coexistence with a 2D liquid that exists at low temperature and has a critical point, a commensurate solid, and an incommensurate solid. There is a reasonably sharp transition to a second layer where the sequence of phase transitions repeats itself. An example of the phase diagram is shown in Fig. 7.

Fig. 7

Phase diagram for ⁴He on grafoil: a First layer, G = gas, F = fluid, C = commensurate solid, DWF = domain wall fluid, SIC = striped incommensurate solid. b Second layer, S = second layer solid. From [29]

In bulk liquid ⁴He, the heat capacity has a lambda-shaped singularity which is the origin of the name of the superfluid transition. As the coverage is decreased, the total heat capacity and the heat capacity per atom decrease. The peaks become truncated, and the superfluid onset temperature decreases. Torsional oscillator [29] and third sound [50] using graphite substrates have provided more detailed information about the interaction of superfluidity and other 2D phase transitions. On graphite, even though the first layer has a liquid phase, it is not superfluid even at 20 mK. Superfluidity is observed in the second layer, but it is strongly affected by 2D liquid–vapor coexistence and solidification. These effects are weaker in the third layer and become insignificant in higher layers. Preplating graphite with H₂ or HD forms a composite substrate which preserves the uniformity of the graphite, but has a much weaker adsorption potential for helium. On HD preplated graphite, superfluidity is also not observed in the first layer of helium but is observed in the second layer [65]. Where superfluidity is observed, there is no corresponding feature in the heat capacity, which is consistent with the higher coverage data of Fig. 8.

Fig. 8

Heat capacity peak associated with superfluidity for a series of helium coverages measured in layers denoted by n. At 11 layers, the lambda shape of the 3D heat capacity is well established, while at n = 3.62, the peak is greatly reduced. The arrows locate the temperature at which the thermal time constant goes to zero, indicating superfluid onset. Note that superfluid onset and the heat capacity peaks do not coincide. From [53]

⁴He and ³He are chemically identical, but ⁴He has no nuclear spin and obeys Bose statistics, while ³He has a nuclear spin of 1/2 and obeys Fermi statistics. Despite this difference, the structure of the bulk solid–liquid–gas phase transitions in the two isotopes is qualitatively similar. ³He is less tightly bound than ⁴He, so the liquid–vapor critical temperature is lower (3.3 K versus 5.2 K), and the minimum pressure required for solidification at T = 0 is higher (3.2 MPa versus 2.5 MPa). Quantum statistics profoundly affects superfluidity in the two isotopes. The superfluid transition temperature of pure ³He is approximately 1000 times lower than in ⁴He and involves a spin pairing mechanism.

The non-superfluid phase of thin films of ³He on graphite [49, 54, 66] is also similar to those in ⁴He. One possible difference in the behavior of the two isotopes is the question of the existence of a 2D liquid–vapor transition, which is unambiguous in ⁴He but is controversial [66, 67] in ³He. Recent work [68, 69] supports the picture of 2D liquid–gas coexistence in the first three layers. Other experiments have utilized preplating the graphite surface with either hydrogen [70, 71] or ⁴He to study ³He films in a weaker and more uniform substrate [72].

In addition to phase transitions between superfluid, solid, liquid, and gas, bulk ³He–⁴He mixtures have a miscibility gap with a tricritical point [73] at T = 0.87 K and ³He concentration of 70%. Bulk mixtures with ³He concentration greater than 6% at temperatures below 0.87 K will separate into ³He rich phase that floats on top of a ⁴He rich phase; the ⁴He rich phase is superfluid, but the ³He rich phase is not. Even outside the miscibility gap region where the bulk phases are completely miscible, addition of ³He to ⁴He strongly affects the liquid–vapor surface tension. ³He has a larger zero point energy than ⁴He, so ³He will preferentially adsorb to the surface of a dilute solution and occupy the so-called Andreev bound state. The resulting 2D Fermi gas produces a pressure which reduces the surface tension. Experiments on third sound propagation in mixture films a few layers thick at temperatures below 0.5 K have been interpreted in terms of a phase separated sandwich structure [74,75,76] in which the ³He phase floats on top of the ⁴He-rich phase. Heat capacity measurements on dilute solutions provide evidence [77] for lateral phase separation, i.e., 2D “puddles” of the ³He rich phase.

6 Film Growth and Wetting

Before the 1990s, experiments on 2D quantum films were carried out primarily on disordered substrates such as glass or Mylar, or on crystallographically ordered graphite. In both of these cases, the interaction of the helium with the substrate is large compared to the interactions of the helium with itself. On graphite, the strong substrate potential produces registered solid phases and distinct layer-by-layer growth which involves a sequence of 2D phase transitions in the first few layers, as discussed above. On disordered substrates, the strong potential washes out the distinct layers and forms 2–3 layers of solid which is often referred to by experimentalists as “dead layers,” while theorists [28, 78] often use the more sophisticated term “Bose glass.” Since these substrates obviously affect superfluidity in thin films, efforts were made to produce weaker substrates by preplating disordered materials with hydrogen [79,80,81], with the goal of more closely approximating ideal 2D behavior. A lattice gas model [82] characterized by an atom–substrate energy and an atom–atom interaction energy provided a quantitative way to distinguish between strong and weak substrates and the surface phase transitions that occur on each of them. The strong substrate case shown in Fig. 9 has a series of first-order phase transitions that separate films of 0, 1, 2… layers. The layering transitions end in critical points. Isotherms below the critical temperatures give distinct steps at layer completion, while isotherms above the layering critical temperatures give smooth isotherms. In either case, the film thickness approaches infinity as the chemical potential approaches the bulk coexistence value. Another word used to describe this situation is that the adsorbate “wets” the substrate.

Fig. 9

Lattice gas phase diagram in the $\mu$-T plane (left) and associated coverage isotherms (right) in the strong substrate limit. $\mu _0$ is the bulk coexistence chemical potential. There is a sequence of layering transitions labeled 0,1,2.. which end in critical points $T_{{\rm c}}(1)$, $T_{{\rm c}}(2)$...The layer critical points approach the roughening temperature $T_{{\rm R}}$ at bulk coexistence. For temperatures below the layering critical points, such as A, the isotherm will have distinct steps. For temperatures above the layering critical points, such as B, the isotherm will be smooth. From [82]

The opposite case in which the atom–atom interaction is larger than the interaction with the substrate is shown in Fig. 10. Somewhat surprisingly, there is a temperature $T_{{\rm w}}$ which separates regions of essentially zero thickness from a region of infinite thickness at coexistence, so the substrate is wet above $T_{{\rm w}}$ and dry below. $T_{{\rm w}}$ is called the wetting temperature, and the transition between wet and dry states at coexistence is a first-order wetting transition. Even more surprisingly, this first-order phase transition persists into the bulk gas region of the phase diagram where the substrate is in equilibrium with unsaturated vapor. This phase transition, which is called the prewetting transition, extends from $T_{{\rm w}}$ at coexistence to a critical point $T_{{\rm PC}}$, as shown in Fig. 10. If the pressure or chemical potential is varied at constant temperature, the adsorbed film will make an abrupt transition from a thin state to a thick state as it crosses the prewetting line. The size of the jump in film thickness varies along the prewetting line; at $T_{{\rm w}}$, the jump is infinite, while at $T_{{\rm PC}}$, the jump goes to zero. Exactly on the prewetting line, films of two different thicknesses can coexist, which is roughly analogous to the coexistence of low density vapor and high density liquid in 3D.

Fig. 10

Lattice gas phase diagram in the $\mu$-T plane (left) and associated coverage isotherms (right) in the weak substrate limit. $\mu _0$ corresponds to bulk coexistence. There is a wetting temperature $T_{{\rm w}}$ below which the substrate is essentially dry. Emanating from $T_{{\rm w}}$ is a first-order phase transition line called “prewetting” that separates a thin film phase from a thick film phase. The prewetting line ends in a critical point at $T_{{\rm PC}}$. For temperatures below the wetting temperature $T_{{\rm w}}$, such as A, the coverage isotherm will remain at very small values even at bulk coexistence. For temperatures between $T_{{\rm w}}$ and $T_{{\rm PC}}$, such as indicated by arrow B, the isotherm will have a discontinuous jump in coverage as the chemical potential crosses the prewetting line; after the discontinuity, the coverage smoothly goes to infinity at bulk coexistence, i.e., the fluid wets the substrate. At temperatures above $T_{{\rm PC}}$, such as C, the coverage is a smooth function of the chemical potential which goes to infinity at bulk coexistence. From [82]

This scenario of the wetting behavior of a fluid on a “weak” substrate was initially worked out in detail for a lattice gas model, but it is quite general. In particular, it does not depend on quantum properties or quantum mechanics; it only requires that the interaction of the fluid with itself is large compared to the interaction with the substrate. Helium has a particularly weak interaction with itself, as indicated by its very low critical temperature, so helium was widely regarded as a “universal wetting agent,” because its interaction with any known substrate was stronger than the helium–helium interaction. For these reasons, helium was an unlikely fluid to use in a study of wetting transitions.

This changed in 1991 when Cheng et al. [83] had two insights. The first was to work out the wetting properties of a fluid interacting with the substrate with a van der Waals-type potential

$$ V(z)=\frac{4 C_3^3}{27 D^2 z^9}-\frac{C_3}{z^3} $$

(7)

where $C_3$ measures the long-range interaction of an atom with the substrate, and D measures the depth of the minimum of the potential. A thick film will lower its energy by an amount $\int _{{\rm zmin}}^{\infty } \rho _{{\rm l}} V(z) \mathrm{d}z$, where ${\hbox {zmin}}={(\frac{2 C_3}{3 D})}^\frac{1}{3}$ is the position of the minimum of V(z) and $\rho _{{\rm l}}$ is the density of the liquid. The energetic cost of forming a film is the energy required to form the liquid–vapor interface and the liquid–substrate interface. The liquid–vapor interfacial energy is simply the experimentally measured surface tension $\sigma _{{\rm lv}}$. $\sigma _{{\rm lv}}$ has a value of approximately 0.003 J/m² at T = 0, is approximately constant up to T = 2 K, and then monotonically decreases to zero at the bulk critical point $T_{{\rm c}}=5.2$ K. The liquid–substrate surface tension $\sigma _{{\rm ls}}$ is not easy to measure directly, so the authors of Ref. [83] made the approximation $\sigma _{{\rm sl}}=\sigma _{{\rm lv}}$; this approximation is somewhat justified by the observation that zmin for a weak substrate is quite large, so the physical environment at the liquid–vapor interface and the liquid–substrate interface is actually quite similar. Using this approximation, the criterion for a wetting transition at $T_{{\rm w}}$ is

$$ 2 \sigma _{{\rm lv}}(T_{{\rm w}}) = \int _{{\rm zmin}} ^{\infty } \rho _{{\rm l}} V(z) \mathrm{d}z $$

(8)

Because $\sigma _{{\rm lv}}$ is a monotonically decreasing function of temperature, we expect that for $T<T_{{\rm w}}$, the cost of forming the interfaces exceeds the gain of the dense phase falling into the substrate potential, so the substrate will be dry, while at higher temperatures, a thick film will be stable.

The second insight was that the value of D for helium interacting with alkali metals, and cesium in particular, was exceptionally low. The physical reason for this is that cesium is the biggest atom in the periodic table with the lowest ionization energy, which reflects the fact that the outer electrons are weakly bound in large orbitals. This means that the electron cloud extends unusually far from a cesium surface, so the balance between the long-range attraction and the Pauli repulsion occurs at an unusually large distance, which results in a low binding energy. The binding energy is so low that they predicted that ⁴He would not wet cesium.

It was experimentally challenging to test this prediction, because cesium is extremely chemically reactive, which is directly related to its loosely bound outer electrons. It is a silver-colored metal that melts at slightly above room temperature, and spontaneously combusts in air, so preparing a clean Cs surface requires special care. Nacher and Dupont-Roc [84] used a sealed glass tube with a small amount of helium with the two ends separated by a cesium ring. They measured the thermal conductance of the tube, which is ordinarily dominated by the superfluid film, but in their setup, the superfluid film was interrupted by the cesium ring (but not by a sodium or potassium ring). They concluded that cesium was not wet by ⁴He at 1.8 K. Ketola and Hallock  [85] prepared a cesium barrier on a glass slide using a commercial getter. They found that third sound would not propagate across the barrier at 1.4K if the helium film thickness was less than about ten layers. Rutledge and Taborek  [86, 87] used a quartz microbalance technique, which did not rely on superfluidity and could detect the “dead layer,” the normal fraction in the superfluid state, and the normal fluid film for a wide range of film thickness or vapor pressure. They made high-quality cesium films by evaporating elemental metal from a small oven at 4K. The cesium was loaded into the oven in a sealed glass ampule which was broken at low temperature. Adsorption isotherms on these surfaces were very unusual. At low temperatures, there was no “dead layer” and essentially no adsorption from zero pressure up to the saturated vapor pressure. At higher temperatures, there was no adsorption until a critical pressure below saturation was reached, and then, a film abruptly formed which continued to thicken as saturation was approached. A detailed analysis of these isotherms showed that the wetting temperature was approximately 1.95K, above which the substrate became wet via a prewetting transition which ended in a critical point at 2.5K, although a rounded step in the isotherm could be seen even above 4K. This was the first experimental realization of the prewetting type of phase diagram [88] illustrated in Fig. 10.

Wetting is a first-order phase transition that involves a discontinuity in the order parameter (the film thickness). First-order phase transitions are typically hysteretic, because the phase transition requires the nucleation of a small region of the new phase which has a free energy barrier because of the interface which must be formed. Nucleation is a thermally activated process, and experimentally observable rates of nucleation require a finite amount of supercooling or superheating, so, for example, the solid→liquid transition and the liquid→solid transition take place at slightly different temperatures. Wetting is an extreme example of this type of hysteresis because the nucleation barrier itself becomes singular at coexistence where the film thickness diverges. If a dry cesium surface initially below $T_{{\rm w}}$ is heated in contact with helium vapor along the coexistence curve, near $T_{{\rm w}}$ it is relatively easy to nucleate small drops of liquid that eventually grow and cover the surface with a thick film of liquid. On the other hand, if a cesium surface initially above $T_{{\rm w}}$ which is covered by a thick film of liquid is cooled below $T_{{\rm w}}$ along the coexistence curve, nucleation of even a small dry patch requires the formation of a large amount of liquid–vapor interface which is energetically prohibitive. Experiments show that a thick helium film on cesium will persist indefinitely [87] even when cooled far below $T_{{\rm w}}$, and this metastability is explained by a detailed analysis of the nucleation rates [89] (Fig. 11).

Fig. 11

Frequency shift of a QCM covered with a thick (100 layers) film of cesium as a function of ⁴He vapor pressure measured as a fraction of the saturated vapor pressure $P_0$ for three different temperatures. 1 Hz of frequency shift corresponds to 5 atomic layers of helium. At high temperatures in (a), more than 40 layers are adsorbed at $P=P_0$. At low temperatures below the wetting temperature in (c), less than five layers are adsorbed at $P=P_0$. Near but below the wetting temperature in (b), the coverage is very low until $P=0.995 P_0$ where the film abruptly thickens to about 20 layers; this is the prewetting step. All of these isotherms stand in distinct contrast to those on a strong substrate as shown in Fig. 5. From [87]

A wetting transition with its associated prewetting transition is generic features of a fluid interacting with a “weak” substrate  [90, 91]. The details of the phase diagram depend on the strength of the interaction between the fluid and the substrate. A convenient way to tune this interaction is to form a composite substrate of a semi-infinite “strong” material such as quartz or gold with a thin film of a “weak” material, e.g., cesium. For cesium thickness greater than about 50 layers, the substrate behaves like bulk cesium, but for thinner layers, the effective interaction is stronger, which has the effect of lowering the wetting temperature [92]. On thick cesium substrates, the wetting temperature and the bulk lambda temperature almost coincide, which means that thick prewetted films are almost always normal, and also raises the suspicion that wetting and superfluidity are somehow coupled. Experiments on thin cesium [91, 93] for which the wetting temperature is decisively below $T_\lambda$ show that the K–T transition and prewetting are distinct independent transitions. As shown in Fig. 12, a thick superfluid film can be formed by crossing the prewetting line at low temperature, in which case the thick film is “born” superfluid, while at higher temperatures, the film makes distinct transitions from thin→thick normal and thick normal→thick superfluid.

Fig. 12

P–T phase diagram for ⁴He adsorbed on a thin cesium substrate 4.2 layers thick for which the wetting temperature has been depressed to $T_{{\rm w}}=1.5$ K. The circles show the position of the prewetting thin→thick transition, and the triangles show the position of the KT transition. From  [93]

Although cesium is the weakest substrate for ⁴He, all of the alkali metals are much weaker than conventional substrates like graphite or glass. Theoretical calculations  [94, 95] suggested that thick substrates of cesium, rubidium, and potassium should all have a finite ⁴He wetting temperature, while sodium was expected to be on the borderline and lithium was expected to wet at all temperatures. Calculations show that Cs and Rb should have almost identical wetting properties, but this prediction was not corroborated by experiment. Most experiments [96,97,98] show that ⁴He on Rb has a prewetting-like thin→thick transition, but Rb is always wet at coexistence, implying that $T_{{\rm w}}=0$ (see, however, [99] which concludes $T_{{\rm w}}>300$ mK). Rb, Na, and K all behave similarly [97, 100, 101] in the sense that at pressures substantially below the saturated vapor pressure, the surfaces are essentially dry and there is no “dead layer” of strongly bound solid. They all have an abrupt prewetting transition which occurs near bulk coexistence (within a few percent of the saturated vapor pressure) at temperatures below the prewetting critical point. In contrast to the thin cesium case, for the lighter alkali metals the KT transition line appears to hit the prewetting line exactly at the prewetting critical point, forming a tricritical point. Lithium appears to be a true intermediate case between conventional strong substrates and the heavy alkalis. Although there is no solid layer at low pressure, there is also no abrupt prewetting transition; a fluid film grows continuously and almost linearly as the vapor pressure is increased  [102], corresponding to a binding energy of approximately 13K. Superfluid onset in this system is a particularly clean and simple example of the KT transition which is not obscured by either solid-like underlayers or by prewetting.

Probes such as adsorption isotherms, third sound, and heat transport measurements are designed to work with flat, uniform liquid films which can exist only above the wetting temperature. Although the thermodynamically stable phase below the wetting temperature is an essentially dry substrate (with perhaps a 2D adsorbed gas), long-lived metastable states of liquid in contact with the substrate can be prepared in the form of droplets with a finite contact angle. Droplets on a substrate are never in equilibrium with bulk fluid because the Laplace pressure due to their curvature implies that the internal pressure is always higher than the saturated vapor pressure; because of this pressure difference, all droplets will eventually evaporate. Evaporation can be quite slow, and on shorter time scales, a drop minimizes its surface energy $E_{{\rm S}}$ subject to an approximate constraint of constant volume. For the axisymmetric case specified by a drop height h(r), the energy functional is

$$ E_{{\rm S}}=\int _{0}^{R} \sigma _{{\rm lv}} 2 \pi r\sqrt{1+h'(r)^2} +(\sigma _{{\rm ls}}-\sigma _{{\rm sv}})2 \pi r+\lambda 2 \pi r h(r) \mathrm{d}r $$

(9)

$\sigma _{{\rm lv}}, \sigma _{{\rm ls}}, \sigma _{{\rm sv}}$ are the surface energy of the liquid–vapor, liquid–solid, and solid–vapor interfaces, respectively. $\lambda$ is a Lagrange multiplier to enforce volume conservation. The contact line is at r = R, so h(R) = 0. Minimizing this functional is a standard problem of calculus of variations with variable endpoints because R is not specified a priori. Functional minimization yields a nonlinear differential equation for the drop profile

$$ h''(r)= \frac{-(h'(r)+h'(r)^3)}{r}+\frac{\lambda (1+h'(r)^2)^{3/2}}{\sigma _{{\rm lv}}} $$

(10)

and an endpoint condition

$$ \frac{1}{\sqrt{1+h'(R)^2}}=\cos \theta _{{\rm c}} = \frac{\sigma _{{\rm sv}}-\sigma _{{\rm sl}}}{\sigma _{{\rm lv}}} $$

(11)

The physical content of Eq. 10 is that the mean curvature of the drop surface is a constant that depends on the drop volume; this implies that the drop shape is a spherical cap. This is strictly true only if gravitational forces are negligible compared to surface forces, which is quantified by saying that $R<\sqrt{2 \sigma _{{\rm lv}}/(\rho g)}$. If gravity is not negligible, a gravitational potential energy term must be added to 9, and the drop profiles become “pancakes” rather than spherical caps [103]. Equation 11, which is known as the Young equation, says that the contact angle $\theta _{{\rm c}}$ is determined by various interfacial energies and is independent of the drop volume; this result is valid for both spherical cap and “pancake” drops.

The Young equation 11 provides a way to understand the wetting transition as it is approached from the dry state where $\theta _{{\rm c}} >0$. For quantum fluids, $\sigma _{{\rm sv}}-\sigma _{{\rm sl}}>0$, which means the substrate prefers the liquid to the vapor. Despite the preference for the liquid, a drop will not spread out indefinitely as long as $\sigma _{{\rm lv}}(T)>\sigma _{{\rm sv}}-\sigma _{{\rm sl}}$, which means that the potential benefit of spreading out on the substrate is more than canceled by the cost of forming liquid–vapor interface. In this case, the fluid does not completely wet the substrate, and the drop will spread to a finite radius R with a contact angle $\theta _{{\rm c}}>0$ given by Eq. 11. Although all of the surface energies in Eq. 11 in principle depend on temperature, the temperature dependence of $\sigma _{{\rm lv}}(T)$ is the dominant effect, with ${\mathrm{d}}\sigma _{{\rm lv}}(T)/{\mathrm{d}}T<0$ and $\sigma _{{\rm lv}}(T_{{\rm c}})=0$. If the temperature of a drop with a finite contact angle is raised, eventually a temperature $T_{{\rm w}}$ will be reached at which $\sigma _{{\rm lv}}(T_{{\rm w}})=\sigma _{{\rm sv}}-\sigma _{{\rm sl}}$ and $\theta _{{\rm c}}=0$ which corresponds to a flat film of liquid which completely wets the substrate. Measuring the temperature dependence of the contact angle and locating the temperature at which $\theta _{{\rm c}}=0$ are an alternative way of finding the wetting temperature $T_{{\rm w}}$ and for determining the temperature dependence of the surface energies.

Measurements [104,105,106,107] of the contact angle of ⁴He on Cs as a function of temperature are summarized in Fig. 13. Although the details of the method of Cs surface preparation and contact angle measurement affect the quantitative results, qualitatively all of the data show that the contact angle goes to zero near T = 2 K with an approximately square root dependence on temperature, as expected from Eq. 11.

Fig. 13

Contact angle of ⁴He on Cs as a function of temperature. Solid circles, squares, and triangles are for various surfaces from [107], open squares are data from [106], and open triangles are from [104]. From [107]

The wetting criterion defined in Eq. 8 involves a balance between the substrate surface potential and the surface tension of the fluid, so another way to tune the wetting properties is to change the surface tension. This can be carried out by considering isotopic mixtures of ³He and ⁴He. The surface tension of ³He is substantially lower than ⁴He, so pure ³He wets Cs at all temperatures [108]. Although mixtures of the isotopes are miscible in the bulk at all concentrations for temperatures above 0.8 K, the interfaces represent a perturbation which typically prefers one component or another. ³He has a higher zero point energy than ⁴He, so a mixture can lower its energy by pushing ³He to the vapor interface where it is less confined. Because of this effect, a dilute solution of ³He will form a 2D gas of ³He at the liquid–vapor interface. ³He has a binding energy of about 2.2K to the interface, so the population of the bound state (sometimes called the Andreev state) varies with temperature in this range. The 2D gas at the interface exerts a negative pressure and reduces the surface tension by an amount that depends on concentration and temperature. These effects have surprising consequences for wetting of helium mixtures, which were first worked out in reference [109] and experimentally verified in reference [110]. Dilute solutions of ³He in ⁴He on Cs have two wetting temperatures and exhibit reentrant wetting. At high temperatures, the mixture wets because the surface tension is low for conventional thermal reasons. As the temperature is lowered, the surface tension increases and the film makes a transition from wet→non-wet. As the temperature is lowered further, the ³He bound states are populated which lowers the surface tension so much that the interface goes from non-wet→wet. A phase diagram which shows this behavior is shown in Fig. 14. In order to reconcile theory and experiment, it is necessary to include the effects of ³He bound states and a 2D gas at the liquid–substrate interface as well as the liquid–vapor interface; this further supports the idea that the liquid–substrate interface is very similar to the liquid–vapor interface.

Fig. 14

X3-T phase diagram for ³He–⁴He mixture in contact with a cesium substrate. If the ³He concentration X3 is constant at, e.g., 5%, the substrate will be wet for T > 1.7 K, non-wet for 0.85 < T < 1.7, and wet again for T < 0.85. The dotted line is the theoretical phase boundary assuming a ³He 2D gas only on the liquid–vapor interface, while the solid curve (which matches the data) includes the effects of a 2D gas on the liquid–Cs interface. From [110]

7 Hydrogen Films

Hydrogen has a low mass and a large zero point energy, so quantum effects strongly influence its phase diagram, but hydrogen behaves quite differently than helium. Perhaps the biggest difference is that the low temperature ground state is a solid instead of a liquid; the triple point of hydrogen where solid, liquid, and vapor coexist is $T_t=13.8$ K. The stability of the solid state is due to the much stronger interparticle interactions in hydrogen as compared to helium. Solidification precludes superfluidity(at least naively, see, however, [111, 112]), so attempts to search for superfluid hydrogen have focused on metastable states. Under normal conditions, hydrogen is a molecule H₂ which can exist in two nuclear spin states called ortho (nuclear spins aligned) and para (nuclear spins anti parallel) hydrogen. Near the triple point, liquid hydrogen is almost entirely in the para form which is a boson and might be expected to become superfluid near 3K if it could be prevented from freezing [113, 114], but this has not been successful so far in macroscopic or even mesoscopic samples. Two exotic types of hydrogenic superfluidity have been observed: 16 parahydrogen molecules around an organic molecule [115] and in extremely dilute spin polarized atomic hydrogen gas [116].

Despite the absence of conventional superfluidity, hydrogen is an interesting quantum material that has been used in several studies of film growth and wetting, both as a substrate and as an adsorbate. Although hydrogen is much more polarizable than helium, solid hydrogen is a weak substrate because its density is very low. Third sound experiments using ⁴He on hydrogen  [79, 80] show that helium wets solid hydrogen, but the dead layer is much lower than in conventional substrates and superfluidity can be observed in helium films of submonolayer coverage adsorbed on hydrogen. Forming solid hydrogen substrates is experimentally challenging because solid hydrogen, and indeed any solid material, will not wet another solid (in the sense of grow to infinite thickness at coexistence) even if the attractive interaction is strong. The reason for this is that even on a crystallographically perfect substrate there typically is a lattice mismatch elastic strain energy that makes the free energy cost of a thick solid film very high [117]. On a realistically rough substrate, bending strain energy further adds to the cost of forming a solid film on a solid substrate [118]. Near the triple point where the free energy of solid and liquid phases becomes similar, compound films which contain both phases can grow to modest thickness [119], and above the triple point, the liquid phase will fully wet a strong substrate. This scenario is called triple point wetting [120] and has been observed for hydrogen on silver [121, 122]. Another counterintuitive aspect of solid hydrogen films is that they are remarkably mobile even at temperatures far below the triple point  [123,124,125], so quench condensed films do not retain their morphology.

On weak substrates, liquid hydrogen is expected to have a wetting phase diagram similar to helium, but shifted to higher temperatures [126]. Adsorption of H₂ on rubidium shows prewetting features and a wetting temperature near 18K [101]. The wetting temperature of hydrogen on cesium is approximately 20.6K, which was determined using adsorption isotherms above the wetting temperature and optical imaging of drops below the wetting temperature [127].

8 Conclusion

In this review, we have attempted to provide an elementary introduction to the experimental tools and theoretical models which have historically been used to study films of quantum fluids. Superfluidity in films of ⁴He is the most obvious and spectacular manifestation of quantum effects. Even after the basic phenomena of film flow and third sound were well established, it took nearly 20 years of concerted effort by a large group of researchers to unravel some of the conflicting theoretical and experimental information to eventually come to a consensus on the nature of 2D superfluidity. The quantum constant $\hbar$ enters the analysis in the strength of a quantized vortex, but the statistical mechanics of the phase transition is essentially classical; the essential ingredient is 2D dimensionality, not quantum mechanics. Although helium films were the first experimental system in which the hallmark features of the KT transition were observed, this classical phase transition has subsequently been seen in room temperature systems as diverse as colloids, magnets, and ultracold gases [128,129,130,131,132]. The extreme purity of helium and the particularly low background signal and high sensitivity of experimental probes in the cryogenic environment have been repeatedly exploited to make initial studies of phase transitions which were widely applicable in other systems. Examples include solid, liquid and vapor monolayer phases and the phase transitions between them, and the existence of wetting transitions and prewetting, which have also been seen in classical fluids  [133, 134]. Many of the basic issues in thin film superfluidity and thin film growth have been resolved, and future work will explore the properties of quantum films on substrates with novel chemical or structural properties  [26, 135,136,137] and utilize the remarkable properties of thin quantum films to manipulate electrons and other particles [138,139,140,141].