Control of the Rolling Motion of a Spherical Robot on an Inclined Plane

Abstract

In this work we consider the controlled motion of a pendulum spherical robot on an inclined plane. The algorithm for determining the control actions for the motion along an arbitrary trajectory and examples of numerical simulation of the controlled motion are given.

This paper is an extension of recent studies [1] on the controlled motion of a spherical robot of pendulum type moving on an inclined plane. In [1], equations of controlled motion of a spherical robot of pendulum type on an inclined plane are presented and integrals of motion and partial solutions (with constant control) are found. A linear stability analysis of partial solutions is carried out.In this paper, using the results obtained in [1–4], an algorithm is presented for constructing an explicit control during motion along a given trajectory on an inclined plane, in particular, in a straight line and a circle.

1 EQUATIONS OF MOTION OF A SPHERICAL ROBOT OF PENDULUM TYPE ON AN INCLINED PLANE

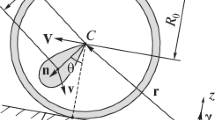
Consider the motion of a spherical robot of pendulum type rolling without slipping on an inclined absolutely rough plane. The spherical robot is a spherical shell of radius ${{R}_{o}}$ (Fig. 1) with an axisymmetric pendulum fixed at its center. The pendulum (Lagrange top) has mass m, the distance from the center of the spherical shell to the center of mass of the pendulum is ${{R}_{t}}$, and in the system of principal axes of the top the central tensor of inertia has the form ${{{\mathbf{i}}}_{0}} = \operatorname{diag} (i,\,i,\,i + j)$. The system is set in motion by forced oscillations of the pendulum. In this paper, we address a model problem in which it is assumed that the mechanism setting the pendulum in motion produces control torque Q, applied at the point C of attachment of the pendulum.

Fig. 1.

Schematic model of a spherical robot on an inclined plane.

All vectors describing the motion of the spherical robot will be referred to a fixed (inertial) coordinate system $Oxyz$ (the $Oxy$-plane coincides with the inclined plane of rolling of the spherical robot, the unit vector ${\boldsymbol{\beta }}$ is directed to the observer perpendicularly to the plane of the figure, and the unit vector ${\boldsymbol{\gamma }}$ is directed along the outer normal to the inclined plane), see Fig. 1.

The velocity of the center of mass of the top ${\mathbf{v}}$ is determined from the condition that the velocity of the center of the shell ${\mathbf{V}}$ is equal to that of the point of suspension of the pendulum. This condition is expressed by the (holonomic) constraint

$${\mathbf{v}} = {\mathbf{V}} + {{R}_{t}}{\boldsymbol{\omega }} \times {\mathbf{n}},$$

((1))

where n is the vector directed along the symmetry axis of the pendulum and ${\boldsymbol{\omega}}$ is the angular velocity of the pendulum.

The velocity of the center of the shell is related to the angular velocity of the shell, ${\mathbf{\Omega }}$, by the condition that there is no slipping at the point of contact $P$:

$${\mathbf{V}} = {\mathbf{\dot {r}}} = {{R}_{o}}{\mathbf{\Omega }} \times {\mathbf{\gamma }},$$

((2))

where ${\mathbf{r}} = (x,y)$ are the coordinates of the center of the sphere, ${\mathbf{\gamma }} = (0,\,0,\,1)$, and ${\mathbf{\Omega }}$ is the angular velocity of the shell.

With respect to the chosen coordinate system and in view of (1) and (2), the equations describing the controlled motion of the system of interest on an inclined plane have the form (for a detailed derivation, see [1]):

$$\begin{gathered} {\mathbf{J\dot {\Omega }}} + m{{R}_{o}}{{R}_{t}}{\mathbf{\gamma }} \times ({\boldsymbol{\dot {\omega }}} \times {\mathbf{n}}) \\ \, = - m{{R}_{o}}{{R}_{t}}{\mathbf{\gamma }} \times ({\boldsymbol{\omega}} \times {\mathbf{\dot {n}}}) + (m + M){{R}_{o}}{\mathbf{\gamma }} \times {\mathbf{g}} - {\mathbf{Q}}, \\ i{\boldsymbol{\dot {\omega }}} + mR_{t}^{2}{\mathbf{n}} \times ({\boldsymbol{\dot {\omega }}} \times {\mathbf{n}}) + m{{R}_{o}}{{R}_{t}}{\mathbf{n}} \times ({\mathbf{\dot {\Omega }}} \times {\mathbf{\gamma }}) \\ = m{{R}_{t}}{\mathbf{n}} \times {\mathbf{g}}\, - \,j({\boldsymbol{\omega}},{\mathbf{n}}){\mathbf{\dot {n}}}\, - \,j({\boldsymbol{\dot {\omega }}},{\mathbf{n}}){\mathbf{n}}\, - \,mR_{t}^{2}{\mathbf{n}} \times ({\boldsymbol{\omega}} \times {\mathbf{\dot {n}}})\, + \,{\mathbf{Q}}, \\ {\mathbf{\dot {n}}} = {\boldsymbol{\omega}} \times {\mathbf{n}}, \\ \end{gathered} $$

((3))

where J = $\operatorname{diag} (I + (M + m)R_{o}^{2},I + (M + m)R_{o}^{2},I)$, M, I are the mass and the central moment of inertia of the shell, ${\mathbf{g}} = {\text{g}}( - \sin\delta ,0, - \cos\delta )$ is the vector of free-fall acceleration, and $\delta$ is the angle of inclination of the plane of motion.

Let ${{\delta }_{ * }}$ denote the angle of inclination of the plane at which the symmetry axis of the pendulum is horizontal and the line of action of gravity ${{{\mathbf{F}}}_{g}} = (m + M){\mathbf{g}}$, applied to the center of mass of the entire system, passes through the point of contact of the shell with the plane of motion P. Then

$$\sin{{\delta }_{*}} = {{R}_{c}}{\text{/}}{{R}_{o}},$$

where ${{R}_{c}} = m{{R}_{t}}{\text{/}}(m + M)$ is the distance from the center of the spherical shell to the center of mass of the spherical robot.

In [1], it was shown that in the case of constant control action of the form

$${\mathbf{Q}} = (m + M){{R}_{o}}{\mathbf{\gamma }} \times {\mathbf{g}}$$

and at the inclination angle of the plane $\delta < {{\delta }_{*}}$, the system (3) admits two families of steady-state solutions:

$$\begin{gathered} {\mathbf{\Omega }} = {{{\mathbf{\Omega }}}_{0}},\quad {\boldsymbol{\omega}} = {{\omega }_{0}}{\mathbf{n}}{\text{*}},\quad {\mathbf{n}}{\text{*}} = (n_{1}^{*},n_{2}^{*},n_{3}^{*}), \\ n_{1}^{*} = \frac{{\sin\delta {{R}_{o}}}}{{{{R}_{c}}}}(\cos\delta \pm \sqrt {R_{c}^{2}{\text{/}}R_{o}^{2} - \sin{^{2}}\delta } ),\quad n_{2}^{*} = 0, \\ n_{3}^{*} = \frac{{\cos\delta {{R}_{o}}}}{{{{R}_{c}}}}( - \sin\delta \tan \delta \pm \sqrt {R_{c}^{2}{\text{/}}R_{o}^{2} - \sin{^{2}}\delta } ), \\ \end{gathered} $$

((4))

where ${{{\mathbf{\Omega }}}_{0}}$, ${{\omega }_{0}}$ are the parameters of the family. The solutions (4) correspond to motion on an inclined plane in a straight line with constant angular velocity of the shell ${{{\mathbf{\Omega }}}_{0}}$, which, like the angular velocity of rotation of the pendulum about its symmetry axis ${{\omega }_{0}}$, can take any value and is defined from the initial conditions.

2 CONTROLLED MOTION AT AN ARBITRARY ANGLE OF INCLINATION

Consider the problem of the controlled motion of a spherical robot, formulated as follows.

Suppose we are given the position of the spherical robot,r(0), the position of the pendulum${\mathbf{n}}(0)$, the angular velocity of rotation of the pendulum${\boldsymbol{\omega}}(0)$and the velocity of rotation of the shell about the normal to the plane of motion${{\Omega }_{\gamma }}(0)$at an initial instant of time. Can control actionsQ be chosen in such a way that the spherical robot (its center) moves along a prescribed trajectory${\mathbf{r}}(t) = (x(t),y(t),0)$for a given time interval?

For the motion of the spherical robot of pendulum type on a horizontal plane this problem has been solved in [2, 5]. In particular, in [5] an explicit algorithm is presented which determines control actions for motion along a given trajectory. In [2], an additional integral for the case of uniformly accelerated motion in a straight line is found and it is shown that in this case the system (3) is reduced to one degree of freedom, where the angle of deviation of the pendulum from the vertical position in the plane along the direction of motion has been chosen as a generalized coordinate.

In [2, 5], it is also pointed out that a necessary condition for controlled motion is that an inequality which holds for motion on an inclined plane

$$i + mR_{t}^{2} > m{{R}_{o}}{{R}_{t}}$$

must be satisfied. This can be done by appropriately choosing mass and geometric characteristics of the system.

Below we present an algorithm that makes it possible to solve the problem of determining a control input for motion on an inclined plane.

(1) Define the law of motion along the trajectory

$${\mathbf{r}}(t) = (x(t),y(t),0).$$

((5))

From the condition that there is no slipping at the point of contact (2), we obtain expressions for the change in angular velocity ${\mathbf{\Omega }}(t)$ and acceleration ${\mathbf{\dot {\Omega }}}(t)$:

$${\mathbf{\Omega }}(t) = \frac{1}{{{{R}_{o}}}}{\mathbf{\gamma }} \times {\mathbf{V}} + {{\Omega }_{\gamma }}{\mathbf{\gamma }},\quad {\mathbf{\dot {\Omega }}}(t) = \frac{1}{{{{R}_{o}}}}{\mathbf{\gamma }} \times {\mathbf{\dot {V}}} + {{\dot {\Omega }}_{\gamma }}{\mathbf{\gamma }}.$$

((6))

The projection ${{\Omega }_{\gamma }}$ of the angular velocity of the spherical shell onto the axis Oz is in the general case an arbitrary function of time.

In what follows we shall assume that ${{\Omega }_{\gamma }} = 0$. This assumption corresponds to the rubber rolling model [6] (it is assumed that there is no slipping and spinning at the point of contact).

Substituting the trajectory Eq. (5) into (6) taking the assumption ${{\Omega }_{\gamma }} = 0$, into account, we obtain explicit dependences ${\mathbf{\Omega }}(t),{\mathbf{\dot {\Omega }}}(t)$. Here we assume that the initial angular velocity of the shell ${\mathbf{\Omega }}(0)$ is matched with the trajectory ${\mathbf{r}}(t)$ and that Eqs. (6) are satisfied at the initial instant of time.

(2) Introduce new variables ${\mathbf{X}} = (\theta ,\xi ,{{\omega }_{\theta }},{{\omega }_{\xi }},{{\omega }_{n}})$ related to the variables ${\mathbf{n}},{\boldsymbol{\omega}}$ by

$$\begin{gathered} {\mathbf{n}} = (\cos\xi \sin\theta ,\sin\xi \sin\theta , - \cos\theta ), \\ {\boldsymbol{\omega}} = ({{\omega }_{\theta }}\sin\xi + \sin\theta \cos\xi ({{\omega }_{\xi }}\cos\theta + {{\omega }_{n}}), \\ - {{\omega }_{\theta }}\cos\xi + \sin\theta \sin\xi ({{\omega }_{\xi }}\cos\theta + {{\omega }_{n}}), \\ {{\omega }_{\xi }}\sin{^{2}}\theta - {{\omega }_{n}}\cos\theta ). \\ \end{gathered} $$

((7))

The variables ${{\omega }_{n}}$, $\theta$, and $\xi$ have the obvious physical meaning: ${{\omega }_{n}}$ is the angular velocity of rotation of the pendulum about its symmetry axis, $\theta$ is the angle of deviation of the pendulum from the line drawn from the center of the sphere to the point of contact of the plane (see Fig. 1), and $\xi$ is the angle between the axis $Ox$ and the projection of the vector ${\mathbf{n}}$ onto the inclined plane. The variables ${{\omega }_{\theta }}$, ${{\omega }_{\xi }}$ are related to $\theta$ and $\xi$ by

$$\dot {\theta } = {{\omega }_{\theta }},\quad \dot {\xi } = {{\omega }_{\xi }}.$$

((8))

(3) Eliminating the control ${\mathbf{Q}}$ from the system, add the first two equations of (3). Substitute the explicit dependences ${\mathbf{\dot {\Omega }}}(t)$ obtained earlier into the resulting equation and the third equation of (3). The resulting equation, written in the variables X, and Eqs. (8) form a closed system of five differential equations explicitly depending on time:

$${\mathbf{A}}({\mathbf{X}},t){\mathbf{\dot {X}}} = {\mathbf{b}}({\mathbf{X}},t),$$

((9))

where ${\mathbf{A}}({\mathbf{X}},t)$, ${\mathbf{b}}({\mathbf{X}},t)$ are, respectively, the matrix and the vector of the coefficients of the equations, which depend explicitly on time.

(4) Integrating (numerically) the resulting system with given initial conditions ${\mathbf{X}}(0)$, find the dependence ${\mathbf{X}}(t)$. Further, knowing ${\mathbf{X}}(t)$, find the explicit dependence of the control torque ${\mathbf{Q}}(t)$ from the first equation of (3).

2.1 Uniform Motion of a Spherical Robot along an Arbitrary Straight Line

2.1.1. Reduction of the system to one degree of freedom. For uniform motion in a straight line with velocity ${{{v}}_{0}}$ we represent the law of motion along the trajectory (5) in the form

$${\mathbf{r}}(t) = ({{{v}}_{0}}t\cos\psi ,{{{v}}_{0}}t \sin\psi ,0),$$

((10))

where $\psi$ is the angle between the axis Ox and the direction of motion of the center of the spherical robot.

Substituting (7) and (10) into the sum of the first two equations of (3) and the third equation of (3) taking (6) into account, we obtain the following system of equations

$$\begin{gathered} {{{\dot {\omega }}}_{\theta }}\; = - \frac{1}{{G(\theta )}}(\sin\theta (m{{R}_{o}}{{R}_{t}}\omega _{\theta }^{2} - ({{i}_{0}}\cos\theta - m{{R}_{o}}{{R}_{t}})\omega _{\xi }^{2} \\ \, - (i + j){{\omega }_{n}}{{\omega }_{\xi }} + m{\text{g}}{{R}_{t}}\cos\delta ) \\ \, - ((m + M){{R}_{o}} - m{{R}_{t}}\cos\theta ){\text{g}}\sin\delta \cos\xi ), \\ \end{gathered} $$

$$\begin{gathered} {{{\dot {\omega }}}_{\xi }}\; = - \frac{1}{{G(\theta )\sin\theta }}(2G(\theta )\cos\theta {{\omega }_{\theta }}{{\omega }_{\xi }} + (i + j){{\omega }_{n}}{{\omega }_{\theta }} \\ \,\left. { + \,((m + M){{R}_{o}}\cos\theta - m{{R}_{t}}){\text{g}}\sin\delta \sin\xi } \right), \\ \end{gathered} $$

((11))

$$\begin{gathered} {{{\dot {\omega }}}_{n}} = - \frac{{{{R}_{o}}\sin\theta }}{{G(\theta )(i + j)}}((i + j)m{{R}_{t}}{{\omega }_{n}}{{\omega }_{\theta }} \\ \, + ((m + M)i + mMR_{t}^{2}){\text{g}}\sin \delta \sin\xi ), \\ \dot {\theta } = {{\omega }_{\theta }},\quad \dot {\xi } = {{\omega }_{\xi }}, \\ \end{gathered} $$

where $G(\theta ) = {{i}_{0}} - m{{R}_{o}}{{R}_{t}}\cos\theta$, ${{i}_{0}} = i + mR_{t}^{2}$.

We note that Eqs. (11) do not depend on the direction of motion $\psi$ and the initial velocity ${{{v}}_{0}}$, so the calculations below hold for any direction of motion $\psi \in [0,2\pi ]$ and for any initial velocity bounded only by physically realizable values.

The system (11) admits an integral that is linear in the angular velocities

$$\begin{gathered} F = {{\omega }_{n}}(i + j)(\cos\delta \cos\theta - \sin\delta \sin\theta \cos\xi ) \\ \, - {{\omega }_{\theta }}G(\theta )\sin\delta \sin\xi + {{\omega }_{\xi }}\sin\theta (m{{R}_{o}}{{R}_{t}}\sin\delta \cos\xi \\ \, - {{i}_{0}}(\cos\delta \sin\theta + \sin\delta \cos\theta \cos\xi )). \\ \end{gathered} $$

((12))

Thus, in view of (12) the system (11) can be reduced to a system of four differential equations, which need to be solved with the given initial conditions ${\mathbf{X}}(0)$.

In the general case, such systems are non-Hamiltonian in nature and may exhibit chaotic behavior such as strange attractors. For a detailed discussion of Hamiltonization of such systems, see, for example, [7, 8]. Thus, a control that is unstable with respect to small perturbations can arise in the system of interest under some initial conditions.

In the example we consider here, the system (11) admits an invariant manifold lying on the zero level set of the integral F and defined by the equations

$$\xi = 0,\quad {{\omega }_{\xi }} = 0,\quad {{\omega }_{n}} = 0.$$

((13))

This manifold corresponds to oscillations of the pendulum in the vertical plane along the axis Ox (the pendulum does not rotate about its symmetry axis).

If ${\mathbf{X}}(0)$ lies on the manifold (13) at the initial instant of time, the system (11) simplifies and its solution can be analyzed explicitly.

2.1.2. Analysis of a system with one degree of freedom. On the invariant manifold (13), the system (9) reduces to a system with one degree of freedom:

$$\begin{gathered} {{{\dot {\omega }}}_{\theta }} = - \frac{{m{{R}_{t}}\sin\theta }}{{G(\theta )}}({{R}_{o}}\omega _{\theta }^{2} + {\text{g}}\cos\delta ) \\ \, + \frac{{{\text{g}}\sin\delta }}{{G(\theta )}}\left( {(m + M){{R}_{o}} - m{{R}_{t}}\cos\theta } \right), \\ \dot {\theta } = {{\omega }_{\theta }}. \\ \end{gathered} $$

((14))

To determine a control torque that ensures uniform motion in a straight line according to the law (10), we substitute the relations thus obtained into the first equation of (3) and obtain:

$$\begin{gathered} {\mathbf{Q}} = (0,m{{R}_{o}}{{R}_{t}}(\omega _{\theta }^{2}\sin\theta - {{{\dot {\omega }}}_{\theta }}\cos\theta ) \\ \, - (m + M){\text{g}}{{R}_{o}}{{R}_{t}}\sin\delta ,0). \\ \end{gathered} $$

We analyze the system (14) in more detail. This system admits an integral of motion that is quadratic in angular velocity and is an analog of the integral of generalized energy in the reference system whose motion is uniformly accelerated:

$$\begin{gathered} C = \frac{{G{{{(\theta )}}^{2}}\omega _{\theta }^{2}}}{2} - m{\text{g}}{{R}_{t}}\cos\delta \\ \, \times \left[ {G(\theta )\cos\theta + \frac{{m{{R}_{o}}{{R}_{t}}}}{2}(2 + co{{s}^{2}}\theta )} \right] \\ \, - {\text{g}}\sin\delta \left[ {{{R}_{o}}\theta \left( {{{i}_{0}}(m + M) + \frac{{{{m}^{2}}R_{t}^{2}}}{2}} \right)} \right. \\ \left. {\, - \frac{{m{{R}_{t}}}}{2}\sin\theta (G(\theta ) + {{i}_{0}} + 2(m + M)R_{o}^{2})} \right]. \\ \end{gathered} $$

((15))

Figure 2 shows a phase portrait of the system (3) on the plane $(\theta ,\,\,{{\omega }_{\theta }})$ in the case of uniform motion of the spherical robot in an arbitrary straight line for different values of the angle of inclination of the plane $\delta$ and the following mass and geometric parameters of the system:

$$\begin{gathered} m = M = 1,\quad {{R}_{t}} = 0.25,\quad {{R}_{o}} = 1, \\ i = 0.23,\quad j = 0.23,\quad I = 2{\text{/}}3. \\ \end{gathered} $$

Fig. 2.

Phase portrait of the system (3) in the case of uniform motion in a straight line on an inclined plane at different angles of inclination δ.

For the above parameters the value of the critical angle of inclination ${{\delta }_{ * }} \approx 0.125$ rad.

At $\delta < {{\delta }_{ * }}$ (Figs. 2a, 2b) and the chosen mass and geometric parameters of the system on the phase plane there are two fixed points corresponding to the partial solutions (4) with ${{\omega }_{0}} = {{\omega }_{n}} = 0$, whose stability is investigated in [1]. Under the initial conditions from the region bounded by the separatrix, the solutions (4) correspond to unbounded motion on an inclined plane in a straight line with constant angular velocity of the shell, which can take any value and is determined from the initial conditions.

When $\delta = {{\delta }_{ * }}$ (Fig. 2c), a bifurcation occurs at which the two fixed points merge to form a single point [1]. As the numerical experiment has shown (see Fig. 2c), this point is unstable.

For $\delta > {{\delta }_{ * }}$ there exist no closed trajectories (see Fig. 2d) and there are no fixed points. The absolute value of the angular velocity of the pendulum ${{\omega }_{\theta }}$ increases indefinitely on average linearly in time (see Fig. 3а). This increase is due to the presence of a linear (in $\theta$) term in the integral (15).

Fig. 3.

(a) Dependence ${{\omega }_{\theta }}(t)$ plotted for the initial conditions $\theta (0) = - \delta$, ${{\omega }_{\theta }}(0) = 0$, and $\delta > {{\delta }_{ * }}(\delta = 0.175)$. (b) Ascent height $h{\text{/}}{{{v}}_{0}}$ as a function of the initial position of the pendulum ${{\theta }_{0}} = \theta (0)$ for uniform motion in a straight line under the initial conditions ${{\omega }_{\theta }}(0) = 0$ and $\delta > {{\delta }_{ * }}$$(\delta = 0.175)$, $\omega _{\theta }^{{{\text{max}}}} = 4$.

2.1.3. Physical interpretation. In a real physical system the angular velocity of rotation of the pendulum relative to the spherical shell, which is controlled by the motor, is bounded by some maximal value $\omega _{\theta }^{{{\text{max}}}}$, which is determined by the structural features of the spherical robot. When it is reached during rolling with velocity ${{{v}}_{0}}$, the absolute angular velocity of the pendulum is

$${{\omega }_{\theta }} = {{{v}}_{0}}{\text{/}}{{R}_{o}} + \omega _{\theta }^{{{\text{max}}}}.$$

((16))

When $\delta > {{\delta }_{ * }}$, the value of (16) is reached in finite time ${{T}_{{{\text{max}}}}}$ (see Fig. 3a). Consequently, the time of uniform motion and the ascent height, defined as h = ${{{v}}_{0}}{{T}_{{{\text{max}}}}}{\text{sin}}\delta$, are bounded and depend on the initial deviation of the pendulum $\theta (0) = {{\theta }_{0}}$ and the initial velocity ${{\omega }_{\theta }}(0)$.

Figure 3b shows the dependence $h{\text{/}}{{{v}}_{0}}$ for ${{\omega }_{\theta }}(0)$ = 0, which allows one to determine the optimal initial position of the pendulum in which the ascent height will be maximal (in the above example this is the value ${{\theta }_{0}}$ = 1.02 rad).

When $t > {{T}_{{{\text{max}}}}}$ the motion of the spherical robot up the inclined plane does not stop, but ceases to be uniform. In particular, even if the control is switched off completely, the motion of the spherical robot upwards will be uniformly decelerated until a complete stop. The choice of an optimal control regime for further motion upwards to the maximal possible height is an interesting open question.

2.2 Uniform Motion of the Spherical Robot in a Circle

Consider an example of determination of control actions for the uniform motion of a spherical robot in a circle on an inclined plane. In this case, the law of motion along the trajectory can be written as

$${\mathbf{r}}(t) = \left( {{{R}_{1}}\cos\left( {\frac{{2\pi t}}{T}} \right),\,\,{{R}_{1}}\sin\left( {\frac{{2\pi t}}{T}} \right),\,\,0} \right),$$

((17))

where ${{R}_{1}}$ is the radius of the circle and T is the time it takes for the spherical robot to pass a complete circle.

For numerical integration of the resulting equations we define the angular velocities and the initial position of the shell in accordance with (17) and the initial position of the pendulum, which corresponds to the steady-state solution (4), and direct the initial angular velocity of the pendulum along the perpendicular to the vector n the plane $Oxz$ (i.e., along the vector ${\mathbf{n}} \times {\mathbf{\beta }}$):

$$\begin{gathered} \theta (0) = \arccos n_{3}^{ * },\quad \xi (0) = 0, \\ {{\omega }_{\theta }}(0) = 0,\quad {{\omega }_{\xi }}(0) = 9.02,\quad {{\omega }_{n}}(0) = 0. \\ \end{gathered} $$

((18))

Substituting the resulting functions into the first equation of (3), we obtain the time dependences of the control torque vector components ${\mathbf{Q}}(t)$.

Figure 4 shows the angular velocities of the pendulum ${{\omega }_{\theta }}$, ${{\omega }_{\xi }}$, ${{\omega }_{n}}$, the angles $\theta$ and $\xi$ and the control torque vector components ${{Q}_{1}}$, ${{Q}_{2}}$ as functions of time for uniform motion of the spherical robot along a circle of radius ${{R}_{1}} = 2$ for time T = 5, which were obtained under the initial conditions (18) and at the angle of inclination of the plane $\delta < {{\delta }_{ * }}$ (δ = 0.1).

Fig. 4.

The angular velocities of the pendulum ${{\omega }_{\theta }}$, ${{\omega }_{\xi }}$, ${{\omega }_{n}}$ the angles $\theta$ and $\xi$, and the control torque vector components versus time for uniform motion of the spherical robot in a circle of radius ${{R}_{1}} = 2$ for time T = 5, under the initial conditions (18) and at the angle of inclination of the plane $\delta = 0.1$.

As can be seen in Fig. 4, the time dependences of the controls and phase variables are quasi-periodic. The periodic character of the controls can be obtained by a numerical search for periodic solutions (9).

The algorithm and the examples presented above of explicit control for motion in a straight line and a circle can be used to construct control along a more complex trajectory (composed of individual segments), by analogy with gait control [2, 4, 9].