1 Introduction

This paper investigates one of the modifications of the spherical robot moving by displacing its center of mass, a robot of pendulum type which is a spherical shell with an axisymmetric spherical pendulum fastened at its center.

Spherical robots are mobile robotic systems with enhanced performance: the spherical shell is completely symmetric and cannot fall or topple over, but the system can autonomously move in space. The internal structure by means of which the spherical robot moves in space can be totally enclosed to protect the internal electromechanical systems against adverse environmental conditions.

In addition, the spherical robot (as a system with rolling) is an interesting system for modeling and testing of various motion models. Different internal mechanisms can be used. A detailed overview of existing internal structures of spherical robots and the history of development of this area of robotics can be found in the dissertation by Ylikorpi [1] and in Refs. [2,3,4,5,6,7,8,9].

The dynamics of a spherical robot of pendulum type has been investigated previously in Refs. [10,11,12,13,14,15,16]. The authors obtained steady-state solutions of free motion on horizontal and inclined planes and analyzed their stability. For the case of controlled motion, explicit algorithms for the control of motion along a prescribed trajectory, including those with feedback, were obtained and elementary maneuvers involved in controlling gaits were presented which allow acceleration (deceleration) during straight-line motion and enable rotation through a given angle.

The motion planning problem for a spherical robot driven by a pendulum with two degrees of freedom is considered in Ref. [17]. The proposed algorithm constructs a path consisting of straight-line segments, and then the movement along each segment is designed based on the dynamic model of the robot.

In Refs. [10,11,12,13,14,15,16] it was assumed that the spherical shell rolls without slipping (subject to the nonholonomic constraint) and that there is no dissipation. In this case, the system without control has additional linear integrals of motion and an invariant measure (see also [18, 19]) and is integrable. But, as is well known, such an approximation corresponds to a point contact, which is not the case in a natural experiment.

The influence of friction during rolling arising on the contact area is a complicated problem which is yet to be solved. To date, multiparameter friction models [20,21,22,23,24], based on Contensou’s model [25], have been developed and used in some systems with rolling. But these models, on the one hand, require considerable computational costs, on the other hand, they are not always in agreement with experiment (see [26,27,28] and references therein). In addition, such systems should consider the possibility of transition between rolling and slipping [29]. The reader is also referred to [30,31,32], where the authors introduce a precession nonlinear model of the controlled motion of a pendulum-driven ball robot along a straight line.

In this paper, we explore the dynamics of a pendulum-driven spherical robot, taking into account the linear model of viscous rolling friction [33,34,35]. According to this model, the spherical robot is acted upon by the torque of rolling resistance which is proportional to the angular velocity of the spherical shell of the system. The model is relatively simple; nevertheless, there are experimental studies [36,37,38, 42] which confirm the adequacy of the friction model with very good accuracy.

We present equations of motion which describe the rolling of a spherical robot on a horizontal plane, taking the torque of rolling resistance into account. In this work, we find steady-state solutions which represent motions with constant velocity along a straight line. In this case, the pendulum is deflected through a constant angle from the vertical axis under constant control action. In what follows, using the motion model under consideration, we propose an algorithm for designing elementary maneuvers which ensures transition between two steady motions of the system.

2 Equations of motion of a pendulum-driven spherical robot on a horizontal plane with rolling resistance present

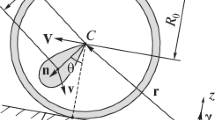
The spherical robot is a spherical shell of radius \(R_o\) (Fig. 1) at whose center an axisymmetric 3-DOF pendulum (Lagrange’s top) is fastened. In what follows, we will refer to the pendulum as a top. The system is set in motion by forced oscillations of the pendulum. In this paper, we address a model problem in which it is assumed that the device actuating the pendulum generates control torque \({\varvec{Q}}\), applied at the point C of attachment of the pendulum.

Fig. 1
figure 1

a A schematic model of a spherical robot with an axisymmetric pendulum drive, b a prototype of the spherical robot which was developed at the Laboratory of nonlinear analysis and new types of vehicles (Udmurt State University)

Full size image

To describe the dynamics of the spherical robot, we define a fixed (inertial) coordinate system Oxyz with unit vectors \({\varvec{e}}_1, {\varvec{e}}_2, {\varvec{e}}_3\) in such a way that the plane Oxy coincides with the surface on which the spherical robot rolls. The axis Oz is directed vertically downwards (Fig. 1).

Here and below the vectors and the matrices are denoted in boldface font. The vectors projected onto units vectors \({\varvec{e}}_1, {\varvec{e}}_2, {\varvec{e}}_3\). The normal vector to the surface of rolling is denoted as \(\varvec{\upgamma }=(0, 0, -1)\).

The position and configuration of the system are completely defined by the coordinates of the center of the sphere, \({\mathbf {r}}=(x, y, -R_o)\in {\mathbb {R}}^2\), and by two orthogonal matrices of rotation of the shell, \(\mathbf{S}_s\in SO(3)\), and the top, \(\mathbf{S}_t\in SO(3)\), relative to the fixed coordinate system.

The kinetic energy of the system has the form [10, 15]

$$\begin{aligned} T=\dfrac{1}{2}M{\varvec{V}}^2+\frac{1}{2}(\varvec{\Omega }, \mathbf{I}\varvec{\Omega }) +\dfrac{1}{2} m{\varvec{v}}^2+ \dfrac{1}{2}(\varvec{\upomega }, \mathbf{i_0}\,\varvec{\upomega }), \end{aligned}$$
(1)

where M, \(\mathbf{I}=I\mathbf{E}\) are the mass and the central tensor of inertia of the shell, \(\mathbf{E}\) is the identity matrix, m, \(\mathbf{{i_0}}=\mathrm {diag}(i,i,i+j)\) are the mass and the central tensor of inertia of the top, \({\varvec{V}}=(\dot{x}, \dot{y}, 0)\) and \(\varvec{\Omega }=(\Omega _x, \Omega _y, \Omega _z)\) are the velocity of the center of mass and the angular velocity of the shell, and \({\varvec{v}}\) and \(\varvec{\upomega }\) are the velocity of the center of mass and the angular velocity of the pendulum, respectively.

The change in the angular momentum relative to the center of the spherical shell and in the linear momentum of the shell can be written as

$$\begin{aligned} \begin{aligned} I\dot{\varvec{\Omega }}=R_o{\varvec{N}}_o\times \varvec{\upgamma }-{\varvec{Q}}+{\varvec{M}}_f,\\ M\dot{{\varvec{V}}}= {\varvec{N}}_o+{\varvec{N}}_t+M{\varvec{g}}, \end{aligned} \end{aligned}$$
(2)

where \({\varvec{N}}_o\), \({\varvec{N}}_t\) are the reaction forces acting on the shell at the contact point P and at the point of attachment of the top C, respectively, \({\varvec{M}}_f\) is the torque of rolling resistance acting on the shell from the plane, \({\varvec{Q}}\) is the control torque, and \({\varvec{g}}=(0, 0, \mathrm g)\) is the vector of free-fall acceleration.

We will assume that the torque of rolling resistance is proportional to the horizontal component of the angular velocity of the shell and has the form

$$\begin{aligned} {\varvec{M}}_f=-\mu \varvec{\upgamma }\times (\varvec{\Omega }\times \varvec{\upgamma }), \end{aligned}$$
(3)

where \(\mu \) is the constant coefficient. The choice of this model of viscous resistance is motivated by the results of investigating the model problems of rigid bodies rolling on horizontal surfaces, such as a tippe top, a Celtic stone, disks, which allowed, in addition to experimental validation, a qualitatively explanation of the complex dynamic phenomena accompanying their motion: inversion, turn, retrograde motion [39,40,41,42]. In this paper, we neglect the spinning resistance, because the spinning resistance is negligibly small in the case of point contact

The equations of motion for the top relative to its center of mass have the form

$$\begin{aligned} \begin{aligned}&\dfrac{d}{dt}\left( i\varvec{\upomega }+j(\varvec{\upomega },{\varvec{n}}){\varvec{n}} \right) =R_t{\varvec{n}}\times {\varvec{N}}_t+{\varvec{Q}},\\&m\dot{{\varvec{v}}}=m{\varvec{g}}-{\varvec{N}}_t, \end{aligned} \end{aligned}$$
(4)

where \({\varvec{n}}\) is the vector directed along the symmetry axis of the pendulum, and \(R_t\) is the distance from the center of the spherical shell to the center of mass of the pendulum (see Fig. 1).

The velocity of the center of mass of the top is defined from the condition that the velocities of the center of the shell and the suspension point of the pendulum be the same, which is expressed by a (holonomic) constraint of the form

$$\begin{aligned} {\varvec{v}}={\varvec{V}}+R_t\varvec{\upomega }\times {\varvec{n}}. \end{aligned}$$
(5)

The velocity of the center of the shell, \({\varvec{V}}\), is related to the angular velocity of the shell, \(\varvec{\Omega }\), by the condition that there be no slipping at the contact point P:

$$\begin{aligned} {\varvec{V}} =R_o\varvec{\Omega }\times \varvec{\upgamma }, \end{aligned}$$
(6)

Eliminating the reaction forces \({{\varvec{N}}}_o,{{\varvec{N}}}_t\) from (2) and (4) taking (3), (5) and (6) into account, and adding an evolution equation for the vector \({\varvec{n}}\), we obtain a reduced system of equations for the controlled motion on a horizontal plane of a spherical shell with an axisymmetric top fastened at the geometric center of the shell:

$$\begin{aligned} \begin{array}{ll} &{}\mathbf{J}\dot{\varvec{\Omega }}+ mR_oR_t\varvec{\upgamma }\times (\dot{\varvec{\upomega }}\times {\varvec{n}}) \\ &{}=-mR_oR_t \varvec{\upgamma }\times (\varvec{\upomega }\times \dot{{\varvec{n}}})-{\varvec{Q}} -\mu \varvec{\upgamma }\times (\varvec{\Omega }\times \varvec{\upgamma }),\\ &{}i_0\dot{\varvec{\upomega }}+j_0(\dot{\varvec{\upomega }}\cdot {\varvec{n}}){\varvec{n}}+ mR_oR_t{\varvec{n}}\times (\dot{\varvec{\Omega }}\times \varvec{\upgamma })\\ &{}=mR_t{\varvec{n}}\times {\varvec{g}} -j_0 (\varvec{\upomega }\cdot {\varvec{n}})\varvec{\upomega }\times {\varvec{n}} +{\varvec{Q}},\\ &{}\dot{{\varvec{n}}}=\varvec{\upomega }\times {{\varvec{n}}}, \end{array} \end{aligned}$$
(7)

where \(\mathbf{J}=\mathrm {diag}(I_0, I_0, I),\)    \(I_0=I+(M+m)R_o^2, \quad i_0=i+mR_t^2, \quad j_0=j-mR_t^2.\)

To completely describe the system dynamics in absolute space, we need to supplement Eqs.  (6) and (7) with kinematic relations for matrices \(\mathbf{S}_s\) and \(\mathbf{S}_t\).

3 Steady-state solutions

To find steady-state solutions to the system of interest, we equate the derivatives \(\dot{\varvec{\Omega }},\dot{\varvec{\upomega }},\,\dot{{\varvec{n}}}\) in (7) to zero and obtain the system of equations

$$\begin{aligned} \begin{array}{ll} {\varvec{Q}}+\mu \varvec{\upgamma }\times (\varvec{\Omega }\times \varvec{\upgamma })=0,&{}\\ mR_t{\varvec{n}}\times {\varvec{g}} +{\varvec{Q}}=0,&{}\\ \varvec{\upomega }\times {\varvec{n}}=0.&{} \end{array} \end{aligned}$$
(8)

This yields the following statement.

Proposition 1

The system (7) admits the family of steady-state solutions

$$\begin{aligned} \begin{array}{ll} \varvec{\Omega }&{}=\dfrac{mR_t}{\mu }{\varvec{n}}\times {\varvec{g}}+ \Omega _{\gamma }\varvec{\upgamma },\\ \varvec{\upomega }&{}=\omega _n {{\varvec{n}}},\\ {\varvec{n}}&{}=\left( \sin \theta \cos \varphi ,\,\,\sin \theta \sin \varphi ,\,\, \cos \theta \right) , \end{array} \end{aligned}$$
(9)

where \(\Omega _\gamma , \omega _n, \theta , \varphi \) are the parameters of the family, with the control action

$$\begin{aligned} {\varvec{Q}}=-mR_t{\varvec{n}}\times {\varvec{g}}, \end{aligned}$$
(10)

The statement is easy to prove using an explicit solution to the system (8).

The parameters \(\omega _n\) and \(\Omega _\gamma \) define the angular velocity of rotation of the pendulum about its symmetry axis and of the spherical shell about the normal to the plane, respectively. The angles \(\theta \) and \(\varphi \) completely define the position of the pendulum in space: \(\theta \) is the angle of deflection of the pendulum from the vertical and \(\varphi \) is the angle between the axis Ox and the plane of the pendulum’s oscillation (Fig. 2).

The system admits two types of motion corresponding to steady-state solutions: motions of a robot in a straight line with constant velocity such that the pendulum is tilted at a constant (arbitrary) angle relative to the vertical, and the rotation of the spherical robot through a given angle \(\psi \) about the vertical by rotating the pendulum about its symmetry axis with angular velocity \(\omega _n\).

Fig. 2
figure 2

Definition of the angles \(\theta \) and \(\varphi \)

Full size image

Corresponding to the solutions (9) is the motion of the center of mass along a straight line in the direction defined by the angle \(\varphi \), with constant angular velocity of the shell, \(\varvec{\Omega }\), and with constant velocity of the center of mass of the system

$$\begin{aligned} |V|=\dfrac{m g R_o R_t\sin \theta }{\mu }. \end{aligned}$$
(11)

It follows from (11) that the velocity of motion with the solutions (9) is bounded

$$\begin{aligned} |V|\leqslant \dfrac{m g R_o R_t}{\mu }. \end{aligned}$$
(12)

The stability analysis of the partial solution (9) is an open question, which we will not consider in this paper.

4 Control using gaits

In this section, we consider control using gaits. We define a gait as elementary controlled motion of a system (acceleration or rotation through a given angle) which ensures transition from one steady motion (9) to another in a given time interval T.

Let us formulate the problem of the controlled motion of a spherical robot using gaits as follows.

Let the initial and final states of the system (7) correspond to the steady-state solutions (9) with the following parameter values:

$$\begin{aligned} t= & {} 0:\quad \Omega _\gamma =\Omega _\gamma ^{(1)}, \omega _n=\omega _n^{(1)}, \theta =\theta _1, \varphi =\varphi _1, \end{aligned}$$
(13)
$$\begin{aligned} t= & {} T: \quad \Omega _\gamma =\Omega _\gamma ^{(2)}, \omega _n=\omega _n^{(2)}, \theta =\theta _2, \varphi =\varphi _2. \end{aligned}$$
(14)

Can a control action \({\varvec{Q}}(t)\) be chosen so as to ensure transition between given steady-state solutions in the time interval T?

This problem can also be formulated in the form of a boundary-value problem for a system of differential equations.

To do this, we first add up the first two equations of (7), thereby eliminating the control \({\varvec{Q}}\) from the system. We obtain a system of six differential first-order equations in the variables \({\varvec{n}}, \varvec{\Omega }, \varvec{\upomega }\). Supplementing these equations with boundary conditions which follow from (9), (13) and (14), we obtain

$$\begin{aligned} \begin{array}{l} \mathbf{J}\dot{\varvec{\Omega }} +mR_oR_t\bigl (\varvec{\upgamma }\times (\dot{\varvec{\upomega }}\times {\varvec{n}}) +{\varvec{n}}\times (\dot{\varvec{\Omega }}\times \varvec{\upgamma })\bigr )\\ +i_0\dot{\varvec{\upomega }}+j_0(\dot{\varvec{\upomega }}\cdot {\varvec{n}}){\varvec{n}}= mR_t{\varvec{n}}\times {\varvec{g}} -\mu \varvec{\upgamma }\times (\varvec{\Omega }\times \varvec{\upgamma }) \\ -j_0 (\varvec{\upomega }\cdot {\varvec{n}})\, \varvec{\upomega }\times {\varvec{n}} -mR_oR_t\bigl ( (\varvec{\upomega }\cdot {\varvec{n}})\varvec{\upgamma }\times \varvec{\upomega }-\omega ^2 \varvec{\upgamma }\times {{\varvec{n}}})\bigr ) ,\\ \dot{{\varvec{n}}}=\varvec{\upomega }\times {\varvec{n}},\\ \end{array} \end{aligned}$$
(15)
$$\begin{aligned} \begin{array}{l} {\varvec{n}}(0)={\varvec{n}}_1, ~\varvec{\upomega }(0)=\omega _n^{(1)}{\varvec{n}}_1, \varvec{\Omega }(0)=\dfrac{m R_t}{\mu } {\varvec{n}}_1\times {\varvec{g}}+ \Omega _\gamma ^{(1)}\varvec{\upgamma }, \end{array} \end{aligned}$$
(16)
$$\begin{aligned} \begin{array}{l} {\varvec{n}}(T)={\varvec{n}}_2, ~\varvec{\upomega }(T)=\omega _n^{(2)}{\varvec{n}}_2, \varvec{\Omega }(T)=\dfrac{m R_t}{\mu } {\varvec{n}}_2\times {\varvec{g}}+ \Omega _\gamma ^{(2)}\varvec{\upgamma }, \end{array} \end{aligned}$$
(17)

where \({\varvec{n}}_1= {\varvec{n}}(\theta _1, \varphi _1), {\varvec{n}}_2= {\varvec{n}}(\theta _2, \varphi _2)\).

Remark 1

Equations (15) have a redundant number of unknown functions (nine in six equations). Therefore, in solving the posed boundary-value problem we can define some three functions in the form of explicit functions of time in such a way that equations (15) and the boundary conditions (16), (17) are satisfied.

4.1 The algorithm of gaits design

In this section we solve the posed boundary-value problem and consider the algorithm of gaits design.

Step 1. Define the vectors \({\varvec{n}}(t), \varvec{\upomega }(t)\) in the form of explicit functions of time depending on the parameters and satisfying the equation for \(\dot{{\varvec{n}}}\) (15) with the corresponding boundary conditions (16), (17). In the general case, this can be done by defining three functions \(\theta (t), \varphi (t), \omega _n(t)\) which satisfy the following conditions:

$$\begin{aligned} \begin{aligned}&\theta (0)=\theta _1, ~{\dot{\theta }}(0)=0, ~\varphi (0)=\varphi _1, ~{\dot{\varphi }}(0)=0, ~\omega _n(0)=\omega _n^{(1)},\\&\theta (T)=\theta _2, ~{\dot{\theta }}(T)=0, ~\varphi (T)=\varphi _2, ~{\dot{\varphi }}(T)=0, ~\omega _n(T)=\omega _n^{(2)}.\\ \end{aligned} \end{aligned}$$
(18)

In this case, the vectors \({\varvec{n}}\) and \(\varvec{\upomega }\) will depend on these functions as follows:

$$\begin{aligned} \begin{array}{rcl} {\varvec{n}}(t)&{}=&{}\bigl ( \sin \theta (t)\cos \varphi (t),\,\,\sin \theta (t)\sin \varphi (t),\,\, \cos \theta (t)\bigr ),\\ \varvec{\upomega }(t)&{}=&{}{\varvec{n}}(t)\times \dot{{\varvec{n}}}(t)+\omega _n(t){\varvec{n}}(t). \end{array} \end{aligned}$$
(19)

Remark 2

The boundary conditions for the derivatives \({\dot{\theta }}(t)\) and \({\dot{\varphi }}(t)\) follow from the boundary conditions for the angular velocities \(\varvec{\upomega }\) and the equation for \(\dot{{\varvec{n}}}\) (15).

In this paper, we choose the functions \(\theta (t),\) \(\varphi (t)\) and \(\omega _n(t)\) in the form

$$\begin{aligned} \begin{aligned}&\theta (t,\alpha ,T)=\alpha \sin ^2\left( \dfrac{\pi t}{T}\right) + (\theta _2-\theta _1)\sin ^2\left( \dfrac{\pi t}{2T}\right) +\theta _1 ,\\&\varphi (t)= (\varphi _2-\varphi _1)\sin ^2\left( \dfrac{\pi t}{2T}\right) +\varphi _1,\\&\omega _n(t)=\omega _n=\mathrm{const}. \end{aligned} \end{aligned}$$
(20)

where \(\alpha \) is a still unknown parameter defining the oscillation amplitude of the top, T is the time of one maneuver, and the angles \(\theta _1, \theta _2\), \(\varphi _1, \varphi _2\) are the parameter values of the steady-state solutions (13), (14) at the initial and final times.

The choice of the form of the functions \(\theta (t)\) and \(\varphi (t)\) is based on the analysis of the possibility of technical implementation and their maximal simplicity. In the general case, such gaits can be formed using arbitrary functions satisfying condition 18. As a justification of the choice of a specific form of functions one can formulate various optimality criteria, however, these investigations are beyond the scope of this paper due to their complexity.

Remark 3

It follows from (19) that for given \({\varvec{n}}_2\) the parameters \(\theta _2\) and \(\varphi _2\) are defined up to the change of variables

$$\begin{aligned} \begin{array}{llll} 1.&{} \theta \rightarrow -\theta , \quad \varphi \rightarrow \varphi +(2k+1)\pi , &{} ~k\in {\mathbb {Z}},\\ 2.&{} \theta \rightarrow \theta +2\pi n, \quad \varphi \rightarrow \varphi +2\pi k, &{} ~n, k\in {\mathbb {Z}}. \end{array} \end{aligned}$$
(21)

It also follows from (20) that different values of n and k correspond to different dependences \({\varvec{n}}(t)\) under the same boundary conditions (16), (17), i.e., by changing the values of n and k one can perform a countable number of maneuvers enabling transition between the same steady-state solutions.

Remark 4

The functions (20) generalize the control used to accelerate the spherical robot along a straight line in a nonholonomic setting (without dissipation, \(\mu =0\)) [13]. We recall that a stable steady-state solution in the absence of rolling resistance is rolling motion along a straight line with constant velocity, in which case the pendulum is in the lower position and can rotate about its symmetry axis with constant velocity \(\omega _n\).

Step 2. Substitute (19) and (20) into the first equation of (15). We obtain a nonautonomous system of differential first-order equations for defining the angular velocity of the shell:

$$\begin{aligned} \varvec{{\dot{\Omega }}}={\varvec{f}}(\varvec{\Omega }, t), \end{aligned}$$
(22)

where \({\varvec{f}}\) is a function linear in \(\varvec{\Omega }\).

Integrating the system (22) with the initial conditions (16) gives the function \(\varvec{\Omega }\left( t, \alpha , \theta _2, \varphi _2, \omega _n, \Omega _\gamma ^{(2)}\right) \). We require that at the final time \(t=T\) the angular velocity \(\varvec{\Omega }(t=T)\) satisfies the boundary condition (17), i.e.,

$$\begin{aligned} \varvec{\Omega }\left( T, \alpha , \theta _2, \varphi _2, \omega _n, \Omega _\gamma ^{(2)}\right) = \dfrac{m R_t}{\mu } \,{\varvec{n}}_2(\alpha , \theta _2, \varphi _2)\times {\varvec{g}} +\Omega _\gamma ^{(2)}\varvec{\upgamma }. \end{aligned}$$
(23)

Solving Eq. (23) for the control parameters \(\alpha , \omega _n \) and/or part of the boundary conditions \(\theta _2, \varphi _2, \Omega _\gamma ^{(2)}\), we obtain an explicit form of control (20).

As we will see below, particular gaits will require that only part of the boundary conditions (16), (17) be satisfied, and the solution to the system (23) will reduce to solving one or two equations relative to the projections of the angular velocity \(\varvec{\Omega }\) onto the axes of the coordinate system Oxyz.

Step 3. Substitute the control parameters thus found into Eq. (22) and integrate it. Use the resulting function \(\varvec{\Omega }(t)\) to define the control torques \({\varvec{Q}}(t)\) from (7) in explicit form.

Step 4. To construct the trajectory of motion, it is necessary to substitute the function \(\varvec{\Omega }(t)\) into Eq. (6) and to integrate it with initial conditions corresponding to the position of the center of the shell of the spherical robot at the initial time (for example, \(x(0)=0,~y(0)=0\)).

We consider the above algorithm for two gaits: acceleration of the ball to a given velocity in the case of motion along a straight line and rotation through a given angle.

4.2 Acceleration along a straight line

Let us define the control \({\varvec{Q}}(t)\) which causes the center of mass of the spherical robot to accelerate from some (physically realizable) velocity \(V_1\) to velocity \(V_2\) in a given time T and to move without changing its direction, for example, along the axis Ox. Assume that the pendulum does not rotate about its symmetry axis.

The values of the parameters of the functions (20) corresponding to the gait considered have the form

$$\begin{aligned} \begin{aligned} {\sin \theta _1}&=\dfrac{\mu V_{1}}{m g R_o R_t}, \quad {\sin \theta _2}=\dfrac{\mu V_{2}}{m g R_o R_t}, \\ \omega _n&=0, \quad \varphi _1=0, \quad \varphi _2=0. \end{aligned} \end{aligned}$$
(24)

We note that the first equation of (15), taking into account (19) and (20) with parameters (24), admits an invariant manifold given by

$$\begin{aligned} \Omega _x=0, \quad \Omega _z=\mathrm{const}. \end{aligned}$$
(25)

This manifold corresponds to rolling of the spherical shell along the axis Ox with variable angular velocity.

On the manifold (25) the boundary conditions (16), (17) for \(\Omega _z\) take the form \(\Omega _z{(0)} = \Omega _z{(T)}= \Omega _\gamma ^{(1)}=\Omega _\gamma ^{(2)}=\mathrm{const}\). For simplicity we will assume that this constant is zero.

Thus, on the invariant manifold (25) the boundary-value problem (15) reduces to one differential first-order equation for the projection \(\Omega _y\) of the angular velocity of the shell onto the axis Oy with the following boundary conditions:

$$\begin{aligned} \begin{aligned} {\dot{\Omega }}_y&=-\dfrac{\mu \Omega _y+i_0\ddot{\theta } +mR_oR_t(\dot{\theta }^2\sin \theta -\ddot{\theta }\cos \theta ) +mg R_t\sin \theta }{I_0-mR_oR_t\cos \theta },\\ \Omega _y(0)&=-\dfrac{V_1}{R_o}, \quad \Omega _y(T)=-\dfrac{V_2}{R_o}, \end{aligned} \end{aligned}$$
(26)

where \(\theta \), \(\dot{\theta }\), \(\ddot{\theta }\) are explicit functions of time and parameters \(\alpha \) and T (20) and depend on \(V_2\), see (24).

To solve the boundary-value problem (26), we integrate the resulting differential equation with the initial condition \(\Omega _y(0)\) and plot a curve of the final angular velocity \(\Omega _y(T)\) as a function of \(\alpha \). The intersection of this curve with the straight line \(-V_2/R_o\) corresponds to the value of \(\alpha \) at which the boundary conditions of the problem (26) are satisfied.

As an example, Fig. 3 shows graphs of the function \(\Omega _y(T)\) (26) versus \(\alpha \), which correspond to acceleration of the spherical robot from rest (\(\theta _1=0\)) to velocity \(V_2=0.72\) m/s (\(\theta _2=0.258~\mathrm {rad}\)) in the time intervals \(T=1\) s and \(T=2\) s, with the friction coefficient \(\mu =0.001\) kg \(\cdot \)m\(^2\)/s.

The simulation was performed using the following mass-geometric parameters corresponding to the parameters of the full-scale specimen (see Fig. 1b), with the mass expressed in kg, the distance in m and the moment of inertia in kg\(\cdot \)m\(^2\):

$$\begin{aligned} \begin{aligned}&m=0.32, \quad M=0.06, \quad R_o=0.06, \quad R_t=0.015,\\&i=j=0.2244\cdot 10^{-3}, \quad I=0.144 \cdot 10^{-3}. \end{aligned} \end{aligned}$$
(27)
Fig. 3
figure 3

a Graphs of the function \(\Omega _y(T)\) (26) of \(\alpha \) for different values of T and equal other parameters (27). b An enlarged fragment of a, \(\alpha _0=0.34~\mathrm {rad}\)—the value of \(\alpha \) which satisfies the boundary-value problem (26) for \(T=2\) s

Full size image

In this example, during the gait the projection \(\Omega _y\) of the angular velocity onto the axis Oy of the shell decreases from zero to the value \(-V_2/R_o=-12\) rad/s. The intersection of the function \(\Omega _y(T)\) with the straight line \(-V_2/R_o\) for \(T=2\) s corresponds to the value \(\alpha _0=0.34~\mathrm {rad}\) (see Fig. 3b).

Next, following the algorithm described above, we substitute the value \(\alpha =\alpha _0\) into Eq. (26) and integrate it. The resulting function \(\Omega _y(t)\) can now be used to define the control torques \({\varvec{Q}}=(Q_x, Q_y, Q_z)\) from (7):

$$\begin{aligned} \begin{array}{rcl} Q_x&{}=&{}0, \\ Q_y&{}=&{} \dfrac{ mR_oR_t\cos \theta \left( \mu \Omega _y(t) +mR_oR_t({\dot{\theta }}^2\sin \theta -\ddot{\theta }\cos \theta )\right) }{I_0-mR_oR_t\cos \theta }\\ &{} &{}+\dfrac{I_0(i_0\ddot{\theta }+m g R_t\sin \theta )}{I_0-mR_oR_t\cos \theta }, \\ Q_z&{}=&{}0. \end{array} \end{aligned}$$
(28)

The graphs of the angle \(\theta \), velocity V, control \(Q_y\) and the angular velocity of the pendulum, \(\omega _y\), versus time for the example considered are shown in Fig. 4. It can be seen that during the gait the velocity of the center of the spherical shell, V, increases monotonically, and the projection of the angular velocity at the final time instant takes values corresponding to the steady-state solutions (9).

Fig. 4
figure 4

Graphs of the angle \(\theta \), velocity V, control \(Q_y\), the projection \(\omega _y\) of the angular velocity of the pendulum onto the axis Oy, plotted versus time, in the case of acceleration from rest to velocity \(V_2=0.72\) m/s during one gait for \(\alpha _0=0.34~\mathrm {rad}\)

Full size image

Remark 5

Figure 3 shows that in the example considered the equation \(\Omega _y(T)=-V_2/R_o\) has two roots. For the second root \(\alpha _0=3.73 ~\mathrm {rad}\) the velocity V during a gait changes nonmonotonically (see Fig. 5).

If there are several roots, then the choice of one of them which will be used in the future to develop a maneuver can be made based on the technical limitations of the torque and angular velocity of the drive motors.

Fig. 5
figure 5

Velocity V and control \(Q_y\), plotted versus time, in the case of acceleration from rest to velocity \(V_2=0.72\) m/s during one gait for \(\alpha _0=3.73~\mathrm {rad}\)

Full size image

4.3 Motion with changing direction

Consider a gait used to turn the spherical robot through a given angle.

Let the spherical robot move at an initial time instant (in accordance with the steady-state solution (9)) along the axis Ox with constant velocity \(V_1\). As before, we assume that during the maneuver the pendulum does not rotate about its symmetry axis. In addition, at the initial time instant the shell of the spherical robot does not rotate about the vertical axis.

Thus, we define part of the parameters (18) of the pendulum’s motion and choose initial conditions for the angular velocity of the shell

$$\begin{aligned}&\varphi _1=0, \quad \sin \theta _1=\dfrac{\mu V_{1}}{m g R_t}, \quad \omega _n=0,\end{aligned}$$
(29)
$$\begin{aligned}&\Omega _x(0)=0, \quad \Omega _y(0)=-V_1/R_o, \quad \Omega _z(0)=0. \end{aligned}$$
(30)

Let us require that, as a result of the maneuver, the spherical robot turn through a given angle \(\psi \) and move along a straight line in the direction of the vector

$$\begin{aligned} \varvec{\tau }=(\cos \psi ,\sin \psi , 0) \end{aligned}$$
(31)

in accordance with the steady-state solution (7). This requirement imposes a restriction on the final position of the pendulum: \(\varphi _2=\psi ,\) and defines the boundary conditions for the angular velocity of the shell at the end of the maneuver

$$\begin{aligned} \begin{array}{l} {\Omega }_x(T)-\dfrac{mg R_t}{\mu }\sin \theta _2\sin \psi =0, \\ {\Omega }_y(T)+\dfrac{mg R_t}{\mu }\sin \theta _2\cos \psi =0, \end{array} \end{aligned}$$
(32)

where \(\theta _2\) is a still undefined parameter of the maneuver which defines the final position of the pendulum and the velocity of the spherical robot.

Remark 6

In this case, we impose no restriction on the angular velocity of rotation of the shell about the vertical at the end of the maneuver \(\Omega _z(T)\). This is due to the fact that, at any value of \(\Omega _z(T)\), the final motion will be the steady-state solution (7).

In accordance with the above algorithm, we solve the problem (22) with the boundary conditions (30), (32). For this we substitute the solution of the system (22) for \(\Omega _x, \Omega _y\) with the initial condition (30) into conditions (32). We obtain a system of two equations in the parameters of the maneuver, \(\alpha \) and \(\theta _2\). Solving this system numerically, we obtain parameter values at which the required maneuver can be performed.

Figure 6 gives an example of the trajectory of the contact point of the spherical robot with parameters (27) for rotation through the angle \(\psi =\pi /3\) in the time interval \(T=2\). The robot rolls with the initial velocity \(V_1=0.12\) m/s and the friction coefficient \(\mu =0.001\) kg\(\cdot \)m\(^2\)/s. The corresponding graphs of controls \({\varvec{Q}}(t)\) are shown in Fig. 7. The parameters of the maneuver are \( \theta _{2}=-0.025~\mathrm{{rad}}, ~\alpha =-0.076. \)

Fig. 6
figure 6

Trajectory of the contact point of the spherical robot rotating through the angle \(\psi =\pi /3\) in the time interval \(T=2\) s

Full size image
Fig. 7
figure 7

Graphs showing the projections of the vector of controls \({\varvec{Q}}\) versus time for rotation through the angle \(\psi =\pi /3\) in the time interval \(T=2\) s

Full size image

Interestingly, in the above example, \(\theta _2<0\). Consequently, after the maneuver the spherical robot moves along a straight line turned through the angle \(\psi =\pi /3\) relative to the axis Ox, but in the direction opposite to the vector \(\varvec{\tau }\) (see Fig. 6). This is due to the fact that the functions \(\theta (t)\) and \(\varphi (t)\) are defined up to the change of variables (21), see Remark 3.

We also note that the system of Eq. (32) can have several roots \((\theta _2, \alpha )\). If \(\theta _2>0\), then the trajectory of the contact point of the spherical robot at the end of the maneuver is directed along the vector \(\varvec{\tau }\).

As an illustration of this statement, we give two more examples. In the first case, for the value \(\psi =7\pi /3\) we have \(\theta _2=0.018>0\) (see Fig. 8), and at the end of the maneuver, the spherical robot moves along the vector \(\varvec{\tau }\). In the second case, for the value \(\psi =-2\pi /3\), we have \(\theta _2=-0.024<0\) (see Fig. 9), and at the end of the maneuver, the spherical robot moves in a direction similar to that of the first case, but opposite to the vector \(\varvec{\tau }\) (31).

Fig. 8
figure 8

a Trajectory of the contact point of the spherical robot and b the corresponding vertical projection of the angular velocity for rotation in the time interval \(T=2\) through the angle \(\psi =7\pi /3\)

Full size image
Fig. 9
figure 9

(a) Trajectory of the contact point of the spherical robot and (b) the corresponding vertical projection of the angular velocity for rotation in the time interval \(T=2\) through the angle \(\psi =-2\pi /3\)

Full size image

Remark 7

During the gait the vertical projection of the angular velocity changes nonmonotonically, and at time \(t=T\) it takes a nonzero value (see Figs. 8b, 9b). Thus, the rotation is accompanied by changes in the velocity of spinning of the shell of the spherical robot about the vertical axis.

4.4 Discussion

In this section we discuss the question of the necessity of incorporating friction into models describing the controlled motion of systems with rolling.

In Ref. [13], the controlled motion of a pendulum-driven spherical robot in a nonholonomic setting without dissipation was considered. Algorithms for calculating the control actions required to perform various gaits, including acceleration and rotation through a given angle, were developed. The trajectory of the spherical robot obtained according to this algorithm for rotation through the angle \(\psi =\pi /3\) with the initial velocity of motion \(V_1=0.4\) m/s is shown in Fig. 10a (solid line). We denote the corresponding control by \(Q_{nh}\).

If one uses the control \(Q_{nh}\) for maneuvering using the model with friction, then the result of the maneuver does obviously not coincide with the planned result. For example, the dotted line in Fig. 10a indicates the trajectory of the spherical robot obtained using the model with rolling friction (7) and with model control \(Q_{nh}\). The figure shows that the direction of rotation at the end of the gait does not correspond to the planned direction. Moreover, in an environment with friction, the spherical robot stops predictably after control is turned off.

To estimate the influence of the friction coefficient on the angle of rotation, we present a graph (see Fig. 10b) of the angle \(\varphi (T)\) at which the spherical robot moves after the gait \(Q_{nh}\) versus the friction coefficient. It can be seen that, as the value of \(\mu \) increases, the deviation of the trajectory from the required direction \(\psi =\pi /3\) increases.

Fig. 10
figure 10

a Trajectory of motion of the contact point of the spherical robot during rotation through the angle \(\psi =\pi /3\) in the time interval \(T=2\) in the nonholonomic model [11] (solid line, \(\mu =0\)), and with the same control (\(Q_{nh}\)) on a “rough” surface (dotted line). b The angle of rotation versus the friction coefficient during motion with a control corresponding to the nonholonomic model on a “rough” surface (with friction). For \(\mu =0\), the angle of rotation is \(\psi =\pi /3\)

Full size image

As the friction coefficient \(\mu ^*\) exceeds some critical value, the direction of motion after the maneuver becomes constant. Such a dependence is due to the fact that at large friction coefficients the initial velocity of the spherical robot (in the direction of the axis Ox) decays in a time interval smaller than the duration of the maneuver. As a result, the final direction of motion is influenced only by the direction in which the pendulum is deflected with control \(Q_{nh}\). In the chosen example, this direction coincides with the axis Oy, and hence \(\varphi (T)\) takes the value \(\pi /2\).

Thus, even at small values of the friction coefficient, control using the nonholonomic model can lead to fairly large errors in the final position or in the direction of motion. As the friction coefficient exceeds a critical value, control using nonholonomic gaits is impossible in principle.

5 Experimental validation of the model

To test the proposed algorithm for controlling the spherical robot and to estimate the chosen friction model, experimental investigations for the prototype (see Fig. 1b) described above have been conducted. In the course of the experiments, the velocity and the trajectory of the spherical robot were recovered using a marker-based motion capture system Vicon. The prototype is a transparent spherical shell inside which a one-degree-of freedom pendulum is placed below which a rotor is mounted. In practice, this design allows the implementation of only one maneuver, which is described in Sect. 4.2, namely, the motion along a straight line. The transparent shell of the prototype of the spherical robot makes it possible to place inside the robot markers of the motion capture system for recovering the motion parameters.

The shell of the spherical robot is made of PET material, and acrylic sheet was used as the underlying surface. The value of the coefficient of viscous rolling friction for this pair of materials was \(\mu = 0.002\), and was defined using the method tested to describe the free motion of spherical bodies [38, 42]. In the course of the experiments the spherical robot moving from rest along a straight line on a horizontal plane was to accelerate up to 0.25 m/s for time \(T = 2\) s.

For the the initial conditions, the parameters of the function \(\theta (t)\) are defined by the solution to Eq. (23) taking the mass and geometric parameters of the spherical robot (27). For implementation of the above-mentioned maneuver, the functions defining the maneuver have the following form:

$$\begin{aligned} \begin{aligned}&\theta (t)=0.1182\sin ^2\left( \dfrac{\pi t}{2}\right) + 0.178\sin ^2\left( \dfrac{\pi t}{4}\right) ,\\&\varphi (t)= 0,\quad \omega _n(t)=0. \end{aligned} \end{aligned}$$
(33)

In the experiments, the angle of rotation of the pendulum about the vertical was specified and maintained by the robot control system using the function (33).

Figure 11 shows trajectories and the corresponding velocities of the spherical robot performing this maneuver. The solid lines are the graphs obtained in the experiments, and the dotted lines indicate the simulation results. A video of the experiment can be found at https://youtu.be/yq30Ksm-pr0.

Fig. 11
figure 11

a Trajectories of motion of the spherical robot for control action (33) in experiment (solid line) and simulation (dotted line). b The velocities of spherical robots obtained from experimental data (solid line) and in simulations(dotted line)

Full size image

The deviations of the trajectory and the velocity of the spherical robot performing a maneuver in the experiments from the simulation results are due to nonideality of the geometry and measurement errors of the mass and inertia parameters of the prototype. But even despite this fact, the results of the experiment are in good quantitative agreement with the simulation results within the framework of the model of viscous rolling resistance.

6 Conclusion

In this paper, the model of the controlled motion of a spherical robot with an axisymmetric pendulum drive is considered taking rolling resistance into account.

It is shown that the system admits steady-state solutions only under constant control action, and the center of mass of the system moves uniformly along a straight line. Much of the focus of the paper is on designing elementary maneuvers (gaits) which ensure transition between two steady-state motions of the system: acceleration along a straight line and rotation through a given angle. These gaits can serve as a basis for designing algorithms for controlled motion along an arbitrary trajectory. The more general motion planning problem for driving a spherical robot from an initial to the desired configuration can be considered as a task for representing the trajectory of motion as a sequence of sections of straight lines and rotations between them. Then the proposed algorithm can be implemented.

The steady-state solutions obtained can be used in the future to construct models of the controlled motion of a spherical robot with feedback [14, 43,44,45,46]. The question of the stability of partial solutions (9) of the system considered remains also open.

The results of the experimental investigations confirm the adequacy of the proposed model of viscous rolling resistance and the possibility of using it to form control actions for the spherical robot. It would also be of interest to perform an experimental validation of the motion model used for more complicated controls. The proposed model of viscous rolling resistance can be easily implemented both for describing the rolling dynamics of free bodies and for developing of control for actuated rolling robots. But this model cannot be implemented when sliding arises. If sliding is difficult to eliminate, then other friction models should be investigated and applied.

We note that in this paper we have analyzed motion and defined control relative to a fixed coordinate system. On the other hand, controlled motion is in practice often implemented using a control action defined relative to the shell of the spherical robot (see, e.g., [7, 36, 44]). Generalization of the results obtained to the case of this (more realistic) model of a controlled spherical robot is also an open problem.