A Pseudo-Second Order Kinetic Equation for Sorption Processes

Abstract

The problem of substantiating a pseudo-second order equation in the kinetics of sorption processes is considered. A simple way is presented of transforming the Langmuir kinetic equation written for a process within a limited volume into a polynomial relation in the form of the sum of difference terms of first- and second-order kinetic equations. It is shown that such a relation is reduced to a good approximation of a pseudo-second order equation over a much wider range of conditions determined by the equilibrium and kinetic characteristics of the sorbent and the experimental parameters than was predicted earlier. It is established that the errors of such a theoretical approximation are either negligible or do not exceed the corresponding errors at the initial stage of kinetic experiments within a confined space. It is concluded that the applicability of the pseudo-second order model is independent of the mechanisms determining the rate of sorption and does not require concepts of chemisorption or special equations of kinetics controlled via chemical reactions or diffusion.

INTRODUCTION

The kinetic model of sorption based on a pseudo-second order equation became extraordinarily popular after the works of Ho and McKay [1, 2], which demonstrated a simple and almost universal way of describing experimental data. Most current studies of the kinetics of sorption processes use this model, and dozens of articles are published annually. We shall refer only to a few reviews and original works of recent years with a great many cited sources [3–6]. A uniform approach to describing the sorption kinetic has emerged: Experimental results are compared to linearized integral forms of kinetic equations of the pseudo-first and pseudo-second orders:

$${\text{ln}}\left( {1 - \frac{{{{q}_{{\text{t}}}}}}{{{{q}_{{\text{e}}}}}}} \right) = - {{k}_{{\text{I}}}}t,$$

((1))

$$\frac{t}{{{{q}_{{\text{t}}}}}} = \frac{1}{{{{k}_{2}}q_{{\text{e}}}^{2}}} + \frac{t}{{{{q}_{{\text{e}}}}}},$$

((2))

where q_t and q_e are the averaged current and equilibrium concentrations, respectively, in a sorbent; and k with different subscripts are rate constants. If the experimental data are better described by model (2), it is concluded that the process proceeds via chemisorption or is controlled by chemical reactions [3]; otherwise, diffusion control is most often assumed. One reason for such an approach (which cannot be considered correct) is the lack of theoretical substantiation of the pseudo-second order kinetic equation dq_t/dt = k₂(q_e – q_t)² and the conditions of its applicability to sorption processes. Another reason is probably that this form of the equation was first proposed as an empirical relation for describing the kinetics of sorption in processes that were interpreted as heterogeneous chemical reactions [7].

Among studies that have made an important contribution to developing the theoretical concepts of the equations of the pseudo-first and pseudo-second orders were the works of Azizian [8] and Liu and Shen [9], which showed the possibility of approximately deriving these equations using the Langmuir kinetic model [10]. However, we consider these derivations to be mathematically cumbersome, incapable of completely substantiating the conditions of different models’ applicability, and contradict one another in predicting such conditions. Another problem is the need to correctly interpret Langmuir’s classic work [10] in the context of modern knowledge. It can be seen from his reasoning and comments that he treated any adsorption on the surface of a material from the viewpoint of early twentieth century science as a “pseudochemical” or chemical process. However, few notice that the kinetic and equilibrium relations formulated in [10] do not require assumptions of the process’s mechanism because they were derived using a model of the condensation of components on a surface and their subsequent evaporation.

It would seem that the possibility of deriving a pseudo-second order equation from Langmuir’s classic model, which was shown by Azizian [8] and Liu and Shen [9], was perceived by many researchers as additional proof of the relationship of this equation to the chemisorption mechanism. This was noted by Plazinski et al. [11], who analyzed their theoretical works. They also showed [12] that the pseudo-second order equation can be applied to diffusion-controlled processes in sorbent granules. In [13, 14], a first-order difference equation for obtaining an approximate description of diffusion processes was used to prove there was no relationship between the control mechanism and the form of the corresponding kinetic equations, and to demonstrate the possibility of obtaining an approximate derivation of the pseudo-second order equation from it. It was shown that such a derivation is possible if the initial kinetic equation becomes nonlinear when two conditions are met simultaneously: (1) the boundary concentration of a component being sorbed is not constant over time, which is characteristic of kinetic experiments in a confined space (the batch technique) and (2) the equilibrium sorption isotherm is nonlinear.

This work continues the study on substantiating the relationship between the pseudo-second order equation to known kinetic models and determining specific features of this equation and its conditions of applicability.

MODELING THE KINETIC PROCESS

In analogy with the equation for the kinetics of the accumulation of an adsorbate from the gas phase on the surface of an adsorbent that was presented in Langmuir’s fundamental work [10], sorption from liquid can be described by the equation

$$\frac{{d{{q}_{{\text{t}}}}}}{{dt}} = {{k}_{{{\text{L}}{\text{,1}}}}}~{{c}_{{\text{t}}}}({{q}_{{\Sigma }}} - {{q}_{{\text{t}}}}) - {{k}_{{{\text{L}}{\text{,2}}}}}~{{q}_{{\text{t}}}},$$

((3))

where q_t is the current concentration of the component in the sorbent phase; k_L,1(time⁻¹ concentration⁻¹) and k_L,2(time^–1) are the kinetic coefficients of the sorption and desorption processes, respectively; q_Σ is the maximum number of sites accessible to the component being sorbed in the sorbent; (q_Σ – q_t) is the concentration of free (unoccupied) sites; and c_t is the current concentration of the component in the solution.

Once equilibrium is reached (q_t = q_e, c_t = c_e), the right- and left-hand sides of Eq. (3) become zero, producing the familiar expression for the Langmuir equilibrium isotherm

$${{q}_{{\text{e}}}} = \frac{{{{q}_{{{\Sigma \;}}}}({{k}_{{{\text{L}}{\text{,1}}}}}{\text{/}}{{k}_{{{\text{L}}{\text{,2}}}}}){{c}_{{\text{e}}}}}}{{1 + A{{c}_{{\text{e}}}}}} = \frac{{{{q}_{{\Sigma }}}A{{c}_{{\text{e}}}}}}{{1 + A{{c}_{{\text{e}}}}}},$$

where A = k_L,1/k_L,2 is the Langmuir constant (concentration⁻¹). Kinetic equation (3) must be solved in order to describe sorption before equilibration. If the concentration of the component in the solution during the mass-transfer process does not change and remains equal to the initial concentration, we have constant boundary condition c_t = c₀ = const. In practice, this condition can be satisfied to a good approximation in, e.g., a dynamic or static process (in a column or a reactor) of contact between sorbent grains of total volume ω_v (or weight ω_m) with large volume V of solution:

$$V{{c}_{0}} \gg \omega {{q}_{{\text{e}}}},$$

((4))

where q_e is the equilibrium concentration in the sorbent.

It was shown in [13] that the kinetics of such processes, regardless of the type of the isotherm, can be described by the familiar first-order kinetic equation

$$\frac{{d{{q}_{{\text{t}}}}}}{{dt}} = ~{{k}_{1}}~({{q}_{{\text{e}}}} - {{q}_{{\text{t}}}}),$$

((5))

which is more convenient than Eq. (3) because it includes only one kinetic constant and has simple integral form (1). Note that the formulations of kinetic equations (3) and (5) are not based on concepts of mechanisms that could be either physical adsorption or chemisorption controlled by diffusion or chemical reactions.

Equation (5) was first proposed by Lagergren in [15] and was then substantiated by a number of researchers, including Glückauf and Tikhonov, in solving dynamic diffusion problems [16, 17].

If condition (4) is not met (i.e., if the kinetic experiment is performed in batch mode), the concentration of the solution changes (falls over time) during the mass-transfer process, and material balance condition ΔcV = Δqω yields

$${{c}_{{\text{t}}}} = \left( {{{c}_{0}} - \frac{\omega }{V}{{q}_{{\text{t}}}}} \right).$$

((6))

We can now rewrite Langmuir kinetic equation (3) for a confined space as

$$\frac{{d{{q}_{{\text{t}}}}}}{{dt}} = {{k}_{{{\text{L}}{\text{,1}}}}}({{q}_{{\Sigma }}} - {{q}_{{\text{t}}}})\left( {{{c}_{0}} - {{q}_{{\text{t}}}}\frac{\omega }{V}} \right) - {{k}_{{{\text{L}}{\text{,2}}}}}~{{q}_{{\text{t}}}}.$$

((7))

Equation (7) can be written as

$$\begin{gathered} \frac{{d{{q}_{{\text{t}}}}}}{{dt}} = {{k}_{{{\text{L}}{\text{,1}}}}}[({{q}_{{\Sigma }}} - {{q}_{{\text{e}}}}) + ({{q}_{{\text{e}}}} - ~{{q}_{{\text{t}}}})] \\ \times \;\left[ {\left( {{{c}_{0}}\, - \,\frac{\omega }{V}{{q}_{{\text{e}}}}} \right)\, + \,\frac{\omega }{V}({{q}_{{\text{e}}}}\, - \,{{q}_{{\text{t}}}})} \right]\, - \,{{k}_{{{\text{L}}{\text{,2}}}}}{{q}_{{\text{e}}}}\, + \,{{k}_{{{\text{L}}{\text{,2}}}}}({{q}_{{\text{e}}}}\, - \,{{q}_{{\text{t}}}}). \\ \end{gathered} $$

((8))

Under equilibrium conditions dq_t/dt = 0 and q_t = q_e, it follows from Eq. (7) that

$${{c}_{0}} - \frac{\omega }{V}{{q}_{{\text{e}}}} = \frac{{{{k}_{{{\text{L}}{\text{,2}}}}}{{q}_{{\text{e}}}}}}{{{{k}_{{{\text{L}}{\text{,1}}}}}({{q}_{{\Sigma }}} - {{q}_{{\text{e}}}})}}.$$

((9))

Simple transformations of Eq. (8) with allowance for Eq. (9) yield

$$\frac{{d{{q}_{{\text{t}}}}}}{{dt}} = {{k}_{1}}({{q}_{{\text{e}}}} - ~{{q}_{{\text{t}}}}) + {{k}_{2}}{{({{q}_{{\text{e}}}} - {{q}_{{\text{t}}}})}^{2}},$$

((10))

where

$${{k}_{1}} = {{k}_{{{\text{L}}{\text{,1}}}}}\left[ {\frac{{{{q}_{{\Sigma }}}}}{{A({{q}_{{\Sigma }}} - {{q}_{{\text{e}}}})}} + \frac{\omega }{V}({{q}_{{\Sigma }}} - ~{{q}_{{\text{e}}}})} \right],$$

((11))

$$~{{k}_{2}} = {{k}_{{{\text{L}}{\text{,1}}}}}\frac{\omega }{V}.$$

((12))

The dimensions of the parameters in Eqs. (8)–(12) should match one another. For example, if we choose dimensions q, mg/g; c, g/L (mg/mL); V, L (mL); ω = ω_m, g; and t, s, which are widely used in practice, Langmuir constant A has the dimension L/g (mL/mg). The corresponding coefficients are k_L,1, s⁻¹ L/g (s⁻¹ mL/mg) and k_L,2, s⁻¹; and the kinetic coefficients of Eq. (10) are k₁, s⁻¹; and k₂, s⁻¹ g/m.

Using the Langmuir kinetic equation written for a limited volume, expression (10) was thus derived in virtually one line, in the form of the sum of difference relations of the pseudo-first and pseudo-second orders with coefficients that depend on the experimental conditions and characteristics of the sorbent. The derivation made in this work differs from the more awkward procedure performed by Liu and Shen [9] in that parameter q_e is not eliminated from the expressions for kinetic coefficients k₁ and k₂. This elimination seems useless, since the other sides of final equation (10) contain this parameter anyway. If necessary, the q_e value can be calculated from the initial experimental data using Eq. (9) if we know Langmuir constant A and maximum sorbent capacity q_Σ.

Azizian [8] was the first to show the possibility of obtaining an approximate derivation of individual equations of the pseudo-first and pseudo-second orders from the Langmuir kinetic equation. However, these mathematical transformations are very cumbersome and require numerous assumptions. This was likely behind the conclusion [8] that the first-order kinetic model is more characteristic of high initial concentrations of the component sorbed in the solution, and the second-order kinetic model is better at low c₀. This conclusion turns out to be wrong, as was proven in [13, 14].

CONDITIONS FOR THE APPLICABILITY OF THE MODEL BASED ON THE PSEUDO-SECOND ORDER EQUATION

In the above rigorous derivation of Eq. (10), it is important to determine the conditions under which it can be reduced to individual equations of the first or second orders. From a formal mathematical viewpoint, Liu and Shen’s trivial estimate [9], which states that at k₂(q_e – q_t) ⪢ k₁ the process kinetics can be approximately described using the pseudo-second order equation. This inequality of course requires the validity of the milder condition k₂q_e ⪢ k₁. However, many experimental data suggest this condition could be invalid, but the kinetics of sorption can still be described with the pseudo-second order equation [6, 14, 18].

Let us show that the wide applicability of the pseudo-second order kinetics model is due to specific features of integral equation (2) used for the linearization of experimental data, and to specific features related to errors in kinetic experiments within a confined space.

1. Unlike other models (including ones based on the first-order equation) whose range of applicability limited to the interval of variation in q_t(t), Eq. (2) also describes to a good approximation the equilibrium part, since t/q_t ≈ t/q_e follows from q_t ≈ q_e. For inexperienced researchers, this creates an opportunity to “improve” the applicability of the pseudo-second order kinetic model by including more equilibrium or near-equilibrium experimental points in an analysis.

2. In contrast to, e.g., constructing experimental curves using Eq. (1), in which all the points of the kinetic curve are of equal importance for the correlation coefficient, the initial points are virtually unimportant in constructing the curves with Eq. (2): the closer the process is to equilibrium, the more important value t/q_t at the corresponding point is to constructing the linearized experimental curve. Parameter 1/k_II$q_{{\text{e}}}^{2}$ (the third term of Eq. (2)) is incommensurably small when compared to the values at such points, as can be seen in curves t/q_t = f(t).

3. It is at the initial points of the kinetic curve, where c_t ≈ c₀, that the experimental errors in performing kinetic experiments in a confined space to obtain data based only on measuring the current concentration of the component being sorbed in a solution can be quite high. This problem was analyzed in detail in [13, 19]. It was found that the relative error in determining current concentration q_t of the component in the sorbent is, along with parameter t/q_t, found as

$$\frac{{{\Delta }{{q}_{{\text{t}}}}}}{{{{q}_{{\text{t}}}}}} \approx \frac{{{\Delta }(t{\text{/}}{{q}_{{\text{t}}}})}}{{t{\text{/}}{{q}_{{\text{t}}}}}} > 2\frac{{{\Delta }c}}{c}\frac{{{{c}_{0}}}}{{{{c}_{0}} - {{c}_{{\text{t}}}}}},$$

where Δc/c is the relative error in measuring the concentration of the component in the solution using one analytical means (instrument) or another.

Returning to the problem of describing the kinetic process for batch sorption (under varying boundary conditions) with the equilibrium Langmuir isotherm, note that Liu and Shen’s [9] condition of applicability for the pseudo-second order equation, k₂(q_e – q_t) ⪢ k₁ is functional and cannot be used in practice.

Let us try to find a practically useful condition. Let k₁ = αk₂q_e, where α is a certain positive number. Instead of Eq. (10), we can now write

$$\begin{gathered} \frac{{d{{q}_{{\text{t}}}}}}{{dt}}\, = \,{{k}_{2}}[\alpha {{q}_{{\text{e}}}}({{q}_{{\text{e}}}}\, - \,{{q}_{{\text{t}}}})\, + \,{{({{q}_{{\text{e}}}}\, - \,{{q}_{{\text{t}}}})}^{2}}]\, = \,{{\left( {\frac{{\alpha \, + \,2}}{2}} \right)}^{2}}q_{{\text{e}}}^{2}\, \\ + \;\left[ {\alpha + 1 - {{{\left( {\frac{{\alpha + 2}}{2}} \right)}}^{2}}} \right]q_{{\text{e}}}^{2} - (\alpha + 2){{q}_{{\text{e}}}}{{q}_{{\text{t}}}} + q_{{\text{t}}}^{2}. \\ \end{gathered} $$

((13))

If the condition

$$\left| {\alpha + 1 - {{{\left( {\frac{{\alpha + 2}}{2}} \right)}}^{2}}} \right| \ll {{\left( {\frac{{\alpha + 2}}{2}} \right)}^{2}}$$

((14))

is satisfied, we can write the sought pseudo-second order equation instead of Eq. (13):

$$\frac{{d{{q}_{{\text{t}}}}}}{{dt}} \approx {{k}_{2}}{{\left[ {\left( {\frac{{\alpha + 2}}{2}} \right){{q}_{{\text{e}}}} - {{q}_{{\text{t}}}}} \right]}^{2}} = {{k}_{2}}{{(q_{{\text{e}}}^{*} - {{q}_{{\text{t}}}})}^{2}}.$$

((15))

We rewrite condition (14) in the form

$$\left| {\alpha + 1 - {{{\left( {\frac{{\alpha + 2}}{2}} \right)}}^{2}}} \right| \leqslant 0.1{{\left( {\frac{{\alpha + 2}}{2}} \right)}^{2}},$$

((16))

assuming that the difference between the absolute values of the left- and right-hand sides is an order of magnitude. Inequality (16) has a simple solution: α ≤ 0.925. We can therefore write the first condition under which the kinetics of the sorption process within a confined space according to the Langmuir isotherm is described to a good approximation by the pseudo-second order equation

$${{k}_{1}} \leqslant 0.9~{{k}_{2}}{{q}_{{\text{e}}}}$$

((17))

instead of polynomial (10).

We now show that the approximate description of Eq. (10) by the pseudo-second-order equation can also be made (contrary to Liu and Shen’s opinion [9]) under another condition,

$${{k}_{2}}{{q}_{{\text{e}}}} \ll {{k}_{1}}.$$

((18))

We integrate Eq. (10), reducing it to an expression for a tabular integral:

$$\begin{gathered} - \mathop \smallint \limits_0^{{{q}_{{\text{t}}}}} \frac{{d({{q}_{{\text{e}}}} - ~{{q}_{{\text{t}}}})}}{{[{{k}_{1}} + {{k}_{2}}({{q}_{{\text{e}}}} - ~{{q}_{{\text{t}}}})]({{q}_{{\text{e}}}} - ~{{q}_{{\text{t}}}})}} \\ = - \frac{1}{{{{k}_{1}}}}\ln \left| {\frac{{({{k}_{2}}{{q}_{{\text{e}}}} + {{k}_{1}})({{q}_{{\text{e}}}} - ~{{q}_{{\text{t}}}})}}{{[{{k}_{2}}({{q}_{{\text{e}}}} - {{q}_{{\text{t}}}}) + {{k}_{1}}]{{q}_{{\text{e}}}}}}} \right| = t. \\ \end{gathered} $$

We now transform it and obtain a solution in the form

$${{q}_{{\text{t}}}} = {{q}_{{\text{e}}}}\frac{{({{k}_{2}}{{q}_{{\text{e}}}} + {{k}_{1}})[1 - ~\exp ( - {{k}_{1}}t)]}}{{[{{k}_{2}}{{q}_{{\text{e}}}}[1 - ~\exp ( - {{k}_{1}}t)] + {{k}_{1}}]}}.$$

((19))

When k₂q_e ⪡ k₁, Eq. (19) is reduced to the relation q_t ≈ q_e[1 – exp(–k₁t)], an integral expression for pseudo-first order equation (5). Using such an approximation, we present the expression for q_t as the sum of individual integral kinetic equations:

$$\begin{gathered} {{q}_{{\text{t}}}} = {{q}_{{{\text{t}}{\text{,I}}}}} + {{q}_{{{\text{t}}{\text{,II}}}}} \approx \left[ {\mathop {{{q}_{{\text{e}}}}}\limits_{_{{_{{_{{_{{}}}}}}}}}^{} [1 - \exp( - {{k}_{1}}t)]} \right. \\ - \;\left. {\frac{{{{{({{q}_{{\text{e}}}} - ~{{q}_{{{\text{e}}{\text{,I}}}}})}}^{2}}{{k}_{2}}t}}{{1 + ({{q}_{{\text{e}}}} - ~{{q}_{{{\text{e}}{\text{,I}}}}}){{k}_{2}}t}}} \right] + \frac{{q_{{{\text{e}}{\text{,II}}}}^{2}{{k}_{2}}t}}{{1 + {{q}_{{{\text{e}}{\text{,II}}}}}{{k}_{2}}t}}, \\ \end{gathered} $$

((20))

where q_e – q_e,I = q_e,II, and ${{q}_{{{\text{t}}{\text{,II}}}}} = q_{{{\text{e}}{\text{,II}}}}^{2}{{k}_{2}}t{\text{/}}[1 + {{q}_{{{\text{e}}{\text{,II}}}}}{{k}_{2}}t]$ is the result from integrating pseudo-second order equation dq_t,II/dt = k₂(q_e,II – q_t)². Note that function q_t can be split into q_t,I and q_t,II in infinitely many ways at different ratios between quantities q_e,I and q_e,II.

Let us consider individual parts of expression (20) in different time intervals of the kinetic process. In the interval 0 < t ⪡ 1/(q_e – q_e,I)k², the part within the square brackets is reduced to the expression

$$\begin{gathered} {{q}_{{{\text{t}}{\text{,I}}}}} \approx {{q}_{{\text{e}}}}[1 - {\text{exp}}( - {{k}_{1}}t)] - {{({{q}_{{\text{e}}}} - ~{{q}_{{{\text{e}}{\text{,I}}}}})}^{2}}{{k}_{2}}t \\ \approx {{q}_{{\text{e}}}}[1 - {\text{exp}}( - {{k}_{1}}t)] - ({{q}_{{\text{e}}}} - ~{{q}_{{{\text{e}}{\text{,I}}}}}) \\ \times \;\{ 1 - ~{\text{exp}}[ - {{k}_{2}}({{q}_{{\text{e}}}} - ~{{q}_{{{\text{e}}{\text{,I}}}}})t]\} \\ \end{gathered} $$

((21))

(since exp(–x) ≈ 1 – x when x ⪡ 1).

Using expression (21), we can estimate characteristic time t_1/2 of the first of the two kinetic processes described by sum (20):

$$\begin{gathered} \frac{{{{q}_{{{\text{e}}{\text{,I}}}}}}}{2} = {{q}_{{\text{e}}}}[1 - {\text{exp}}( - {{k}_{1}}{{t}_{{1/2}}})] - ({{q}_{{\text{e}}}} - ~{{q}_{{{\text{e}}{\text{,I}}}}}) \\ \times \;\{ 1 - {\text{exp}}[ - {{k}_{2}}({{q}_{{\text{e}}}} - ~{{q}_{{{\text{e}}{\text{,I}}}}}){{t}_{{1/2}}}]\} ~ \\ > ~\;{{q}_{{\text{e}}}}[1 - {\text{exp}}( - {{k}_{1}}{{t}_{{1/2}}})] - ({{q}_{{\text{e}}}} - ~{{q}_{{{\text{e}}{\text{,I}}}}})[1 - {\text{exp}}( - {{k}_{1}}{{t}_{{1/2}}})]. \\ \end{gathered} $$

((22))

It follows for q_t,I that ${{\left. {{{t}_{{1/2}}}} \right|}_{{{{q}_{{{\text{t}}{\text{,I}}}}}}}} < - {\kern 1pt} \ln \left( {1{\text{/}}2} \right){\text{/}}{{k}_{1}}$ or ${{\left. {{{t}_{{1/2}}}} \right|}_{{{{q}_{{{\text{t}}{\text{,I}}}}}}}} < 0.693{\text{/}}{{k}_{1}}$.

The characteristic time of the second kinetic process described by the last term of expression (20), a pseudo-second order equation, is easy to find in the form ${{\left. {{{t}_{{1/2}}}} \right|}_{{{{q}_{{{\text{t}}{\text{,II}}}}}}}} = 1{\text{/}}({{q}_{{{\text{e}}{\text{,II}}}}}{{k}_{1}})$.

Under the accepted condition (k₂q_e ⪡ k₁), it is obvious that ${{\left. {{{t}_{{1/2}}}} \right|}_{{{{q}_{{{\text{t}}{\text{,I}}}}}}}} \ll {{\left. {{{t}_{{1/2}}}} \right|}_{{{{q}_{{{\text{t}}{\text{,II}}}}}}}}$.

To simplify further analysis, we assume that beginning at a certain time exceeding the characteristic duration of the first kinetic process ($t > {{\left. {{{t}_{{1/2}}}} \right|}_{{{{q}_{{{\text{t}}{\text{,I}}}}}}}}$) (e.g., starting from t ≥ 1/k₁), approximate equality q_t,I ≈ q_e,I (the accuracy of which grows over time) is valid. We can then write

$$\begin{gathered} {{q}_{{\text{t}}}} = {{q}_{{{\text{t}}{\text{,I}}}}} + {{q}_{{{\text{t}}{\text{,II}}}}} \approx {{q}_{{{\text{e}}{\text{,I}}}}} + \frac{{q_{{{\text{e}}{\text{,II}}}}^{2}{{k}_{2}}t}}{{1 + {{q}_{{{\text{e}}{\text{,II}}}}}{{k}_{2}}t}} \\ = \frac{{{{q}_{{{\text{e}}{\text{,I}}}}} + {{q}_{{{\text{e}}{\text{,I}}}}}~{{q}_{{{\text{e}}{\text{,II}}}}}{{k}_{2}}t + q_{{{\text{e}}{\text{,II}}}}^{2}{{k}_{2}}t}}{{1 + {{q}_{{{\text{e}}{\text{,II}}}}}{{k}_{2}}t}}. \\ \end{gathered} $$

((23))

Returning to various ways of splitting function q_t into q_t,I and q_t,II, we choose one that meets the condition

$${{q}_{{{\text{e}}{\text{,I}}}}} \ll q_{{{\text{e}}{\text{,II}}}}^{2}{{k}_{2}}{\text{/}}{{k}_{1}}.$$

((24))

Under condition (24), quantity q_e,I in the numerator of the last term of Eq. (21) can be ignored, since this approximation has the maximum error at chosen initial time t = 1/k₁. Multiplying the inverse values of the left and right sides of expression (23) by t we obtain

$$\frac{t}{{{{q}_{{\text{t}}}}}} \approx \frac{t}{{{{q}_{{\text{e}}}}}} + \frac{1}{{{{k}_{2}}{{q}_{{\text{e}}}}{{q}_{{{\text{e}}{\text{,II}}}}}}},$$

((25))

which, under chosen conditions (18) and (24), coincides with the form of Eq. (2).

To completing this part of our analysis, let us consider the validity of the above assumption q_t,I ≈ q_e,I. The maximum theoretical error at initial point t = 1/k₁ can be estimated in analogy with the transformation in expression (22):

$$\begin{gathered} \frac{{{\Delta }q}}{q} = \frac{{{{q}_{{{\text{e}}{\text{,I}}}}} - {{{\left. {{{q}_{{{\text{t}}{\text{,I}}}}}} \right|}}_{{1/{{k}_{1}}}}}}}{{{{q}_{{{\text{e}}{\text{,I}}}}}}} \\ < \frac{{{{q}_{{{\text{e}}{\text{,I}}}}} - {{q}_{{{\text{e}}{\text{,I}}}}}[1 - \exp ( - 1)]}}{{{{q}_{{{\text{e}}{\text{,I}}}}}}} \approx 0.37. \\ \end{gathered} $$

The maximum experimental error at the same point at an average relative error of 5% in determining the concentration in the solution is

$$\frac{{{\Delta }q}}{q} > \frac{{0.1{{c}_{0}}}}{{{{c}_{0}} - {{c}_{{\text{t}}}}}} = 0.1\left( {\frac{{{{c}_{{\text{e}}}} + {{q}_{{\text{e}}}}\frac{\omega }{V}}}{{{{q}_{{\text{t}}}}\frac{\omega }{V}}}} \right)$$

$$ \approx 0.1\left[ {\frac{{\frac{{V{{q}_{{\text{e}}}}}}{{\omega A\left( {{{q}_{{\Sigma }}} - {{q}_{{\text{e}}}}} \right)}} + {{q}_{{\text{e}}}}}}{{{{q}_{{{\text{e}}{\text{,I}}}}} + \frac{{{{k}_{2}}}}{{{{k}_{1}}}}q_{{{\text{e}}{\text{,II}}}}^{2}}}~} \right]$$

$$ \approx 0.1\left[ {\frac{{\frac{V}{{\omega A\left( {{{q}_{{\Sigma }}} - {{q}_{{\text{e}}}}} \right)}} + 1}}{{\frac{{{{k}_{2}}}}{{{{k}_{1}}}}{{q}_{{{\text{e}}{\text{,II}}}}}}}~} \right] \gg 0.1$$

at a denominator value of k₂q_e,II/k₁ ⪡ 1.

Our assumptions are thus within the possible experimental error in a kinetic experiment in a confined space.

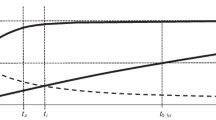
Figure 1 illustrates linearized time dependences t/q_t corresponding to the pseudo-second order model for the total kinetic process and its constituents. Figure 1 also traces the change in the error of such an approximation over time, relative to the change in the possible experimental error.

Fig. 1.

Integral kinetic dependences (1) t/q_t,I = t/q_e,I and (2) $~t{\text{/}}{{q}_{{{\text{t}}{\text{,II}}}}}$ = $t{\text{/}}{{q}_{{{\text{e}}{\text{,II}}}}}$ + $1{\text{/}}({{k}_{2}}q_{{{\text{e}}{\text{,II}}}}^{2})$ and (3) the dependence $t{\text{/}}{{q}_{{\text{t}}}}$ = $t{\text{/}}{{q}_{{\text{e}}}}$ + $1{\text{/}}({{k}_{2}}q_{{{\text{e}}{\text{,II}}}}^{2})$ for the total kinetic process q_t ≈ q_t,I + q_t,II at t ≥ 1/k₁ (left ordinate axis). The changes in the (4) theoretical and (5) experimental errors with time (right ordinate axis).

Our analysis shows that under conditions (17) and (18), the kinetic process modeled with the Langmuir equation for a limited volume can be approximately described by a pseudo-second order equation. For practical purposes, condition k₂q_e ≤ 0.1k₁ can be used instead of (18). Note too that the above considerations and mathematical transformations were made with no assumptions about the mechanism of sorption and the controlling kinetic steps.

CONCLUSIONS

Within the problem of substantiating the use of a pseudo-second order equation for describing sorption processes, it was shown how the kinetic Langmuir model written for a limited volume at varying boundary concentrations of the component can easily be transformed into polynomial expression dq_t/dt = k₁(q_e − q_t) + k₂(q_e − q_t)². If condition k₁ ≤ 0.9k₂q_e or k₂q_e ≤ 0.1k₁ is satisfied, it can be reduced to a good approximation of a pseudo-second order equation. The possibility of using this equation is unrelated to the kinetic mechanism.