INTRODUCTION

In one of our earlier articles dedicated to the kinetics of batch sorption processes, it was shown that their possible description by means of pseudo first- or pseudo second-order kinetic equations was not governed by the diffusion or chemical limiting mechanisms of these processes. It is associated with our ability to deduce these equations from a nonlinear kinetic equation, with an error not exceeding the characteristic errors of experimental kinetic curves:

$$\frac{{d{{q}_{t}}}}{{dt}} = {{k}_{{\text{I}}}}({{q}_{s}} - {{q}_{t}}) = {{k}_{{\text{I}}}}\left[ {f\left( {{{c}_{0}} - {{q}_{t}}\frac{\omega }{V}} \right) - {{q}_{t}}} \right],$$
((1))

where kI is the mass transfer coefficient for a particular component; qt is its current average concentration in a sorbent; and qs is its surface concentration on the sorbent, which is in equilibrium with the concentration in a solution at the interface and is determined as a function of equilibrium isotherm qs = f(cs,t) = f(c0 – qtω/V), where c0 is the initial concentration in the solution, and ω/V is the ratio of the volume (or sorbent mass) to the solution’s volume.

Equation (1) is a consequence of the Tikhonov–Glückauf linear difference equation [1–3] as applied to an experiment in a limited volume (the batch technique) in which a component’s concentration in a solution falls at the interface during the process.

The kinetic process was modeled for different types of isotherms, and it was shown that if the equilibrium in the system obeyed the Langmuir isotherm in the range of solution concentrations up to c0 (at which qe = qΣAc0/(1 + Ac0), where qe and qΣ are the equilibrium and limiting capacities, and А is a constant); relation (1) can then be reduced to an approximate pseudo first-order equation using parameters \(k_{{\text{I}}}^{*}\) and \(q_{{e{\text{,I}}}}^{*}\) (which are constant for the full kinetic process and are determined by the conditions of the experiment):

$$\begin{gathered} \frac{{d{{q}_{t}}}}{{dt}} \approx k_{{\text{I}}}^{*}(q_{{e{\text{,I}}}}^{*} - {{q}_{t}}) \\ = \;{{k}_{{\text{I}}}}\left( {1 + \frac{{\omega {{q}_{e}}}}{{V{{c}_{0}}}}} \right)\left[ {\frac{{{{q}_{e}}}}{{1 + {{q}_{e}}\omega {\text{/}}(V{{c}_{0}})}} - {{q}_{t}}} \right], \\ \end{gathered} $$
((2))

being integrated in the usual way with regard to the parameter magnitudes as ln(1 – qt/\(q_{{e{\text{,I}}}}^{*}\)) = –\(k_{{\text{I}}}^{*}\)t.

We have shown that for a Langmuir isotherm, there is another variant where Eq. (1) is reduced to approximate relationship (3) representing the sum of pseudo first- and pseudo second-order equations

$$\frac{{d{{q}_{t}}}}{{dt}} \approx k_{{\text{I}}}^{*}(q_{e}^{*} - {{q}_{t}}) + k_{{{\text{II}}}}^{*}{{(q_{e}^{{{\text{**}}}} - {{q}_{t}})}^{2}}.$$
((3))

This expression was deduced earlier by Liu and Shen [4] through transforming the classical kinetic Langmuir equation in [5].

Our analysis brought us to the parameters

$$k_{{\text{I}}}^{*} = {{k}_{{\text{I}}}}\left( {1 + \frac{{{{q}_{e}}\omega (3 - 4A{{c}_{0}})}}{{7V{{c}_{0}}}}} \right),$$
((4))
$$q_{e}^{*} = \frac{{{{q}_{e}}}}{{49}}\left[ {\frac{{49 - 4{{{(1 + A{{c}_{0}})}}^{2}}\frac{{{{q}_{\Sigma }}\omega }}{{V{{c}_{0}}}}}}{{1 + \frac{{{{q}_{e}}\omega (3 - 4A{{c}_{0}})}}{{7V{{c}_{0}}}}}}} \right],$$
((5))
$$k_{{{\text{II}}}}^{*} = \frac{{{{k}_{{\text{I}}}}{{q}_{e}}\omega }}{{{{q}_{\Sigma }}V{{c}_{0}}}},$$
((6))
$$q_{e}^{{{\text{**}}}} = \frac{{2{{q}_{\Sigma }}}}{7}(1 + A{{c}_{0}}) = \frac{{2{{q}_{e}}{{{(1 + A{{c}_{0}})}}^{2}}}}{{A{{c}_{0}}}}.$$
((7))

We found that relation (3) can in turn be reduced to approximate pseudo second-order equation dqt/dt ≈ \(k_{{{\text{II}}}}^{*}\)(〈\(q_{e}^{{{\text{**}}}}\)〉 – qt)2 with fixed equilibrium parameter

$$\left\langle {q_{e}^{{{\text{**}}}}} \right\rangle = 4(q_{e}^{{{\text{**}}}} - q_{e}^{{\text{*}}})q_{e}^{{\text{*}}}{\text{/}}q_{e}^{{{\text{**}}}},$$
((8))

being integrated and linearized in the familiar form

$$t{\text{/}}{{q}_{t}} = 1{\text{/}}\left( {k_{{{\text{II}}}}^{*}{{{\left\langle {q_{e}^{{{\text{**}}}}} \right\rangle }}^{2}}} \right) + t{\text{/}}\left\langle {q_{e}^{{{\text{**}}}}} \right\rangle .$$

This form of the integral pseudo second-order equation has become very popular among researchers, especially after the works of Ho and McKay [6, 7].

We also modeled the sorption kinetics for the polymolecular BET sorption isotherm adapted for liquid media in [8] with AM and AP constants, respectively, for a monolayer (Langmuir sorption) and multilayer sorption. It was shown in this case too that nonlinear kinetic Eq. (1) leads to relation (3) for the sum of different order equations with fixed parameters:

$$\begin{gathered} k_{{\text{I}}}^{*} = {{k}_{{\text{I}}}}\left[ {1 + \frac{{{{q}_{{e,{\text{M}}}}}\omega }}{{V{{c}_{0}}}}{\text{/}}(1 - {{A}_{P}}{{c}_{0}})} \right] \\ \times \;\left[ {1 + \frac{{4{{q}_{{e,{\text{M}}}}}\omega }}{{V{{c}_{0}}}}{\text{/}}(1 - {{A}_{P}}{{c}_{0}})} \right], \\ \end{gathered} $$
((9))
$$\begin{gathered} q_{{e,{\text{BET}}}}^{{{\text{*}}{\kern 1pt} }} = \frac{{{{q}_{{e,{\text{M}}}}}}}{{49(1 - {{A}_{P}}{{c}_{0}})}} \\ \times \;\left\{ {\frac{{49 - 2{\text{/}}\left( {\frac{{{{q}_{{e,{\text{M}}}}}}}{{{{q}_{{\Sigma ,{\text{M}}}}}}} - \frac{{{{A}_{P}}{{c}_{0}}}}{{1 - {{A}_{P}}{{c}_{0}}}}} \right)}}{{\left[ {1 + \frac{{{{q}_{{e,{\text{M}}}}}\omega }}{{V{{c}_{0}}}}{\text{/}}(1 - {{A}_{P}}{{c}_{0}})} \right]\left[ {1 + \frac{{4{{q}_{{e,{\text{M}}}}}\omega }}{{V{{c}_{0}}}}{\text{/}}(1 - {{A}_{P}}{{c}_{0}})} \right]}}} \right\}, \\ \end{gathered} $$
((10))
$$k_{{{\text{II}}}}^{{{\text{**}}}} = \frac{{{{k}_{{\text{I}}}}{{{\left( {\frac{{{{q}_{{e,{\text{M}}}}}\omega }}{{V{{c}_{0}}}}} \right)}}^{2}}\left( {\frac{{{{q}_{{e,{\text{M}}}}}}}{{{{q}_{{\Sigma ,{\text{M}}}}}}} - \frac{{{{A}_{P}}{{c}_{0}}}}{{1 - {{A}_{P}}{{c}_{0}}}}} \right)}}{{2{{q}_{\Sigma }}{{A}_{M}}{{c}_{0}}(1 + {{A}_{M}}{{c}_{0}}){{{(1 - {{A}_{P}}{{c}_{0}})}}^{3}}}},$$
((11))
$$q_{{e,{\text{BET}}}}^{{{\text{**}}{\kern 1pt} }} = \frac{{2(1 + {{A}_{M}}{{c}_{0}})(1 - {{A}_{P}}{{c}_{0}})}}{{\left( {\frac{{7\omega }}{{V{{c}_{0}}}}} \right)\left( {\frac{{{{q}_{{e,{\text{M}}}}}}}{{{{q}_{{\Sigma ,{\text{M}}}}}}} - \frac{{{{A}_{P}}{{c}_{0}}}}{{1 - {{A}_{P}}{{c}_{0}}}}} \right)}}.$$
((12))

In subsequent analysis of Eq. (3) with parameters for the BET isotherm, it was shown that the contribution from the first summand can be ignored, and the approximate kinetic equation can be presented simply as a pseudo second-order equation with parameters (11) and (12).

The conditions (criteria) under which all of the above approximations were possible were determined as

$$K{{R}_{{\text{L}}}} = \frac{{V(1 + A{{c}_{0}})}}{{5A\omega {{q}_{e}}}} \geqslant 1,$$
((13))
$$K{{R}_{{{\text{BET}}}}} = \frac{{{{A}_{M}}[1 - {{A}_{P}}{{c}_{0}}]}}{{{{A}_{P}}[1 + {{A}_{M}}{{c}_{0}}]}} \geqslant 1$$
((14))

for the Langmuir and BET isotherms, respectively.

In this work, the proposed models were validated by comparing the calculated parameters and the data obtained in kinetic experiments.

COMPARING CALCULATIONS AND EXPERIMENTAL DATA

Langmuir Isotherm

The relations deduced in this work were tested for their applicability to describing experimental results obtained at the Laboratory of Physical Chemistry of Thermal Water, Institute for Geothermal Research, Dagestan Scientific Center, Russian Academy of Sciences, on the adsorption of ions on diverse activated coals (ACs). Some of these results were presented in [9, 10]. KM-2, OKM-2, and FKM-2 (the latter two being obtained by treating KM-2 coal with nitric and phosphoric acids, respectively) ACs were used as sorbents. The sorption equilibrium and kinetics of the studied ions were examined on both polarized and unpolarized sorbents. Table 1 lists some of the results of these studies in the denotations used in this work.

Table 1.   Equilibrium and kinetic characteristics of coals obtained in batch experiments in limited volumes: V = 8 × 10−2 L, m = 2 g
Full size table

Systems in which the equilibrium is described by the Langmuir equation and the experimental results on kinetics are described by a pseudo second-order equation with high correlation coefficients are taken as the examples. The initial concentration of solutions at which the kinetic studies were performed was in the nonlinear part of the isotherm. Tables 1 and 2 summarize the experimental and calculated data. Data on the equilibrium capacity of ACs given in column 3 of Table 1 characterize the saturation of the material with the target component at its maximum concentration in a solution. With good approximation, we may assume that qmax ≈ qΣ. The data in column 4 correspond to the equilibrium capacity of sorbents at an equilibrium concentration equal to the concentration in the initial solution in the kinetic experiments. They are consistent with the equilibrium coefficients (columns 6 and 7) obtained in processing the results from the kinetic experiments using the kinetic equations for the pseudo first- and pseudo second-orders, respectively. At the same time, the ratios of the kinetic coefficients in the same dimensionalities appear to be overestimated if we consider that condition \(k_{{{\text{II}}}}^{*}q_{e}^{{{\text{**}}}}\) ≤ \(k_{{\text{I}}}^{*}\) must be satisfied. This is most likely due to large experimental errors in determining the kinetic coefficient when a linearized pseudo second-order equation is used. A segment cut across the Y axis (equal to a very low value of 1/(\(q_{e}^{2}\)kII)) changes greatly upon a minor change in the slope of the line: 1/qt = f(t).

Table 2.   Calculated data for the kinetics of sorption on the studied samples
Full size table

Table 2 presents the calculated values of parameters that should be obtained (in accordance with the above relationships) for different kinetic models: pseudo first-order (column 3), pseudo second-order (column 6), and a combined model as the sum of equations for the first and second orders (columns 4 and 5).

The latter were used as auxiliary values for calculating the equilibrium parameter of the pseudo second-order kinetic equation. The parameters that can be compared are presented in the columns 4, 6, and 7 in Table 1, and in the columns 4 and 6 in Table 2. It is seen that with rare exceptions, the coincidence between calculated values qe and the experimental values obtained from the isotherms is no worse than the data of the kinetic experiments given in Table 1 (within possible experimental errors). This testifies to the adequacy of the above theoretical analysis. As for the disagreement between the dimensionless parameters based on the kinetic coefficients, we believe it is better to use the calculated values (column 7, Table 2) that do not contradict the physical sense of the relations between the different order equations instead of the experimental data (column 8, Table 1), which are difficult to obtain with acceptable accuracy. Processing the data according to the linearized integral form for the pseudo second-order kinetics prevents us from claiming accuracy in determining the kinetic coefficients.

Yet another set of experimental data that we used was taken from [11]; these data were published in [12–14]. One of the authors of this work, together with colleagues from Tambov Technical University, have experimentally investigated the equilibrium and kinetics of lead sorption on nanostructured materials: TAUNIT-M; industrial carbon nanotubes with 6–10 graphene layers, produced by NanoTechCenter Ltd., Tambov; PANI, carbon nanotubes modified by polyaniline under oxidizing conditions; PMAG and PMNG, aqueous pastes of thick- and thin-layered graphene with 15–25 and 3–5 layers respectively; HC, highly porous carbon (a nanocomposite from mesoporous carbon and grapheme); SLOGS, a thin-layered oxidized graphene suspension with hydrogel structure. The author synthesized the graphene materials independently. For purposes of comparison, the authors of the cited works also analyzed the properties of a familiar sorption material, activated birch charcoal (ABC) produced by Sorbent, Perm. Table 3 summarizes some results from [10–13] in the denotation used in this work.

Table 3.   Equilibrium and kinetic characteristics of sorbents, obtained in batch experiments: V = 1.5 × 10−2 L, с0 = 103 mg/L (3.5 × 103 is for PANI)
Full size table

Data on the equilibrium capacity of sorbents (column 3) characterize saturation of the material with the target component at its maximum concentration in a solution. With good approximation, we may assume that qmax ≈ qe. The data in column 4 correspond to the equilibrium capacity of sorption materials at an equilibrium concentration equal to the one in the initial solution, c0 = 103 mg/L; i.e., they correspond to the cross sections of isotherms at ce = 103 mg/L. These data may therefore be used for comparison with the experimental data obtained as a result of kinetic experiments with the same initial concentration. The experimental equilibrium data given in Table 3 were included after thorough verification of all results obtained in [11–14]. Only in one case were the data refined (the qΣ and A values were interrelated). The corrected values are given in parentheses.

Comparison of the calculated data (Table 4) on the equilibrium parameters for different kinetic models (highlighted in columns 4 and 6) and the experimental data (columns 4, 6, and 7, Table 3) also demonstrate their good agreement, along with the data described earlier for sorption systems.

Table 4.   Calculated data for the kinetics of sorption on the studied samples
Full size table

As before, the calculated and experimental dimensionless parameters based on the kinetic coefficients deviate strongly.

BET ISOTHERM

Let us compare the calculated data with the results from experiments on the sorption of an organic compound (phosphatidylcholine (PC), a biologically active phospholipide) on highly ordered mesoporous nanostructured silica-based materials: MCM-41 (Süd-Chemie, Germany) and its analogs MMC-1 and MMS-1, synthesized by one of the authors according to the procedures in [15, 16]. The researchers at the Chair of Analytical Chemistry, Voronezh University, recently presented their results from studying the equilibrium and kinetics of PC sorption on the abovementioned sorbents characterized by porosity and specific surface, and on industrial silica gel (IMID) [17–20]. The same experimental results were presented in [20].

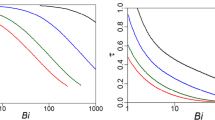
Figure 1 shows the linearized kinetic dependences obtained using pseudo second-order Eq. (2) for PC sorption on the studied sorbents, which we calculated from the primary kinetic data for c0 = 6 mmol/L.

Fig. 1.
figure 1

Integral kinetic curves of PC sorption in t/qt vs. t coordinates on sorption materials: (1) MCM-41, (2) MMC-1, (3) MMS-1, and (4) silica gel.

Full size image

Tables 5 and 6 list the kinetic parameters obtained in processing the experimental dependences shown in Fig. 1 in combination with the data on BET isotherms and kinetic coefficients \(k_{{\text{I}}}^{*}\) from [20] and the parameters calculated from model relations (9)–(12) and (14).

Table 5.   Equilibrium and kinetic characteristics of sorbents, obtained in a batch experiment: ωm = 0.3 g, V = 3 × 10−2 L, c0 = 6 mmol/L
Full size table
Table 6.   Calculated data for the kinetics of sorption on the studied samples
Full size table

The experimental kinetic data on silica gel poorly obey the model of pseudo second-order kinetics; neither do they correspond to criteria relation (14). It was therefore difficult to obtain and calculate parameters q and k. For highly ordered mesoporous materials (MCM-41, MMC-1, and MMS-1), calculated and experimental parameters \(q_{e}^{{{\text{**}}}}\) coincide with one another (column 6, Table 5 and column 7, Table 6).

Unlike the previous section, the dimensionless parameter for the relations of kinetic coefficients (column 5, Table 6) was taken here with coefficient \(q_{{e,{\text{BET}}}}^{{{\text{**}}}}\)/\(q_{{e,{\text{BET}}}}^{{\text{*}}}\). This is because the model calculations using relations (10) and (12) gave parameters not comparable in value, and in describing the same kinetic process by first- and second-order differential equations, condition kI\(q_{e}^{{\text{*}}}\) ~ kII(\(q_{e}^{{{\text{**}}}}\))2 must be satisfied at its initial stage (at qt ≪ qe). The calculated and experimental values of the dimensionless parameters based on the kinetic coefficients differ considerably, as before.

CONCLUSIONS

Calculated and experimental equilibrium and kinetic parameters were compared for a large number of processes, including the sorption and electrosorption of metal ions on ACs, lead sorption on nanostructured carbon materials, and PC sorption on ordered mesoporous nanostructured silica-based materials. There is good coincidence between the calculated equilibrium data and the respective experimental results obtained in kinetic experiments. At the same time, poor correspondence is observed between calculated and experimental dimensionless parameters based on the relationships of kinetic coefficients for different order equations, due likely to large errors in determining these parameters in experiments.

It was shown that the results from kinetic experiments can be described by models of pseudo-first or pseudo-second order kinetics that were deduced from the nonlinear mass transfer equation for the batch processes in a limited volume. This means that based on the possibility of such a description, we cannot reach any conclusions on the limiting kinetic mechanisms.