INTRODUCTION

The technique proposed in [1] is extended to the three-dimensional case. The study of the characteristics of wave scattering by bodies of complex geometry is of great interest in such areas as astrophysics, optics, acoustics, etc. Such studies are usually carried out using the T-matrices method [2]. This method is very popular, which is confirmed, in particular, by review [3], which provides links to more than 250 publications for 2015–2017. The popularity of the T-matrices method is largely due to the fact that using this method it is relatively easy to perform such an important procedure, for example, in astrophysics, as averaging the scattering characteristics of a body over the angles of its orientation relative to the incident field. However, as was shown earlier in our works (for example, [2, 4]), the traditional method of T-matrices is correct for a fairly narrow class of scatterer geometries.

The T-matrices method proposed by P. Waterman in the early 1960s [5] was subsequently widely used in radio physics, acoustics, astrophysics, and other areas of science. Its popularity is explained by the simplicity and convenience of calculating the characteristics of scattering of compact objects that are important in applications. Earlier in our works it was shown that the traditional method of T-matrices is correct only for so-called “Rayleigh bodies” [2]. Thus, it is of interest to extend the technique of this method to the problems of wave scattering by bodies of sufficiently arbitrary shape.

The T-matrices method (MTM) is commonly understood as the procedure for finding matrix-connecting decomposition coefficients over some (usually angular or spherical) basis of the field scattered by an object when a plane wave [1] is incident on it, called “scattering coefficients” (see below). The elements of the T-matrix are independent of the angle of incidence of the primary wave and are determined only by the geometry of the scatterer and the type of boundary conditions at its boundary. This makes it easy to carry out averaging scattering characteristics over the angles of incidence of the primary wave (orientation angles of the scatterer), which are important in a number of applications [3]. The traditional (classical) version of the T-matrices method [5], as well as its recently developed modified versions [1, 4, 6, 7], are applicable, as shown in [1] and earlier works of the authors, to solving diffraction problems only on scatterers with an analytical boundary. At the same time, in astrophysics, radar, and other areas, the problem of wave scattering by bodies with boundary breaks, thin screens, etc., is highly in demand. Thus, it is of great interest to extend the T-matrices technique to the problem of wave scattering by bodies with a nonanalytical boundary. This paper presents an approach based on the continued boundary conditions method (CBCM) [2, 8].

As is known [9], in the optical field, the intensity of the electromagnetic field can be approximately expressed through one complex scalar function, i.e., the diffraction vector problem can be approximately replaced by the scalar one. In this paper, we consider the three-dimensional scalar problem of the diffraction of a plane wave on the bodies of rotation, in particular, on fractal-like bodies with a complex cross section.

DERIVATION OF BASIC RELATIONSHIPS

Let us proceed to the presentation of the proposed approach. Let us consider diffraction on a compact obstacle in the form of a body of revolution bounded by a piecewise-smooth surface S. Let the Dirichlet condition be satisfied on boundary S of the scatterer

$${{\left. U \right|}_{S}} = 0.$$
((1))

Here, \(U({\mathbf{r}}) = {{U}^{0}}({\mathbf{r}}) + {{U}^{1}}({\mathbf{r}})\) is the full field, where \({{U}^{0}}({\mathbf{r}})\) is the incident field and \({{U}^{1}}({\mathbf{r}})\) is the scattered (secondary) field. For the incident field, consider a plane wave

$$\begin{gathered} {{U}^{0}}({\mathbf{r}}) = \exp ( - ikr(\sin \theta \sin {{\theta }_{0}}\cos (\varphi - {{\varphi }_{0}}) \\ + \;\cos \theta \cos {{\theta }_{0}})), \\ \end{gathered} $$
((2))

where \({{\theta }_{0}}\), \({{\varphi }_{0}}\) are the angles of incidence of the wave, k is the wavenumber of the medium surrounding the body, and \((r,\theta ,\varphi )\) are the spherical coordinates. At infinity, the radiation condition for the scattered field is satisfied:

$$\frac{{\partial {{U}^{1}}}}{{\partial r}} + ik{{U}^{1}} = o\left( {\frac{1}{r}} \right),\quad r \to \infty .$$
((3))

As is known (for example, [2]), for the diffraction field, the following representation takes place:

$$\int\limits_S {\left\{ {U({\mathbf{r}})\frac{{\partial {{G}_{0}}({\mathbf{r}};{\mathbf{r}}')}}{{\partial n'}} - \frac{{\partial U({\mathbf{r}}')}}{{\partial n'}}{{G}_{0}}({\mathbf{r}};{\mathbf{r}}')} \right\}ds'} = {{U}^{1}}({\mathbf{r}}),$$
((4))

wherein

$${{G}_{0}}({\mathbf{r}};{\mathbf{r}}') = \frac{1}{{4\pi }}\frac{{\exp ( - ik\left| {{\mathbf{r}} - {\mathbf{r}}'} \right|)}}{{\left| {{\mathbf{r}} - {\mathbf{r}}'} \right|}} = \frac{1}{{4\pi }}\frac{{{{e}^{{ - ikR}}}}}{R}$$
((5))

is the fundamental solution of the Helmholtz equation (Green function of free space) in the three-dimensional case. Subject to condition (1), representation (4) will take the following form:

$$\int\limits_S {\frac{{\partial U({\mathbf{r}}')}}{{\partial n'}}{{G}_{0}}({\mathbf{r}};{\mathbf{r}}')ds'} = - {{U}^{1}}({\mathbf{r}}),$$
((6))

where \(\partial {\text{/}}\partial n'\) means differentiation in the direction of the outward normal to surface S. Requiring, in accordance with CBCM, the fulfillment of condition (1) on surface \({{S}_{\delta }}\) located at \({{{\mathbf{R}}}^{3}}{\backslash }\bar {D}\), where \(D\) is the region inside S [2, 8], using (6) we obtain the following Fredholm integral equation of the first kind with a smooth core:

$${{\left. {\int\limits_S {\frac{{\partial U({\mathbf{r}}')}}{{\partial n'}}{{G}_{0}}({\mathbf{r}};{\mathbf{r}}')ds'} } \right|}_{{{{S}_{\delta }}}}} = {{\left. {{{U}^{0}}({\mathbf{r}})} \right|}_{{{{S}_{\delta }}}}}.$$
((7))

Note that, most often, as \({{S}_{\delta }}\) [2, 8], a surface is chosen that encloses S and is separated from it by some sufficiently small distance \(\delta \), that is, an equidistant surface is considered. Let the scatterer is a body of revolution, the equation of the boundary S of which is given in parametric form

$$\left\{ \begin{gathered} x = \rho (t)\cos \varphi , \hfill \\ y = \rho (t)\sin \varphi , \hfill \\ z = z(t), \hfill \\ \end{gathered} \right.$$
((8))

where \((\rho ,\varphi ,z)\) are the cylindrical coordinates. In this case, parameter t varies on the interval \([0,{{t}_{{\max }}}]\). Then the equations of displaced surface \({{S}_{\delta }}\) are written as follows:

$$\left\{ \begin{gathered} x = {{\rho }_{\delta }}(t)\cos \varphi , \hfill \\ y = {{\rho }_{\delta }}(t)\sin \varphi , \hfill \\ z = {{z}_{\delta }}(t), \hfill \\ \end{gathered} \right.$$
((9))

where \({{\rho }_{\delta }}(t) = \rho (t) + {{n}_{\rho }}(t)\delta \), \({{z}_{\delta }}(t) = z(t) + {{n}_{z}}(t)\delta \), while \({{n}_{\rho }}\) and \({{n}_{z}}\) are the coordinates of the normal to surface of the body S. Now, using the notation

$${{\left. {\frac{1}{2}\frac{{\partial U({\mathbf{r}}')}}{{\partial n'}}} \right|}_{S}}ds' \equiv J(t',\varphi ')dt'd\varphi ',$$
((10))

Eq. (7) takes the form

$${{\left. {\frac{1}{{2\pi }}\int\limits_0^{2\pi } {\int\limits_0^{{{t}_{{\max }}}} {J(t',\varphi ')} } \frac{{{{e}^{{ - ikR}}}}}{R}dt'd\varphi '{\kern 1pt} } \right|}_{{{{S}_{\delta }}}}} = {{\left. {{{U}^{0}}({\mathbf{r}})} \right|}_{{{{S}_{\delta }}}}},$$
((11))

where

$$R = \sqrt {{{\rho }_{\delta }}{{{(t)}}^{2}} + \rho {{{(t')}}^{2}} - 2{{\rho }_{\delta }}(t)\rho (t')\cos (\varphi - \varphi ') + {{{({{z}_{\delta }}(t) - z(t'))}}^{2}}} .$$

In addition, taking into account the Fourier expansions

$$\begin{gathered} {{\left. {{{U}^{0}}({\mathbf{r}})} \right|}_{{{{S}_{\delta }}}}} = {{U}^{0}}(t,\varphi ) = \sum\limits_{s = - \infty }^\infty {U_{s}^{0}(t){{e}^{{is\varphi }}}} ,\quad J(t',\varphi ') = \sum\limits_{s = - \infty }^\infty {{{I}_{s}}(t'){{e}^{{is\varphi '}}}} , \\ {{\left. {\frac{{{{e}^{{ - ikR}}}}}{R}} \right|}_{{{{S}_{\delta }}}}} \equiv K(t,t',\tau ) = \sum\limits_{s = - \infty }^\infty {{{K}_{s}}(t,t'){{e}^{{is\tau }}}} \\ \end{gathered} $$
((12))

(where \(\tau = \varphi - \varphi '\)), Eq. (11) reduces to the following system of one-dimensional integral equations (SIE):

$$\int\limits_0^{{{t}_{{\max }}}} {{{I}_{s}}(t')} {{K}_{s}}(t,t')dt' = U_{s}^{0}(t),\quad s = \overline { - Q,Q} ,$$
((13))

where \(Q\) is the upper limit of summation in relationships (12) and

$$\begin{gathered} {{K}_{s}}(t,t') = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\frac{{{{e}^{{ - ikR(t,t',\tau )}}}}}{{R(t,t',\tau )}}} {{e}^{{ - is\tau }}}d\tau , \\ U_{s}^{0}(t) = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {{{U}^{0}}(t,\varphi ){{e}^{{ - is\varphi }}}d\varphi } . \\ \end{gathered} $$
((14))

System (13) can be solved, for example, by the Krylov–Bogolyubov method. To this end, we represent the unknown functions \({{I}_{s}}(t')\) in the form

$${{I}_{s}}(t') \cong \sum\limits_{n = 1}^N {{{I}_{{n,s}}}{{\Phi }_{n}}(t')} ,\quad s = \overline { - Q,Q} ,$$
((15))

where \({{\Phi }_{n}}(t')\) are impulse functions of the form

$${{\Phi }_{n}}(t') = \left\{ \begin{gathered} 1,\quad t \in [{{t}_{n}} - \Delta {\text{/}}2,{{t}_{n}} + \Delta {\text{/}}2], \hfill \\ 0,\quad t \notin [{{t}_{n}} - \Delta {\text{/}}2,{{t}_{n}} + \Delta {\text{/}}2]. \hfill \\ \end{gathered} \right.$$
((16))

Here, \({{t}_{n}} = \frac{{{{t}_{{\max }}}}}{N}\left( {n - \frac{1}{2}} \right)\), \(n = \overline {1,N} \), \(\Delta = \frac{{{{t}_{{\max }}}}}{N}\) is the grid step, and \(N\)is the number of basis functions. In addition, substituting (15) into SIE (13) and equating the left and right sides of the obtained equalities at the c-ollocation points selected on surface \({{S}_{\delta }}\), we obtain the following systems of algebraic equations for quantities \({{I}_{{n,s}}}\):

$$\sum\limits_{n = 1}^N {K_{{mn,s}}^{{}}} {{I}_{{n,s}}} = U_{{m,s}}^{0},\quad s = \overline { - Q,Q} ,\quad m = \overline {1,N} ,$$
((17))

where the matrix elements and the right parts are calculated by the formulas

$$K_{{nm,s}}^{{}} = \int\limits_{{{t}_{n}} - \Delta /2}^{{{t}_{n}} + \Delta /2} {{{K}_{s}}({{t}_{m}},t)dt} ,\quad U_{{m,s}}^{0} = U_{s}^{0}({{t}_{m}}).$$
((18))

Note that, in order to efficiently calculate the matrix elements in system (17), that is, the values \({{K}_{s}}({{t}_{m}},t')\), the algorithm given in [10] was used. To speed up the computation, we found external integrals in formula (18) using an adaptive method (allowing one to calculate integrals from rapidly changing functions), only for the matrix elements located near the main diagonal, and the remaining matrix elements were calculated using Gauss quadrature with two nodes.

The correctness of the obtained results is controlled by calculating the magnitude of the discrepancy at points of surface \({{S}_{\delta }}\) located in the middle between the points of collocation. One of the criteria for the correctness of the results obtained is also the optical theorem, which is written in the form [11]

$$\begin{gathered} \frac{{{{k}^{2}}\sigma }}{{4\pi }} \equiv \frac{1}{{4\pi }}\int\limits_\Omega {{{{\left| {f(\theta ,\varphi ;{{\theta }_{0}},{{\varphi }_{0}})} \right|}}^{2}}\sin \theta d\theta d\varphi } \\ = - \operatorname{Im} f(\theta = {{\theta }_{0}},\varphi = {{\varphi }_{0}}), \\ \end{gathered} $$
((19))

where \(f(\theta ,\varphi ;{{\theta }_{0}},{{\varphi }_{0}})\) is the scattering diagram, the expression for which is given below. As an estimate of the accuracy of the optical theorem, we will calculate the value \({{\Delta }_{{ot}}}\), which is the relative difference between the left and right sides in formula (19).

For the following, it will be convenient to rewrite systems (17) in the matrix notation:

$${{{\mathbf{K}}}_{s}}{{{\mathbf{I}}}_{s}} = {{{\mathbf{a}}}_{s}},\quad s = \overline { - Q,Q} ,$$
((20))

where \({{{\mathbf{K}}}_{s}} = \left\| {K_{{mn,s}}^{{}}} \right\|\), \({{{\mathbf{a}}}_{s}} = \left\| {U_{{m,s}}^{0}} \right\|\), \(m,n = \overline {1,N} \). Finding coefficients \({{I}_{{n,s}}}\) from systems (20) taking into account formulas (6), (10), (12), and (15), we obtain the following representation for the scattered field:

$${{U}^{1}}(\rho ,z) = - \sum\limits_{s = - Q}^Q {\sum\limits_{n = 1}^N {{{I}_{{n,s}}}\int\limits_{{{t}_{n}} - \frac{\Delta }{2}}^{{{t}_{n}} + \frac{\Delta }{2}} {{{K}_{s}}(\rho ,z,t')dt'} } } {{e}^{{is\varphi }}},$$
((21))

where

$${{K}_{s}}(\rho ,z,t') = \frac{1}{{2\pi }}\int\limits_0^{2\pi } {\frac{{{{e}^{{ - ikR}}}}}{R}} {{e}^{{ - is\tau }}}d\tau ,$$
$$R = \sqrt {{{\rho }^{2}} + \rho {{{(t')}}^{2}} - 2\rho \rho (t')\cos \tau + {{{(z - z(t'))}}^{2}}} .$$

Turning to the asymptotics of expression (21) at \(r \to \infty \), we obtain the representation for the scattering diagram:

$$\begin{gathered} f(\theta ,\varphi ,{{\theta }_{0}},{{\varphi }_{0}}) = - \sum\limits_{s = - Q}^Q {\sum\limits_{n = 1}^N {{{i}^{s}}{{I}_{{n,s}}}} } \\ \times \;\int\limits_{{{t}_{n}} - \frac{\Delta }{2}}^{{{t}_{n}} + \frac{\Delta }{2}} {{{J}_{s}}(k\rho (t)\sin \theta )} \exp (ikz(t)\cos\theta )dt{{e}^{{is\varphi }}}. \\ \end{gathered} $$
((22))

Here, \({{J}_{s}}(x)\) are the cylindrical Bessel functions. In formula (22), coefficients \({{I}_{{n,s}}}\) depend on angles of incidence \({{\theta }_{0}}\), \({{\varphi }_{0}}\) of the plane wave.

Let us consider the question of finding a scattering diagram averaged over the angles of incidence of a plane wave (for example, in the case of an equally probable distribution of angles of incidence \({{\theta }_{0}}\), \({{\varphi }_{0}}\)):

$$\left\langle {f(\theta ,\varphi )} \right\rangle = \frac{1}{{4\pi }}\int\limits_0^{2\pi } {\int\limits_0^\pi {f(\theta ,\varphi ,{{\theta }_{0}},{{\varphi }_{0}})\sin {{\theta }_{0}}d{{\theta }_{0}}d{{\varphi }_{0}}} } .$$
((23))

First, we give a standard scheme for finding the averaged diagram using the T-matrices method. Everywhere outside the sphere depicted around S, in accordance with the addition theorem [12], we have

$$\begin{gathered} \frac{{\exp ( - ikR)}}{R} = - ik\sum\limits_{p = 0}^\infty {\sum\limits_{q = - p}^p {(2p + 1)} } \\ \times \;\frac{{(p - q)!}}{{(p + q)!}}h_{p}^{{(2)}}(kr){{j}_{p}}(kr')P_{q}^{p}(\cos\theta )P_{q}^{p}(\cos\theta '){{e}^{{iq(\varphi - \varphi ')}}}. \\ \end{gathered} $$
((24))

Taking into account the determination of the values of \({{K}_{s}}(r,\theta ,t')\) from (24), we obtain

$$\begin{gathered} {{K}_{s}}(r,\theta ,t') = - ik\sum\limits_{p = |s|}^\infty {(2p + 1)\frac{{(p - s)!}}{{(p + s)!}}} h_{p}^{{(2)}}(kr) \\ \times \;{{j}_{p}}(kr'(t'))P_{p}^{s}(\cos\theta )P_{p}^{s}(\cos\theta '{\text{(}}t'{\text{))}}{\text{,}} \\ \end{gathered} $$
((25))

where \({{j}_{p}}(x)\) are the spherical Bessel functions, \(h_{p}^{{(2)}}(x)\) are the spherical Hankel functions of the second kind, \(P_{p}^{s}(x)\) are the associated Legendre functions, and \(r'(t')\), \(\theta '(t'{\text{)}}\) are the spherical coordinates of a point on the contour of the axial section of the body. Now, from (21) and (25), we obtain

$$\begin{gathered} {{U}^{1}}({\mathbf{r}}) = ik\sum\limits_{s = - \infty }^\infty {\sum\limits_{p = |s|}^\infty {(2p + 1)\frac{{(p - s)!}}{{(p + s)!}}} } \,h_{p}^{{(2)}}(kr)P_{p}^{s}(\cos\theta ){{e}^{{is\varphi }}} \\ \times \;\sum\limits_{n = 1}^N {{{I}_{{n,s}}}\int\limits_{{{t}_{n}} - \frac{\Delta }{2}}^{{{t}_{n}} + \frac{\Delta }{2}} {{{j}_{p}}(kr'{\text{(}}t))P_{p}^{s}(\cos\theta '(t))dt'} } . \\ \end{gathered} $$
((26))

Let us rewrite relation (26) in the form standard for MTM:

$${{U}^{1}}({\mathbf{r}}) = \sum\limits_{s = - \infty }^\infty {\sum\limits_{p = |s|}^\infty {{{c}_{{p,s}}}} } h_{p}^{{(2)}}(kr)P_{p}^{s}(\cos\theta ){{e}^{{is\varphi }}},$$
((27))

where

$$\begin{gathered} {{c}_{{p,s}}} = ik(2p + 1)\frac{{(p - s)!}}{{(p + s)!}} \\ \times \;\sum\limits_{n = 1}^N {{{I}_{{n,s}}}\int\limits_{{{t}_{n}} - \frac{\Delta }{2}}^{{{t}_{n}} + \frac{\Delta }{2}} {{{j}_{p}}(kr'(t))P_{p}^{s}(\cos\theta '(t))dt} } . \\ \end{gathered} $$
((28))

In the matrix notations, we will have

$${{{\mathbf{c}}}_{s}} = {{{\mathbf{J}}}_{s}}{{{\mathbf{I}}}_{s}} = ({{{\mathbf{J}}}_{s}}{{{\mathbf{K}}}_{s}}^{{ - 1}}){{{\mathbf{a}}}_{s}} = {{{\mathbf{T}}}_{s}}{{{\mathbf{a}}}_{s}},\quad {{{\mathbf{J}}}_{s}} = \left\| {{{J}_{{s,pn}}}} \right\|,$$
((29))
$$\begin{gathered} {{J}_{{s,pm}}} = ik(2p + 1)\frac{{(p - s)!}}{{(p + s)!}} \\ \times \;\int\limits_{{{t}_{n}} - \frac{\Delta }{2}}^{{{t}_{n}} + \frac{\Delta }{2}} {{{j}_{p}}(kr'(t))P_{p}^{s}(\cos\theta '(t))dt} . \\ \end{gathered} $$
((30))

Here, \({{{\mathbf{T}}}_{s}} = {{{\mathbf{J}}}_{s}}{{{\mathbf{K}}}_{s}}^{{ - 1}}\) is the \(T\)-matrix for the sth azimuthal harmonic. In the case in which the primary field is plane wave (2) propagating at angle of \({{\theta }_{0}}\) to the \(Oz\)axis,

$$U_{s}^{0} = \exp( - ik{{z}_{\delta }}(t)\cos {{\theta }_{0}}){{( - i)}^{s}}{{J}_{s}}(k{{\rho }_{\delta }}(t)\sin{{\theta }_{0}}).$$
((31))

At \(kr \to \infty \), we have

$$h_{p}^{{(2)}}(kr) \cong {{i}^{{p + 1}}}\frac{{{{e}^{{ - ikr}}}}}{{kr}},\quad {{U}^{1}}({\mathbf{r}}) \cong \frac{{{{e}^{{ - ikr}}}}}{{kr}}f(\theta ,\varphi ).$$
((32))

Thus, from (27), we obtain

$$f(\theta ,\varphi ) = \sum\limits_{s = - \infty }^\infty {\sum\limits_{p = |s|}^\infty {{{c}_{{ps}}}} } {{i}^{{p + 1}}}P_{p}^{s}(\cos\theta ){{e}^{{is\varphi }}}.$$
((33))

As noted in the Introduction, in many applications, a scattering diagram averaged over the angles of orientation of the body is of interest. Averaging over orientation angles (taking into account (23)) leads to the ratio

$$\left\langle {f(\theta )} \right\rangle = \sum\limits_{p = 0}^\infty {\left\langle {{{c}_{{p0}}}} \right\rangle {{i}^{{p + 1}}}P_{p}^{{}}(\cos\theta )} ,$$
((34))

wherein

$$\left\langle {{{{\mathbf{c}}}_{0}}} \right\rangle = {{{\mathbf{T}}}_{0}}\left\langle {{{{\mathbf{a}}}_{0}}} \right\rangle ,$$
((35))

where \(\left\langle {{{{\mathbf{a}}}_{0}}} \right\rangle = \left\| {\left\langle {U_{{m,0}}^{0}} \right\rangle } \right\|\), \(m = \overline {1,N} \). For example, in the case of an equally probable distribution of orientation angles (angles of incidence of a primary plane wave), we obtain

$$\begin{gathered} \left\langle {U_{{m,0}}^{0}} \right\rangle = \frac{1}{2}\int\limits_0^\pi {{{J}_{0}}(k{{\rho }_{\delta }}({{t}_{m}})\sin {{\theta }_{0}})} \\ \times \;\exp (ik{{z}_{\delta }}({{t}_{m}})\cos {{\theta }_{0}}))\sin {{\theta }_{0}}d{{\theta }_{0}}. \\ \end{gathered} $$
((36))

The averaged diagram can also be found directly from formula (22). Then,

$$\begin{gathered} \left\langle {f(\theta )} \right\rangle = - \sum\limits_{n = 1}^N {\left\langle {{{I}_{{n,0}}}} \right\rangle } \int\limits_{{{t}_{n}} - \frac{\Delta }{2}}^{{{t}_{n}} + \frac{\Delta }{2}} {{{J}_{0}}(k\rho (t)\sin \theta )} \\ \times \;\exp (ikz(t)\cos\theta )dt, \\ \end{gathered} $$
((37))

where coefficients \(\left\langle {{{I}_{{n,0}}}} \right\rangle \) are found from system (20) (at \(s = 0\)), in which the right-hand sides are replaced by the values of (36).

We present the averaged sphere diagram. As is known, the scattering diagram of a sphere of radius a in the case of the Dirichlet condition on its surface has the form

$$\begin{gathered} f(\theta ,\varphi ,{{\theta }_{0}},{{\varphi }_{0}}) = - i\sum\limits_{p = 0}^\infty {\sum\limits_{q = - p}^p {(2p + 1)\frac{{(p - q)!}}{{(p + q)!}}} \frac{{{{j}_{p}}(ka)}}{{h_{p}^{{(2)}}(ka)}}} \\ \times \;P_{p}^{q}(\cos\theta )P_{p}^{q}(\cos{{\theta }_{0}})\exp (iq(\varphi - {{\varphi }_{0}})). \\ \end{gathered} $$
((38))

Calculating integral (23), we obtain

$$\left\langle {f(\theta ,\varphi )} \right\rangle = - i\frac{{{{j}_{0}}(ka)}}{{h_{0}^{{(2)}}(ka)}}.$$
((39))

Thus, the averaged diagram of the sphere, as expected, is constant.

CALCULATION RESULTS

In Table 1, the results of calculating the modulus of the scattering diagram of an ideally reflecting cone (the Dirichlet conditions are fulfilled on the body surface) with a cross section of an equilateral triangle with the side \(2ka = 20\) and an ideal cylinder with a square cross section with the side \(2ka = 20\) are presented. The plane wave is incident perpendicular to the axis of rotation of the body. The scattering diagram was calculated at \(\varphi = 0\). Parameter \(k\delta = {{10}^{{ - 3}}}\). The numerical results given in Table 1 were obtained by two methods: using the modified method of discrete sources (MMDS) and CBCM. Note that MMDS cannot be directly applied to the diffraction problem on the bodies with boundary breaks (such as a cone and cylinder); therefore, to solve the problem using MMDS, the bodies’ axial section contour was approximated by a smooth contour (for example, [13]). In particular, when solving the problem of diffraction on a cylinder, the body boundary was approximated by the surface of a superellipsoid of revolution. As can be seen from Table 1, the relative difference of the results obtained using MMDS and CBCM does not exceed 5 × 10–3 in the case of diffraction on a cone and 4 × 10–2 for a cylinder.

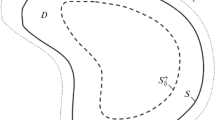
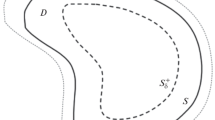
Table 1. Comparison of results obtained using MMDS and CBCM
Full size table

In Table 2, the results of checking the accuracy of the optical theorem for the abovementioned bodies (a cone and cylinder), as well as for a body of revolution with a Koch snowflake cross section and a Sierpinski curve cross section (two iterations were considered) are presented [14]. In the latter two cases, the maximum size of the body section along the x axis was equal to \(2ka = 20\). The geometries of these fractal-like bodies are shown in Figs. 1 and 2. The number of collocation points at one wavelength for all six forms of the body section was\({{N}_{\lambda }} = 30\). The number of angular harmonics was chosen to be \(Q = 24\). A plane wave was incident perpendicular to the axis of the body. As follows from Table 1, the relative difference between the right and left sides of equality (19), i.e., the value of \({{\Delta }_{{{\text{ot}}}}}\), does not exceed 5 × 10–5. Thus, the diffraction problem is solved on the basis of the CBCM with high accuracy.

Table 2. Accuracy of the optical theorem correspondence for different geometries
Full size table
Fig. 1.
figure 1

Cross section of the body in the form of the Koch snowflake: (a) is the first iteration, (b) is the second iteration.

Full size image
Fig. 2.
figure 2

Cross section of the body in the form of the Sierpinski curve: (a) is the first iteration, (b) is the second iteration.

Full size image

Let us consider the results concerning the calculation of the scattering diagram of wave averaged over the angles of incidence. As a test, we compared the values of the averaged sphere diagram obtained using the CBCM and using the exact formula (39). The radius of the sphere was \(ka = 10\). The angular dependences of the averaged diagram module are shown in Fig. 3. Curve 1 in the figure illustrates the exact value of the averaged diagram obtained from (39), and curves 2 and 3 relate to the case when value of parameter \(k\delta \) was \({{10}^{{ - 3}}}\) and \({{10}^{{ - 4}}}\), respectively. As can be seen, with decreasing parameter \(\delta \), the approximate solution approaches an exact one.

Fig. 3.
figure 3

The angular dependence of the averaged diagram for the sphere.

Full size image

In Figs. 4 and 5, the angular dependences of the averaged scattering diagram for a particle with a cross section in the form of a Koch snowflake and in the form of a Sierpinski curve, respectively, are shown. The maximum size of the body section along the x axis was equal to \(2ka = 20\). Parameter \(k\delta \) was equal to \({{10}^{{ - 3}}}\). It should be noted that if, in the two-dimensional case, the type of the averaged scattering diagram made it possible to form a first idea about the geometry of the scatterer [1], then in the three-dimensional case such obvious correspondence is not observed, apparently because of its more complex geometry.

Fig. 4.
figure 4

The angular dependence of the averaged diagram for the body with the cross section in the form of the Koch snowflake. Curves 1 and 2 correspond to the first and second iteration.

Full size image
Fig. 5.
figure 5

The angular dependence of the averaged diagram for the body in the form of the Sierpinski curve. Curves 1 and 2 correspond to the first and second iteration.

Full size image